晶体学中的旋转矩阵和平移矢量
S.霍夫米勒
1.旋转矩阵和平移向量
旋转矩阵(R(右))和平移向量(t吨)它们是对晶体内对称性的有力描述,有助于确定原点规格,确定相位限制、系统缺失、系统增强和半非变量,区分中心反射和无中心反射、一般反射和空间反射,并有助于正确确定空间群。
每个空间组都有若干个等效位置。这些可能来自1,如P(P)1到192,如Fm公司三米,Fm公司三c(c),Fd公司三米,Fd公司三米和Fd公司三c(c).每个原子在一个点上(x个,年,z(z))也是位置对称的结果( ). 列出了中所有空间组的等效位置国际X射线晶体学表等效位置通过以下方式相互关联对称运算每个对称运算都是一对R(右)和t吨。一个等效位置通过旋转和按该顺序应用的平移从另一个位置导出。单词rotation不仅表示2、3、4或6倍旋转,还表示点或平面中的反射。平移沿单元的轴或对角线。两个等效位置之间的关系可以表示为:
). 列出了中所有空间组的等效位置国际X射线晶体学表等效位置通过以下方式相互关联对称运算每个对称运算都是一对R(右)和t吨。一个等效位置通过旋转和按该顺序应用的平移从另一个位置导出。单词rotation不仅表示2、3、4或6倍旋转,还表示点或平面中的反射。平移沿单元的轴或对角线。两个等效位置之间的关系可以表示为:
|
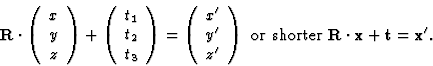 |
(1) |
例子:
空间组P(P)1只有一个等效位置(x个,年,z(z)). 因此,该空间群中唯一的对称运算是单位矩阵,我

例子:
空间组P(P)三1具有3个等效位置:(x个,年,z(z)), (-年,x个-年,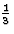 +z(z))和(年-x个, -x个,
+z(z))和(年-x个, -x个,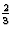 +z(z)). 对称操作为:
+z(z)). 对称操作为:
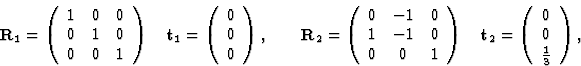
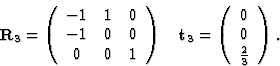
请注意
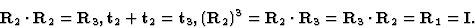
每个空间群的不同对称运算总是可以从最多3个唯一的、不可进一步简化的对称运算中导出(3,因为空间是三维的)。所有其他对称运算都可以通过以下方式从唯一运算中导出:
|
![\开始{displaymath}\textbf{R} _ i+\textbf(文本框){t} _ i=\文本bf{R} _米(\textbf{R} _n(n)\{\……t}_m)\cdots]+\textbf{t} _0(0)\}\+\textbf{t} _n(n))+\textbf{t} _米,\结束{displaymath}](https://www.iucr.org/__data/assets/image/0019/13744/img9.gif) |
(2) |
哪里米,n个和哦对于3个唯一的对称操作,可以是1、2或3。2.结构因素
对于每个空间组、每个结构和每个反射(香港特别行政区)我们知道:
|
![\开始{显示方式}F(hkl)=\sum^N_{j=1}F_j\cdot\exp[2{\pi}i(hk_j+ky_j+lz_j)],结束{显示方法}](https://www.iucr.org/__data/assets/image/0018/13671/img10.gif) |
(3) |
哪里
- F类(香港特别行政区)是折射率为的反射的振幅和相位(小时,k,我).F类(香港特别行政区)称为结构因子。
- (f)j个是原子的散射因子j个.
- N个是单位单元中的原子数。
- x个j个年j个z(z)j个是x个-,年-和z(z)-原子坐标j个.
在以下方面(总部+基尔+里兹)经常写总部使公式更短。
结构系数取决于
- 1.单位细胞中的原子种类。
- 2.单位单元内原子的位置。
由于空间群的对称性给出了原子相对位置的信息,F类(香港特别行政区)将变得依赖于对称性。这对相位和振幅都适用F类(香港特别行政区). 这种依赖的形式将从以下几页中清晰可见。
3.特殊反射
在具有的空间组中n个同等职位(R(右)我x个+t吨我),我= 1, 2,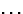 ,n个通过以下方式总结对结构因子的贡献,可以计算出结构因子:
,n个通过以下方式总结对结构因子的贡献,可以计算出结构因子:
|
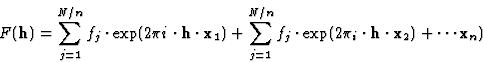 |
(4) |
即,首先添加第一个等效位置的所有原子,然后通过R(右)2+t吨2添加,依此类推,直到单位单元中的所有原子都添加完毕。根据(1),每个等效位置可以写成接收+t吨如果将此表达式插入(4)中,为了简单起见,我们看一个具有2个等价位置的空间群,我们得到:
|
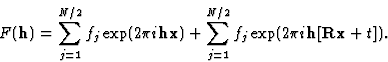 |
(5) |
这些总和中的第二个可以重写,因为![\开始{displaymath}\exp(2{\pi}i\textbf{h}[\textbf{Rx}+\textbf{t}])=\exp](https://www.iucr.org/__data/assets/image/0004/13675/img14.gif)
|
![\开始{displaymath}\phantom{J\exp(2{\pi}i\textbf{h}[\textbf{Rx}+\textbf-{t}])}=\exp](https://www.iucr.org/__data/assets/image/0005/13676/img15.gif) |
(6) |
![\开始{displaymath}\phantom{M=I\exp(2{\pi}I\textbf{h}[\textbf{Rx}+\textbf{t}])}=\exp。\结束{显示方式}](https://www.iucr.org/__data/assets/image/0006/13677/img16.gif)
如果将(5)和(6)结合起来,我们得到:
|
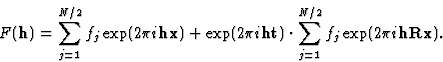 |
(7) |
很明显,在一般情况下,结构两部分的贡献在振幅和相位上都不同。然而,如果这两种贡献相等,即振幅相同,则会出现几个有趣的情况。当且仅当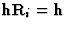 或
或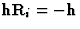 至少一个
至少一个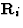 ,
,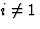 .
.4.相位限制
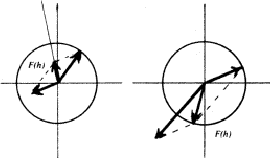
在来自晶胞的两个部分的贡献具有不同幅度的一般情况下,F类(香港特别行政区)可以表示为不同长度(=振幅)和不同方向(=相位)的两个矢量之和,如图1所示。
图1:结构因素F类(小时) =F类(香港特别行政区)表示为单位单元两部分贡献的矢量和。在一般情况下,这两部分的振幅和相位都不同。
 |
的阶段F类(香港特别行政区)可以采用0到360之间的任何值 .特殊情况是
.特殊情况是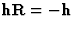 将限制相位的可能值F类(香港特别行政区). 这叫做相位限制如果(7)中第一次出资的阶段为
将限制相位的可能值F类(香港特别行政区). 这叫做相位限制如果(7)中第一次出资的阶段为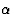 和ht(高温)=0,则第二次贡献的阶段变为
和ht(高温)=0,则第二次贡献的阶段变为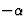 如图2所示,这两个贡献之和的唯一可能相位值为0和180
如图2所示,这两个贡献之和的唯一可能相位值为0和180 ,或如果以弧度0和
,或如果以弧度0和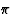 .如果
.如果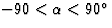 ,的阶段F类(香港特别行政区)变为0
,的阶段F类(香港特别行政区)变为0 ,如果
,如果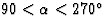 的阶段F类(香港特别行政区)将为180
的阶段F类(香港特别行政区)将为180 .的阶段F类香港特别行政区表示为
.的阶段F类香港特别行政区表示为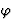 这里是为了将其与贡献的阶段区分开来。
这里是为了将其与贡献的阶段区分开来。
图2:在晶胞的两半具有相等振幅贡献但相位相反的特殊情况下( 和
和 ),生成的反射将具有相位限制。
),生成的反射将具有相位限制。
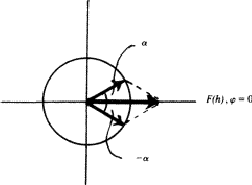 |
我们说(香港特别行政区)相位限制为0(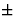 180
180 ).
).
中心对称空间群中的所有反射都具有相位限制0(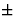 180
180 ). 非中心对称空间群中的大多数反射都没有相位限制,但一些特殊反射具有相位限制。阶段不一定限制为0(
). 非中心对称空间群中的大多数反射都没有相位限制,但一些特殊反射具有相位限制。阶段不一定限制为0(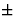 180
180 )-相位限制,如45
)-相位限制,如45 , 60
, 60 , 90
, 90 等等。所有相位限制均为
等等。所有相位限制均为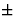 180
180 或模180
或模180 为了澄清这一点,我们做了一个比较详细的例子。
为了澄清这一点,我们做了一个比较详细的例子。
什么是相位限制(小时01)在空间组中P(P)三121(第152号)?等效位置为:
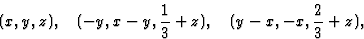
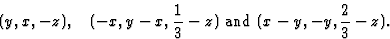
旋转矩阵和平移向量为: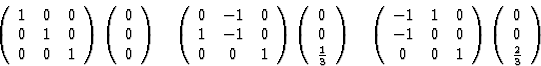
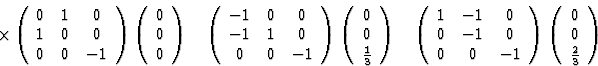
而等效位置由旋转矩阵和平移向量通过接收+t吨等效反射通过以下公式导出小时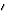 =人力资源.同时(xyz公司)写为列向量(香港特别行政区)必须写为行向量。
=人力资源.同时(xyz公司)写为列向量(香港特别行政区)必须写为行向量。反射相当于(香港特别行政区)是:
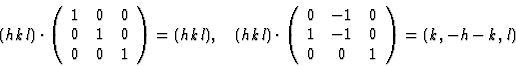
等等,给予(香港特别行政区), (k,小时-k,我), (-小时-k,小时,我), (k,小时, -我), (-小时-k,k, -我)和(小时, -小时-k, -我). 反思(小时01)相当于(0-小时, 1), (-小时,小时, 1), (0,小时, -1), (-小时,0,-1)和(小时, -小时, -1). 所有这些反射都具有相同的振幅,但它们的相位可能不同,我们将在后面看到。当且仅当(香港特别行政区)R(右)我= (-小时, -k, -我),即反射的Friedel对由任何R(右)我.如果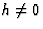 只有R(右)5创建一对Friedel(小时01).
只有R(右)5创建一对Friedel(小时01).
这些结果被引入到(7)中。如果单位单元中超过一半原子的第一次求和对振幅的结构因子有贡献|F类|和相位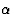 ,单位单元中的另一半原子将贡献振幅|F类|但具有相位exp(2
,单位单元中的另一半原子将贡献振幅|F类|但具有相位exp(2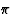 我ht(高温))
我ht(高温))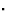 (
(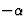 ). exp值(2
). exp值(2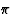 我ht(高温))是exp(2)的缩写
我ht(高温))是exp(2)的缩写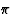 我[ht(高温)1+千吨2+书信电报三])在这种情况下等于exp(2
我[ht(高温)1+千吨2+书信电报三])在这种情况下等于exp(2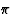 我[
我[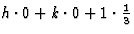 ])或exp(2
])或exp(2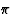 我/3) 或+120
我/3) 或+120 (注意+号!)。因此,第二个和的相位为120
(注意+号!)。因此,第二个和的相位为120
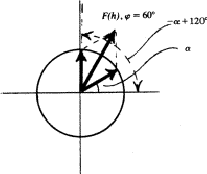
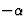 如图3中的几何解释所示,由此产生的结构系数将出现在第60阶段
如图3中的几何解释所示,由此产生的结构系数将出现在第60阶段 或240
或240 .
.
图3:相位限制不是0或180的反射 .
.
 |
与一般反射相比,具有相位限制的反射通常很强或很弱。这是因为在相位受限反射的情况下,这两个贡献要么都很大,要么都很小,而在一般情况下,它们的振幅是独立的。根据其出现极端振幅值的概率,将所有反射分为两类:偏心反射或中心反射。没有相位限制的反射称为偏心反射,有相位限制的反射称为中心反射。中心反射和无中心反射的概率分布如此不同,以至于通常可以区分空间群P(P)1和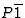 仅来自强度数据。中心概念不应与中心对称或中心(也拼写为中心)混淆。中心对称指的是空间组,而中心仅指单个反射。尽管中心对称空间组中的所有反射都是中心反射,但并非非中心对称空间群中的所有折射都是无中心反射。
仅来自强度数据。中心概念不应与中心对称或中心(也拼写为中心)混淆。中心对称指的是空间组,而中心仅指单个反射。尽管中心对称空间组中的所有反射都是中心反射,但并非非中心对称空间群中的所有折射都是无中心反射。
5.系统性缺勤
如果小时 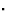 R(右)=小时和小时
R(右)=小时和小时 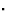 t吨
t吨 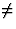 0(模1)然后是反射小时消失或缺失,即其振幅为
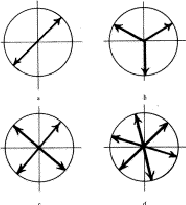
0(模1)然后是反射小时消失或缺失,即其振幅为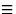 0.如果我们有2倍对称,如P(P)21,这两个对结构因子的贡献相等,但方向正好相反,并且它们相互抵消。如图4a所示。在具有三重对称性的空间群中,例如P(P)三1,在以下情况下,将有系统地缺席反思人力资源=小时和小时
0.如果我们有2倍对称,如P(P)21,这两个对结构因子的贡献相等,但方向正好相反,并且它们相互抵消。如图4a所示。在具有三重对称性的空间群中,例如P(P)三1,在以下情况下,将有系统地缺席反思人力资源=小时和小时 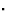 t吨=
t吨=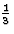 或
或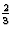 ,如图4所示。由于三重对称性,原子被分为三组,而不是像二重对称那样分为两组。4或6倍对称的情况与3倍的情况非常相似,只有我们现在有4或6个贡献,每个贡献大小不同,但相差90
,如图4所示。由于三重对称性,原子被分为三组,而不是像二重对称那样分为两组。4或6倍对称的情况与3倍的情况非常相似,只有我们现在有4或6个贡献,每个贡献大小不同,但相差90 和60
和60 分别是。见图4c和4d。
分别是。见图4c和4d。
图4:具有(a)2倍、(b)3倍、(c)4倍和(d)6倍对称元素的空间群中系统缺失的增加。
 |
6.系统增强,ε
第三种也是最后一种特殊反射是人力资源=小时和ht(高温)=0(模1)。2个(或3个或4个或6个或更多)捐款数额相等,并且具有相同的阶段,因此相互扩大。预期强度(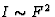 )这种反射的大小是一般反射的2倍(或3倍或4倍或6倍以上)。增强因子称为ε(
)这种反射的大小是一般反射的2倍(或3倍或4倍或6倍以上)。增强因子称为ε(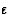 )很容易导出为旋转矩阵的个数R(右)我可以应用于小时并给予回报小时.
)很容易导出为旋转矩阵的个数R(右)我可以应用于小时并给予回报小时.
例子:
在P(P)2有两种对称操作:
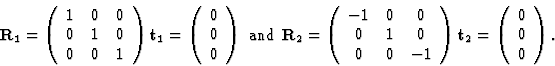
类型(0)的所有反射k0)将满足标准人力资源=小时和ht(高温)对称操作均为0,因此这些反射具有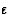 = 2. 很明显
= 2. 很明显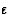 不是系统性缺勤的影响。见图5。
不是系统性缺勤的影响。见图5。7.相移
与等效位置类似,由于这些,存在等效反射。两个等效反射,小时和小时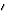 始终具有相同的振幅,即|F类(小时)| = |F类(小时
始终具有相同的振幅,即|F类(小时)| = |F类(小时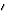 )|,但它们的阶段可能不同。然而,相位以一种容易推断的方式相互关联。两个等效反射之间的相位差称为相移现在将显示相移是如何产生的以及它有多大。
)|,但它们的阶段可能不同。然而,相位以一种容易推断的方式相互关联。两个等效反射之间的相位差称为相移现在将显示相移是如何产生的以及它有多大。
两次反射小时和小时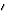 如果存在R(右)我这样的话
如果存在R(右)我这样的话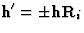 .根据弗里德尔定律小时始终等于-小时两次等效反射的相位关系如下:
.根据弗里德尔定律小时始终等于-小时两次等效反射的相位关系如下:
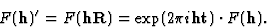
证明:
为了简单起见,对二次对称性进行了证明。对于较高的对称性,可以使用类似的策略。如果x个和接收+t吨是相等的位置,那么R(右)-1(x个-t吨)也是一个等价的位置,因为x个引起x个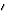 ,x个
,x个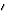 引起x个,通过相同的对称操作:
引起x个,通过相同的对称操作:
![\开始{displaymath}\textbf{R}^{-1}([\textbf{Rx}+\textbf2}]-\textbf2{t})=\text。。。tbf{Rx})=(\textbf{R}^{-1}\textbf{R})\tdot\textbf{x}=\textbf-x}。\结束{显示方式}](https://www.iucr.org/__data/assets/image/0019/13717/img52.gif)
R(右)-1是的逆矩阵R(右),即。R(右)- 1R(右)=我。我们在计算时将利用这一点F类(小时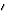 ) =F类(人力资源):
) =F类(人力资源):
|
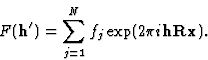 |
(8) |
与(5)类似,我们现在对一半以上的单位单元求和:
|
![\开始{displaymath}F(\textbf{h}^{prime})=\sum^{N/2}_{j=1}F_j\exp(2{\pi}i\……2{\pi}i\textbf{hR}[\textbf-{R}^{-1}\{\textbv{x}-\textbf{t}\}])。\结束{显示方式}](https://www.iucr.org/__data/assets/image/0003/13719/img54.gif) |
(9) |
利用右后- 1=我.
|
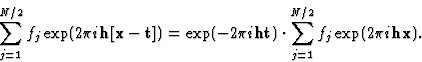 |
(10) |
exp一词(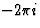 ht(高温))因为它是一个常量,所以可以将其置于总和之外。注意指数的减号!我们现在得到
ht(高温))因为它是一个常量,所以可以将其置于总和之外。注意指数的减号!我们现在得到
|
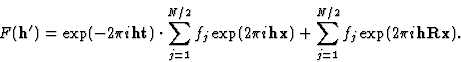 |
(11) |
(11) 与(7)相比:
|
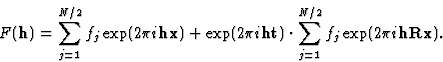 |
(7) |
除了相位项exp外,两个表达式(11)和(7)是相同的(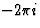 小时)将其应用于(7)的两个和,得到(11)。因此F类(小时)和F类(小时
小时)将其应用于(7)的两个和,得到(11)。因此F类(小时)和F类(小时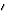 )振幅相等但相位不同(
)振幅相等但相位不同(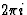 ht(高温)).
ht(高温)).相移称为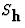 和等于exp(
和等于exp(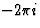 ht(高温)). 注意减号!
ht(高温)). 注意减号!
|
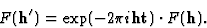 |
(12) |
这通常以其他形式书写,表示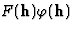 :
: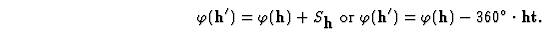
由于相移取决于平移矢量,因此通过平移矢量=0的对称运算得出的等效反射的所有相位都是相等的。将给出不同相位的等效反射示例。推导所有反射的相位,其等效于(小时0 1)在空间组中 P(P)三121.等效反射在第4节中推导。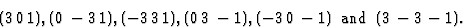
如果第一个反射(3 0 1)为+60 ,然后第二个变为
,然后第二个变为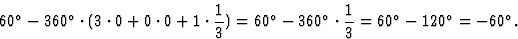
以类似的方式,其他反射的相位为60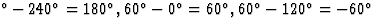 和
和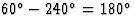 .
.请注意,第五次反射(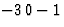 )也是(3 0 1)的弗里德尔对。根据弗里德尔定律,任何反射的相位都必须减去其弗里德尔对的相位。在所有对称操作产生等效反射(也是其Friedel伴侣)的情况下,我们有两个相位值指示。如果(香港特别行政区)是
)也是(3 0 1)的弗里德尔对。根据弗里德尔定律,任何反射的相位都必须减去其弗里德尔对的相位。在所有对称操作产生等效反射(也是其Friedel伴侣)的情况下,我们有两个相位值指示。如果(香港特别行政区)是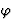 然后是(-小时-k-我)是
然后是(-小时-k-我)是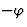 根据弗里德尔定律,相位为
根据弗里德尔定律,相位为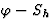 由于相移。我们现在有一个方程组:
由于相移。我们现在有一个方程组:
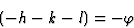
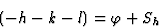
用解决方案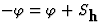 ,即。
,即。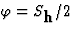 (模数180
(模数180 自从
自从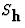 当然是360模
当然是360模 ). 这种推导相位限制的替代方法显然比第4节中的方法更为相关。
). 这种推导相位限制的替代方法显然比第4节中的方法更为相关。以类似的方式,系统性缺失的反射可以显示为具有两个矛盾相位指示的反射。在P(P)21(0k0)-反射k奇数已灭绝。的等效位置P(P)21是(x个,年,z(z))和(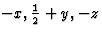 ). 反思(香港特别行政区)和(-小时,k, -我)等效,相移为k/2.因此,像(0 3 0)这样的反射本身是等效的,但生成的等效反射具有与原始反射相差180的相位
). 反思(香港特别行政区)和(-小时,k, -我)等效,相移为k/2.因此,像(0 3 0)这样的反射本身是等效的,但生成的等效反射具有与原始反射相差180的相位 。(0 3 0)的相位同时
。(0 3 0)的相位同时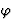 和
和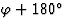 ,当然,只有当反射的振幅为0时,这才有可能!
,当然,只有当反射的振幅为0时,这才有可能!
进一步阅读的建议
Hall,S.R.,结构不变量应用中的对称性考虑。北约直接法和帕特森法高级研究学校,意大利帕尔马(1970年)。
Luzzati,V.,《使用统计方法检测对称元素》。国际X射线冷冻表第二卷,第355-356页。伯明翰,基诺奇出版社(1959年)。
Main,P.,《关于定义起源和反形态》,M.M.Woolfson(编辑),晶体学中的直接方法(讲稿),约克(1974年)。
Rogers,D.,《X射线强度的概率分布》。四、 确定晶体类别和空间群的新方法,《水晶学报》. 3 (1950) 455-464. 互惠空间的统计性质,J.S.Rollett(编辑),晶体学中的计算方法伦敦,佩加蒙出版社(1965)。
Sheldrick,G.M.,结构因子代数,in国际结晶学学院(课堂讲稿)。五、课程。求解晶体结构的直接方法。第1部分。Erice,主任G.Allegra教授。(1978).
![]()
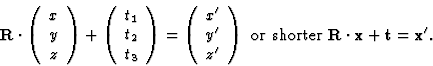

![]()
![]()
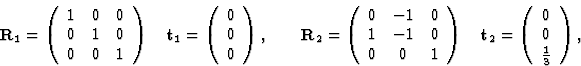
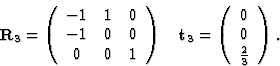
![]()
![\开始{显示方式}F(hkl)=\sum^N_{j=1}F_j\cdot\exp[2{\pi}i(hk_j+ky_j+lz_j)],结束{显示方法}](https://www.iucr.org/__data/assets/image/0018/13671/img10.gif)
![]()
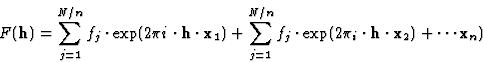
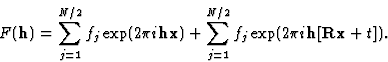
![]()
![]()
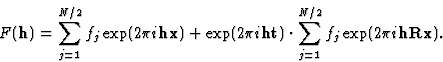
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
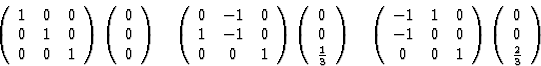
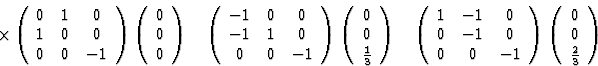
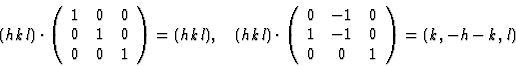
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
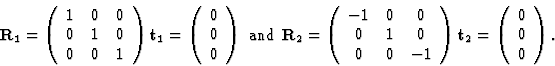
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
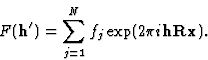
![\开始{displaymath}F(\textbf{h}^{prime})=\sum^{N/2}_{j=1}F_j\exp(2{\pi}i\……2{\pi}i\textbf{hR}[\textbf-{R}^{-1}\{\textbv{x}-\textbf{t}\}])。\结束{显示方式}](https://www.iucr.org/__data/assets/image/0003/13719/img54.gif)
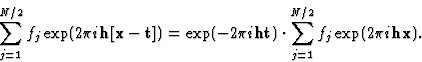
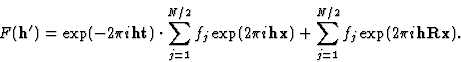
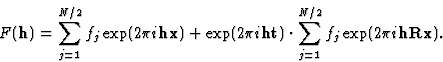
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()