晶体物理学导论
晶体物理性质的描述
埃尔文·哈特曼
介绍
大多数讨论物质物理性质的物理学专著通常来自各向同性材料,概括而言,包括对结晶体行为的有限描述。这种表述方式无疑是有利的,然而,它意味着对各种性质进行单独的讨论,不可避免地模糊了晶体性质理论中适用的一般原理和方法。本工作的目的是在统一处理中讨论和总结晶体的物理特性,并通过一些典型示例说明统一描述这些特性的原理和方法。
作为引言,为了获得清晰的晶体物理图像,让我们分别研究各向同性和各向异性介质中的介电常数问题。
图1:偶极子的形成(a)在各向同性中,(b)在各向异性绝缘体中。
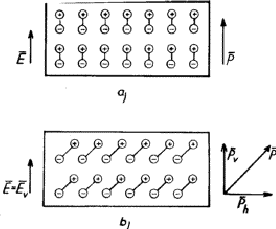 |
在各向同性绝缘体中,介电极化过程中产生的偶极子与电场平行(图1a),因此电极化矢量之间的关系(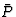 )和电场(
)和电场(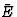 )也就是磁化率,可以用一个单一值来表征(
)也就是磁化率,可以用一个单一值来表征(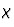 ).
).
|
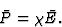 |
(1.1) |
然而,在各向异性介质中,介电极化过程中形成的偶极子通常与电场不平行。图1b描述了一个相对简单的情况,其中偶极子虽然布置在与电场平行的平面上(由图中的平面表示),但方向不同。在这种情况下,极化矢量(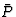 )由于垂直电场(
)由于垂直电场(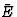 =
=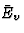 ))不仅有垂直(
))不仅有垂直(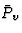 )也是一个水平组件(
)也是一个水平组件(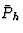 ). 因此,在图1b的情况下,有两个数量(
). 因此,在图1b的情况下,有两个数量(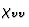 ;
;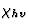 )描述垂直电场和极化之间的关系是必要的,所讨论的两个矢量的分量由方程连接
)描述垂直电场和极化之间的关系是必要的,所讨论的两个矢量的分量由方程连接
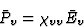 |
(1.2) |
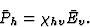 |
一般来说,当研究三维空间中的介电极化时,人们发现,忽略高阶效应x个1,x个2,x个三坐标系——电场矢量分量之间的下列方程(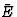 = [E类1,E类2,E类三])和极化的成分(
= [E类1,E类2,E类三])和极化的成分(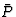 = [P(P)1,P(P)2,P(P)三]):
= [P(P)1,P(P)2,P(P)三]):
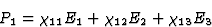
|
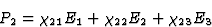 |
(1.3) |
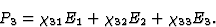
这意味着总共需要九个数据来描述电场和极化之间的关系。通过向量代数,可以表明,在正交坐标变换的情况下,方程(1.3)变换中的九个系数是两个向量分量的乘积,即它们是二阶张量的分量。因此,各向异性介质中的介电极化率可以用二阶张量来描述。
方程式(1.3)可以缩写形式重写
|
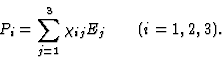 |
(1.4) |
用爱因斯坦的符号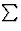 如果在同一术语中后缀出现两次,则可以省略符号。因此,等式(1.4)采用以下形式
如果在同一术语中后缀出现两次,则可以省略符号。因此,等式(1.4)采用以下形式
|
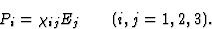 |
(1.5) |
在接下来的讨论中,将使用爱因斯坦公约。
2.作为张量的物理性质
在引言中已经证明,各向异性介质的介电极化率可以用二阶张量来描述,该张量表示两个物理量之间的关系,即极化矢量和电场矢量之间的关系。类似地,各种物理性质的大部分可以用张量来描述,张量建立了可测量物理张量之间的关系。每个标量都是零秩的,每个向量都是一阶张量。通常在晶体物理学中,一组3第页数量与第页从旧坐标到新坐标转换下的指数作为第页向量称为秩的极张量(或真张量)第页.
因此,如果[B类ijk公司...n个]和[A类pqr(pqr)...u个]张量表示物理量,这些量之间关系的一般形式可以用爱因斯坦的约定写成(在一阶近似中),如下所示
|
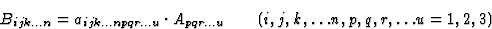 |
(2.1) |
其中张量[一ijk公司...净功率因数...u个]表示连接两个物理量的物理性质。根据张量代数,如果[A类pqr(pqr)...u个]表示(f)-等级和[B类ijk公司...n个]一个克-秩张量[一ijk公司...净功率因数...u个],表示物理属性,必须是((f)+克)-秩张量。
让我们考虑一些例子。在给定状态下,物质的密度表示其质量和体积之间的关系,它们由0阶张量表示,因此密度由0阶张量表示(即标量)。晶体的热释电性质用一阶张量描述。热释电张量(本质上是一个向量)表示一阶张量(电极化向量)和零阶张量之间的关系。除了介电常数外,电导率、导热系数、热膨胀等也可以用二阶张量表示。表1总结了其他示例,包括可以用高阶张量表示的特性。
晶体还有一些不能用张量直接表示的各向异性性质,这些性质(本文不讨论)例如抗拉强度、流动应力、表面能、生长和溶解速度等。
表1:表示物理特性的张量
| 性质或效果 |
张量表示法 |
张量秩 |
独立组件的最大数量 |
定义方程式 |
定义方程中的物理量 |
|
| 密度 |
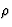 |
|
1 |
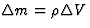 |
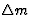 群众 群众 |
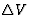 体积 体积 |
| 比热 |
c(c) |
|
1 |
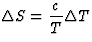 |
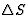 熵 熵 |
T型温度 |
| 热释电 |
[第页我] |
1 |
三 |
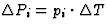 |
[P(P)我]电介质极化 |
T型温度 |
| 电热效应 |
[第页我] |
1 |
三 |
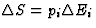 |
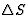 熵 熵 |
[E类我]电场 |
| 介电常数 |
![$[\varepsilon_{ij}]$](https://www.iucr.org/education/pamphlets/18/full-text/img28.gif) |
2 |
6 |
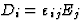 |
[D类我]电位移 |
[E类j个]电场 |
| 磁导率 |
![$[\mu_{ij}]$](https://www.iucr.org/education/pamphlets/18/full-text/img30.gif) |
2 |
6 |
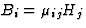 |
[B类我]磁感应 |
[H(H)j个]磁场 |
| 电导率 |
![$[\sigma_{ik}]$](https://www.iucr.org/education/pamphlets/18/full-text/img32.gif) |
2 |
6 |
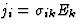 |
[j个我]电流密度 |
[E类k个]电场 |
| 电阻率 |
![$[\rho_{ik}]$](https://www.iucr.org/education/pamphlets/18/full-text/img34.gif) |
2 |
6 |
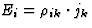 |
[E类我]电场 |
[j个k个]电流密度 |
| 导热系数 |
[k个ij公司] |
2 |
6 |
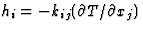 |
[小时我]热流密度 |
![$[\部分T/\部分x_j]$](https://www.iucr.org/education/pamphlets/18/full-text/img37.gif) 温度梯度 温度梯度 |
| 热膨胀 |
![$[\alpha_{ij}]$](https://www.iucr.org/education/pamphlets/18/full-text/img38.gif) |
2 |
6 |
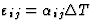 |
![$[\varepsilon_{ij}]$](https://www.iucr.org/education/pamphlets/18/full-text/img28.gif) 拉紧 拉紧 |
T型温度 |
| 塞贝克效应 |
![$[\beta_{ik}]$](https://www.iucr.org/education/pamphlets/18/full-text/img40.gif) |
2 |
9 |
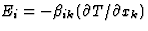 |
[E类我]电场 |
![$[\部分T/\部分x_k]$](https://www.iucr.org/education/pamphlets/18/full-text/img42.gif) 温度梯度 温度梯度 |
| 珀尔贴效应 |
![$[\pi_{ik}]$](https://www.iucr.org/education/pamphlets/18/full-text/img43.gif) |
2 |
9 |
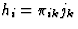 |
[小时我]热流密度 |
[j个k个]电流密度 |
| 霍尔效应 |
![$\rho_{ikl}]$](https://www.iucr.org/education/pamphlets/18/full-text/img45.gif) |
三 |
9 |
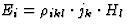 |
[E类我]电场 |
[j个k个]电流密度[H(H)我]磁场 |
| 直接压电效应 |
[d日ijk公司] |
三 |
18 |
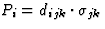 |
[P(P)我]电介质极化 |
![$[\sigma_{jk}]$](https://www.iucr.org/education/pamphlets/18/full-text/img48.gif) 强调 强调 |
| 逆压电效应 |
[d日ijk公司] |
三 |
18 |
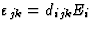 |
![$[\varepsilon_{jk}]$](https://www.iucr.org/education/pamphlets/18/full-text/img50.gif) 拉紧 拉紧 |
[E类我]电场 |
| 压磁效应 |
[q个里吉] |
三 |
18 |
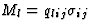 |
[M(M)我]磁极化 |
![$[\sigma_{ij}]$](https://www.iucr.org/education/pamphlets/18/full-text/img52.gif) 强调 强调 |
| 电光效应 |
[第页ijk公司] |
三 |
18 |
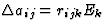 |
[一ij公司]介电抗渗性 |
[E类k个]电场 |
| 二次谐波产生 |
[d日ijk公司] |
三 |
18 |
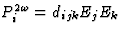 |
![$[P_i^{2\omega}]$](https://www.iucr.org/education/pamphlets/18/full-text/img55.gif) 频率介电极化 频率介电极化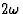 |
![$[E_j],\,[E_k]$](https://www.iucr.org/education/pamphlets/18/full-text/img57.gif) 电场 电场 |
| 二阶弹性刚度 |
[c(c)国际jkl] |
4 |
21 |
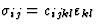 |
![$[\sigma_{ij}]$](https://www.iucr.org/education/pamphlets/18/full-text/img52.gif) 强调 强调 |
![$[\varepsilon_{kl}]$](https://www.iucr.org/education/pamphlets/18/full-text/img59.gif) 拉紧 拉紧 |
| 二阶弹性柔度 |
[秒国际jkl] |
4 |
21 |
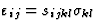 |
![$[\varepsilon_{ij}]$](https://www.iucr.org/education/pamphlets/18/full-text/img28.gif) 拉紧 拉紧 |
![$[\sigma_{kl}]$](https://www.iucr.org/education/pamphlets/18/full-text/img61.gif) 强调 强调 |
| 压水效应 |
![$[\pi_{ijkl}]$](https://www.iucr.org/education/pamphlets/18/full-text/img62.gif) |
4 |
36 |
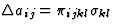 |
[一ij公司]介电抗渗性 |
![$[\sigma_{kl}]$](https://www.iucr.org/education/pamphlets/18/full-text/img61.gif) 强调 强调 |
| 二次电光效应 |
[对国际jkl] |
4 |
36 |
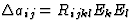 |
[一ij公司]介电抗渗性 |
![$[E_k],\,[E_l]$](https://www.iucr.org/education/pamphlets/18/full-text/img65.gif) 电场 电场 |
| 电致伸缩 |
![$[\gamma_{iljk}]$](https://www.iucr.org/education/pamphlets/18/full-text/img66.gif) |
4 |
36 |
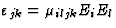 |
![$[\varepsilon_{jk}]$](https://www.iucr.org/education/pamphlets/18/full-text/img50.gif) 拉紧 拉紧 |
![$[E_i],\,[E_l]$](https://www.iucr.org/education/pamphlets/18/full-text/img68.gif) 电场 电场 |
| 三阶弹性应力 |
[c(c)ijklmn公司] |
6 |
56 |
![$\Phi=\frac{1}{2} c(c)_{ijkl}\cdot\eta{ij}\cdoteta{kl}+\frac{1}{6} c(c)_{ijklmn}\cdot\eta{ij}\cdot \eta_{kl}\cdoteta_{mn}]$](https://www.iucr.org/education/pamphlets/18/full-text/img69.gif) |
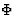 变形能[c(c)国际jkl]二阶刚度 变形能[c(c)国际jkl]二阶刚度 |
![$[\eta_{ij}],\,[\eta _{kl}],\n,[\esta _{mn}]$](https://www.iucr.org/education/pamphlets/18/full-text/img71.gif) 拉格朗日有限应变分量 拉格朗日有限应变分量 |
3.物理性质的内在对称性
张量的秩决定了张量分量的数量。0,1,2,3,4,5,6-秩张量的分量数为1,3,9,27,81243729。然而,某些对称性大大减少了独立分量的数量。这些可能是物理性质固有的固有对称性,也可能是晶体对称性,它们对独立成分数量的影响将在下一节中讨论。
在某些情况下,内在对称性遵循所讨论物理性质的定义。因此,例如在弹性情况下,它遵循应力张量和变形张量的对称性,以及二阶弹性刚度的四阶张量[c(c)国际jkl](见表1)相对于(ij公司)和(kl公司)排列。这样,四阶弹性张量的独立系数从81个减少到36个。进一步,变形张量的对称性遵循[d日ijk公司]压电张量(见表1)j个和k个后缀,这意味着压电张量的独立分量不超过18个。
物理性质中固有的对称性在大多数情况下可以通过热力学推理找到。对于平衡性质,即指热力学可逆变化的性质,可以通过研究热力学势来揭示性质的固有对称性。对于输运过程的物理性质特征,本征对称性是Onsager原理的结果。
为了说明平衡性质的热力学讨论,让我们考虑一个更复杂的例子,从这个例子中,不仅张量的对称性代表单个物理性质(弹性张量、电学张量和磁学张量)而且代表各种性质的张量之间的关系也变得明显。在示例中,同时研究了弹性、热、电和磁效应。自变量应为压力[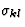 ],电场[E类k个],磁场[H(H)我]和温度[T型]而变形[
],电场[E类k个],磁场[H(H)我]和温度[T型]而变形[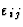 ],极化[P(P)我],磁化强度[M(M)我]和熵[S公司]被选为因变量。上述数量的差异明显与以下关系有关:
],极化[P(P)我],磁化强度[M(M)我]和熵[S公司]被选为因变量。上述数量的差异明显与以下关系有关:
|
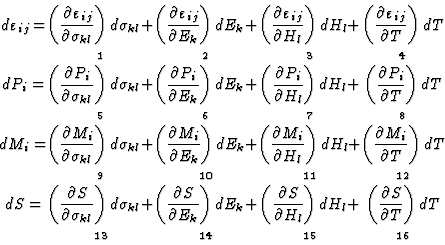 |
(3.1) |
偏导数具有以下效应的特征:
1.弹性变形。
2.往复(或逆向)压电效应。
3.往复(或逆向)压磁效应。
4.热膨胀。
5.压电效应。
6.极化。
7.磁电极化。
8.热释电。
9.压磁效应。
10.往复(或逆向)磁电极化。
11.磁极化。
12.热磁学。
13.压热效应。
14.电致变色效应。
15.磁热效应。
16.传热。
为了认识方程组(3.1)偏导数之间的关系,让我们讨论系统的吉布斯势
|
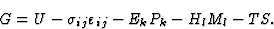 |
(3.2) |
记住,根据热力学第一定律和第二定律,内能的总微分是
|
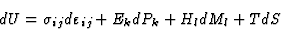 |
(3.3) |
我们得到吉布斯势的全微分的表达式
|
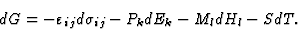 |
(3.4) |
同时,可以用自变量的偏导数描述吉布斯势的总微分:
|
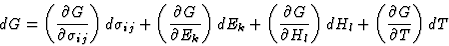 |
(3.5) |
那就是
|
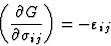 |
(3.6) |
|
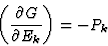 |
(3.7) |
|
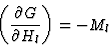 |
(3.8) |
|
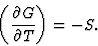 |
(3.9) |
通过研究吉布斯势的二阶偏导数,并考虑偏微分序列的可换性,得出如下结论:[秒国际jkl],电介质[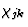 ]和抗磁性[
]和抗磁性[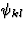 ]张量,如下面等式(3.10)-(3.12)所定义的,是对称的
]张量,如下面等式(3.10)-(3.12)所定义的,是对称的
|
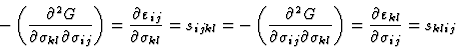 |
(3.10) |
|
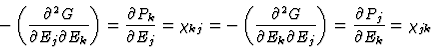 |
(3.11) |
|
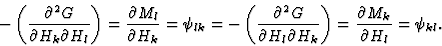 |
(3.12) |
此外,对偏导数的研究不仅证明了上述张量的对称性,而且表明代表直接效应和互易效应的张量分量相互对应。让我们研究一下下列偏导数
|
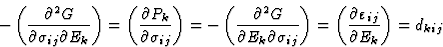 |
(3.13) |
|
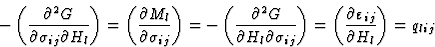 |
(3.14) |
|
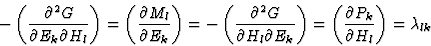 |
(3.15) |
|
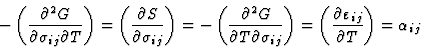 |
(3.16) |
|
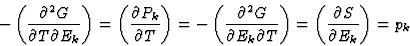 |
(3.17) |
|
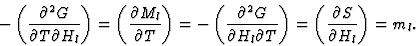 |
(3.18) |
从上述方程式可以看出,以下两者之间存在对应关系:(a) 张量的分量表示压电效应和互反压电效应(等式3.13),
(b) 表示压磁效应和压磁效应倒数的张量分量(等式(3.14)),
(c) 表示磁电极化和互易磁电极化的张量分量(等式(3.15)),
(d) 表示压热效应和热膨胀的张量分量(等式(3.16)),
(e) 表示热释电和电热效应的张量分量(等式(3.17)),
(f) 表示热磁和磁热效应的张量分量(等式(3.18))。
考虑到上述陈述,并仅限于一阶效应,对方程(3.1)进行积分,得到以下方程组
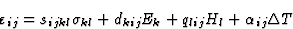
|
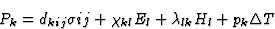 |
(3.19) |
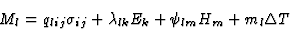
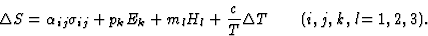
也许值得让读者注意的是,方程组(3.19)代表16=9+3+3+1方程,这些方程的右边包含16个项,因为每个项中出现两次后缀意味着根据爱因斯坦约定求和。此外,变形张量[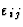 ]和应力张量[
]和应力张量[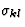 ]是对称的,因此方程组(3.19)总共包含13个独立方程和13个自变量。
]是对称的,因此方程组(3.19)总共包含13个独立方程和13个自变量。
正如已经指出的,输运过程的固有对称性特征是Onsager互易关系的结果。然而,重要的是要强调,只有适当地选择了与之相连的通量和热力学力,这种关系才有效。为了简单起见,让我们研究一下电导率的情况。热力学力[X(X)k个]附于电流密度[j个我]是
|
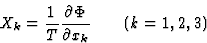 |
(3.20) |
哪里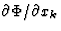 表示k个-的第个组件
表示k个-的第个组件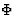 电位梯度和T型是温度。
电位梯度和T型是温度。在这种情况下,线性电流定律为
|
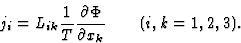 |
(3.21) |
此方程的展开形式为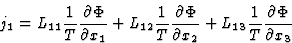
|
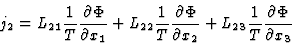 |
(3.22) |
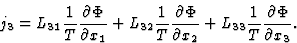
根据Onsager的互惠关系L(左)伊克电导率系数与足量的互换性对称,即。
电导率系数与比电导率张量分量之间的关系[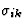 ]很容易找到。定义公式[
]很容易找到。定义公式[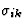 ]张量(见表1),为
]张量(见表1),为
|
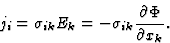 |
(3.24) |
然而,通过比较方程(3.21)和(3.24),我们很容易看出
|
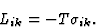 |
(3.25) |
另一方面,从等式(3.23)和(3.25)可以看出,代表特定电导率的张量的对称性非常明显。通过适当选择与之对应的通量和热力学力来讨论复合输运过程,不仅讨论了各种张量的对称性,而且还讨论了代表各种性质的张量之间的关系,这些关系遵循Onsager互易关系。例如,在讨论热电效应时,电导张量和热导张量的对称性遵循Onsager原理以及代表塞贝克效应的张量之间的关系[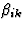 ]和珀尔贴张量[
]和珀尔贴张量[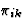 ](见表1)。
](见表1)。
|
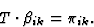 |
(3.26) |
此外,需要注意的是(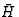 )磁场的形式
)磁场的形式
|
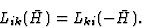 |
(3.27) |
4.诺依曼原理
上一节已经证明,物理性质的固有对称性减少了独立张量分量的数量。物理性质张量的独立分量和某些分量的零值的进一步减少是因为晶体对称性对物理性质的对称性产生了一些影响。这一事实由19世纪已经提出的纽曼原理来表达,根据该原理晶体任何物理性质的对称元素必须包括晶体点群的所有对称元素:
|
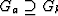 |
(4.1) |
哪里克k个表示晶体的对称组,克一是表示物理性质的张量的对称组,符号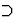 指示子组属于该组。晶体的对称群通常是指从晶体形式导出的32个点群,然而,有时也应考虑最近引入的90个磁性群或更一般的122个Shubnikov群(见[10-14])。根据诺依曼原理,代表任何物理性质的张量对于给定晶体类的每个对称操作都应该是不变的。不变性条件减少了独立张量分量的数量,因为它表示张量分量之间的关系。为了描述这些关系,有必要在一定程度上讨论张量分量的变换。
指示子组属于该组。晶体的对称群通常是指从晶体形式导出的32个点群,然而,有时也应考虑最近引入的90个磁性群或更一般的122个Shubnikov群(见[10-14])。根据诺依曼原理,代表任何物理性质的张量对于给定晶体类的每个对称操作都应该是不变的。不变性条件减少了独立张量分量的数量,因为它表示张量分量之间的关系。为了描述这些关系,有必要在一定程度上讨论张量分量的变换。众所周知的正交变换方程x个1,x个2,x个三系统到另一个类似的正交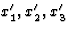 根据定义,该系统用于第一、第二、第三和第四阶极性张量:
根据定义,该系统用于第一、第二、第三和第四阶极性张量:
|
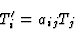 |
(4.2) |
|
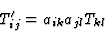 |
(4.3) |
|
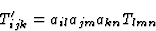 |
(4.4) |
|
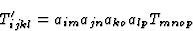 |
(4.5) |
这使我们得到了方程中表示的通用极化传感器变换符号:
|
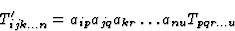 |
(4.6) |
其中一ij公司方向余弦是(一ij公司)矩阵(一ij公司)矩阵根据矩阵方程连接原始坐标和“新”坐标
|
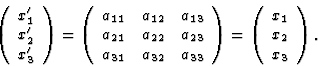 |
(4.7) |
在某些情况下,描述物理性质的张量不是极性的,而是轴向的(例如,描述光学活动或压磁的张量)。对于轴向(或伪)张量,可以使用以下转换关系作为定义
|
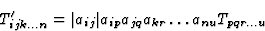 |
(4.8) |
其中|一ij公司|表示矩阵行列式的值(一ij公司)如果变换操作包含纯旋转,则其值为(+1);如果变换除旋转外还包含反转,则值为(-1),这意味着对称操作也会改变轴的方向。不难发现表示任何物理性质的张量是极性的还是轴向的,因为这可以很容易地通过定义所讨论的物理性质的方程(2.1)来确定。如果只有一个张量[A类pqr(pqr)...u个]和[B类ijk公司...n个]式(2.1)中是轴向的(例如磁场是一阶轴向张量),也是性质张量[一ijk公司...净功率因数...u个]如等式(2.1)所定义的,张量是轴向的,在其他情况下张量是极性的。
应该注意的是,如果还考虑了磁点群,则表示张量分量变换性质的方程(4.6)和方程(4.8)仅对常规对称运算有效。然而,如果传统的对称运算与反对称运算中实际发生的时间反演相结合(参见[10-14]),则无论何时方程式(2.1),方程式(4.6)和(4.8)的右侧都应分别乘以(-1)定义物理性质包含磁矢量量(磁场、磁感应强度、磁化矢量)的奇数倍。表示这类属性的张量称为C类-张量。1有关此问题的更详细讨论,请参阅文献。1-3
考虑到变换方程(4.6)和(4.8)以及上述备注,现在可以定义给定晶体类别的极张量和轴向张量分量之间的关系,因为张量对于任何对称操作的不变性都需要该关系
|
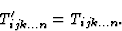 |
(4.9) |
因此,在极张量的情况下,如果矩阵(一ij公司)描述了给定晶体类的任何常规对称操作,张量分量必须根据诺依曼原理满足方程
|
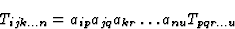 |
(4.10) |
考虑到轴向张量不变性的条件,考虑到等式(4.8)和(4.9),我们可以写下
|
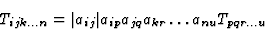 |
(4.11) |
当然,在反对称操作和前面讨论的情况下C类-张量等式(4.10)和(4.11)的右侧乘以(-1)。对于每个张量分量,(4.10)和(4.11)类型的方程应分别有效,以便张量分量必须满足这些方程组。由于这适用于给定晶体类的每个对称操作,张量分量之间的方程组数量将等于给定晶体类中可能执行的对称操作的数量。然而,在给定晶体类别的情况下,为了获得代表任何物理性质的张量分量之间的每一种关系,不必为每一种对称操作分别记下(4.10)和(4.11)类型的方程组。群论中众所周知,对于不同的晶体类别,每个对称操作都可以从几个基本对称操作中推导出来。应用与这些基本操作相对应的矩阵(生成矩阵)就足以获得因晶体类在给定张量上的对称性而产生的效果。表2和表3总结了每个传统晶体类别的一系列生成矩阵。
这些相互关系起初似乎有些复杂,但举一个简单的例子,将有助于更好地理解。让我们考虑三方系统的晶体类3中热电张量的形式,假设x个三坐标系的轴是三重旋转轴。如表2和表3所示,与对称操作相关的坐标变换可以用以下矩阵进行描述
|
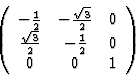 |
(4.12) |
考虑到等式(4.10)中表示的极张量的不变性条件,可以得到张量分量的下列方程
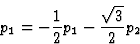
|
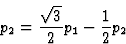 |
(4.13) |
第页三=第页三.
从这些方程可以得出第页1=第页2=0且仅限第页三可以不同于零,因此三角系第3类晶体的热释电张量的形式为第页= [0; 0;第页三].
表2:32个点群(晶体类)的生成矩阵。Koptsik之后13
|
| 晶体系统 |
类别符号 |
生成矩阵 |
对称元素数量 |
选择x个1,x个2,x个三晶体物理轴与对称轴的关系 |
|
| |
|
| |
国际 |
Schoenflies公司 |
|
|
|
|
|
| 三联诊所 |
1 |
C类1 |
M(M)0 |
1 |
|
|
| |
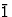 |
S公司2=C类我 |
M(M)1 |
2 |
|
|
| 单诊所 |
2 |
C类2 |
M(M)2 |
2 |
|
|
| |
米 |
C类1小时=C类秒 |
M(M)三 |
2 |
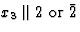 |
|
| |
2/米 |
C类2小时 |
M(M)2,M(M)三 |
4 |
|
|
| 正交晶系 |
222 |
V(V)=D类2 |
M(M)4,M(M)2 |
4 |
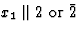 |
|
| |
毫米2 |
C类2v(v) |
M(M)5,M(M)2 |
4 |
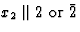 |
|
| |
毫米 |
V(V)小时=D类2小时 |
M(M)5,M(M)6,M(M)三 |
8 |
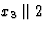 |
|
| 正方形 |
4 |
C类4 |
M(M)7 |
4 |
|
|
| |
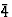 |
S公司4 |
M(M)8 |
4 |
|
|
| |
422 |
D类4 |
M(M)7,M(M)4 |
8 |
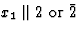 |
|
| |
4/米 |
C类4小时 |
M(M)7,M(M)三 |
8 |
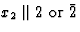 |
|
| |
4毫米 |
C类4v(v) |
M(M)7,M(M)5 |
8 |
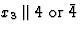 |
|
| |
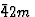 |
V(V)d日=D类2d日 |
M(M)8,M(M)4 |
8 |
|
|
| |
4/毫米 |
D类4小时 |
M(M)7,M(M)三,M(M)5 |
16 |
|
|
| 三角(Trigonal) |
三 |
C类三 |
M(M)9 |
三 |
|
|
| |
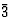 |
S公司6=C类三我 |
M(M)10 |
6 |
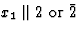 |
|
| |
32 |
D类三 |
M(M)9,M(M)4 |
6 |
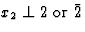 |
|
| |
三米 |
C类三v(v) |
M(M)9,M(M)5 |
6 |
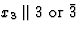 |
|
| |
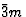 |
D类三d日 |
M(M)10,M(M)5 |
12 |
|
|
| 六边形 |
6 |
C类6 |
M(M)11 |
6 |
|
|
| |
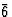 |
C类三小时 |
M(M)12 |
6 |
|
|
| |
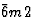 |
D类三小时 |
M(M)12,M(M)5 |
12 |
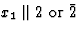 |
|
| |
622 |
D类6 |
M(M)11,M(M)4 |
12 |
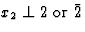 |
|
| |
6/米 |
C类6小时 |
M(M)11,M(M)三 |
12 |
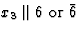 |
|
| |
6/毫米 |
C类6v(v) |
M(M)11,M(M)5 |
12 |
|
|
| |
6/毫米 |
D类6小时 |
M(M)11,M(M)5,M(M)三 |
24 |
|
|
| 立方(Cubic) |
23 |
T型 |
M(M)13,M(M)2 |
12 |
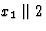 |
|
| |
米三 |
T型小时 |
M(M)14,M(M)2 |
24 |
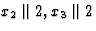 |
|
| |
432 |
O(运行) |
M(M)13,M(M)7 |
24 |
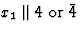 |
|
| |
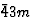 |
T型d日 |
M(M)13,M(M)8 |
24 |
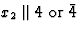 |
|
| |
米三米 |
O(运行)小时 |
M(M)14,M(M)7 |
48 |
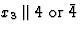 |
|
|
表3:生成矩阵
|
| |
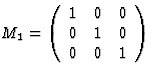 |
身份 |
|
|
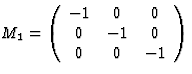 |
反转 |
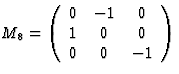 |
关于的四重反演x个三轴 |
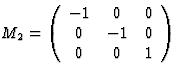 |
关于的双重旋转x个三轴 |
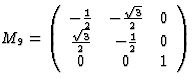 |
三倍旋转x个三轴 |
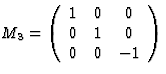 |
反射x个1x个2飞机 |
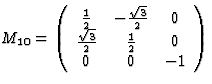 |
关于的三重反演x个三轴 |
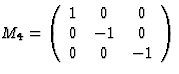 |
关于的双重旋转x个1轴 |
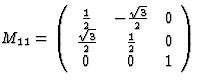 |
六倍旋转x个三轴 |
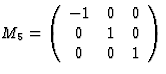 |
反射x个2x个三飞机 |
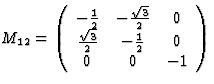 |
关于六倍反转x个三轴 |
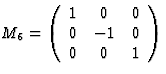 |
反射x个1x个三飞机 |
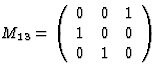 |
[111]方向的三倍旋转 |
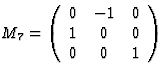 |
四倍旋转x个三轴 |
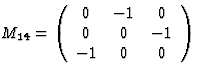 |
[111]方向的三重反演 |
|
本例中使用的方法可以应用于所有情况,尽管对于更高秩的张量,在许多情况下它可能相当令人厌烦。
Fumi制定的直接检查方法可以节省大量时间(三角类和六角形类除外),4虽然原则上与之前的治疗方法没有区别,但其结果是时间相对较短。Fumi的方法基于这样一个事实,即在正交坐标系中,极张量分量的变换方式与相应坐标的乘积相同(参见等式(4.6))。然而,人们必须小心,不要改变因素的顺序,例如,不要改变产品x个1x个2人不会写字x个2x个1.
Fumi的方法可以通过一个考虑极性二阶张量形式的简单示例来研究,例如单斜晶系第2类晶体的介电常数张量。假设双重对称轴与x个2坐标轴对称操作符将按以下方式转换坐标
|
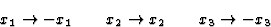 |
(4.14) |
或者用更简洁的方式
|
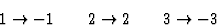 |
(4.15) |
由此可知
|
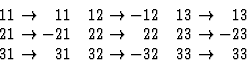 |
(4.16) |
那就是
|
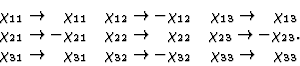 |
(4.17) |
同时,根据诺依曼原理,每个组件都应该转换为自身
|
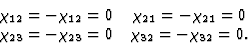 |
(4.18) |
因此,对于单斜系的第2类,磁化率张量的形式为
|
![\开始{displaymath}\left[\begin{array}{ccc}\chi{11}&0&\chi{13}\\0&\ch{22}&0\\chi{31}&0&\chi{33}\end{arrary}\right]\end{displayth}](https://www.iucr.org/education/pamphlets/18/full-text/img153.gif) |
(4.19) |
在本征对称性导致介电敏感性的情况下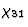 等于
等于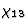 即张量(4.19)是对称的。
即张量(4.19)是对称的。由各种晶体类别的张量分量组成的张量或矩阵的形式可以在特殊文献中找到,例如参见[1、2、5-7、16、17]。
最后,应该注意到,在某些情况下,简单的几何考虑可以确定代表物理特性的张量的独立分量。很容易看出,具有对称中心的晶体中不可能存在热释电效应。这意味着对于这些晶体,热电张量的每个分量都是零,第页=[0,0,0],因为在这些晶体中,如果偏振矢量指向给定的方向,根据诺依曼原理,矢量也应出现在相反的方向,因此其值只能为零。
5.给定方向上的物理属性值
人们经常在文献中找到一些数据,这些数据给出了给定方向上某些物理性质的值。在本章中,将分别以电导率和杨氏模量的方向依赖性为例,说明给定方向上物理性质大小的概念,以及该值与相应张量分量之间的关系。
电场方向上的电导率定义为平行于电场的分量与电流密度的比值(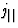 )电场的大小(E类),即。
)电场的大小(E类),即。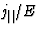 .让电场的分量E类我=英语我,其中n个我表示我-单位向量的第个分量(
.让电场的分量E类我=英语我,其中n个我表示我-单位向量的第个分量(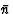 )指向电场的方向。的组件j个电流密度与
)指向电场的方向。的组件j个电流密度与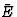 是张量符号
是张量符号
|
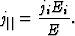 |
(5.1) |
因此单位矢量方向上的比电导率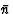 将
将
|
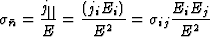 |
(5.2) |
其中一个已经
|
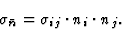 |
(5.3) |
因此,公式(5.3)得出了以下方向的电导率值之间的关系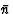 以及电导张量的分量。类似的关系给出了物理性质的值,这些物理性质可以用晶体介质给定方向上的二阶张量(例如导热系数、介电常数、热膨胀)表示。
以及电导张量的分量。类似的关系给出了物理性质的值,这些物理性质可以用晶体介质给定方向上的二阶张量(例如导热系数、介电常数、热膨胀)表示。方程式(5.3)可通过两种方式应用。一种可能性是根据测量的电导率值和相应的方向余弦计算张量分量。为此,人们应该测量不同方向上的电导率,这些方向不是通过对称性连接的,测量的次数是独立分量数量的两倍。应用等式(5.3)的另一种可能性与第一种可能性完全相反。借助已知的张量分量,可以计算任意方向的电导率值。
对于只有两个独立张量分量的四方、三角和六角形系统的晶体,方程(5.3)变得相当简化(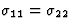 和
和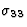 )
)
|
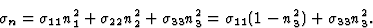 |
(5.4) |
如果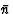 矢量和x个三晶体的主轴由
矢量和x个三晶体的主轴由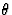 得到以下方程
得到以下方程
|
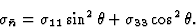 |
(5.5) |
组件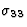 通常表示为
通常表示为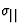 和的组件
和的组件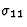 作为
作为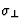 参考平行于晶体主轴(即三倍、四倍或六倍轴)和垂直于该轴的电导率值。使用这些符号,可以重写公式(5.5),以获得
参考平行于晶体主轴(即三倍、四倍或六倍轴)和垂直于该轴的电导率值。使用这些符号,可以重写公式(5.5),以获得
|
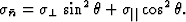 |
(5.6) |
作为另一个例子,我们将研究杨氏模量的方向依赖性。首先应说明,拉伸方向的杨氏模量定义为纵向应力的比值(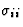 )和纵向应变(
)和纵向应变(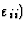 。如果
。如果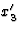 坐标系的轴放置在
坐标系的轴放置在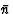 单位向量在这个方向上的杨氏模量显然是
单位向量在这个方向上的杨氏模量显然是
|
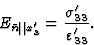 |
(5.7) |
根据方程式(3.19)(如果不存在外场)
|
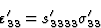 |
(5.8) |
一个人得到
|
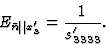 |
(5.9) |
因此,为了找到杨氏模量的方向依赖性,有必要了解张量分量的变化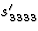 在各个方向。然而,这种依赖关系由
在各个方向。然而,这种依赖关系由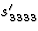 张量分量。
张量分量。
|
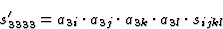 |
(5.10) |
哪里一三我,一三j个,一三k个,一三我表示的方向余弦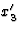 轴平行于
轴平行于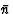 晶体物理坐标系的单位矢量;因此
晶体物理坐标系的单位矢量;因此
|
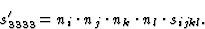 |
(5.11) |
从这个方程和等式(5.9)可以得到立方系晶体的杨氏模量
|
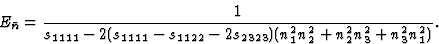 |
(5.12) |
这意味着,即使是立方晶体,杨氏模量也与方向有关。6.高阶效应
两种物理性质之间的关系不一定是线性的。因变量和自变量之间的关系通常可以用泰勒展开表示。例如,用幂级数展开来描述强场中极化的电场依赖性
|
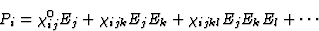 |
(6.1) |
其中张量[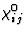 ]描述线性或一阶效应,张量[
]描述线性或一阶效应,张量[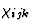 ]代表二阶效应等等。(二阶效应解释了当光通过没有对称中心的晶体时,会产生双频光波)。
]代表二阶效应等等。(二阶效应解释了当光通过没有对称中心的晶体时,会产生双频光波)。决定效果的顺序有一定的自由度,这取决于研究效果的方面。因此,在上例中,如果不是张量[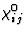 ]关于极化矢量电场的微分(即[
]关于极化矢量电场的微分(即[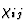 ]张量)被视为介电常数,先前的二阶效应可以被视为一阶效应,它描述了介电常数的电场依赖性。从方程式中可以看出这一点
]张量)被视为介电常数,先前的二阶效应可以被视为一阶效应,它描述了介电常数的电场依赖性。从方程式中可以看出这一点
|
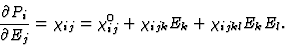 |
(6.2) |
电阻率对磁场的依赖性类似
|
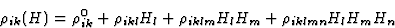 |
(6.3) |
其中[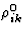 ]张量表示没有磁场时的电阻率;张量[
]张量表示没有磁场时的电阻率;张量[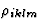 ]描述了由磁场引起的电阻率变化,以及张量[
]描述了由磁场引起的电阻率变化,以及张量[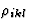 ]和[
]和[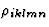 ]参考一阶和二阶霍尔效应。
]参考一阶和二阶霍尔效应。最后应该注意的是,在弹性理论中,二阶效应的系数称为三阶弹性刚度,因为更适合开始讨论非线性应力-变形与能量函数的关系,能量函数的三阶导数提供了主要二阶效应的系数。
7.用矩阵表示法描述物理特性
前面的章节已经表明,晶体的各种物理性质可以用张量来描述。然而,特别是对于高秩张量,大量后缀可能会变得不方便。在许多情况下,引入一种新的符号,即矩阵符号,适合减少后缀的数量。由于固有对称性,表示物理性质的张量的独立分量的数量通常会大幅减少,这可能会鼓励矩阵表示法的引入。
让我们首先考虑一个简单的例子。出于某种目的(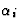 )矩阵由对称的二阶分量构成[
)矩阵由对称的二阶分量构成[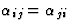 ]张量
]张量
|
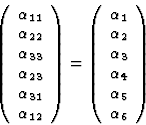 |
(7.1) |
|
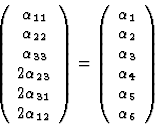 |
(7.2) |
从公式(7.1)和(7.2)可以很容易地看出,在这两种情况下,相同的张量分量与相同的矩阵元素相连,即张量分量的后缀和矩阵项之间的关系是明确的
|
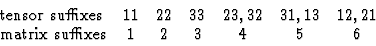 |
(7.3) |
通过引入矩阵表示法,在1、2和3旁边的新后缀现在也可以取值4、5和6的条件下,后缀的数量减少了。虽然张量分量后缀和矩阵元素之间的关系是明确的,但张量分量和矩阵元素的关系定义为乘数。下面给出了几个解释该因素作用的示例。
矩阵表示法的优点在使用三阶和更高阶张量时变得显而易见。在晶体物理中经常出现的一个三阶张量是压电张量,它根据方程描述了晶体上的有效应力与产生的电极化之间的关系
|
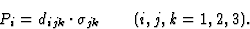 |
(7.4) |
三阶压电张量的分量数为3三=27,这意味着组件可以写在三维立方表中,其中层表示第一个后缀,第二个后缀表示行,第三个后缀表示列。然而,考虑到[d日ijk公司]张量相对于的可换性是对称的k个和j个后缀(见第3段)通过引入新的符号,这些后缀的数量减少了。后缀对jk公司只能根据(7.3)用一个替换。元素(d日在里面)压电矩阵的[d日ijk公司]张量分量如下
|
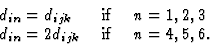 |
(7.5) |
一旦压电矩阵的符号如上文(7.5)所述被接受,并且根据等式(7.1)由应力张量的分量生成矩阵,就可以得到以下矩阵方程
|
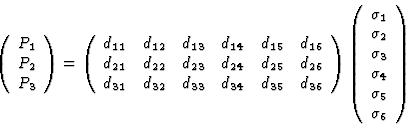 |
(7.6) |
考虑到一个后缀在一个术语中出现两次意味着与这个后缀相加的惯例,(7.6)可以用更紧凑的形式重写
|
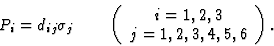 |
(7.7) |
值得注意的是,一些作者在解释n个=压电矩阵的4、5和6个元素。然而,这排除了方程(7.7)中对电极化矢量和机械应力之间关系的紧凑描述。
类似地,代表各种物理性质的其他矩阵可以由不同的作者以不同的方式定义。因此,在尝试使用文献中公布的数值时,应考虑作者使用的各种定义。
最后,为了证明矩阵表示法的优点,让我们研究晶体的弹性。胡克定律在张量符号中采用以下形式
|
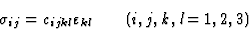 |
(7.8) |
其中[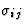 ]表示应力张量和
]表示应力张量和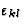 是变形张量的分量。
是变形张量的分量。现在,由于[c(c)国际jkl]张量分别相对于前两个和后两个后缀对称,根据(7.3),可以用一个新后缀分别替换这些后缀。
关于(c(c)锰)矩阵可以由方程定义
|
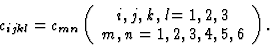 |
(7.9) |
由的组件组成矩阵[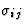 ]根据(7.1)的应力[
]根据(7.1)的应力[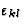 ]根据(7.2)和[c(c)国际jkl]根据(7.9)胡克定律的弹性张量可以用以下矩阵方程描述
]根据(7.2)和[c(c)国际jkl]根据(7.9)胡克定律的弹性张量可以用以下矩阵方程描述
|
 |
(7.10) |
或者,考虑到求和的惯例,采用更紧凑的形式。
|
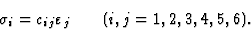 |
(7.11) |
用应力表示应变可以得到方程
|
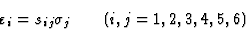 |
(7.12) |
其中(秒ij公司)是矩阵的倒数(c(c)ij公司)这就得出了方程
|
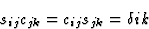 |
(7.13) |
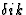 表示克罗内克三角洲。
表示克罗内克三角洲。简单计算表明,上述元素之间(秒锰)矩阵和的组件[秒国际jkl]张量表示[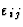 ]应变和[
]应变和[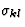 ]分别强调以下对应关系成立
]分别强调以下对应关系成立
|
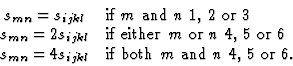 |
(7.14) |
最后需要注意的是,如果使用矩阵表示法,后缀的数量并不代表矩阵元素的转换公式。例如,在坐标变换的情况下,压电矩阵的元素(d日ij公司)与矩阵元素不同的变换(c(c)ij公司)弹性。
8.居里原理
晶体的对称性取决于晶体的状态。如果由于一些外部影响,晶体的状态发生变化,那么晶体的对称性也可能发生变化。晶体给定状态的对称性可以使用居里原理从没有任何外部影响的晶体对称性和外部影响的对称性来确定。
根据居里的观点,当各种自然现象相互叠加形成一个系统时,不对称性被叠加起来,只留下那些元素,这些元素在每一种现象中单独存在。居里所说的不对称是指缺少对称元素的总和。8居里原理本身可以在晶体物理学中表述为:受外部影响的晶体对称群(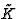 )由晶体对称群的最大公共子群给出,不受影响(K(K))和外部影响的对称群(克)同时考虑这些群的对称元素的相互位置:9
)由晶体对称群的最大公共子群给出,不受影响(K(K))和外部影响的对称群(克)同时考虑这些群的对称元素的相互位置:9
|
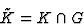 |
(8.1) |
居里原理用另一句话表达:受外部影响的晶体将只显示那些在没有影响和没有影响的晶体中常见的对称元素.5
作为一个例子,让我们研究ADP(磷酸二氢铵)晶体在不同方向电场中的对称性变化。这些晶体的基态对称性为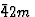 也就是说,它有四个反转轴(其本身也包含两个旋转轴)。四重反转轴位于两个相互垂直的对称平面的相交线上。两个双轴垂直于四倍反转轴,位于45
也就是说,它有四个反转轴(其本身也包含两个旋转轴)。四重反转轴位于两个相互垂直的对称平面的相交线上。两个双轴垂直于四倍反转轴,位于45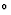 对称平面。图2和图3分别用公理表示法和赤平表示法证明了这一点。电场的对称性为
对称平面。图2和图3分别用公理表示法和赤平表示法证明了这一点。电场的对称性为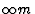 也就是说,它对应于一个圆锥体的对称性,该圆锥体具有一个无限倍的旋转轴,其中包含低对称性的每个可能的旋转轴(也包括两个轴),此外,无限倍旋转轴位于无穷多个镜平面的交线上。
也就是说,它对应于一个圆锥体的对称性,该圆锥体具有一个无限倍的旋转轴,其中包含低对称性的每个可能的旋转轴(也包括两个轴),此外,无限倍旋转轴位于无穷多个镜平面的交线上。
图2:ADP晶体在[001]方向电场中的对称性降低。
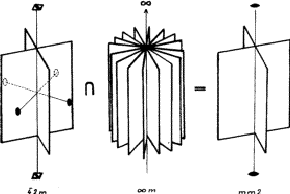 |
图3:ADP晶体在不同方向电场中对称性的变化。
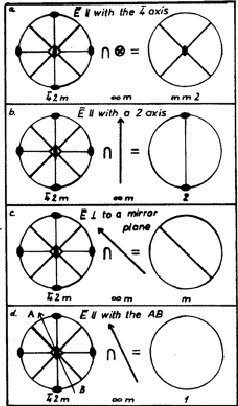 |
首先,让我们研究电场指向[001]方向的情况,这意味着电场的矢量与晶体的四倍反转轴平行。电场的对称元素不包括反转轴,因此根据居里原理,得到的对称元素并不包含该轴。然而,应该注意的是,四重反转轴还包含一个二重旋转轴,这是电场的对称元素,因此,晶体在[001]方向电场中的对称元素也将包含此二重轴。在基本对称元素中,两个镜面也是电场的对称元素,因此它们在晶体中也是守恒的。垂直于镜平面交线的两个旋转轴不属于电场的对称元素,因此它们将消失。总结电场和该场中晶体的常见对称元素,我们有两个相互垂直的镜面,在镜面相交线上有一个双重旋转轴。因此,ADP晶体在[001]方向的电场中的对称性被降低为正交晶系的对称性毫米两点组(图2和3a)。如果电场作用于[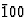 ]方向,即沿垂直于四倍反转轴的两倍旋转轴,晶体的镜面与电场的镜面不一致,导致镜面消失。此外,四重反转轴(连同与反转轴相连的两重旋转轴),以及从另外两个两重轴中消失的一个轴,因为电场只有一个方向的旋转对称性。这样,只有双旋转轴(沿其有效电场)保持守恒,因此晶体的对称性降低到单斜点群2(如图3b所示)。如果电场影响[
]方向,即沿垂直于四倍反转轴的两倍旋转轴,晶体的镜面与电场的镜面不一致,导致镜面消失。此外,四重反转轴(连同与反转轴相连的两重旋转轴),以及从另外两个两重轴中消失的一个轴,因为电场只有一个方向的旋转对称性。这样,只有双旋转轴(沿其有效电场)保持守恒,因此晶体的对称性降低到单斜点群2(如图3b所示)。如果电场影响[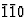 ]方向,即在一个镜像平面中,常见的对称元素将是一个镜像面:晶体对称性被简化为点群米单斜系(图3c)。最后,如果电场指向任意方向[香港特别行政区]方向,与前面讨论的方向不同,晶体的对称元素与电场不一致。因此,不保留对称元素。在这种情况下,晶体的对称性被简化为三斜晶系的平凡点群1(图3d)。
]方向,即在一个镜像平面中,常见的对称元素将是一个镜像面:晶体对称性被简化为点群米单斜系(图3c)。最后,如果电场指向任意方向[香港特别行政区]方向,与前面讨论的方向不同,晶体的对称元素与电场不一致。因此,不保留对称元素。在这种情况下,晶体的对称性被简化为三斜晶系的平凡点群1(图3d)。
从前面可以看出,最初的光学单轴ADP晶体在电场的影响下将表现为光学双轴晶体。
应该指出,居里原理只是对称群叠加大原理的一个特例。然而,对这一主题的详细讨论超出了本文的范围,可以参考舒布尼科夫和科普茨克的著作。10
致谢
作者要感谢M.P.Shaskolskaya教授、N.V.Perelomova博士和M.M.Tagieva博士的有用建议和宝贵讨论。此外,他还感谢同事们阅读了手稿和有用的评论。
工具书类
1.伯斯,R.R。,对称性和磁性,阿姆斯特丹,North-Holland Publishing Company(1964)。
2.巴加万塔姆,S。,晶体对称性和物理性质,伦敦,纽约,学术出版社(1966)。
3.Yu Sirotin。I.和Shaskolskaya,M.P。,晶体物理基础莫斯科,和平号出版社(1982年)。
4.Fumi,F.G。,《水晶学报》. 5 (1952) 44.
5.奈伊,J.F。,晶体的物理性质,牛津,克拉伦登出版社(1957)。
6.史密斯,A.C.,贾纳克,J.F.,阿德勒,R.B。,固体中的电子传导,纽约,McGraw-Hill图书公司(1967年)。
7.Hellwege,K.-H.(编辑),Landolt-Börnstein,《新系列》,第三组,第11卷,柏林,海德堡,纽约,斯普林格-Verlag(1979)。
8.居里。,机动第118页,巴黎,法国体育协会(1908年)。
9.Koptsik,V.A。,苏联。物理学。克里斯特. 2 (1957) 99.
10.Shubnikov,A.V.和Koptsik,V.A。,科学与艺术中的对称,纽约和伦敦,Plenum出版社(1977年)。
11.Shubnikov,A.V.和Belov,N.V。,彩色对称牛津,佩加蒙出版社(1964年)。
12.Juretschke,Hellmut,J。,晶体物理学马萨诸塞州,W.A.Benjamin,Inc.Reading(1974)。
13.Koptsik,V.A.公司。,舒布尼科夫群(俄语),莫斯科,莫斯科大学出版社(1966年)。
14.Opechowski,W.和Guccione,R.,《磁对称性》,G.T.Rado和H.Suhl(编辑),磁性第II/A卷,第105页,纽约,伦敦,学术出版社(1965)。
15.Shuvalov,L.A.(编辑),现代晶体学Ⅳ.晶体的物理性质《施普林格固体科学系列》,第37卷。施普林格-弗拉格,准备中。
16.伍斯特,W.A。,晶体物理性质的张量和群论牛津,克拉伦登出版社(1973)。
17.Perelomova,N.V.和Tagieva,N.M.,《晶体物理问题及其解决方案》,莫斯科,和平号出版社(1983年)。
在每一本被引用的书中都可以找到更多的参考文献。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
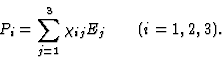
![]()
![]()
![]()
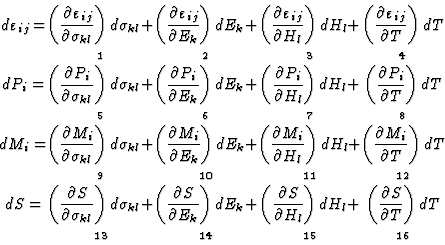
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
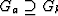
![]()
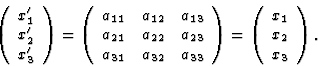
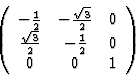
![]()
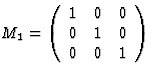
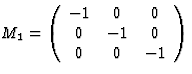
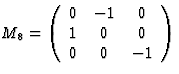
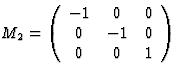
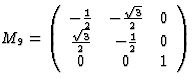
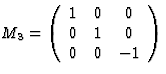
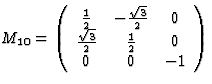
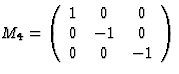
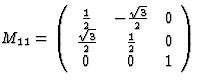
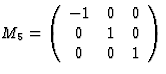
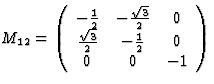
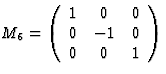
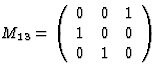
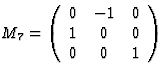
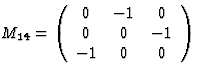
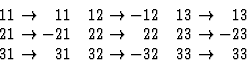
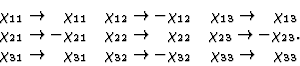
![\开始{displaymath}\left[\begin{array}{ccc}\chi{11}&0&\chi{13}\\0&\ch{22}&0\\chi{31}&0&\chi{33}\end{arrary}\right]\end{displayth}](https://www.iucr.org/education/pamphlets/18/full-text/img153.gif)
![]()
![]()
![]()
![]()
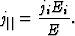
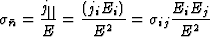
![]()
![]()
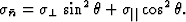
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
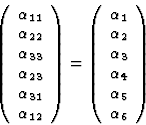
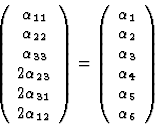
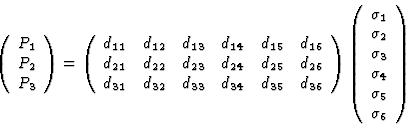

![]()
![]()
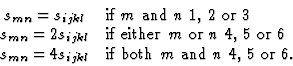
![]()
![]()
![]()
![]()
![]()
![]()