对称
L.S.牙科眼镜
1.简单的对称操作
对称的一般概念几乎为每个人所熟悉。从形式上来说,它可以用各种方式定义。简明牛津词典上写着“1。(美产生于)身体各部分或任何整体之间的适当比例、平衡、和谐、保持。2.这种结构允许物体被一个点、线或平面或辐射线或平面分割成两个或多个在尺寸和形状以及相对于分割点的位置等方面完全相似的部分,完全相似的部分彼此面对或中心重复,…”。
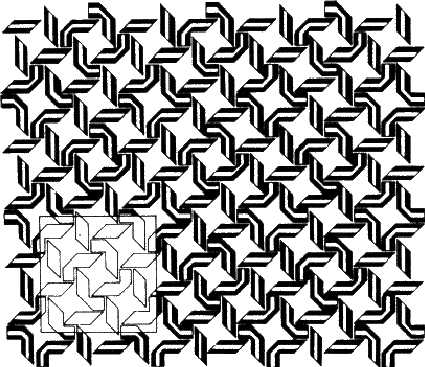
第二个定义是与结晶学关系最密切的,因此与我们有关,但我也包括了第一个定义,因为在我看来,它表达了为什么主题既令人满意又令人愉快。对称性和艺术密不可分,如图1.1所示。然而,图1.1的对称性比第一眼看到的要复杂得多,所以我们将从考虑更简单的东西开始。
图1.1。基于十四世纪波斯瓷砖设计的图案。
 |
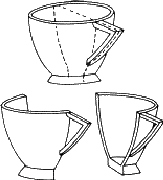
一个茶杯就可以开始了(图1.2)。这是一个可以被平面分成两部分的对象的示例。由于这两个部分是彼此的镜像,这个对称元素被称为镜像平面。在茶杯的一半上操作此元素会生成另一半:如果将半个茶杯的切边靠在镜子上,则整个茶杯的外观将重新生成。在现实生活中,茶杯很少被切成薄片(尽管这是在卡通版的《爱丽丝梦游仙境》中完成的),但你可以用苹果或梨来试试。如果产生的两个相似部分没有保持对称,如茶杯的情况,则称为非对称单元.
图1.2。一个茶杯,显示出其对称的镜面。(摘自L.S.Dent Glasser,《晶体学及其应用》:Van Nostrand Reinhold,1977年)
 |
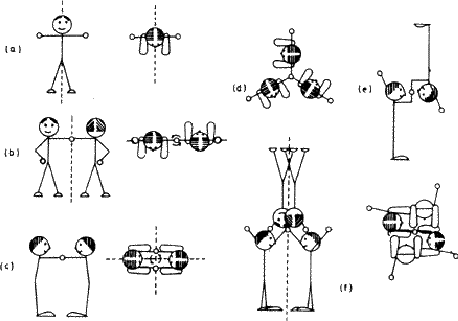
花等生物物体经常表现出对称性。此人-以下简称“其” -如图1.3a所示,也有一个镜面,前提是它竖立在中间,将头发分开(我们忽略了它的内部器官)。这个数字的每一半都是一个不对称的单位。移动手臂或腿会破坏对称性,然后可以将整个图形视为非对称单元。我们将使用这个小人物,无论有没有镜像平面,来进一步说明对称元素,并构建更复杂的群体。
-如图1.3a所示,也有一个镜面,前提是它竖立在中间,将头发分开(我们忽略了它的内部器官)。这个数字的每一半都是一个不对称的单位。移动手臂或腿会破坏对称性,然后可以将整个图形视为非对称单元。我们将使用这个小人物,无论有没有镜像平面,来进一步说明对称元素,并构建更复杂的群体。
如图1.3b所示,如果人像与同卵双胞胎手牵手,则形成的群体不再具有镜面。另一方面,将组旋转180度 围绕一个轴(如图所示)使每个图形与其孪生图形重合。此组具有旋转轴,在这种情况下是双重的,因为在每个图形返回其原始位置之前,必须执行两次操作。图1.3c显示了不同的握手方法如何产生一组将镜平面与双轴结合的物体;在图1.3d中,相同的三元组显示出三重轴。(你能识别图1.1中的四重轴吗?它有任何两重轴或镜像对称吗?)
围绕一个轴(如图所示)使每个图形与其孪生图形重合。此组具有旋转轴,在这种情况下是双重的,因为在每个图形返回其原始位置之前,必须执行两次操作。图1.3c显示了不同的握手方法如何产生一组将镜平面与双轴结合的物体;在图1.3d中,相同的三元组显示出三重轴。(你能识别图1.1中的四重轴吗?它有任何两重轴或镜像对称吗?)
图1.3。一些对称元素,由人形代表。(a) 在立面图和平面图中以虚线显示的镜像平面。(b) 两条旧轴线,沿着立面图中的虚线,垂直穿过平面图中紧握的双手。(c) 双轴与镜面的组合;对称元素的位置仅在平面图中给出。(d) 三倍轴,仅在平面图中显示。(e) 对称中心(紧握双手的中心)。(f) 四重倒置轴,在立面图和平面图中,沿着虚线并穿过紧握的双手的中心。(摘自L.S.Dent Glasser,第19章,水泥化学:学术出版社,1964年。)
 |
孤立对象或对象组可以显示任意数量的镜像平面和任意类型的轴;相同组的无限阵列的对称性,例如在晶体中发现的,由于必须将这些单元在三维中组合在一起而受到限制。这一限制意味着在结晶学中,只会遇到对称中心(图1.3e)、镜像平面、二倍、三倍、四倍和六倍以及相应的反转轴。反转轴包括旋转加上通过点的反转;图1.3f表示四倍反转轴,旋转四分之一圈,然后通过紧握双手中间的一个点反转。一个单反转轴相当于对称中心(图1.3e),一个双反转轴等同于镜像平面。(最后一个等价性在其他情况下很重要,因为它建立了镜像平面作为双重对称算子。)
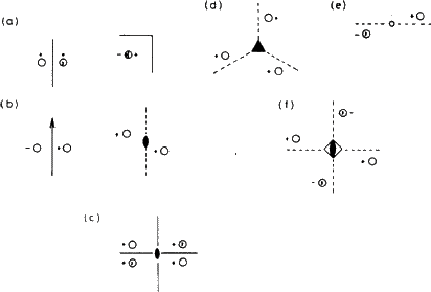
用我们刚刚使用的方式来说明对称元素不是很方便:我们不是画小人物,而是用圆圈来表示不对称单位:传统上,开放的圆圈代表右手单位,镜像中有逗号的圆圈或对映体(即左手装置)。图1.4显示了与图1.3相同的组,以这种正式的速记方式表示。
图1.4。图1.3中的排列使用传统符号重新绘制。此处以不同方向绘制(a)的右侧组,省略(c)和(f)的左侧组。符号+和-表示纸张平面上方和下方的相等距离:开圆圈表示一只手的不对称单位,带逗号的圆圈表示其对映体。(a) 镜像平面(m),垂直于(左侧)和纸张平面。(b) 两倍轴(2)在纸张平面上(左),垂直于纸张平面(右)。(c) 双重轴和镜面的组合。请注意,这些元素中的任何两个都会创建第三个元素。(d) 三个折叠轴(3)。(e) 对称中心(1)。(f) 四倍反转轴( ).
).
 |
即使这样,在书面文本中也很不方便,因为在文字中,镜像平面被赋予了符号米,而轴和相应的反转轴称为 符号1(表示单轴)表示完全没有对称性,而相应的反转轴(
符号1(表示单轴)表示完全没有对称性,而相应的反转轴(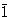 )如前所述,相当于对称中心。
)如前所述,相当于对称中心。
2.有限群中对称元素的组合
孤立对象或对象组显示的完整对称性是点编组,所有对称元素都至少有一个公共点。我们已经在图1.3c和1.4c中遇到了这样一组对称元素,包括两个相交于双轴的镜面。请注意,这些元素中的任何一个都不能被排除在组之外,因为任何两个元素的出现都会创建第三个元素。因此,其中两个元素足以定义整体,而这个特殊的点群通常被赋予短符号毫米,而不是完整的符号2毫米或毫米2
类似地,三个在三重轴上相交的镜面(图2.1a)由3充分表示米.完整符号3毫米不需要,因为“米的是冗余的,由三个轴对另一个轴的作用创建。图2.1b显示了垂直于双重旋转轴的镜面;这是符号2/米,“/”表示“垂直于”。(请注意,该组合在旋转轴与镜面相交的点处产生对称中心。)
图2.1:。对称元素及其点群符号的一些组合。等价物Schoenflies公司符号在括号中给出。
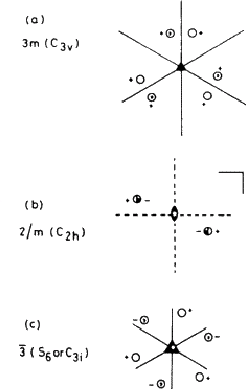 |
这个命名系统是结晶学中最常用的一个系统,它在很大程度上是自解释的,很少有实践可以为任何符号画出适当的对称元素和非对称单元集合。还有一个使用中的旧系统,对我们的目的来说并不方便;图2.1中的示例Schoenflies公司符号在结晶学后面的括号中给出(赫尔曼·莫金)符号:表1给出了两者之间的一致性。一个主要区别是我们称之为反转轴的操作符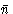 (=n个-折叠旋转加上通过点的反转)被交替轴取代S公司n个(=旋转加上平面反射)Schoenflies公司符号。此外,如图2.1c所示,n个可能发生变化:三重反转轴对应六重交替轴。虽然这可能不方便,但它确实说明了三重对称和六重对称之间的区别有时是一个定义问题,因此是任意的。
(=n个-折叠旋转加上通过点的反转)被交替轴取代S公司n个(=旋转加上平面反射)Schoenflies公司符号。此外,如图2.1c所示,n个可能发生变化:三重反转轴对应六重交替轴。虽然这可能不方便,但它确实说明了三重对称和六重对称之间的区别有时是一个定义问题,因此是任意的。
与有限群有关的晶体对称运算有32种不同的组合,因此有32个点群或晶体类; 晶体通常通过其外部形态的对称性来揭示其所属的类别。这些晶体类别根据其内容物的对称性对单元单元形状的限制(见下一节)方便地分组为系统。表1总结了这一点。
表1:晶体系统和类别(等效Schoenflies公司括号中为后者命名)
| 系统 |
特征对称性 |
单元单元形状 |
晶格类型 |
课程 |
| 三联诊所 |
无 |
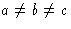 * * |
P(P) |
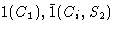 |
| |
|
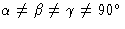 |
|
|
| 单诊所 |
一个双轴(2或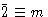 ) ) |
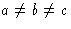 |
P(P),C类(或一) |
$](https://www.iucr.org/education/pamphlets/13/full-text/img15.gif) |
| |
|
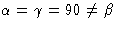 |
|
2/米(C类2小时) |
| 正交晶系 |
三个相互垂直的双轴 |
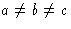 |
P(P),C类, |
222(D类2),毫米2(C类2v(v)) |
| |
|
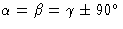 |
(或一或B类) |
毫米(D类2小时) |
| |
|
|
我,F类 |
|
| 正方形 |
一个四倍轴 |
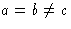 |
P(P),我 |
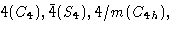 |
| |
|
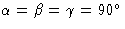 |
|
422(D类4), 4nn个(C类4v(v)) |
| |
|
|
|
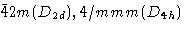 |
| 三角(Trigonal) |
一个三重轴 |
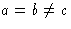 |
P(P)<R(右) |
3(C类三), 3(S公司6,C类三我), 32(D类三) |
| |
|
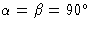 |
三米(C类三v(v)), 3米(D类三d日) |
|
| |
|
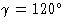 |
|
|
| 六边形 |
一个六倍轴 |
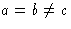 |
P(P) |
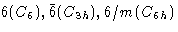 |
| |
|
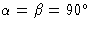 |
|
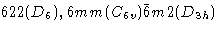 |
| |
|
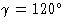 |
|
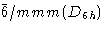 |
| 立方 |
四个三重轴(沿立方体的主体对角线) |
一=b条=c(c) |
P(P),我,F类 |
23(T型),米3(T型小时), 432(O(运行)) |
| |
|
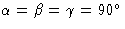 |
|
43米(T型d日),米三米(O(运行)小时) |
*也就是说,没有任何限制。
3.阵列中的对称元素
如果你回头看图1.1,你会发现它将对称元素与重复图案结合在一起。我们称这种重复图案为阵列; 在不改变方向的情况下可以重复生成图案的最小方便平行四边形称为单位电池二维单元如图1.1所示;请注意,虽然原点的选择有点随意,但形状并非如此。(通过确定定义重复单元的其他方式进行检查。)
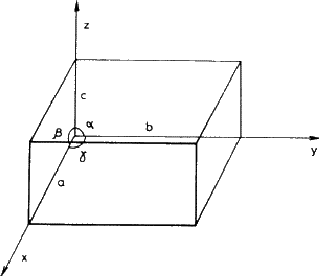
在三维阵列中,如晶体中,单位单元是由截距定义的平行管a、 b、c在三个轴上(x、 y,z)以及它们之间的角度,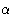 ,
,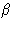 ,
,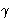 ,如图3.1所示。如果内容没有对称性或只有一个对称中心,则单位细胞可以具有这种非常一般的形状;更对称的单元内容以表1中给出的方式限制轴间角的值和边缘的相对尺寸。因此,双对称的单一方向(单斜系统)使两个角度成直角,但对第三个或边缘尺寸没有限制;在另一个极端,立方对称产生的细胞边缘都相等,角度都是90
,如图3.1所示。如果内容没有对称性或只有一个对称中心,则单位细胞可以具有这种非常一般的形状;更对称的单元内容以表1中给出的方式限制轴间角的值和边缘的相对尺寸。因此,双对称的单一方向(单斜系统)使两个角度成直角,但对第三个或边缘尺寸没有限制;在另一个极端,立方对称产生的细胞边缘都相等,角度都是90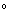 (即立方体!)。
(即立方体!)。
图3.1。通用单位单元,显示重复距离,一,b条,c(c)沿着x个,年和z(z)轴和轴间角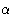 ,
,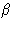 ,
,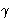 .
.
 |
阵列可以具有我们已经讨论过的任何对称元素,包括完全没有对称性(图3.2),也可以具有有限对象中不可能的其他类型的对称性。考虑图3.3,该图显示了八名船员划船的鸟瞰图;只要他们受过良好的训练,他们就会呈现出对称的外观,但这并不是迄今为止所介绍的任何对称元素都能准确描述的外观。很明显,这与镜面有关,但在图3.3中,每个赛艇运动员都是一条赛艇前后的镜像。任何图形都与下一个图形相关,方法是沿着船移动一个位置,然后通过镜像平面进行反射。这种对称操作称为-非常描述性地-滑翔机由于滑翔面结合了反射和平移的操作,所以它只出现在扩展阵列中。
将旋转和平移相结合的类似操作称为-同样具有描述性-a螺旋轴作为具有这种对称性的物体的一个实际例子,螺栓确实比螺钉好,因为大多数螺钉都会逐渐变细到一个点,但驱动螺钉或使用螺旋钻的动作非常生动地说明了螺旋轴的操作。其他常见的具有螺旋轴的物体有螺旋楼梯、弹簧和一些攀援植物。图3.4显示了正式示例,以及滑翔平面的正式表示。
图3.2。重复图案的阵列:图案和阵列都不包含任何对称元素。
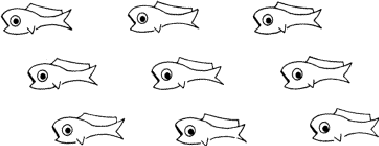 |
图3.3。一张精心训练的“八号”的风格化鸟瞰图,显示了平移对称操作:每个赛艇运动员通过平移和反射的组合与下一个赛艇运动员相关联。
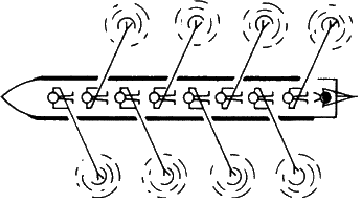 |
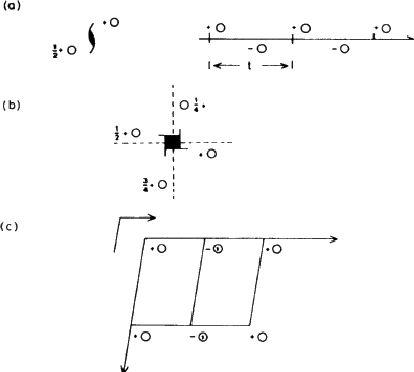
图3.4。平移对称元素。(a) 双螺旋轴,21,垂直于纸张平面(左)和纸张平面(右)显示。每转半圈,都会经过一半的重复距离进行平移。(b) 四倍螺旋轴,41.(c)滑翔机。整个页面从左到右的翻译伴随着纸张平面的反射。
 |
螺旋轴的通用符号为N个n个,其中N个是轴的顺序(2、3、4或6),以及n个/N个以重复单位的分数表示的平移距离。因此,41,如图3.4b所示,表示非对称装置移动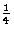 每个轴上的重复单元
每个轴上的重复单元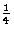 绕着那条轴线旋转。滑翔机由一个表示滑翔方向的字母表示:字母a、 b条和c(c)意味着滑翔方向与a、 b条和c(c)轴,而n个和d日指滑动方向对角穿过单位细胞表面或沿着身体对角线的滑动面。
绕着那条轴线旋转。滑翔机由一个表示滑翔方向的字母表示:字母a、 b条和c(c)意味着滑翔方向与a、 b条和c(c)轴,而n个和d日指滑动方向对角穿过单位细胞表面或沿着身体对角线的滑动面。
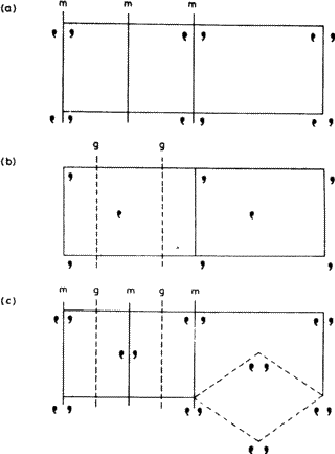
平行平移和非平移对称元素的组合对图案重复的方式产生了有趣的影响。考虑图3.5。3.5a中的图案包含镜像平面:请注意,两个镜像平面与页面上的每个重复单元相关联。3.5b中的图案基于滑翔机相关的类似图案(克); 还有两个与页面上的每个重复单元相关联。在3.5c中,有平行的镜面和滑动面,因此矩形单元中心的图案分组与角落的图案分组相同。这种模式称为居中而3.5a和3.5b被称为原始的。通常可以为居中图案定义较小的原始单元格,例如3.5c右下角概述的菱形单元格。然而,这通常不是这样做的,部分原因是这样的细胞形状不太方便,但更重要的是因为其轴线不再与图案的对称元素具有正确的关系。
图3.5。非平移和平移对称元素及其组合。(a) 镜面,(b)滑动面,(c)平行镜面和滑动面,形成中心图案。虚线勾勒出一个可能的(但不方便的)原始单元格。
 |
4.空间组
正如非平移对称元素可以组合成描述有限群对称性的点群符号一样,无限数组的对称性也可以被总结和符号化。添加翻译大大增加了可能性,因此代替32点组230空间组需要描述无限阵列的对称性。以下是完整的列表及其描述国际X射线晶体学表(见第5节)。这里所要做的就是尝试给出空间群符号的含义以及如何解释它。
典型的空间编组符号包括: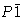 ,C类2/米,伊布卡,
,C类2/米,伊布卡,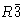 ,Fm公司三米,P(P)212121。您会注意到它们都以大写字母开头。这使得晶格类型,它告诉您单位单元是原始的还是居中的。P(P)表示原始,A、 B,或C类指以垂直于a、 b条或c(c)轴,F类指以所有面为中心,我指身体居中-居中于细胞中央(来自德语,英恩森特里特)-和R(右)指菱形,这是三角系统特有的一种特殊类型的定心。下面的一组符号为您提供了水晶类,从而提供了系统。因此在
,Fm公司三米,P(P)212121。您会注意到它们都以大写字母开头。这使得晶格类型,它告诉您单位单元是原始的还是居中的。P(P)表示原始,A、 B,或C类指以垂直于a、 b条或c(c)轴,F类指以所有面为中心,我指身体居中-居中于细胞中央(来自德语,英恩森特里特)-和R(右)指菱形,这是三角系统特有的一种特殊类型的定心。下面的一组符号为您提供了水晶类,从而提供了系统。因此在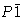 ,符号
,符号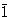 告诉你这个系统是三斜的(见表1)。同样地C类2/米属于2类/米从表1中可以看出,它是单斜的。
告诉你这个系统是三斜的(见表1)。同样地C类2/米属于2类/米从表1中可以看出,它是单斜的。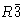 和Fm公司三米同样容易分别指定为三角系和立方系。伊贝卡问题稍微多一些;符号b条,c(c)和一如前一节所述,请参阅滑翔机。要找到晶体类别,只需用等效的非平移元素替换任何平移对称元素:这一规则适用于滑动面和螺旋轴。因此伊布卡属于类毫米,为正交;最后一个例子,P(P)212121,属于222类,也是正交的。符号也给出了各种对称元素的位置。正如毫米意味着镜面垂直于正交系的三个相互垂直的轴,所以伊布卡告诉我们,在以身体为中心的阵列中b条垂直于x个轴,c(c)垂直于年和一垂直于z(z).
和Fm公司三米同样容易分别指定为三角系和立方系。伊贝卡问题稍微多一些;符号b条,c(c)和一如前一节所述,请参阅滑翔机。要找到晶体类别,只需用等效的非平移元素替换任何平移对称元素:这一规则适用于滑动面和螺旋轴。因此伊布卡属于类毫米,为正交;最后一个例子,P(P)212121,属于222类,也是正交的。符号也给出了各种对称元素的位置。正如毫米意味着镜面垂直于正交系的三个相互垂直的轴,所以伊布卡告诉我们,在以身体为中心的阵列中b条垂直于x个轴,c(c)垂直于年和一垂直于z(z).
第页,共页国际餐桌描述Pnma公司如图5.1所示,从中可以看出全部的对称元素集合包括许多未在空间组符号中列出的元素。符号中只给出了基本元素;多余的符号被省略,就像它们来自点编组符号一样。
5.X射线晶体学国际表格,第一卷
国际X射线晶体学表包含大量有关结晶学各个方面的信息,第一卷涉及对称性。除此之外,它还介绍了比此处更详细、更高级的对称性考虑。它还列出了所有空间组的信息,我们现在将考虑这一点。图5.1再现了空间组列表中的一个典型页面,我们将使用它来解释一些重要功能。
图5.1。第一卷第151页,摘自1965年版《X射线晶体学国际表》(经国际晶体学联合会实物许可)。
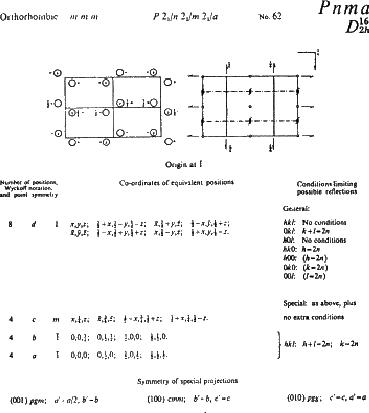 |
空间组符号-Pnma公司-在页面顶部以粗体字给出,以及等效的Schoenflies公司符号。更换平移元件n个和一通过非翻译等价物米给出水晶类毫米,系统正交:此信息也在页面顶部给出。同一行上有:(1)完整符号P(P)21/n个21/米21/一(包括平行于a、 b条和c(c)(2)空间组号,62。空间群以逻辑顺序列出,以增加其晶体类的对称性,从1号开始,P(P)1,它完全没有对称性,以高度对称的立方群结尾国际航空公司三d日,编号230。
在这条顶线的正下方是两张图,分别以不对称单位(左侧)和对称元素集合(右侧)表示空间组。它们被投影到页面下方z(z)轴,使用年轴从左到右水平穿过页面和x个轴向下。空间组符号告诉我们有一个n个-垂直于x个轴,垂直于年轴和一-垂直于z(z)轴(即平行于纸张平面);这些线在右手图上分别显示为点灰线、粗实线和带箭头的直角线。(箭头表示滑翔的方向一; 小人物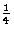 表示滑翔机c(c)/图平面上方4。)冗余的双螺旋轴也出现了,并创建了一些对称中心。
表示滑翔机c(c)/图平面上方4。)冗余的双螺旋轴也出现了,并创建了一些对称中心。
这些对称操作的效果可以在左图中找到。镜面的效果特别容易看到(请参阅图1.4)。在你找到这个之后,看看滑翔面和螺旋轴的影响;图5.2中给出了一个键。所有反射面成组出现,由半个单元边缘隔开;它们在这里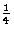 和
和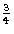 因为原点选择在对称中心(这具有计算优势)。
因为原点选择在对称中心(这具有计算优势)。
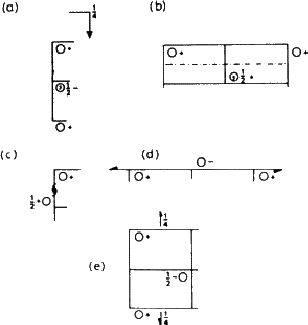
图5.2:。由中一些对称元素的运算生成的等价群Pnma].(a)一个一-滑动平面平行于纸张平面。该组在图中向下移动一/2,然后反射。(b) 安n个-垂直于同一组移动b条/右侧2个c(c)/2在反射前垂直放置。(c) 、(d)、(e)螺旋轴移动组一/2,b条/2和c(c)/2个,同时旋转180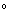 .
.
 |
此处我们关注的页面的其余功能是等效位置的坐标列表。随机放置在单元格中的非对称组(位于x、 y,z例如,由左图左上角的“+”处的开圆表示的位置)必须与其他七组匹配,总共八组。应用于晶体结构,这意味着发生在这种晶体结构中的原子一般立场必须是单元单元中总共八个类似原子中的一个;这对确定化学公式很有帮助。在表中,首先列出了与该一般位置相对应的坐标:8是等效位置的数量,d日是一个简单的字母,作为引用集合的方便方式,1表示站点没有对称性。
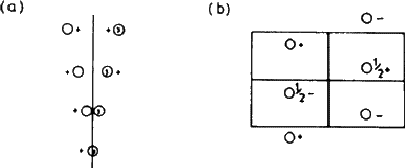
图5.3。特殊位置上的群或原子。(a) 将非对称群移动到镜像平面上的效果;它不再通过镜子产生一个等价的群,但它现在必须拥有一个对称的镜面。(b) 如果一个原子被放置在特殊位置c(c)在里面Pnma公司细胞中必须还有三个类似的原子,如图所示排列(而不是一般情况下的七个)。
 |
假设现在该组从x、 y,z到x个,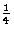 ,z(z)-也就是说,在镜面上(图5.3)。这使其与镜像相一致,并将组数减少到四个。这种情况在第4行开始处进行了总结c(c)...; 现在场地的对称性米,并且只有四个等效位置,而不是八个。剩下的两条线显示了在一个或另一个对称中心上选择位置的效果。我们在此不使用页面上的其余信息。
,z(z)-也就是说,在镜面上(图5.3)。这使其与镜像相一致,并将组数减少到四个。这种情况在第4行开始处进行了总结c(c)...; 现在场地的对称性米,并且只有四个等效位置,而不是八个。剩下的两条线显示了在一个或另一个对称中心上选择位置的效果。我们在此不使用页面上的其余信息。
最后一段对这种对称信息的一种实际应用进行了非常简短的说明。假设金属硫酸盐,MSO4,在这个空间组中结晶,每个细胞有四个公式单位。四个人M(M)和S公司原子必须位于其中一个位置,a、 b条或c(c); 硫原子形成硫酸盐基团的一部分。SO公司4群是四面体,四面体没有对称中心,但做有镜面:因此硫原子必须占据位置c(c),在镜面上(也必须有两个氧原子附着在上面)。将此信息与债券长度知识相结合,应能制定出试验结构。
- …“它”
- 这样就避免了任何性别歧视!
![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()