100篇关于震级的论文
Tom Leinster发布
里程碑!据我统计,现在有100篇论文量级,包括几个共有73位作者发表论文。你可以在量级参考文献.
在这里,我将快速做两件事:告诉你当前的一些热点那么,更重要的是-描述世界上几个尚未得到应有关注的地区有,那里甚至可能有一些低垂的水果。
发布时间:UTC下午11:04|永久链接|发表评论
3d旋转和7d叉积(第2部分)
John Baez发布
关于Mathstodon保罗·施瓦恩提出了一个与八元数有关的有趣问题。我们能显式地描述保持7d叉积的7d空间?
我在这里解释了这个问题:
这引发了一场激烈的对话,其中包括Layra Idarani、Greg Egan和Paul Schwahn本人。结果是一个令人震惊的新公式的7d交叉产品方面的三维交叉产品。
让我总结一下。
发布时间:UTC上午10:23|永久链接|后续行动(23)
镧系元素与例外李群G2
John Baez发布
这个镧系元素这14个元素是由它们的电子一个接一个地填满所谓的f子壳。它们在这里:
镧、铈、镨、钕、丙、钐、铕、钆、铽、镝、钬、铒、铥、镱。
它们也被称为“稀土',但该术语通常也适用于另外3个元素。为什么?这本身就是一个迷人的谜。但现在对我来说重要的是另一件事:镧系元素和特殊的Lie群G之间的明显联系2!
唉,这种联系对我来说仍然非常神秘,所以我恳求你的帮助。
发布于UTC晚上10:15|永久链接|后续行动(9)
野生结极难分类
John Baez发布
在现实世界中,绳结中的绳子有一些非零厚度。在数学中,结是由无限薄的物质组成的。这使得数学结可以以无限复杂的方式打结——这种方式对于非零厚度的结来说是不可能的!这些被称为“野生”结。
看看这个疯狂的结亨利·塞格曼的视频只有一个点需要零厚度。所以我们说它在一点上是野生的。但有些结在许多点上都很疯狂。
甚至还有疯狂的绳结每一个点!为了构建这些,你需要在越来越多的地方递归地放入野性,直到永远。我想看到这样一个到处都是野结的好照片。我还没见过。
野生结极难分类。这不仅仅是一种感觉,而是一个定理。瓦迪姆·库利科夫(Vadim Kulikov)表明,野结比任何一种可以用一阶经典逻辑和可数符号描述的可数结构更难分类!
粗略地说,这意味着野结是如此复杂,以至于我们无法用我们能写下来的任何东西对它们进行分类。这使它们与“驯服”的结有很大不同:即不野生的结。是的,驯服的结很难分类,但离得远那个很难。
发布于UTC下午12:23|永久链接|后续行动(5)
3d旋转和7d叉积(第1部分)
John Baez发布
有一个三维向量的点积和叉积。但还有一个点积和十字积在7个维度上遵循许多相同的恒等式!在其他维度中,没有什么真正像这样。
以下内容是众所周知的:保留点和叉积称为。它由旋转组成。我们说在上具有“不可约表示”因为不存在的线性子空间通过中的每个转换映射到自身,除了和整个空间。
呵呵。但有件事更令人惊讶:似乎在上也有不可约表示其中每个变换都在7维中保留点积和叉积!
那是对的,没有错别字。有不的不可约表示在它保留了点积和叉积。保存点积很容易。但7维的叉积是一个奇怪的东西,它打破了旋转对称性。
那里是显然,这是一个小得多的群体的不可约表示在这样可以保留点和叉积。但我之所以知道这一点,是因为人们说丹金证明了这一点!更严格地说,Dynkin似乎说的子组其中的不可约表示在仅限于此子组时保持不可约。我想明确地看到一个。
发布时间:UTC下午4:36|永久链接|随访(39)
复杂圆环上的线束(第五部分)
John Baez发布
这个艾森斯坦整数 是表单的复数哪里和是整数和它们构成复数的子环和格:
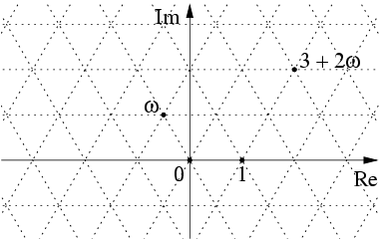
上次我解释了空间属于赫密特矩阵秘密地是四维闵可夫斯基时空,而其子集
是三维双曲空间。因此属于带有Eisenstein整数项的hermitian矩阵在Minkowski时空中形成了一个格,我推测正是由六角形瓷砖蜂窝-Coxeter发现的双曲线空间中的高度对称结构,如下所示:

现在,格雷格·伊根和我将证明这个猜想。
发布时间:UTC上午10:40|永久链接|后续行动(2)
复杂圆环上的线束(第四部分)
John Baez发布
上次我引入了一个二维复数变体,称为艾森斯坦曲面
哪里是的格子艾森斯坦整数。我们制定了Néron–Severi集团 这个曲面的:也就是说,这个曲面上全纯线丛的一组等价类,如果它们同构为拓扑的线束。我们得到了一个很好的答案:
哪里包括以Eisenstein整数为项的hermitian矩阵。
现在,我们将了解这与“六角形瓷砖蜂窝”的关系:

我们将在这张图片中看到艾森斯坦表面的所谓“主极化”和六边形中心之间的显式双射!我们不会证明它有效,我希望稍后再这样做。但我们会做好一切准备。
复杂圆环上的线束(第三部分)
John Baez发布
你认为这个系列已经过时了。但它只是处于休眠状态!
在第1部分,我解释了复杂环面上全纯线束的分类分成两部分:
在第2部分,我解释了复圆环的对偶性,它是复向量空间对偶性的派生。我用这句话具体描述了Néron–Severi团队.
但对我来说,有趣的是这些例子。今天,让我们实际计算一个Néron–Severi组,并开始看看它是如何导致罗伊斯·纳尔逊(Roice Nelson)的这幅非凡画面的:

这是与詹姆斯·多兰的合作。
发布时间:UTC上午11:31|永久链接|后续行动(3)
从肯特继续
由David Corfield发布
约翰真的是在十七年前打破了新闻在这个博客上,我终于找到了一份永久的学术工作?这是一个漫长的等待——我在获得博士学位后签订了十二年的临时合同。
现在我决定离开肯特大学。该大学正面临财政困难,已下令削减包括哲学在内的一些课程。无论他们的计划多么明智,我在这里的时间都将在今年7月结束。
接下来呢?我现在退休有点早。如果有人有什么建议,我很高兴听到。
我们在我加入肯特大学的前一年开始写这个博客。为了帮助思考问题,在接下来的几周里,我想我应该重新审视一下这些年来这里发展起来的一些主题,看看它们是如何演变的:
- 高等几何:对埃朗格程序进行分类
- 范畴理论与机器学习相结合
- 二元性
- 分类逻辑
- 范畴理论在哲学中的应用
- 通过历史发展理解(数学和科学)理论变化的合理性
发布时间:UTC上午9:45|永久链接|后续行动(11)
作为集的双射的模性定理
John Baez发布
来宾发帖人布鲁斯·巴特利特
约翰在计算椭圆曲线上的点方面做了一些很棒的文章(第1部分,第2部分,第3部分). 所以我想我应该抓住这个机会,把我对椭圆曲线的模块性定理的理解提升到这里,它将椭圆曲线定义为集合之间的显式双射。据我所知,文献中并没有以这种形式确切地阐述这一点。有一些方面我不理解(显性同系);也许有人可以帮忙。
发布时间:UTC下午4:06|永久链接|后续行动(11)
五次曲线、二十面体和椭圆曲线
John Baez发布
这里的老一辈人会记得布鲁斯·巴特利特和乌斯·施赖伯经常谈论2-向量空间之类的东西的日子。后来,我喜欢与布鲁斯和格雷格·伊根就五面体和二十面体进行对话。现在,布鲁斯发表了一篇很棒的文章,将这些主题与椭圆曲线联系起来!
这是一本解释性的书,读起来很有趣。
发布于UTC上午10:31|永久链接|后续行动(2)
勾股三元组与射影线
John Baez发布
毕达哥拉斯式三元组可能看起来很可爱,但它们与代数中的一些重要思想有关。要开始看到这一点,请注意缩放任何毕达哥拉斯三元组给出单位圆上具有有理坐标的点:
相反,单位圆上任何具有有理坐标的点都可以放大以得到毕达哥拉斯三元组。
现在,如果你是拓扑学家或微分几何家,你就会知道单位圆与真实的射影线同构作为拓扑空间,作为光滑流形。你甚至可能知道它们作为真正的代数变体是同构的。但你可能从未想过理性的单位圆上的坐标形成同构于理性的射影线.
这是真的!从那以后是再加上一个无穷大点,这意味着有一种方法可以将有理数转化为毕达哥拉斯三元组。显式地解决这个问题,这提供了一个很好的显式方法来获得所有毕达哥拉斯三元组。另一个好处是,我们看到具有有理坐标的点是稠密的在单位圆中。
发布时间:UTC上午9:52|永久链接|后续行动(3)
半简单类型,第二部分:主要结果
Mike Shulman发布
(由Astra Kolomatskaia和Mike Shulman联合撰写)
这是我们论文的三篇系列说明文章的第二部分显示类型理论与半简单类型在这一部分中,我们介绍了本文的主要结果。
发布时间:UTC凌晨2:41|永久链接|后续行动(2)
类别理论者的机器学习工作
John Baez发布
前特斯拉工程师乔治摩根创办了一家名为Symbolica公司利用范畴理论改进机器学习。
当马斯克和他的人工智能主管安德烈·卡佩西(Andrej Karpathy)不听摩根(Morgan)的担忧,即当前的深度学习技术无法“扩展到无限并解决所有问题”时,摩根离开了特斯拉(Tesla),创办了Symbolica。亿万富翁维诺德·科斯拉(Vinod Khosla)给了他200万美元,以证明类别理论的想法可能有所帮助。
科斯拉后来说:“他说得很可信。所以我们说,‘去雇佣范畴理论领域最优秀的人。’”他说,虽然他仍然相信OpenAI在构建大型语言模型方面的持续成功,但他对摩根的想法“相对乐观”,这将是一个“重大贡献”如果它按预期工作,则发送给AI。所以他又投资了3000万美元。
发布时间:UTC下午4:29|永久链接|后续行动(7)
为什么数学很无聊
John Baez发布
我正在写一篇短文,其中有一些关于如何写数学论文的想法,标题颇具挑衅性。它很快就要到期了,所以如果你对这份草稿有任何想法,我希望很快能听到!
发布于UTC晚上10:21|永久链接|后续行动(36)



















