Tanya Khovanova的数学博客

2022年12月，我写了一篇博文Uncrossed Knight’s Tours，介绍了德里克·基斯曼（Derek Kisman）在计算最大的非交叉骑士在大小为M-N的矩形棋盘上的巡游时取得的惊人成就，其中M很小，N可以非常非常大。

数据显示出一些渐近周期性，我想知道如何从数学上证明它。我没有意识到德里克已经证明了这一点。由于我对编程一无所知，我认为程序只是输出了数据，而且不认为它们能证明任何东西。我错了。似乎不需要其他证据。德里克试图用动态编程的术语向我解释细节，但我不确定能否在这里重现。

让我们回忆一下这个问题。考虑一个M-by-N棋盘和一个按照标准国际象棋规则移动的骑士：在一个方向跳一个方块，在正交方向跳两个方块。骑士必须访问尽可能多的方块，不重复，然后返回其起始方块。此外，骑士可能永远不会穿越自己的道路。如果你想象骑士的路径由连接其访问的方块中心的直线段组成，这些线段必须形成一个简单的多边形。总之，给定M和N，我们要计算最长的非交叉骑士的巡游长度。

需要明确的是：这些程序、它们的输出数据、经验证的答案和图像都是由德里克·基斯曼（Derek Kisman）提供的。我只是一个谦逊的信使，展示了我对计算证明力量的新认识。

图中显示了德里克的3乘13棋盘解决方案。有一个由虚线标记的3×4重复图案。同样的巡演适用于长度为10、11和12的木板。因此，对于宽度为3、长度为10至13（含）的棋盘，最长的无交叉骑士巡游长度为10。我们可以用索引N将3×N棋盘的答案写为一个序列，其中-1表示不可能进行巡演。序列以N=1:-1、-1、-1，4、6、6、6,6、6,10、10,10、10、10,14、……开始…。

我们可以在不编程的情况下证明这个序列是正确的。假设巡更从最左边的列开始。如果我们从列的中间开始，整个行程将以菱形和长度为4的行程结束，顺便说一下，这是N=5时最长的行程。因此，对于较大的N，我们必须从一个角开始。从那里，只有两种可能的行动。我们可以看到，延拓是唯一的，并且，渐近地，我们每增加一列就获得一步。也就是说，渐近地，最长巡更的长度除以N是1。

德里克在下面的顺序中使用了一个额外的符号：每个循环都在括号中。任何两个连续循环的差值都是相同的常数。所以要无限期地继续这个序列，只需知道前两个循环就足够了。

闭路：3xN（渐近线1）：-1，-1，-1…

我继续使用Derek计算的其他示例：

闭路：4xN（渐近线2）：-1、-1、-1，[4]、[6]…

闭路：5xN（渐近线2 3/5）：-1，-1，4，6，[8，12，14，18，20，22，24，28，30，34]，[34，38，40，44，46，48，50，54，56，60]…

闭路：6xN（渐近线4）：-1，-1，6，8，12，12，18，22，24，28，32，36，[38]，[42]…

封闭游览：7xN（渐近线4 10/33）：-1，-1，6，10，14，18，24，26，32，36，42，44，48，54，58，62，66，72，74，80，84，88，94，98，100，106，112，114，118，124，128，130，[136，140，144，148，154，158，162，166，170，176，180，184，188，192，196，200，204，210，214，218，222，226，232，236，240，244，248，254，256，260，266270274]， [278, 282, 286, 290, 296, 300, 304, 308, 312, 318, 322, 326, 330, 334, 338, 342, 346, 352, 356, 360, 364, 368, 374, 378, 382, 386, 390, 396, 398, 402, 408, 412, 416], …

闭路：8xN（渐近线6）：-1，-1，6，12，18，22，26，32，36，42，46，52，58，[64，70，76，80，88，92]，[100，106，112，116，124，128]…

闭路：9xN（渐近线6 6/29）：-1，-1，6，14，20，24，32，36，42，50，56，60，68，74，80，86，94，98，106，114，118，126，132，136， [144, 150, 156, 162, 168, 174, 180, 186, 192, 200, 206, 212, 218, 224, 230, 236, 242, 250, 254, 262, 268, 274, 280, 286, 292, 300, 304, 312, 318, 324, 330, 336, 342, 348, 354, 360, 366, 372, 378, 386, 392, 398, 404, 410, 416, 422, 428, 436, 440, 448, 454, 460, 466, 474, 478, 486, 492, 498], [504, 510, 516, 522, 528, 534, 540, 546, 552, 560, 566, 572, 578, 584, 590, 596, 602, 610, 614, 622, 628, 634, 640, 646, 652, 660, 664, 672, 678, 684, 690, 696, 702, 708, 714, 720, 726, 732, 738, 746, 752, 758, 764, 770, 776, 782, 788, 796, 800, 808, 814, 820, 826, 834, 838, 846, 852, 858], …

闭合巡视：10xN（渐近线8）：-1，-1，10，16，22，28，36，42，50，54，64，70，78，84，92，100，[106]，[114]，…我没有这个案例的图像。

您可能已经注意到，对于偶数M，渐近线等于M-2。奇数M的渐近线略大于M-1的渐近线上。

德里克还计算了开放时间最长的骑士之旅：骑士不必回到起始位置的旅行。

开放巡视：2xN（渐近线1/2）：-1，-1，[2，2]，[3，3]…

开放巡视：3xN（渐近线1）：-1，2，3，5，6，7，[9]，[10]…

开放巡视：4xN（渐近线2）：-1、2、5、[6]、[8]、…

开放游览：5xN（渐近线3）：-1、3、6、8、11、15、17、20、23、26、29、[32、35、38、41、44、46]、[50、53、56、59、62、64]…

开放游览：6xN（渐近线4）：-1、3、7、10、15、18、22、26、30、33、[36]、[40]、…

开放线路：7xN（渐近线5）：-1、4、9、12、17、22、25、31、36、[40]、[45]、…

开放线路：8xN（渐近线6）：-1、4、10、14、20、26、31、36、43、48、54、60、[64]、[70]、…

开放巡视：9xN开放（渐近线7）：-1、5、11、16、23、30、36、43、48、56、62、68、75、[82、88、94]、[103、109、115]……我没有这个案例的图像。

本文中有许多有趣的新序列，它们的计算非常重要。我希望有人将它们添加到OEIS数据库中。

2018年国际大学生编程竞赛（ICPC）有一个非常困难的问题，这是数学家感兴趣的。这个问题是由超级指挥官德里克·基斯曼提出的。问题是这样的参加比赛.

问题J.无交叉骑士之旅。一个著名的谜题是使用骑士“巡游”8×8棋盘上的所有方块，骑士是一块只能在一个方向上跳跃一个方块，在正交方向上跳跃两个方块的棋子。骑士必须访问棋盘的每一个方格，不得重复，然后返回其起始方格。有很多方法可以做到这一点，棋盘的大小是可控的，所以这是一个人类可以解决的合理难题。

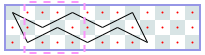
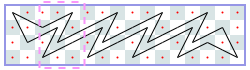
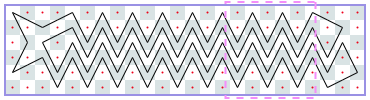
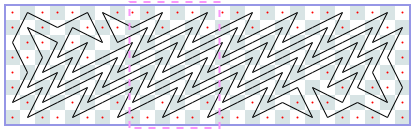
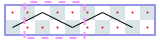
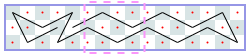
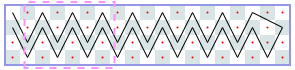
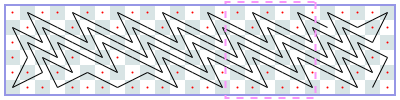
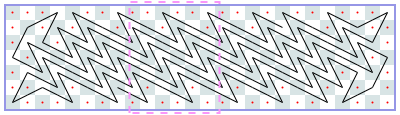
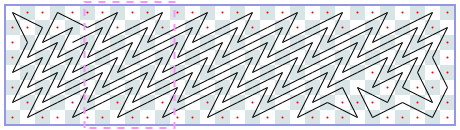
然而，你可以使用电脑，并且有一些编码技能！因此，我们将在矩形m×n棋盘上为您提供此问题的更难版本，并附加一个约束条件：骑士可能永远不会穿越自己的路径。如果你想象它的路径由直线段组成，这些直线段连接着它所跳跃的方块的中心，那么这些线段必须形成一个简单的多边形；也就是说，没有两个线段相交或接触，除非连续的线段在它们的公共端点接触。这个限制使得不可能访问每个方块，因此您必须最大化骑士访问的方块数。我们保留骑士必须返回起始方格的限制。图J.1显示了第一个样本输入的最佳解决方案，即6×6电路板。

输入由包含两个整数m（1≤m≤8）和n（1≤n≤10）的单行组成¹⁵)，给出矩形棋盘的尺寸。

数学家对标准的8×8棋盘上的骑士之旅了解很多。但这个难题中的一个极限是如此巨大，以至于这个计算难题的答案构成了一个新的数学发现。不出所料，在比赛中没有人解决这个难题。写得很好的解决方案摘要可在ICPC网站上找到。解决方案需要动态编程，并认识到旅游必须有重复的模式。

由于比赛期间没有人解决这个问题，除了解决方案总结外，德里克在网上发布了他的创新代码下面的两张图（由德里克·基斯曼提供）显示了他对6×24棋盘上最长的封闭巡演和6×26棋盘上的最长开放巡演的回答。

德里克读了我的博客帖子后，对无交叉骑士之旅产生了兴趣，2014年莫斯科数学节在那里，我向七年级学生提出了在该节上给出的以下问题。

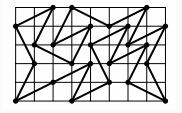
问题。在一个5×8的矩形内，Bart绘制了沿着1×2矩形对角线的闭合路径。找到尽可能长的路径。

2014年数学节组织者为16条对角线上方的每条对角线额外加分。有趣的是，组织者混淆了试图找到17条对角线是没有用的，因为对角线的数量必须是均匀的。下面显示的官方解决方案有24条对角线。

在解决方案手册中，组织者提到他们不知道自己问题的最佳答案。他们希望尽可能长的路径符合他们的官方解决方案。

在德里克的符号中，上述问题相当于在6×9网格上找到最大的非交叉骑士的闭合巡游。德里克证明，实际上，24是最大巡游。在证明这一点的同时，他还计算了无数其他董事会的答案。

我们可以走得更远：超越数亿。让我们考虑在m×n板上发生了什么，其中m是固定的，n是天文大的。假设f_米（n） 是m×n板和g板上非交叉骑士封闭巡游的最大尺寸_米（n） 是非交叉开放式巡回赛中规模最大的一次。

答案到处都有重复的模式，除了在黑板的两端。我们预计可能的重复模式数量是有限的。此外，对于大型板，只有最密集的图案才会出现。这意味着渐近地，函数f和g都是n的线性函数。此外，由于每个模式都是周期性的，所以长板末端的行为也应该成为周期性的。因此，固定m的f和g的差函数最终将变为周期函数。（这里是f的差分函数，我表示D（f_米)定义如下：D（f_米)（n） =英尺_米（n+1）–f_米（n） .）

这意味着我们可以解决更困难的问题。我们不需要n的极限。对于给定的m和任意n，应该可以计算这些函数（即使n远大于千兆）。我在这里过于乐观了。首先，我们需要一些数学理论来找到周期行为开始的边界，并估计周期的大小。假设我们可以证明对于D（f₆)（n） ，最终周期必须在n达到A之前开始，并且最终周期的长度不超过B。然后，我们需要计算函数f的A+2B值₆（n） 知道任意n的函数。

德里克实际上计算了函数f_米（n） 和g_米（n） 对于m到9和n到无穷大。更准确地说，他发现了我上面描述的循环。多么了不起的成就！

我的儿子阿列克谢·拉杜尔失业了。在寻找新工作时，他写了几篇关于编程思想的文章。我是一个自豪而快乐的母亲。虽然我不能理解他的代码，但我理解他的尖端文章。以下是他迄今为止发表的四篇文章的链接。他也是一位出色的作家。你不必相信我的话。每个环节都附有文章的开头。

• 数字福克斯成功的狐狸所知道的一定比刺猬所知道的总和还要多，因为它必须知道事物之间的联系。这一事实是设计用于解决某些问题的计算机系统的关键。阅读更多信息
• 自动微分简介自动微分可能是你从未听说过的最好的科学计算技术之一。如果你同时使用计算机和实数，我认为你至少会从对AD的基本理解中受益，我希望本文能提供这一点；阅读更多信息
• 论编译人员的聪明“足够聪明的编译器”已经成为Lisp社区中的一个比喻：一个神话般的野兽，它承诺语言和界面设计者几乎无限的自由，并让他们的输出因其外观而陷入性能困境。几年前，我还年轻，参加了一个研究项目，建造了一个这样的东西。忽略了大量的星号、脚注和警告，我们最终做出了一些本质上令人印象深刻的东西：你为编译时资源中的抽象边界付费，但它们最终在运行时是免费的。一个原型最近刚刚开源，所以现在是谈论它的好时机。阅读更多信息
• 编译器的聪明2：如何这个编译器的聪明这篇文章用广义的、哲学的笔触描述了过度激进的编译游戏的名称。在这里，我想详细介绍一下Mandelbrot示例，以便感兴趣的读者可以看到一种特定的方法来实际完成该级别的优化。阅读更多信息

共享：

我最喜欢的帽子拼图是由康斯坦丁·诺普和亚历山大·沙波瓦洛夫发明的。它于2013年3月在城镇锦标赛:

一位苏丹决定对他的100位圣人进行测试。先哲们会一个接一个地排成一行，这样最后一个人就能看到其他人。苏丹有101顶帽子，每顶帽子都有不同的颜色，圣人知道所有的颜色。苏丹把所有的帽子都戴在圣人头上，只有一顶没有戴。圣人只能看到他们面前人们帽子的颜色。然后，按照他们想要的任何顺序，每个智者都会猜测自己头上帽子的颜色。每个人都能听到之前所有的猜测，但除此之外，圣人无法说话。他们不允许重复已经宣布的颜色。每个猜错颜色的人都会被砍下脑袋。猜对的人就可以自由了。测试规则在测试前一天发给他们，届时他们有机会就一项策略达成一致，该策略将最大限度地减少测试期间死亡的人数。这个战略应该是什么？

我非常喜欢它，所以我写了一篇关于它的论文。你可以在那里找到解决方案。共享：

有一个数组包含从1到的所有整数n个以某种顺序，除了缺少一个整数。建议一个有效的算法来查找缺失的数字。

当我开车送他离开机场时，一位朋友向我提出了上述问题。他刚刚参加了一次面试，面试中他们给了他两个问题。这个问题可以在线性时间和常数空间中求解。

但我的朋友对下一个问题感到非常兴奋：

有一个数组包含从1到的所有整数n个按照一定的顺序，除了一个整数缺失，另一个整数重复。建议一个有效的算法来找到这两个数字。

我的朋友发现了一种算法，它也适用于线性时间和恒定空间。然而，面试官并不知道这个解决方案。面试官希望算法能在n个日志n个时间。

该公司声称，他们正在寻找世界上最聪明的人，我的朋友为他们提供了一个令人印象深刻的解决方案。尽管他很兴奋，我还是预测他们不会雇佣他。猜猜谁是对的？

我这样反应是因为我自己的故事。许多年前，我在一家公司面试，该公司也需要世界上最聪明的人。在采访中，那家伙给了我一张问题清单，但他说他并不指望我能解决所有的问题，只有几个。这些问题太难了，他想和我坐在一起读，以确保我理解它们。

问题是奥运会风格，这是我的专长。当我们在读的时候，我解出了一半。在接下来的一个小时里，我解决了剩下的问题。面试官大吃一惊。他告诉我，他和他的同事们一直在努力解决一个长期以来无法解决的问题。他让我试试。我也解决了这个问题。你猜怎么着？我没有被录用。因此，我对朋友采访的反应。

好消息是：我仍然记得他们无法解决的问题：

一辆汽车在一条有几个加油站的环形道路上。加油站的汽油不足，加油站和车内的总可用汽油量正好足以让汽车绕马路行驶一圈。道路上真的有一个地方可以让汽车开始行驶，在每个加油站停下来加油，这样汽车就可以完成一整圈而不会耗尽汽油吗？假设汽车油箱足够大，不会出现限制。

共享：

Sid Dhawan是我们RSI 2011数学系的学生之一。他在扎卡里·阿贝尔.

如果没有一个子集可以远离其余的多边形，那么一组多边形是互锁的。众所周知，由四个或更少的正方形构成的多边形不会互锁。达万和他的导师的项目是研究大型多民族的相互联系。他们完全做到了。

他们很快证明了你可以用八个或更多的正方形来连锁波利米诺。然后他们证明了五角大楼不能连锁。这给他们留下了一个灰色区域：六个或七个正方形的波利米诺会发生什么？在绘制了许多美丽的图片后，他们终于找到了我们所附图片中呈现的结构。该系统由12个六边形和5个五边形组成，并且是刚性的。你不能移动任何东西。这意味着六边形可以相互交错，从而解决了灰色区域。

你可以在他们的论文中找到证据和细节“连锁多民族的复杂性”正如你可以通过标题猜到的那样，本文还讨论了复杂性。作者证明，确定一个包含六边形或较大多边形的系统的互锁性是很难的。共享：

几年前，我的儿子谢尔盖发明了以下游戏。两个人，爱丽丝和鲍勃，在一个数字上意见一致，比如说，四。爱丽丝拿起一个干净的魔方，偷偷地做了四个动作。Bob得到了生成的立方体，必须在不超过四步的时间内将其旋转到初始状态。鲍勃不需要追溯爱丽丝的动作。他只需要找到一条返回的捷径，最好是最短的。如果他成功了，他就得了一分，然后轮到爱丽丝了。

如果他们有解决魔方的经验，他们可以增加难度，用五到六个动作玩这个游戏。

顺便问一下，如果你知道最佳方法，你需要多少步才能解出魔方上的任何位置？这个立方体太复杂了，人们不可能总是知道最佳的方法。他们认为上帝可以，所以他们把所有可能的魔方位置集的直径称为上帝的数字。最近证明上帝的数字是20如果Alice和Bob可以将难度增加到20，这意味着他们可以找到从立方体的任何位置返回初始状态的最短路径，或者简而言之，他们将掌握上帝的算法。共享：

我最近发表了我最喜欢的新数学题:

一副由36张扑克牌组成的扑克牌（四副牌，每副9张）面朝下躺在一个通灵者面前。通灵者命名上层卡片的花色；之后，卡片被翻过来给他看。然后通灵者命名下一张牌的花色，依此类推。通灵者的目标是尽可能多次正确猜测花色。
卡片的背面是不对称的，所以每张卡片可以通过两种方式放置在卡片组中，通灵者可以看到顶部卡片的方向。通灵者的助手知道牌组中牌的顺序；他不被允许改变顺序，但他可以用这两种方式中的任何一种来调整任何卡片的方向。
灵媒有可能在助手了解牌的顺序之前，提前与助手进行安排，以确保至少（a）19张牌，（b）23张牌的花色能够被正确猜测吗？
如果你为超过19张的卡片设计了一个猜测策略，也要解释一下。

如果通灵者只允许看卡片的背面，那么传递的信息量是2³⁶，这与适用于18张卡的信息量相同。这样的猜测次数是可以实现的：每两张牌的背面都可以提示这对牌中第二张牌的花色。这样，通灵者就能猜出牌组中所有偶数牌的套牌。所以问题是要改进它。使用通灵者被允许翻转的卡片上的信息也有帮助。

问题出在书上2000-2005年莫斯科数学奥林匹克运动会.书和俄语博客讨论就如何猜出一半以上的牌提供许多不同的想法。

以下是想法列表。

想法1。数卡片。如果你数牌，你就会知道最后几张牌的花色。

想法2。交易。正如我们之前所讨论的，通灵者可以正确猜测偶数牌的套数。通过随机猜测奇数卡片，她平均可以正确猜出4.5张额外卡片的套数。不幸的是，这并不能保证。但等一下。如果我们用第二张牌的套牌知识来交换奇数牌中的多数套牌呢？

想法3。三张牌。假设我们有三张牌。三位可以提供以下知识：多数色，加上多数色中第一张和第二张牌的套色。因此，三位信息将允许通灵者从三张牌中猜出两张牌的套牌。

想法4。哪张卡。假设助理给一套偶数卡片发信号。在没有损失的情况下，通灵者可以猜出偶数牌，并为下一张牌重复相同的套牌。如果这是计划，助理可以选择两张卡片中的哪一张来描述。这两张牌中哪一张与通灵者的猜测相匹配提供了额外的信息。

想法5。令人惊讶。假设我们有一个策略来通知灵媒一些卡片。假设助理故意在其中一张牌上失败。然后，这张卡片的索引向通灵者提供信息。

我让我的读者使用这些想法来为19、23、24甚至26张卡片找到解决方案。共享：

我最近发表了一篇文章没有奶牛的二元公牛有以下困惑：

维克多正在接受的测试包括n个“真”或“假”问题。起初，维克多不知道任何答案，但他被允许参加多次相同的测试。每次完成测试后，维克多都会得到分数，也就是正确答案的数量。维克多利用这个机会重新测试，找出所有正确的答案。我们表示为a（n）维克多需要参加测试的最少次数，以确保他能找出所有答案。证明这一点a（30）≤24、和a（8）≤6.

维克多可以使用两种不同的策略来取得成功。首先，在每次尝试之后，他可以使用每个分数作为反馈，为下一次测试准备答案。这种策略称为适应的。另一种类型的策略称为非自适应这是一个他事先准备好所有考试答案，却不知道中间分数的考试。

在不失一般性的情况下，我们可以假设在第一次测试中，维克多对所有问题的回答都是“真的”。我称之为基础测试。

我想描述一下我的证据a（30）≤24不平等意味着，平均而言，四次尝试可以解决五个问题。假设我们已经证明了a（5）=4根据这一点，让我们制定出24个测试，以确保维克多能找出30个正确答案。

正如我前面提到的，第一个测试是基本测试，维克多回答每个问题都是“真”。第二个测试，他将前五个答案改为“假”，从而计算出前五个问题中有多少个“真”答案。这相当于对前五个问题进行基础测试。我们可以在另外三个测试中解决前五个问题，然后继续下一组五个问题。我们不需要对最后五个问题进行基础测试，因为我们可以通过了解总分和前五组的答案，计算出最后五个中“正确”答案的数量。因此，我们表明a（mn）≤ma（n）特别是，a（5）=4暗示a（30）≤24.

现在我需要证明a（5）=4。我从一个信念的飞跃开始。我假设存在一种非适应性策略，即维克多可以提前安排所有四项测试。第一个测试是TTTTT，我用T表示“真”，用F表示“假”。假设下一个测试我改变了其中一个答案，就说第一个。如果在那之后，我能在两次尝试中找出剩下的四个答案，那就意味着a（4）=3。这意味着a（28）≤21因此，a（30）≤23如果是这样的话，问题就不会要求我证明这一点a（30）≤24通过这种元推理，我可以得出以下结论a（4）≠3，这很容易检查。由此我推断，所有其他测试都应该在多个答案上与基础测试不同。改变其中一个答案相当于改变四个答案，改变两个答案等同于改变三个答案。因此，我们可以假设所有其他测试都包含两个“错误”答案。在不失一般性的情况下，第二个测试是FFTTT。

假设在第三个测试中，我从最后三个问题中选择了两个“错误”答案，例如TTFFT。第三个测试提供了与TTTTF测试完全相同的信息，但我已经解释过，只有一个“错误”答案是个坏主意。因此，我的下一个测试应该与之前的非基础测试重叠一个“错误”答案。我们可以得出结论，第三个测试将是FTFTT。另外，不应该有任何一组问题维克多在每次测试中都回答相同。事实上，如果小组中的一个答案是“假”，另一个是“真”，维克多将无法找出哪个是哪个。这唯一地将最后一个测试标识为FTTFT。

所以，如果这四个测试有效，它们应该是这样的：TTTTT，FFTTT，FTFTT，FTTFT。让我证明，这四项测试确实让维克多能够找出所有答案。将模块2最后三次测试的结果汇总起来，Victor将得到前四个问题的正确答案数的相等值。由于他知道正确答案的总数，他可以推断出最后一个问题的正确答案。之后，他将知道前四个问题以及每对问题的正确答案数量。我将把它留给我的读者来完成证明。

Knop和Mednikov在他们的论文中证明了以下引理：

如果有一种非自适应方法来计算测试n个问题由k个尝试，然后有一种非自适应的方法用2计算测试n+k−1问题由2提出k个尝试。

他们的证据是这样的。让我们把所有问题分成三个不重叠的组一个,B、和C类包含n个,n个、和k−1相应地提出问题。根据我们的假设，有一种非适应性的方法可以找出以下问题的答案一个或B使用k个尝试。让我们从一个我们将其更改为“false”k−1非基础测试一个₁, …,一个_k-1型类似地，我们表示来自B作为B₁, …,B_k-1型.

我们的第一个测试是由所有“正确”答案组成的基本测试。对于第二个测试，我们将答案改为一个确定有多少“正确”答案一个。此外，我们还有k−1类型问题总和：我们在中将答案切换为问题一个_我¼B类_我（C）_我; 和类型差异：我们将答案切换为（A∖A_我)¼B类_我.中“错误”答案之和的奇偶性A−A（A−A）_我+B类_我和一个_我+B类_我+C类_我与中的相同一个加C类_我.但我们知道一个第二次测试的分数。因此，我们可以推导C类_我之后，我们有两个带有两个未知数的方程，可以得出一个_我和B_我.从中知道“正确”答案的数量一个和C类，我们可以推导出B.了解一个和一个_我给出了所有答案一个。类似于B.量化宽松政策。

这个引理足够强大，可以回答最初的难题。的确，a（2）=2暗示a（5）≤4、和a（3）=3暗示a（8）≤6。共享：

以下是公牛和奶牛问题出现在2008年秋季城镇锦标赛上：

一个测试由30个正确或错误的问题组成。测试结束后（回答了所有30个问题），维克多得到了分数：正确答案的数量。维克多不知道答案，但被允许参加多次相同的测试。维克多能想出一个策略来保证他能在第29次尝试后找出所有答案吗？在第24次尝试之后？

让我们假设我们有一个更普遍的问题。有n个问题，以及a（n）是我们需要进行测试以确保能够找出答案的最小次数。首先，我们可以尝试所有答案的组合。这样我们就可以保证在2之后知道所有答案^n个尝试。下一个想法是从基线测试开始，例如，说所有答案都是正确的。然后我们逐个改变答案，看看分数是上升还是下降。更改后n个−1个答案，我们将知道第一个答案n个−1个问题。另外，我们知道真实答案的总数，所以我们知道所有问题的答案。我们刚刚展示了这一点a（n）≤n个.

这不足以回答问题中的预热问题。我们需要一些更微妙的东西。

让我们谈谈问题的第二部分。正如我们所知，24=4●6。因此，要解决第二部分，平均而言，我们需要在每四次测试中找到五个正确答案。这是真的吗a（5）≤ 4? 如果是这样，我们可以用它来证明吗a（30）≤ 24?

以下三个案例是最有趣的证明：a（5）= 4,a（8）≤6，以及a（30）≤ 24. 试试看！

顺便说一下，K.Knop和L.Mednikov写了一篇论文(俄语版本)他们证明了这一点a（n）不超过最小的数字k个这样，从1到k个至少是n个− 1. 这意味着他们证明了a（30）≤16.份额：