Tanya Khovanova的数学博客

我删除了之前关于所罗门结的帖子。原因很简单。我犯了信任维基百科的错误。我确信所罗门结的连接数是2。然后维基百科说是0，所以我修正了我帖子中的“错误”。我的一位读者纠正了我。所以，我重新检查了一下，删除了我的帖子，并修复了维基百科上的文章。现在，我有一篇关于这个结的新帖子。

所罗门结实际上并不是数学意义上的一个结。它是一个链接，因为它由两个循环组成。它以最简单的链接之一而闻名。最简单的是取消链接两个循环未链接的链接。下一个最简单的是Hopf链接。接下来就是所罗门节了。

通常，链接的简单性与其交叉口编号，这是链接投影到平面上的最小交叉数。unlink的交叉数为0，Hopf链路的交叉数是2，Solomon结的交叉数则是4。然而，链接号造成了混乱，所以我将对此进行解释。

这个链接编号是链接的不变量，描述一个循环围绕另一个循环的次数。对于未链接的，它等于零；对于Hopf链接，它等于一；对于Solmon的结，它等于二。

我经常很难通过查看链接的图片来计算链接数。这就是我开始编织链接的原因：通过摆弄链接来找到链接编号很容易。第一张图片显示了所罗门链接的钩编标准表示。第二张图片显示了相同的链接，但我滑动了红色的环，使其围绕绿色环的一小部分扭曲，现在看起来像一个片段。然后，我可以计算红圈绕绿圈的次数。重要的是要记住方向。在第二张图片中，可以看到红色环绕绿色环两圈，但方向相同，使链接数为2。

到目前为止，链接数似乎随着交叉数的增加而增加。这是我最喜欢的链接，怀特黑德链接的用武之地。它打破了以前的模式。它的交叉数是5，所以它比所罗门的链接稍微复杂一些。但它的链接数是零，这对于链接来说是不寻常的。事实上，Whitehead链接是链接数为零的最简单的链接，但我已经在我的帖子中写过了乌克兰Whitehead链接.

数学博物馆组织一个两年一次的娱乐数学会议，名为MOVES：各种娱乐学科的数学。作为一名数学再创作者，我参加了所有的活动。最后一次会议于2023年8月举行，专门讨论纤维艺术的数学。几年前，我不会相信我和艺术有什么关系。然而，近年来，我开始为我的课堂编织数学对象，所以我不仅决定参加，还提交了一份演讲提案。

谈话建议被接受了。当我完成幻灯片时，我意识到我为25分钟的演讲创造了太多的对象。因此，我将演讲分为七个部分，并请观众选择。我很幸运，他们选择了我最兴奋的部分，但我只有7节中的4节。

今天，我发布了几张幻灯片中的图片，展示了布伦尼人的链接。

A类布伦尼链路是一组无法分离的循环，但如果任何一个循环被移除，它们都会分崩离析。Brunnian链接最著名的例子是波罗米安环我已经写过了。在第一张图片中，博罗米安环位于右侧。它们之所以出名，是因为它们是最简单的布伦尼联系。

推广Borromean环有两种自然的方法。一种方法是使用相同的三个循环，但使它们彼此缠绕更多。第二种方法是增加循环数。

第一张图片的左侧显示了三个缠结的环，它们比波罗米安环更为缠绕。左侧链路的交叉数为12，而博罗米安环的交叉数是6。

第二张图片显示了两条布伦尼链，其中有三条以上的环。左连杆有四个环，而右连杆有五个环。

为什么我会把彩色边框钩编到不同的条纹上，使我的生活变得复杂？

回答：我想强调他们的边界。

你能认出图片中的物体吗？最左边的是莫比乌斯带。我用钩针编织了一个长长方形。然后，我没有将短边连接成圆柱体，而是将一侧扭曲了180度，然后将它们缝合在一起。对于其他两个对象，我分别进行了360度和540度的扭曲。

我用绿色纱线做带子的内部。当条带中的扭曲是360度的倍数时，生成的曲面是可定向的，并且有两个边界。我用了两种不同的颜色来强调这个事实。在其他情况下，生成的曲面是不可定向的，并且只有一个边界，因此我只对边界使用了一种颜色。

为边框使用额外颜色的目的是使其更加突出。例如，很容易看出莫比乌斯带的边界是一个圆形。中间部分的边界由两个环组成，不同的颜色使这两个边界明显相连。最后一个对象有一个边界，颜色可以帮助您注意到它的边界是一个三叶结！

如果我们在扭曲中增加度数，边界会发生什么？你能理解吗？你愿意用钩针编织来解决这个难题吗？

A类链接定义为三维空间中的两条闭合曲线。第一张图片显示了一条黄色曲线和一条蓝色曲线的链接示例。这个链接编号是链接的简单数值不变量。直观地说，它表示每条曲线绕另一条曲线的次数。例如，如果可以将两条曲线拉开，则链接数为零。

当我研究链接数时，我会看到一张链接的图片，试图计算这个数字。这让人困惑。在我开始钩编之后，这才变得容易。例如，第二张图片显示了与第一张图片相同的链接，但略有重新排列。我简单地沿着蓝色的圈滑动黄色的圈，直到我清楚地看到蓝色的圈的一部分是一条直线，黄色的圈围绕着它旋转。现在，很容易看到黄色的圈绕着蓝色的圈旋转了3次，使链接编号为3。

唯一需要记住的是，在计算绕组数量时，我需要考虑方向。环路可能先顺时针转动，然后逆时针转动。在这种情况下，链接数就是两者之间的差值。

我钩编了很多链接，现在我和我的学生计算链接数没有问题。

在我钩编之后惠特尼雨伞，我很兴奋，我发现了如何钩针穿过现有的织物层。我决定用我的技能钩编“correct-er”Klein瓶子。

克莱因瓶子是一个只有一面的很酷的数学表面，类似于莫比乌斯带。与条带不同，克莱因瓶没有边界，使其成为不可定向的流形。制作克莱因瓶的问题是克莱因瓶无法嵌入3D空间。因此，所有克莱因瓶的3D模型都必须自我交互。但是我看到的所有模型，包括玻璃模型和钩编帽子，你可以在那里买到ACME克莱因瓶，有孔。

我意识到我的钩针编织方法可能会让我制作出更准确的克莱因瓶模型，即无孔的模型。

现在是时候泄露我的秘密了。这个想法很简单，但其实不然。这两张图片显示了从不同角度观察，相同的黄色圆柱体钩住绿色方形。我先钩编绿色方块，然后钩编一半黄色圆柱。后来，我不得不把整团黄色纱线穿过绿色广场中间的一个小孔。然后，我用钩子把每一根黄色的针从绿色方块的一边穿过自己的小孔拉到另一边，并在新的一边完成了针迹。在第三张图片中，你可以看到我的克莱因酒瓶有两种颜色。你也许能看到里面的第二种颜色，而不是一个洞。

我在钩编惠特尼的雨伞时发明了这种方法。我必须把整团纱线穿过一个小孔，每排一次。我仍然恐惧地记得它的单调。

喝完酒后，我决定试试投影飞机。在第四张图片中，你可以看到两个投影平面和两个带孔的投影平面。对于前者，我从下半球开始，对于后者，我从圆柱体开始。我不需要钩针穿过，也不需要把纱线穿过小孔。我只是把一排钩针穿过另一排。我把最简单的钩针任务留到了最后！

我用埃舍尔的镶嵌来教壁纸组。埃舍尔是数学家中最好的画家，也是画家中最好的数学家。他的名声有助于激励我的班级。另外，他有很多漂亮的画可供选择。

然而，他的细分还有另一层。许多绘画不仅是对壁纸组的研究，而且也是对组-子组的研究。例如，考虑一下左边这些红色/灰色/黑色的鱼。三条不同的反射线相交于三个不同的点。第一点是三条黑鱼相互亲吻的地方。其他两点对应于灰色和红色的鱼吻。在orbifold符号中，这个对称群是*333。

但是，同一个图形有另一个对称组。我们只需要忽略颜色。也就是说，我们认为所有的鱼都是一样的。在这种情况下，三条反射线相交的三个不同点成为同一个点：鱼类亲吻的点，而不管它们的颜色如何。新的对称组有一个额外的元素：120度旋转，三种不同颜色的鱼的三个鳍相互接触。因此，新的对称群是3*3。

埃舍尔使用颜色创建了许多组及其子组的示例。但有时，他更微妙。在我之前的一篇帖子中，埃舍尔炮弹的黑暗秘密，我讨论了我最喜欢的Escher的飞机细分。在那张图中，当我们忽略其中一个黑色外壳上的标记时，第二组就出现了。

这是另一个关于群和子群的壮观例子，一个双曲平面与天使和魔鬼的镶嵌。你在画中看到两个不同的对称组了吗？

惠特尼雨伞是我想要钩针编织的一个很酷的表面。雨伞一直延伸到无穷远处，我根本不想钩针整把伞。我想把惠特尼雨伞的有限部分围绕在最激动人心的地方。

结果如图所示。从技术上讲，我编织的不是惠特尼雨伞，而是拓扑等效的表面。我最自豪的是我用钩针编织自我交融部分的秘密而痛苦的方法。总有一天我会把它洒出来。

正如维基百科所定义的那样：惠特尼伞是所有直线的集合，这些直线穿过固定抛物线的点，垂直于平行于抛物线轴的固定直线，并位于其垂直平分面上。如果你看这张图片，固定的直线是自相交线，它是颜色相互交织的线段的延续。你可以找到抛物线，它是由伞两侧的双色边缘形成的曲线。哎呀，我忘了这些雨伞中只有三把是由两种颜色制成的。

惠特尼雨伞是一个规则曲面，这意味着对于每个点，曲面上都有一条穿过该点的直线。直纹曲面可以直观地描述为由移动直线扫过的一组点。

哦，看，缝合的行可以假装是这些直线。事实上，如果我折叠这些东西，缝合的行是直线。但是，当我把边做成抛物线时，行就不再是直的了。在真正的惠特尼雨伞中，如果你沿着交叉线看，直线之间的距离比沿着抛物线更近。但在钩编中，行与行之间的距离必须固定。如果我的钩针被折叠起来，它们就会变成矩形和直纹表面。真正的惠特尼雨伞不会折叠成飞机。

Whitney伞是著名的R映射的唯一稳定奇点²至R^三。我感谢保罗·塞德尔给我发来证明。这个奇点非常有名，甚至有两个名字：夹点和尖点虽然我的钩针并不完全是惠特尼雨伞，但它们显示了这种独特性。万岁！我找到了一种秘密的方法钩针最著名的稳定奇点！

我最喜欢的埃舍尔平面镶嵌是带壳的。这是令人惊叹的，它背后的数学是美丽的。我想感谢已故的约翰·康威教我这幅画的秘密。

数学家对镶嵌感兴趣是因为镶嵌背后的对称性。该细分具有平移和旋转对称性。你能找到它们吗？

当我让我的学生找到旋转对称性时，他们立即告诉我，他们看到了两个不同的4折叠点，也就是90度旋转保留图形的点。有一点，我称之为G，是四克绿色的贝壳相遇，我称之为R的一个点是四个第页涡流炮弹相遇。

正如你可能已经猜到的那样，学生们的答案并不十分正确。这幅画还有更多。看一个深棕色的外壳，看起来像一个弯曲的矩形。这个形状有标记。现在看一个特定的点R及其四个最近的棕色外壳。你可以看到，围绕着这个点R，棕色的壳交替着它们的方向：这些壳的黑暗面要么朝向点R，要么远离点。

这幅作品的最大秘密在于它包含两个对称群：一个群和一个子群。如果我们忽略棕色外壳上的标记，将它们视为一种纯色，那么R点确实是一个4倍对称点。此外，棕色形状的中心是一个2倍对称点。因此，这个简化图的对称组在orbifold符号中是442。

如果我们考虑棕色外壳的标记，那么R点不是4倍旋转，而是2倍旋转。点G保持4倍旋转的特性。如果你知道你的对称群，你可以得出结论，应该有另一个4倍的旋转。但它在哪里？

我会泄露我的答案。对称点G不再是一个对称点。绿色贝壳在两个不同的点交汇。棕色贝壳的黑暗面对着其中一个，并将目光从另一个身上移开。

这幅图的秘密在于它展示了两个对称群：群442及其子群442，具有不同的基本区域。要了解这个秘密，你必须仔细观察一个深棕色的贝壳，找到它较暗的一面。

我不喜欢用手做东西。但我住在苏联。所以我知道如何钩针、编织和缝纫，因为当时在俄罗斯，我们没有选择。我总是做得不好。我唯一擅长的是补袜子：我不得不经常这么做。顺便说一句，我找不到一个视频，告诉我如何用妈妈教我的方法补袜子。

然后我来到了美国。我突然发现自己身处一个富裕的社会，在那里买新东西比花时间用手做事情便宜。所以我高兴地放弃了我的手艺。

在我28年没有用手工作之后，有一天我的课需要双曲线曲面，我找不到任何可以买的。双曲曲面因在欧几里德第五公理不起作用时提供了一个示例而闻名。这些双曲曲面局部看起来很平坦，因此可以在任何给定的方向上继续一条线。如果你在这样的表面上画一条线，并选取一个不在这条线上的点，那么你可以通过这个点画出许多与给定线平行的线。

我的学生比我不喜欢钩针更重要，所以我决定自己动手。我向我的朋友黛比请教，她知道如何钩针编织，她给我的不仅仅是建议。她给了我一个钩子和一根纱线，并提醒我如何操作钩子。她用一个小圆圈开始了我。在那之后，我所要做的就是在圆圈的周长上为每一针增加两针。成品是一个绿色圆球状的东西，就像照片中的大脑。

在起始圆之外，这个“大脑”的每个小表面段看起来都一样，使“大脑”成为一个恒定曲率的表面。

我选择了2比1的比例，为之前的每一针增加了两针。有了这个比率，我平坦的表面开始看起来像一个球，速度非常快。每排的周长增加了一倍。因此，我钩编的每一行花去的总时间与我花在整件事情上的总时间相同。我花了几个小时研究这个“大脑”，我一直在想：该死，这么做是徒劳的。尽管这很让人恼火，但让我坚持下来的是我最初的决定：继续用尽黛比给我的所有纱线。最终，按照这个比例，我工作的一半时间都花在了最后一排。份额：

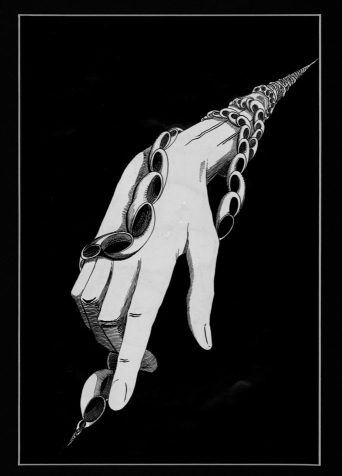左侧的Fomenko图纸来自原始俄罗斯版本同伦拓扑Fuks、Fomenko和Gutenmacher。德米特里·福克斯我九年级时在苏联数学奥林匹克运动会上取得了成功，并在这本书上签了名。多年来，我一直不知道这幅画的意思，并被它迷惑了。现在这本书已经重新出版，并附有解释，以不可承受的价格提供了英文版。你可以在Fomenko的书中找到这幅画和其他许多素描数学印象虽然插图中的注释令人困惑，但这是可以负担得起的。因此，我对这幅插图的含义有自己的解释。

这个手镯是贝壳做的。每个壳都是一个中空的圆锥体，其顶点粘在圆锥体开口边缘的一个点上，从而为每个中空圆锥体提供了自己的把手。在另一幅画的一部分（左图）中，福门科展示了手镯是如何由一支由微小奴隶组成的军队建造的。首先他们建造外壳，然后将其连接在一起。

它们是如何将壳相互连接的？下一个壳的边缘粘在上一个壳手柄上。让我提醒你，将圆环上的一点连接到圆锥体顶点的直线称为母线。想象一下，一条母线将圆锥体的顶点连接到圆环上该顶点所粘附的点。这条母线变成了壳中的一个圆，我称之为把手圆。因此，下一个壳的边缘粘在上一个壳把手的圆上。

现在考虑壳的基本群。轮辋可以收缩到手柄圆上。此外，圆锥体本身可以收缩到手柄圆上。如果我们把几个壳粘在一起，结果是可以收缩到最后一个壳的手柄圆。

现在让我们回到手镯上。壳在两个方向上都变小，并在两点处结束。前端端点在拓扑上比后端更有趣。除前端外的每个点都有一个可收缩的邻域，而前端则没有。或者用科学术语来说：手镯给出了一个空间的例子，该空间具有一个点，该点的空间是“1-lc”，但没有每个（切赫）1-圈边界的开放邻域。份额：