2022年12月,我写了一篇博客文章《无交叉骑士之旅》,讲述了德里克·基斯曼在M乘N的矩形棋盘上计算最大无交叉骑士之旅的惊人成就,其中M很小,N可以非常非常大。
数据显示出一些渐近周期性,我想知道如何从数学上证明它。我没有意识到德里克已经证明了这一点。由于我对编程一无所知,我以为程序只是输出数据,不认为它们能证明任何东西。我错了。似乎不需要其他证据。德里克试图用动态编程的术语向我解释细节,但我不确定能否在这里重现。
让我们回忆一下这个问题。考虑一个M乘N的棋盘和一个按照标准国际象棋规则移动的骑士:在一个方向跳一个方格,在正交方向跳两个方格。骑士必须访问尽可能多的方块,不重复,然后返回其起始方块。此外,骑士可能永远不会穿越自己的道路。如果你想象骑士的路径由连接其访问的方块中心的直线段组成,这些线段必须形成一个简单的多边形。总之,给定M和N,我们要计算最长的非交叉骑士的巡游长度。
需要明确的是:这些程序、它们的输出数据、经验证的答案和图像都是由德里克·基斯曼(Derek Kisman)提供的。我只是一个谦逊的信使,表达了我对计算证明能力的新认识。
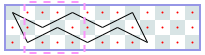
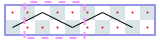
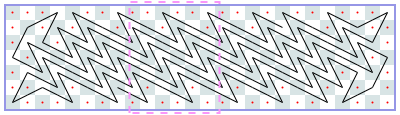
图中显示了德里克的3乘13棋盘解决方案。有一个由虚线标记的3×4重复图案。同样的巡演适用于长度为10、11和12的木板。因此,对于宽度为3、长度为10至13(含)的棋盘,最长的无交叉骑士巡游长度为10。我们可以用索引N将3×N棋盘的答案写为一个序列,其中-1表示不可能进行巡演。序列以N=1:-1、-1、-1,4、6、6、6,6、6,10、10,10、10、10,14、……开始…。
我们可以在不编程的情况下证明这个序列是正确的。假设巡更从最左边的列开始。如果我们从列的中间开始,整个行程将以菱形和长度为4的行程结束,顺便说一下,这是N=5时最长的行程。因此,对于较大的N,我们必须从一个角开始。从那里,只有两种可能的行动。我们可以看到,延拓是唯一的,并且,渐近地,我们每增加一列就获得一步。也就是说,渐近地,最长巡更的长度除以N是1。
德里克在下面的顺序中使用了一个额外的符号:每个循环都在括号中。任何两个连续循环的差值都是相同的常数。所以要无限期地继续这个序列,只需知道前两个循环就足够了。
闭路:3xN(渐近线1):-1,-1,-1…
我继续使用Derek计算的其他示例:
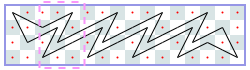
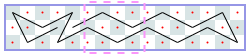
闭路:4xN(渐近线2):-1、-1、-1,[4]、[6]…
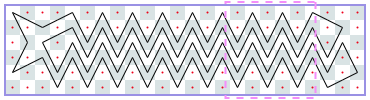
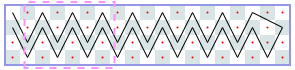
闭路:5xN(渐近线2 3/5):-1,-1,4,6,[8,12,14,18,20,22,24,28,30,34],[34,38,40,44,46,48,50,54,56,60]…
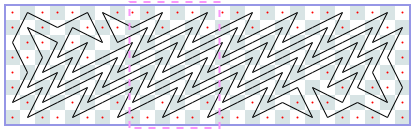
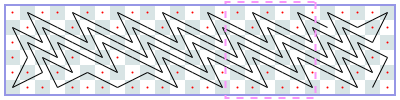
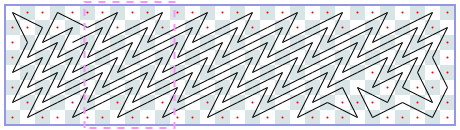
闭路:6xN(渐近线4):-1,-1,6,8,12,12,18,22,24,28,32,36,[38],[42]…
封闭游览:7xN(渐近线4 10/33):-1,-1,6,10,14,18,24,26,32,36,42,44,48,54,58,62,66,72,74,80,84,88,94,98,100,106,112,114,118,124,128,130,[136,140,144,148,154,158,162,166,170,176,180,184,188,192,196,200,204,210,214,218,222,226,232,236,240,244,248,254,256,260,266270274], [278, 282, 286, 290, 296, 300, 304, 308, 312, 318, 322, 326, 330, 334, 338, 342, 346, 352, 356, 360, 364, 368, 374, 378, 382, 386, 390, 396, 398, 402, 408, 412, 416], …
闭路:8xN(渐近线6):-1,-1,6,12,18,22,26,32,36,42,46,52,58,[64,70,76,80,88,92],[100,106,112,116,124,128]…
闭路:9xN(渐近线6 6/29):-1,-1,6,14,20,24,32,36,42,50,56,60,68,74,80,86,94,98,106,114,118,126,132,136, [144, 150, 156, 162, 168, 174, 180, 186, 192, 200, 206, 212, 218, 224, 230, 236, 242, 250, 254, 262, 268, 274, 280, 286, 292, 300, 304, 312, 318, 324, 330, 336, 342, 348, 354, 360, 366, 372, 378, 386, 392, 398, 404, 410, 416, 422, 428, 436, 440, 448, 454, 460, 466, 474, 478, 486, 492, 498], [504, 510, 516, 522, 528, 534, 540, 546, 552, 560, 566, 572, 578, 584, 590, 596, 602, 610, 614, 622, 628, 634, 640, 646, 652, 660, 664, 672, 678, 684, 690, 696, 702, 708, 714, 720, 726, 732, 738, 746, 752, 758, 764, 770, 776, 782, 788, 796, 800, 808, 814, 820, 826, 834, 838, 846, 852, 858], …
闭合巡视:10xN(渐近线8):-1,-1,10,16,22,28,36,42,50,54,64,70,78,84,92,100,[106],[114],…我没有这个案例的图像。
您可能已经注意到,对于偶数M,渐近线等于M-2。奇数M的渐近线略大于M-1的渐近线上。
德里克还计算了最长的开放骑士巡游:骑士不必回到起始位置的巡游。
开放巡视:2xN(渐近线1/2):-1,-1,[2,2],[3,3]…
开放巡视:3xN(渐近线1):-1,2,3,5,6,7,[9],[10]…
开放巡视:4xN(渐近线2):-1、2、5、[6]、[8]、…
开放游览:5xN(渐近线3):-1、3、6、8、11、15、17、20、23、26、29、[32、35、38、41、44、46]、[50、53、56、59、62、64]…
开放游览:6xN(渐近线4):-1、3、7、10、15、18、22、26、30、33、[36]、[40]、…
开放线路:7xN(渐近线5):-1、4、9、12、17、22、25、31、36、[40]、[45]、…
开放式旅游:8xN(渐近线6):-1,4,10,14,20,26,31,36,43,48,54,60,[64],[70]…
开放巡视:9xN开放(渐近线7):-1、5、11、16、23、30、36、43、48、56、62、68、75、[82、88、94]、[103、109、115]……我没有这个案例的图像。
本文中有许多有趣的新序列,它们的计算非常重要。我希望有人能将它们添加到OEIS数据库中。
共享: