Invariant Co-Ordinate Selection

Tyler, David E.; Critchley, Frank; Dümbgen, Lutz; Oja, Hannu

doi:10.1111/j.1467-9868.2009.00706.x

总结

提出了一种通过比较多元散度的不同估计来探索多元数据的通用方法。该方法基于一个散射矩阵相对于另一散射矩阵的特征值-特征向量分解。特别地，本文证明了特征向量可以用于生成多元数据的仿射不变坐标系。因此，我们将此方法视为不变坐标选择通过绘制关于这个新的不变坐标系的数据，可以揭示各种数据结构。例如，在某些独立分量模型下，证明了不变坐标对应于独立分量。另一个例子涉及椭圆分布的混合物。在这种情况下，可以证明，即使数据点的类标识未知，不变坐标的子集也对应于Fisher线性鉴别子空间。给出了一些示例。

仿射不变性,聚类分析,独立成分分析,混合物模型,多元诊断,多元散射,主要组成部分,投影追踪,稳健的统计数据

1.简介

当从多元正态分布抽样时，样本均值向量和样本方差-协方差矩阵是数据集的充分总结。为了防止非正态性，特别是长尾分布和离群值，我们可以用多元位置和散布（或伪协方差）的稳健估计来代替样本均值和协方差矩阵。已经提出了多元位置向量和散布矩阵的各种稳健估计。其中包括多元M（M）-估计（Huber，1981; 马龙娜，1976)最小体积椭球估计和最小协方差行列式估计（Rousseeuw，1986),S公司-估计值（Davies，1987; Lopuhaä，1985)，基于项目的估算（Maronna等。,1992; 泰勒，1994),τ-估计值（Lopuhaä，1991)，受约束M（M）-估计（肯特和泰勒，1996)和MM估计（Tatsuoka和Tyler，2000; 泰勒，2002)以及这些估算的一步版本（Lopuhaä，1999). 在计算多元位置和散布的稳健估计后，通常可以通过检查相应的稳健马氏距离来检测异常值；例如，见卢梭和勒罗伊(1987).

如果大部分数据来自多元正态分布，或者更普遍地说，来自椭圆对称分布，则通过位置和散布统计汇总多元数据集，然后检查相应的马氏距离图中可能的异常值是合适的。然而，如果数据来自非对称分布，那么不同的位置统计数据估计的是不同的中心趋势概念。此外，如果数据来自椭圆对称分布以外的分布，即使是对称分布，那么不同的散布统计并不一定估计相同的人口数量，而是反映了潜在分布的不同方面。这表明，比较多元分散度的不同估计可能有助于揭示与椭圆对称分布的有趣偏离。这种数据结构在马氏距离图中可能不明显。

在本文中，我们提出了一种基于多元散度不同估计值比较的通用多元方法。该方法基于一个散射矩阵相对于另一散射矩阵的特征值-特征向量分解。这种分解的一个重要特性是，相应的特征向量为多元观测值生成仿射不变坐标系，因此我们将此方法视为不变坐标选择（ICS）。通过绘制关于这个新的不变坐标系的数据，可以揭示各种数据结构。例如，当数据来自椭圆分布的混合时，由不变坐标子集跨越的空间给出Fisher线性判别子空间的估计，即使数据点的类标识未知。另一个例子涉及某些独立的组件模型。这里，通过使用不变坐标获得的变量对应于独立分量的估计。

论文组织如下。第2节建立一些要在论文中使用的符号和概念。特别是，仿射等变散布矩阵的一般概念在第2.1节中简要回顾了几类散布矩阵第2.2节。中讨论了通过使用一个散射矩阵相对于另一散射矩阵的特征值-特征向量分解来比较两个不同散射矩阵的思想第3节中给出了ICS变换的不变性第4节.第5节对上述椭圆混合模型下的ICS变换进行了理论研究(第5.1节)、和在独立组件模型下(第5.2节). 结果在第5.1节表示以下标题下给出的结果的大致概括广义主成分分析作者：Ruiz-Gazen(1993)还有Caussinus和Ruiz-Gazen(1993,1995). 主要对ICS在实践中的工作方式感兴趣的读者可能希望跳过第5节第一次阅读时。在第6节给出了在实现ICS时可能考虑的散布矩阵选择的一般讨论，以及一些示例，说明了ICS转换在诊断图中的实用性。进一步的讨论、开放性研究问题以及ICS与其他方法的关系，请参见第7节.所有正式证明均为附录A一个名为ICS的R包（诺德豪森、Oja和泰勒，2008)可免费用于实现ICS方法。

2.散布矩阵

2.1. 仿射等方差

让F类_Y（Y）表示多元随机变量的分布函数Y（Y）∈ ℜ^第页，并让 ${P（P）}_{第页}$ 表示所有对称正定阶矩阵的集合第页仿射等变多元位置和散布泛函μ(F类_Y（Y）) ∈ ℜ^第页和 $V（V） ({F类}_{Y（Y）}) \in {P（P）}_{第页}$ 分别是满足以下性质的分布函数Y（Y）^*=是的+b条，使用A类非奇异和b条∈ ℜ^第页,

\begin{matrix} μ ({F类}_{{Y（Y）}^{*}}) = A类 μ ({F类}_{Y（Y）}) + b条, \\ V（V） ({F类}_{{Y（Y）}^{*}}) = A类 V（V） ({F类}_{Y（Y）}) {A类}^{'} . \end{matrix}

(1)

仿射等变位置泛函和散射泛函的经典示例是平均向量μ_Y（Y）=E类[Y（Y）]方差-协方差矩阵∑_Y（Y）=E类[(Y（Y）−μ_Y（Y）)(Y（Y）−μ_Y（Y）)^′]如果它们存在的话。就我们的目的而言，可以稍微放宽散布矩阵的仿射等方差，只需要其形状分量的仿射等方差。散布矩阵的形状分量 $V（V） \in {P（P）}_{第页}$ 指的是V（V），说吧 $S公司 (V（V）)$ ⁠，因此

S公司 (V（V）) = S公司 (λ V（V）) 对于任何 λ > 0

(2)

因此，我们说V（V）(F类_Y（Y）)是仿射等变的，如果

V（V） ({F类}_{{Y（Y）}^{*}}) \propto A类 V（V） ({F类}_{Y（Y）}) {A类}^{'} .

(3)

对于第页-尺寸样本n个,Y（Y）={年₁,…,年_n个}仿射等变多元位置和散布统计 $\hat{μ}$ 和 $\hat{V（V）}$ 分别通过将上述定义应用于经验分布函数来定义，即它们是满足以下性质的统计量：对于任何非奇异A类以及任何b条∈ ℜ^第页,

年_{我} \to 年_{我}^{*} = A类 年_{我} + b条 （f） o个 第页 我 = 1, \dots, n个 \Rightarrow (\hat{μ}, \hat{V（V）}) \to ({\hat{μ}}^{*}, {\hat{V（V）}}^{*}) = (A类 \hat{μ} + b条, A类 \hat{V（V）} {A类}^{'}) .

(4)

同样 $\hat{V（V）}$ 称为仿射等变，如果

{\hat{V（V）}}^{*} \propto A类 \hat{V（V）} {A类}^{'} .

(5)

样本平均向量 $\bar{年}$ 和样本方差–协方差矩阵S公司_n个分别是仿射等变位置和散布统计的示例，以及中引用的所有估计第1节.

通常，在实践中， $\hat{V（V）}$ 对方差-协方差矩阵进行归一化处理，使其在多元正态模型中保持一致。因此，归一化版本如下所示 $\tilde{V（V）} = \hat{V（V）} / β$ ⁠，其中β>0是这样的V（V）(F类_Z轴) =βI什么时候Z轴具有标准的多元正态分布。就我们的目的而言，只考虑非正规化散射矩阵就足够了 $\hat{V（V）}$ 因为我们提出的方法仅依赖于达到比例的散射矩阵，即仅依赖于散射矩阵的形状。

在椭圆对称下，仿射等变位置泛函和散射泛函具有相对简单的形式。回想一下，椭圆对称分布定义为球对称分布的仿射变换产生的分布，即，如果Z轴∼质量保证对于任何第页×第页正交矩阵问，然后是Y（Y）=亚利桑那州+μ被称为具有中心椭圆对称分布μ∈ ℜ^第页和形状矩阵Γ=AA公司^′; 参见比洛多和布伦纳的例子(1999). 如果Y（Y）也是绝对连续的，那么它具有形式的密度

（f） (年; μ, Γ, 克) = det（探测） {(Γ)}^{- 1 / 2} 克 {{(年 - μ)}^{'} Γ^{- 1} (年 - μ)} 对于 年 \in ℜ^{第页},

(6)

对于一些非负函数克和 $Γ \in {P（P）}_{第页}$ ⁠如定义所示，椭圆对称分布的形状参数Γ仅在标量倍数内定义良好，即，如果Γ满足给定椭圆对称分布形状矩阵的定义，则λΓ也适用于任何情况λ>0.在绝对连续的情况下，如果对函数没有任何限制克，则参数Γ与克可以通过设置，例如，det（Γ）=1或tr（Г）来规范化形状参数=第页再次说明，这对于我们的目的是不必要的，因为只有Γ的形状分量，如表达式中所定义的(2)，并定义了椭圆对称分布的这些形状分量。

在椭圆对称下，任何仿射等变位置泛函都对应于对称中心，而任何仿射等变散射泛函都与形状矩阵成正比，即。μ(F类_Y（Y）) =μ和V（V）(F类_Y（Y）)∝Γ. 特别地，μ_Y（Y）=μ和∑_Y（Y）当一阶矩和二阶矩分别存在时。一般来说，如果V（V）(F类_Y（Y）)是否有函数满足条件(3)，然后V（V）(F类_Y（Y）)∝Γ.

如中所述第1节对于一般分布，仿射等变位置泛函不一定相等，仿射等变散布泛函也不一定成比例。因此，这些功能的相应样本版本正在估计不同的人群特征。这些泛函的差异在某种程度上反映了分布与椭圆对称分布的不同。

备注1。所有仿射等变位置泛函相等且所有等变散射泛函彼此成比例的分布类比椭圆分布类更广。例如，对于F类_Y（Y）什么时候Y（Y）=亚利桑那州+μ随着Z轴每个组件都是可交换和对称的，即。Z轴∼DJZ公司对于任何置换矩阵J型和任何对角矩阵D类具有对角线元素±1。我们推测这是该属性所属的最广泛的类。此类包含椭圆对称分布，因为这些分布对应于Z轴具有球对称分布的。

2.2. 分散统计分类

从概念上讲，样本的最简单替代方法意味着 $\bar{年}$ 和样本协方差矩阵S公司_n个分别是加权样本均值和样本协方差矩阵，权重取决于经典马氏距离。这些定义如下

\begin{matrix} \hat{μ} = {\sum^{​}}_{我 = 1}^{n个} {u个}_{1} (秒_{0, 我}) 年_{我} / {\sum^{​}}_{我 = 1}^{n个} {u个}_{1} (秒_{0, 我}), \\ \hat{V（V）} = {\sum^{​}}_{我 = 1}^{n个} {u个}_{2} (秒_{0, 我}) (年_{我} - \bar{年}) {(年_{我} - \bar{年})}^{'} / {\sum^{​}}_{我 = 1}^{n个} {u个}_{2} (秒_{0, 我}), \end{matrix}

(7)

哪里 $秒_{0, 我} = {(年_{我} - \bar{年})}^{'} {S公司}_{n个}^{- 1} (年_{我} - \bar{年})$ ⁠、和u个₁(秒)和u个₂(秒)是一些适当选择的权重函数。通过仅将上述散射方程应用于两两差异的样本，即对称化数据集，可以获得样本协方差矩阵的其他简单替代方案

{Y（Y）}^{秒} = {年_{我} - 年_{j个} Ş===================================================================================================== 我, j个 = 1, \dots, n个, 我 \neq j个},

(8)

样本平均值为0。尽管加权平均值和协方差矩阵以及加权协方差矩阵的对称化版本可能会降低异常值的权重，但它们具有无限的影响函数和零崩溃点。

多元位置和散布统计的一个更稳健的类是由多元M（M）-估计，可分别视为自适应加权样本均值和样本协方差矩阵。更具体地说，它们被定义为M（M）-估计方程

\begin{matrix} \hat{μ} = {\sum^{​}}_{我 = 1}^{n个} {u个}_{1} (秒_{我}) 年_{我} / {\sum^{​}}_{我 = 1}^{n个} {u个}_{1} (秒_{我}), \\ \hat{V（V）} = {\sum^{​}}_{我 = 1}^{n个} {u个}_{2} (秒_{我}) (年_{我} - \hat{μ}) {(年_{我} - \hat{μ})}^{'} / {\sum^{​}}_{我 = 1}^{n个} {u个}_{三} (秒_{我}), \end{matrix}

(9)

哪里 $秒_{我} = {(年_{我} - \hat{μ})}^{'} {\hat{V（V）}}^{- 1} (年_{我} - \hat{μ})$ ⁠、和u个₁(秒),u个₂(秒)和u个_三(秒)也是一些适当选择的权重函数。我们建议读者参考Huber(1981)和玛丽娜(1976)关于多元的一般理论M（M）-估计值。表达式中给出的方程(9)是隐式方程 $(\hat{μ}, \hat{V（V）})$ 因为重量取决于相对于 $(\hat{μ}, \hat{V（V）})$ ⁠，即打开 ${d日}_{我} (\hat{μ}, \hat{V（V）}) = \sqrt 秒_{我}$ ⁠然而，存在相对简单的算法来计算多元M（M）-估计值。参数的最大似然估计μ给定扩散函数的椭圆分布的Γ克在表达式中(6)是的特殊情况M（M）-估计值。

从稳健性的角度来看，多变量的一个常见缺陷M（M）-估计是它们在更高维度上相对较低的细分。具体来说，它们的分解点以1为界/(第页+1）。随后，提出了许多高击穿点估计，如最小体积椭球、最小协方差行列式、S公司-估算，基于项目的估算τ-估计，受限M（M）-估计值和MM估计值，所有这些都在第1节。所有高崩溃点估计都是计算密集型的，除小数据集外，通常使用近似或概率算法进行计算。对于高维的超大数据集，高分解点多元估计的计算复杂性尤其具有挑战性，这仍然是一个开放和活跃的研究领域。

通过表达式给出加权样本均值和协方差矩阵的定义(7)可以很容易地通过使用任何初始仿射等变位置和散布统计进行推广 ${\hat{μ}}_{0}$ 和 ${\hat{V（V）}}_{0}$ 分别，即。

\begin{matrix} \hat{μ} = {\sum^{​}}_{我 = 1}^{n个} {u个}_{1} (秒_{0, 我}) 年_{我} / {\sum^{​}}_{我 = 1}^{n个} {u个}_{1} (秒_{0, 我}), \\ \hat{V（V）} = {\sum^{​}}_{我 = 1}^{n个} {u个}_{2} (秒_{0, 我}) (年_{我} - {\hat{μ}}_{0}) {(年_{我} - {\hat{μ}}_{0})}^{'} / {\sum^{​}}_{我 = 1}^{n个} {u个}_{2} (秒_{0, 我}), \end{matrix}

(10)

现在在哪里 $秒_{0, 我} = {(年_{我} - {\hat{μ}}_{0})}^{'} {\hat{V（V）}}_{0}^{- 1} (年_{我} - {\hat{μ}}_{0})$ ⁠在单变量设置中，这种加权样本均值和方差有时被称为一步W公司-估计值（汉佩尔等。,1986; Mosteller和Tukey，1977)，因此我们将其多元版本称为多元一步W公司-估计值。给定位置和散布统计，相应的一步W公司-估计为替代位置和散布统计提供了一个计算简单的选择。

用于获取数据集的位置和散布统计信息的任何方法Y（Y）也可以应用于其对称版本Y（Y）^秒生成散布统计。对于对称化数据，任何仿射等变位置统计量总是0。

本节中讨论的位置和散布统计的功能或人口版本可以通过替换Y（Y）具有人口分布函数F类_Y（Y）。对于M（M）-估计和一步到位W公司-估计，这只是意味着替换表达式中的平均值(9)和(10)分别具有预期值。对于对称数据，通过替换Y（Y）^秒几乎可以肯定的极限 ${F类}_{Y（Y）}^{S公司}$ ⁠，的分布函数Y（Y）^秒=Y（Y）₁−Y（Y）₂，其中Y（Y）₁和Y（Y）₂是的独立副本Y（Y）.

3.比较散布矩阵

比较正定对称矩阵在各种多元统计问题中自然而然地出现。也许最明显的情况是我们希望比较两个或更多不同组的协方差结构；参见Flury示例(1988). 其他众所周知的情况发生在多元方差分析中，其中的兴趣在于比较组内和组间平方和和交叉积矩阵，以及典型相关分析，其中，有趣的是比较一组变量的协方差矩阵与其基于另一组变量线性预测器的协方差阵。这些方法要么涉及多个群体，要么涉及两组不同的变量。对单个群体中单个变量集的不同散射估计的比较关注较少。然而，在艺术中可以找到这方面的一些工作等。(1982)、Caussinus和Ruiz-Gazen(1990,1993,1995)、病原体等。(2003)和Ruiz-Gazen(1993)，这将在后面的章节中讨论。

通常，通过考虑一个矩阵相对于另一个矩阵的特征值和特征向量，可以总结出两个正定对称矩阵之间的差异。更具体地说，假设 ${V（V）}_{1} \in {P（P）}_{第页}$ 和 ${V（V）}_{2} \in {P（P）}_{第页}$ ⁠一个特征值，比如ρ_j个，以及相应的特征向量小时_j个，第页，共页V（V）₂相对于V（V）₁对应于矩阵方程的非平凡解

{V（V）}_{2} {小时}_{j个} = ρ_{j个} {V（V）}_{1} {小时}_{j个} .

(11)

等效地，ρ_j个和小时_j个分别是的特征值和对应的特征向量 ${V（V）}_{1}^{- 1} {V（V）}_{2}$ ⁠。由于大多数读者可能更熟悉对称矩阵的特征值-特征向量理论，我们注意到ρ_j个也表示对称矩阵的特征值 $M（M） = {V（V）}_{1}^{- 1 / 2} {V（V）}_{2} {V（V）}_{1}^{- 1 / 2} \in$ ⁠，其中 ${V（V）}_{1}^{1 / 2} \in {P（P）}_{第页}$ 表示的唯一正定对称平方根V（V）₁。因此，我们可以选择第页有序特征值，ρ₁≥ρ₂≥ … ≥ρ_第页>0和特征向量的正交集q个_j个,j个= 1,…,第页，因此Mq公司_j个=ρ_j个q个_j个.两者之间的关系小时_j个和的特征向量M（M）由提供 ${q个}_{j个} \propto {V（V）}_{1}^{1 / 2} {小时}_{j个}$ ⁠，等等 ${小时}_{我}^{'} {V（V）}_{1} {小时}_{j个} = 0$ 对于我≠j个这产生了以下的同时对角化V（V）₁和V（V）₂:

\begin{matrix} {H（H）}^{'} {V（V）}_{1} H（H） = {D类}_{1}, \\ {H（H）}^{'} {V（V）}_{2} H（H） = {D类}_{2} \end{matrix}

(12)

哪里H（H）=(小时₁…小时_第页),D类₁和D类₂是具有正项的对角矩阵 ${D类}_{1}^{- 1} {D类}_{2} = Δ = d日我一克 (ρ_{1}, \dots, ρ_{第页})$ ⁠.在不失一般性的情况下，我们可以D类₁=我通过标准化小时_j个以便 ${小时}_{j个}^{'} {V（V）}_{1} {小时}_{j个} = 1$ ⁠。或者，我们可以D类₂=我。这样的规范化对于我们的目的来说是不必要的，我们只是喜欢一般形式(12)因为它反映了V（V）₁和V（V）₂注意，矩阵 ${V（V）}_{1}^{- 1} {V（V）}_{2}$ 具有光谱值分解

{V（V）}_{1}^{- 1} {V（V）}_{2} = H（H） Δ {H（H）}^{- 1} .

(13)

中特征值和特征向量的各种有用解释方程式（11）可以随时提供V（V）₁和V（V）₂是相同总体或样本的两个不同散布矩阵。我们首先注意到特征值ρ₁,…,ρ_第页仿射变换下的最大不变量用于比较V（V）₁和V（V）₂，即，如果我们定义一个函数G公司(V（V）₁,V（V）₂)这样的话G公司(V（V）₁,V（V）₂) =G公司(成人影片₁A类^′,成人影片₂A类^′)对于任何非奇异A类，然后G公司(V（V）₁,V（V）₂) =G公司(D类₁,D类₂) =G公司(我，Δ），带有D类₁,D类₂Δ的定义如上所述。此外，Δ在这种变换下是不变的。由于散布矩阵往往仅在标量倍数范围内得到很好的定义，因此更自然地会对两者之间的差异感兴趣V（V）₁和V（V）₂达到相称性。在这种情况下，如果我们考虑一个函数G公司(V（V）₁,V（V）₂)这样的话G公司(V（V）₁,V（V）₂) =G公司(λ₁成人影片₁A类^′,λ₂成人影片₂A类^′)对于任何非奇异A类以及任何λ₁>0和λ₂>0，然后G公司(V（V）₁,V（V）₂) =G公司{我，Δ/det（Δ）^1/第页}，即本例中的最大不变量为

(ρ_{1}, \dots, ρ_{第页}) / {({\prod^{​}}_{我 = 1}^{第页} ρ_{我})}^{1 / 第页}

或者，换句话说，我们对(ρ₁,…,ρ_第页)多达一个公共标量乘数。

特征值的一个更有用的解释来自以下最优性性质，它很容易遵循标准特征值-特征向量理论。对于小时∈ ℜ^第页，让

κ (小时) = {小时}^{'} {V（V）}_{2} 小时 / {小时}^{'} {V（V）}_{1} 小时 .

(14)

对于V（V）₁=V（V）₁(F类_Y（Y）)和V（V）₂=V（V）₂(F类_Y（Y）),κ(小时)表示变量的两个不同尺度之比的平方小时^′Y（Y）回想一下，峰度的经典度量对应于两个尺度度量之比的四次幂，即四阶中心矩的四次方根和标准差。因此κ(小时)²可以被视为“相对”峰度的广义度量。由于分散矩阵，此处使用相对项V（V）₁和V（V）₂不一定规范化。如果两者都有V（V）₁和V（V）₂进行规范化，以便它们在多元正态模型下的方差-协方差矩阵中一致，然后偏差为κ(小时)从1表示非正态性。但总的来说，比率κ(小时₁)²/κ(小时₂)²不依赖于任何特定的规范化。

最大可能值κ(小时)超过小时∈ ℜ^第页是ρ₁在以下方向达到最大值小时₁同样κ(小时)是ρ_第页在以下方向达到最小值小时_第页。一般来说，我们有

啜饮 {κ (小时) Ş===================================================================================================== 小时 \in ℜ^{第页}, {小时}^{'} {V（V）}_{1} {小时}_{j个} = 0, j个 = 1, \dots, 米 - 1} = ρ_{米},

(15)

上确界获得于小时_米、和

inf公司 {κ (小时) Ş===================================================================================================== 小时 \in ℜ^{第页}, {小时}^{'} {V（V）}_{1} {小时}_{j个} = 0, j个 = 米 + 1, \dots, 第页} = ρ_{米},

(16)

下确界在小时_米这些连续优化结果表明，使用坐标绘制数据或分布Z轴=H（H）^′Y（Y）可以揭示有趣的结构。我们将在后面的章节中探讨这个想法。

备注2。转型的另一个动机Z轴=H（H）^′Y（Y）如下所示。假设Y（Y）首先通过使用分散函数“标准化”V（V）₁(F类)满足条件(3)，即。X（X）=V（V）₁(F类_Y（Y）)^−1/2Y（Y）.如果Y（Y）椭圆对称于μ_Y（Y），然后X（X）中心是球对称的μ_X（X）=V（V）₁(F类_Y（Y）)^−1/2μ_Y（Y）。如果第二个散射函数随后应用于X（X），说吧V（V）₂(F类)满足条件(3)，然后V（V）₂(F类_X（X）)∝我，因此没有投影X（X）比任何其他的投影都有趣X（X）然而，如果Y（Y）不是椭圆对称的，那么V（V）₂(F类_X（X）)不一定与我这表明主成分分析X（X）基于V（V）₂(F类_X（X）)可能会揭示一些有趣的预测。通过进行谱值分解V（V）₂(F类_X（X）) =QDQ公司^′，其中问是正交矩阵，然后构造主成分变量问^′X（X），我们获得

问^{'} X（X） = {H（H）}^{'} Y（Y） = Z轴, 具有 D类 = Δ,

(17)

无论何时H（H）被规范化，以便H（H）^′ V（V）₁(F类_Y（Y）)H（H）=我.

4.不变坐标系

在本节和下一节中，我们将研究变换的属性Z轴=H（H）^′Y（Y）更详细的信息，以及第6节我们给出了一些示例，说明在诊断图中使用转换时的实用性。为了简单起见，除非另有说明，否则我们将使用散布矩阵的函数或总体形式来说明任何理论性质。然后，样本版本根据经验分布作为特例。当然，示例是针对示例版本给出的。始终假设以下条件，并在下文中使用以下符号。

条件1。对于Y（Y）∈ ℜ^第页有分布F类_Y（Y），让V（V）₁(F类)和V（V）₂(F类)是满足条件的两个散射泛函(3)此外，假设两者V（V）₁(F类)和V（V）₂(F类)在处唯一定义F类_Y（Y）.

定义1。让H（H）(F类)=(小时₁(F类)…小时_第页(F类))是定义为方程式（11）和(12)，使用ρ₁(F类) ≥ … ≥ρ_第页(F类)是相应的特征值，无论何时V（V）₁和V（V）₂被认为是V（V）₁(F类)和V（V）₂(F类)分别是。

众所周知，主成分变量在原始变量的平移和正交变换下是不变的，但在其他一般仿射变换下不是不变的。这里提出的变换的一个重要性质，即。Z轴=H（H）(F类_Y（Y）)^′Y（Y），即得到的变量在任何仿射变换下都是不变的。

定理1。除了条件1之外，假设根ρ₁(F类_Y（Y）),…,ρ_第页(F类_Y（Y）)都是不同的。那么对于仿射变换Y（Y）^*=是的+b条，使用A类非奇异，
$ρ_{j个} ({F类}_{{Y（Y）}^{*}}) = γ ρ_{j个} ({F类}_{Y（Y）}) 的 j个 = 1, \dots, 第页$
(18)
对一些人来说γ>0.此外Z轴=H（H）(F类_Y（Y）)^′Y（Y）和Z轴^*=H（H）(F类_Y（Y）*)^′Y（Y）^*在坐标位置和比例上最多不同，即对于某些常数α₁,…,α_第页和β₁,…,β_第页，使用α_j个≠0j个= 1,…,第页,
${Z轴}_{j个}^{*} = α_{j个} {Z轴}_{j个} + β_{j个} 对于 j个 = 1, \dots, 第页 .$
(19)

由于财产(19)我们指的是转换后的变量Z轴=H（H）(F类_Y（Y）)^′Y（Y）作为不变坐标系以及将它们作为ICS获得的方法。如果将单变量标准化应用于转换的变量，那么Z轴_j个和 ${Z轴}_{j个}^{*}$ 差异仅为±1倍。

前面定理的一个推广允许可能的多个根，可以表述如下。

定理2。让Y、 Y（Y）^*,Z轴和Z轴^*定义见定理1。除了条件1之外，假设根ρ₁(F类_Y（Y）),…,ρ_第页(F类_Y（Y）)包括米不同的值，比如ρ₍₁₎>…>ρ_(米)，使用ρ_(k个)具有多样性第页_k个对于k个= 1,…,米，因此第页₁++第页_米=第页。然后，表达式(18)仍然有效。此外，假设我们划分 ${Z轴}^{'} = ({Z轴}_{(1)}^{'}, \dots, {Z轴}_{(米)}^{'})$ ⁠，其中Z轴_(k个)∈ ℜ^pk系列然后，对于一些非奇异矩阵C类_k个秩序井然第页_k个还有一些第页_k个-量纲向量β_k个,
${Z轴}_{(k个)}^{*} = {C类}_{k个} {Z轴}_{(k个)} + β_{k个} 对于 k个 = 1, \dots, 米,$
(20)
即由以下构件跨越的空间 ${Z轴}_{(k个)}^{*}$ 与以下组件跨越的空间相同Z轴_(k个).

与任何特征值-特征向量问题一样，特征向量并没有很好的定义。对于不同的根，特征向量被很好地定义为标量倍数。对于复数根，比方说重数第页₀，对应的第页₀特征向量可以选择为跨越相应的线性无关向量第页₀-维特征空间。因此Z轴_(k个)定理2中没有很好的定义。可以构造一些任意规则来定义Z轴_(k个)独特地。然而，这在这里是不必要的，因为无论我们使用哪种规则来定义Z轴_(k个)唯一的是，定理2的结果成立。

5.非椭圆模型下的不变坐标选择

什么时候？Y（Y）具有椭圆对称分布，所有根ρ₁(F类_Y（Y）),…,ρ_第页(F类_Y（Y）)是相等的，因此ICS转换Z轴=H（H）(F类_Y（Y）)^′Y（Y）是任意的。ICS的目的是检测Y（Y）来自椭圆对称分布。在本节中，从理论上证明了两类非椭圆对称模型的ICS变换行为，即椭圆分布混合模型和独立分量模型。

5.1. 椭圆分布的混合

实际上，数据往往来自混合分布，混合是某些未测量的分组变量的结果。在聚类分析中，发现不同的组通常被视为一个问题。Art提出的一种聚类方法等。(1982)基于首次通过尝试识别Fisher线性判别子空间来降低聚类问题的维数。为了做到这一点，他们给出了一种迭代算法来近似组内平方和和交叉积矩阵W公司_n个，然后考虑 ${W公司}_{n个}^{- 1} ({T型}_{n个} - {W公司}_{n个})$ ⁠，其中T型_n个是总平方和和交叉积矩阵。Art提出的方法等。(1982)主要由启发式论证激发，并得到蒙特卡洛研究的支持。

随后，Ruiz-Gazen(1993)还有Caussinus和Ruiz-Gazen(1993,1995)对于具有等方差-协方差矩阵的多元正态分布的位置混合，即使在群识别未知的情况下，也可以一致地估计Fisher的线性判别子空间，前提是q个子空间的，是已知的。他们的结果基于与q个最大特征值 ${S公司}_{1, n个}^{- 1} {S公司}_{n个}$ ⁠，其中S公司_n个是样本方差–协方差矩阵和S公司_1,n个要么是一步走W公司-估计(7)或其对称版本。他们还要求S公司_1,n个不同于S公司_n个由于它们的证明涉及扩展函数形式的S公司_1,n个关于的功能版本S公司_n个在本小节中，我们证明了这些结果基本上可以推广到任何一对散射矩阵，并且在具有比例散射参数的椭圆分布的混合情况下，这些结果是成立的。

为了简单起见，我们首先考虑具有比例协方差矩阵的两个多元正态分布的混合的ICS变换的性质。考虑到比例协方差矩阵，可以将点质量污染作为混合组分之一包含在内，因为点质量污染是通过使比例常数变为0来获得的。

定理3。除了条件1，假设
$Y（Y） \sim_{d日} (1 - α) {N个}_{第页} (μ_{1}, Γ) + α {N个}_{第页} (μ_{2}, λ Γ),$
其中0<α<1,μ₁≠μ₂,λ>0和 $Γ \in {P（P）}_{第页}$ ⁠。然后，要么
（a）
ρ₁(F类_Y（Y）)>ρ₂(F类_Y（Y）)=… =ρ_第页(F类_Y（Y）),
（b）
ρ₁(F类_Y（Y）)=… =ρ_第页−1(F类_Y（Y）)>ρ_第页(F类_Y（Y）)，或
（c）
ρ₁(F类_Y（Y）)=… =ρ_第页(F类_Y（Y）).
对于第页>2，如果情况（a）成立，则小时₁(F类_Y（Y）)∝Γ⁻¹(μ₁−μ₂)如果情况（b）成立，则小时_第页(F类_Y（Y）)¦Γ⁻¹(μ₁−μ₂). 对于第页=2，如果ρ₁(F类_Y（Y）)>ρ₂(F类_Y（Y）)，然后要么小时₁(F类_Y（Y）)或小时₂(F类_Y（Y）)与Γ成正比⁻¹(μ₁−μ₂).

因此，取决于案例（a）或案例（b）是否成立，小时₁或小时_第页分别对应于Fisher线性判别函数（参见示例Mardia等。(1980))，即使组身份未知。关于为什么我们可能认为这是成立的一个直观解释是，任何散布估计都包含关于组间变异性的信息，即组间差异μ₁和μ₂以及组内变异性或形状，即Γ。因此，我们可以通过使用两种不同的离散度估计值来区分这两种变异性来源。但我们在定理3的证明中并没有使用这种直觉；我们的证明也不是基于Ruiz-Gazen使用的扰动参数的推广(1993)还有Caussinus和Ruiz-Gazen(1995)在得出上述结果时。相反，定理3的证明附录A只依赖不变性参数。

在定理3中，情况（a）或情况（b）是否成立取决于V（V）₁(F类)和V（V）₂(F类)以及混合物的性质。显然，如果案例（a）成立，那么V（V）₁(F类)和V（V）₂(F类)则情况（b）成立。案例（c）仅适用于非常特殊的情况。特别是，情况（c）适用于μ₁=μ₂，在这种情况下Y（Y）具有椭圆对称分布。什么时候？μ₁≠μ₂也就是说，当混合物本身不是椭圆时，情况（c）仍然可能成立。但这不仅取决于V（V）₁(F类)和V（V）₂(F类)而且还要考虑参数的特定值α, μ₁,μ₂、Γ和λ.

例如，假设V（V）₁(F类)=Σ(F类)人口协方差矩阵，以及 ${V（V）}_{2} (F类) = K（K） (F类)$ 哪里

K（K） (F类) = E类 [{(Y（Y） - μ_{Y（Y）})}^{'} Σ {(F类)}^{- 1} (Y（Y） - μ_{Y（Y）}) \times (Y（Y） - μ_{Y（Y）}) {(Y（Y） - μ_{Y（Y）})}^{'}] .

(21)

除了易于分析外，散射函数 $K（K） (F类)$ 是独立成分分析的经典算法中出现的一种算法，将在后面的章节中进行更详细的讨论。对于特殊情况λ=1且当μ₁≠μ₂如果我们允许η=α(1−α)则可以证明情况（a）适用于η>1/6，情况（b）适用于η<1/6，案例（c）适用于η= 1/6. 此外，对于这三种情况中的任何一种，我们都有ρ₁(F类_Y（Y）)−ρ_第页(F类_Y（Y）) =η|1−6η|θ²/(1+ηθ)²，其中θ=(μ₁−μ₂)^′Γ⁻¹(μ₁−μ₂).

在Caussinus和Ruiz-Gazen研究了其他例子(1993,1995). 在他们的工作中，V（V）₂(F类)=Σ(F类)和V（V）₁(F类)对应于一步对称版本的功能版本W公司-估计(7).解释一下，他们为这个案子展示了λ=1，并且对于权重函数类u个₂(秒) =u个(βs)该情况（a）适用于足够小的情况β前提是η<1/6. 然而，他们没有注意到，这种情况（a）或（b）可以适用于其他值β和η.条件的原因η<1/6出现在他们的工作中，以及上一段的讨论中，是因为他们的证明涉及扩展u个(βs)关于u个(秒)，使用矩阵 $K（K） (F类)$ 然后在线性项中出现相应的一步展开式W公司-∑的估计(F类).

定理3很容易推广到两个椭圆分布的混合，它们具有相同的形状矩阵，但可能具有不同的位置向量和不同的扩展函数，即，如果Y（Y）具有密度

{（f）}_{Y（Y）} (年) = (1 - α) （f） (年; μ_{1}, Γ, 克_{1}) + α （f） (年; μ_{2}, Γ, 克_{2}),

其中0<α<1,μ₁≠μ₂和（f）(年;μ,Γ,克)由表达式定义(6)，则定理3的结果成立。注意，这种混合分布包括两种混合成分来自同一椭圆族但具有比例形状矩阵的情况。此特殊情况对应于设置克₂(秒) =克₁(秒/λ)，因此（f）(年;μ₂,Γ,克₂) =（f）(年;μ₂,λΓ,克₁).

将这些结果推广到k个下面的定理给出了可能具有不同中心和不同扩展函数，但形状矩阵相同的椭圆对称分布。更具启发性地说，这个定理暗示了Fisher的线性鉴别子空间（参见示例Mardia等。(1980))对应于不变坐标的某些子集的跨度，即使群标识未知。

定理4。除了条件1，假设Y（Y）具有密度
${（f）}_{Y（Y）} (年) = det（探测） {(Γ)}^{- 1 / 2} {\sum^{}}_{j个 = 1}^{k个} α_{j个} 克_{j个} {{(年 - μ_{j个})}^{'} Γ^{- 1} (年 - μ_{j个})},$
哪里α_j个>0用于j个= 1,…,k、 α₁+…+α_k个= 1, $Γ \in {P（P）}_{第页}$ 和克₁,…,克_k个是非负函数。此外，假设中心μ₁,…,μ_k个跨越一些q个-维度超平面，具有0<q个<第页然后，使用定理2的符号表示多个根，至少有一个根ρ_(j个),j个= 1,…,米，重数大于或等于第页−q个此外，如果没有根的重数大于第页−q个，则有一个具有多重性的根第页−q个，说吧ρ_(t吨)，因此
$跨度 {Γ^{- 1} (μ_{j个} - μ_{k个}) Ş===================================================================================================== j个 = 1, \dots, k个 - 1} = 跨度 {{H（H）}_{q个} ({F类}_{Y（Y）})},$
(22)
哪里H（H）_q个(F类_Y（Y）)=(小时₁(F类_Y（Y）),…,小时_{第页1+…+pt（磅）−1}(F类_Y（Y）),小时_{第页1+…+pt（磅）+1}(F类_Y（Y）),…,小时_第页(F类_Y（Y）)).

定理4中只有一个根具有多重性的条件第页−q个在定理3中，当k个= 2. 与定理3后的讨论类似，除特殊情况外，此条件通常成立。对于给定的选择V（V）₁(F类_Y（Y）)和V（V）₂(F类_Y（Y）)，这些特殊情况取决于参数的特定值。

5.2. 独立组件分析模型

独立成分分析（ICA）在许多经常遇到多元数据的应用领域中是一种非常流行的方法。有关详细概述，请参阅Hyvärinen等。(1981). 最常见的ICA模型假设Y（Y）以卷积形式出现第页独立分量或变量，即。Y（Y）=BX公司，其中B类是非奇异的，并且X（X），说吧X（X）₁,…,X（X）_第页，都是独立的。ICA的主要目标是恢复混合矩阵B类这样我们就可以“取消混合”Y（Y）获得独立组件X（X）^*=B类⁻¹Y（Y）在这个ICA模型下，混合矩阵中存在一些不确定性B类，因为模型也可以表示为Y（Y）=B类₀X（X）₀，其中B类₀=b质量∧和X（X）₀=Λ⁻¹问^′十、问是置换矩阵，∧是具有非零项的对角矩阵。的组件X（X）₀然后也是独立的。在至多一个独立组件的情况下X（X）₁,…,X（X）_第页具有正态分布，众所周知，这是B类以及独立组件X（X）=B类⁻¹Y（Y）可以很好地定义排列和组件缩放因子。

对称分布的ICS和ICA之间的关系在下一个定理中给出。

定理5。除了条件1，假设Y（Y）=BX公司+μ，其中B类是非奇异的，并且X（X），说吧X（X）₁,…,X（X）_第页，相互独立。此外，假设X（X）对称于0，即。X（X）∼_d日−X（X）和根ρ₁(F类_Y（Y）),…,ρ_第页(F类_Y（Y）)都是不同的。然后，转换后的变量Z轴=H（H）(F类_Y（Y）)^′Y（Y）由独立组件组成，或者更具体地说，Z轴和X（X）最多不同于排列和/或组件位置和比例。

从定理5的证明中可以看出X（X）对称分布在0左右可以放宽到只要求第页−1个组件X（X）在0左右对称分布。同样值得注意的是，所有根都是不同的条件比最多只能包含X（X）是正常的。这是因为通常很容易表明，如果X（X）仅通过位置偏移和/或比例变化而彼此不同，则至少有一个根的重数大于1。

如果X（X）不是关于0的对称，那么我们可以对称化Y（Y）在应用定理5之前，即假设Y（Y）=BX公司+μ具有X（X）拥有独立的组件，并让Y（Y）₁和Y（Y）₂是…的独立副本Y（Y）.然后Y（Y）^秒=Y（Y）₁−Y（Y）₂=BX公司^秒，其中X（X）^秒=X（X）₁−X（X）₂是关于零的对称且具有独立分量。因此，定理5可以应用于Y（Y）^秒此外，由于卷积矩阵B类两者都是一样的Y（Y）和Y（Y）^秒，则转换后的变量 $Z轴 = H（H） {({F类}_{Y（Y）}^{秒})}^{'} Y（Y）$ 和X（X）最多不同于排列和/或组件位置和比例，其中 ${F类}_{Y（Y）}^{秒}$ 指的是对称分布F类_Y（Y），即Y（Y）^秒.

对称化的替代方案Y（Y）就是两者都选V（V）₁(F类)和V（V）₂(F类)从而满足以下要求独立财产.

定义1。仿射等变散射泛函V（V）(F类)如果V（V）(F类_X（X）)是一个对角矩阵，只要X（X）相互独立，前提是V（V）(F类_X（X）)存在。

假设这个财产，Oja等。(2006)建议使用备注2中定义的标准化变量的主成分来获得ICA问题的解决方案。他们的解决方案可以重述如下。

定理6。除了条件1，假设Y（Y）=BX公司+μ，其中B类是非奇异的，并且X（X），说吧X（X）₁,…,X（X）_第页，相互独立。进一步，假设这两个散射泛函V（V）₁(F类)和V（V）₂(F类)满足定义1中给出的独立性属性和根ρ₁(F类_Y（Y）),…,ρ_第页(F类_Y（Y）)都是不同的。然后，转换后的变量Z轴=H（H）(F类_Y（Y）)^′Y（Y）由独立组件组成，或者更具体地说，Z轴和X（X）最多不同于排列和/或组件位置和比例。

协方差矩阵∑(F类)当然，满足定义1是众所周知的。它还可以直接显示散射函数 $K（K） (F类)$ 定义于方程式（21）也是如此。定理6是Cardoso提出的早期ICA算法的推广(1989)基于a的谱值分解峰度矩阵Cardoso的算法，他称之为四阶盲辨识算法，可以证明它等价于选择V（V）₁(F类)=Σ(F类)和 ${V（V）}_{2} (F类) = K（K） (F类)$ 在定理6中。

值得注意的是，定义1给出的独立性属性比属性弱

{X（X）}_{我} 一 n个 d日 {X（X）}_{j个} 是独立的 \Rightarrow V（V） {({F类}_{X（X）})}_{我, j个} = 0

(23)

协方差矩阵满足性质(23)，而 $K（K） (F类)$ 没有。

一个经常被忽视的观察结果是(23)通常不适用于稳健散射泛函，即独立性不一定意味着零伪相关。除协方差矩阵外，散射泛函是否满足性质是一个公开的问题(23)此外，稳健分散泛函一般不满足较弱的定义1。然而，在对称分布下，对于一般的散布矩阵，独立性在以下意义上是成立的。

定理7。让V（V）(F类)是满足条件的散射函数(3)。假设X（X）围绕某个中心对称μ∈ ℜ^第页，包含的组件X（X）相互独立。如果V（V）(F类_X（X）)存在，则它是对角矩阵。

因此，给定一个散布函数V（V）(F类)，我们可以通过定义V（V）^秒(F类) =V（V）(F类^秒)，其中F类^秒表示的对称分布F类Taskinen最近研究了利用对称化获得满足独立性的散射泛函等。(2007).

最后，我们注意到这一部分的结果可以在两个方向上推广。首先，我们考虑多个根的情况，然后我们考虑只包含X（X）都是独立的。

定理8。除了条件1，假设Y（Y）=BX公司+μ，其中B类是非奇异的，并且X（X），说吧X（X）₁,…,X（X）_第页，相互独立。此外，假设
（a）
X（X）对称于0，即。X（X）∼_d日−X（X），或
（b）
二者都V（V）₁(F类)和V（V）₂(F类)满足定义1。
然后，对于变换后的变量，使用定理2的符号表示多重根Z轴=H（H）(F类_Y（Y）)^′Y（Y）随机向量Z轴₍₁₎,…,Z轴_(米)相互独立。
定理9。除了条件1，假设Y（Y）=BX公司+μ，其中B类非单数，以及 ${X（X）}^{'} = ({X（X）}_{(1)}^{'}, \dots, {X（X）}_{(米)}^{'})$ 具有相互独立的组件X（X）₍₁₎∈ ℜ^第页1,…,X（X）_(米)∈ ℜ^下午，使用第页₁+…+第页_米=第页进一步，假设X（X）对称于0，根ρ₁(F类_Y（Y）),…,ρ_第页(F类_Y（Y）)都是不同的。然后，有一个分区{J型₁,…,J型_米}共{1，…，第页}基数为J型_k个存在第页_k个对于k个= 1,…,米这样，对于转换后的变量Z轴=H（H）(F类_Y（Y）)^′Y（Y）随机向量
${Z轴}_{(1)} = {{Z轴}_{j个}, j个 \in {J型}_{1}}, \dots, {Z轴}_{(米)} = {{Z轴}_{j个}, j个 \in {J型}_{米}}$
相互独立。更具体地说，Z轴_(j个)和X（X）_(j个)是彼此的仿射变换。

从中定理9的证明附录A，可以注意到，如果X（X）_(j个)s不是对称的。如果X（X）不是对称的，定理8和9可以应用于Y（Y）^秒，对称版本的Y（Y）.将定理6推广到以下情况：X（X）如果是独立的，则需要修改独立性属性。定义1、定理6和定理7的这种推广相当简单，因此这里不进行形式化处理。

备注3。定理9中给出的设置的多个根的一般情况更有问题。问题源于多重根可能与特定的X（X）_(j个)而是有两种或两种以上的不同X（X）_(j个)s.例如，考虑一下这种情况 ${X（X）}^{'} = ({X（X）}_{(1)}^{'}, {X（X）}_{(2)})$ ⁠，使用X（X）₍₁₎∈ ℜ²和X（X）₍₂₎∈ ℜ. 对于这种情况，V（V）₁(F类_X（X）)⁻¹ V（V）₂(F类_X（X）)是块对角线，具有2级和1级对角线块。三个特征值ρ₁(F类_Y（Y）),ρ₂(F类_Y（Y）)和ρ_三(F类_Y（Y）)对应于2阶对角块的两个特征值和最后一个对角元素，但不一定分别对应。所以，如果ρ₁(F类_Y（Y）) =ρ₂(F类_Y（Y）)>ρ_三(F类_Y（Y）)，这并不意味着最后一个对角线元素对应于ρ_三(F类_Y（Y）)，因此Z轴₍₁₎∈ ℜ²和Z轴₍₂₎∈ ℜ, 如定理2所定义的，不一定是独立的。

6.讨论和示例

虽然本文的理论结果基本上适用于任何一对散布矩阵，但在实践中，散布矩阵的选择会影响最终的ICS方法。根据我们的经验，对于一些数据集，散点矩阵的选择似乎对ICS变量的诊断图没有太大影响，特别是当数据与其中一个混合模型或一个独立成分模型一致时第5节然而，对于其他一些数据集，生成的诊断图可能对散布矩阵的选择非常敏感。通常，不同的散布矩阵对可能会揭示数据中不同类型的结构，因为偏离椭圆分布的情况可能有多种形式。因此，任何一对特定的散布矩阵是否对所有情况都是最佳的，这一点值得怀疑。与其事先选择两个散布矩阵，特别是当一个散布矩阵处于完全探索性的情况下，不知道会发生什么，不如考虑一些不同的散布矩阵对，并将所得的ICS转换视为互补的。

通过对所使用的散布矩阵的属性的基本了解，可以大致了解散布矩阵对如何影响所产生的ICS方法。为了进行讨论，我们将散射矩阵分为三大类。I类分散统计将指那些在分解点基本为零的意义上不稳健的统计。此类包括样本协方差矩阵以及一步W公司-由表达式定义的估计(7)和他们的对称版本。这类中的其他散布统计是多元符号和秩散布矩阵；参见Visuri示例等。(2000). 第二类分散统计是指那些具有有界影响函数和正分解点，但分解点不大于1的适度稳健统计/(第页+1). 此类主要包括多变量M（M）-估计，但它还包括在对数据应用凸壳剥离或椭球壳剥离后获得的样本协方差矩阵；见多诺霍和加斯科(1992). 第三类散布统计指的是高击穿点散布矩阵，详见第2.2节.II类或III类散射矩阵的对称版本，以及一步W公司-散布估计(10)使用初始II类或III类散布矩阵进行降权重的，分别被视为II类或II类散布矩阵本身。

如果一个或两个散布矩阵都来自I类，那么产生的ICS转换可能会受到一些异常值的严重影响，而代价是在数据中查找其他结构。此外，即使没有虚假的离群值和混合模型或独立成分模型第5节保持不变，但对于长尾分布，则所得样本ICS转换可能是对相应总体ICS转换的无效估计。Nordhausen、Oja和Ollila报道的模拟研究(2008)已经表明，对于ICA，通过为ICS变换选择稳健的散布矩阵，可以获得更好的性能。然而，由于其计算简单，如果已知数据集不包含任何虚假的异常值，或者如果诊断的目的是查找此类异常值，如Caussinus和Ruiz-Gazen中所建议的那样，使用I类散布矩阵是有用的(1990).

如果我们使用II类或III类散布矩阵，那么我们仍然可以通过绘制相应的稳健马氏距离来发现虚假的离群值。然而，由此产生的ICS转换不会受到虚假异常值的严重影响。离群值对第二类散布矩阵的影响比第三类散布矩阵更大，尽管即使高比例的假离群值也未必会影响第二类散射矩阵。对于严重影响II类散射矩阵的异常值，它们通常需要位于一个聚类中；参见示例Dümbgen和Tyler(2005). 的结果第5.1节尽管建议在进行ICS转换后可以识别此类聚集的异常值，即使它们不能通过基于II类统计的稳健马氏距离进行识别。

除非我们只对50%的“内部”数据的结构感兴趣，否则使用两个III类散点矩阵进行ICS转换可能不会产生好的结果。例如，假设数据来自两个多元正态分布的60-40混合，平均值相差很大，但协方差矩阵相等。然后，III类散射矩阵主要由60%分量的特性决定。因此，当为ICS使用两个III类散布矩阵时，相应的ICS根将趋于相等或几乎相等。在所有根都相等的情况下，定理3不适用。在根几乎相等的情况下，由于采样变化，样本ICS变换可能无法令人满意地揭示Fisher线性判别函数。

对于用于ICS转换的一对散布矩阵，一个合理的一般选择是使用一个II类和一个III类散布矩阵。如果我们希望避免III类散布阵所涉及的计算复杂性，那么使用两个II类散布矩阵就足够了。特别是，我们可以选择崩溃点接近1的II类散射矩阵/(第页+1），例如M（M）-椭圆Cauchy分布（Dümbgen和Tyler，2005)，以及相应的一步W公司-估计ψ(秒) =s u₂(秒)→0作为秒→∞. 这么简单W公司-散射估计具有重降影响函数。根据我们的经验，使用ICS的III类散布矩阵似乎并没有揭示任何其他方法无法获得的数据结构。

这里的评论和建议都是高度推测性的。什么样的散射矩阵对最适合检测特定类型的偏离椭圆分布的问题仍然是一个悬而未决的问题。特别是，有兴趣发现在ICS方法中使用至少一个III类散布矩阵对哪种类型的数据结构有利。最有可能的是，当使用非常高维的数据集时，可能会产生一些优势，在这种情况下，计算III类散射矩阵所需的计算强度会大大增强；参见罗塞乌和范德里森的例子(1999).

我们在以下示例中演示了一些概念。这些示例说明了一些数据集如何使用ICS转换来构建诊断图。它们还可以作为前几节中所述理论的例证。

6.1. 示例1

卢梭和范德里森(1999)分析了由以下内容组成的数据集n个=677块金属板第页=测量了9个特性。对于该数据集，他们计算了样本均值和协方差矩阵以及中心和散布的最小协方差行列式估计。他们的论文有助于说明使用高崩溃点多元估计或III类统计来发现数据集中多个离群值的优势。

对于我们的示例，我们选择了两个II类位置和散布统计。第一次估计 $({\hat{μ}}_{1}, {\hat{V（V）}}_{1})$ 被视为从椭圆柯西分布导出的最大似然估计。这对应于M（M）-估计(9)具有u个₁(秒) =u个₂(秒)=(第页+1)/(秒+1）和u个_三(秒)=1. 这个M（M）-估计这个方程M（M）-众所周知，估计通常承认一个唯一的解，无论初始值如何，都可以通过简单的重加权算法找到该解。

对于我们的第二个估计 $({\hat{μ}}_{2}, {\hat{V（V）}}_{2})$ ⁠，我们取样本平均向量和样本协方差矩阵，只使用由柯西公式导出的马氏距离测量的内部50%的数据M（M）-估计，即。 ${d日}_{我} ({\hat{μ}}_{1}, {\hat{V（V）}}_{1})$ ⁠。这对应于多元一步W公司-散布估计(10)具有u个₁(秒) =u个₂(秒) =我(秒≤1）和u个_三(秒)=1，并有初步估计 ${\hat{μ}}_{0} = {\hat{μ}}_{1}$ 和 ${\hat{V（V）}}_{0} = {\hat{σ}}_{1}^{2} \hat{V（V）}$ ⁠，其中 $\hat{σ} = 米 e（电子） d日我一 n个 {{d日}_{我} ({\hat{μ}}_{1}, {\hat{V（V）}}_{1}), 我 = 1, \dots, n个}$ ⁠.

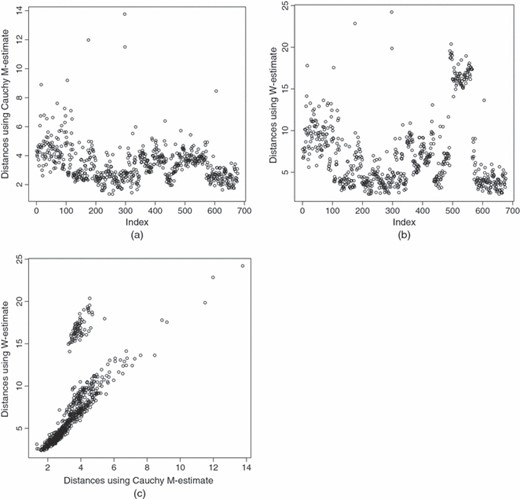
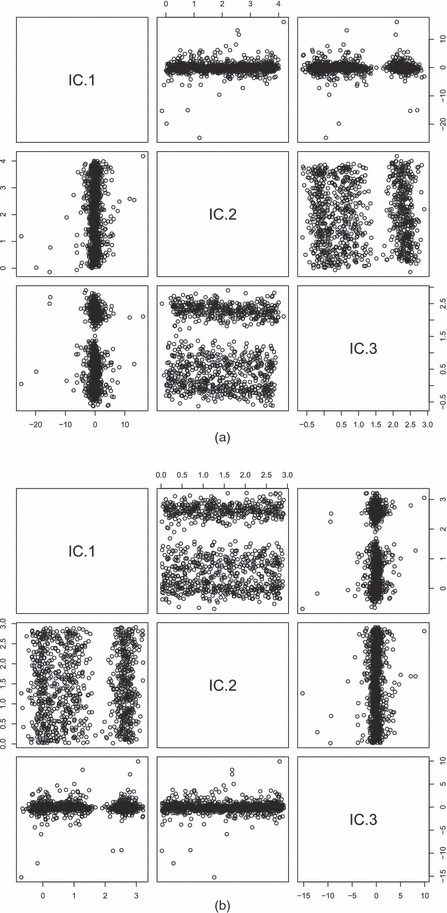
图1（a）和1（b）显示的Mahalanobis距离图 ${d日}_{我} ({\hat{μ}}_{1}, {\hat{V（V）}}_{1})$ 和 ${d日}_{我} ({\hat{μ}}_{2}, {\hat{V（V）}}_{2})$ 分别使用图1（c）是这两组距离的散点图。这些图与基于经典马氏距离和基于Rousseeuw和van Driessen中给出的最小协方差行列式的图有些相似(1999). 如卢梭和范德里森所述(1999),图1（b）和1（c）表明，至少有三个不同的组：前100个点，指数为491-565的点，其余的点。指数本身是在获得马哈拉诺比距离时未考虑的因素。它代表一种生产秩序，显然是一个重要因素。指数的影响在个别变量的一些曲线图中也很明显。

图1

新标签中打开下载幻灯片

示例1：基于（a）的马氏距离 ${\hat{V（V）}}_{1}$ ⁠，（b） ${\hat{V（V）}}_{2}$ 和（c） ${\hat{V（V）}}_{1}$ 与 ${\hat{V（V）}}_{2}$

马哈拉诺比斯距离图的比较图1（c）表示数据并非来自椭圆对称分布。否则，两个距离的散点图将近似为线性，因为两个位置统计将估计相同的中心，而两个散点矩阵将估计比例常数范围内的相同人口形状矩阵，因此，由此产生的马哈拉诺比斯距离将大致成比例。数据的非椭圆性质很可能归因于指数因子产生的混合物。

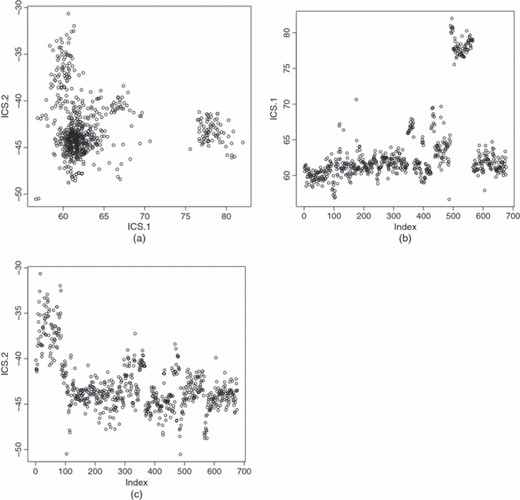
中给出的仿射不变图图1不要揭示图中观察到的三组是否对应于三个簇，因为马哈拉诺比斯距离没有显示点之间的相对距离。数据的更完整的仿射不变视图可以从基于散布矩阵的数据ICS变换的成对图中获得 ${\hat{V（V）}}_{1}$ 和 ${\hat{V（V）}}_{2}$ 如上所述。对于此分析，生成的ICS根为 $小时 ({\hat{ρ}}_{1}, \dots, {\hat{ρ}}_{9}) = (19.94, 5.27, 3.68, 3.41, 2.89, 2.61, 2.12, 1.69, 1.62)$ ⁠.图2（a）显示了前两个ICS组件的散点图，其中图2（b）和2（c）分别示出了前两个ICS组件。在这些图中也可以看到这三组。此外，我们可以确定各组之间的差异。特别值得注意的是，与索引491-565相关的组基本上位于其他数据的特定方向，即由第一个ICS组件确定的方向，而前100个点基本上位于不同的方向，由第二个ICS部件确定。最后，如果我们绘制其他ICS组件，各种孤立的异常值也会变得可见。

图2

新标签中打开下载幻灯片

示例1：第一和第二ICS坐标基于 ${\hat{V（V）}}_{1}$ 和 ${\hat{V（V）}}_{2}$

6.2. 示例2

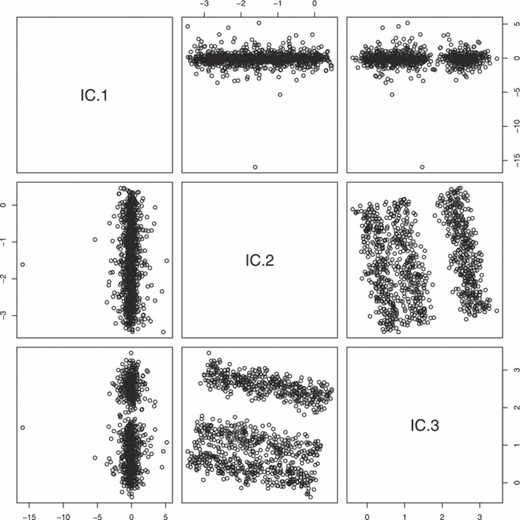
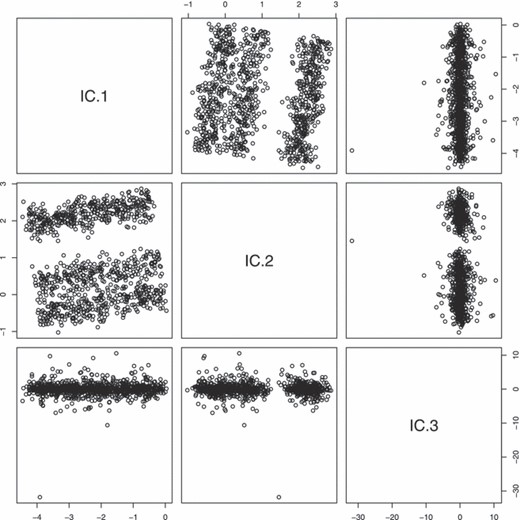
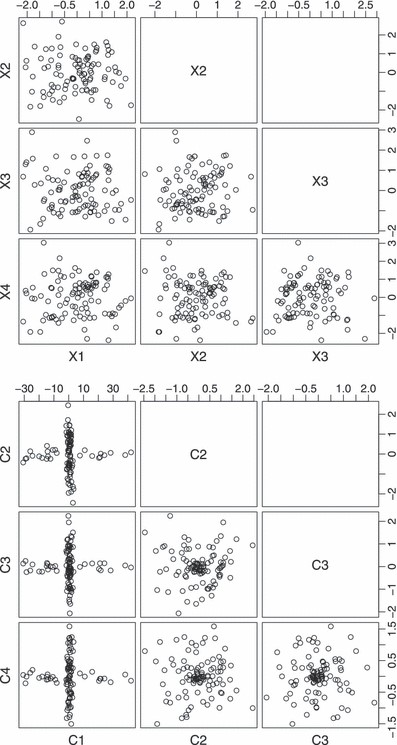
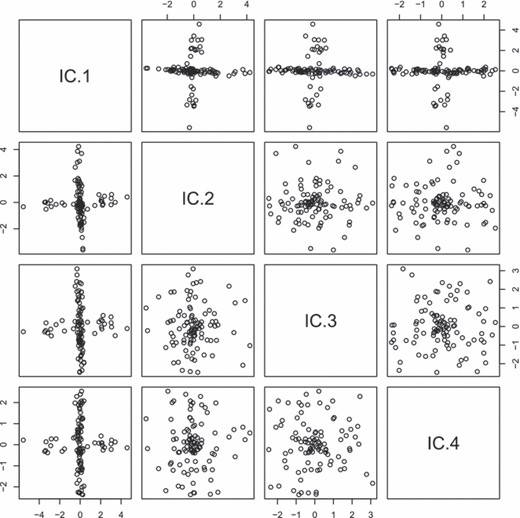
中给出的配对图图3（a）产生于模拟大小的随机样本n个=500来自a第页=4维分布。可以说，这个数据集似乎没有什么特别值得注意的地方。样本方差–中数据集的协方差矩阵图3（a）是单位矩阵，因此主成分分析不指示任何特定的兴趣方向。然而，如果我们将ICS转换应用于这些数据，我们可以发现数据中有趣的隐藏结构，如中给出的配对图所示图3（b）。相应的ICS根为 $({\hat{ρ}}_{1}, {\hat{ρ}}_{2}, {\hat{ρ}}_{三}, {\hat{ρ}}_{4}) = (1.49, 1.13, 0.81, 0.73)$ ⁠。对于本例，原始数据年_我对应于通过模拟单位圆上的均匀分布而生成的分布的仿射变换，其中添加了平均值为0、标准偏差为0.01的独立正态噪声，并与标准正态分布和t吨-分布在5个自由度上。请注意，无论模拟数据如何进行仿射变换，得到的ICS坐标始终由以下公式给出图3（b）.

图3

新标签中打开下载幻灯片

示例2：（a）模拟四维数据集和（b）ICS通过使用 ${S公司}_{n个}$ 和 ${K（K）}_{n个}$

这里用于ICS转换的两个散布矩阵是样本协方差矩阵S公司_n个和散射矩阵的样本版本 $K（K） (F类)$ 在中给出方程式（21），即

{K（K）}_{n个} = \frac{1}{n个} {\sum^{​}}_{我 = 1}^{n个} {{(年_{我} - \bar{年})}^{'} {S公司}_{n个}^{- 1} (年_{我} - \bar{年}) \times (年_{我} - \bar{年}) {(年_{我} - \bar{年})}^{'}} .

(24)

${K（K）}_{n个}$ 可以视为一步到位W公司-散布估计(7)通过按经典马氏距离平方加权每个点，即选择u个₂(秒) =秒和u个_三(秒)=1，带 $秒_{我} = {(年_{我} - \bar{年})}^{'} {S公司}_{n个}^{- 1} (年_{我} - \bar{年})$ ⁠.作为对散布的估计， ${K（K）}_{n个}$ 通过实际对异常值进行加权获得。即使两者都不是S公司_n个也不是 ${K（K）}_{n个}$ 是对散布的稳健估计，它们可以揭示此特定数据集中的结构，因为它不包含虚假的异常值。如果我们只考虑马哈拉诺比距离或其稳健版本，那么无论有无假离群值，这样的结构都很难检测到。与中显示的结果类似图3（b）在ICS转换中使用几乎任何其他散点矩阵对时都会出现这种情况。

请注意第5.2节直接适用于此示例，但此示例属于备注3中讨论的类型。对于这个例子的功能版本，我们有 ${X（X）}^{'} = ({X（X）}_{(1)}^{'}, {X（X）}_{(2)}, {X（X）}_{(三)})$ ⁠，其分布X（X）₍₁₎∈ ℜ²单位圆上的均匀分布加上方差为0.1的二元球面法向噪声，X（X）₍₂₎∈ ℜ 具有标准正态分布，X（X）₍₃₎∈ ℜ 有一个t吨-5自由度分布X（X）₍₁₎,X（X）₍₂₎和X（X）₍₃₎相互独立。通过使用不变性参数，可以表明，无论选择哪两个散布矩阵，至少有两个根ρ₁(F类_Y（Y）),…,ρ₄(F类_Y（Y）)是相等的，因此最多有三个不同的根。对于三个不同根的情况，与多个根相关联的两个ICS变量对应于X（X）₍₁₎，并且与两个不同根相关联的ICS变量对应于X（X）₍₂₎和X（X）₍₃₎.三个不同根的情况往往成立，除了非常特殊的选择V（V）₁(F类)和V（V）₂(F类). 特别是，它可以显示为支持选择V（V）₁(F类)=Σ(F类)和 ${V（V）}_{2} (F类) = K（K） (F类)$ ⁠，最小的根是多个根，最大的根与X（X）₍₂₎第二大根与X（X）₍₃₎。因此，中显示的结果图3如预期。

6.3. 其他示例

我们在这里简要解释一些其他示例的结果。第一个是经典的Fisher虹膜数据，可以在统计包R（R Development Core Team，2005). 此数据集包括第页=4个测量值，即萼片长度、萼片宽度、花瓣长度和花瓣宽度n个=150朵鸢尾花。这150朵花属于三种不同的鸢尾属植物。假设我们忽略了数据的组分类，并对n个=150个数据点，使用样本协方差矩阵和CauchyM（M）-估计。结果表明，第一个ICS分量与第一个线性判别函数几乎相同，如果我们使用品种作为组变量进行判别分析，则会得到第一个线性鉴别函数，两者之间的样本相关性为0.99，尽管前者没有考虑组分类。对于我们可以选择的几乎任何一对散布矩阵，本例中ICS方法的结果都是相似的。这可以归因于数据与中讨论的混合物模型一致第5.1节并且没有任何明显的异常值。

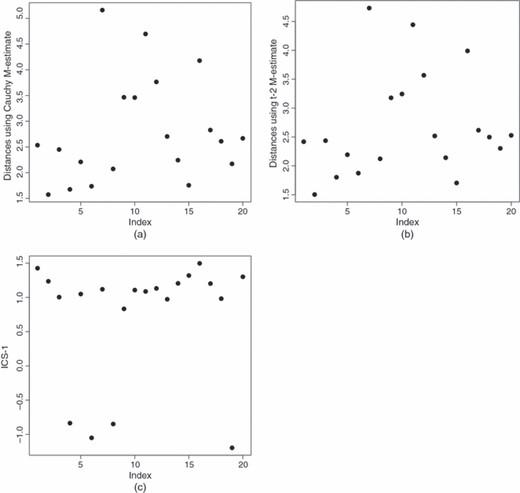
下一个示例使用Rousseeuw和Leroy中给出的修改后的木材重力数据集(1987). 该数据集经常用作说明异常值检测方法的示例。它包括n个=20个观察值第页=6个维度，其中四个观测值是原始作者放入数据集中的人工异常值。卢梭和勒罗伊(1987)演示了经典的异常值检测方法如何无法发现这些异常值，而使用基于高崩溃点位置和散布统计的马氏距离很容易发现这些异常。对于这个数据集，我们计算了一个CauchyM（M）-估计值和at吨₂M（M）-估计值，其分解点分别为1/7=0.143和1/8=0.125。与示例1不同，对应的马哈拉诺比斯距离图都不是图4（a）和4（b），显示任何异常值，并且这两个图非常相似。由于污染比例为4/20=0.20，因此我们预计马哈拉诺比斯距离不会基于这两者之一M（M）-如果异常值形成一个簇，估计值将揭示异常值；见泰勒(2002). 然而，如果异常值确实形成了一个集群，那么第5.1节建议基于这两个散射估计的ICS变换可以将数据的主要聚类与四个异常值的聚类分离。这里的情况就是这样，所有四个异常值都清楚地出现在第一个ICS坐标中；看见图4（c）。这里的结果再次与ICS转换中使用的散布矩阵无关。

图4

新标签中打开下载幻灯片

修改木材重力数据集的ICS示例

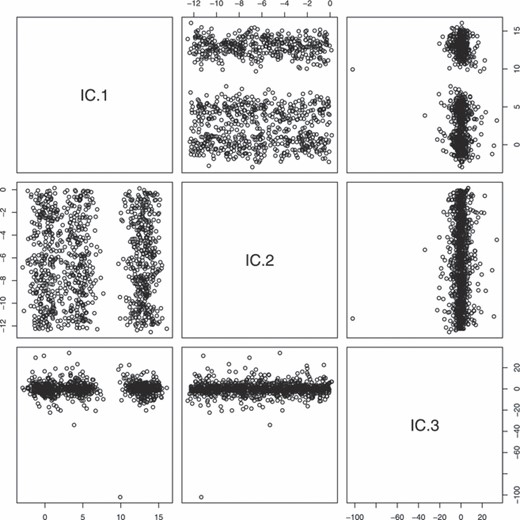
最后一个例子，考虑RANDU数据集，也可以在R（R开发核心团队，2005);图5（a）。这包括n个=300个观察值第页=3维，假设由随机数生成器获得。然而，实际上，数据位于平行平面上，在原始坐标中并不明显。然而，如果我们使用样本协方差矩阵将该数据集转换为ICS坐标S公司_n个和一步到位W公司-基于以下公式给出的成对差异的估计

\hat{V（V）} = \frac{2}{n个 (n个 - 1)} {\sum^{​}}_{我 = 1}^{n个 - 1} {\sum^{​}}_{j个 = 我 + 1}^{n个} \frac{(年_{我} - 年_{j个}) {(年_{我} - 年_{j个})}^{'}}{{{(年_{我} - 年_{j个})}^{'} {S公司}_{n个}^{- 1} (年_{我} - 年_{j个})}^{2}},

(25)

然后，数据中的平行平面结构在成对图中变得明显；看见图5（b）。

图5

新标签中打开下载幻灯片

RANDU数据集上的ICS示例

在最后一个示例中，数据产生的假定分布不是椭圆分布，而是单位立方体内的均匀分布，这属于备注1中讨论的分布类别。因此，我们可以预计，偏离这种假定分布的情况将反映在ICS分析中。数据集中的平行线可以看作是由对称奇异分布的位置混合引起的。因此，在第5.1节，虽然由于混合组分不是严格的椭圆分布，因此不直接适用，但给出了为什么可以检测到这种模式的一些理由。然而，对于这个示例，生成的ICS对图对所使用的散布矩阵的选择相当敏感。特别是，如果我们替换分母中的平方项方程式（25）拥有的力量q个，然后针对q个<1.5 RANDU数据集中的行不是很明显。相反，结果似乎并不严重依赖于q个对于q个>1.5.

7.结束语

7.1. 与投影追踪的关系

除了与混合模型和ICA的关系外，ICS方法背后的概念与投影寻踪方法有相似之处，特别是与Huber(1985)被称为III类投影追踪方法，即研究数据仿射不变方面的方法。在投影追踪中，我们通常寻求有趣的，通常是指非正常的数据投影；参见库克示例等。(1993)、弗里德曼和图基(1974)、胡贝尔(1985)还有琼斯和西布森(1987). 在投影追踪上下文中，对投影有趣之处的评估仅取决于特定投影的分布。一般来说，投影追踪方法中的追踪往往是计算密集型的。相比之下κ(小时)它是由方程式（14）ICS中使用的严格来说并不是线性组合分布的函数小时^′Y（Y）而是取决于多元分布F类通过V（V）₁(F类)和V（V）₂(F类). 的顺序优化κ(小时)由提供方程式（15）和(16)具有特征向量的解析解，因此计算量不高。从这个意义上说，ICS可以被视为一种无需追求努力的投影追求。

投影寻踪本身与ICA之间的关系有很好的记录；参见Hyvärinen示例等。(2001). 几乎所有针对ICA问题提出的算法都倾向于投影寻踪性质。然而，一个值得注意的例外是Cardosa之前提出的算法(1989). 同样值得注意的是，Peña和Prieto观察到基于峰度的投影追踪与多元正态混合之间的关系(2001). 他们表明，对于协方差矩阵相等的两个多元正态分布的混合物，经典峰度系数最小的投影或最大的投影对应于混合物两个元素之间的Fisher线性判别函数。Yenyukov也得到了类似的结果(1988)当使用稳健方差与样本方差之比作为投影指数时。他还建议使用κ(小时)基于样本协方差矩阵和协方差矩阵的稳健估计，作为此类投影指数的近似值。

7.2. 其他相关方法

如中所述第1节，ICS可以被视为Ruiz-Gazen所指内容的更一般的表述(1993)还有Caussinus和Ruiz-Gazen(1995)作为广义主成分分析。从矩阵开始，他们就使用了这个术语方程式（11）通常被称为广义特征值-特征向量问题。然而，文献中经常使用广义主成分分析这一术语来描述主成分的各种无关推广。因此，为了将该方法与其他被称为广义主成分的方法区分开来，并强调该方法的中心特性，我们使用ICS术语。此外，我们不认为ICS是主成分分析的泛化；我们也不认为ICS是主成分分析或稳健版主成分分析的竞争对手，而是一种补充方法。主成分分析涉及了解数据云的扩散或散布，这是仿射不变设置中无法识别的属性。正如Huber建议的那样(1985)通过探索数据集的仿射不变量及其位置-尺度信息，可以更全面地理解数据集。

最近，克里奇利等。(2007)建议对标准化数据进行主成分分析，如备注2所述，他们称之为主轴分析。因此，当我们采取以下措施时，他们的建议与ICS转换的特殊情况相对应 ${\hat{V（V）}}_{1} = {S公司}_{n个}$ ⁠，样本协方差矩阵，以及 ${\hat{V（V）}}_{2}$ 是一个一步重加权协方差矩阵，其权重对应于经典平方马氏距离的倒数，即。 ${\hat{V（V）}}_{2}$ 是一步到位的W公司-表达式中定义的估计(7)带权重函数u个₂(秒)=1/秒和u个_三(秒)=1，使用样本均值和协方差矩阵作为初始估计。他们将其方法称为主轴分析，因为 ${\hat{V（V）}}_{2}$ 取决于标准化样本向量 ${X（X）}_{我} = {S公司}_{n个}^{- 1 / 2} ({Y（Y）}_{我} - \bar{Y（Y）})$ 仅通过其对相反方向±X（X）_我/‖X（X）_我‖. 克里奇利内部等。(2007)当数据来自椭圆分布的混合分布，甚至可能具有不同形状矩阵的分布时，给出了启发性的论点，以激励主轴分析用于检测分离良好的簇。

生成仿射不变坐标的另一种方法是Chakraborty和Chaudhuri提出的变换-重传（TR）方法，这在多元非参数统计领域是众所周知的(1996,1998). 在单样本问题中，TR方法的基本思想是通过将每个观测值乘以包含第页观察结果。尽管TR方法在n个观察结果，除非第页用于标准化的观测值是随机选择的，或者使用一些置换不变准则来选择它们。无论如何，用泛函来表示TR方法是困难的，这使得TR变换的理论性质难以研究。然而，TR变换并不是数据的探索性变换，而是用于生成仿射不变多元非参数检验的步骤。同样，ICS转换也可用于生成此类测试（参见Nordhausen示例等。(2006))或者通常用于定义单变量概念的多变量版本。的仿射等变分量多元中值Y（Y）∈ℜ^P（P）例如，可以定义为μ_Y（Y），其中 $μ_{Y（Y）}^{'} = (米 e（电子） d日我一 n个 ({Z轴}_{1}), \dots, 米 e（电子） d日我一 n个 ({Z轴}_{第页})) H（H） {({F类}_{Y（Y）})}^{- 1}$ 具有Z轴=H（H）(F类_Y（Y）)^′Y（Y）对应于ICS转换。在这种情况下，ICS的主要重点不是降维，而是完整的仿射不变坐标系。

7.3. 总结和继续研究

在本文中，我们引入了ICS的概念，作为探索多元数据的通用仿射不变方法。在消除了多元数据集中中心和分散的影响后，ICS基本上解决了数据集中是否还有其他感兴趣的内容的问题。本文还展示了ICS变换在椭圆混合模型和ICA模型下的理论行为。

从统计建模的角度来看，有人可能会认为，除了非常具体的问题外，ICA模型似乎不切实际。尽管如此，ICA算法在许多经常应用多元方法的领域中越来越流行，并且即使ICA模型看起来不现实，通常也会产生有趣的结果。本文的原始目标之一是给出一个关于为什么会这样的无模型解释。本文将ICS与混合模型和ICA相关联的结果提供了这样的解释。

如中所述第6节，本文的理论结果基本上适用于两个散布矩阵的任何选择。然而，ICS变换的统计可变性和鲁棒性特性确实取决于所使用的特定散射矩阵。中给出的关于混合模型下ICS的结果第5.1节建议该方法可能具有一些天然的稳健性，至少在检测离群值簇方面，即使估计本身不是特别稳健。

与所有特征向量方法一样，ICS变换的稳定性将取决于理论根的扩散ρ₁(F类),…,ρ_第页(F类)，这又取决于散射矩阵的选择。作者及其学生目前正在研究散射矩阵的选择对所得ICS方法的影响，以及与ICS方法相关的统计特性。与其事先选择两个散布矩阵，一个很有前途的策略似乎是允许数据根据观测到的各自根的分离情况，从一大类散布矩阵中选择两个散射矩阵。不幸的是，这种数据驱动的方法使得对结果方法统计特性的理论研究更具挑战性。

讨论Tyler、Critchley、Dümbgen和Oja的论文

J.T.肯特(利兹大学)

这是一篇令人愉快的论文。与统计中的许多最佳想法一样，它是基于一个简单但优雅的想法，这导致了发现数据模式的强大新方法。用户需要做的只是指定两个散射函数（有效地为特定数据集指定两个度量），然后执行相对特征分析。正如本文的示例所表明的，这种新方法在广泛的环境中证明了其价值。

双重度量在多元分析中有着悠久的历史。最简单的例子可能是主成分分析本身，它涉及一个矩阵（通常是样本协方差矩阵）相对于另一个矩阵的特征分解（通常是隐含的单位矩阵）。另一个例子出现在多元方差分析中，它也被称为判别分析，根据“组间”和“组内”平方和和乘积矩阵B类和W公司（或者，根据T型=B类+W公司和W公司)尽管在这种情况下，需要事先了解分组结构。这两个例子涉及数据的二次函数，而本文的重点是数据的非二次函数。

随机变量的最简单非二次函数U型是峰度，它的形式是kurt(U型) =E类(U型⁴)−3，当U型居中并按比例缩放，以使平均值为0，方差为1。区分三种情况很有用：

（a）
库尔特(U型)=0，在正态下成立，以及备选方案
（b）
库尔特(U型)>0和
（c）
库尔特(U型)<0,

这可以分别称为“超高斯”和“亚高斯”情况。超高斯情形出现在长尾分布中，而亚高斯情形则出现在两个具有不同平均值的正态分布的“平衡”混合中。这里的平衡意味着混合比例离 $\frac{1}{2}$ 方差也没有太大差异。当方差相等时，可以显式地刻画平衡混合物的类别；例如，请参见，第5.1节Peña和Prieto（2001）。

在中查找结构的一种方法第页-维数随机向量Y（Y）（具有均值0和协方差矩阵∑）是为了寻找线性组合一最大化绝对的峰度|kurt(一^′年)|该准则构成了独立成分分析（ICA）标准算法之一的基础。然而，上面的段落表明，当怀疑存在集群时，更好的方法可能是将签署峰度库尔特(一^′Y（Y）)这导致了所谓的“子ICA”算法；看，比如布格里恩和肯特(2005)了解更多详细信息。

所有四阶矩的集合形成一个四向数组（因此不定义度量）。由于峰度涉及四次函数一在这个四向阵列上，这些算法中的任何一种都必须进行数值优化。

本文通过将四阶矩的全四向数组替换为选定的四阶矩矩阵来解决这个数值问题， $K（K） = E类 {({Y（Y）}^{'} Σ^{- 1} Y（Y）) Y（Y） {Y（Y）}^{'}}$ 在里面方程式（21），并将四次优化替换为二次优化。因此，一个自然的问题是，哪种标准能够更深入地了解多元数据的结构，

k个 u个 第页 t吨 (一^{'} Y（Y）) 或 一^{'} K（K） 一 / 一^{'} Σ 一 ?

此外，这里有什么见解可以为更一般的散射泛函的分析提供指导吗？

我还想到了其他几个问题。

（a）
特征值的排序：论文几乎没有区分 ${V（V）}_{1}^{- 1} {V（V）}_{2}$ 和 ${V（V）}_{2}^{- 1} {V（V）}_{1}$ ⁠将其中一个矩阵标记为比另一个矩阵“更稳健”，并区分最大特征值和最小特征值的解释是否有帮助（参见上述子ICA）？
（b）
估算数据中心：这一主题在论文中几乎没有得到讨论，但它似乎具有潜在的重要性。位置功能的选择重要吗，特别是对于倾斜数据？还是对称化成功地解决了这个问题？如果不使用对称化，在定义矩阵时是否需要强制执行位置的通用估计V（V）₁和V（V）₂?
（c）
第三个时刻：本文使用并扩展了四阶矩（峰度）。是否值得调查和扩展第三矩（偏度）？
（d）
高维度：本文中的示例涉及适度维的数据集。是否有机会利用高维数据进行洞察(n个<第页或n个≪第页)，在正规化之后？

让我以一个更哲学的问题结束。作者利用稳健性理论的思想来激励本文中的方法，该理论是为了防止异常值而开发的。然而，本文更多关注的是模式检测，这是一个更微妙的问题。为一个问题开发的方法为另一个问题提供了工具，这仅仅是偶然的发现吗，还是有更深层次的东西在发生？

这是一篇引人入胜的论文，为多元数据中的模式搜索开辟了一个全新的方向。我很高兴提议投感谢票。

特雷弗·林格罗斯(斯温顿克兰菲尔德大学)

多元分析往往似乎是一个随机分类的模糊相关方法的集合体，而不是一个相干的领域，因此，看到一篇展示了几种方法之间联系的论文是非常令人鼓舞的，更重要的是，它揭示了一系列潜在有用的推广和特殊情况。

作者正确地指出，当表面上相同参数的不同稳健估计值产生不同的答案时，这不一定是坏事，因为这些差异中包含信息。类似地，在介绍统计学的讲座中，我们经常提到，对于对称分布的样本，平均值、中位数和模式都大致相同，因此，如果它们都不同，那么它会告诉我们一些有用的信息。本文提供了一种在多元环境中进行此类比较的令人信服的方法，读者可以通过类比了解在多元方差分析和典型变量分析中组内和组间协方差矩阵的类似用法。

然而，支持投票的人的工作更为关键，因此我们可能会问一个明显的问题，即拟议的方法在实践中的效果如何，特别是它们对我们现有的方法有什么补充？有些例子不太令人信服。在口头陈述中，人们承认，事实上，在木材重力数据的矩阵图中可以很清楚地看到外围集群。忽略响应变量和解释变量之间的区别（如本文所述），主成分分析（PCA）解的双点图（前两个轴上79%的方差）清楚地选择了聚类，并表明它们在x个₂和x个₅以及其他变量的低于平均值，这在原始数据中可以清楚地看到。同样，作者在《诺德豪森》中指出，在费希尔虹膜数据中区分物种也很容易，因为简单的矩阵图再次显示出花瓣大小的明显差异等。(2008)这种简单的PCA几乎与不变坐标选择一样好。诚然，这是一篇主要是理论性的论文，所以这些数据集是为了说明而不是为了真正感兴趣，但即使考虑到这一点，它们看起来还是过于简单。类似地，Nordhausen中不变坐标选择作为独立分量分析的图像混合示例等。(2008)（第24-26页），通过使用PCA可以几乎同样好地执行（在R中），在本例中，PCA似乎能够更好地处理输出混合数超过输入信号数的情况。

我们倾向于在已发表的作品中使用和重复使用相同的玩具示例，这是对我们所有人的批评，这很容易让愤世嫉俗的局外人怀疑我们的方法只在某些有限的情况下有效。特别是，我想建议暂停进一步公开使用费希尔虹膜数据！

我有两个最后的评论。首先，本文主要关注新轴上的坐标分数，但在许多情况下，特征向量系数也会引起关注。可以生成有意义的Biplot吗？其次，最后一段提到了基于观测到的特征值分离的离散矩阵的数据驱动选择（假设分离越大越好）。无论如何，样本特征值通常比总体特征值分布得更广，这将倾向于从这些高估的分离值中挑选出最大的一个。不过，这是好是坏？在搜索离群值时，它可能会变得很好，但在尝试对分布的大部分进行建模时，它会变得很糟糕。

在阅读这篇论文时，作者们显然是从不同的角度分别开始这项工作的。其中一位作者证实了这一点：他们是独立工作的，直到其中三人意识到他们在一次会议上都在谈论同一件事。这是一个令人愉快的自我参照方面的文件，这三个独立的组成部分的工作可以由读者混合。

然而，上述批评并不多见，因为这是一篇非常有趣的论文，它为更多研究方法及其实际应用的论文指明了方向。近年来，多元统计的发展似乎落后于回归建模和贝叶斯方法等领域，本文将有助于激发该领域的新兴趣。这份文件是一份非常受欢迎的补充文件，我毫不犹豫地附议感谢票。

感谢票以鼓掌方式通过。

戴维·潘戴文(布鲁塞尔自由大学)

除了在检测偏离椭圆度方面所起的作用外，不变坐标选择（ICS）还可能有助于在文献中提供的许多多元模型中为手头的数据选择合适的模型：椭圆模型的（混合）、第5.2节（另见诺德豪森等. (2009年b))，斜椭圆模型（例如，请参见Genton(2004))等。这一讨论部分支持了这一说法，提出了一种非正式的图形方法，使我们能够“测试”零假设 $ℋ_{0}^{集成电路}$ IC模型的适用范围。

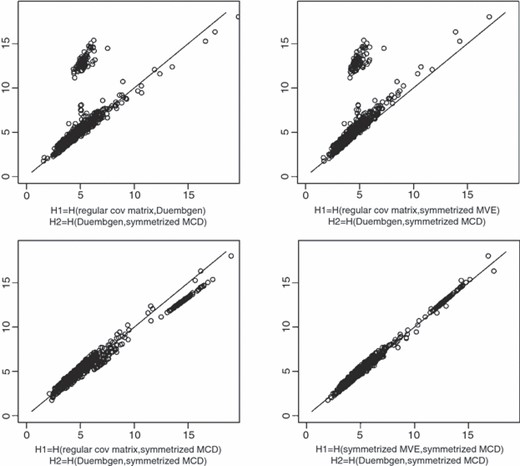
在图1（c），它显示了两个位置-散布估计 $({\hat{μ}}_{我}, {\hat{V（V）}}_{我}), 我 = 1, 2$ ⁠，可用于检测偏离椭圆度的情况，基于这样一个事实，对于任何这样的耦合，在椭圆度下，我们应该 ${d日}_{我} ({\hat{μ}}_{2}, {\hat{V（V）}}_{2}) \approx λ {d日}_{我} ({\hat{μ}}_{1}, {\hat{V（V）}}_{1})$ 对一些人来说λ>0.对于 $ℋ_{0}^{集成电路}$ ⁠，我们可以类似地考虑使用三个或四个不同的散布估计来推导——典型地，通过定理5——一对一致估计 ${\hat{H（H）}}_{我}, 我 = 1, 2$ ⁠，用于基础混合矩阵H（H）（显然，对 ${\hat{H（H）}}_{1}, {\hat{H（H）}}_{2}$ 和H（H）这里，例如Z轴-R包ICS的标准化；参见诺德豪森等。(2008)详细信息）。虽然结果之间的距离合适（Frobenius类型） ${\hat{H（H）}}_{1}$ 和 ${\hat{H（H）}}_{2}$ 将为 $ℋ_{0}^{集成电路}$ ⁠，一个直接的图形工具，其精神与图1（c），是的散点图ICS距离 $({d日}_{我}^{内部控制系统} ({\hat{H（H）}}_{1}), {d日}_{我}^{内部控制系统} ({\hat{H（H）}}_{2})), 我 = 1, \dots, n个$ 具有

{d日}_{我}^{内部控制系统} ({\hat{H（H）}}_{我}) : = \sqrt {{({\hat{H（H）}}_{我}^{'} {Y（Y）}_{我} - {\hat{μ}}_{我}^{内部控制系统})}^{'} {({\hat{Λ}}_{我}^{内部控制系统})}^{- 2} ({\hat{H（H）}}_{我}^{'} {Y（Y）}_{我} - {\hat{μ}}_{我}^{内部控制系统})},

哪里 ${\hat{μ}}_{我}^{内部控制系统}$ 是我第ICS和 ${\hat{Λ}}_{我}^{内部控制系统}$ 是对角矩阵，收集了相应的边际中值绝对偏差。低于 $ℋ_{0}^{集成电路}$ ⁠，这种散点图中的所有点都应该大致位于主对角线上，这使我们能够检测到可能违反 $ℋ_{0}^{集成电路}$ ⁠.

在这里，各种散布矩阵的选择也是一个微妙的问题。但仍有人可能会认为，将分散矩阵与不同的稳健性属性相结合可以揭示有趣的特征。如图所示（使用与中相同的数据第6.1节)英寸图6，有趣的是，只有完全基于稳健散布矩阵的图似乎与 $ℋ_{0}^{集成电路}$ ⁠.

图6

ICS距离的散点图（diICS（H^1），diICS，H^2），i=1，…，n，其中H^1=H（Vl1，V^l2）

新标签中打开下载幻灯片

ICS距离散点图 $({d日}_{我}^{我 C类 S公司} ({\hat{H（H）}}_{1}), {d日}_{我}^{我 C类 S公司} ({\hat{H（H）}}_{2})), 我 = 1, \dots, n个$ ⁠，使用 ${\hat{H（H）}}_{1} = H（H） ({V（V）}_{我 1}, {\hat{V（V）}}_{我 2})$

然而，正如论文中漂亮地显示的那样，ICS的相关性远远超出了IC模型，我祝贺作者们在这十年里在多元统计领域所做的最令人耳目一新和鼓舞人心的工作之一。

默文·斯通（伦敦大学学院）

这篇有用的论文从任何数据附带的笛卡尔坐标开始，逐渐发展到矩阵，最后达到仿射不变性，换句话说，就是坐标自由的露天几何！

我怀疑作者是否依赖于第2节——4在编写需要使用坐标和矩阵的计算机程序之前，要有信心做到这一点。如果坐标自由的伟大代表保罗·哈尔莫斯（Paul Halmos）深入研究概率和统计学，无论何时何地，只要坐标和矩阵妨碍我们理解，那么这篇论文的读者就可以不用读代数了。

现在供应替代稀粥还为时不晚。

（a）
关于多元分析的最薄、影响最小的书籍中的几个概念和术语： $V（V）$ 是变量的向量空间（由第页名称）和 $ε$ 是其评价者的双重空间e（电子）变量的评估v（v）（可能的“观察”，如果v（v）是一个名称）是双线性乘积[e（电子）,v（v）].V（V）₁和V（V）₂内部产品是否打开 $V（V）$ 以及所谓的“协方差算子”（线性 $V（V） \to ε$ ⁠).
（b）
实现不动点理论可以为简化等效特征分析打开大门V（V）₁和V（V）₂: $S公司 = {υ : ({V（V）}_{1} + {V（V）}_{2}) (υ, u个) = 1 和 ({V（V）}_{1} - {V（V）}_{2}) (υ, u个) \geq 0 对于一些固定的 u个}$ 是的闭合曲面(V（V）₁+V（V）₂)-半球 $V（V）$ ⁠.转型 $T型 : S公司 \to S公司$ 定义为 $秒 \to ρ (秒) {V（V）}_{2}^{- 1} {V（V）}_{1} 秒$ 是连续的。所以 $S公司$ 有一个固定点小时具有V（V）₂小时=ρ(小时)V（V）₁小时因此，你可以带着“去看照片”的意愿从这里开始拍摄。
（c）
我在这里提到的图片可以下载，在Stone中有更详细的解释(2008). 它们令人放心的特征是仿射不变量，就像三条线在一个点上相遇一样明显，对于统计学家来说，简单地发现它们可能比数独更有益和解放。

克里斯蒂安·海宁(伦敦大学学院)

作者很好地为一类投影方法提供了框架，以可视化多元数据集。关于形状矩阵选择的评论主要集中在稳健性方面。我认为其他考虑因素也很重要，在许多情况下，选择比论文所建议的更重要。

我展示了一种情况，在这种情况下，论文和ICS软件包中建议的选择并不奏效，而另一种形状矩阵效果更好。

这需要一个质量定义，这取决于感兴趣的模式，这里是聚类。在三维数据集中具有一维有趣模式的基准情况下，一个好的投影方法应该提供什么？与高维情况下的预期类似，图案应该沿着第一个或最后一个不变坐标出现。

示例数据集的三个变量是独立于t吨₂-分布、均匀分布和包含300个点的混合 $N个 (0, 1), 300$ 点来自 $N个 (4, 2.25)$ 和400分 $N个 (12, 1)$ ⁠.图7显示了具有ICS软件默认值的解决方案 $({V（V）}_{1} = {S公司}_{n个} 和 {V（V）}_{2} = κ_{n个})$ ⁠; 这与解决方案类似V（V）₁Cauchy的最大似然（ML），V（V）₂ML用于t吨₂). 在第三个坐标上，簇模式不是最清晰可见的。在图8，ML用于t吨₂并使用了最小协方差行列式（MCD）。这显示了沿着第二个坐标的图案。

图7

新标签中打开下载幻灯片

ICS绘图S公司_n个和 $κ_{n个}$

图8

新标签中打开下载幻灯片

带ML的ICS绘图t吨₂和MCD

图9显示了最佳解决方案，它源于MCDV（V）₂和V（V）₁（“局部形状”）定义如下。

图9

新标签中打开下载幻灯片

带有局部形状和MCD的ICS绘图

（a）
计算点之间的马氏距离矩阵（例如，基于20%崩溃点的MCD）。
（b）
对于每个点，计算其10%最近邻居的协方差矩阵。
（c）
通过追踪将所有这些矩阵标准化，以统一每个点的影响。
（d）
合并协方差矩阵。

将该矩阵与全局协方差矩阵结合使用，可以得到局部结构与全局结构不同的坐标。

这里有另一个想法。

（a）
计算数据的仿射不变聚类。
（b）
使用集群内的池协方差矩阵。

结论：如果聚类感兴趣，那么选择分散矩阵来探索全局是有利的与在集群结构中。

A.P.Dawid公司(剑桥大学)

本文的中心思想非常简洁：在存在两种不同的分散度度量的情况下，定义变量的两种不同内积，我们可以应用同时对角化来定义一组“自然”的基本变量，以便进一步分析和显示数据。然而，只有当所选的一对分散度量可以被视为自然时，该集合才是自然的。但是，即使在这种情况下，为什么还要停止两种这样的措施呢-在许多问题中，会有各种有趣的分散度量。不幸的是，所提出的理论要求的不是一个，不是三个，而是正好两个分散度量。

关于两个以上的适当治疗（以对称的方式），有什么有用的吗？

会后收到了以下书面材料。

亨利·考瑟斯(图卢兹数学研究所)和安妮·鲁伊斯·加森(图卢兹经济学院)

我们祝贺作者们发表了非常有趣的论文，该论文在散射矩阵比较的理论知识方面取得了重大进步。从我们的角度来看，有几个问题值得进一步关注。第一个问题是图形显示尺寸的选择，这是自投影追踪方法早期以来的一个关键问题（Sun，1991)：哪些投影是重要的，即哪些投影包含真正的结构，而不仅仅是对应于椭圆分布的随机变化？例如，在定理4的框架内k个或者，更准确地说，包含kμ_j个? 这个实际问题的答案取决于所涉及的矩阵乘积的特征值的分布。我们给出了Caussinus中特定散射矩阵的初步理论结果等。(2003年a)用于检测异常值和因果关系等。(2003年3月)用于检测组。另一个问题是不变量坐标选择和分类的互补使用。通过不变坐标选择选择的坐标可以用来可视化可能的组，建议它们的数量，并提高聚类算法的效率。这些不同的方面在Caussinus和Ruiz-Gazen中进行了说明(2007)鼓励进一步研究。第三个问题涉及选择要与感兴趣的结构进行比较的（类）散布矩阵。根据我们的经验，许多选择都会导致显示异常值。由于在实践中，数据集中通常存在离群值，因此它们可以掩盖其他有趣的特征。要显示示例2或RANDU数据集中的组或特殊结构，在选择要比较的散布估计值时需要格外小心，尤其是在存在离群值的情况下。基于两两差异的散布矩阵似乎特别有趣。一类散布矩阵取决于一个调整参数，其选择也具有挑战性。正如Tyler及其同事所引用的，我们的一些结果导致选择较小的参数值；在查找异常值时，基本上就是这种情况。然而，在其他有趣的情况下，我们的实践和一些有限的未发表的结果导致了不同的值，例如2，出现在因果关系中的值等。(2003年a). 我们希望作者有兴趣进一步调查这些不同的问题。

克里斯托夫·克劳斯(鲁汶卡索利克大学)

本文介绍了一种新的多元数据分析工具，称为不变坐标选择。我认为本文中的观点是新的和创新的，并且本文很可能会在多元分析中产生新的研究流。我祝贺作者们发表了这篇引人入胜的论文，并对他们的工作进行了清晰的阐述。

该方法很容易实施：计算V（V）₁和V（V）₂，使用V（V）₁和V（V）₂两个散布矩阵。这个想法只有在以下情况下才有效V（V）₁和V（V）₂是不同的散布矩阵。这种方法之所以没有被早期发现，可能是因为大多数统计学家只使用协方差矩阵。分散矩阵在稳健性文献中是众所周知的，但应用这里的方法并不要求分散矩阵是稳健性的。我认为最重要的贡献如下。

（a）
引入“不变坐标系”：数据的仿射变换不会改变坐标系。主成分分析仅对正交变换具有此性质。不变坐标系取决于两个散射矩阵的选择，并产生椭圆分布的任意变换。同样在主成分中，计算所选散射矩阵（通常为协方差矩阵）的特征向量，并获得球面分布的任意旋转。
（b）
不变坐标选择检索的结果
- （i）
  独立成分分析模型的独立成分和
- （ii）
  椭圆分布混合的Fisher线性鉴别子空间。

如果我们既没有椭圆分布的混合，也没有独立的成分分析模型，那么对选定坐标的解释就依赖于投影追踪论证，其中推广了峰度的广义度量。请注意，峰度的度量是根据给定的多元分布条件定义的。对于任意的单变量分布，如何定义这种广义峰度度量尚不清楚。

虽然多元统计中的大多数理论都依赖于椭圆分布，但作者超越了这一点，开辟了一个全新的研究领域。我喜欢读这篇论文，我再次向作者表示祝贺。

彼得·菲尔兹莫瑟(维也纳科技大学)

我祝贺作者的这一有趣贡献，它结合并概括了几种方法。推广了Caussinus和Ruiz-Gazen关于广义主成分分析的工作，Fisher线性判别子空间是一个特例。此外，还考虑了独立分量分析和投影追踪。对于后一种方法，不变坐标选择（ICS）不需要追踪。相反，可以使用标准投影寻踪指数来评估ICS生成的坐标对的“趣味性”。此外，正如作者已经指出的那样，可以使用不同的散布矩阵对来寻找有趣的投影。另一个想法是使用散布矩阵的线性组合，并以与现在相同的方式组合它们方程式（13）根据线性组合的系数，可以获得对多元数据结构的不同见解。

ICS的一个有趣的方面是，成对图提供了解释异常值的可能性。例如，在示例1中(图2)前两个ICS组件的方向是指九个变量的贡献。因此，通过检查这些“加载”，可以根据原始变量解释异常值组。

最后，多亏了可用的R包“ICS”，我用高维数据做了一些实验。我生成了两个1000维的多元正态分布数据云，第一个云由2000个观测值组成，第二个云由200个观测值构成，两者都集中在原点。协方差矩阵是第一个云的单位矩阵和第二个云的乘以1.2的单位矩阵。因此，几乎不可能在任何配对图中区分这两组。使用“ics”功能的默认参数，我们可以看到两组在第一个和最后一个ics方向上的行为略有不同。当采用原始数据和加权数据的经典协方差矩阵时，通过多元异常值检测方法获得的权重，我们可以清楚地看到这两组数据。这里我使用了一种非仿射等变的离群值检测方法（Filzmoser等。,2008)尽管ICS的理论结果不再成立，但实际结果非常有用。

马克·哈林(布鲁塞尔自由大学)

这篇文章汇集并统一了几个统计领域的基本思想——主成分、判别分析、稳健性、不变性、统计深度、灵活建模、独立成分分析……——无疑是我多年来读过的最令人兴奋和耳目一新的文章之一。

专注于使用两种不同的散射（或形状）度量V（V）₁(F类)和V（V）₂(F类)在检测偏离椭圆度时，有一个问题自然会浮现在我们的脑海中，这是作者没有研究过的：对于给定的非椭圆F类，有没有“最有效”或“最具对比度”的选择F类↦V（V）_j个(F类),j个=1,2-最大化，例如，缩放版本之间的适当距离(ρ₁,…,ρ_第页)和（1，…，1）？很可能，这个问题与构建球形度的“最优”测试（传统Mauchly的稳健替代方案）有关(1940)和约翰(1972)测试可以在泰勒身上找到(1982,1987)Hallin和Paindaveine(2006)). 回答这样一个问题将非常有用，例如在以最佳方式恢复独立组件分析模型中的独立组件的问题中。

然而，仿射不变性或等方差并不是我们对散布矩阵所要求的唯一不变性F类↦V（V）_j个(F类),j个= 1,2. 另一组同样相关的变换没有提到，它也保留了椭圆性：单调径向变换更准确地说，假设某个位置θ=θ(F类)已选定，考虑分散函数F类↦V（V）(F类)（在本文的意义上），并让

\begin{matrix} {第页}_{V（V）} : = {{(Y（Y） - θ)}^{'} {V（V）}^{- 1} (Y（Y） - θ)}^{1 / 2}, \\ {U型}_{V（V）} : = {V（V）}^{- 1 / 2} (Y（Y） - θ) / {V（V）}^{- 1 / 2} (Y（Y） - θ) = {V（V）}^{- 1 / 2} (Y（Y） - θ) / {第页}_{V（V）} . \end{matrix}

然后，Y（Y）（具有分配功能F类_Y（Y）)是椭圆的当且仅当 ${Y（Y）}_{V（V）}^{克} : = θ + 克 ({第页}_{V（V）}) {V（V）}^{1 / 2} {U型}_{V（V）}$ （具有分配功能 $第页 \mapsto 克 (第页)$ 也是椭圆形的，其中第页↦克(第页)是的任意连续单调递增变换 $ℝ^{+}$ 这样的话克（0）=0和lim_第页→∞{克(第页)}=∞. 经典不变性论证表明 $V（V） ({F类}_{{Y（Y）}_{V（V）}^{克}})$ 成比例（形状相等）V（V）(F类_Y（Y）)对于任何克和F类_Y（Y）-本文所考虑的散射泛函仅限于椭圆族时才具有的一个性质F类_Y（Y）s.径向变换下的这种不变性严重限制了可容许的散射泛函类；注意Tyler提出的功能(1987)满足条件-但确实存在其他解决方案。

在经验版本中（表示为 ${F类}_{Y（Y）}^{(n个)}$ 样本的经验分布函数Y（Y）₁,…,Y（Y）_n个大小为n个)，类似的不变性参数意味着 ${V（V）}^{(n个)} : = V（V） ({F类}_{Y（Y）}^{(n个)})$ 应在以下方面进行测量U型_{V（V）(n个);我}:=(V（V）^(n个))^−1/2(Y（Y）_我−θ)/‖(V（V）^(n个))^−1/2(Y（Y）_我−θ)和等级 ${R（右）}_{{V（V）}^{(n个)}; j个}^{(n个)}$ 的距离第页_{V（V）(n个);我}:={(Y（Y）_我−θ)^′(V（V）^(n个))⁻¹(Y（Y）_我−θ)}^1/2,我= 1,…,n个。这对于有限的n个，但它适用于M（M）-Tyler提出的估计器(1987)在渐近形式下，对于R（右）-Hallin开发的形状估算器等。(2006).

丹尼尔·佩尼亚和朱利亚·维拉多马(马德里卡洛斯三世大学)

作者提出了一种非常通用的方法，通过将数据投影到矩阵的某些特征向量上来生成仿射不变坐标系 ${V（V）}_{1}^{- 1} {V（V）}_{2}$ ⁠，其中V（V）₁和V（V）₂是任意一对（稳健的）仿射等变散布矩阵。这些投影显示了偏离椭圆分布的情况，可以视为基于峰度的投影追踪方法（参见方程式（14）). 投影方向最大化和最小化峰度对于Peña和Prieto中的稳健多元估计是有用的(2001亿)，他还证明了聚类方向的最优性（Peña和Prieto，2001年a). 他们使用数值优化来找到这些最佳方向。本文的一个重要贡献是，这些方向也可以作为某些一般类峰度矩阵的特征向量获得。

因此，我们有两种方法可以找到峰度的极端方向。第一种方法是通过数值优化，第二种方法是找到一些广义峰度矩阵的特征向量等。(2008)我们在一个特定的案例中比较了这两种方法。给定多元随机向量X（X）平均值μ和协方差矩阵∑，我们建议计算峰度矩阵的特征向量K（K）=E类(Z轴^T型ZZZ公司^T型)，其中Z轴=Σ^−1/2(X（X）−μ). 使用此矩阵相当于选择V（V）₁=∑，以及V（V）₂=E类{Z轴^T型Z轴(X（X）−μ)(X（X）−μ)^T型}在本文中。然后我们证明，如果比率n个/第页很大，其中n个是样本量和第页维数，维数矩阵的估计第页是可靠的，估计其特征向量变得准确和有用。此外，在这种情况下，数值优化需要大量计算。然而，当n个/第页由于规模较小，估计矩阵元素的精度有限，并且特征向量对于显示聚类并不有用。由于使用了峰度矩阵K（K）基于现有的基于峰度的算法，我们可以在Peña和Prieto中使用该算法(2001年a)何时n个/第页很小。一个有趣的问题是这两个过程在不同散射矩阵的更普遍情况下的性能。那么，仅仅使用任何一对稳健的散布矩阵都不能保证识别簇，而极端峰度的方向在这种情况下是有效的。

沃纳·A·斯塔尔和马丁·梅克勒(苏黎世Eidgenössiche Technische Hochschule)

本文介绍了一个优雅的理论，并导出了一个非常有用的工具，用于在多元数据中查找模式。我们热烈祝贺作者的这项工作。

该评论回顾了旨在获得良好稳健性特性的多元工具的基准分布，该分布在Hampel第5.5a节中介绍等。(1986)我们称之为“手推车”。它是一个被部分污染的平坦正态分布的混合物ε= 1/第页粗误差集中在一维子空间附近。让

{G公司}_{0} = (1 - \frac{1}{第页}) {N个}_{第页} {0, d日 我 一 克 (σ_{1}^{2}, 1, \dots, 1)} + \frac{1}{第页} H（H）,

哪里第页是尺寸和H（H）是指Y（Y），其中Y（Y）⁽¹⁾具有对称分布 ${({Y（Y）}^{(1)})}^{2} ~ {X（X）}_{第页 - 1}^{2}$ 并且独立于 ${Y（Y）}^{(2)}, \dots, {Y（Y）}^{(第页)} ~ {N个}_{第页} (0, σ_{2}^{2} 我_{第页 - 1})$ (图10（b）). 然后，旋转此分布，使X（X）⁽¹⁾-轴指向空间对角线方向（1，1，…，1），然后重新缩放组件以获得G公司注意，两者的协方差矩阵G公司₀和G公司会倾向于我_第页对于σ₁→0和σ₂→0，所有已知的高分解点（“III类”）协方差估计的“廉价替代品”都无法检测到异常值部分H（H）。有关更多详细信息和R函数，请参阅http://stat.ethz.ch/research/areas/robustive.

图10

新标签中打开下载幻灯片

手推车分布样本的散点图矩阵，第页=4，以及从中获得的不变坐标

手推车轮子是人为造成的吗？“轮子”描述了变量之间具有强线性关系的多元正态分布，这是多元统计研究的一种情况。异常值是“令人讨厌的”，但使它们更真实并不会使检测结构的问题变得更容易。因此，稳健的多元程序应通过此基准测试。

图10（a）显示了来自的示例G公司对于第页=4和σ₁=0.1和σ₂= 0.2. 任何结构似乎都很难识别。使用鲁棒MCD协方差作为V（V）₂经验协方差矩阵为V（V）₁非常清楚地显示了结构(图10（b）). 请注意，如果我们遵循作者的建议，使用温和或非稳健的散布估计作为V（V）₁以及更稳健的估计V（V）₂.

因此，如果使用高击穿散射矩阵，则不变坐标选择通过基准。基于II类散射矩阵和一步法的更便宜的替代方案W公司-应用于它的估计(第6节通常会遗漏结构。如果完整的III类估计值太昂贵，我们建议只限制常用重采样算法的基本子集的数量，以找到这样的估计值，并使用相应的“不安全”估计值作为V（V）₂.

这个作者随后以书面形式回复如下。

我们感谢所有讨论者所作的富有洞察力和总体上令人鼓舞的发言。他们提出的许多观点也是我们的主要关注点，我们希望我们的论文能够激励其他人进一步发展这一主题。讨论者已经指出了许多重要的未决问题。

我们不是逐一回应讨论者，而是讨论他们反复出现的主要主题。

分散度和统计可变性的选择

贡献中更突出的主题之一是选择散布矩阵。这当然是一个值得更好理解的重要话题。然而，散射矩阵的一个好选择可能取决于手头的问题，例如，关注点是混合问题、独立成分分析（ICA）问题还是其他问题。

大多数讨论倾向于集中于不变坐标选择（ICS）在检测混合或簇中的作用。在这种情况下，人们应该尝试定义一个散布矩阵，以便可以将其视为组内分散。这基本上就是Hennig博士提出的局部形状矩阵。（根据定义，该矩阵不是仿射等变的，但可以通过替换tr来实现(V（V）_伊姆河)带det(V（V）_伊姆河)在其定义中。）这也是Art提出的聚类算法背后的激励思想等。(1982)，以及在Caussinus教授和Ruiz Gazen教授的讨论中以及在Lutz Dümbgen解释RANDU示例中使用的散射矩阵选择的口头陈述中注意到的基于大的成对差异的降权散射矩阵背后的想法。

然而，如果第5节我们的研究结果表明，在推导ICS坐标时所用的散布矩阵的选择在理论上与足够大的样本量无关。正如Hallin教授和Ringrose博士所指出的，主要考虑的是ICS根的理论分离，ρ₁(F类),…,ρ_第页(F类)，以及样本散布矩阵的统计可变性 ${\hat{V（V）}}_{1}$ 和 ${\hat{V（V）}}_{2}$ ⁠如果理论根没有很好地分离，则散布矩阵中的一些适度统计变异性可能会导致ICS坐标估计不佳。然而，理论ICS坐标并不取决于散射矩阵的选择，至少在以下定理的背景下是这样的第5节。研究ICS根和坐标的统计可变性是一个相当简单的问题，至少是渐近的。然而，对于一个特定的基础模型，基于两个给定的散射泛函来理解根的理论分离这一更重要的问题似乎是非常具有挑战性的，并且关于这一主题的任何结果都非常受欢迎。

为了进一步说明这些观点，请考虑Hennig博士提出的示例。这个有趣的例子是作为一个聚类问题提出的，但它不属于第5.1节相反，它提供了ICA模型的一个很好的示例。定理5指出，本质上任何两个散布矩阵都应该揭示结构。此外，正如在定理5之后的讨论中所指出的，这里不需要独立性或对称性，因为三个边缘中的两个是对称的。Hennig首先考虑的散射矩阵，即。S公司_n个和 $κ_{n个}$ ⁠，可能不合适，因为由于t吨₂-分配。（奇怪的是t吨₂-组分很容易找到，困难在于从均匀组分中分离混合组分。）否则，任何定义良好的散布矩阵对都应该找到足够大样本大小的独立分量，即使它们不是专门针对这个特定问题的。

图11（a）和11（b）显示了在选择Dümbgen散射矩阵时Hennig博士示例的结果 ${\hat{V（V）}}_{2}$ 在这两个数字中t吨₂M（M）-散射估计及其对称化版本分别选择为 ${\hat{V（V）}}_{1}$ ⁠.来自图11对称版本似乎能更好地恢复独立分量，在对称版本中，样本ICS根之间的距离更大，即（1.26，0.98，0.80）图11（a）与（1.53、0.87、0.75）图11（b）这表明，正如肯特教授、考斯辛教授和鲁伊兹·加森教授所评论的那样，对称化可能有好处，至少对于中等样本量来说是这样的。似乎对这两个散布矩阵使用一个共同的中心可能也是有利的。ICS使用t吨₂M（M）-以t吨₂M（M）-对位置的估计给出了一个类似于图11（b）。使用公共中心可以避免使用对称数据时所需的额外计算。

图11

Hennig示例的ICS：（a）V^1，t2M估计，以及V^2，Dümbgen散射；（b）对称化t2M估计和V^2，Dümbgen散射

新标签中打开下载幻灯片

Hennig的ICS示例：（a） ${\hat{V（V）}}_{1}$ ⁠，的t吨₂M（M）-估计，以及 ${\hat{V（V）}}_{2}$ ⁠Dümbgen散射；（b） ${\hat{V（V）}}_{1}$ ⁠，对称化的t吨₂M（M）-估计，以及 ${\hat{V（V）}}_{2}$ ⁠Dümbgen的分散

这个例子也揭示了肯特教授关于大小ICS根之间区别的问题。杜姆布根矩阵在广义上可能被视为比这两个矩阵更“稳健”t吨₂M（M）-估计及其对称版本。在图11（a）尽管如此t吨₂-组件与最大根相关，而在图11（b）它与最小的根有关。

统计推断和一般分布

我们的论文没有给出统计推断的任何结果，而是将此主题留作进一步研究。正如Caussinus教授和Ruiz-Gazen教授所指出的，当我们假设一个混合模型时，有一些有趣的开放推理问题。然而，也许最基本的问题是，首先要确定ICS根之间是否存在显著差异。否则，ICS方法就是简单地探索噪声。

在Kankainen可以找到一些关于使用两个散射矩阵来测试多元正态性的工作等. (2007). 在Wang中(2008)样本ICS根用于测试数据来自椭圆分布的假设。还得到了椭圆分布和偏椭圆分布混合情况下这些试验的局部幂函数。

Hallin教授提出的关于此类测试中散布矩阵的最佳选择的问题再次取决于手头的问题，即替代模型。针对一般多元分布检验椭圆度假设的问题远比检验椭圆分布类中的球形假设复杂。即使在考虑两个多元正态分布的平均混合时，我们在一些初步工作中注意到，对于某些混合，一对散布矩阵可能比另一对更强大，而对于其他混合，则相反。

对于中讨论的模型以外的分布第5节，理论ICS坐标本身可能严重依赖于散射泛函。在这种情况下，正如Dawid教授所思考的那样，使用两个以上的散射泛函可能有助于探索这些更复杂的非椭圆结构。基于两个以上散射矩阵的比较生成新的坐标系更加困难，因为通常三个或更多散射泛函不能同时对角化。（请注意，定理5规定，对于定理中考虑的ICA模型，所有散射泛函都可以同时对角化。）也许可以发展一些Filzmoser教授建议的近似同时对角化法。近似同时对角化技术已在ICA的另一个上下文中开发；参见Cardoso和Souloumiac示例(1996).

Paindaveine博士的贡献提出了一个聪明的应用程序，它使用了两个以上散布矩阵中包含的信息，即一种图形方法，用于访问不同ICS坐标系统的变化程度。由此获得的见解可用于诊断第5节是适当的。他所展示的图表表明，在实践中应考虑广泛的散布矩阵，因为一些散布矩阵对可能会给出类似的ICS结果，而另一些可能会给出不同的结果。

理论ICS根相等的假设与该假设等价V（V）₁∝V（V）₂。通过考虑假设，还可以使用来自几个散布矩阵的信息来开发替代的、也许更强大的椭圆度测试V（V）₁∝V（V）₂…∝V（V）_k个扩展了Paindaveine博士的想法，还可以使用几个散点矩阵来测试是否与第5节对于这种测试，我们将感兴趣的是测试散射矩阵是否可以同时对角化，而不是测试散射矩阵之间是否成比例。这些都是未来研究的挑战性课题。

高维数据和投影追踪

一些讨论者提出了高维数据的话题，尤其是当样本量n个相对于尺寸较小第页。对于n个≤第页+1，所有仿射等变样本散布矩阵彼此成比例（参见示例Tyler(2009))，因此ICS方法在这种情况下不适用。什么时候？n个相对于而言不太大第页正如Peña教授和Viladomat博士所指出的，由于散布矩阵的统计可变性，ICS不太可能成功地发现潜在结构，除非这些结构是极端的。

作为第页以倍数增加n个目前尚不清楚ICS的根和坐标是否会收敛到任何地方。在无限维空间中，如何定义协方差算子以外的仿射等变散射算子？在此设置中，以及在以下设置中n个/第页不是很大，我们可能需要放宽仿射等方差的要求，并按照肯特教授的建议，引入某种类型的正则化。

使用一维投影指数导出的ICS方法和投影寻踪方法之间的差异是一个自然的问题。例如，肯特教授质疑使用库尔特的区别(一^′Y（Y）)和使用 $一^{'} κ 一 / 一' Σ 一$ ⁠Peña教授和Viladomat博士报告了最近比较这两种测量方法的一些工作，我们很想阅读。他们指出，当混合组分的散布矩阵不同（或者更准确地说，当它们不成比例时）时，ICS理论不能保证识别簇，而在这种情况下，具有极端单变量峰度的投影是有效的。据我们所知，在这种情况下，投影寻踪理论只保证在协方差矩阵相等或分量分离良好时识别正态混合的分量。可以证明后一种情况也适用于ICS。克里奇利考虑了这种特殊情况等. (2007).

我们通常不建议使用 $K（K）$ 和∑作为ICS中的散布矩阵。对于这种选择，ICS的结果可能过于集中于少数伪异常值，并且对于长尾分布（包括混合模型），该方法的统计可变性可能很高。然而，这对散布矩阵很有趣，不仅因为它们在最早的ICA算法之一FOBI中的作用，而且因为它们可以进行分析处理，因此有助于更好地从理论上理解该方法。例如，在定理3后讨论的两个多元正态分布的混合中，证明了当混合比例满足 $α (1 - α) \frac{1}{6}$ 然后 $一^{'} K（K）一 / 一^{'} Σ 一$ 是恒定的，因此没有方向可以与其他方向区分。如果我们检查两个单变量正态分布混合的峰度公式（参见Preston(1953))，我们对库尔特得出了相同的结论(一^′Y（Y）)也就是说，它是常数。ICA模型下的两个度量之间也存在关系，即

一_{j个}^{'} K（K） 一_{j个} / 一_{j个}^{'} Σ 一_{j个} = 库尔特 (一_{j个}^{'} Y（Y）)

什么时候 ${一^{'}}_{j个} Y（Y）$ 是独立组件之一；参见诺德豪森等。(2008).

内容和风格

正如林格罗斯博士所观察到的，本文中给出的示例旨在清楚地说明论文中给出的理论。因此，通过使用简单的主成分分析（PCA）也可以找到一些示例中的结构。然而，问一问ICS可以做什么，而PCA不能做什么，这是一个公平的问题。这个问题也可以用判别分析来回答，我们中的一些人有咨询应用领域研究人员的经验，这些研究人员确实从主成分分析中获得了答案，尽管问题是判别分析。多元分析的研究人员都知道，可以很容易地构造PCA无法揭示组间差异的示例，特别是当平均值相对于组内协方差矩阵在最小主成分方向上发生变化时。这种情况下，当组识别未知时，将导致ICS和PCA之间的类似差异。

其他例子可以在大量的独立分量分析文献中找到，其中其发展的主要动机之一是主成分分析经常无法在多元数据集中找到重要的结构。如果将主成分分析应用于我们的示例2，则无论主成分分析使用的散布矩阵如何，都无法找到底层结构。实际上，ICS根可能有显著差异，但在ICS坐标图中可能看不到明显的结构、组或异常值。尽管该理论向我们保证，基本分布比椭圆分布更复杂，因此需要对数据进行更深入的理解，而不是简单的位置-散布汇总，更仔细地检查ICS坐标可能会有所启发。然而，这样的例子并不能很好地解释最初的情况。

是否应该暂停Fisher的虹膜数据是一个有争议的问题。由于不需要详细解释数据集，因此它们在论文中占用最小空间或在演示中占用最小时间的同时，也可以用于演示。此外，如果一种方法在虹膜数据上表现不佳，那么理论可能会受到怀疑。其他领域也有自己的宠物数据集来说明方法和理论（虹膜数据是宠物而不是玩具），例如计算机视觉中著名的Lena图像。

我们赞赏斯通教授对ICS变量的无坐标公式。多元统计的无坐标方法无疑为这个主题提供了一个理论上优雅而简洁的观点。肯特教授的评论也暗示了他在提到双重指标时采用的无协调方法。通过简单地注意到对于有限维向量空间上的任何两个内积，都有一个相对于两个内积正交（但不一定正交）的基（ICS基），可以以无坐标的方式更优雅地陈述两个散射矩阵总是可以同时对角化的说法。或者，与其提出通常的技术难题来关联对称矩阵的谱值分解 ${V（V）}_{1}^{- 1 / 2} {V（V）}_{2} {V（V）}_{1}^{- 1 / 2}$ 到的特征值和特征向量 ${V（V）}_{1}^{- 1} {V（V）}_{2}$ 我们可以注意到，ICS只是对应于对称算子的通常谱值分解 ${V（V）}_{1}^{- 1} {V（V）}_{2}$ ⁠，其中对称性是相对于内积的 $(x个, 年) = {x个}^{T型} {V（V）}_{1}^{- 1} 年$ ⁠。我们中的一些人在演示中提到了这些更抽象的概念，有时会收到这样的疑问：为什么把观众与抽象混淆了？因此，在呈现结果时，一个共同的考虑因素是目标受众，对于本文来说，目标受众是那些对通用多元方法感兴趣的人。将ICS解释为标准化数据的PCA可能对从业者特别有吸引力。

在将ICS推广到无限维希尔伯特空间的任何尝试中，无坐标方法都是有益的。这里，相对于两个不同内积的相互正交基的概念以及对称算子的谱值分解（或Karhunen–Loève分解）仍然成立。协方差算子也可以在无坐标格式中定义；参见Eaton示例(1983). 然而，其他散射泛函，无论是在有限维还是无限维空间中，如何以无坐标的方式来表示尚不清楚。

稳健性

一些讨论者指出了稳健性在ICS中的作用。克罗克斯博士对我们论文的关键点进行了非常深入的讨论，并特别指出了ICS是如何在稳健统计中思考问题的自然结果。稳健性社区的研究人员熟悉在一般假设下，使用竞争函数（和估计）测量（估计），假设是相同的总体参数。稳健统计通常侧重于自动调整异常值，以便它们不会影响大多数数据的解释。然后，自然会在多元设置中询问位置-散布摘要是否合理，即使是对于大多数数据，例如30–30–40的混合数据。

对于许多统计数据而言，通常导致“崩溃”的异常值类型不仅仅是虚假的异常值，而是具有自身模式的异常值。最极端的情况是点质量污染。有人可能会争辩说，这种数据结构与混合模型相混淆，作为替代方案，可以尝试识别这种模式，同时容纳虚假的异常值。统计数据，而非高崩溃点统计数据，往往会用任何离群值结构模糊大多数结构。然而，如修改后的木材重力数据示例所示，当ICA中同时使用两个这样的散布统计数据时，单独的模式可能会更明显。

Stahel和Mächler给出的示例也出现了类似的现象，该示例最初用于汉佩尔等。(1986)来说明边缘击穿在这个例子中，大部分数据位于某个子空间附近。正如他们在贡献分散统计中正确指出的那样，这些统计数据附近没有崩溃点 $\frac{1}{2}$ 未能发现大多数数据的近似奇异性。虽然这并不意味着基于两个较低崩溃点统计的ICS也无法检测到这种模式。尽管此示例与中考虑的混合模型或ICA模型之一不对应第5节结果表明，ICS坐标在理论上并不依赖于所使用的两个散射矩阵。

为了看到这一点，我们首先注意到，由于ICS的不变性，考虑G公司₀.分配G公司₀在形式变换下是不变的QX公司，即，如果X（X）具有分发G公司₀，那么也是QX公司什么时候问是块与块的对角线q个₁₁=±1和问₂₂是一个3×3的正交矩阵。因此，任何仿射等变散射矩阵V（V）在G公司₀必须与元素成块对角线v（v）₁₁和V（V）₂₂=v（v）₂₂我_三，其中我_三是3×3识别矩阵。因此， ${V（V）}_{1}^{- 1} {V（V）}_{2}$ 具有相同的块对角线形式，因此第一个或最后一个ICS坐标将对应于中的第一个变量G公司₀其他三个坐标将对应于中最后三个坐标的旋转G公司₀（特殊情况除外，当V（V）₁和V（V）₂理论上是成比例的）。再次，选择的问题取决于理论根的分离以及根的统计可变性。对于足够大的样本量，应检测任意两种散射选择的模式，并且任何一种都不需要有高的击穿点。图12举例说明了这一点n个=100来自G公司₀使用样本协方差矩阵和柯西M（M）-估计。

图12

Stahel的ICS–Mächler的示例：V^1，t1M-估计，V^2，样本协方差

新标签中打开下载幻灯片

Stahel的ICS–Mächler示例： ${\hat{V（V）}}_{1}$ ⁠，的t吨₁M（M）-估计，以及 ${\hat{V（V）}}_{2}$ ⁠，样本协方差

其他备注

我们还没有能够详细回应稿件中的所有评论。林格罗斯博士和菲尔兹莫瑟教授提出了ICS坐标的双平面图主题，因此我们希望简要地指出，因果窦已经考虑过这种双平面图等。（2003）在广义PCA的背景下。肯特教授提出了第三时刻可能延长的问题。在这里，我们注意到诺德豪森最近在这个主题上的一些工作等。(2009年a).

我们再次感谢所有讨论者的贡献，希望我们的回答能有所启发。然而，总的来说，仍有很多工作要做，需要新的方法来更好地理解多元数据的性质，尤其是当我们远离椭圆分布的舒适性时。

致谢

作者感谢克劳斯·诺德豪森（Klaus Nordhausen）在为示例和插图提供R代码方面的帮助，感谢安妮·鲁伊斯·加森（Anne Ruiz-Gazen）提请我们注意关于广义主成分分析的文献，感谢斯特凡·凡·阿尔斯特（Stefan Van Aelst）提供对示例1中使用的数据集的访问。

第一作者的研究得到了国家科学基金会拨款DMS-0604596的支持。第三位作者的研究得到了瑞士国家科学基金会的支持。

工具书类

艺术

,

D。

,

格纳纳德西坎

,

对。

和

Kettering公司

,

J.R.公司。

(

1982

)

基于数据的聚类分析指标

.

实用程序。数学。A类

,

21

,

75

——

99

.

谷歌学者

OpenURL占位符文本

书目数据库

比洛多

,

M。

和

布伦纳

,

D。

(

1999

)

多元统计理论

.

纽约

:

施普林格

.

卡多佐

,

J.-F.公司。

(

1989

)利用高阶矩进行源分离。在

程序。国际协调声学、语音和信号处理

，第页。

2109

——

2112

.

格拉斯哥

:

电气和电子工程师协会

.

科西尼斯

,

H。

,

费克里

,

M。

,

哈卡姆

,

秒。

和

鲁伊斯·加赞

,

答：。

(

2003

)

多变量异常值的监测显示

.

计算统计。数据分析。

,

44

,

237

——

252

.

谷歌学者

交叉引用

书目数据库

科西尼斯

,

H。

和

鲁伊斯·加森

,

A类

. (

1990

)通过广义主成分分析对多维数据进行有趣的预测。在

程序。压缩机90

，第页。

121

——

126

,

海德堡

:

物理

.

科西尼斯

,

H。

和

鲁伊斯·加森

,

答：。

(

1993

)投影寻踪和广义主成分分析。在

统计数据分析和稳健性的新方向

（编辑

秒。

摩根塔勒

,

E.公司。

龙凯蒂

和

水务局。

斯塔勒

)，第页。

35

——

46

,

巴塞尔

:

Birkhä用户

.

科西尼斯

,

H。

和

鲁伊斯·加森

,

答：。

(

1995

)通过主成分分析找到典型结构的指标。在

数据科学及其应用

（编辑

年。

护送员

和

C类

.

林下（Hayashi）

)，第页。

177

——

192

.

东京

:

学术出版社

.

查克拉博蒂

,

B。

和

乔杜里

,

第页。

(

1996

)

构造仿射等变多元中值的变换与重传技术

.

程序。美国数学。Soc公司。

,

124

,

2539

——

2547

.

谷歌学者

交叉引用

书目数据库

查克拉博蒂

,

B。

和

乔杜里

,

第页。

(

1998

)

关于一种自适应变换——多元位置的重传估计

.

J.R.统计。Soc.B公司

,

60

,

145

——

157

.

谷歌学者

交叉引用

书目数据库

厨师

,

D。

,

布亚

,

答：。

和

卡布雷拉

,

J。

(

1993

)

基于正交函数展开的投影寻踪指数

.

J.计算图。统计师。

,

2

,

225

——

250

.

谷歌学者

交叉引用

书目数据库

克里奇利

,

F、。

,

皮雷

,

答：。

和

阿马多

,

C、。

(

2007

)

主轴分析

.

开放大学

,

米尔顿·凯恩斯

。未发布。

戴维斯

,

P.L.公司。

(

1987

)

多元位置参数和离散矩阵S估计的渐近性

.

安。统计师。

,

15

,

1269

——

1292

.

谷歌学者

交叉引用

书目数据库

多诺霍

,

D.L.公司。

和

加斯科

,

M。

(

1992

)

基于半空间深度和投影轮廓的位置估计的分解特性

.

安。统计师。

,

20

,

1803

——

1827

.

谷歌学者

OpenURL占位符文本

书目数据库

杜姆布根

,

L。

和

泰勒

,

D.E.博士。

(

2005

)

关于一些多元M-泛函的击穿性质

.

扫描。J.统计。

,

32

,

247

——

264

.

谷歌学者

交叉引用

书目数据库

Flury公司

,

B。

(

1988

)

常见主成分和相关多元模型

.

纽约

:

威利

.

弗里德曼

,

J.H。

和

Tukey公司

,

J·W·。

(

1974

)

一种用于探索性数据分析的投影寻踪算法

.

IEEE传输。计算。

,

23

,

881

——

890

.

谷歌学者

OpenURL占位符文本

书目数据库

汉普尔

,

F.R.公司。

,

龙凯蒂

,

电子显微镜。

,

卢梭

,

P.J.公司。

和

斯塔勒

,

水务局。

(

1986

)

稳健统计：基于影响函数的方法

.

纽约

:

威利

.

胡贝尔

,

P.J.公司。

(

1981

)

稳健的统计

.

纽约

:

威利

.

胡贝尔

,

P.J.公司。

(

1985

)

投影追踪

.

安。统计师。

,

13

,

435

——

475

.

谷歌学者

OpenURL占位符文本

书目数据库

海瓦里宁

,

答：。

,

卡胡宁

,

J。

和

奥哈

,

E.公司。

(

2001

)

独立成分分析

.

纽约

:

威利

.

琼斯

,

M.C.公司。

和

西布森

,

对。

(

1987

)

什么是投影追踪（讨论）？

J.R.统计。社会学硕士

,

150

,

1

——

36

.

谷歌学者

交叉引用

书目数据库

肯特

,

J.T.公司。

和

泰勒

,

D.E.博士。

(

1996

)

多元位置和散布的约束M估计

.

安。统计师。

,

24

,

1346

——

1370

.

谷歌学者

交叉引用

书目数据库

Lopuhaä

,

小时。

(

1989

)

多元位置和协方差的S估计与M估计的关系

.

安。统计师。

,

17

,

1662

——

1683

.

谷歌学者

交叉引用

书目数据库

Lopuhaä

,

小时。

(

1991

)

多变量τ-位置和散布的估计

.

可以。J.统计。

,

19

,

307

——

332

.

谷歌学者

交叉引用

书目数据库

Lopuhaä

,

小时。

(

1999

)

多元位置和离散度重加权估计的渐近性

.

安。统计师。

,

27

,

1638

——

1665

.

谷歌学者

交叉引用

书目数据库

马尔迪亚

,

K.与。

,

肯特

,

J.T.公司。

和

比比

,

J·M·。

(

1980

)

多变量分析

.

伦敦

:

学术出版社

.

玛丽娜

,

注册会计师。

(

1976

)

多元位置和散射的鲁棒M-估计

.

安。统计师。

,

4

,

51

——

67

.

谷歌学者

交叉引用

书目数据库

玛丽娜

,

注册会计师。

,

斯塔勒

,

水务局。

和

尤海

,

V·J。

(

1992

)

基于投影的多元散度偏差稳健估计

.

J.Multiv.公司。分析。

,

42

,

141

——

161

.

谷歌学者

交叉引用

书目数据库

莫斯特勒

,

成本加运费。

和

Tukey公司

,

J·W·。

(

1977

)

数据分析和回归

.

阅读

:

出版商

.

诺德豪森

,

英国。

,

奥哈

,

H。

和

奥利拉

,

E.公司。

(

2008

)

基于双分散矩阵的稳健独立分量分析

.

澳大利亚。J.统计。

,

37

,

91

——

100

.

谷歌学者

OpenURL占位符文本

书目数据库

诺德豪森

,

英国。

,

奥贾

,

H。

和

泰勒

,

D.E.博士。

(

2006

)关于不变多元符号和秩检验的有效性。在

塔尔莫·普基拉的节日

（编辑

J。

伊索塔洛

,

体育。

李斯基

,

秒。

蓬塔宁

和

G.P.H.公司。

斯泰恩

)，第页。

217

——

232

.

坦佩雷

:

坦佩雷大学

.

诺德豪森

,

英国。

,

奥哈

,

H。

和

泰勒

,

D.E.博士。

(

2008

)探索多元数据的工具：ICS包。

J.统计。软件。

,

28

，编号6。

奥哈

,

H。

,

Sirkiä

,

秒。

和

埃里克松

,

J。

(

2006

)

散布矩阵和独立分量分析

.

澳大利亚。J.统计。

,

35

,

175

——

189

.

谷歌学者

OpenURL占位符文本

书目数据库

佩尼亚

,

D。

和

普列托

,

F。J。

(

2001

)

使用投影进行聚类识别

.

《美国统计杂志》。助理。

,

96

,

1433

——

1445

.

谷歌学者

交叉引用

书目数据库

R开发核心团队

(

2005

)

R：统计计算语言与环境

.

维也纳

:

R统计计算基金会

。（可从网址：http://www.R-project.org.)

卢梭

,

P.J.公司。

(

1986

)高崩溃点的多元估计。在

数理统计及其应用

（编辑

西。

格罗斯曼

,

G。

普弗拉格

,

一、。

温克责

和

西。

维尔茨

)，第页。

283

——

297

.

多德雷赫特

:

雷德尔

.

卢梭

,

P.J.公司。

和

范德里森

,

英国。

(

1999

)

最小协方差行列式估计的快速算法

.

技术计量学

,

41

,

212

——

223

.

谷歌学者

交叉引用

书目数据库

卢梭

,

P.J.公司。

和

勒罗伊

,

答：。

(

1987

)

稳健回归与异常检测

.

纽约

:

威利

.

鲁伊斯·加森

,

答：。

(

1993

)

估计robuste d'une矩阵离散与投影

.博士论文.

保罗·萨巴蒂尔大学

,

图卢兹

.

塔斯基宁

,

秒。

,

锡尔凯

,

秒。

和

奥贾

,

H。

(

2007

)

基于对称散布矩阵的独立分量分析

.

计算统计。数据分析。

,

51

,

5103

——

5111

.

谷歌学者

交叉引用

书目数据库

龙冈

,

英国标准。

和

泰勒

,

D.E.博士。

(

2000

)

非椭圆分布下S-泛函和M-泛函的唯一性

.

安。统计师。

,

28

,

1219

——

1243

.

谷歌学者

交叉引用

书目数据库

泰勒

,

D.E.博士。

(

1994

)

基于投影的多元位置和散布统计的有限样本分解点

.

安。统计师。

,

22

,

1024

——

1044

.

谷歌学者

交叉引用

书目数据库

泰勒

,

D.E.博士。

(

2002

)

高崩溃点多元M估计

.

Estadística公司

,

54

,

213

——

247

.

谷歌学者

OpenURL占位符文本

书目数据库

维萨里

,

秒。

,

科维恩

,

五、。

和

奥哈

,

H。

(

2000

)

符号和秩协方差矩阵

.

J.统计。计划信息。

,

91

,

557

——

575

.

谷歌学者

交叉引用

书目数据库

Yenyukov公司

,

I.S公司

. (

1988

)通过投影追踪检测结构。在

程序。压缩机88

，第页。

47

——

58

.

海德堡

:

物理

.

讨论中的参考文献

艺术

,

D。

,

格纳纳德西坎

,

对。

和

Kettering公司

,

J.R.公司。

(

1982

)

基于数据的聚类分析指标

.

实用程序。数学。A类

,

21

,

75

——

99

.

谷歌学者

OpenURL占位符文本

书目数据库

布格里恩

,

J.B.公司。

和

肯特

,

J.T.公司。

(

2005

)独立成分分析：一种聚类方法

定量生物学、形状分析和小波论文集

（编辑

秒。

理发室

,

P.D.公司。

巴克斯特

,

K.与。

马尔迪亚

和

R.E.公司。

墙壁

)，第页。

111

——

114

.

利兹

:

利兹大学出版社

.

卡多佐

,

J.-F.公司。

和

苏卢米亚克

,

答：。

(

1996

)

同时对角化的雅可比角

.

SIAM J.数学。分析。申请。

,

17

,

161

——

164

.

谷歌学者

交叉引用

书目数据库

科西尼斯

,

H。

,

费克里

,

M。

,

哈卡姆

,

秒。

和

鲁伊斯·加森

,

答：。

(

2003年a

)

多变量异常值的监控显示

.

计算统计。数据分析。

,

44

,

237

——

252

.

谷歌学者

交叉引用

书目数据库

科西尼斯

,

H。

,

哈卡姆

,

秒。

和

鲁伊斯·加森

,

答：。

(

2003年3月

)

投影、关系、控制、群和结构多样

.

修订版统计。申请。

,

51

,

37

——

58

.

谷歌学者

OpenURL占位符文本

书目数据库

科西尼斯

,

H。

和

鲁伊斯·加森

,

A类

. (

2007

)分类和广义主成分分析。在

数据分析和分类的部分贡献

（编辑

第页。

布里托

,

第页。

贝特朗

,

G。

Cucumel公司

和

F、。

德卡瓦略

)，第页。

539

——

548

.

柏林

:

施普林格

.

克里奇利

,

F、。

,

皮雷

,

A类

.和

阿马多

,

C类

. (

2007

)

主轴分析

未发表的手稿。

伊顿

,

M.L.公司。

(

1983

)

多元统计：向量空间方法

.

纽约

:

威利

.

Filzmoser公司

,

第页。

,

玛丽娜

,

对。

和

沃纳

,

M。

(

2008

)

高维异常识别

.

计算统计。数据分析。

,

52

,

1694

——

1711

.

谷歌学者

交叉引用

书目数据库

让东

,

M.G.公司。

(

2004

)

偏椭圆分布及其应用：超越正态性的旅程

.

博卡拉顿

:

查普曼和霍尔——CRC

.

哈林

,

M。

,

奥哈

,

H。

和

潘达文

,

D。

(

2006

)

形状的半参数有效等级推理：II，最优R（右）-形状估计

.

安。统计师。

,

34

,

2757

——

2789

.

谷歌学者

OpenURL占位符文本

书目数据库

哈林

,

H。

和

潘达文

,

D。

(

2006

)

形状的半参数有效等级推理：I，球形度的最佳等级测试

.

安。统计师。

,

34

,

2707

——

2756

.

谷歌学者

OpenURL占位符文本

书目数据库

汉佩尔

,

F.R.公司。

,

龙凯蒂

,

电子显微镜。

,

卢梭

,

P.J.公司。

和

斯塔勒

,

水务局。

(

1986

)

稳健统计：基于影响函数的方法

.

纽约

:

威利

.

约翰

,

秒。

(

1972

)

用于测试正态分布球度的统计量的分布

.

生物特征

,

59

,

169

——

174

.

谷歌学者

交叉引用

书目数据库

坎凯南

,

答：。

,

塔斯基宁

,

秒。

和

奥贾

,

H。

(

2007

)

基于位置向量和散点矩阵的多项式检验

.

统计师。方法。申请。

,

16

,

357

——

379

.

谷歌学者

交叉引用

书目数据库

莫奇来

,

J·W·。

(

1940

)

法线球度测试n个-变量分布

.

安。数学。统计师。

,

11

,

204

——

209

.

谷歌学者

交叉引用

书目数据库

诺德豪森

,

英国。

,

奥哈

,

H。

和

奥利拉

,

E.公司。

(

2009年a

)多元模型和前四个矩。在

Thomas P.Hettmansperger的Festschrift

（编辑

D.右。

亨特

,

J·L·。

罗森伯格

和

D。

理查兹

). 待发布。

诺德豪森

,

英国。

,

奥哈

,

H。

和

潘达文

,

D。

(

2009年b

)

对称独立分量模型中位置的符号库检验

.

J.Multiv.公司。分析。

,

100

,

821

——

834

.

谷歌学者

交叉引用

书目数据库

诺德豪森

,

英国。

,

奥哈

,

H。

和

泰勒

,

D.E.博士。

(

2008

)通过ICS/ICA探索多元数据的工具。在

R包，版本1.1-1

（可从http://cran.r-project.org.)

佩尼亚

,

D。

和

普列托

,

F。J。

(

2001年a

)

使用投影进行聚类识别

.

《美国统计杂志》。助理。

,

96

,

1433

——

1445

.

谷歌学者

交叉引用

书目数据库

佩尼亚

,

D。

和

普列托

,

F。J。

(

2001亿

)

稳健协方差矩阵估计和多元异常值检测（附讨论）

.

技术计量学

,

43

,

286

——

310

.

谷歌学者

交叉引用

书目数据库

佩尼亚

,

D。

,

普列托

,

F。J。

和

维拉多马

,

J。

(

2008

)

峰度矩阵的特征向量作为揭示簇结构的有趣方向

。待发布。

普雷斯顿

,

E.J.公司。

(

1953

)

将统计分布分析为两个正态分量的图解法

.

生物特征

,

40

,

460

——

464

.

谷歌学者

交叉引用

书目数据库

石头

,

M。

(

2008

)

转到图片：特征向量作为不动点

.研究报告。

伦敦大学学院

,

伦敦

。（可从http://www.ucl.stats.uk/research/reports/psfiles/rr299.pdf.)

太阳

,

J。

(

1991

)

探索性投射追踪的显著性水平

.

生物特征

,

78

,

759

——

769

.

谷歌学者

交叉引用

书目数据库

泰勒

,

D.E.博士。

(

1982

)

径向估计和球度检验

.

生物特征

,

69

,

429

——

436

.

谷歌学者

交叉引用

书目数据库

泰勒

,

D.E.博士。

(

1987

)

多元散度的无分布M估计

.

安。统计师。

,

15

,

234

——

251

.

谷歌学者

交叉引用

书目数据库

泰勒

,

D.E.博士。

(

2009

)

关于稀疏数据集的多元位置和散布统计的注记

.技术报告.

新泽西州立大学统计系

,

皮斯卡塔韦

.

王

,

J。

(

2008

)

非对称模型下稳健统计的一些性质

.博士论文.

新泽西州立大学

,

皮斯卡塔韦

.

附录A：证明

A.1、。定理1和2的证明

From属性(3)，因此有γ₁>0和γ₂>0，这样V（V）₁(F类_Y（Y）*) =γ₁A伏₁(F类_Y（Y）)A类^′和V（V）₂(F类_Y（Y）*) =γ₂A伏₂(F类_Y（Y）)A类^′根据定义，V（V）₂(F类_Y（Y）*)小时_j个(F类_Y（Y）*) =ρ_j个(F类_Y（Y）*)V（V）₁(F类_Y（Y）*)小时_j个(F类_Y（Y）*)等等

{V（V）}_{2} ({F类}_{Y（Y）}) {A类}^{'} {小时}_{j个} ({F类}_{{Y（Y）}^{*}}) = γ ρ_{j个} ({F类}_{{Y（Y）}^{*}}) {V（V）}_{1} ({F类}_{Y（Y）}) {A类}^{'} {小时}_{j个} ({F类}_{{Y（Y）}^{*}}),

(26)

哪里γ=γ₁/γ₂。这意味着该条件(18)持有。如果ρ_j个(F类_Y（Y）)是一个不同的根，那么方程式（26）也意味着小时_j个(F类_Y（Y）) =一_j个A类^′ 小时_j个(F类_Y（Y）*)对于某些标量一_j个≠0，依此类推

{Z轴}_{j个} = {小时}_{j个} {({F类}_{Y（Y）})}^{'} Y（Y） = 一_{j个} {小时}_{j个} {({F类}_{{Y（Y）}^{*}})}^{'} A类 Y（Y） = 一_{j个} {小时}_{j个} {({F类}_{{Y（Y）}^{*}})}^{'} ({Y（Y）}^{*} - b条) = 一_{j个} {Z轴}_{j个}^{*} - {b条}_{j个},

这就完成了定理1的证明。现在考虑多个根的情况，比如ρ_(k个)≡ρ_j个1(F类_Y（Y）)=… =ρ_j个2(F类_Y（Y）)其中j个2 =j个1+第页_k个-1，并让H（H）_(k个)(F类)=(小时_j个1(F类),…,小时_j个2(F类)). 作为多重根的结果，精确的选择H（H）_(k个)(F类)有些武断，除非指定了有关如何选择其列的规则。然而H（H）_(k个)(F类)是唯一定义的，因此，无论我们使用什么规则来定义H（H）_(k个)(F类),方程式（26）意味着 ${H（H）}_{(k个)} ({F类}_{年}) = {A类}^{'} {H（H）}_{(k个)} ({F类}_{Y（Y） *}) {B类}^{'}_{k个}$ 对于一些非奇异矩阵B类_k个。这意味着

{Z轴}_{(k个)} = {H（H）}_{(k个)} {({F类}_{Y（Y）})}^{'} Y（Y） = {B类}_{k个} {H（H）}_{(k个)} {({F类}_{{Y（Y）}^{*}})}^{'} A类 Y（Y） = {B类}_{k个} {H（H）}_{(k个)} {({F类}_{{Y（Y）}^{*}})}^{'} ({Y（Y）}^{*} - b条) = {B类}_{k个} {Z轴}_{(k个)}^{*} - {b条}_{j个},

这就完成了定理2的证明。

A.2、。定理3和4的证明

由于定理3是定理4的特例，因此只需证明后者。使用定理4的符号，让 ${M（M）}_{0} = Γ^{- 1 / 2} (M（M） - μ_{k个} {1^{'}}_{k个})$ ⁠，其中M（M）=(μ₁…μ_k个)和1_k个∈ ℜ^k个是1s的向量。自M（M）₀有等级q个，矩阵的三角分解给出了

{M（M）}_{0} = P（P） (\begin{matrix} {T型}_{u个} & 0 \\ 0 & 0 \end{matrix}) = P（P） ({t吨}_{1} \dots {t吨}_{q个} 0) = P（P） T型

具有P（P）是一个正交的有序矩阵第页和T型_u个是阶上三角矩阵q个.分配X（X）=P（P）^′Γ^−1/2(Y（Y）−μ_k个)然后是k个带中心的球面分布t吨₁,…,t吨_k个，其中t吨_q个+1=… =t吨_k个=0，和扩散函数克_我,我= 1,…,k个，即X（X）由提供

{（f）}_{X（X）} (x个) = {\sum^{​}}_{j个 = 1}^{k个} α_{j个} 克_{j个} {{(x个 - {t吨}_{j个})}^{'} (x个 - {t吨}_{j个})} .

The distributions ofX（X）和QX公司因此，对于任何正交问表单的

问 = (\begin{matrix} 我_{q个} & 0 \\ 0 & 问_{22} \end{matrix}),

哪里我_q个是顺序的单位矩阵q个和问₂₂是一个正交矩阵第页−q个因此，给定一个散布函数V（V）(F类)满足条件(3),V（V）(F类_X（X）) =V（V）(F类_QX公司)⑪Q V型(F类_X（X）)问^′，对于任何此类问，等等

V（V） ({F类}_{X（X）}) = (\begin{matrix} {V（V）}_{11} ({F类}_{X（X）}) & {V（V）}_{12} ({F类}_{X（X）}) \\ {V（V）}_{12} {({F类}_{X（X）})}^{'} & {V（V）}_{22} ({F类}_{X（X）}) \end{matrix}) = (\begin{matrix} {V（V）}_{11} ({F类}_{X（X）}) & {V（V）}_{12} ({F类}_{X（X）}) 问_{22}^{'} \\ 问_{22} {V（V）}_{12} {({F类}_{X（X）})}^{'} & 问_{22} {V（V）}_{22} ({F类}_{X（X）}) 问_{22}^{'} \end{matrix})

(27)

对于任何正交矩阵问₂₂。注意等式在表达式中成立(27)而不仅仅是比例性，因为上块对角矩阵是相等的（且非零）。通过做出适当的选择问₂₂在表达式中(27)我们获得V（V）₁₂(F类_X（X）)=0和V（V）₂₂(F类_X（X）) =γI_{第页−q个}，对于一些γ>因此，对于两个散射泛函V（V）₁(F类)和V（V）₂(F类),

{V（V）}_{1} {({F类}_{X（X）})}^{- 1} {V（V）}_{2} ({F类}_{X（X）}) = (\begin{matrix} {V（V）}_{1, 11} {({F类}_{X（X）})}^{- 1} {V（V）}_{2, 11} ({F类}_{X（X）}) & 0 \\ 0 & (γ_{2} / γ_{1}) 我 \end{matrix}) .

此矩阵至少有一个根，其重数大于或等于第页−q个通过定理2，我们知道V（V）₁(F类_Y（Y）)⁻¹ V（V）₂(F类_Y（Y）)与根成正比V（V）₁(F类_X（X）)⁻¹ V（V）₂(F类_X（X）)，因此至少有一个根ρ_(j个)具有大于或等于的多重性第页−q个.

假设现在没有根的重数大于第页−q个，根据定理2适用于V（V）₁(F类_X（X）)⁻¹V（V）₂(F类_X（X）)以及到V（V）₁(F类_Y（Y）)⁻¹ V（V）₂(F类_Y（Y）). 对于V（V）₁(F类_X（X）)⁻¹ V（V）₂(F类_X（X）)，一个具有多重性的根第页−q个必须是γ₂/γ₁。此外q个-由特征向量跨越的维子空间V（V）₁(F类_X（X）)⁻¹ V（V）₂(F类_X（X）)，除了与γ₂/γ₁，与跨越的子空间相同(我_q个0)^′，或等价地，它与跨越的子空间相同T型.从形状等变属性(3)，我们有V（V）₁(F类_X（X）)⁻¹ V（V）₂(F类_X（X）)∝P（P）^′Γ^1/2 V（V）₁(F类_Y（Y）)⁻¹ V（V）₂(F类_Y（Y）)Γ^−1/2P（P），因此如果一是的特征向量V（V）₁(F类_X（X）)⁻¹ V（V）₂(F类_X（X）)然后小时=Γ^−1/2帕是的特征向量V（V）₁(F类_Y（Y）)⁻¹ V（V）₂(F类_Y（Y）). 如果特征向量一与根关联γ₂/γ₁，然后小时与某个根相关联，例如ρ_(t吨)，具有多重性第页−q个.由所有特征向量跨越的子空间V（V）₁(F类_Y（Y）)⁻¹ V（V）₂(F类_Y（Y）)，除了与ρ_(t吨)，因此与跨越的子空间相同 $Γ^{- 1 / 2} P（P） T型 = Γ^{- 1 / 2} {M（M）}_{0} = Γ^{- 1} (M（M） - μ_{k个} {1^{'}}_{k个})$ ⁠，因此方程式（22）持有。

答3。定理5的证明

对称性X（X），以及X（X）拥有独立组件意味着 $X（X） ~_{d日} S公司 X（X）$ 对于任何对角矩阵 $S公司$ 只有1s和−1s作为条目，即对于这种形式的矩阵 $S公司 = 诊断 (\pm 1, \dots, \pm 1)$ ⁠因此，对于任何散射函数V（V）(F类)满足形状等变性质(3)，因此 $V（V） ({F类}_{X（X）}) = V（V） ({F类}_{S公司 X（X）}) = S公司 V（V） ({F类}_{X（X）}) S公司$ ⁠，对于任何此类 $S公司$ ⁠。最后一个等式来自属性(3)因为对角线分量V（V）(F类_X（X）)和S V系列(F类_X（X）)S公司都是一样的。通过选择 $S公司 V（V） ({F类}_{X（X）}) S公司$ ⁠，我们注意到V（V）(F类_X（X）)必须为0。继续，我们的结论是V（V）(F类_X（X）)是一个对角矩阵。

对于两个散射泛函V（V）₁(F类)和V（V）₂(F类),V（V）₁(F类_X（X）)⁻¹ V（V）₂(F类_X（X）)是对角矩阵。根据定理1，它如下所示 ${V（V）}_{1} {({F类}_{X（X）})}^{- 1} {V（V）}_{2} ({F类}_{X（X）}) \propto {P（P）}_{σ} Δ ({F类}_{Y（Y）}) {P（P）}^{'}_{σ}$ ⁠，式中Δ(F类_Y（Y）)=诊断{ρ₁(F类_Y（Y）),…,ρ_第页(F类_Y（Y）)}和P（P）是置换矩阵。使用属性(3)再次给予

{V（V）}_{1} {({F类}_{Y（Y）})}^{- 1} {V（V）}_{2} ({F类}_{Y（Y）}) \propto {({B类}^{'})}^{- 1} {V（V）}_{1} {({F类}_{X（X）})}^{- 1} {V（V）}_{2} ({F类}_{X（X）}) {B类}^{'} \propto {({B类}^{'})}^{- 1} {P（P）}_{σ} Δ ({F类}_{Y（Y）}) {P（P）}_{σ}^{'} {B类}^{'},

通过谱值分解(13)意味着 $H（H） ({F类}_{Y（Y）}) = {({B类}^{'})}^{- 1} {P（P）}_{σ} D类$ 一类非奇异对角矩阵 $D类$ ⁠。然后定理如下

Z轴 = H（H） {({F类}_{Y（Y）})}^{'} Y（Y） = D类 {P（P）}_{σ}^{'} {B类}^{- 1} (B类 X（X） + μ) = D类 {P（P）}_{σ}^{'} X（X） + D类 {P（P）}_{σ}^{'} {B类}^{- 1} μ .

A.4、。定理6的证明

紧接着，如果V（V）(F类)是满足定义1的散射函数，那么V（V）(F类_X（X）)是一个对角矩阵。证明的其余部分与定理5的证明相同。

答5。定理7的证明

通过等方差，我们可以假定μ= 0. 然后通过定理5的证明的第一部分给出证明。

A.6、。定理证明8

定理8的证明类似于定理5和6的证明。唯一的区别是矩阵 $D类$ 在证明的最后，不一定是对角矩阵，而是一个具有对角顺序块的块对角矩阵第页₁,…,第页_米.

A.7、。定理9的证明

定理9的证明是定理5证明的推广。在这个证明中，对顺序矩阵块的引用第页指的是将矩阵划分为维度块第页_我×第页_j个对于我,j个=1，…，米上的对称条件X（X）以及以下假设X（X）具有相互独立的子向量，意味着 $X（X） ~_{d日} S公司 X（X）$ 对于任何块对角矩阵 $S公司$ 具有形式为±的对角块我_pk系列,k个= 1,…,米因此，对于任何散射函数V（V）(F类)满足形状等变特性(3)，因此 $V（V） ({F类}_{X（X）}) = V（V） ({F类}_{S公司 X（X）}) = S公司 V（V） ({F类}_{X（X）}) S公司$ ⁠，对于任何此类 $S公司$ ⁠。最后一个等式来自属性(3)因为块对角线分量V（V）(F类_X（X）)和 $S公司 V（V） ({F类}_{X（X）}) S公司$ 都是一样的。通过选择第一个对角线块 $S公司$ 将是−我_第页1和其他对角块我_pk系列对于k个= 2,…,第页然后以这种方式继续，我们得出结论V（V）(F类_X（X）)是块对角矩阵。

对于两个散射泛函V（V）₁(F类)和V（V）₂(F类),V（V）₁(F类_X（X）)⁻¹ V（V）₂(F类_X（X）)是块对角矩阵。应用谱值分解(13)对角线元素给出了 ${V（V）}_{1, 我 j个} {({F类}_{X（X）})}^{- 1} {V（V）}_{2, 我 j个} ({F类}_{X（X）}) = {H（H）}_{j个} Δ_{j个} {H（H）}_{j个}^{- 1}$ ⁠，带Δ_j个是对角阶矩阵第页_j个对于j个=1，…，米.设Δ为阶对角矩阵第页带对角块Δ_j个，并让H（H）是有序的块对角矩阵第页带对角块H（H）_j个因此，V（V）₁(F类_X（X）)⁻¹ V（V）₂(F类_X（X）) =H（H）ΔH（H）⁻¹根据定理2 $Δ \propto {P（P）}_{σ} Δ ({F类}_{Y（Y）}) {P（P）}^{'}_{σ}$ ⁠，式中Δ(F类_Y（Y）)■诊断{ρ₁(F类_Y（Y）),…,ρ_第页(F类_Y（Y）)}和P（P）是块置换矩阵。应用属性(3)再次给予

{V（V）}_{1} {({F类}_{Y（Y）})}^{- 1} {V（V）}_{2} ({F类}_{Y（Y）}) \propto {({B类}^{'})}^{- 1} {V（V）}_{1} {({F类}_{X（X）})}^{- 1} {V（V）}_{2} ({F类}_{X（X）}) {B类}^{'} \propto {({B类}^{'})}^{- 1} H（H） {P（P）}_{σ} Δ ({F类}_{Y（Y）}) {P（P）}_{σ}^{'} {H（H）}^{- 1} {B类}^{'} .

将其与光谱值分解进行比较(13)对于V（V）₁(F类_Y（Y）)⁻¹ V（V）₂(F类_Y（Y）)给予 $H（H） ({F类}_{Y（Y）}) = {({B类}^{'})}^{- 1} H（H） {P（P）}_{σ} D类$ 一类非奇异对角矩阵 $D类$ ⁠因此，

Z轴 = H（H） {({F类}_{Y（Y）})}^{'} Y（Y） = D类 {P（P）}_{σ}^{'} {H（H）}^{'} {B类}^{- 1} (B类 X（X） + μ) = D类 {P（P）}_{σ}^{'} {H（H）}^{'} X（X） + β,

哪里 $β = D类 {P（P）}^{'}_{σ} {H（H）}^{'} {B类}^{- 1} μ$ ⁠.自 $D类 {P（P）}^{'}_{σ} = {P（P）}_{σ} D类$ ⁠，那么它就这样

{P（P）}_{σ}^{'} (Z轴 - β) = {({Z轴}_{(1)}^{'}, \dots, {Z轴}_{(米)}^{'})}^{'} - {P（P）}_{σ}^{'} β = D类 {H（H）}^{'} X（X）,

具有 ${Z轴}_{(j个)} = {D类}_{j个} {H（H）}^{'}_{j个} {X（X）}_{(j个)}$ ⁠，用于j个=1，…，米因此，定理9成立。

本文根据牛津大学出版社标准期刊出版模式的条款出版和发行(https://academic.oup.com/journals/pages/open_access/funder_policies/chorus/standard_publication_model)

下载所有幻灯片

月份：	总浏览次数：
2023年3月	5
2023年4月	19
2023年5月	16
2023年6月	10
2023年7月	11
2023年8月	10
2023年9月	6
2023年10月	9
2023年11月	10
2023年12月	25
2024年1月	15
2024年2月	13
2024年3月	10
2024年4月	5

文章内容

不变坐标选择

总结

1.简介

2.散布矩阵

2.1. 仿射等方差

2.2. 分散统计分类

3.比较散布矩阵

4.不变坐标系

5.非椭圆模型下的不变坐标选择

5.1. 椭圆分布的混合

5.2. 独立组件分析模型

6.讨论和示例

6.1. 示例1

6.2. 示例2

6.3. 其他示例

7.结束语

7.1. 与投影追踪的关系

7.2. 其他相关方法

7.3. 总结和继续研究

讨论Tyler、Critchley、Dümbgen和Oja的论文

分散度和统计可变性的选择

统计推断和一般分布

高维数据和投影追踪

内容和风格

稳健性

其他备注

致谢

工具书类

讨论中的参考文献

附录A：证明

A.1、。定理1和2的证明

A.2、。定理3和4的证明

答3。定理5的证明

A.4、。定理6的证明

答5。定理7的证明

A.6、。定理证明8

A.7、。定理9的证明

引文

意见

海拔高度

电子邮件警报

通过引用文章

最新的

阅读次数最多

被引用次数最多

此功能仅对订阅服务器可用