2013年7月25日

积分八元数（下）

约翰·贝兹

现在我想谈谈这对我们有什么帮助。特别是，它如何将11维超重力与台球游戏联系起来！

我还想生动详细地解释一下Cayley整数和\（\mathrm的作用{PSL}_2（\mathbf{O}）\）“看起来像”-以及一些低维示例，这些示例来自实数、复数和四元数中的其他类型的整数。这将迫使我学习一些有趣的东西。但我认为最好是从整体上开始，如果我有时间的话，稍后再回到细节上来。

重力台球

基本思想是这样的。

假设你遵循广义相对论的解决方案，就像我们的宇宙回到大爆炸。然后在某些条件下，当我们返回时，每一小块空间都会与其他空间“解耦”。这意味着，在极限状态下，当你回到大爆炸时，描述广义相对论的复杂非线性偏微分方程会减少到普通的空间中每个点度量的微分方程。

更好的是，随着时间的推移，这些方程简化为方程，就像那些描述牛顿点粒子在高维双曲空间区域内反弹的方程一样！这就像一个理想化的无摩擦台球的高维版本，在台球桌的墙壁之间无休止地弹跳：

图中的桌子，直墙被半圆覆盖，是已知给予混乱如果够长的话。也就是说，台球的未来位置以一种非常敏感的方式取决于它的初始位置和速度。初始条件的微小变化会在每次球穿过球台时使球的位置发生越来越大的变化，这使得预测未来的情况变得不切实际。

数学物理学家认为很多关于不同类型的台球桌会发生什么，包括高维桌和弯曲黎曼流形的桌，有或没有边界。正如你所料，在负曲率的流形上，如双曲线空间，附近的轨迹往往会漂移得很远。因此，人们认为，在许多情况下，将广义相对论推回大爆炸会导致混乱！

有一些显而易见的问题你应该想知道。

例如：一个理想化的无摩擦台球可以在桌子上无休止地反弹。当我说“预测未来会发生什么是不切实际的”时，我是在使用这个事实。但你只需要回到过去有限量在你到达宇宙大爆炸之前。那么，这两个问题怎么可能是同构的呢？

答案很有趣：我们需要取时间的对数让它与台球问题同构！作为\（t\到0\），它的对数一直向下到\（-\infty\）。所以宇宙无限次地反弹，无序地改变形状越来越快当我们回到宇宙大爆炸的时候。

这里的想法可以追溯到一些俄罗斯人，包括Evgeny Lifshitz，他因一系列被大家称为“Landau and Lifshit”的物理教科书而闻名：

• V.A.Belinskii、I.M.Khalatnikov和E.M.Lifshitz，相对论宇宙学中奇点的振荡方法，高级物理。 19(1970), 525.

所以我所说的现象被称为“BKL奇点”。您可以在此处阅读更多信息：

• 维基百科，BKL奇点.

为了澄清一点，我应该补充一点，台球反射到硬墙上的模型只是一个极限情况。起初，墙是“软”的：我们有一个球在平滑的势场中运动。但随着时间的推移，它们变得“更难”或更陡峭。

此外，我应该强调的是，这幅图只适用于在任何给定时间空间都是均匀但非各向同性的宇宙学，尤其是所谓的“Bianchi IX模型”。这个短语指的是三维实李代数分为九个科，这也对空间均匀宇宙学进行了分类。

在现实世界中，我们可以预期空间不是很均匀，然后为了论证BKL奇异性的重要性，我们需要论证不同的空间小块从每个as（t到0）解耦。我不确定当然，如果我们认真对待（t到0）极限，我们需要考虑量子引力，包括各种形式的物质。。。

但也许我应该说清楚：我在这是为了美丽的数学。我不在乎这些东西是否与现实世界有关。但在寻求美丽的数学时，运用物理思想仍然很好。

如果我们这样做了，那么当空间不是三维的，而是具有其他维度时，它自然会引导我们思考宇宙台球。然后，一本很好的“字典”出现了，它将其中一些可能性与台球在不同维度的双曲空间区域中弹跳联系起来。

在这本词典中，如果时空是（n）维的，并且在我们的引力理论中存在（d）“dilaton场”，我们会得到一个弹球在（n+d-2）维双曲空间的区域内反弹。根据其他细节，双曲线空间中的该区域可能具有有限或无限体积：

第一种情况产生混沌运动；在第二种情况下，台球通常会反弹一点，然后反弹到无穷远。（我从在这里.)

在最好的情况下，这个区域是作用于双曲空间上的Coxeter群的基本域！

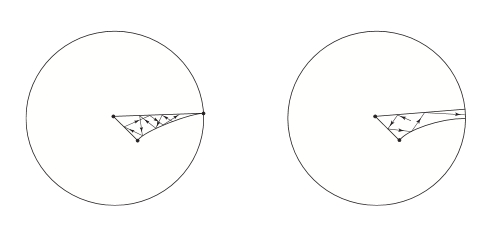
例如，Belinskii、Khalatnikov和Lifshitz最初研究的案例是4d时空中没有物质的纯重力。这意味着（n=4）和（d=0）：没有膨胀剂。这使我们的台球在双曲线平面上运动。通过大量的工作，您可以显示该区域看起来像这里的任何一个三角形：

这些三角形是称为三角形群的基本域。对于任何自然数\（p，q，r \）(p、 q、r)三角形组具有遵循关系的生成器\（s_1、s_2、s_3\）

$$s_1^2=s_2^2=s_3^2=1$$

$$（s_1 s_2）^p=（s_2 s_3）^q=（s_3 s_1）^r$$

该组是一个简单的示例考克斯特群.如果

$$\压裂{1}{p}+\压裂{1'{q}+\裂缝{1}}{r}<1$$

它作用于双曲线平面上，每个生成器都充当一条直线上的反射。该组动作具有基本域，这些域是带内角的三角形\（\pi/p、\pi/q、\pi/r\）。例如，Hermann Weyl研究的三角形群具有如下基本域：

如果\（p，q \）或\（r \）变为无穷大，那么从技术上讲我们没有Coxeter群，但我们仍然可以通过删除包含该数字的关系来获得一个群。该群仍然作用于双曲线平面。。。但是三角形的一些角移到了无穷远处，也就是上面圆盘的边缘。一种极端情况是\（（\infty，\infty，\inffy）\）三角形组，它给出了以下结果：

（2,3，infty）三角形组来自4d时空中无物质的重力，并不极端：每个三角形在无穷远处只有一个顶点。如果我们稍微推广一下这些图，并让我们用无穷大标记一条边，我们可以为其写下一个Coxeter图：

这个组非常重要：它正是\（\mathrm{PGL}（2，\mathbb{Z}）\）。所以它是偶数部分-由对反射-是模群\（\mathrm{PSL}（2，\mathbb{Z}）\）。

还有很多其他有趣的例子。但让我跳到关键点：这本关于引力理论和台球的字典对数学上最令人兴奋的引力理论说了什么：11维超重力，有（n=11）和（d=0）？如果我们看最简单的纯玻色子解，我们会得到一个台球在9维双曲空间的区域内弹跳。这个区域就是我上次描述的Coxeter群的基本域：{电子}_{10}\)!

记住，这个组是由9维双曲空间中的10个反射生成的。每一个反射都是我们台球桌的一面墙。而这个组的偶数部分——由成对反射产生的部分，给出了方向-保护变换——正是（mathrm{PSL}（2，mathbf{O}）），其中\（mathbf}O}\）是Cayley整数！

要了解更多信息，我推荐本文：

• 蒂鲍特·达穆尔、索菲·德贝尔、马克·亨诺和克里斯蒂安·肖姆隆德，爱因斯坦台球与有限维单李代数的超扩张.

或者更温和的说法是：

• 蒂鲍特·达穆尔，庞加莱、相对论、台球和对称.

还有很多话要说。。。其中大部分我都不知道。所以下一次我将回到现实中，开始详细描述Cayley整数。人们不需要知道奇特的物理或群论就能理解和享受它们。你真的只需要知道如何加、减、乘、除。。。思考8维的形状。

©2013 John Baez版权所有
baez@math.removethis.ucr.andis.edu
家