整数八元数（上）

2013年7月23日

整数八元数（上）

约翰·贝兹

关于群同构的一件大事

$$\mathrm{PSL}（2，\mathbb{R}）\cong\mathrm{SO}_0(2,1) $$

这给了我们两种思考双曲平面对称群的方法。一方面，它包括分数线性变换具有真实条目：

$$z\mapsto\frac{az+b}{cz+d}\四元a，b，c，d\in\mathbb{R}$$

作用于\（\mathbb｛C｝\）中的上半平面，这是考虑双曲平面的一种方法。另一方面，它是三维时空洛伦兹群的身份成分，作用于双曲面

$$\{（t，x，y）\in\mathbb{R}^{3}：t^2-x^2-y^2=1，t>0\}$$

哪个是另一个思考双曲线平面的方式。

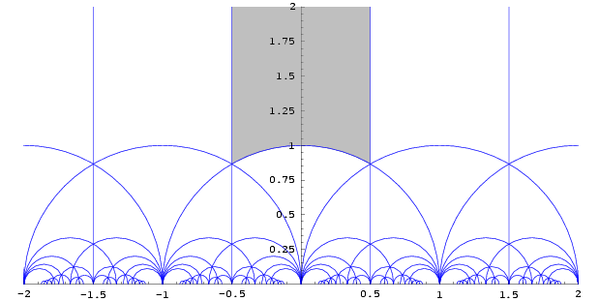
但真正重要的是，因为字段\（mathbb{R}\）包含作为离散子环的整数，\（mathrm{PSL}（2，mathbb}R}）\）包含模群\（\mathrm{PSL}（2，\mathbb{Z}）\）作为离散子群，作用于双曲平面，基本域如下：

这将三维时空的洛伦兹组与数论……多亏了模块形式理论之类的东西。部分观点是\（\mathrm｛PSL｝（2，\mathbb｛Z｝）\）不仅仅是\（\mathrm｛PSL｝（2，\mathbb｛R｝）\）的离散子群。这是一个算术组! 非常非常粗略地说，这就像一个代数群，但它是用类似整数的环来定义的，而不是用字段。

这是一个更奇妙的事实。八元数代数（mathbb{O}）包含一个（非结合！）离散子环（mathbf{O}），有时称为Cayley整数，Coxeter整数，或屋大维人如果你忽略了可以乘法八元数的事实，你可以把八元数看作是一个8维的真实内积空间。。。然后Cayley整数在这个向量空间中形成一个格，也就是说，直到重新缩放，除了\（\mathrm）{E} _8个\)根晶格！

因此，每个Cayley整数都有240个最近的邻居，按如下模式排列：

你应该在8个维度中想象。

这已经很好了。但是Cayley整数在乘法下是闭合的，这使得更神奇的事情发生了！

例如，它允许我们定义组的算术子组（\mathrm{PSL}（2，\mathbf{O}）

$$\mathrm{PSL}（2，\mathbb{O}）\cong\mathrm{SO}_0(9,1) $$

这作用于9维双曲空间

$$\{x\in\mathbb{R}^{10}:\；x_0^2-x_1^2-\cdots-x_9^2=1，\；x_0>0\}$$

更好的是，这个作用于9d双曲空间的奇妙离散群与\（\mathrm）有关{E} _8个\). 实际上，\（\mathrm{PSL}（2，\mathbf{O}）\）是考克斯特群\（\mathrm{电子}_{10} \），由考克塞特图像\（\mathrm{E} _8个\)，但更长：

该组为每个点有一个生成器\（s_i\），具有关系$$s_i^2=1$$对于每个点，$$s_i s_j s_i=s_j s _j$$对于由边缘连接的任何一对点，以及$$s_i s_j=s_j s_i$$对于配对不由边缘连接。这些生成器中的每一个都作为超平面在9维双曲空间中的反射。所以，它被称为双曲Coxeter群.由产品生成的子组二生成器被称为该组的偶数部分，它与\（\mathrm相同{PSL}_2（\mathbf｛O｝）\）。

同样的事情以更简单的方式发生在\（\mathrm{PSL}_2（mathbb{Z}）：它是双曲Coxeter群在双曲平面上作用的偶数部分，基本域如下：

您可以通过为\（\mathrm获取基本域来获得这些{PSL}_2（\mathbb{Z}）\），我之前在上半平面中向您展示过，并将它们切成两半。

所以，多亏了Cayley整数，我们知道在9维双曲空间中有一个类似但更精彩的画面！不幸的是，这个博客太低了，无法容纳它。

此Coxeter图：

也可以看作是Dynkin图-是一种危险的大类型，因为它提供了无限维的李代数，a双曲Kac–Moody代数.这个李代数也名称为\（\mathrm｛E｝_{10} \），它与我刚才描述的Coxeter组密切相关：Weyl群李代数。

李代数{电子}_{10} \）与物理学有着诱人而神秘的联系。理想情况下，我会在本系列中解释一些关于它们的内容。至少，我想说双曲Coxeter群是如何像\（\mathrm{电子}_{10} \）与超对称量子宇宙学台球! 但我今天想向大家推荐的论文是：

阿克塞尔·克莱恩施密特（Axel Kleinschmidt）、赫尔曼·尼科莱（Hermann Nicolai）、雅各布·帕尔姆克维斯特（Jakob Palmkvist）、，双曲Weyl群与四赋范除代数.

有一些不太宏大的目标，所以这是一个很好的起点。它描述了同构

$$\开始{数组}{ccl}\mathrm{PSL}（2，\mathbb{R}）&\cong&\mathrm{SO}_0(2,1) \\\mathrm{PSL}（2，\mathbb{C}）&\cong&\mathrm{SO}_0（3,1）\\\mathrm{PSL}（2，\mathbb{H}）&\cong&\mathrm{SO}_0(5,1) \\\mathrm{PSL}（2，\mathbb{O}）&\cong&\mathrm{SO}_0(9,1) .\结束｛数组｝$$

工作，重点是非对易性（对于四元数（mathbb{H}）和八元数（mathbb{O}））和非结合性（对于（mathbb{O}\））引入的微妙之处。它描述了\（\mathbb{R}，\mathbb2{C}，\ mathbb}H}）和\（\mathbb{O}）中“整数”的各种子环，以及这些子环如何产生算术群。并且，它描述了这些与双曲Coxeter群的关系。即使你不关心（有趣的、遥远的、高度理论化的、无法通过实验验证的）物理的潜在应用，这也是一个非常漂亮的数学。

你也可以阅读评论上n个-品类咖啡馆，并在那里发表自己的意见或提出问题！