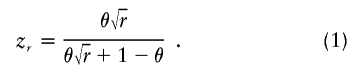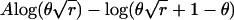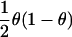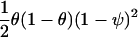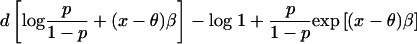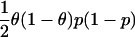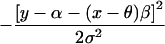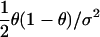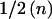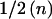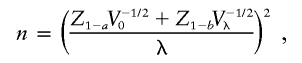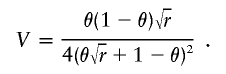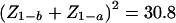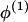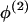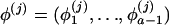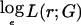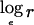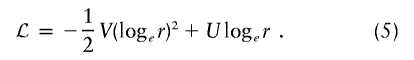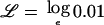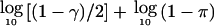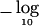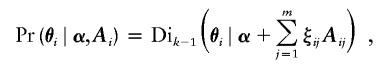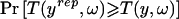摘要 可以利用来自不同大陆的人群之间的混合来检测疾病易感性位点,在这些位点上,风险等位基因在这些人群之间的分布存在差异。 我们首先在配子混合和基因座祖先的测量没有不确定性的极限情况下检验了这种方法的统计能力和映射分辨率。 我们表明,对于一种罕见的疾病,最有效的设计是只研究受影响的个体。 在一个典型的非裔美国人群体中(双向混合比例为0.8/0.2,血统交叉率为每100 cM 2),一项对800名受影响个体的研究有90%的检测能力 P(P) 值<10 −5 一个在人群之间产生2的风险比的基因座,预期的映射分辨率(该基因座位置的95%置信区间的大小)为4cM。实际上,要从标记数据推断基因座祖先需要贝叶斯计算密集型方法,如程序ADMIXMAP中所实现的那样。 仅受影响的研究设计需要关于给定基因座祖先的每个等位基因频率的强有力的先验信息。 我们展示了如何结合来自未摄入和混合人群的数据来估计研究中混合人群中的这些祖先特异性等位基因频率,从而考虑到未摄入和混杂人群中等位基因的频率差异。 使用基于非裔美国人遗传结构的模拟数据,我们表明,在使用3-cM间距祖先信息含量为36%的标记进行连锁测试时,可以提取60%的信息。 与经典连锁研究一样,最有效的策略是在初始基因组搜索中使用中等密度的标记,然后用额外的标记使假定连锁区域饱和,以提取几乎所有有关基因座祖先的信息。
背景 由于基因原因,疾病风险不同的种族群体之间的混合提供了一种自然实验,原则上可以利用这种实验以与实验杂交相同的方式定位基因。 虽然应用这种方法需要先进的统计方法,但实际上,它检测联系所依赖的基本原理很简单。 例如,假设某个基因座的风险等位基因在人群之间的分布存在差异,从而使欧洲人患骨质疏松性骨折的风险比西非人高出两倍。 如果我们根据在该基因座上是否有0、1或2个欧洲血统基因拷贝对欧洲/西非混合血统的个体进行分类,那么具有2个拷贝的个体的疾病风险将是具有0个欧洲血缘基因拷贝的个体高出的两倍。 我们不必直接比较这三组之间的疾病风险(这需要队列设计)。 相反,我们只能研究病例,在每个配子上的每个位点比较具有欧洲血统的基因拷贝的观察和预期比例。
虽然这种方法的理论是由麦凯格概述的( 1998 )它的实际应用有待于统计方法和标记面板的发展,这些标记可以为祖先提供信息。 为了将用于近交系间实验杂交的连锁分析方法推广到最近混合的人群,必须克服三个主要问题:
1. 被人口分层搞糊涂了。 在实验杂交中,所有个体都有相同的混合史。 在混合的人类种群中,混合的历史尚不清楚,不同个体的混合比例也不同。 这导致疾病与非连锁基因座的祖先相关。 这个问题可以通过调节每个人父母的混合比例来解决(麦凯格 1998 ). 为了满足母体混合物的条件,我们可以在广义线性模型中调整母体混合物(Hoggart等人。 2003 )或者将观察到的基因座祖先与每个个体的预期基因座祖先(给定父母混合)进行比较。
2 人类族群不是近亲繁殖的。 实验杂交通常使用自交系,通过使用标记位点,在每个菌株中固定不同的等位基因。 对于祖先大陆定义的人类种群,我们可以预先选择标记,以显示这些大陆群种群之间的极端等位基因频率差异。 然而,即使是这些标记也不能为祖先提供完美的信息。 这个问题可以通过多点分析来解决,该分析结合了染色体上所有标记的信息,以提取每个位点的祖先信息(Falush等人。 2003 ;Hoggart等人。 2003 ).
三。 祖先群体中的等位基因频率未知。 在一次实验杂交中,已知祖先菌株中的等位基因频率。 对于混合人群,祖先特异性等位基因频率的估计值——每个等位基因的概率,考虑到研究位点配子的祖先——存在不确定性。 这是因为构成混合种群的祖先亚群通常无法精确定义,而且对于其中一些亚群,没有未被接纳的后代可供研究。 如本文所述,通过结合来自未摄入和混合人群的数据来估计祖先特异性等位基因频率,可以克服这个问题。
在未对祖父母进行分型的远交系(Sillanpaa和Arjas)之间的实验杂交分析中也出现了类似的问题 1999 )以及通过使用异质小鼠种群对数量性状基因座进行精细定位(Mott等人。 2000 ).
研究设计和混合映射的统计能力 在本节中,我们检验了在没有不确定性的情况下测量基因座祖先和配子混合比例的极限情况下混合映射的统计能力。 我们后来表明,如果对全基因组的祖先信息标记进行分型,然后用额外的标记饱和假定连锁的区域,以提取关于基因座祖先的高比例信息,那么这些条件几乎可以满足。
统计功率计算 检测产生λ效应大小的基因座(其中λ可以是对数比值比β或对数风险比 记录器 )具有I类错误概率 一 和II类错误概率 b、, 所需观察次数 n个 由提供
哪里 V(V) 0 和 V(V) λ 分别表示在零假设和替代假设下由单个观察所提供的预期信息。 在只受影响的设计中,高风险亚群中具有比例混合θ的单个配子所提供的预期信息为
对于固定 r、 V(V) 最大化为 θ=(1+ 第页 1/4 ) -1 因此,信息量最大的配子是那些与高危亚群的混合比例略低于50%的配子。 对于中等效果大小, V(V) λ ≈ V(V) 0 和
因此,根据方程式( 4 ),所需信息 纳伏 0 对于90%功率( Z轴 1- b =1.28 )检测尺寸的影响 λ=1 单方面 P(P) 值<10 −5 ( Z轴 1- 一 =4.27 )近似值为 。90%功率所需的样本量,以检测 P(P) 值<10 −5 通过将所需信息(30.8)除以单个观测值的预期信息,即可轻松计算出 表1 。任何其他效果大小所需的样本大小是通过将这些数字除以效果大小的平方来计算的。 因此,在非洲裔美国人中,西非混合物的平均比例θ为~0.8(Parra et al。 1998 ),一个只受影响的设计需要800个人的90%的检测能力 P(P) 值<10 −5 ,一个导致血统风险比率的基因座 第页 =2 ( 记录器 =0.69 ).
统计建模 上述理论结果基于这样一个假设,即配子混合和基因座祖先可以在没有不确定性的情况下推断出来。 实际上,标记数据只能提供关于配子混合和基因座祖先的不完全信息。 我们之前已经描述了ADMIXMAP程序,该程序对混合进行建模,如何在遗传关联研究中通过群体分层来控制混杂(Hoggart et al。 2003 ; 遗传流行病学组 网站)。 我们现在描述这个程序在混合映射中的应用。
建模外加剂 Hoggart等人之前详细描述了ADMIXMAP拟合的基本模型( 2003 ). (计算方法见 附录A 程序STRUCTURE(Falush等人。 2003 ). 研究中的人群被建模为 k 祖先亚群。 我们将“配子混合物”定义为父母基因组中每个亚群都有祖先的比例; 这与配子基因组中每个亚群都有祖先的比例并不完全相同。 混合种群中配子混合物的分布由带参数向量的Dirichlet分布建模 α=(α 1 ,…,α k ) ADMIXMAP中可以指定配子分类的两种可选模型:随机模型,其中两个亲本配子独立于此Dirichlet分布; 或两个亲本配子的混合比例相同的分类交配模型。 这些选择代表着极端; 原则上,该模型可以扩展,以估计单个混合物的配合程度。
每个配子上不同基因座间祖先的随机变化由以下公式建模 k 独立泊松到达过程。 由于这些到达过程的相对强度由配子θ的混合比例指定,因此只需要一个额外的参数:到达过程强度的总和,用τ表示。 尽管祖先的随机变化并不完全遵循独立泊松到达过程的模型,即使在无干扰的假设下(麦凯格 1998 ),此建模假设简化了问题。 如果混合发生在单个脉冲中,τ的预期值是自未被吸收的祖先以来经过的世代数(Falush等人。 2003 ). 参数τ决定混合映射研究的分辨率以及提取每个位点祖先信息所需的标记密度。 τ值越高,绘图分辨率越高,但提取给定比例信息所需的标记密度也越高。 对于具有给定亚种群混合比例θ的配子,祖先交叉率ρ(来自该亚种群的祖先与来自其他亚种群之一的祖先之间的转换密度)由下式给出 ρ=2θ(1-θ)τ .
该模型假设基因座之间没有等位基因关联,这取决于基因座祖先。 如果两个或多个标记靠得很近,不能依赖这个假设,那么这些标记被归为一个单一的“复合位点”。假设在任何给定配子的复合位点内的所有标记位置上,祖先都是相同的,因为在这个短距离内,混合可能会被忽略。 在复合位点,单倍型和单倍型频率被建模,而不是等位基因和等位基因频率。 给定一个位点的祖先,观察到的等位基因或未观察到的单倍型的可能性是多项式,其概率由祖先特异性等位基因(或单倍型)频率指定。 该程序对每个位点的单倍型和祖先特异性等位基因(或单倍型)频率的后向分布进行采样。
一个性状对配子混合物的依赖性建模 对于病例对照或横断面设计,指定了一个广义线性模型,用于描述性状对两个配子平均混合比例的依赖性,以及用户指定的任何其他解释变量。 对于数量性状,这是一个线性回归模型; 对于二元性状,这是一个logistic回归模型。 通过对性状对个体混合的依赖性建模,程序可以使用性状值和基因型数据推断配子混合比例。 即使是仅对受影响个体(包括对照组)进行连锁测试,拟合逻辑回归模型也有助于模型推断配子混合和等位基因频率。
建模通道频率 在一个基因座上观察每个可能的等位基因或单倍型的概率,考虑到该基因座配子的祖先,由混合群体中的祖先特异等位基因(或单倍体)频率指定。 ADMIXMAP允许以三种方式之一指定祖先特异性等位基因频率:
对于大多数由大陆群之间最近混合形成的种群,有关祖先特异性等位基因频率的一些信息可从构成混合种群的大陆群的现代未被接纳后代中获得。 我们可以假设这些未被接纳的后代中的等位基因频率与混合群体中相应的祖先特异性等位基因的频率相同; 我们将其称为“无色散”假设。 如果等位基因频率是从相对较小的未摄入个体样本中估计出来的,则有必要考虑估计中的抽样误差。 在贝叶斯框架内,这很简单,在该框架中,上一次研究的后验分布成为下一次研究之前的分布。 因此,我们可以将祖先特异性等位基因频率的Dirichlet先验分布指定为后验分布,该后验分布是通过结合参考先验分布获得的, 迪 (0.5,…,0.5) ,以及来自未纳入人群的数据的可能性。 这个分布的参数只需在未摄入人群样本中每个等位基因的观察计数上加上0.5即可获得。 我们可以通过基于后验预测检查概率构建模型诊断来测试无离散假设,如 附录B 对于每个亚群体,该测试比较了混合群体中观察到的和复制的等位基因计数的可能性,给出了特定于祖先的等位细胞频率。 该测试在每个基因座进行计算,并(通过对所有基因座的对数可能性求和)作为每个亚群的汇总测试。
如果有证据表明无色散假设被违反,我们可以拟合色散模型。 与假设没有离散的模型相比,在估计混合人群中的祖先特异性等位基因频率时,这使得来自现代未被接纳后代的等位基因频数数据(“历史”等位基因频数)的权重较小。 这是通过为等位基因频率指定一个类似于Lockwood等人所描述的层次模型来实现的( 2001 ). 对于每个大陆组,混合人群中的祖先特异性等位基因频率 以及未被接纳人群中相应的“历史”频率 独立于Dirichlet分布绘制, 迪 (μ) .对于带有 一 等位基因, μ=(μ 1 ,…,μ 一 ) 和 。我们重新参数化Dirichlet分布,以便 每个位点的等位基因频率分布如下
哪里 我 指数位置和 j个 索引混合种群中的一个子种群( j个 =1 )或相应的未被接纳的大陆集团( j个 =2 ). 离散参数η控制Dirichlet分布的方差,并规定每个大陆群中的所有位点都是相同的。 这与Wright的 如果 标准 (赖特 1951 ),由 如果 标准 =(1+η) -1 (Lockwood等人。 2001 ). 在我们的应用中,η指数在现代未被接纳后代的“历史”等位基因频率与混合人群中相应的祖先特异性等位基因的频率之间的离散度。 η值越大,等位基因频率的离散度越小。
模拟表明,为了从具有模糊先验分布的混合群体样本的数据中可靠地估计离散参数η,标记面板必须包含紧密相连的标记序列,以便可以准确推断基因座祖先, 或者混合比例在样本个体之间必须有很大差异,因此可以根据观察到的等位基因频率对个体混合比例的依赖性来推断祖先特异性等位基因的频率。 在迄今为止报道的研究中,我们只使用了宾夕法尼亚州立大学的标记面板(Shriver等人。 2003 ),它只有几个短序列的连锁标记。 在这种情况下,有必要根据各大陆群内各亚群之间等位基因频率的方差估计,为离散参数η指定一个信息先验值。 例如, 如果 标准 西非各亚群之间的差异估计为~0.02(Cavalli-Sforza et al。 1994 ). 如果现代西非人之间的等位基因频率和非洲裔美国人中相应的祖先特异性等位基因的频率的离散度与西非亚群之间的离散度相似,这表明η的优先模式应为~50。 同样, 如果 标准 据估计,欧洲各亚群之间的η值为~0.002,表明η值的先验模式应为~500。 由于离散参数η将取决于如何选择标记,以及在大陆组内抽样何种亚群组合来估计等位基因频率,因此η的先验值应反映出这种不确定性。
根据贝叶斯推断的原理,我们可以使用ADMIXMAP生成的祖先特异性等位基因频率的后验分布,在随后对来自同一混合群体的新样本的研究中指定这些等位基因的频率的先验分布。 从这一阶段开始,只要我们可以假设来自同一混合群体的不同样本之间的祖先特异性等位基因频率没有差异,我们就不需要指定离散模型。 为了简化计算,ADMIXMAP生成的等位基因频率的后验分布近似为Dirichlet分布,可用于指定后续研究的先验值。 通过将Dirichlet分布的协方差矩阵的均值和行列式与ADMIXMAP生成的等位基因频率的后验均值和后验协方差矩阵行列式相等,计算出该分布的参数。
外加剂映射的应用 悬挂机构测试 ADMIXMAP中提供的链接测试是基于丢失数据可能性的得分测试。 使用这种方法,可以直接测试形式的任何无效假设 λ=λ 0 ,其中 λ 0 是贝叶斯模型中指定的值。 基本算法已在其他地方进行了描述(McKeigue et al。 2000 ;Hoggart等人。 2003 ). 对于完整数据的每次实现,我们计算实现的分数(对数似然梯度 λ 0 )和实现的信息(减去对数似然的二阶导数 λ 0 ). 对于一项仅受影响的研究,测试无效假设 记录器 =0 ,单个配子在任何给定位点的实际得分和信息都可以从表达式中导出( 2 )作为 ( A类 -θ)/2 和 θ(1-θ)/4 分别为。 比分 U型 被评估为已实现分数的后验期望,以及观察到的信息 V(V) 通过从完整信息(实现信息的后验期望)中减去缺失信息(实现分数的后验方差)来计算。 在零假设下, U型 t吨 V(V) -1 U型 有一个χ 2 分配。
与完全贝叶斯方法相比,该评分测试算法具有以下几个优点:(1)计算效率高,因为可以在一次马尔可夫链蒙特卡罗采样器运行中测试多个假设; (2)它只需要拟合一个零模型,避免了零模型可能产生的困难(例如确定偏差); 以及(3)相对于直接测量潜在变量的理想实验,观察到的信息与完整信息的比率是研究设计效率的有用估计。 在大样本中,分数检验与似然比检验是渐近等价的。 此外,渐近地,对数似然近似为二次方(参见等式[ 5 ]).
另一种测试受影响设计中特定基因座连锁的方法是计算一个似然比,该似然比比较了零假设下的似然比, H(H) 0 根据另一种假设,没有与研究中的基因座相关的疾病基因座, H(H) 1 研究中的基因座的人口风险率为 第页 .
信息内容映射 与无限密集的标记图相比,信息内容图衡量标记集检测连锁的充分性,该标记图允许在没有不确定性的情况下推断基因座祖先和配子混合。 这使我们能够确定应在地图中添加其他标记的位置。 我们可以通过使用每个位点的受影响分数测试中观察到的信息与完整信息的比率来构建此信息内容图。 为此,测试应该在未经选择的个人样本上进行评估,对于这些人,我们可以假设零假设是正确的。 地图的信息内容必须针对研究中的每个混合人群分别进行评估,因为它取决于混合历史以及祖先特异性等位基因频率。 与经典连锁研究一样,提取特定比例信息所需的标记密度与单个标记的信息含量之间存在权衡。
有几种可能的方法来计算祖先的标记信息内容。 在本文中,祖先标记信息内容的引用值基于预期比例 (f) 通过对基因座进行分型,单个配子上基因座祖先的先验方差减少了(麦凯格 1998 ;Molokhia等人。 2003 ). 这种测量方法对我们的目的很有用,因为它相当于如果没有来自连锁标记基因座的信息,只受影响的分数测试的效率。 另一种措施, 我 n个 , Rosenberg等人提出( 2003 ). 尽管的绝对值 (f) 和 我 n个 不同的是,这两种方法对标记的信息内容排序相似。
排除映射 排除图显示了基因组上每个位置的影响大小 第页 可以在给定的LOD得分阈值下排除。 这可以用来排除其他标记的输入区域,因为已经获得的数据足以排除研究旨在检测的大小的影响。 为了构建排除图,我们需要将对数似然作为每个位点的效应大小的函数。 如上所述,近似对数似然的二次函数 -说吧, ℒ -可以从分数中获得 U型 和信息 V(V) 在分数测试中计算。 对于仅受影响的测试,对数似然是以下函数的函数 ;如果我们任意设置 ℒ=0 ,此功能为
要根据LOD得分−2的传统标准计算排除阈值,我们可以替换 并求解此二次方程以计算 第页 可能性比 第页 =1 与真正的对数似然函数(在配子混合和基因座祖先的测量没有不确定性的极限情况下计算)相比,这个近似值是相当准确的,除了以下值 第页 远离null,这与排除映射无关。
映射分辨率 通过调整Kruglyak和Lander使用的方法,可以计算通过混合映射和仅受影响设计检测到的疾病位点位置的预期置信区大小( 1995 b )在受影响相对对的连锁研究中,生成置信区大小的概率分布。 我们假设配子混合和基因座祖先是在没有不确定性的情况下测量的,就像在一个无限稠密的标记图被键入的极限情况下一样。 对于受影响个体的单个配子 z(z) 第页 疾病所在地高危亚群的血统由方程式给出( 1 ). 因此,似然比对比了疾病位点与效应大小的假设 第页 位于给定的地图位置,假设该位置与疾病无关,则为两个贝努利可能性与参数之比 z(z) 第页 和θ。
克鲁格利克和兰德( 1995 b )利用随机游动理论导出置信区大小分布的近似值 C类 γ 其具有包含疾病基因座的概率γ。 在疾病位点的区域,LOD评分表现为随机行走,条件是通过疾病位点的预期值。 在一项仅受影响的地图研究中,这种行走步长是恒定的,
上下阶跃概率为π 1-π 分别,其中
置信区 C类 γ 定义为包含LOD分数超过阈值水平的所有点的最小间隔 Z轴 * - T型 γ ,其中 Z轴 * 是最大LOD分数。 T型 γ 由提供 .
为了计算置信区大小的分布,我们需要跃迁次数的分布 S公司 LOD分数永久降至以下所需 Z轴 * - T型 γ 在一项受影响的相关研究中,这些转换是在从共同祖先遗传的成对配子上共享0到1个基因拷贝之间进行的。 在混合映射研究中,单配子上的低风险和高风险亚群的祖先状态之间存在转换。 这些跃迁被建模为带有强度参数的泊松到达过程 ν=[ρ + (1- z(z) 第页 )+ρ - z(z) 第页 ] n个 疾病易感性位点区域的per-morgan,其中 n个 是受影响配子的数量 ρ + 和 ρ - 分别是向较高和较低LOD分数过渡的密度。 因此,对于来自高危亚群的具有比例混合θ的配子,这些转换的密度由下式给出 ρ + =θτ 和 ρ - =(1-θ)τ ,其中τ是上面定义的密集度参数之和。 所有祖先交叉的平均密度 n个 疾病位点区域的配子是 ν=[θτ(1- z(z) 第页 )+(1-θ)τ z(z) 第页 ] n个 每个摩根。 连续到达的距离服从指数分布,平均值为 1/ν 。以下是到达的距离 S公司 变换具有带形状参数的gamma分布 S公司 和标度参数ν。 此分布的样本可以通过模拟生成,从而使我们能够计算置信区大小的分布 C类 γ .
数据源 对三个非裔美国人样本和一个西班牙裔美国人样本进行了双列标记分型,这些双列标记是从一组38个标记中挑选出来的,用于提供西非、欧洲和美洲原住民血统的信息。 非裔美国人样本包括对费城202名个体的横断面研究,分型为26个位点; 对华盛顿特区232名个体在34个位点进行的横断面研究[ 2003 ]有关此集合的详细信息); 和393名居住在华盛顿特区的个体被纳入前列腺癌病例对照研究,分型为27个位点(见Kittles等人[ 2001 ]和[ 2002 ]有关此集合的详细信息)。 西班牙裔美国人样本是科罗拉多州圣路易斯山谷居民的横断面样本,根据Hoggart等人的描述,在21个标记位点上分型,从诊所确诊的糖尿病病例丰富( 2003 ).
未被接纳的西非人、欧洲人和美洲原住民的样本被分为38个祖先信息标记的同一组。 西非样本由369名个体在所有38个基因座上分型,欧洲样本由229名个体,在35个基因座分型,美洲原住民样本由182名个体在35个位点分型。 有关这些数据集的更多详细信息,请参见Shriver等人( 2003 ).
结果 祖先交配率的估计和映射分辨率 表2 显示了基于三个非裔美国人样本和一个西班牙裔美国人样本的密集度总和参数τ的估计值。 95%的可信区间很宽,因为这些研究中使用的标记面板只包括少数连锁标记序列。 结合这些研究,我们估计非裔美国人的τ为~6/100 cM。Falush等人( 2003 )在伊利诺伊州梅伍德的一个非裔美国人样本中,估计τ的后验平均值为9.8,可信区间为7-13,可信区间90%。
表2。
强度总和参数
人口 个人数量 标记数量 中值的 95%可信区间
非裔美国人:
前列腺癌 393 64 5.7 4.3–7.2
费城 202 26 6.1 3.3–10.6
华盛顿特区 232 33 7.1 4.6–10.8
西班牙裔美国人:
圣路易斯山谷 446 21 8.1 5.1–12.4
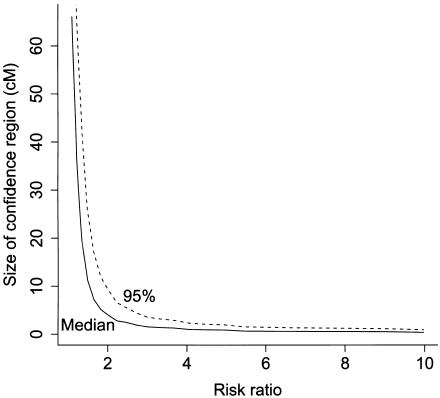
强度总和为6意味着,对于混合比例0.8/0.2,祖先交叉率为每100 cM~2( 2×0.80×0.20×6 ). 由此,我们计算了在无不确定性地测量基因座祖先和配子混合的极限情况下,非裔美国人混合映射研究的预期分辨率。 图1 显示了置信区大小分布的中位和上百分之95,相对于祖先风险比绘制 第页 样本量为800人,混合比例为0.8,来自高危人群 τ=6 。对于 第页 =2 ,置信区的预期大小为4 cM。由于尺度参数ν与样本大小呈线性关系 编号:, 置信区大小的期望与 1/ n个 因此,对于1 cM的预期绘图分辨率,具有祖先风险比的基因座需要约3200个个体 第页 =2 ,约9000人 第页 =1.5 .
图1。
疾病位点位置95%置信区间大小的中位数和上95%与800名固定样本大小的风险比相对应,混合比例为0.8,来自高危人群和 τ=6 .
测试链接、信息内容映射和排除映射 为了证明ADMIXMAP在使用密集标记图进行混合映射中的应用,我们模拟了一项基于指定为具有混合比例的双向混合的非洲裔美国人的遗传结构的仅受影响的研究 θ=0.8 来自高危人群和密集度总和 τ=6 每个摩根。 对于每个个体,标记基因型产生于两条100 cM长的染色体上,每1 cM间隔一个标记,其中一条包含一个疾病位点,其祖先风险比为2,位于染色体的中间,另一条没有疾病位点。 这些标记是双列的,等位基因1在高危亚群中的频率为0.8,在低危亚群中为0.2(相当于祖先的信息含量 (f) =0.36 [麦凯格 1998 ]或 我 n个 =0.28 [罗森博格等人。 2003 ]). 这两个数据集还包括200个未链接的双列标记,这些标记为祖先提供了充分的信息,以代表配子混合物的信息,这些信息可通过在基因组中对数百个其他祖先信息标记进行分型获得。
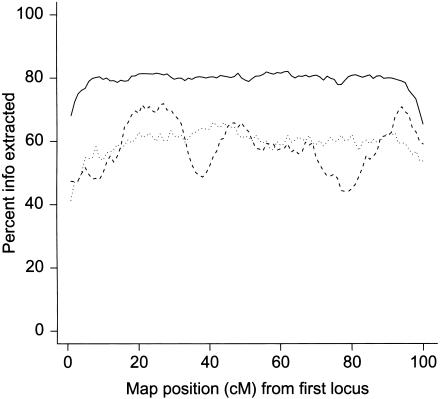
利用ADMIXMAP对这项模拟研究进行了三项分析:(1)一项使用所有标记位点的基因型数据; (2)每第二和第三个连锁标记位点的基因型在两条染色体上设置为“缺失”,以模拟标记均匀分布在3 cM的研究; (3)在两条染色体上各使用33个随机选择的标记,以模拟一项平均间隔为3 cM的标记间距不均匀的研究。包括缺失基因型的位点,可以确保程序计算在这些位置提取的信息的比例, 这样我们就可以评估提取的信息在标记位点之间脱落的程度。 图2 显示了 P(P) 三种分析中包含疾病位点的染色体的评分测试中计算的值。 在每次分析中,都会在一个广阔的区域内检测到联系。 图3 显示了在没有疾病位点的染色体上提取的信息的比例。 在标记间距为1cM的情况下,对于染色体的中间90%,提取的信息比例>80%。 标记均匀分布在3 cM处,提取的信息比例为染色体中部90%的约60%,标记位点之间的信息仅略有下降。 在平均3-cM间距但随机间隔标记的情况下,一些标记位点之间的信息降至~50%。 数字 4 和 5 显示祖先风险比率超出的估计阈值 第页 对于含有疾病位点的染色体和不含疾病位点的基因组,LOD得分分别为−2时可以排除该位点。 即使标记物间距为3-cM,血统风险比 第页 ⩾2 在整个染色体上LOD评分为−2时被排除在外,没有疾病位点。 在包含疾病位点的染色体上,可以排除祖先风险比>2的区域,标记间隔为1 cM比标记间隔为3 cM大。
图2。
的绘图 P(P) 长度为100 cM的染色体的模拟数据值,疾病位点在50 cM时的风险比为2。 实线, 标记间距为1 cM; 虚线, 每3cM间隔一个标记; 虚线, 标记随机间隔,平均间隔为3 cM。
图3。
长度为100 cM且无疾病位点的染色体的模拟数据的信息内容图。 实线, 标记间距为1 cM; 虚线, 标记间隔3 cM; 虚线, 标记随机间隔,平均间隔为3 cM。
图4。
长度为100 cM的染色体的模拟数据的排除图,疾病位点在50 cM时的风险比为2。 实线, 标记间距为1 cM; 虚线, 标记间隔3 cM; 虚线, 以3cM的平均间距随机间隔的标记。
图5。
长度为100 cM且无疾病位点的染色体的模拟数据的排除图。 实线, 标记间距为1 cM; 虚线, 标记间隔3 cM; 虚线, 标记随机间隔,平均间隔为3 cM。
祖先特异性等位基因/单倍型频率的估计 为了测试从相同混合人群的连续样本中了解祖先特异性等位基因频率的能力,我们使用了上述三个非洲裔美国人数据集。 总的来说,这三个数据集包括37个祖先信息标记,其中23个标记在所有三个数据集中都是通用的; Shriver等人给出了标记的详细信息( 2003 ). 该模型由三个亚群组成:西非、欧洲和美洲原住民。 如果我们假设非裔美国人中的祖先特异性等位基因频率不随居住地区而变化,那么对祖先特异性等位基因频率的连续更新将使估计的等位基因频度与真实值的拟合度更接近。 为了验证这一预测,我们计算了两组等位基因频率估计值:(1)估计值为未纳入人群的西非样本的平均频率,(2)估计值是通过将离散模型与“历史”拟合而获得的后验分布的平均值 来自未混合的西非人群和来自华盛顿特区和费城数据集的样本给出的等位基因频率作为研究中的混合人群。 由于这些研究中的标记物数量太少,无法对分散参数进行可靠推断,因此为这些参数指定了信息先验。 西非等位基因频率的离散参数的先验值规定为 η∼ 镓 (4,0.04) 其95%的质量在20至200之间。 欧洲等位基因频率的离散参数的先验值规定为 η∼ 镓 (6,0.02) 其98%的质量在100到1000之间。 由于在这些非裔美国人样本中,关于美洲原住民等位基因频率的信息很少,因此美洲原住族等位基因的频率离散参数的优先权规定为 η∼ 镓 (1,000,10) ,平均值为100,方差为10。
图6 比较这两组等位基因频率估计值与前列腺癌数据集的拟合度。 每一组估计值都用于指定一个具有固定等位基因频率的模型,并计算这些等位基因频度的错误指定分数测试。 由于等位基因频率估计仅基于抽样未纳入人群,因此对四个基因座的错误指定等位基因的频率测试在1%水平上显著,在 P(P) 值<10 −5 其中两个。 通过在离散模型中结合来自未服用和混合人群(华盛顿特区和费城)的数据,根据后验分布进行等位基因频率估计,只有两个基因座的等位基因错误频率在1%水平上显著。 当用一个模型分析前列腺癌数据集时,原始和更新的非洲特异性等位基因频率估计之间的拟合也得到了类似的改善,在该模型中,等位基因频率被指定为具有先前分布的随机变量,而不是固定的。 为了测试这种模型的适合性,我们必须使用基于后验预测检查概率的模型诊断,如上文“ 建模通道频率 “第节。 在离散模型中,基于使用来自未摄入人群的数据的先验分布,后验预测检验概率从使用非洲特定等位基因频率的原始先验分布的模型中的0.06增加到使用更新的先验分配的模型中0.27。 有关预测检查概率的计算,请参见 附录B .
图6。
的绘图 P(P) 根据西非未纳入人群的频率估计值,对指定模型中错误指定的非洲等位基因频率进行测试获得的值( 水平轴 )以及通过将来自未被接纳和混合人群(华盛顿特区和费城)的数据合并到离散模型中,以频率估计值指定的模型( 垂直轴 ). 错误规格测试在以下位置显著 P(P) 第一个模型指定的等位基因频率值<.01显示为黑色方块。
讨论 早期的作者建议,可以利用混合体产生的连锁信息,通过测试混合体产生疾病的等位基因关联(Chakraborty和Weiss)来定位疾病易感基因 1988 ). Stephens等人( 1994 )为此方法引入了术语“混合链接不平衡映射”(MALD)。 相反,本文中描述的方法依赖于测试疾病与从标记数据推断的基因座祖先的关联。 与基因座祖先对疾病风险影响的测试相比,依赖等位基因关联测试的方法有两个严重的局限性:它们不能使用仅受影响的设计,也不能在多点分析中结合来自连锁标记的信息来提取祖先信息。
我们已经表明,对于一种罕见的疾病,病例和对照的比较所传达的信息仅为相同总样本量的受影响研究的四分之一。 由于等位基因关联测试无法结合来自连锁标记的信息,因此其检测导致疾病风险种族差异的基因座的效率受到单个标记基因座的祖先信息含量的限制。 选择用于提供祖先信息的标记通常具有<40%的平均祖先信息含量。 因此,有了一张密集的标记图,可以为祖先提供信息,一项针对等位基因关联的病例对照研究测试将传递不到十分之一的信息( 0.25×0.40 )与总样本量相同的受影响混合映射研究一样多的信息。 即使对于一种常见疾病,只研究病例也比比较病例和对照更有效,除非该疾病的流行率>50%。 对于患病率>50%的疾病,最有效的设计是只研究未受影响的个体。
检测对疾病风险种族差异贡献不大的基因座所需的样本量(祖先风险比为1.5–2)在现实范围内,即使在非洲裔美国人中,平均混合比例(0.8/0.2)远不是混合映射研究的最佳选择。 我们已经表明,如果对非洲裔美国人进行的此类研究如我们所建议的那样有力,95%置信区间的预期大小为~4 cM。实际上,在染色体上检测到与疾病位点的联系, 我们不会计算该基因座位置的置信区间,而是扩展统计模型,以在完全贝叶斯分析中估计该疾病基因座的影响大小和位置,从而获得该基因座的位置的后验区间。
如果检测到与疾病风险中的种族差异相关,可以采用几种策略进行精细绘图。 一种方法,如前所述(Hoggart等人。 2003 )是为了构建一个以基因座祖先为条件的等位基因关联测试,从而消除混合产生的远程信号。 另一种可能的策略是筛选最近选择的证据(Sabeti等人。 2002 ),因为不同种族之间风险等位基因的差异分布很可能是由差异选择压力造成的。
混合映射的预期分辨率和所需的标记密度取决于强度参数之和,或者等效地,取决于祖先交叉率。 我们估计非裔美国人的强度总和和血统交叉率分别为~6/100cM和2/100cM。 我们的模拟表明,要使用一组平均信息含量为0.36的标记在初始基因组搜索中提取至少60%的基因组信息,平均标记间距需要为3 cM。 这需要整个基因组约1200个标记。 标记没有必要均匀分布,因为在这个标记密度下,标记位点之间的信息不会减少很多。
Kruglyak和Lander之前为多点家族连锁研究阐述的许多原则( 1995 a、, 1995 b )可以扩展到混合映射研究。 一个例子是计算置信区分布的算法,如本文所述。 另一个是标记信息内容和所需标记密度之间的权衡。 在平均信息含量高达0.36的标记不可用的情况下,同样比例的信息可以通过信息较少的标记组成的更密集的地图来提取。 与家族连锁研究一样,最有效的策略是使用标记集进行初始基因组搜索,该标记集足以在大多数基因组中排除研究设计检测的大小的影响, 然后用额外的标记饱和假定连锁的区域,以提取几乎所有关于祖先的信息。 本文中的模拟结果表明,相对低密度(每3 cM 1个)的标记图可能足以进行初始基因组搜索。 混合作图研究的统计能力和作图分辨率的计算可以基于假设密集的标记图,这样配子混合和基因座祖先就可以在没有不确定性的情况下进行测量。
对混合填图的一个批评是,它假定每个经历混合的祖先大陆群都具有同质性。 因此,例如,有人认为,非洲内部的遗传异质性使得仅仅将现代非裔美国人的遗传结构建模为两个基因库的混合物是不现实的:西非和欧洲(特威利格和戈林 2000 ). 然而,ADMIXMAP中使用的模型并没有假设西非各亚群之间的遗传同质性; 它假设只有在非洲裔美国人的非洲血统基因库中(同样,在欧洲血统基因库中)具有同质性。 这是一个更现实的假设; 尽管奴隶来自西非不同地区,但来自这些不同非洲亚群的基因很可能在随后的运动中混合。 同质性假设可以通过扩展Hoggart et al( 2003 )测试每个亚群中的残余分层。
如果大陆组内存在异质性,则可用于取样的未纳入组可能无法代表那些进行混合的组。 因此,例如,我们无法对非洲亚种群的确切组合进行取样,而这些亚种群构成了现代非裔美国人中非洲血统基因库的组成部分。 大陆组内的遗传异质性也可能导致混合种群中祖先特异性等位基因频率与现代未混合西非、欧洲和美洲原住民的等位基因频度发生变化。 我们已经用实际数据证明,通过结合来自未摄入和混合人群的数据,可以更准确地估计祖先特异性等位基因频率,允许在未摄入和混杂人群之间分散等位基因的频率。 由于对祖先特异性等位基因频率有很强的先验性,混合映射研究的设计可以基于仅对受影响个体进行分型,而无需对对照组进行分型以独立于病例样本估计等位基因的频率。 为了充分利用这一方法,研究人员应该建立一个共同的祖先信息标记小组,用于混合映射研究,并汇集其控制数据,以便所有可用数据都可以用于估计混合人群中的祖先特异性等位基因频率。
与其他检测疾病易感基因的方法相比,混合映射有三个主要优点:它比家族连锁研究具有更高的统计能力(McKeigue 1998 )与全基因组关联研究相比,它需要更少的标记进行基因组搜索,并且不受等位基因异质性的影响(Terwilliger和Weiss 1998 ). 通过混合映射检测基因座的能力不取决于该基因座上疾病等位基因的数量,而仅取决于该位点的疾病等位蛋白库在祖先亚群之间的分布是否存在差异。 即使在没有检测到疾病风险的总体种族差异的地方,也有可能存在这种基因座。 在存在混合种群的地方,混合映射的可行性取决于标记多态性的全基因组面板的可用性,这些标记多态性可为经历混合的不同亚种群之间的祖先提供信息。 为此,可以使用任何类型的标记:SNP、插入/缺失多态性或微卫星。 尽管微卫星的多态性信息含量高于双列标记,但它们不一定具有更高的祖先信息含量。 公共领域中SNP等位基因频率的数据积累使得可以选择显示大陆组之间极端频率差异的子集,而无需筛选未选择的标记。 ADMIXMAP可用于评估给定混合种群中标记面板祖先的信息内容。 可以在必要时添加标记,直到在基因组上的所有位置提取的信息比例超过某个指定的最小值。
我们注意到,ADMIXMAP作为一个通用程序,用于从混合或分层人群中建模基因型和表型数据,除了混合映射之外,还有几个应用。 STRUCTURE计划(Falush等人。 2003 )适用于种群混合的类似模型,但不包括性状对个体混合依赖性的回归模型,也不包括连锁检验。 我们已经将ADMIXMAP用于检测和控制隐藏人群分层描述为遗传关联研究中的混淆因素(Hoggart等人。 2003 ). 其他应用包括估计疾病风险与个体混合因素的关系(Molokhia等人。 2003 )识别与其他亚群混血或有血统的外围个体(在其他同质人群中),并从犯罪现场采集的DNA样本中预测与个体混合比例密切相关的特征(如皮肤色素沉着和眼睛颜色)。
致谢 我们感谢T.Smith、C.Bonilla、E.Parra、B.Falkner和W.Chen允许我们使用他们的数据。 对于编程方面的帮助和建议,我们要感谢R.Sharp和N.Wetters。 这项工作得到了国家卫生研究院拨款DK53958和HG02154(均为M.D.S.)、MH60343(为P.M.M.)和RR03048(为R.A.K.)的支持。
附录A:计算方法 ADMIXMAP通过马尔可夫链蒙特卡罗模拟,在给定观测数据的情况下,生成所有未观测变量的后验分布。 有了密集的标记图,就有必要对每条染色体上所有位点的祖先状态进行联合采样,以确保采样器快速混合。 如Falush等人所述,这是使用隐马尔可夫模型正向算法实现的( 2003 ). 为了允许配子混合比例的共轭更新,我们引入了二进制变量的辅助向量 ξ=(ξ 1 ,…,ξ 米 -1 ) 对于每个配子。 这些矢量的坐标取值如下 ξ j个 =1 如果来自 k 轨迹之间发生了独立的泊松过程 j个 和轨迹 j个 +1 、和 ξ j个 =0 否则。 然后根据定义为
哪里 k 是经过混合的亚群数量, α 是描述总体水平混合的Dirichlet分布的参数,以及 A类 ij公司 是长度向量 k 带元素 我 如果基因座祖先来自 我 第个亚群,否则为0。
为了减少模型参数之间的后验协方差,从而确保样本的快速混合,回归模型中的每个解释变量都以样本均值为中心; 这些平均值的估计是在老化期间进行的。 在线性回归模型中,回归参数的完全条件分布是多元正态的。 使用逻辑回归模型,回归参数的完全条件分布可以用正态分布来近似,我们将其用作Metropolis-Hastings算法中的提议分布。 由于密集度总和参数τ的完整条件分布是对数曲线,因此可以使用自适应拒绝采样器(Gilks和Wild 1992 ). 除密集度总和参数τ外,所有人口级参数在10次迭代后的自相关都很低。 通过为该参数选择合理的起始值,可以缩短老化所需的迭代次数。 当前版本的程序无法包含有关相位的先验信息,尽管它对每个位点的祖先状态和单倍型的联合后验分布进行了采样。
附录B:后验预测测试(贝叶斯 P(P) 数值) 如果拟合模型的替代方案不能指定为连续参数与其指定值的偏差,则可以基于后验预测检验概率(Rubin 1984 ). 对于每个缺失数据的实现,重复观察 年 代表 由后验预测分布生成,并与观测数据进行比较 年 通过一些测试统计 T型 后验预测检验概率定义为测试统计量值从 年 代表 比计算值更极端 是的, ,其中ω是模型参数。 该概率通过ω的后验分布和 年 代表 .如果ω中没有后验不确定度,则该程序相当于经典的精确测试,其中 P(P) 当零假设为真时,在实验的假设重复中,数值在区间0-1上具有均匀分布。 在ω中有后验不确定性时,后验预测检验概率比经典检验概率更保守 P(P) 值,因为它们在null下的假设重复实验中的分布缩小到预期值0.5。 如果测试被用作模型诊断,而不是用于正式的统计推断,那么这不是一个严重的问题。
工具书类
Cavalli-Sforza LL,Menoozz P,Piazzi A(1994)人类基因的历史和地理。 普林斯顿大学出版社 [ 谷歌学者 ]
Chakraborty R,Weiss KM(1988)混合作为一种工具,用于发现连锁基因并检测基因座之间的等位关联差异。 美国国家科学院院刊85:9119–9123 [ 内政部 ] [ PMC免费文章 ] [ 公共医学 ] [ 谷歌学者 ]
Devlin B,Roeder K,Wasserman L(2003)多点关联模型分析。 基因流行病学25:36–47 10.1002/gepi.10237 [ 内政部 ] [ 公共医学 ] [ 谷歌学者 ]
Falush D,Stephens M,Pritchard JK(2003)利用多位点基因型数据推断种群结构:连锁位点和相关等位基因频率。 遗传学164:1567–1587 [ 内政部 ] [ PMC免费文章 ] [ 公共医学 ] [ 谷歌学者 ]
Gilks WF,Wild P(1992)吉布斯采样的自适应抑制采样。 应用统计41:337–348 [ 谷歌学者 ]
Hoggart CJ、Parra EJ、Shriver MD、Bonilla C、Kittles RA、Clayton DG、McKeigue PM(2003)分层人群中遗传关联混淆的控制。 美国人类遗传学杂志72:1492–1504 [ 内政部 ] [ PMC免费文章 ] [ 公共医学 ] [ 谷歌学者 ]
Jeffreys H(1961)《概率论》,第三版,牛津大学出版社,牛津 [ 谷歌学者 ]
Kilpikari R,Sillanpaa MJ(2003)定量和定性性状中多点关联的贝叶斯分析。 基因流行病学25:122–135 10.1002/gepi.10257 [ 内政部 ] [ 公共医学 ] [ 谷歌学者 ]
Kittles RA、Chen W、Panguluri RK、Ahaghotu C、Jackson A、Adebamowo CA、Griffin R、Williams T、Ukoli F、Adams-Campbell L、Kwagyan J、Isaacs W、Freeman V、Dunston GM、Massac A(2002)《非裔美国人的CYP3A4-V与前列腺癌:因人口分层导致的因果关系还是混杂关系? 人类基因110:553–560 10.1007/s00439-002-0731-5 [ 内政部 ] [ 公共医学 ] [ 谷歌学者 ]
Kittles RA、Panguluri RK、Chen W、Massac A、Ahaghotu C、Jackson A、Ukoli F、Adams-Campbell L、Isaacs W、Dunston GM(2001)Cyp17启动子变异与非裔美国人前列腺癌侵袭性相关。 癌症流行病学生物标记Prev 10:943–947 [ 公共医学 ] [ 谷歌学者 ]
Kruglyak L,Lander ES(1995年 一 )完成定性和定量性状的多点同胞对分析。 《美国人类遗传学杂志》57:439–454 [ PMC免费文章 ] [ 公共医学 ] [ 谷歌学者 ]
——— (1995 b )复杂性状的高分辨率遗传作图。 美国人类遗传学杂志56:1212–1223 [ PMC免费文章 ] [ 公共医学 ] [ 谷歌学者 ]
Lockwood JR,Roeder K,Devlin B(2001)等位基因频率的贝叶斯层次模型。 基因流行病学20:17–33 [ 内政部 ] [ 公共医学 ] [ 谷歌学者 ]
McKeigue PM(1998)绘制疾病风险中种族差异的基因:通过调节父母的混合情况来检测混合人群中的联系的方法。 《美国人类遗传学杂志》63:241–251 [ 内政部 ] [ PMC免费文章 ] [ 公共医学 ] [ 谷歌学者 ]
McKeigue PM、Carpenter JR、Parra EJ、Shriver MD(2000年)《用贝叶斯方法估计混合种群中的混合和检测连锁:应用于非洲裔美国人》。 《人类遗传学年鉴》64:171–186 10.1046/j.1469-1809.2000.6420171.x [ 内政部 ] [ 公共医学 ] [ 谷歌学者 ]
Molokhia M、Hoggart C、Patrick AL、Shriver M、Parra E、Ye J、Silman AJ、McKeigue PM(2003)加勒比人群中系统性红斑狼疮风险与西非混合型狼疮风险的关系。 人类遗传学112:310–318 [ 内政部 ] [ 公共医学 ] [ 谷歌学者 ]
Mott R、Talbot CJ、Turri MG、Collins AC、Flint J(2000)《远缘动物种群数量性状基因座精细定位方法》。 美国国家科学院院刊97:12649–12654 10.1073/pnas.230304397 [ 内政部 ] [ PMC免费文章 ] [ 公共医学 ] [ 谷歌学者 ]
Parra EJ、Marcini A、Akey J、Martinson J、Batzer MA、Cooper R、Forrester T、Allison DB、Deka R、Ferrell RE、Shriver MD(1998)《利用人群特异性等位基因估算非裔美国人混合比例》。 《美国人类遗传学杂志》63:1839–1851 [ 内政部 ] [ PMC免费文章 ] [ 公共医学 ] [ 谷歌学者 ]
Rosenberg NA,Li LM,Ward R,Pritchard JK(2003)遗传标记对祖先推断的信息性。 《美国人类遗传学杂志》73:1402–1422 [ 内政部 ] [ PMC免费文章 ] [ 公共医学 ] [ 谷歌学者 ]
Rubin DB(1984)应用统计学家的贝叶斯合理相关频率计算。 安统计12:1151-1172 [ 谷歌学者 ]
Sabeti PC、Reich DE、Higgins JM、Levine HZ、Richter DJ、Schaffner SF、Gabriel SB、Platko JV、Patterson NJ、McDonald GJ、Ackerman HC、Campbell SJ、Altshuler D、Cooper R、Kwiatkowski D、Ward R、Lander ES(2002),从单倍型结构检测人类基因组中最近的阳性选择。 自然419:832–837 10.1038/nature01140 [ 内政部 ] [ 公共医学 ] [ 谷歌学者 ]
Shriver MD、Parra EJ、Dios S、Bonilla C、Norton H、Jovel C、Pfaff C、Jones C、Massac A、Cameron N、Baron A、Jackson T、Argyropoulos G、Jin L、Hoggart CJ、McKeigue PM、Kittles RA(2003)《皮肤色素沉着、生物地理祖先和混合图谱》。 人类基因112:387–399 [ 内政部 ] [ 公共医学 ] [ 谷歌学者 ]
Sillanpaa MJ,Arjas E(1999)来自不完全远系后代数据的多个数量性状基因座的贝叶斯映射。 遗传学151:1605–1619 [ 内政部 ] [ PMC免费文章 ] [ 公共医学 ] [ 谷歌学者 ]
Stephens JC,Briscoe D,O'Brien SJ(1994),《通过混合连锁不平衡在人群中进行绘图:限制和指南》。 美国人类遗传学杂志55:809–824 [ PMC免费文章 ] [ 公共医学 ] [ 谷歌学者 ]
Terwilliger JD,Göring HH(2000)《20世纪和21世纪的基因图谱:统计方法、数据分析和实验设计》。 人类生物学72:63–132 [ 公共医学 ] [ 谷歌学者 ]
Terwilliger JD,Weiss(1998)复杂疾病的连锁不平衡映射:幻想还是现实? Curr Opin生物技术公司9:578–594 10.1016/S0958-1669(98)80135-3 [ 内政部 ] [ 公共医学 ] [ 谷歌学者 ]
Wright S(1951)种群的遗传结构。 安·尤根15:159–171 [ 内政部 ] [ 公共医学 ] [ 谷歌学者 ]