Geometry of q-Exponential Family of Probability Distributions

Amari, Shun-ichi; Ohara, Atsumi

doi:10.3390/e13061170

开放式访问第条

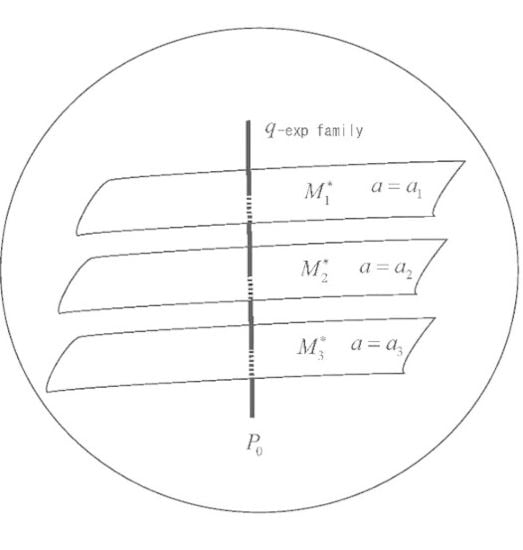
的几何形状q个-概率分布的指数族

通过

顺义阿玛里

^1,*和

阿萨米·奥哈拉

^2,*

¹

日本柴达木市和谷市广泽2-1日成脑科学研究所数学神经科学实验室351-0198

²

日本福井市福井市文桥3-9-1，福井大学工程研究生院电气与电子工程系，邮编：910-8507

^*

应向其发送信件的作者。

熵 2011,13(6), 1170-1185;https://doi.org/10.3390/e13061170

收到的意见：2011年2月11日/修订日期：2011年6月1日/接受日期：2011年6月2日/出版日期：2011年6月14日

（本文属于特刊信息与统计物理中的距离第二卷)

下载

浏览地物

版本注释

摘要

:

统计物理中的吉布斯分布是概率分布的指数族，它以勒让德变换的形式具有对偶性的数学基础。最近对复杂系统的研究发现，许多分布服从幂律，而不是标准的吉布斯分布。Tslis家族q个-熵就是捕捉这种现象的典型例子。我们对待q个-吉布斯分布或q个-通过将指数函数推广到q个-幂函数族，用于研究各种复杂或非标准的物理现象。我们为q个-指数族与先前给出的不同。它具有从勒让德变换导出的双平面几何结构，保角几何有助于理解它q个-最大熵定理的版本是由q个-勾股定理。我们还证明了q个-护送分布是一种贝叶斯MAP（最大后验概率）估计量。

关键词：

q个-指数族;q个-熵;信息几何;q个-勾股定理;q-Max-Ent定理;共形变换

图形摘要

1.简介

统计物理学是建立在微观状态的吉布斯分布基础上的，它形成了统计学中已知的概率分布的指数族。重要的宏观量，如能量、熵、自由能、，等。然而，最近的研究表明，有些非标准复杂系统服从幂律，而不是吉布斯型分布的指数律。请参见[1,2]以及其中引用的大量文献。

查利斯[三]定义了q个-熵来阐明这种类型的各种物理现象，随后是关于这个主题的许多相关研究工作（参见[1]). 概念q个-吉布斯分布或q个-概率分布的指数族是从这个框架中自然导出的（另请参见[4]). 然而，其数学结构尚未得到足够的研究[2,5,6]，而吉布斯型分布和指数分布族已经得到了很好的研究[7]. 我们需要一个数学（几何）基础来研究q个-指数族。本文为q个-基于信息几何的指数族[8]，给出了q个-势函数，q个-熵和q个-统一发散。

我们定义q个-由一个黎曼度量和一对对偶仿射连接组成的几何结构。通过使用这个框架，我们证明了q个-指数分布是双重平坦的，其中q个-勾股定理成立。这自然会导致相应的q个-与Tsallis情形类似的最大熵定理q个-熵[1,9,10]. 这个q个-结构自家庭以来无处不在

{S公司}_{n个}

在所有离散概率分布中，始终可以赋予q个-任意指数族q个。可以将q个-任何概率分布族的结构。此外，它与α-几何形状[8]它是常曲率的信息几何结构之一。这种新的对偶平坦结构不同于由信息几何中的不变量引起的旧的对偶平坦结构，也可以通过对α-几何形状[11,12]，使用保角和射影几何中的技术[13,14,15].

本框架为分析受幂律约束的物理现象准备了数学工具。勒让德变换在推导几何对偶结构方面再次发挥了基本作用。有许多应用q个-从几何学到信息论([16]和统计数据，包括贝叶斯q个-统计数据。

通过使用正凸函数而不是q个-指数函数（参见[2,17]). 一个很好的例子是κ-指数族[18,19,20]，但我们在此不作说明。

2q个-吉布斯或q个-指数分布族

2.1. q-对数与q-指数函数

第一步是将对数函数和指数函数推广到包括幂函数族，其中对数函数和幂函数被作为极限情况包括在内[1,5,21]. 这也用于定义α-信息几何中的分布族[8]. 我们定义q个-对数乘以

{日志}_{q个} (u个) = \frac{1}{1 - q个} ({u个}^{1 - q个} - 1), u个 > 0

(1)

及其逆函数q个-指数，按

{经验}_{q个} (u个) = {\{1 + (1 - q个) u个\}}^{\frac{1}{1 - q个}}, u个 > - 1 / (1 - q个)

(2)

对于一个积极的q个具有

q个 \neq 1

.极限情况

q个 \to 1

减少到

\begin{matrix} {日志}_{1} (u个) & = & 日志 u个 \end{matrix}

(3)

\begin{matrix} {经验}_{1} (u个) & = & 经验 u个 \end{matrix}

(4)

因此

{日志}_{q个}

和

{经验}_{q个}

为定义

q个 > 0

.

2.2。q-指数族

指数分布族的标准形式写为

第页 (x个, θ) = 经验 \{\sum θ^{我} {x个}_{我} - ψ (θ)\}

(5)

就适当措施而言

μ (x个)

，其中

x个 = ({x个}_{1}, \dots, {x个}_{n个})

是一组随机变量和

θ = (θ^{1}, \dots, θ^{n个})

是描述底层系统的规范参数。吉布斯分布属于这种类型。在这里，

ψ (θ)

称为自由能，即累积量生成函数。

吉布斯分布的幂函数形式如下

\begin{matrix} 第页 (x个, θ) & = & {经验}_{q个} \{θ \cdot x个 - ψ_{q个} (θ)\} \end{matrix}

(6)

\begin{matrix} {日志}_{q个} \{第页 (x个, θ)\} & = & θ \cdot x个 - ψ_{q个} (θ) \end{matrix}

(7)

哪里

θ \cdot x个 = \sum θ^{我} {x个}_{我}

。这是q个-吉布斯分布或q个-指数族[4]，我们用S公司，其中的域x个受到限制

第页 (x个, θ) > 0

持有。功能

ψ_{q个} (θ)

，调用了q个-自由能或q个-势函数，由归一化条件确定：

\int {经验}_{q个} \{θ \cdot x个 - ψ_{q个} (θ)\} d日 x个 = 1

(8)

我们更换的位置

d日 μ (x个)

通过

d日 x个

为了简短起见。功能

ψ_{q个}

取决于q个，但我们以后会忽略后缀q个在大多数情况下。关于q个-指数族可以在[2,4,19]. 这个q个-高斯分布由下式给出

第页 (x个, μ, σ) = {经验}_{q个} \{- \frac{{(x个 - μ)}^{2}}{2 σ^{2}} - ψ (μ, σ)\}

（9）

并在[22,23,24,25]详细说明。这里，我们需要引入一个向量随机变量

x个 = (x个, {x个}^{2})

和一个新参数

θ

，它是的向量值函数μ和σ，以标准形式表示(7). 有趣的是x个在中q个-高斯情况取决于q个如果

0 < q个 < 1

因此q个-和

{q个}^{'}

-当

q个 \neq {q个}^{'}

.

应该指出的是q个-指数族本身与α-信息几何中的分布族[8]. 这里，我们介绍了一种不同的几何结构，概括了[24].

我们主要使用家庭

{S公司}_{n个}

离散分布的

(n个 + 1)

元素

X（X） = \{{x个}_{0}, {x个}_{1}, \dots, {x个}_{n个}\}

尽管我们可以很容易地将结果推广到连续随机变量的情况。这里是随机变量x个接管价值观X（X）我们还处理了

0 < q个 < 1

，以及的极限情况

q个 = 0

或者我给那些著名的。

让我们把

{第页}_{我} = 探针 \{x个 = {x个}_{我}\}

用向量表示概率分布

第页 = ({第页}_{0}, {第页}_{1}, \dots, {第页}_{n个})

，其中

\sum_{我 = 1}^{n个} {第页}_{我} = 1

(10)

概率x个也写为

第页 (x个) = \sum_{我 = 0}^{n个} {第页}_{我} δ_{我} (x个)

(11)

哪里

δ_{我} (x个) = \{\begin{matrix} 1, & x个 = {x个}_{我}, \\ 0, & 否则 . \end{matrix}

(12)

定理 1

家庭

{S公司}_{n个}

离散概率分布的结构q个-任意指数族q个.

证明

我们接受

{日志}_{q个}

分配的

第页 (x个)

第页，共页(11). 对于任何功能

（f） (u个)

，我们有

（f） \{\sum_{我 = 1}^{n个} {第页}_{我} δ_{我} (x个)\} = \sum_{我 = 0}^{n个} （f） ({第页}_{我}) δ_{我} (x个)

(13)

通过采取

δ_{0} (x个) = 1 - \sum_{我 = 1}^{n个} δ_{我} (x个)

(14)

考虑到离散分布(11)可以改写为(8)作为

{日志}_{q个} 第页 (x个) = \frac{1}{1 - q个} \{\sum_{我 = 1}^{n个} ({第页}_{我}^{1 - q个} - {第页}_{0}^{1 - q个}) δ_{我} (x个) + {第页}_{0}^{1 - q个} - 1\}

（15）

哪里

{第页}_{0} = 1 - \sum_{我 = 1}^{n个} {第页}_{我}

(16)

被视为

({第页}_{1}, \dots, {第页}_{n个})

因此，

{S公司}_{n个}

是q个-指数族(6)对于任何q个，具有以下内容q个-规范参数、随机变量和q个-势函数：

\begin{matrix} θ^{我} & = & \frac{1}{1 - q个} ({第页}_{我}^{1 - q个} - {第页}_{0}^{1 - q个}), 我 = 1, \dots, n个 \end{matrix}

(17)

\begin{matrix} {x个}_{我} & = & δ_{我} (x个) \end{matrix}

(18)

\begin{matrix} ψ (θ) & = & - {日志}_{q个} {第页}_{0} \end{matrix}

（19）

这就完成了证明。□

请注意q个-电势

ψ (θ)

和规范参数

θ

依靠q个如中所示(17)和(19). 还应注意的是，定理1与[19]说明概率分布的参数化族最多可以属于一个q个-指数族。作者认为米-中的维参数化子流形

{S公司}_{n个}

具有

米 < n个

其中规范参数取决于q个通过变分原理给出。因此，通过表示q个-规范参数依据

θ_{q个} \in {R（右）}^{米}

，我们可以从几何角度重申他的定理，线性子流形的参数化由

θ_{q个} \in {R（右）}^{米}

不是由参数化的线性子流形

θ_{{q个}^{'}} \in {R（右）}^{米}

什么时候

{q个}^{'} \neq q个

另一方面，本定理表明存在q个-标准参数

θ_{q个} \in {R（右）}^{n个}

总的来说

{S公司}_{n个}

对于任何q个流形相对于任何

θ_{q个}

这是一个令人惊讶的新发现。

2.3. q-电位函数

我们研究q个-几何结构S公司. Theq个-log-likelihood是一种线性形式，定义为

我_{q个} (x个, θ) = {日志}_{q个} 第页 (x个, θ) = \sum_{我 = 1}^{n个} θ^{我} {x个}_{我} - ψ (θ)

(20)

通过区分以下方面

θ^{我}

，带有缩写符号

⏴_{我} = \frac{⏴}{⏴ θ^{我}}

，我们有

\begin{matrix} ⏴_{我} 我_{q个} (x个, θ) & = & {x个}_{我} - ⏴_{我} ψ (θ) \end{matrix}

(21)

\begin{matrix} ⏴_{我} ⏴_{j个} 我_{q个} (x个, θ) & = & - ⏴_{我} ⏴_{j个} ψ (θ) \end{matrix}

（22）

由此我们得到了以下重要定理。

定理 2

这个q个-自由能或q个-电势

ψ_{q个} (θ)

是的凸函数

θ_{q个}

.

证明

我们省略了后缀q个为了简单起见。我们有

\begin{matrix} ⏴_{我} 第页 (x个, θ) & = & 第页 {(x个, θ)}^{q个} ({x个}_{我} - ⏴_{我} ψ) \end{matrix}

(23)

\begin{matrix} ⏴_{我} ⏴_{j个} 第页 (x个, θ) & = & q个 第页 {(x个, θ)}^{2 q个 - 1} ({x个}_{我} - ⏴_{我} ψ) ({x个}_{j个} - ⏴_{j个} ψ) - 第页 {(x个, θ)}^{q个} ⏴_{我} ⏴_{j个} ψ \end{matrix}

(24)

以下身份保持不变：

\begin{matrix} \int ⏴_{我} 第页 (x个, θ) d日 x个 & = & ⏴_{我} \int 第页 (x个, θ) d日 x个 = 0 \end{matrix}

(25)

\begin{matrix} \int ⏴_{我} ⏴_{j个} 第页 (x个, θ) d日 x个 & = & ⏴_{我} ⏴_{j个} \int 第页 (x个, θ) d日 x个 = 0 \end{matrix}

(26)

这里，我们定义了一个重要的函数

{小时}_{q个} (θ) = {小时}_{q个} [第页 (x个, θ)] = \int 第页 {(x个, θ)}^{q个} d日 x个

(27)

特别是对于离散型

{S公司}_{n个}

,

{小时}_{q个} (第页) = \sum_{我 = 0}^{n个} {第页}_{我}^{q个}

(28)

对于

0 < q个 < 1

。此功能在以下方面起着关键作用。发件人(25)和(26)，通过使用(23)和(24)，我们有

\begin{matrix} ⏴_{我} ψ (θ) & = & \frac{1}{{小时}_{q个} (θ)} \int {x个}_{我} 第页 {(x个, θ)}^{q个} d日 x个 \end{matrix}

(29)

\begin{matrix} ⏴_{我} ⏴_{j个} ψ (θ) & = & \frac{q个}{{小时}_{q个} (θ)} \int ({x个}_{我} - ⏴_{我} ψ) ({x个}_{j个} - ⏴_{j个} ψ) 第页 {(x个, θ)}^{2 q个 - 1} d日 x个 \end{matrix}

(30)

后者表明

⏴_{我} ⏴_{j个} ψ (θ)

是正定的，因此ψ是凸起的。□

2.4. q-发散

凸函数

ψ (θ)

可以定义两个概率分布之间的Bregman型散度

第页 (x个, θ_{1})

和

第页 (x个, θ_{2})

[8,26,27]. 它是通过使用梯度给出的

\nabla = ⏴ / ⏴ θ

,

{D类}_{q个} [第页 (x个, θ_{1}) : 第页 (x个, θ_{2})] = ψ (θ_{2}) - ψ (θ_{1}) - \nabla ψ (θ_{1}) \cdot (θ_{2} - θ_{1})

(31)

满足非负性条件

{D类}_{q个} [第页 (x个, θ_{1}) : 第页 (x个, θ_{2})] \geq 0

(32)

当且仅当

θ_{1} = θ_{2}

。这提供了一个q个-中的散度

{S公司}_{n个}

不同于

{S公司}_{n个}

[28]. 发散是典型的，因为它是根据对偶平坦结构唯一确定的q个-指数族第3节和第4节。正则散度不同于α-信息几何中使用的散度或传统的Tsallis相对熵（参见本小节末尾的讨论）。请注意，它用于[16].

定理三

对于两个离散分布

第页 (x个) = 第页

和

第页 (x个) = 第页

，的q个-散度由下式给出

{D类}_{q个} [第页 : 第页] = \frac{1}{(1 - q个) {小时}_{q个} (第页)} (1 - \sum_{我 = 0}^{n个} {第页}_{我}^{q个} {第页}_{我}^{1 - q个})

（33）

证明

电位为，来自(19),

ψ (第页) = - {日志}_{q个} {第页}_{0}, ψ (第页) = - {日志}_{q个} {第页}_{0}

(34)

对于第页和第页。我们需要计算

\nabla ψ (θ)

在中给出(29). 在我们的案例中，

{x个}_{我} = δ_{我} (x个)

因此

⏴_{我} ψ = \frac{{第页}_{我}^{q个}}{{小时}_{q个} (第页)}

(35)

通过使用此和(17)，我们获得(33). □

考虑相关的概率分布是有用的，

{\hat{第页}}_{q个} (x个) = \frac{1}{{小时}_{q个} [第页 (x个)]} 第页 {(x个)}^{q个}

(36)

用于定义q个-期望。这被称为q个-护送概率分布[1,4,29]. 介绍q个-随机变量的期望

（f） (x个)

通过

{E类}_{\hat{第页}} [（f） (x个)] = \frac{1}{{小时}_{q个} [第页 (x个)]} \int 第页 {(x个)}^{q个} （f） (x个) d日 x个

(37)

我们可以重写q个-发散(31)对于

第页 (x个), 第页 (x个) \in S公司

作为

{D类}_{q个} [第页 (x个) : 第页 (x个)] = {E类}_{\hat{第页}} [{日志}_{q个} 第页 (x个) - {日志}_{q个} 第页 (x个)]

（38）

因为这些关系(20)和(29). 表达式(38)也适用于

S公司 \times S公司

当它是可积的。这与Tsallis相对熵的定义不同[30,31]

{\tilde{D类}}_{q个} [第页 (x个) : 第页 (x个)] = \frac{1}{1 - q个} (1 - \int 第页 {(x个)}^{q个} 第页 {(x个)}^{1 - q个} d日 x个)

(39)

这等于众所周知的α-散度达到常数因子，其中

α = 1 - 2 q个

（请参见[8,28])，满足不变性准则。我们有

{D类}_{q个} [第页 (x个) : 第页 (x个)] = \frac{1}{{小时}_{q个} [第页 (x个)]} {\tilde{D类}}_{q个} [第页 (x个) : 第页 (x个)]

(40)

这是散度的保角变换，如下所示。另请参见基于仿射微分几何的推导[12].

2.5. q-Riemannian公制

何时

θ_{2}

非常接近

θ_{1}

，通过放置

θ_{1} = θ

,

θ_{2} = θ + d日 θ

利用泰勒展开式，我们得到

{D类}_{q个} [第页 (x个, θ) : 第页 (x个, θ + d日 θ)] = \sum 克_{我 j个}^{q个} (θ) d日 θ^{我} d日 θ^{j个}

(41)

哪里

克_{我 j个}^{(q个)} = ⏴_{我} ⏴_{j个} ψ (θ)

(42)

是一个正定矩阵。我们称之为

[克_{我 j个}^{(q个)} (θ)]

这个q个-费希尔信息矩阵。何时

q个 = 1

，这可简化为以下公式给出的普通Fisher信息矩阵

克_{我 j个}^{(1)} (θ) = 克_{我 j个}^{如果} (θ) = E类 [⏴_{我} 日志 第页 (x个, θ) ⏴_{j个} 日志 第页 (x个, θ)]

(43)

正定矩阵

克_{我 j个}^{(q个)} (θ)

在上定义黎曼度量

{S公司}_{n个}

，给它q个-黎曼构造。

当度量张量

克_{我 j个} (θ)

被转换为

{\tilde{克}}_{我 j个} (θ) = σ (θ) 克_{我 j个} (θ)

(44)

通过一个正函数

σ (θ)

，我们称之为保角变换。参见，例如[13,14,15,32]. 散度的保角变换引入了黎曼度量。

定理 4

这个q个-Fisher信息度量由Fisher度量的保角变换给出

克_{我 j个}^{如果}

作为

克_{我 j个}^{(q个)} (θ) = \frac{q个}{{小时}_{q个} (θ)} 克_{我 j个}^{如果} (θ)

(45)

证明

这个q个-度量由泰勒展开式导出

{D类}_{q个} [第页 : 第页 + d日 第页]

.我们有

\begin{matrix} {D类}_{q个} [第页 (x个, θ) : 第页 (x个, θ + d日 θ)] & = & \frac{1}{(1 - q个) {小时}_{q个} (θ)} \{1 - \int 第页 {(x个, θ)}^{q个} 第页 {(x个, θ + d日 θ)}^{1 - q个} d日 x个\} \\ = & \frac{q个}{{小时}_{q个} (θ)} \{\int \frac{1}{第页 (x个, θ)} ⏴_{我} 第页 (x个, θ) ⏴_{j个} 第页 (x个, θ) d日 x个\} d日 θ^{我} d日 θ^{j个} \end{matrix}

(46)

使用身份(25)和(26). 何时

q个 = 1

，这是Fisher提供的信息(43). 因此q个-Fisher信息由(45). □

黎曼度量定义切线向量的长度

X（X） = ({X（X）}^{1}, \dots, {X（X）}^{n个})

在

θ

通过

{∥ X（X） ∥}^{2} = \sum 克_{我 j个} (θ) {X（X）}^{我} {X（X）}^{j个}

(47)

类似地，对于两个切线向量X（X）和Y（Y），其内积定义为

〈 X（X）, Y（Y） 〉 = \sum 克_{我 j个} {X（X）}^{我} {Y（Y）}^{j个}

(48)

何时

〈 X（X）, Y（Y） 〉

消失，X（X）和Y（Y）据说是正交的。两个向量的正交性，或更一般的角度X（X）和Y（Y）虽然它们的大小发生了变化，但不会因保角变换而改变。

3.双平面结构q个-指数族

3.1. 勒让德变换与q熵

给定一个凸函数

ψ (θ)

，Legendre变换定义为

η = \nabla ψ (θ)

(49)

哪里

\nabla = (⏴ / ⏴ θ^{我})

是梯度。由于

θ

和

η

是一对一的，我们可以考虑

η

作为另一个坐标系S公司.

双势函数定义为

φ (η) = \underset{θ}{最大值} \{θ \cdot η - ψ (θ)\}

(50)

相对于

η

。原始坐标从以下给定的逆变换中恢复

θ = \nabla φ (η)

(51)

哪里

\nabla = (⏴ / ⏴ η_{我})

，所以

θ

和

η

是双重通信。

以下定理给出了这些量之间的明确关系。

定理 5

双坐标

η

由提供

η = {E类}_{\hat{第页}} [x个]

(52)

双电势由下式给出

φ (η) = \frac{1}{1 - q个} \{\frac{1}{{小时}_{q个} (第页)} - 1\}

(53)

证明

关系(52)立即从(29). 从勒让德对偶性来看，对偶势满足

φ (η) + ψ (θ) - θ \cdot η = 0

(54)

什么时候

θ

和

η

通过以下方式相互通信

η = \nabla ψ (θ)

因此，

\begin{matrix} φ (η) & = & \sum_{我 = 1}^{n个} θ^{我} η_{我} - ψ (θ) \end{matrix}

(55)

\begin{matrix} = & {E类}_{\hat{第页}} [{日志}_{q个} 第页 (x个, θ)] \end{matrix}

(56)

\begin{matrix} = & \frac{1}{(1 - q个) {小时}_{q个} (θ)} (1 - \int {第页}^{q个} (x个, θ) d日 x个) \end{matrix}

(57)

\begin{matrix} = & \frac{1}{1 - q个} (\frac{1}{{小时}_{q个} (θ)} - 1) \end{matrix}

(58)

这是一个凸函数

η

. □

我们称之为q个-双电势

φ (η) = E类 [{日志}_{q个} 第页 (x个, θ)] = \frac{1}{1 - q个} \{\frac{1}{{小时}_{q个}} - 1\}

(59)

负片q个-熵，因为它是q个-自由能

ψ (θ)

。有各种定义q个-熵。Tslis家族q个-熵[三]最初由定义

{H（H）}_{查利斯} = \frac{1}{1 - q个} ({小时}_{q个} - 1)

(60)

而Rényiq个-熵[33]是

{H（H）}_{雷尼} = \frac{1}{1 - q个} 日志 {小时}_{q个}

(61)

它们通过单调函数相互关联。何时

q个 \to 1

，所有这些都减少到香农熵。

我们对

{H（H）}_{q个} = \frac{1}{1 - q个} (1 - \frac{1}{{小时}_{q个}}) = \frac{{H（H）}_{查利斯}}{{小时}_{q个}}

(62)

也与前面的单调连接，但从q个-几何图形。熵

{H（H）}_{q个}

被称为标准化q个-熵，在[16,34,35,36,37].

3.2. q-平直结构

有两个双重耦合的坐标系

θ

和

η

在里面q个-指数族S公司具有两个势函数

ψ (θ)

和

φ (η)

对于每个q个.两个凸函数引入了两个仿射结构ψ和φ参见对偶平面空间的信息几何[8]. 尽管S公司是由q个-费希尔信息矩阵(45)，但我们可能会考虑S公司作为仿射流形，其中

θ

是仿射坐标系。它们代表物理系统的密集量。对偶，我们引入对偶仿射结构S公司，其中

η

是另一个仿射坐标系。它们代表着广泛的数量。我们可以在中定义两种类型的直线或测地线S公司由于q个-仿射结构。

对于两种分布

第页 (x个, θ_{1})

和

第页 (x个, θ_{2})

在里面S公司，一条曲线

第页 (x个, θ (吨))

据说是一个q个-测地线连接它们，当

θ (吨) = 吨 θ_{1} + (1 - 吨) θ_{2}

(63)

哪里吨是曲线的参数。对偶，以双坐标表示

η

，何时

η (吨) = 吨 η_{1} + (1 - 吨) η_{2}

(64)

保持不变，曲线称为对偶曲线q个-测地线。

更一般地q个-测地线连接两个分布

{第页}_{1} (x个)

和

{第页}_{2} (x个)

由给定

{日志}_{q个} 第页 (x个, 吨) = 吨 {日志}_{q个} {第页}_{1} (x个) + (1 - 吨) {日志}_{q个} {第页}_{2} (x个) - c（c） (吨)

(65)

哪里

c（c） (吨)

是一个规范化术语。这被改写为

第页 {(x个, 吨)}^{1 - q个} = 吨 {第页}_{1} {(x个)}^{1 - q个} + (1 - 吨) {第页}_{2} {(x个)}^{1 - q个} - c（c） (吨)

(66)

双重，双重q个-测地线连接

{第页}_{1} (x个)

和

{第页}_{2} (x个)

通过将护送分布用作

\hat{第页} (x个, 吨) = 吨 {\hat{第页}}_{1} (x个) + (1 - 吨) {\hat{第页}}_{2} (x个)

(67)

自从歧管S公司有一个q个-黎曼结构，两个切向量的正交性由黎曼度量定义。我们用仿射坐标重写了两条测地线的正交性。让我们考虑两个小偏差

{d日}_{1} 第页 (x个)

和

{d日}_{2} 第页 (x个)

属于

第页 (x个)

，也就是说，来自

第页 (x个)

到

第页 (x个) + {d日}_{1} 第页 (x个)

和

第页 (x个) + {d日}_{2} 第页 (x个)

，被视为的两个（无穷小）切线向量S公司在

第页 (x个)

.

引理1

两个偏差的内积

{d日}_{1} 第页

和

{d日}_{2} 第页

由给定

〈{d日}_{1} 第页 (x个), {d日}_{2} 第页 (x个)〉 = \int {d日}_{1} \hat{第页} (x个) {d日}_{2} {日志}_{q个} 第页 (x个) d日 x个

(68)

证明

通过简单的计算，我们得出

\int {d日}_{1} \hat{第页} (x个) {d日}_{2} {日志}_{q个} 第页 (x个) d日 x个 = \frac{q个}{{小时}_{q个}} \int \frac{{d日}_{1} 第页 (x个) {d日}_{2} 第页 (x个)}{第页 (x个)} d日 x个

(69)

其中右侧是形式为的黎曼内积(46). □

推论。

两条曲线

θ_{1} (吨)

和

η_{2} (吨)

，相交于

吨 = 0

，是正交的

〈 {\dot{θ}}_{1} (0), {\dot{η}}_{2} (0) 〉 = 0

.给，

{\dot{θ}}_{1} (吨)

和

{\dot{η}}_{2} (吨)

表示的导数

θ_{1} (吨)

和

η_{2} (吨)

通过吨分别是。

两个测地线和正交性在S公司如下所示。

4q个-毕达哥拉斯和q个-Max-Ent定理

对偶平坦黎曼流形承认广义毕达哥拉斯定理及其投影定理[8]. 我们在案例中陈述了这些内容。

q个-毕达哥拉斯语 定理。

对于三种分布

{第页}_{1} (x个), {第页}_{2} (x个)

和

{第页}_{三} (x个)

在里面S公司，它认为

{D类}_{q个} [{第页}_{1} : {第页}_{2}] + {D类}_{q个} [{第页}_{2} : {第页}_{三}] = {D类}_{q个} [{第页}_{1} : {第页}_{三}]

(70)

当双测地线连接时

{第页}_{1} (x个)

和

{第页}_{2} (x个)

正交于

{第页}_{2} (x个)

到测地线连接

{第页}_{2} (x个)

和

{第页}_{三} (x个)

（请参见图1).

图1。 q个-勾股定理。

给定分布

第页 (x个) \in S公司

和子流形

M（M） \subset S公司

，一个分发

第页 (x个) \in M（M）

据说是q个-投影（双q个-投影）

第页 (x个)

到M（M），当q个-测地线（对偶q个-测地线）连接

第页 (x个)

和

第页 (x个)

与…正交M（M）在

第页 (x个)

(图2).

图2。 q个-的投影第页到M（M）.

q个-投影定理.

让M（M）是的子流形S公司.给定

第页 (x个) \in S公司

，重点

第页 (x个) \in M（M）

使其最小化

{D类}_{q个} [第页 (x个) : 第页 (x个)]

由对偶函数给出q个-的投影

第页 (x个)

到M（M）.要点

第页 (x个) \in M（M）

使其最小化

{D类}_{q个} [第页 (x个) : 第页 (x个)]

由q个-的投影

第页 (x个)

到M（M）.

我们向大家展示q个-Tsallis情形下的max-ent定理q个-熵[1,4,9,11]是上述情况的直接后果q个-毕达哥拉斯和q个-投影定理。

q个-Max-Ent定理.

概率分布最大化q个-熵

{H（H）}_{查利斯}, {H（H）}_{R（右） \overset{´}{e（电子）} 纽约}

和

{H（H）}_{q个}

在下面q个-线性约束米随机变量

{c（c）}_{k个} (x个)

和各种值

一_{k个}

{E类}_{\hat{第页}} [{c（c）}_{k个} (x个)] = 一_{k个}, k个 = 1, \dots, 米

(71)

表格aq个-指数族

{日志}_{q个} 第页 (x个, θ) = \sum_{我 = 1}^{米} θ^{我} {c（c）}_{我} (x个) - ψ (θ)

(72)

用标准分析方法很容易得到证明。在这里，我们给出一个几何证明。让我们考虑子空间

{M（M）}^{*} \subset S公司

其成员

第页 (x个)

满足米约束

{E类}_{\hat{第页}} [{c（c）}_{k个} (x个)] = \int \hat{第页} (x个) {c（c）}_{k个} (x个) d日 x个 = 一_{k个}, k个 = 1, \dots, 米 .

(73)

因为约束在对偶仿射坐标中是线性的

η

或

\hat{第页} (x个)

,

{M（M）}^{*}

是的线性子空间S公司关于对偶仿射连接。让

{第页}_{0} (x个, θ_{0})

是由以下定义的均匀分布

θ_{0} = 0

，这意味着

{第页}_{0} (x个, θ_{0}) = 常数

来自(6). 让

\bar{第页} (x个) \in {M（M）}^{*}

成为q个-的投影

{第页}_{0} (x个)

到

{M（M）}^{*}

(图3). 然后，散度

{D类}_{q个} [第页 : {第页}_{0}]

从

第页 (x个) \in {M（M）}^{*}

到

{第页}_{0} (x个)

分解为

{D类}_{q个} [第页 : {第页}_{0}] = {D类}_{q个} [第页 : \bar{第页}] + {D类}_{q个} [\bar{第页} : {第页}_{0}]

(74)

让

η_{第页}

是的双重坐标

第页 (x个)

。因为散度写为

{D类}_{q个} [第页 : {第页}_{0}] = ψ (θ_{0}) + φ (η_{第页}) - θ_{0} \cdot η_{第页}

(75)

最小值

{D类}_{q个} [第页 : {第页}_{0}]

在…之间

第页 (x个) \in {M（M）}^{*}

只是

\bar{第页} (x个)

也是熵的最大化

- φ (η_{第页})

.

The trajectories of

\bar{第页} (x个)

对于各种值

一_{k个}

形成与…正交的平坦子空间

{M（M）}^{*}

意味着它们形成了q个-形式的指数族(6)（请参见图3). 切线方向

d日 \hat{第页} (x个)

属于

{M（M）}^{*}

满足

\int d日 \hat{第页} (x个) {c（c）}_{k个} (x个) d日 x个 = 0, k个 = 1, \dots, 米 .

(76)

因此q个-形式的指数族

{日志}_{q个} 第页 (x个, ξ) = \sum_{我 = 1}^{米} ξ_{我} {d日}_{我} (x个) - ψ (ξ)

(77)

与…正交

{M（M）}^{*}

，何时

\int d日 \hat{第页} (x个) d日 {日志}_{q个} 第页 (x个, ξ) d日 x个 = 0

(78)

这意味着

{d日}_{我} (x个) = {c（c）}_{我} (x个)

。因此，我们有q个-指数族(72)最大化q个-熵。

图3。 q个-Max-Ent定理。

5q个-贝叶斯MAP估计

鉴于N个iid观测

{x个}_{1}, \dots, {x个}_{N个}

从统计模型

M（M） = \{第页 (x个, ξ)\}

，我们有

第页 ({x个}_{1}, \dots, {x个}_{N个}, ξ) = \prod_{我 = 1}^{N个} 第页 ({x个}_{我}, ξ)

(79)

自

{日志}_{q个} u个

是一个单调递增函数q个-可能性

我_{q个} ({x个}_{1}, \dots, {x个}_{N个}, ξ) = {日志}_{q个} 第页 ({x个}_{1}, \dots, {x个}_{N个}, ξ)

(80)

与普通的最大似然估计器（mle）相同。然而q个-最大化q个-护送日志，

\frac{1}{q个} \hat{我} ({x个}_{1}, \dots, {x个}_{N个}, ξ) = 日志 第页 ({x个}_{1}, \dots, {x个}_{N个}, ξ) - \frac{1}{q个} 日志 {小时}_{q个} (ξ)

（81）

与此不同。我们证明了q个-mle是贝叶斯MAP（最大后验概率）估计量。这澄清了q个-护卫长。

这个q个-护送mle是q个-护送分发，

{\hat{ξ}}_{q个} = 参数 最大值 \hat{第页} ({x个}_{1}, \dots, {x个}_{N个}, ξ)

(82)

定理 6

这个q个-护卫长

{\hat{ξ}}_{q个}

是具有先验分布的贝叶斯MAP估计量

π (ξ) = {小时}_{q个} {(ξ)}^{- N个 / q个}

(83)

证明

贝叶斯MAP是具有先验的后验分布的最大化器

π (ξ)

第页 (ξ | {x个}_{1}, \dots, {x个}_{N个}) = \frac{π (ξ) 第页 ({x个}_{1}, \dots, {x个}_{N个}, ξ)}{第页 ({x个}_{1}, \dots, {x个}_{N个})}

(84)

这也最大化了

{(π (ξ) 第页 ({x个}_{1}, \dots, {x个}_{N个}, ξ))}^{q个}, 对于 q个 > 0

(85)

另一方面q个-护送mle是

\hat{第页} ({x个}_{1}, \dots, {x个}_{N个}, ξ) = \prod_{我 = 1}^{N个} \hat{第页} ({x个}_{我}, ξ) = \prod_{我 = 1}^{N个} \frac{第页 {({x个}_{我}, ξ)}^{q个}}{{小时}_{q个} (ξ)}

(86)

因此，当

π (ξ) = {小时}_{q个} {(ξ)}^{- N个 / q个}

(87)

这两个估计值是相同的。□

该定理表明，贝叶斯先验在我们的最大值处有一个峰值q个-熵

{H（H）}_{q个}

.

6.结论

自从Tsallis提出q个-熵及其相关理论。幂律也存在于各种通信网络中。它现在是一个热门的研究课题。

然而，我们没有一个几何基础，而普通概率分布族的基础是由信息几何给出的[8]. 本文试图为q个-概率分布族。我们引入了一个新概念q个-几何图形。这个q个-结构无处不在，因为所有离散概率分布族（以及所有连续概率分布族，如果我们忽略无穷维中涉及的微妙问题）都属于q个-任意指数分布族q个也就是说，我们可以介绍q个-任意概率分布族的几何结构，因为任何参数化的概率分布族都会形成嵌入在整个流形中的子流形。

这个q个-结构由一个黎曼度量和一对双重耦合的仿射连接组成，它们位于标准信息几何的框架中。然而q个-结构与由概率分布流形的不变性准则导出的标准结构有本质不同。我们对与q个-从保角变换的角度看熵。这使我们对各种量有了统一的定义，例如q个-熵，q个-发散，q个-势函数及其对偶，以及对已知量的新解释。

这是一个几何基础，我们希望本文能为这一领域的进一步发展做出贡献。

工具书类

C·查利斯。非扩展统计力学导论; 施普林格：美国纽约州纽约市，2009年。[谷歌学者]
Naudts，J。广义热力学; 施普林格：英国伦敦，2011年。[谷歌学者]
Tsallis，C.Boltzmann-Gibbs统计的可能推广。J.Stat.物理。 1988,52，479–487页。[谷歌学者] [交叉参考]
J.Naudts，Theq个-统计物理学中的指数族。美分。欧洲物理杂志。 2009,7, 405–413. [谷歌学者] [交叉参考]
Suyari，H.数学结构源自q个-Tsallis统计中的多项式系数。物理A 2006,368, 63–82. [谷歌学者] [交叉参考]
苏亚里，H。；Wada，T.乘法对偶，q个-三胞胎和μ,ν,q个-从(μ,ν)-多项式系数与Tsallis熵S公司_q个.物理A 2008,387, 71–83. [谷歌学者] [交叉参考]
O.E.巴恩多夫·尼尔森。统计理论中的信息与指数族; 威利：美国纽约州纽约市，1978年。[谷歌学者]
阿玛里，S。；H·长冈。信息几何方法（数学专著翻译）; 牛津大学出版社：英国牛津，2000年。[谷歌学者]
Ohara，A.与Tsallis统计相关的分布几何和相对熵最小化特性。物理学。莱特。A类 2007,370, 184–193. [谷歌学者] [交叉参考]
Furuichi，S.关于最大熵原理和Tsallis统计中Fisher信息的最小化。数学杂志。物理学。 2009,50, 013303. [谷歌学者] [交叉参考]
Ohara，A.广义熵勒让德对偶的几何研究及其在多孔介质方程中的应用。欧洲物理学。J·B 2009,70, 15–28. [谷歌学者] [交叉参考]
Ohara，A。；Matsuzoe，H。；Amari，S.一种具有护送概率的对偶平坦结构及其在α-Voronoi图中的应用。在arXiv公司; 2010; arXiv:cond-mat/1010.4965。[谷歌学者]
Kurose，T.关于1-共形平坦统计流形的发散性。托霍库数学。J。 1994,46, 427–433. [谷歌学者] [交叉参考]
Matsuzoe，H.对比函数几何和保角几何。广岛数学。J。 1999,29, 175–191. [谷歌学者]
Kurose，T.统计流形的保形投影几何。跨学科信息科学 2002,8, 89–100. [谷歌学者] [交叉参考]
基于非加性信息内容的信息理论。物理学。版本E 2001,63，邮编：046105。[谷歌学者] [交叉参考]
Naudts，J.估计量、伴随概率和统计物理中的非指数族。J.伊内克。纯应用程序。数学。 2004,5, 102. [谷歌学者]
Pistone，G.kappa从几何角度建立指数模型。欧洲物理学。J·B 2009,70, 29–37. [谷歌学者] [交叉参考]
Naudts，J.广义指数族和相关熵函数。熵 2008,10, 131–149. [谷歌学者] [交叉参考]
Kaniadakis，G。；Lissia，M。；Scarfone，A.M.变形对数和熵。物理A 2004,340, 41–49. [谷歌学者] [交叉参考]
Yamano，T.的一些性质q个-对数和q个-Tsallis统计中的指数函数。物理A 2002,305, 486–496. [谷歌学者] [交叉参考]
Tsallis，C。；列维，S.V.F。；A.M.C.苏扎。；梅纳德，R.利维分布在自然界普遍存在的统计力学基础。物理学。修订稿。 1995,75，3589–3593，勘误表物理学。修订稿。 1996,77, 5442.. [谷歌学者] [交叉参考]
Tanaka，M.关于q高斯分布族的思考。IEICE（日本） 2002,J85–D2, 161–173. （日语）。[谷歌学者]
张，Z。；钟，F。；Sun，H.幂逆高斯分布的信息几何。应用。科学。 2007,9, 194–203. [谷歌学者]
Ohara，A。；Wada，T.信息几何q个-高斯密度和相关扩散方程解的行为。《物理学杂志》。A：数学。西奥。 2010,43，035002。[谷歌学者] [交叉参考]
Wada，T.广义我o个克-似然函数和Bregman发散。数学杂志。物理学。 2009,50, 113301. [谷歌学者] [交叉参考]
奇乔基，A。；克鲁斯，S。；Amari，S.广义α-β发散及其在稳健非负矩阵分解中的应用。熵 2011,13, 134–170. [谷歌学者] [交叉参考]
阿玛里，S。α-分歧是唯一的，属于两者（f）-分歧和Bregman分歧类。IEEE传输。通知。西奥。 2009,55, 4925–4931. [谷歌学者] [交叉参考]
贝克，C。；Schlögl，F。混沌系统的热力学; 剑桥大学出版社：英国剑桥，1993年。[谷歌学者]
Borland，L。；Plastino，A.R。；Tsallis，C.非广泛恒温学中的信息增益。数学杂志。物理学。 1998,39, 6490–6501. [谷歌学者] [交叉参考]
Furuichi，S.Tsallis相对熵的基本性质。数学杂志。物理学。 2004,45, 4868–4877. [谷歌学者] [交叉参考]
冈本，I。；阿玛里，S。；Takeuchi，K.曲线指数族序列估计程序的渐近理论。Ann.统计。 1991,19, 961–981. [谷歌学者] [交叉参考]
Rényi，A.关于熵和信息的度量。1960年6月20日至7月30日，美国加利福尼亚州伯克利市，第四届伯克利数学、统计和概率研讨会论文集；第547-561页。
P.T.兰斯伯格。；Vedral，V.广义统计力学中的分布和信道容量。物理学。莱特。A类 1998,247, 211–217. [谷歌学者] [交叉参考]
Rajagopal，A.K。；形式不变性对非扩展熵结构的影响。物理学。修订稿。 1999,83, 1711–1714. [谷歌学者] [交叉参考]
Yamano，T.基于非加性信息内容的信源编码定理。物理A 2002,305, 190–195. [谷歌学者] [交叉参考]
Wada，T。；Scarfone，A.M.采用标准线性平均能量的Tsallis公式与采用归一化线性平均能量公式之间的联系q个-平均能量。物理学。莱特。A类 2005,335, 351–362. [谷歌学者] [交叉参考]

分享和引用

MDPI和ACS样式

阿玛里，S.-i。；奥哈拉，A。的几何结构q个-概率分布的指数族。熵 2011,13, 1170-1185.https://doi.org/10.3390/e13061170

AMA风格

Amari S-i、Ohara A。的几何形状q个-概率分布的指数族。熵. 2011; 13(6):1170-1185.https://doi.org/10.3390/e13061170

芝加哥/图拉宾风格

阿玛里、顺义和大原诚美。2011.“几何q个-概率分布的指数族”熵13，编号6:1170-1185。https://doi.org/10.3390/e13061170

文章菜单

的几何形状q个-概率分布的指数族

摘要

1.简介

2q个-吉布斯或q个-指数分布族

2.1. q-对数与q-指数函数

2.2。q-指数族

2.3. q-电位函数

2.4. q-发散

2.5. q-Riemannian公制

3.双平面结构q个-指数族

3.1. 勒让德变换与q熵

3.2. q-平直结构

4q个-毕达哥拉斯和q个-Max-Ent定理

5q个-贝叶斯MAP估计

6.结论

工具书类

分享和引用

文章指标

文章访问统计

更多信息

指导方针

MDPI计划

遵循MDPI