Fast Bivariate P-Splines: The Sandwich Smoother

Xiao, Luo; Li, Yingxing; Ruppert, David

doi:10.1111/rssb.12007

总结

我们提出了一种用于二元平滑的快速惩罚样条方法。单变量P（P）-样条曲线平滑器沿两个坐标同时应用。新的平滑器有一个三明治形状，向裁判建议“三明治平滑器”的名称。三明治平滑器具有张量积结构，简化了渐近分析，并且可以快速计算。通过证明三明治平滑器渐近等价于具有乘积核的二元核回归估计量，我们导出了三明治平滑器的局部中心极限定理，并给出了渐近偏差和方差的简单表达式。据我们所知，这是任何类型的二元样条估计量的第一个中心极限定理。我们的仿真研究表明，即使使用快速广义线性阵列模型算法计算二元样条平滑器，三明治平滑器的计算速度也比其他二元样条平滑器快几个数量级，并且在平均积分平方误差方面与之相当。我们将三明治平滑器扩展到更高维的阵列数据，其中广义线性阵列模型算法提高了三明治平滑器的计算速度。三明治平滑器的一个重要应用是在函数数据分析中估计协方差函数。在这个应用中，我们的数值结果表明，三明治平滑器比局部线性回归快几个数量级。三明治公式的速度很重要，因为函数数据集变得相当大。

渐近，二元平滑，协方差函数，广义线阵模型，非参数回归，惩罚样条曲线，三明治平滑器，薄板花键

1.简介

本文介绍了一种用于二元平滑的快速惩罚样条方法。给出了二元样条光滑器的第一个局部中心极限定理。假设有一个回归函数μ(x个，z)带有 $(x个， z) \in [0 ， 1]^{2}$ ⁠。最初我们假设 $年_{我， j个} = μ ({x个}_{我} ， z_{j个}) + ε_{我， j个} ， 1 \leq 我 \leq {n个}_{1} ， 1 \leq j个 \leq {n个}_{2}$ ⁠，其中 $ε_{我， j个}$ s独立于 $E类 (ε_{我， j个}) = 0$ 和 $E类 (ε_{我， j个}^{2}) = σ^{2} ({x个}_{我} ， z_{j个})$ ⁠和设计要点 ${({x个}_{我} ， z_{j个})}_{1 \leq 我 \leq {n个}_{1} ， 1 \leq j个 \leq {n个}_{2}}$ 具有确定性；因此，数据点的总数为 $n个 = {n个}_{1} {n个}_{2}$ 数据位于矩形网格上。第节4我们将设计假设放宽到固定的设计点而不是规则网格和随机设计点。使用矩形网格上的数据，可以将其组织为 ${n个}_{1} \times {n个}_{2}$ 矩阵Y（Y）。我们建议在Y（Y）所以拟合值矩阵 $\hat{Y（Y）}$ 满足

\hat{Y（Y）} = {S公司}_{1} Y（Y） {S公司}_{2} ，

(1)

哪里 ${S公司}_{1}$ 和 ${S公司}_{2}$ 是更平滑的矩阵x个和z分别是。所以，固定一个协变量，我们沿着另一个协变数平滑，反之亦然，尽管这两个平滑是同时的，正如方程所示(1).估价师(1)在形式上类似于协方差矩阵的三明治公式，它向裁判建议了“三明治平滑器”的名称。我们采用了这个术语。

三明治平滑器的张量积结构允许快速计算，特别是选择平滑参数的广义交叉验证（GCV）标准；参见第节2.2Dierckx公司(1982)提出了一种与估计器结构相同的平滑器(1)，但我们的渐近分析和三明治平滑器的快速实现是新的。为了平滑二维直方图，Eilers和Goeman(2004)研究了一种简化的三明治平滑器，它具有特殊的平滑器矩阵，可以为非负数据提供非负平滑器。三明治平滑器的快速方法可以应用于他们的方法。

对于二元样条平滑，有两个著名的估计量：二元P（P）-样条曲线（Eilers和Marx，2003; 马克思和艾勒斯，2005)和薄板样条，例如薄板回归样条（Wood，2003). 为了方便起见，Eilers–Marx和Wood估计值将分别用E–M和TPRS表示。我们使用E–M，没有说明如何计算估计器。

惩罚样条曲线近年来越来越受欢迎，因为它们使用的节点更少，在更高的维度上比平滑样条曲线或薄板样条曲线需要更少的计算。参见Ruppert等. (2003)或木材(2006)用于方法开发和应用。然而，缺陷样条的理论研究一直是一个挑战。最近才实现了对单变量惩罚样条函数的渐近研究（Hall和Opsomer，2005; Li和Ruppert，2008; 克莱斯肯斯等.,2009; 考尔曼等.,2009; 王等.,2011). 相比之下，光滑样条的渐近收敛速度已经得到了很好的确定；见顾(2002)以获取全面的参考列表。

高维惩罚样条函数的理论研究更具挑战性。据我们所知，文献中不包含中心极限定理或渐近平均和协方差矩阵的显式表达式 $\hat{μ} (x个， z)$ 对于任何类型的二元样条估计。三明治平滑器具有简化渐近分析的张量积结构，我们证明了三明治平滑器与具有乘积核的核估计量渐近等价。利用这个结果，我们得到了三明治平滑器的中心极限定理以及渐近偏差和方差的简单表达式。

为了平滑阵列数据，Currie的广义线性阵列模型（GLAM）等. (2006)利用模型矩阵和数据的数组结构，给出了一种低存储、高速的算法。E-M估计器可以用GLAM算法实现（用E-M-GLAM表示）。三明治平滑器还可以扩展到任意维的数组数据，其中GLAM算法可以提高三明治平滑器的速度；参见第节7.由于章节中的快速方法2.2对于计算GCV标准，GLAM算法用于计算夹层时比用于计算E–M估计器时更快。在第5节表2中。2，我们看到，在广泛的样本大小和节数范围内，三明治平滑器比E–M–GLAM估计器快许多数量级。

本文的其余部分组织如下。在节中2，我们提供了关于三明治平滑器的详细信息。在节中三通过证明三明治平滑器与具有乘积核的二元核估计量的渐近等价，我们建立了三明治平滑器的渐近理论。在节中4，我们考虑不规则间隔的数据。在节中5，我们报告了一项模拟研究。在节中6为了估计函数数据的协方差函数，我们比较了三明治平滑器和局部线性平滑器。我们发现三明治平滑器比局部线性平滑器快许多数量级，并且它们具有相似的平均积分平方误差（MISE）。在节中7，我们将三明治平滑地扩展到维数大于2的数组数据。

用于分析数据的程序可以从http://www.blackwellpublishing.com/rss

2.三明治更光滑

让vec是将矩阵的列堆叠成向量的操作。定义年=vec(Y（Y）)和 $血管内皮细胞 (\hat{Y（Y）}) = \hat{年}$ ⁠应用张量乘积的一个众所周知的恒等式（Seber(2007)，第240页）发送给估计器(1)给予

\hat{年} = ({S公司}_{2} \otimes {S公司}_{1}) 年 .

(2)

身份(2)证明了整体光滑矩阵是两个单变量光滑矩阵的张量积。由于平滑矩阵的分解，我们说我们的模型具有张量积结构。我们将使用P（P）-样条曲线（Eilers和Marx，1996)构造单变量平滑矩阵，即。

{S公司}_{我} = B_{我} (B_{我}^{T型} B_{我} + λ_{我} 天_{我}^{T型} 天_{我})^{- 1} B_{我}^{T型} ， 我 = 1 ， 2 ，

(3)

哪里 $B_{1}$ 和 $B_{2}$ 是的模型矩阵x个和z使用B-样条基（稍后定义），以及 $天_{1}$ 和 $天_{2}$ 是差分阶的差分矩阵 $米_{1}$ 和 $米_{2}$ 分别是。然后，可以使用张量积的恒等式（Seber(2007)，第235-239页），

\begin{matrix} {S公司}_{2} \otimes {S公司}_{1} & = {B_{2} (B_{2}^{T型} B_{2} + λ_{2} 天_{2}^{T型} 天_{2})^{- 1} B_{2}^{T型}} \otimes {B_{1} (B_{1}^{T型} B_{1} + λ_{1} 天_{1}^{T型} 天_{1})^{- 1} B_{1}^{T型}} \\ = (B_{2} \otimes B_{1}) (B_{2}^{T型} B_{2} \otimes B_{1}^{T型} B_{1} + λ_{1} B_{2}^{T型} B_{2} \otimes 天_{1}^{T型} 天_{1} + λ_{2} 天_{2}^{T型} 天_{2} \otimes B_{1}^{T型} B_{1} \\ + λ_{1} λ_{2} 天_{2}^{T型} 天_{2} \otimes 天_{1}^{T型} 天_{1})^{- 1} (B_{2} \otimes B_{1})^{T型} . \end{matrix}

(4)

第二等式中的逆矩阵(4)显示了我们的模型使用带有惩罚的张量积样条（稍后定义）

P（P） = λ_{1} B_{2}^{T型} B_{2} \otimes 天_{1}^{T型} 天_{1} + λ_{2} 天_{2}^{T型} 天_{2} \otimes B_{1}^{T型} B_{1} + λ_{1} λ_{2} 天_{2}^{T型} 天_{2} \otimes 天_{1}^{T型} 天_{1}

(5)

关于系数矩阵。二元张量积样条（Dierckx(1995)，第2章）的定义

\sum_{1 \leq κ \leq {c（c）}_{1} ， 1 \leq 我 \leq {c（c）}_{2}} θ_{κ ， 我} B_{κ}^{1} (x个) B_{我}^{2} (z) ，

哪里 $B_{κ}^{1}$ 和 $B_{我}^{2}$ 是B-样条基函数x个和z分别是， ${c（c）}_{1}$ 和 ${c（c）}_{2}$ 是一元样条函数的基函数数 $Θ = (θ_{κ ，我})_{1 \leq κ \leq {c（c）}_{1} ， 1 \leq 我 \leq {c（c）}_{2}}$ 是系数矩阵。我们使用B-度的样条曲线 ${第页}_{1}$ 和 ${第页}_{2}$ 对于x个和z分别和使用 ${K（K）}_{1} - 1$ 和 ${K（K）}_{2} - 1$ 分别为等距内部节点。然后 ${c（c）}_{1} = {K（K）}_{1} + {第页}_{1}$ 和 ${c（c）}_{2} = {K（K）}_{2} + {第页}_{2}$ ⁠。因此，模型为

Y（Y） = B_{1} θ B_{2}^{T型} + ε ，

(6)

哪里 $B_{1} = {B_{κ}^{1} ({x个}_{第页})}_{1 \leq 第页 \leq {n个}_{1} ， 1 \leq κ \leq {c（c）}_{1}}$ ⁠， $B_{2} = {B_{我}^{2} (z_{秒})}_{1 \leq 秒 \leq {n个}_{2} ， 1 \leq 我 \leq {c（c）}_{2}}$ 和ε是一个 ${n个}_{1} \times {n个}_{2}$ 矩阵，带有(我，j个)第个条目 $ε_{我， j个}$ ⁠.让θ=vec(Θ). 然后估计θ通过最小化给出 $‖ Y（Y） - B_{1} \hat{Θ} B_{2}^{T型} ‖_{F类}^{2} + {\hat{θ}}^{T型} P（P） \hat{θ}$ ⁠，其中规范是Frobenius规范P（P）在方程式中定义(5)因此，系数矩阵的估计 $\hat{Θ}$ 满足 $Λ_{1} \hat{Θ} Λ_{2} = B_{1}^{T型} Y（Y） B_{2}$ ⁠，其中，对于我= 1,2, $Λ_{我} = B_{我}^{T型} B_{我} + λ_{我} 天_{我}^{T型} 天_{我}$ 或者，同等地， $\hat{θ}$ 满足

(Λ_{2} \otimes Λ_{1}) \hat{θ} = (B_{2} \otimes B_{1})^{T型} 年 .

(7)

那么我们受到惩罚的估计是

\hat{μ} (x个 ， z) = \sum_{1 \leq κ \leq {c（c）}_{1} ， 1 \leq 我 \leq {c（c）}_{2}} {\hat{θ}}_{κ ， 我} B_{κ}^{1} (x个) B_{我}^{2} (z) .

(8)

使用等式(5)，很容易证明 $\hat{年} = (B_{2} \otimes B_{1}) \hat{θ}$ 满足方程(1)这证实了所提出的方法使用具有特定惩罚的张量积样条。

2.1. 与E-M估计值的比较

三明治平滑器和E–M估计器之间的唯一区别（Eilers和Marx，2003; 马克思和艾勒斯，2005)就是惩罚。让 ${P（P）}_{E类 - M（M）}$ 表示E–M估计量的惩罚矩阵；然后 ${P（P）}_{E类 - M（M）} = λ_{1} 我_{{c（c）}_{2}} \otimes 天_{1}^{T型} 天_{1} + λ_{2} 天_{2}^{T型} 天_{2} \otimes 我_{{c（c）}_{1}}$ ⁠.二元第一、二罚项P（P）-样条线惩罚Θ分别被称为列惩罚和行惩罚。可以看出，方程中的第一个惩罚项(5)， $B_{2}^{T型} B_{2} \otimes 天_{1}^{T型} 天_{1}$ ⁠，比如 $我_{{c（c）}_{2}} \otimes 天_{1}^{T型} 天_{1}$ ⁠，是“列”惩罚，但它惩罚 $Θ B_{2}^{T型}$ 而不是Θ。我们称之为修改列惩罚。从更仔细的模型中可以看出此修改列惩罚的含义(6).根据模型(6)作为一个模型B-花键底座 $B_{1}$ 和系数 $Θ B_{2}^{T型}$ ⁠，型号(6)变系数模型（Hastie和Tibshirani，1993)在x个系数取决于z因此，我们可以将修改后的列惩罚解释为对单变量的惩罚P（P）-沿x个-轴。同样，罚款期限 $天_{2}^{T型} 天_{2} \otimes B_{1}^{T型} B_{1}$ 对于三明治来说，更平滑的三明治会减少 $B_{1} Θ$ 可以解释为对单变量的惩罚P（P）-沿z-轴。等式中的第三个惩罚(4)对应于两个单变量平滑器的交互。

2.2. 快速实施

通过显示如何通过GCV的快速计算来选择平滑参数，我们导出了三明治平滑器的快速实现。GCV需要计算 $‖ \hat{Y（Y）} - Y（Y） ‖_{F类}^{2}$ 以及整个平滑矩阵的轨迹。我们需要一些初始计算。首先，我们需要奇异值分解

(B_{我}^{T型} B_{我})^{- 1 / 2} 天_{我}^{T型} 天_{我} (B_{我}^{T型} B_{我})^{- 1 / 2} = {单位}_{我} 诊断 (秒_{我}) {单位}_{我}^{T型} ， 对于 我 = 1 ， 2 ，

(9)

哪里 ${单位}_{我}$ 是特征向量矩阵 $秒_{我}$ 是特征值的向量。对于我=1,2，让 ${A类}_{我} = B_{我} (B_{我}^{T型} B_{我})^{- 1 / 2} {单位}_{我}$ ⁠; 然后 ${A类}_{我}^{T型} {A类}_{我} = 我_{{c（c）}_{我}}$ 和 ${A类}_{我} {A类}_{我}^{T型} = B_{我} (B_{我}^{T型} B_{我})^{- 1} B_{我}^{T型}$ ⁠。由此可见我= 1,2, ${S公司}_{我} = {A类}_{我} Σ_{我} {A类}_{我}^{T型}$ 具有 $Σ_{我} = {我_{{c（c）}_{我}} + λ_{我} 诊断 (秒_{我})}^{- 1}$ ⁠.

我们首先计算 $‖ \hat{Y（Y）} - Y（Y） ‖_{F类}^{2}$ ⁠.替换 ${A类}_{我} Σ_{我} {A类}_{我}^{T型}$ 对于 ${S公司}_{我}$ 在方程式中(1)我们获得

\hat{Y（Y）} = {A类}_{1} {Σ_{1} ({A类}_{1}^{T型} Y（Y） {A类}_{2}) Σ_{2}} {A类}_{2}^{T型} = {A类}_{1} (Σ_{1} \tilde{Y（Y）} Σ_{2}) {A类}_{2}^{T型} ，

哪里 $\tilde{Y（Y）} = {A类}_{1}^{T型} Y（Y） {A类}_{2}$ ⁠.让 $\tilde{年} = 血管内皮细胞 (\tilde{Y（Y）})$ ⁠; 然后

\hat{年} = ({A类}_{2} \otimes {A类}_{1}) (Σ_{2} \otimes Σ_{1}) \tilde{年} .

(10)

我们将对向量使用以下运算：一是仅包含正元素的向量， $一^{1 / 2}$ 表示的元素平方根一和1/一表示一。我们可以推导出

‖ \hat{Y（Y）} - Y（Y） ‖_{F类}^{2} = {{\tilde{年}}^{T型} ({\tilde{秒}}_{2} \otimes {\tilde{秒}}_{1})}^{2} - 2 {{\tilde{年}}^{T型} ({\tilde{秒}}_{2}^{1 / 2} \otimes {\tilde{秒}}_{1}^{1 / 2})}^{2} + 年^{T型} 年 ，

(11)

哪里 ${\tilde{秒}}_{我} = 1 / (1_{{c（c）}_{我}} + λ_{我} 秒_{我})$ 对于我=1.2和 $1_{{c（c）}_{我}}$ 是长度为1s的向量 ${c（c）}_{我}$ ⁠。请参阅附录A用于方程推导(11).方程式的右侧(11)显示了每对平滑参数的计算 $‖ \hat{Y（Y）} - Y（Y） ‖_{F类}^{2}$ 只是长度向量的两个内积 ${c（c）}_{2} {c（c）}_{1}$ 和术语 $年^{T型} 年$ 只需对所有平滑参数进行一次计算。

接下来，可以首先使用张量积的另一个恒等式（Seber(2007)，第235页），

信托收据 ({S公司}_{2} \otimes {S公司}_{1}) = 信托收据 ({S公司}_{2}) \cdot 信托收据 ({S公司}_{1}) ，

(12)

然后使用跟踪标识tr(实验室)=tr(文学士)（如果尺寸兼容）（Seber(2007)，第55页），以及 ${A类}_{我}^{T型} {A类}_{我} = 我_{{c（c）}_{我}}$ ⁠，

信托收据 ({S公司}_{我}) = \sum_{κ = 1}^{{c（c）}_{我}} \frac{1}{1 + λ_{我} 秒_{我 ， κ}} ，

(13)

哪里 $秒_{我， κ}$ 是κ的第个元素 $秒_{我}$ ⁠.

总而言之，通过方程式(11)，(12)和(13)我们得到了一个计算GCV的快速实现，它使我们能够有效地选择平滑参数。由于实现速度快，三明治平滑器可以比E-M-GLAM算法快得多；参见第节5.2进行实证比较。对于E–M–GLAM估计量，维数矩阵的逆 ${c（c）}_{1} {c（c）}_{2} \times {c（c）}_{1} {c（c）}_{2}$ 每对都需要 $(λ_{1} ， λ_{2})$ ⁠，而对于三明治更平滑，除了表达式中的初始计算(9)，不需要矩阵求逆。

3.渐近理论

在本节中，我们导出了三明治平滑器的渐近分布，并证明了它与具有乘积核的二元核回归估计量渐近等价。此外，我们还证明了当两阶差分惩罚相同时，三明治平滑器具有最佳收敛速度。

我们将使用最初用于研究平滑样条线的等效核方法（Silverman，1984)也有助于研究P（P）-样条（Li和Ruppert，2008; 王等.,2011). 非参数点估计通常是所有数据点的加权平均值，其权重取决于所使用的点和方法。等效核方法表明，对于某个核函数（等效核）和某个带宽（等效带宽），权重是核回归估计量的渐近权重。首先，我们定义了一个单变量核函数

{H（H）}_{米} (x个) = \sum_{ν = 1}^{米} \frac{ψ_{ν}}{2 米} 经验 (- ψ_{ν} | x个 |) ，

(14)

哪里米是一个正整数 $ψ_{ν}$ s是米复根 ${x个}^{2 米} + (- 1)^{米} = 0$ 有积极的现实部分。在这里 ${H（H）}_{米}$ 是一元惩罚样条函数的等效核（Wang等.,2011). 通过引理1 in附录B， ${H（H）}_{米}$ 为2阶米注意，核的阶决定了核估计的收敛速度。见Wand和Jones(1995)了解更多详细信息。具有乘积核的二元核回归估计 ${H（H）}_{米_{1}} (x个) {H（H）}_{米_{2}} (z)$ 形式为

({nh型}_{n个 ， 1} {小时}_{n个 ， 2})^{- 1} \sum_{我 ， j个} 年_{我 ， j个} {H（H）}_{米_{1}} {{小时}_{n个 ， 1}^{- 1} (x个 - {x个}_{我})} {H（H）}_{米_{2}} {{小时}_{n个 ， 2}^{- 1} (z - z_{j个})} ，

哪里 ${小时}_{n个， 1}$ 和 ${小时}_{n个， 2}$ 是带宽。在适当的假设下，三明治平滑器与上述核估计量渐近等价（命题1）。因为核回归估计量的渐近理论已经建立（Wand和Jones，1995)，可以类似地为三明治平滑器建立渐近理论。为了方便记法，一∼b条意味着一/b条收敛到1。

提议1.假设满足以下条件。

（a）
有一个常数δ>0，这样 $\underset{我， j个}{啜饮} {E类 (| 年_{我， j个} |^{2 + δ})} < \infty$ ⁠.
（b）
回归函数μ(x个，z)具有连续2米四阶导数，其中 $米 = 最大值 (米_{1} ，米_{2})$ ⁠.
（c）
方差函数 $σ^{2} (x个， z)$ 是连续的。
（d）
协变量满足 $({x个}_{我} ， z_{j个}) = ((我 - \frac{1}{2}) / {n个}_{1} ， (j个 - \frac{1}{2}) / {n个}_{2})$ ⁠.
（e）
${n个}_{1} ˜ c（c） {n个}_{2}$ 哪里c（c）是一个常量。

让 ${小时}_{n个， 1} = {K（K）}_{1}^{- 1} (λ_{1} {K（K）}_{1} {n个}_{1}^{- 1})^{1 / 2 米_{1}}$ ⁠， ${小时}_{n个， 2} = {K（K）}_{2}^{- 1} (λ_{2} {K（K）}_{2} {n个}_{2}^{- 1})^{1 / 2 米_{2}}$ 和 ${小时}_{n个} = {小时}_{n个， 1} {小时}_{n个， 2}$ ⁠.假设 ${小时}_{n个， 1} = O（运行） ({n个}^{- ν_{1}})$ 和 ${小时}_{n个， 2} = O（运行） ({n个}^{- ν_{2}})$ 对于某些常数 $0 < ν_{1} ， ν_{2} < 1$ ⁠也假设 $({K（K）}_{1} {小时}_{n个， 1}^{2})^{- 1} = o个 (1)$ 和 $({K（K）}_{2} {小时}_{n个， 2}^{2})^{- 1} = o个 (1)$ ⁠.让 $\hat{μ} (x个， z)$ 使用 $米_{1}$ th-和 $米_{2}$ 四阶差分惩罚和分别 ${第页}_{1} \geq 1$ 和 ${第页}_{2} \geq 1$ 度B-上的样条曲线x个-轴和z-轴分别具有等间距的节点。修复(x个，z) ∈ (0,1)×(0,1). 让 $μ^{*} (x个， z) =$

(n个 {小时}_{n个})^{- 1} \sum_{我 ， j个} 年_{我 ， j个} {H（H）}_{米_{1}} {{小时}_{n个 ， 1}^{- 1} (x个 - {x个}_{我})} {H（H）}_{米_{2}} {{小时}_{n个 ， 2}^{- 1} (z - z_{j个})} .

然后

\begin{matrix} E类 {\hat{μ} (x个 ， z) - μ^{*} (x个 ， z)} = O（运行） [最大值 {({K（K）}_{1} {小时}_{n个 ， 1})^{- 2} ， ({K（K）}_{2} {小时}_{n个 ， 2})^{- 2}}] ， \\ 无功功率，无功功率 {\hat{μ} (x个 ， z) - μ^{*} (x个 ， z)} = o个 {({nh型}_{n个})^{- 1}} . \end{matrix}

所有证明均在附录B.

定理1在命题1中使用相同的符号，并假设命题1中的所有条件和假设都得到满足。为了简化符号，让我们 $米_{三} = 4 米_{1} 米_{2} + 米_{1} + 米_{2}$ ⁠此外，假设 ${K（K）}_{1} ˜ {C类}_{1} {n个}^{τ_{1}}$ 和 ${K（K）}_{2} ˜ {C类}_{2} {n个}^{τ_{2}}$ 具有 $τ_{1} > (米_{1} + 1) 米_{2} / 米_{三}$ ⁠， $τ_{2} > 米_{1} (米_{2} + 1) / 米_{三} ， {小时}_{n个， 1} ˜ {小时}_{1} {n个}^{- 米_{2} / 米_{三}}$ 和 ${小时}_{n个， 2} ˜ {小时}_{2} {n个}^{- 米_{1} / 米_{三}}$ 对于正常数 ${C类}_{1} ， {C类}_{2} ， {小时}_{1}$ 和 ${小时}_{2}$ ⁠。那么，对于任何(x个，z)∈（0,1）×（0,1），我们得到

{n个}^{2 米_{1} 米_{2} / 米_{三}} {\hat{μ} (x个 ， z) - μ (x个 ， z)} \Rightarrow N个 {\tilde{μ} (x个 ， z) ， 五 (x个 ， z)}

(15)

作为分发 ${n个}_{1} \to \infty$ 和 ${n个}_{2} \to \infty$ ⁠，其中

\tilde{μ} (x个 ， z) = (- 1)^{米_{1} + 1} {小时}_{1}^{2 米_{1}} \frac{\partial^{2 米_{1}}}{\partial {x个}^{2 米_{1}}} μ (x个 ， z) + (- 1)^{米_{2} + 1} {小时}_{2}^{2 米_{2}} \frac{\partial^{2 米_{2}}}{\partial z^{2 米_{2}}} μ (x个 ， z) ，

(16)

五 (x个 ， z) = σ^{2} (x个 ， z) \int {H（H）}_{米_{1}}^{2} (u个) d日 u个 \int {H（H）}_{米_{2}}^{2} (v（v）) d日 v（v） .

(17)

备注1.案例 $米_{1} = 米_{2} = 米$ 非常重要。估计量的收敛速度变为 ${n个}^{- 米 / (2 米 + 1)}$ ⁠.石头(1980)得到了非参数估计的最优收敛速度。对于二元光滑函数μ(x个，z)连续2米th导数，估计的相应最优收敛速度μ(x个，z)单位正方形的任何内部点为 ${n个}^{- 米 / (2 米 + 1)}$ ⁠因此，当 $米_{1} = 米_{2} = 米$ ⁠，三明治平滑器达到最佳收敛速度。注意，具有乘积核的二元核估计 ${H（H）}_{米} (x个) {H（H）}_{米} (z)$ 收敛速度也为 ${n个}^{- 米 / (2 米 + 1)}$ ⁠.

备注2.对于单变量情况P（P）-带有米四阶差分惩罚为 ${n个}^{- 2 米 / (4 米 + 1)}$ （见王等. (2011))。因此，二元情形的收敛速度较慢，这表明了“维数诅咒”的影响。

备注3定理1表明，只要足够快，节数的发散率不会影响渐近分布。为了实际使用，我们建议 ${K（K）}_{1} = 最小值 {{n个}_{1} / 2 ， 35}$ 和 ${K（K）}_{2} = 最小值 {{n个}_{2} / 2 ， 35}$ ⁠，以便每个箱子至少有四个数据点。对于单变量P（P）-样条曲线，最小值{n个/Ruppert建议4,35}节(2002).

4.不规则间隔的数据

假设设计点是随机的，我们使用模型 $年_{我} = μ ({x个}_{我} ， z_{我}) + ε_{我} ，我 = 1 ，， n个$ ⁠，即。 $年_{我}$ ⁠， ${x个}_{我}$ 和 $z_{我}$ 现在只有一个索引，而不是i、 j个和以前一样。假设设计点 ${({x个}_{1} ， z_{1}) ，， ({x个}_{n个} ， z_{n个})}$ 独立并从分布中取样F类(x个，z)在 $[0 ， 1]^{2}$ ⁠。三明治平滑器不能直接应用于不规则间隔的数据。这个问题的解决方案是先将数据装箱。我们划分 $[0 ， 1]^{2}$ 变成 $我_{1} \times 我_{2}$ 等尺寸矩形箱的网格和let ${\tilde{年}}_{κ ，我}$ 成为所有人的中庸 $年_{我}$ 使得 $({x个}_{我} ， z_{我})$ 位于(κ，我)第th个bin。如果(κ，我)第th个仓， ${\tilde{年}}_{κ ，我}$ 是任意定义的，例如由最近邻估计量（见下文）。假设 ${\tilde{年}}_{κ ，我}$ 是位于的数据点 $({\tilde{x个}}_{κ} ， {\tilde{z}}_{我})$ ⁠，位于(κ，我)th bin，我们将三明治平滑器应用于网格数据 $\tilde{Y（Y）} = ({\tilde{年}}_{κ ，我})_{1 \leq κ \leq 我_{1} ， 1 \leq 我 \leq 我_{2}}$ 以获得

{\hat{θ}}^{*} = (Λ_{2}^{- 1} \otimes Λ_{1}^{- 1}) {(B_{2} \otimes B_{1})}^{T型} \tilde{年} ，

哪里 $\tilde{年} = 血管内皮细胞 (\tilde{Y（Y）})$ ⁠。那么我们的惩罚估计被定义为

\hat{μ} (x个 ， z) = \sum_{κ = 1}^{{c（c）}_{1}} \sum_{我 = 1}^{{c（c）}_{2}} {\hat{θ}}_{k个 ， 我}^{*} B_{κ}^{1} (x个) B_{我}^{2} (z) .

4.1. 实际实施

为了使上述估算程序与第节中的快速实施协同工作2.2，我们需要处理由于采样变化而导致某些箱子中没有数据的问题。如果中没有数据(κ，我)一个解决方案是定义 ${\tilde{年}}_{κ ，我}$ 为相邻垃圾箱中的平均值。这样做对渐近没有影响，因为箱子最终会有数据。对于小样本，以这种方式填充空单元格可以更平滑地计算三明治，但可能会将空箱子附近的估计值标记为不可靠。

另一种解决方案是使用在数据和平滑参数之间迭代的算法，如下所示。最初，我们让 ${\tilde{年}}_{κ ，我} = 0$ 如果(κ，我)th bin没有数据点。另一种可能性是 ${\tilde{年}}_{κ ，我}$ 对一些人来说是M（M）>0，是M（M）的值年带有(x个，z)最靠近中心的坐标(κ，我)确定平滑参数 $(λ_{1} ， λ_{2})$ 为了最小化GCV，我们只计算有数据的箱子的平方误差之和，而忽略没有数据的箱子。这为我们提供了一对初始平滑参数。然后，对于没有数据的箱子，我们替换 ${\tilde{年}}_{κ ，我}$ s乘以这对平滑参数的估计值。现在，通过更新数据，我们可以获得另一对平滑参数。我们重复上述步骤，直到达到某种收敛。

4.2. 渐近理论

如前所述，我们将单位间隔划分为 $我_{1} \times 我_{2}$ 网格和出租 $我 = 我_{1} 我_{2}$ 是箱子的数量。

定理2.假设满足以下条件。

（a）
有一个常数δ>0，这样 $\underset{我}{啜饮} {E类 (| 年_{我} |^{2 + δ})} < \infty$ ⁠.
（b）
回归函数μ(x个，z)具有连续2米阶导数，其中 $米 = 最大值 (米_{1} ，米_{2})$ ⁠.
（c）
设计要点 ${({x个}_{我} ， z_{我})}_{我 = 1}^{n个}$ 独立并从分布中取样F类(x个，z)具有密度函数（f）(x个，z)和（f）(x个，z)是肯定的 $[0 ， 1]^{2}$ 并具有连续的一阶导数。
（d）
条件启用 ${({x个}_{我} ， z_{我})}_{我 = 1}^{n个}$ ⁠，随机误差 $ε_{我} ， 1 \leq 我 \leq n个$ ⁠，与均值0和条件方差无关 $σ^{2} ({x个}_{我} ， z_{我})$ ⁠.
（e）
方差函数 $σ^{2} (x个， z)$ 是两倍连续可微的。
（f）
$我 ˜ {c（c）}_{我} {n个}^{τ}$ 和 $我_{1} ˜ {c（c）}_{0} 我_{2}$ 对于某些常数 ${c（c）}_{我} ， {c（c）}_{0}$ 和 $τ > 4 米_{1} 米_{2} / (4 米_{1} 米_{2} + 米_{1} + 米_{2})$ ⁠.

修复 $(x个， z) \in (0 ， 1)^{2}$ ⁠然后，使用与定理1相同的符号和假设，我们得到了

{n个}^{2 米_{1} 米_{2} / 米_{三}} {\hat{μ} (x个 ， z) - μ (x个 ， z)} \Rightarrow N个 {\tilde{μ} (x个 ， z) ， 五 (x个 ， z) / （f） (x个 ， z)}

作为分发n个→∞ 哪里 $\tilde{μ} (x个， z)$ 在方程式中定义(16)和五(x个，z)在方程式中定义(17).

备注4.我们在定理2中假设随机设计点。对于固定的设计点，如果我们将条件（c）替换为 $\underset{κ ，我}{啜饮} | {n个}_{κ ，我} / (镍^{- 1}) - （f） ({\tilde{x个}}_{κ} ， {\tilde{z}}_{我}) | = o个 (1)$ 哪里 ${n个}_{κ ，我}$ 是(κ，我)th bin和（f）(x个，z)是一个连续的正函数。

5.仿真研究

本节比较了艾勒和马克思的三明治P（P）-在MISE和计算速度方面，使用GLAM算法（E–M–GLAM）和Wood的薄板回归样条（TPRS）实现的样条。章节5.1结果表明，三明治平滑器的MISE和E–M–GLAM方法大致相当，且小于TPRS方法，而第5.2说明了三明治平滑器相对于其他平滑器的计算优势。

5.1. 回归函数估计

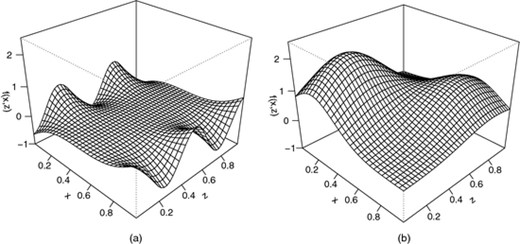
模拟研究中使用了两种测试功能： ${（f）}_{1} (x个， z) = 罪 {2 π (x个 - 0.5)^{三}} 余弦 (4 π z)$ 和

\begin{matrix} {（f）}_{2} (x个 ， z) = \frac{0.75}{π σ_{x个} σ_{z}} 经验 {\frac{- (x个 - 0.2)^{2}}{σ_{x个}^{2}} - \frac{(z - 0.3)^{2}}{σ_{z}^{2}}} + \frac{0.45}{π σ_{x个} σ_{z}} 经验 {\frac{- (x个 - 0.7)^{2}}{σ_{x个}^{2}} - \frac{(z - 0.8)^{2}}{σ_{z}^{2}}} ， \end{matrix}

哪里 $σ_{x个} = 0.3$ 和 $σ_{z} = 0.4$ ⁠。请注意 ${（f）}_{2}$ 用于木材(2003). 两个真实表面如所示图1.

图1

新标签中打开下载幻灯片

（a）表面 ${（f）}_{1}$ 和（b） ${（f）}_{2}$

在两个样本大小下评估了三种平滑器的性能。在较小的样本研究中，每个测试函数都是在单位正方形上的20×30规则网格上采样的，随机误差是独立的，且分布相同 $N个 (0 ， σ^{2})$ 具有σ等于0.1和0.5。在每种情况下，生成100个重复数据集，对于每个重复数据，由三个估计器拟合测试函数，并计算积分平方误差（ISE）。对于样条基和节点设置，根据备注3中的建议，10和15个等距节点用于x个-以及z-两个轴P（P）-样条估计。因此，总共使用了150节来建造B-样条曲线基础。立方（Cubic）B-样条曲线使用二阶差分惩罚。对于薄板回归估计器TPRS，我们使用R包mgcv（Wood，2006). 在本研究中，TPRS的等级为150（即基本维度为150）。对于所有三个估计量，平滑参数由GCV选择。MISE评估了这三种估计器的性能(表1)以及ISE的箱线图(图2).

表1

小样本三个估计量的MISE（20×30网格上的数据）

σ	以下估算结果：
σ	三明治平滑器	E–M–GLAM公司	TPRS公司
${（f）}_{1}$
0.1	$8.13 \times 10^{- 4}$	$9.29 \times 10^{- 4}$	$1.46 \times 10^{- 三}$
0.5	$1.08 \times 10^{- 2}$	$1.18 \times 10^{- 2}$	$1.56 \times 10^{- 2}$
${（f）}_{2}$
0.1	$6.45 \times 10^{- 4}$	$5.73 \times 10^{- 4}$	$6.68 \times 10^{- 4}$
0.5	$9.25 \times 10^{- 三}$	$8.34 \times 10^{- 三}$	$8.06 \times 10^{- 三}$

σ	以下估算结果：
σ	三明治平滑器	E–M–GLAM公司	TPRS公司
${（f）}_{1}$
0.1	$8.13 \times 10^{- 4}$	$9.29 \times 10^{- 4}$	$1.46 \times 10^{- 三}$
0.5	$1.08 \times 10^{- 2}$	$1.18 \times 10^{- 2}$	$1.56 \times 10^{- 2}$
${（f）}_{2}$
0.1	$6.45 \times 10^{- 4}$	$5.73 \times 10^{- 4}$	$6.68 \times 10^{- 4}$
0.5	$9.25 \times 10^{- 三}$	$8.34 \times 10^{- 三}$	$8.06 \times 10^{- 三}$

新标签中打开

表1

小样本三个估计量的MISE（20×30网格上的数据）

σ	以下估算结果：
σ	三明治平滑器	E–M–GLAM公司	TPRS公司
${（f）}_{1}$
0.1	$8.13 \times 10^{- 4}$	$9.29 \times 10^{- 4}$	$1.46 \times 10^{- 三}$
0.5	$1.08 \times 10^{- 2}$	$1.18 \times 10^{- 2}$	$1.56 \times 10^{- 2}$
${（f）}_{2}$
0.1	$6.45 \times 10^{- 4}$	$5.73 \times 10^{- 4}$	$6.68 \times 10^{- 4}$
0.5	$9.25 \times 10^{- 三}$	$8.34 \times 10^{- 三}$	$8.06 \times 10^{- 三}$

σ	以下估算结果：
σ	三明治平滑器	E–M–GLAM公司	第三方程序
${（f）}_{1}$
0.1	$8.13 \times 10^{- 4}$	$9.29 \times 10^{- 4}$	$1.46 \times 10^{- 三}$
0.5	$1.08 \times 10^{- 2}$	$1.18 \times 10^{- 2}$	$1.56 \times 10^{- 2}$
${（f）}_{2}$
0.1	$6.45 \times 10^{- 4}$	$5.73 \times 10^{- 4}$	$6.68 \times 10^{- 4}$
0.5	$9.25 \times 10^{- 三}$	$8.34 \times 10^{- 三}$	$8.06 \times 10^{- 三}$

新标签中打开

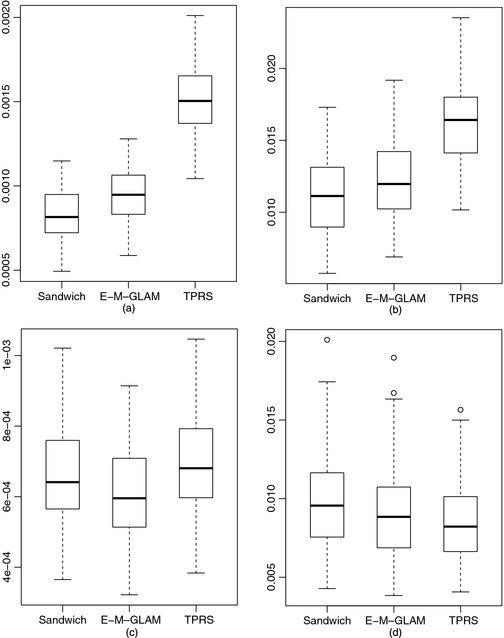
发件人表1我们可以看到，在估计方面，三明治平滑器比E–M–GLAM做得更好 ${（f）}_{1}$ 而E–M–GLAM更适合评估 ${（f）}_{2}$ ⁠中的箱线图图2显示这两个P（P）-样条方法基本上是可比较的。与二者相比P（P）-样条方法，TPRS给出了较大的MISE，只有一例除外。TPRS估算性能相对较差的一种解释 ${（f）}_{1}$ TPRS是各向同性的，只有一个平滑参数，因此在两个方向上应用相同数量的平滑，这可能不适合 ${（f）}_{1}$ 作为 ${（f）}_{1}$ 非常平滑x个并且变化迅速z（请参见图1).

图2

小样本三种估计量ISE的箱线图：（a）f1，σ=0.1；（b） f1，σ=0.5；（c） σ=0.1；（d） σ=0.5

新标签中打开下载幻灯片

小样本三种估计量的ISE的箱线图：（a） ${（f）}_{1}$ ⁠，σ= 0.1; （b） ${（f）}_{1}$ ⁠，σ= 0.5; （c） ${（f）}_{2}$ ⁠，σ= 0.1; （d） ${（f）}_{2}$ ⁠，σ= 0.5

更大样本的模拟研究 ${n个}_{1} = 60$ 和 ${n个}_{2} = 80$ 也完成了。对于这两个人P（P）-样条估计，节点数为 ${K（K）}_{1} = 30$ 和 ${K（K）}_{2} = 35$ ⁠薄板回归样条的秩为1050，这是两个样条中使用的节点总数P（P）-样条估计。所有其他设置与较小样本研究中的设置相同。得出的MISE和箱线图得出了与小样本研究相同的结论。为了简单起见，我们这里不显示结果。

5.2. 计算速度

三种样条平滑器的平滑计算速度 ${（f）}_{2}$ 使用不同数量的数据点进行评估。为了简单起见，我们让 ${n个}_{1} = {n个}_{2}$ 并考虑了这个案子σ= 0.1. 我们为两者选择了结数P（P）-样条平滑器遵循备注3中的建议。我们将TPRS的等级固定为P（P）-样条曲线平滑器。对于两人P（P）-样条平滑器，报告的计算时间是在20×20对数尺度网格上搜索最优平滑参数的情况下 $[- 5 ， 4]^{2}$ ⁠.更精细的网格 $40^{2}$ 还使用了网格点。计算是在运行Windows的2.83-GHz计算机上进行的，该计算机具有3 GB的随机访问内存。表2总结了结果，并表明三明治平滑器是迄今为止最快的方法。请注意，括号中的值是使用更精细网格的计算时间。

表2

在运行Windows且随机访问内存为3G字节的2.83-GHz计算机上，三个估计器的计算时间平均超过100个数据集†

n个	${K（K）}_{1} {K（K）}_{2}$	以下估算值的时间：
n个	${K（K）}_{1} {K（K）}_{2}$	三明治平滑器	E–M–GLAM公司	TPRS公司
$20^{2}$	$10^{2}$	0.06 (0.24)	4.09 (19.74)	0.53
$40^{2}$	$20^{2}$	0.08 (0.30)	94.76 (344.13)	19.50
$80^{2}$	$35^{2}$	0.13 (0.45)	1379.21 (5487.33)	1032.07
$300^{2}$	$42^{2}$	0.18 (0.58)	3798.23 (15192.92)	—
$500^{2}$	$57^{2}$	0.32 (0.89)	21023.44 (84093.76)	—

n个	${K（K）}_{1} {K（K）}_{2}$	以下估算值的时间：
n个	${K（K）}_{1} {K（K）}_{2}$	三明治平滑器	E–M–GLAM公司	TPRS公司
$20^{2}$	$10^{2}$	0.06 (0.24)	4.09 (19.74)	0.53
$40^{2}$	$20^{2}$	0.08 (0.30)	94.76 (344.13)	19.50
$80^{2}$	$35^{2}$	0.13 (0.45)	1379.21 (5487.33)	1032.07
$300^{2}$	$42^{2}$	0.18（0.58）	3798.23 (15192.92)	—
$500^{2}$	$57^{2}$	0.32 (0.89)	21023.44（84093.76）	—

†

夹层平滑器和E–M–GLAM的时间是针对平滑参数值的20×20网格，（括号中）是针对更精细的40×40网格 $n个 = 20^{2} ， 40^{2}$ ⁠， $80^{2}$ ⁠，每个轴的节数由备注3中的建议选择。对于 $n个 = 300^{2}$ 和 $n个 = 500^{2}$ ⁠，三明治平滑器的总节数约为 ${n个}^{三 / 5 + 0.1}$ 如定理1所示。

新标签中打开

表2

在运行Windows且随机访问内存为3G字节的2.83-GHz计算机上，三个估计器的计算时间平均超过100个数据集†

n个	${K（K）}_{1} {K（K）}_{2}$	以下估算值的时间：
n个	${K（K）}_{1} {K（K）}_{2}$	三明治平滑器	E–M–GLAM公司	TPRS公司
$20^{2}$	$10^{2}$	0.06 (0.24)	4.09 (19.74)	0.53
$40^{2}$	$20^{2}$	0.08 (0.30)	94.76 (344.13)	19.50
$80^{2}$	$35^{2}$	0.13 (0.45)	1379.21 (5487.33)	1032.07
$300^{2}$	$42^{2}$	0.18 (0.58)	3798.23 (15192.92)	—
$500^{2}$	$57^{2}$	0.32 (0.89)	21023.44 (84093.76)	—

n个	${K（K）}_{1} {K（K）}_{2}$	以下估算值的时间：
n个	${K（K）}_{1} {K（K）}_{2}$	三明治平滑器	E–M–GLAM公司	TPRS公司
$20^{2}$	$10^{2}$	0.06 (0.24)	4.09 (19.74)	0.53
$40^{2}$	$20^{2}$	0.08 (0.30)	94.76 (344.13)	19.50
$80^{2}$	$35^{2}$	0.13 (0.45)	1379.21 (5487.33)	1032.07
$300^{2}$	$42^{2}$	0.18 (0.58)	3798.23 (15192.92)	—
$500^{2}$	$57^{2}$	0.32 (0.89)	21023.44（84093.76）	—

†

三明治平滑器和E–M–GLAM的时间用于平滑参数值的20×20网格，（括号中）用于更精细的40×40网格 $n个 = 20^{2} ， 40^{2}$ ⁠， $80^{2}$ ⁠，每个轴的节数由备注3中的建议选择。对于 $n个 = 300^{2}$ 和 $n个 = 500^{2}$ ⁠，夹层平滑器的结总数约为 ${n个}^{三 / 5 + 0.1}$ 如定理1所示。

新标签中打开

为了进一步说明其计算能力，将三明治平滑器应用于大小为 $300^{2}$ 和 $500^{2}$ ⁠.对于立方B-样条函数与二阶差分惩罚耦合，定理1建议选择 ${K（K）}_{1} > {n个}^{三 / 10}$ 和 ${K（K）}_{2} > {n个}^{三 / 10}$ ⁠.所以我们让 ${K（K）}_{1} = {K（K）}_{2}$ 具有 ${K（K）}_{1} {K（K）}_{2}$ 接近 ${n个}^{三 / 5 + 0.1}$ 在仿真中。我们还评估了E-M-GLAM的速度。为了节省时间，仅对25对平滑参数运行E–M–GLAM，并将计算时间乘以16或64，以分别在粗网格或细网格上与三明治平滑器的计算时间相比较表2这表明三明治平滑器可以在个人电脑上快速处理大数据，而E-M-GLAM要慢得多。薄板回归样条不适用于这些大数据，因为它需要比计算机提供的更多的内存空间。

总之，这里的模拟研究以及第节中的快速实现2.2显示三明治比其他两个估计值更平滑的优势。因此，当考虑到计算时间时，最好使用三明治平滑器。

6.应用：协方差函数估计

由于函数数据分析已成为一个主要的研究领域，协方差函数的估计已成为二元平滑的一个重要应用。由于函数数据集可能非常大，因此在函数数据分析中，快速计算二元平滑是必不可少的，尤其是在使用bootstrap进行推理时。局部多项式平滑是估计协方差函数的常用方法（参见示例Yao等. (2005)或者姚明和李(2006))而其他平滑方法，如核（Staniswalis和Lee，1998）和惩罚样条（Di等.,2009)也已使用。在本节中，通过模拟研究，我们比较了在固定网格上观察或测量数据时，三明治平滑器和局部多项式用于估计协方差函数的性能。

让{X（X）(t吨):t吨∈[0,1]}是具有连续协方差函数的随机过程K（K）(秒，t吨)=覆盖{X（X）(秒),X（X）(t吨)}. 为了简单起见，我们假设E类{X（X）(t吨)}=0,t吨∈ [0,1]. 假设 ${{X（X）}_{我} (t吨) ，我 = 1 ， \dots ， n个}$ 是上述随机过程的独立实现的集合，我们观察到随机函数 ${X（X）}_{我}$ 在具有测量误差的离散设计点，

{Y（Y）}_{ij公司} = {X（X）}_{我} ({t吨}_{j个}) + ε_{ij公司} ， 1 \leq j个 \leq J型 ， 1 \leq 我 \leq n个 ，

哪里J型是每条曲线的测量次数，n个是曲线的总数 $ε_{ij公司}$ 是独立且同分布的测量误差，平均值为0且方差有限，且与随机函数无关 ${X（X）}_{我}$ ⁠.让 ${Y（Y）}_{我} = ({Y（Y）}_{我 1} ， \dots ， {Y（Y）}_{国际期刊})^{T型}$ ⁠。可以通过平滑样本协方差矩阵来获得协方差函数的估计 ${n个}^{- 1} Σ_{我 = 1}^{n个} {Y（Y）}_{我} {Y（Y）}_{我}^{T型}$ 通过二元平滑器。因为我们要平滑对称矩阵，所以对于三明治平滑器，我们使用两个相同的单变量平滑器矩阵，所以只有一个平滑参数可供选择。我们使用常用的局部线性平滑器（Yao等.,2005; 霍尔等.,2006)用于比较，并且通过留出一条曲线进行交叉验证来选择带宽。我们编写了Yao使用的估计器的R实现等. (2005)，因为他们的代码在MATLAB中。

我们让 $K（K） (秒， t吨) = Σ_{k个 = 1}^{4} λ_{k个} ψ_{k个} (秒) ψ_{k个} (t吨)$ 其中特征值 $λ_{k个} = 0 . 5^{k个 - 1}$ ⁠，k个=1,2,3,4和 ${ψ_{1} ， \dots ， ψ_{4}}$ 是情况1中任一情况的本征函数，

{\sqrt 2 罪 (2 π t吨) ， \sqrt 2 余弦 (2 π t吨) ， \sqrt 2 罪 (4 π t吨) ， \sqrt 2 余弦 (4 π t吨)} ，

或情况2，

{1 ， (2 t吨 - 1) \sqrt 三 ， (6 {t吨}^{2} - 6 t吨 + 1) \sqrt 5 ， (20 {t吨}^{三} - 30 {t吨}^{2} + 12 t吨 - 1) \sqrt 7} .

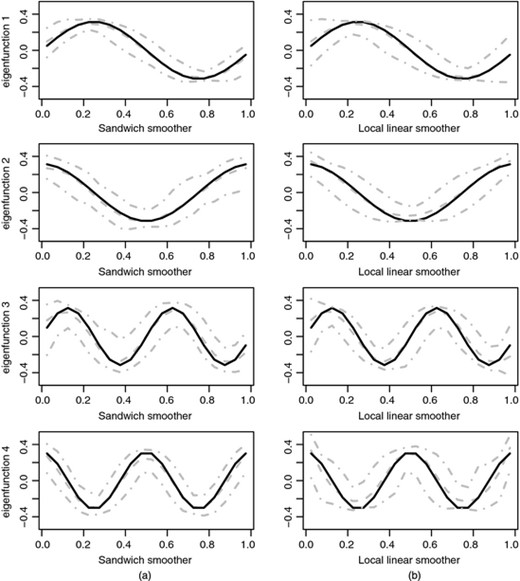
这两组特征函数用于Di等. (2009)、格雷文等. (2010)和Zipunniknov等. (2011). 我们让σ= 0.5. 我们模拟了100个数据集，并根据MISE评估了两个双变量平滑器。结果见表3。来源表3，对于带有的情况1(n个，J型)=（25,20）局部线性平滑器稍好，ISE的平均值和标准偏差较小，对于其他情况，两个平滑器的结果相近。情形1中两个平滑器估计的特征函数(n个，J型)=（25,20）如所示图3这表明这两种平滑器都能很好地估计特征函数。我们发现了类似的结果(n个，J型)=（100,40）（结果未显示）。

表3

估计协方差函数的三明治平滑器和局部线性平滑器的MISE†

（n，J）	案例	三明治更加光滑	局部线性平滑器的结果
(25, 20)	1	0.053 (0.035)	0.050 (0.026)
(25, 20)	2	0.199 (0.139)	0.204 (0.144)
(100, 40)	1	0.014 (0.008)	0.013 (0.008)
(100, 40)	2	0.050 (0.034)	0.050 (0.036)

（n，J）	案例	三明治更光滑的效果	局部线性平滑器的结果
(25, 20)	1	0.053（0.035）	0.050（0.026）
(25, 20)	2	0.199 (0.139)	0.204 (0.144)
(100, 40)	1	0.014 (0.008)	0.013 (0.008)
(100, 40)	2	0.050 (0.034)	0.050 (0.036)

†

括号中的数字是ISE的标准偏差。

新标签中打开

表3

估计协方差函数的三明治平滑器和局部线性平滑器的MISE†

（n，J）	案例	三明治更加光滑	局部线性平滑器的结果
(25, 20)	1	0.053 (0.035)	0.050 (0.026)
(25, 20)	2	0.199 (0.139)	0.204 (0.144)
(100, 40)	1	0.014 (0.008)	0.013 (0.008)
(100, 40)	2	0.050 (0.034)	0.050 (0.036)

（n，J）	案例	三明治更加光滑	局部线性平滑器的结果
(25, 20)	1	0.053 (0.035)	0.050 (0.026)
(25, 20)	2	0.199 (0.139)	0.204 (0.144)
(100, 40)	1	0.014 (0.008)	0.013 (0.008)
(100, 40)	2	0.050（0.034）	0.050 (0.036)

†

括号中的数字是ISE的标准偏差。

新标签中打开

对于情况1（噪声方差为0.25），真实和估计的本征函数用（n，J）=（25,20）重复100次（---，真实本征函数；，逐点中值估计的本征函数；，第5和第95百分位曲线）：（a）三明治平滑器；（b）局部线性平滑器

新标签中打开下载幻灯片

真实和估计的特征函数用(n个，J型)=（25,20）对于情况1（噪声方差为0.25）（---，真本征函数；，逐点中值估计特征函数；第5和第95百分位曲线）：（a）三明治更平滑；（b）局部线性平滑器

我们还通过使用案例1比较了两个平滑器的计算时间J型。对于三明治平滑器，我们搜索了20多个平滑参数。对于局部线性平滑器，我们固定了带宽。请注意，通过保留一条曲线进行交叉验证来选择带宽意味着局部线性平滑器的计算时间将乘以带宽数和曲线数。表4结果表明，即使在协方差函数估计的带宽固定的情况下，三明治平滑器的计算速度也比局部线性平滑器快得多。

表4

平滑a的计算时间J型×J型使用三明治平滑器和局部线性平滑器的协方差矩阵†

J型	三明治平滑器的计算时间（s）	局部线性平滑器的计算时间
40	0.02	2.98
80	0.03	50.04
160	0.05	961.42
320	0.16	13854.40

†

除了一个例外，在运行Windows的2.83-GHz计算机上，计算时间平均超过100个数据集，随机访问内存为3 GB。曲线数固定为100。局部线性平滑器的带宽在计算中是固定的。例外情况是，当J型=320仅为10个数据集的平均值。

新标签中打开

表4

平滑a的计算时间J型×J型使用三明治平滑器和局部线性平滑器的协方差矩阵†

J型	三明治平滑器的计算时间（s）	局部线性平滑器的计算时间
40	0.02	2.98
80	0.03	50.04
160	0.05	961.42
320	0.16	13854.40

†

除了一个例外，在运行Windows的2.83-GHz计算机上，计算时间平均超过100个数据集，随机访问内存为3 GB。曲线数固定为100。局部线性平滑器的带宽在计算中是固定的。例外情况是，当J型=320仅为10个数据集的平均值。

新标签中打开

总之，模拟研究表明，对于协方差函数估计，当功能数据在固定网格上测量时，三明治平滑器在MISE方面与局部线性平滑器相当。三明治平滑器的计算速度比局部线性平滑器快得多。

7.多元P（P）-样条曲线

我们将三明治平滑地扩展到维度大于2的数组数据。假设我们有一个非参数回归模型d日≥3个协变量

年_{我_{1} ， \dots ， 我_{d日}} = μ ({x个}_{我_{1}} ， \dots ， {x个}_{我_{d日}}) + ε_{我_{1} ， \dots ， 我_{d日}} ， 1 \leq 我_{k个} \leq {n个}_{k个} ， 1 \leq k个 \leq d日 ，

因此数据收集在d日-维度网格。为了简单起见，假设协变量在 $[0 ， 1]^{d日}$ ⁠。在双变量情况下，我们对d日-变量函数 $μ ({x个}_{1} ， \dots ， {x个}_{d日})$ 按张量积B-的样条曲线d日变量 $Σ_{κ_{1} ， κ_{2} ， \dots ， κ_{d日}} θ_{κ_{1} ， κ_{2} ， \dots ， κ_{d日}} B_{κ_{1}}^{1} ({x个}_{1}) B_{κ_{2}}^{1} ({x个}_{2}) \dots B_{κ_{d日}}^{d日} ({x个}_{d日}) ，$ 哪里 $B_{κ_{1}}^{1} ， B_{κ_{2}}^{2} ， \dots ， B_{κ_{d日}}^{d日}$ 是B-样条基函数。我们同时平滑所有协变量，以便拟合值和数据满足

\hat{年} = ({S公司}_{d日} \otimes {S公司}_{d日 - 1} \otimes \dots \otimes {S公司}_{1}) 年 ，

(18)

哪里 ${S公司}_{我}$ 是更平滑的矩阵我使用th协变量P（P）-表达式中的样条线(3)，年数据向量首先由 ${x个}_{1}$ ⁠，然后通过 ${x个}_{2}$ ⁠，依此类推，以及 $\hat{年}$ 组织方式与年类似于方程式(7)，系数的估计 $\hat{θ}$ 满足

(Λ_{d日} \otimes Λ_{d日 - 1} \otimes \dots \otimes Λ_{1}) \hat{θ} = (B_{d日} \otimes B_{d日 - 1} \otimes \dots \otimes B_{1})^{T型} 年 ，

被处罚的估计是

\hat{μ} ({x个}_{1} ， {x个}_{2} ， \dots ， {x个}_{d日}) = \sum_{κ_{1} ， κ_{2} ， \dots ， κ_{d日}} {\hat{θ}}_{κ_{1} ， κ_{2} ， \dots ， κ_{d日}} B_{κ_{1}}^{1} ({x个}_{1}) B_{κ_{2}}^{1} ({x个}_{2}) \dots B_{κ_{d日}}^{d日} ({x个}_{d日}) .

7.1. 多元的实现P（P）-样条曲线

在多维网格上平滑数据会出现两个计算问题。第一个问题是，除非 ${S公司}_{我}$ s都很小 ${S公司}_{d日} \otimes {S公司}_{d日 - 1} \otimes \dots \otimes {S公司}_{1}$ 将具有挑战性。第二个问题是平滑参数的选择。由于涉及大量的平滑参数，很难找到使一些模型选择标准（如GCV）最小化的平滑参数。

柯里的GLAM等. (2006)通过利用模型矩阵的数组结构和数据，为第一个问题提供了一个优雅的解决方案。更平滑的矩阵 ${S公司}_{d日} \otimes {S公司}_{d日 - 1} \otimes \dots \otimes {S公司}_{1}$ 多元平滑具有张量积结构；因此 $\hat{年}$ 在方程式中(18)可以通过上的一系列嵌套操作高效计算年通过GLAM算法。例如，考虑d日= 3. 然后 $\hat{年}$ 可以用一行R代码高效计算：#函数“RH”是矩阵对数组的旋转变换

#参见Currie等人（2006）

yhat=矢量（右侧（S3，右侧（S2，右侧，S1，Y）））

我们编写了RH函数的R版本。

第二个问题可以很容易地处理多元快速P（P）-样条曲线。由于平滑矩阵的张量积结构2.2可以推广到多元情况。作为一个例子，我们展示了如何计算平滑矩阵的轨迹 ${S公司}_{我}$ 所以这个表达式(13)为所有人保留我= 1,…,d日; 然后通过以下公式计算平滑矩阵的轨迹

信托收据 ({S公司}_{d日} \otimes {S公司}_{d日 - 1} \otimes \dots \otimes {S公司}_{1}) = Π_{我 = 1}^{d日} 信托收据 ({S公司}_{我})

在表达式中使用标识(12)重复。请注意 $信托收据 ({S公司}_{我})$ 与表达式中的表达式类似(13)为所有人我.

三明治平滑器没有广义线性模型权重矩阵，当它用于二元平滑时，不需要旋转数组，因此我们不认为二元三明治平滑器是GLAM算法。然而，我们对双变量三明治平滑器的实现使用张量积结构来简化计算，与GLAM类似。

7.2. 一个例子

使用 $20^{三}$ 由平滑参数组成的网格，三明治平滑器在运行Macintosh软件和4GB随机访问内存的2.4GHz计算机上大约需要20秒。我们还没有找到其他平滑器的计算时间，但我们可以给出一个粗略的下限。我们看到了表2E–M–GLAM在 $80^{2}$ 在20×20网格上搜索平滑参数的二维网格。在20×20x20网格上搜索以选择平滑参数，GCV计算次数现在增加了20倍。此外，对于每个GCV计算，E–M–GLAM将需要更多的时间来平滑大小为128×128×24的数据，这要大得多。因此，对于计算GCV效率不如三明治平滑器的算法，E–M–GLAM估计器平滑128×128×24数据的计算时间将为数小时。

致谢

这项研究得到了美国国家科学基金会DMS-0805975和美国国立卫生研究院R01-NS060910的部分资助。罗晓的研究得到了国家研究资源中心资助UL1-RR024996的部分支持。李英星的研究得到了国家自然科学基金11201390的部分资助。我们感谢Iain Currie教授对GLAM算法的有益讨论。我们感谢两位审稿人和一位副编辑提出的最有帮助的意见和建议，这些意见和建议极大地改进了本文。我们非常感谢裁判建议使用“三明治平滑剂”这个名字。

工具书类

克莱斯肯斯

，

G.公司。

，

克里沃博科娃

，

T。

和

Opsomer公司

，

J·D·。

(

2009

)

惩罚样条估计的渐近性质

.

生物特征

，

96

，

529

–

544

.

谷歌学者

交叉参考

书目数据库

咖喱

，

身份证号码。

，

德班

，

M。

和

艾尔斯

，

P.H.C.公司。

(

2006

)

广义线性阵列模型及其在多维平滑中的应用

.

J.R.统计。Soc.B公司

，

68

，

259

–

280

.

谷歌学者

交叉参考

书目数据库

迪

，

C、。

，

克拉伊尼恰努

，

C.M.公司。

，

卡福

，

学士学位。

和

旁遮普语

，

N。

(

2009

)

多层次函数主成分分析

.

附录申请。统计师。

，

三

，

458

–

488

.

谷歌学者

交叉参考

书目数据库

迪尔克克斯

，

第页。

(

1982

)

使用样条函数在矩形网格上平滑数据的快速算法

.

SIAM J.数字。分析。

，

19

，

1286

–

1304

.

谷歌学者

交叉参考

书目数据库

迪尔克克斯

，

第页。

(

1995

)

用样条曲线和曲面拟合

.

牛津

:

克拉伦登

.

杜勒特

，

R。

(

2005

)

概率：理论与实例

，第3版。

贝尔蒙特：汤姆森

.

艾尔斯

，

第页。

和

戈曼

，

J。

(

2004

)

使用平滑密度增强散点图

.

生物信息学

，

20

，

623

–

628

.

艾尔斯

，

第页。

和

马克思

，

B。

(

1996

)

使用B样条曲线和惩罚进行灵活平滑（带讨论）

.

统计师。科学。

，

11

，

89

–

121

.

谷歌学者

交叉参考

书目数据库

艾尔斯

，

第页。

和

马克思

，

B。

(

2003

)

基于二维惩罚信号回归的温度相互作用多元校正

.

化学家。智力。实验室系统。

，

66

，

159

–

174

.

谷歌学者

交叉参考

书目数据库

格拉德斯坦

，

一、。

和

雷日克

，

一、。

(

2007

)

积分、级数和乘积表

.

纽约

:

学术出版社

.

格雷文

，

美国。

，

克拉伊尼恰努

，

C、。

，

卡福

，

B。

和

赖希

，

D。

(

2010

)

纵向功能主成分

.

电子。J.统计。

，

4

，

1022

–

1054

.

谷歌学者

交叉参考

书目数据库

顾

，

C、。

(

2002

)

平滑样条方差分析模型

.

纽约

:

施普林格

.

霍尔

，

第页。

，

米勒

，

H。

和

王

，

J。

(

2006

)

用于函数和纵向数据分析的主成分方法的性质

.

安。统计师。

，

34

，

1493

–

1517

.

谷歌学者

OpenURL占位符文本

书目数据库

霍尔

，

第页。

和

运算器

，

J。

(

2005

)

惩罚样条回归理论

.

生物特征

，

92

，

105

–

118

.

谷歌学者

交叉参考

书目数据库

汉森

，

B。

(

2008

)

相依数据核估计的一致收敛速度

.

经济计量学。西奥。

，

24

，

726

–

748

.

谷歌学者

交叉参考

书目数据库

哈斯蒂

，

T。

和

提比什拉尼

，

R。

(

1993

)

变系数模型（含讨论）

.

J.R.统计。Soc.B公司

，

55

，

757

–

796

.

谷歌学者

OpenURL占位符文本

书目数据库

考尔曼

，

G.公司。

，

克里沃博科娃

，

T。

和

法尔迈尔

，

L。

(

2009

)

广义惩罚样条光滑的一些渐近结果

.

J.R.统计。Soc.B公司

，

71

，

487

–

503

.

谷歌学者

交叉参考

书目数据库

锂

，

Y。

和

鲁珀特

，

D。

(

2008

)

关于惩罚样条的渐近性

.

生物特征

，

95

，

415

–

436

.

谷歌学者

交叉参考

书目数据库

马克思

，

B。

和

艾尔斯

，

第页。

(

2005

)

多维惩罚信号回归

.

技术计量学

，

47

，

13

–

22

.

谷歌学者

交叉参考

书目数据库

鲁珀特

，

D。

(

2002

)

为受惩罚的样条线选择节点数

.

J.计算图表。统计师。

，

1

，

735

–

757

.

谷歌学者

OpenURL占位符文本

书目数据库

鲁珀特

，

D。

，

魔杖

，

M。

和

卡罗尔

，

R。

(

2003

)

半参数回归

.

剑桥

:

剑桥大学出版社

.

塞贝尔

，

G.公司。

(

2007

)

统计学家矩阵手册

.

霍博肯

:

威利-国际科学

.

西尔弗曼

，

B。

(

1984

)

样条平滑：等价变量核方法

.

安。统计师。

，

12

，

898

–

916

.

谷歌学者

交叉参考

书目数据库

斯坦尼斯瓦利斯

，

J。

和

李

，

J。

(

1998

)

纵向数据的非参数回归分析

.

美国统计学杂志。助理。

，

93

，

1403

–

1418

.

谷歌学者

交叉参考

书目数据库

石头

，

C、。

(

1980

)

非参数估计的最优收敛速度

.

安。统计师。

，

8

，

1348

–

1360

.

谷歌学者

交叉参考

书目数据库

魔杖

，

M。

和

琼斯

，

M。

(

1995

)

平滑化

.

伦敦

:

查普曼和霍尔

.

王

，

十、。

，

沈

，

J。

和

鲁珀特

，

D。

(

2011

)

广义惩罚样条光滑的一些渐近结果

.

电子。J.统计。

，

4

，

1

–

17

.

谷歌学者

OpenURL占位符文本

书目数据库

木材

，

序号。

(

2003

)

薄板回归样条

.

J.R.统计。Soc.B公司

，

65

，

95

–

114

.

谷歌学者

交叉参考

书目数据库

木材

，

美国。

(

2006

)

广义可加模型：R引言

.

伦敦

:

查普曼和霍尔

.

肖

，

L。

，

锂

，

Y。

，

阿帕纳索维奇

，

T。

和

鲁珀特

，

D。

(

2012

)

P样条的局部渐近性。技术报告

.

康奈尔大学

，

伊萨卡

。（可从http://arxiv.org/abs/1201.0708v3.)

姚明

，

F。

和

李

，

总成本管理。

(

2006

)

函数主成分分析的惩罚样条模型

.

J.R.统计。Soc.B公司

，

68

，

三

–

25

.

谷歌学者

交叉参考

书目数据库

姚明

，

F。

，

米勒

，

H。

和

王

，

J。

(

2005

)

稀疏纵向数据的功能数据分析

.

美国统计学杂志。助理。

，

100

，

577

–

590

.

谷歌学者

交叉参考

书目数据库

齐普尼科夫

，

五、。

，

卡福

，

学士学位。

，

克拉伊尼恰努

，

C.M.公司。

，

尤森

，

D。

，

达瓦特齐科斯

，

C、。

和

施瓦茨

，

B。

(

2011

)

高维数据的多级函数主成分分析

.

J.计算图表。统计师。

，

20

，

852

–

873

.

谷歌学者

交叉参考

书目数据库

附录A：方程推导(11)

首先我们有

‖ \hat{Y（Y）} - Y（Y） ‖_{F类}^{2} = (\hat{年} - 年)^{T型} (\hat{年} - 年) = {\hat{年}}^{T型} \hat{年} - 2 {\hat{年}}^{T型} 年 + 年^{T型} 年 .

可以用公式表示(10)那个

\begin{matrix} {\hat{年}}^{T型} \hat{年} & = {\tilde{年}}^{T型} (Σ_{2} \otimes Σ_{1}) ({A类}_{2} \otimes {A类}_{1})^{T型} ({A类}_{2} \otimes {A类}_{1}) (Σ_{2} \otimes Σ_{1}) \tilde{年} \\ = {\tilde{年}}^{T型} (Σ_{2} \otimes Σ_{1}) (Σ_{2} \otimes Σ_{1}) \tilde{年} \\ = | {\tilde{年}}^{T型} (Σ_{2} \otimes Σ_{1}) |^{2} \\ = {{\tilde{年}}^{T型} ({\tilde{秒}}_{2} \otimes {\tilde{秒}}_{1})}^{2} . \end{matrix}

在这个推导中，|·|表示倒数第二个等式中的欧几里得范数；我们使用的事实是 ${A类}_{我}^{T型} {A类}_{我} = 我_{{c（c）}_{我}}$ 而且两者都是 $Σ_{2}$ 和 $Σ_{1}$ 是对角矩阵。类似地，我们得到

{\hat{年}}^{T型} 年 = {{\tilde{年}}^{T型} ({\tilde{秒}}_{2}^{1 / 2} \otimes {\tilde{秒}}_{1}^{1 / 2})}^{2}

从而建立方程(11).

附录B：定理证明

引理1.单变量核函数 ${H（H）}_{米} (x个)$ 在表达式中定义(14)满足

\int_{- \infty}^{\infty} {x个}^{我} {H（H）}_{米} (x个) d日 x个 = {\begin{matrix} 1 ， & 我 = 0 ， \\ 0 ， & 我 很奇怪 ， \\ 0 ， & 我 是均匀的，并且 2 \leq 我 \leq 2 米 - 2 ， \\ (- 1)^{米 + 1} (2 米)! ， & 我 = 2 米 . \end{matrix}

因此 ${H（H）}_{米} (x个)$ 为2阶米.

证明。我们需要计算两种类型的积分： $\int {x个}^{我} 经验 (斧头) 余弦 (bx公司) d日 x个$ 和 $\int {x个}^{我} 经验 (斧头) 罪 (bx公司) d日 x个$ ⁠这些不定积分由Gradshteyn和Ryzhik第230页的结果3和4给出(2007). 然后进行例行计算，得出预期结果。部分引理在Wang中导出等. (2011). 推导的详细信息可以在Xiao中找到等. (2012).

在证明命题1之前，我们需要以下引理。

引理2.使用与命题1中相同的符号，并假设命题1中的所有条件和假设均已满足。对于(x个，z)∈（0,1）×（0,1），有一个常数C类>0，这样

\hat{μ} (x个 ， z) = \sum_{我 ， j个} 年_{我 ， j个} [{\sum_{κ ， 第页} B_{κ}^{1} (x个) B_{第页}^{1} ({x个}_{我}) {S公司}_{κ ， 第页 ， x个}} \sum_{我 ， 秒} B_{我}^{2} (z) B_{秒}^{2} (z_{j个}) {S公司}_{我 ， 秒 ， z} + {\tilde{b条}}_{我 ， j个} (x个 ， z)] ，

哪里 ${\tilde{b条}}_{我， j个} (x个， z) = O（运行） [经验 {- C类最小值 ({小时}_{n个， 1}^{- 1} ， {小时}_{n个， 2}^{- 1})}]$ ⁠.

证明.通过方程式(8)， $\hat{μ} (x个， z) = Σ {\hat{θ}}_{κ ，我} B_{κ}^{1} (x个) B_{我}^{2} (z)$ ⁠。我们只需要考虑 ${\hat{θ}}_{κ ，我}$ 对于其中 $B_{κ}^{1} (x个)$ 和 $B_{我}^{2} (z)$ 都是非零的。因此假设κ和我满足 $κ \in ({K（K）}_{1} x个 - {第页}_{1} - 1 ， {K（K）}_{1} x个 + {第页}_{1} + 1)$ 和 $我 \in ({K（K）}_{2} z - {第页}_{2} - 1 ， {K（K）}_{2} z + {第页}_{2} + 1)$ ⁠.让 $问_{1} = 最大值 ({第页}_{1} ，米_{1})$ 和 $问_{2} = 最大值 ({第页}_{2} ，米_{2})$ ⁠。表示方式 $Λ_{1 ， j个}$ 这个j个第列，共列 $Λ_{1}$ 和 $Λ_{2 ， j个}$ 这个j个第列，共列 $Λ_{2}$ ⁠.如肖所示等. (2012)李和鲁珀特(2008)，有向量 ${S公司}_{κ ， x个}$ 和一个常数 ${C类}_{三} > 0$ 这样，对于 $问_{1} < j个 < {c（c）}_{1} - 问_{1}$ ⁠， ${S公司}_{κ ， x个}^{T型} Λ_{1 ， j个} = δ_{κ ， j个}$ 和，用于 $1 \leq j个 \leq 问_{1}$ 或 ${c（c）}_{1} - 问_{1} \leq j个 \leq {c（c）}_{1}$ ⁠， ${S公司}_{κ ， x个}^{T型} Λ_{1 ， j个} = O（运行） [经验 {- {C类}_{三} {小时}_{n个， 1}^{- 1} 最小值 (x个， 1 - x个)}]$ ⁠.在这里 $δ_{κ ， j个} = 1$ 如果j个=κ和 $δ_{k个， j个} = 0$ 否则。同样，也有向量 ${S公司}_{我， z}$ 和一个常数 ${C类}_{4} > 0$ 这样，对于 $问_{2} < j个 < {c（c）}_{2} - 问_{2}$ ⁠， ${S公司}_{我， z}^{T型} Λ_{2 ， j个} = δ_{我， j个}$ ⁠、和，用于 $1 \leq j个 \leq 问_{2}$ 或 ${c（c）}_{2} - 问_{2} \leq j个 \leq {c（c）}_{2}$ ⁠， ${S公司}_{我， z}^{T型} Λ_{2 ， j个} = O（运行） [经验 {- {C类}_{4} {小时}_{n个， 2}^{- 1} 最小值 (z ， 1 - z)}]$ ⁠.让 ${\tilde{θ}}_{κ ，我} = ({S公司}_{我， z} \otimes {S公司}_{κ ， x个})^{T型} (Λ_{2} \otimes Λ_{1}) \hat{θ}$ 和 $C类 = 最小值 {{C类}_{三} 最小值 (x个， 1 - x个) ， {C类}_{4} 最小值 (z ， 1 - z)}$ ⁠; 然后

{\tilde{θ}}_{κ ， 我} - {\hat{θ}}_{κ ， 我} = \sum_{我 ， j个} {\tilde{b条}}_{我 ， j个 ， κ ， 我} 年_{我 ， j个} ，

(19)

哪里 ${\tilde{b条}}_{我， j个， κ ，我} = O（运行） [经验 {- C类最小值 ({小时}_{n个， 1}^{- 1} ， {小时}_{n个， 2}^{- 1})}]$ ⁠.通过方程式(7)，

{\tilde{θ}}_{κ ， 我} = ({S公司}_{我 ， z} \otimes {S公司}_{κ ， x个})^{T型} (B_{2}^{T型} \otimes B_{1}^{T型}) 年 = ({S公司}_{我 ， z}^{T型} B_{2}^{T型} \otimes {S公司}_{κ ， x个}^{T型} B_{1}^{T型}) 年 = {S公司}_{κ ， x个}^{T型} (B_{1}^{T型} Y（Y） B_{2}) {S公司}_{我 ， z} .

出租 ${S公司}_{κ ，第页， x个}$ 成为第页的第个元素 ${S公司}_{κ ， x个}$ 和类似的 ${S公司}_{我，秒， z}$ 这个秒的第个元素 ${S公司}_{我， z}$ ⁠，我们快递 ${\tilde{θ}}_{κ ，我}$ 作为双倍总和

{\tilde{θ}}_{κ ， 我} = \sum_{第页 ， 秒} {S公司}_{κ ， 第页 ， x个} {\sum_{我 ， j个} B_{第页}^{1} ({x个}_{我}) 年_{我 ， j个} B_{秒}^{2} (z_{j个})} {S公司}_{我 ， 秒 ， z} = \sum_{我 ， j个} 年_{我 ， j个} {\sum_{第页} B_{第页}^{1} ({x个}_{我}) {S公司}_{κ ， 第页 ， x个}} \sum_{秒} B_{秒}^{2} (z_{j个}) {S公司}_{我 ， 秒 ， z} .

(20)

使用方程式(8)和(19)和(20)，我们有

\begin{matrix} \hat{μ} (x个 ， z) & = \sum_{κ ， 我} {\tilde{θ}}_{κ ， 我} B_{κ}^{1} (x个) B_{我}^{2} (z) + \sum_{κ ， 我} ({\hat{θ}}_{κ ， 我} - {\tilde{θ}}_{κ ， 我}) B_{κ}^{1} (x个) B_{我}^{2} (z) \\ = \sum_{我 ， j个} 年_{我 ， j个} [{\sum_{κ ， 第页} B_{κ}^{1} (x个) B_{第页}^{1} ({x个}_{我}) {S公司}_{κ ， 第页 ， x个}} \sum_{我 ， 秒} B_{我}^{2} (z) B_{秒}^{2} (z_{j个}) {S公司}_{我 ， 秒 ， z} + {\tilde{b条}}_{我 ， j个} (x个 ， z)] ， \end{matrix}

哪里 ${\tilde{b条}}_{我， j个} (x个， z) = O（运行） [经验 {- C类最小值 ({小时}_{n个， 1}^{- 1} ， {小时}_{n个， 2}^{- 1})}]$ ⁠.

B.1、。命题1的证明

让 ${\tilde{λ}}_{1} = λ_{1} {K（K）}_{1} {n个}_{1}^{- 1} = ({K（K）}_{1} {小时}_{n个， 1})^{2 米_{1}}$ 和 ${\tilde{λ}}_{2} = λ_{2} {K（K）}_{2} {n个}_{2}^{- 1} = ({K（K）}_{2} {小时}_{n个， 2})^{2 米_{2}}$ ⁠.根据肖的命题5.1等. (2012)，有一些常量 $0 < ϕ_{1} ， ϕ_{2} < \infty$ 使得

\begin{matrix} {n个}_{1} {小时}_{n个 ， 1} \sum_{k个 ， 第页} B_{k个}^{1} (x个) B_{第页}^{1} ({x个}_{我}) {S公司}_{k个 ， 第页 ， x个} & = {H（H）}_{米_{1}} (\frac{| x个 - {x个}_{我} |}{{小时}_{n个 ， 1}}) + δ_{{{第页}_{1} > 米_{1}}} {O（运行） ({\tilde{λ}}_{1}^{- 2 + 1 / 2 米_{1}}) + δ_{{| x个 - {x个}_{我} | < ϕ_{1} / {K（K）}_{1}}} O（运行） ({\tilde{λ}}_{1}^{- {第页}_{1} / ({第页}_{1} - 米_{1}) + 1 / 2 米_{1}})} \\ + 经验 (- ϕ_{2} \frac{| x个 - {x个}_{我} |}{{小时}_{n个 ， 1}}) {O（运行） ({\tilde{λ}}_{1}^{- 1 / 米_{1}}) + \end{matrix}

(21)

在这里 $δ_{{{第页}_{1} > 米_{1}}} = 1$ 如果 ${第页}_{1} > 米_{1}$ 和 $δ_{{{第页}_{1} > 米_{1}}} = 0$ 否则；其他的δ-术语的定义类似。同样，也有一些常量 $0 < ϕ_{三} ， ϕ_{4} < \infty$ 使得

\begin{matrix} {n个}_{2} {小时}_{n个 ， 2} \sum_{我 ， 秒} B_{我}^{2} (z) B_{秒}^{2} (z_{j个}) {S公司}_{我 ， 秒 ， z} = {H（H）}_{米_{2}} (\frac{|z - z_{j个}|}{{小时}_{n个 ， 2}}) + δ_{\{{第页}_{2} > 米_{2}\}} \{O（运行） ({\tilde{λ}}_{2}^{- 2 + 1 / 2 米_{2}}) \\ + δ_{\{|z - z_{j个}| < ϕ_{三} / {K（K）}_{2}\}} O（运行） ({\tilde{λ}}_{2}^{- {第页}_{2} / ({第页}_{2} - 米_{2}) + 1 / 2 米_{2}})\} + 经验 (- ϕ_{4} \frac{|z - z_{j个}|}{{小时}_{n个 ， 2}}) \{O（运行） ({\tilde{λ}}_{2}^{- 1 / 米_{2}}) \\ + δ_{\{米_{2} = 1\}} δ_{\{|z - z_{j个}| ⩽ ({第页}_{2} + 1) {\tilde{λ}}_{2}^{- 1 / 2 米_{2}}\}} O（运行） ({\tilde{λ}}_{2}^{- 1 / 2 米_{2}})\} . \end{matrix}

(22)

让

\begin{matrix} {d日}_{我 ， 1} = \sum_{k个 ， 第页} B_{k个}^{1} (x个) B_{第页}^{1} ({x个}_{我}) {S公司}_{k个 ， 第页 ， x个} - ({n个}_{1} {小时}_{n个 ， 1})^{- 1} {H（H）}_{米_{1}} {{小时}_{n个 ， 1}^{- 1} (x个 - {x个}_{我})} ， \end{matrix}

\begin{matrix} {d日}_{我 ， 2} = \sum_{我 ， 秒} B_{我}^{2} (z) B_{秒}^{2} (z_{j个}) {S公司}_{我 ， 秒 ， z} - ({n个}_{2} {小时}_{n个 ， 2})^{- 1} {H（H）}_{米_{2}} {{小时}_{n个 ， 2}^{- 1} (z - z_{j个})} ， \end{matrix}

\begin{matrix} {b条}_{我 ， j个} (x个 ， z) = \frac{1}{{n个}_{1} {小时}_{n个 ， 1}} {H（H）}_{米_{1}} (\frac{| x个 - {x个}_{我} |}{{小时}_{n个 ， 1}}) {d日}_{我 ， 2} + \frac{1}{{n个}_{2} {小时}_{n个 ， 2}} {H（H）}_{米_{2}} (\frac{| z - z_{j个} |}{{小时}_{n个 ， 2}}) {d日}_{我 ， 2} + {d日}_{我 ， 1} {d日}_{我 ， 2} + {\tilde{b条}}_{我 ， j个} (x个 ， z) . \end{matrix}

从引理2可以得出 $\hat{μ} (x个， z) - μ^{*} (x个， z) = Σ_{我， j个} {b条}_{我， j个} (x个， z) 年_{我， j个}$ ⁠.因此 $E类 {\hat{μ} (x个， z) - μ^{*} (x个， z)} = Σ_{我， j个} {b条}_{我， j个} (x个， z) μ ({x个}_{我} ， z_{j个})$ 和 $无功功率，无功功率 {\hat{μ} (x个， z) - μ^{*} (x个， z)} = Σ_{我， j个} {b条}_{我， j个}^{2} (x个， z) σ^{2} ({x个}_{我} ， z_{j个})$ ⁠.

为了简化符号，表示 $最大值 {({K（K）}_{1} {小时}_{n个， 1})^{- 2} ， ({K（K）}_{2} {小时}_{n个， 2})^{- 2}}$ 通过ξ.我们证明了这一点 $E类 {\hat{μ} (x个， z) - μ^{*} (x个， z)} = O（运行） (ξ)$ 通过展示 $Σ_{我， j个} | {b条}_{我， j个} (x个， z) μ ({x个}_{我} ， z_{j个}) |$ 是O（运行）(ξ). 根据引理2， ${\tilde{b条}}_{我， j个} (x个， z) = O（运行） [经验 {- C类最小值 ({小时}_{n个， 1}^{- 1} ， {小时}_{n个， 2}^{- 1})}]$ ⁠.自 ${小时}_{n个， 1} = O（运行） ({n个}^{- ν_{1}})$ 和 ${小时}_{n个， 2} = O（运行） ({n个}^{- ν_{2}})$ ⁠， ${\tilde{b条}}_{我， j个} (x个， z) = {n个}^{- 1} o个 (ξ)$ 因此 $Σ_{我， j个} | {\tilde{b条}}_{我， j个} (x个， z) μ ({x个}_{我} ， z_{j个}) | = o个 (ξ) .$ 为了简单起见，我们只展示

\sum_{我 ， j个} | \frac{1}{{n个}_{1} {小时}_{n个 ， 1}} {H（H）}_{米_{1}} (\frac{| x个 - {x个}_{我} |}{{小时}_{n个 ， 1}}) {d日}_{我 ， 2} μ ({x个}_{我} ， z_{j个}) | = O（运行） (ξ) ，

(23)

我们在以下情况下使用案例 ${第页}_{2} \leq 米_{2}$ 作为一个例子。因为

\begin{matrix} \frac{1}{{nh型}_{n个}} \sum_{我 ， j个} | {H（H）}_{米_{1}} (\frac{| x个 - {x个}_{我} |}{{小时}_{n个 ， 1}}) 经验 (- ϕ_{4} \frac{| z - z_{j个} |}{{小时}_{n个 ， 2}}) μ ({x个}_{我} ， z_{j个}) | = O（运行） (1) ， \end{matrix}

\begin{matrix} \frac{1}{{nh型}_{n个}} \sum_{我 ， j个} | {H（H）}_{米_{1}} (\frac{| x个 - {x个}_{我} |}{{小时}_{n个 ， 1}}) 经验 (- ϕ_{4} \frac{| z - z_{j个} |}{{小时}_{n个 ， 2}}) δ_{{| z - z_{j个} | \leq ({第页}_{2} + 1) {\tilde{λ}}_{2}^{- 1 / 2 米_{2}}}} μ ({x个}_{我} ， z_{j个}) | = O（运行） ({\tilde{λ}}_{2}^{- 1 / 2 米_{2}}) ， \end{matrix}

和 ${\tilde{λ}}_{2}^{- 1 / 米_{2}} = ({K（K）}_{2} {小时}_{n个， 2})^{- 2}$ ⁠，平等(23)已被证明。情况发生时 ${第页}_{2} > 米_{2}$ 以及期望的结果，包括 ${d日}_{我， 1}$ 可以得到类似的证明。

接下来我们展示一下 $无功功率，无功功率 {\hat{μ} (x个， z) - μ^{*} (x个， z)} = o个 {({nh型}_{n个})^{- 1}}$ ⁠，即。 $Σ_{我， j个} {b条}_{我， j个}^{2} (x个， z) σ^{2} ({x个}_{我} ， z_{j个}) = o个 {({nh型}_{n个})^{- 1}}$ ⁠。请注意 ${b条}_{我， j个}^{2} (x个， z) σ^{2} ({x个}_{我} ， z_{j个})$ 可以扩展为单个术语的总和。与之前的分析类似 ${b条}_{我， j个}^{2} (x个， z) σ^{2} ({x个}_{我} ， z_{j个})$ ⁠，双倍总和我，j个是其中之一 $O（运行） {({nh型}_{n个})^{- 1} {\tilde{λ}}_{1}^{- 2 / 米_{1}}}$ 或 $O（运行） {({nh型}_{n个})^{- 1} {\tilde{λ}}_{2}^{- 2 / 米_{2}}}$ ⁠、或的顺序较小。

B.2节。定理1的证明

命题1表明三明治平滑器渐近等价于具有乘积核的核回归估计量 ${H（H）}_{米_{1}} (x个) {H（H）}_{米_{2}} (z)$ ⁠为了确定核估计量的渐近偏差和方差，我们对多元核密度估计量进行了类似于Wand和Jones中的分析(1995). 根据命题1，

E类 {\hat{μ} (x个 ， z)} = \frac{1}{{nh型}_{n个 ， 1} {小时}_{n个 ， 2}} \sum_{我 ， j个} μ ({x个}_{我} ， z_{j个}) {H（H）}_{米_{1}} (\frac{x个 - {x个}_{我}}{{小时}_{n个 ， 1}}) {H（H）}_{米_{2}} (\frac{z - z_{j个}}{{小时}_{n个 ， 2}}) + O（运行） (ξ) ，

(24)

我们继续使用符号 $ξ = 最大值 {({K（K）}_{1} {小时}_{n个， 1})^{- 2} ， ({K（K）}_{2} {小时}_{n个， 2})^{- 2}}$ ⁠.让

E类 {\hat{μ} (x个 ， z)} = \frac{1}{{nh型}_{n个 ， 1} {小时}_{n个 ， 2}} \sum_{我 ， j个} μ ({x个}_{我} ， z_{j个}) {H（H）}_{米_{1}} (\frac{x个 - {x个}_{我}}{{小时}_{n个 ， 1}}) {H（H）}_{米_{2}} (\frac{z - z_{j个}}{{小时}_{n个 ， 2}}) + O（运行） (ξ) ，

（25）

方程式右侧的第一项（25）是的Riemann有限和 $({小时}_{n个， 1} {小时}_{n个， 2})^{- 1} μ (u个， v（v）) \times$ ${H（H）}_{米_{1}} {{小时}_{n个， 1}^{- 1} (x个 - u个)} {H（H）}_{米_{2}} {{小时}_{n个， 2}^{- 1} (z - v（v）)}$ 在网格上，而第二项是相同函数的积分，以及 $μ_{0} (x个， z)$ 计算这两个术语之间的差异。 $μ_{0} (x个， z)$ 不是随机的，下面的引理4表明 $μ_{0} (x个， z) = O（运行） {最大值 ({n个}_{1}^{- 2} {小时}_{n个， 1}^{- 2} ， {n个}_{2}^{- 2} {小时}_{n个， 2}^{- 2})}$ ⁠.现在等式(24)成为

\begin{matrix} E类 {\hat{μ} (x个 ， z)} = \frac{1}{{小时}_{n个 ， 1} {小时}_{n个 ， 2}} \iint μ (u个 ， v（v）) {H（H）}_{米_{1}} (\frac{x个 - u个}{{小时}_{n个 ， 1}}) {H（H）}_{米_{2}} (\frac{z - v（v）}{{小时}_{n个 ， 2}}) d日 u个 d日 v（v） + μ_{0} (x个 ， z) + O（运行） (ξ) \\ = \iint μ (x个 - {小时}_{n个 ， 1} u个 ， z - {小时}_{n个 ， 2} v（v）) {H（H）}_{米_{1}} (u个) {H（H）}_{米_{2}} (v（v）) d日 u个 d日 v（v） + μ_{0} (x个 ， z) + O（运行） (ξ) . \end{matrix}

(26)

对于方程中的二重积分(26)，我们首先采用泰勒级数展开 $μ (x个 - {小时}_{{n个}_{1}} u个， z - {小时}_{{n个}_{2}} v（v）)$ 在(x个，z)直到 $2 米_{1}$ 关于的th偏导数x个和 $2 米_{2}$ 关于的th偏导数z然后我们抵消那些被引理1消失的积分。由此可以得到渐近平均值的显式表达式：

\begin{matrix} E类 {\hat{μ} (x个 ， z)} - μ (x个 ， z) - μ_{0} (x个 ， z) & = (- 1)^{米_{1} + 1} {小时}_{n个 ， 1}^{2 米_{1}} \frac{\partial^{2 米_{1}}}{\partial {x个}^{2 米_{1}}} μ (x个 ， z) + (- 1)^{米_{2} + 1} {小时}_{n个 ， 2}^{2 米_{2}} \frac{\partial^{2 米_{2}}}{\partial z^{2 米_{2}}} μ (x个 ， z) + o个 ({小时}_{n个 ， 1}^{2 米_{1}}) \\ + o个 ({小时}_{n个 ， 2}^{2 米_{2}}) + O（运行） (ξ) . \end{matrix}

对于任意两个随机变量X（X）和Y（Y），如果var(Y（Y）) =o个{变量(X（X）)}，然后是var(X（X）+Y（Y）)=变量(X（X）)+o个{变量(X（X）)}. 因此，通过让 $X（X） = μ^{*} (x个， z)$ 和 $Y（Y） = \hat{μ} (x个， z) - μ^{*} (x个， z)$ ⁠，我们可以通过命题1得到

\begin{matrix} 无功功率，无功功率 {\hat{μ} (x个 ， z)} = ({nh型}_{n个})^{- 1} σ^{2} (x个 ， z) \int {H（H）}_{米_{1}}^{2} (u个) d日 u个 \int {H（H）}_{米_{2}}^{2} (v（v）) d日 v（v） + o个 {({nh型}_{n个})^{- 1}} . \end{matrix}

为了获得最佳收敛速度，让 ${小时}_{n个， 1}^{2 米_{1}} / {小时}_{n个， 2}^{2 米_{2}}$ 和 ${小时}_{n个， 1}^{4 米_{1}} / ({nh型}_{n个})^{- 1}$ 收敛到一些常数。然后我们有

{小时}_{n个 ， 1} ˜ {小时}_{1} {n个}^{- 米_{2} / 米_{三}} ，

{小时}_{n个 ， 2} ˜ {小时}_{2} {n个}^{- 米_{1} / 米_{三}}

对于一些正常数 ${小时}_{1}$ 和 ${小时}_{2}$ ⁠（回忆一下 $米_{三} = 4 米_{1} 米_{2} + 米_{1} + 米_{2}$ ⁠.）我们需要选择 ${K（K）}_{1}$ 和 ${K（K）}_{2}$ 以便 $最大值 {({K（K）}_{1} {小时}_{n个， 1})^{- 2} ， ({K（K）}_{2} {小时}_{n个， 2})^{- 2}} = o个 ({小时}_{n个， 1}^{2 米_{1}})$ ⁠因此， ${K（K）}_{1} ˜ {C类}_{1} {n个}^{τ_{1}}$ 对于某些正常数 ${C类}_{1}$ 和 $τ_{1} > (米_{1} 米_{2} + 米_{2}) / 米_{三}$ ⁠同样， ${K（K）}_{2} ˜ {C类}_{2} {n个}^{τ_{2}}$ 对于某些正常数 ${C类}_{2}$ 和 $τ_{2} > (米_{1} 米_{2} + 米_{1}) / 米_{三}$ ⁠。很容易验证 $最大值 ({n个}_{1}^{- 2} {小时}_{n个， 1}^{- 2} ， {n个}_{2}^{- 2} {小时}_{n个， 2}^{- 2}) = o个 ({小时}_{n个， 1}^{2 米_{1}})$ ⁠.

引理3.让G公司(x个)是[0,1]中具有连续二阶导数的实函数。让 ${x个}_{我} = (我 - \frac{1}{2}) / n个$ 对于我= 1,…,n个.假设小时=o个（1）以及 $({nh型}^{2})^{- 1} = o个 (1)$ 作为n个→∞. 然后

| \frac{1}{小时} \int_{0}^{1} {H（H）}_{米} (\frac{x个 - u个}{小时}) G公司 (u个) d日 u个 - \frac{1}{nh型} \sum_{我 = 1}^{n个} {H（H）}_{米} (\frac{x个 - {x个}_{我}}{小时}) G公司 ({x个}_{我}) | = O（运行） ({n个}^{- 2} {小时}^{- 2}) ，

哪里 ${H（H）}_{米} (x个)$ 在表达式中定义(14).

证明首先要注意 ${H（H）}_{米} (x个)$ 对称且以1为界。阿尔索 ${H（H）}_{米} (x个)$ 在（−∞，0]上是无穷可微的，并且所有导数都有界米超过（-∞，0]。让 ${L（左）}_{我} = [(我 - 1) / n个，我 / n个]$ 对于我= 1,…,n个.假设在不失一般性的情况下 $\underset{u个 \in [0 ， 1]}{最大值} | G公司 (u个) | \leq 米$ ⁠.我们有

| \frac{1}{小时} \int_{0}^{1} {H（H）}_{米} (\frac{x个 - u个}{小时}) G公司 (u个) d日 u个 - \frac{1}{nh型} \sum_{我 = 1}^{n个} {H（H）}_{米} (\frac{x个 - {x个}_{我}}{小时}) G公司 ({x个}_{我}) | = O（运行） ({n个}^{- 2} {小时}^{- 2}) ，

(27)

和

| G公司 (u个) - G公司 ({x个}_{我}) - (u个 - {x个}_{我}) \frac{\partial G公司}{\partial x个} ({x个}_{我}) | \leq \frac{1}{2} (u个 - {x个}_{我})^{2} \underset{0 \leq x个 \leq 1}{最大值} | \frac{\partial^{2} G公司}{\partial {x个}^{2}} (x个) |

(28)

在不等式的推导中(28)，术语 $O（运行） ({n个}^{- 三} {小时}^{- 1})$ 以下为

| G公司 (u个) - G公司 ({x个}_{我}) - (u个 - {x个}_{我}) \frac{\partial G公司}{\partial x个} ({x个}_{我}) | \leq \frac{1}{2} (u个 - {x个}_{我})^{2} \underset{0 \leq x个 \leq 1}{最大值} | \frac{\partial^{2} G公司}{\partial {x个}^{2}} (x个) |

和

| \int_{{L（左）}_{我}} {G公司 (u个) - G公司 ({x个}_{我})} d日 u个 | = | \int_{{L（左）}_{我}} {G公司 (u个) - G公司 ({x个}_{我}) - (u个 - {x个}_{我}) \frac{\partial G公司}{\partial x个} ({x个}_{我})} d日 u个 |;

术语 $O（运行） ({n个}^{- 三} {小时}^{- 2})$ 来自

| \frac{1}{小时} {{H（H）}_{米} (\frac{x个 - u个}{小时}) - {H（H）}_{米} (\frac{x个 - {x个}_{我}}{小时})} {G公司 (u个) - G公司 ({x个}_{我})} | = O（运行） ({n个}^{- 2} {小时}^{- 2})

自从 $| u个 - {x个}_{我} | \leq {n个}^{- 1}$ 当两者同时存在时u个和 ${x个}_{我}$ 在中 ${L（左）}_{我}$ ⁠注意，我们使用了等式 $\int_{{L（左）}_{我}} (u个 - {x个}_{我}) d日 u个 = 0$ 在上面的推导中，我们稍后也将使用它。组合不等式(27)和(28)，我们有

| \frac{1}{小时} {{H（H）}_{米} (\frac{x个 - u个}{小时}) - {H（H）}_{米} (\frac{x个 - {x个}_{我}}{小时})} {G公司 (u个) - G公司 ({x个}_{我})} | = O（运行） ({n个}^{- 2} {小时}^{- 2})

(29)

为了简单起见，用表示 ${H（H）}_{米}^{(1)} (x个)$ 和 ${H（H）}_{米}^{(2)} (x个)$ 的一阶和二阶导数 ${H（H）}_{米} (x个)$ 分别是。类似地，表示为 ${H（H）}_{米}^{(1)} (0)$ 和 ${H（H）}_{米}^{(2)} (0)$ 的右导数 ${H（H）}_{米} (x个)$ 位于0。如果 $x个 \in {L（左）}_{我}$ ⁠，然后 ${H（H）}_{米} {{小时}^{- 1} (x个 - u个)} - {H（H）}_{米} {{小时}^{- 1} (x个 - {x个}_{我})} = O（运行） ({n个}^{- 1} {小时}^{- 1})$ 因此

| \frac{1}{小时} \int_{{L（左）}_{我}} {{H（H）}_{米} (\frac{x个 - u个}{小时}) - {H（H）}_{米} (\frac{x个 - {x个}_{我}}{小时})} d日 u个 | = O（运行） ({n个}^{- 2} {小时}^{- 2}) ， 如果 x个 \in {L（左）}_{我} .

(30)

如果x个<(我−1)/n个，然后 $x个 \notin {L（左）}_{我}$ ⁠.让

{\tilde{H（H）}}_{米} (u个 ， {x个}_{我} ， x个 ， 小时) = {H（H）}_{米} (\frac{x个 - u个}{小时}) - {H（H）}_{米} (\frac{x个 - {x个}_{我}}{小时}) - \frac{u个 - {x个}_{我}}{小时} {H（H）}_{米}^{(1)} (\frac{x个 - {x个}_{我}}{小时}) - \frac{(u个 - {x个}_{我})^{2}}{2 {小时}^{2}} {H（H）}_{米}^{(2)} (\frac{x个 - {x个}_{我}}{小时}) .

然后 ${\tilde{H（H）}}_{米} (u个， {x个}_{我} ， x个，小时) = O（运行） ({小时}^{- 三} | u个 - {x个}_{我} |^{三})$ ⁠.我们有

\begin{matrix} | \frac{1}{小时} \int_{{L（左）}_{我}} {{H（H）}_{米} (\frac{x个 - u个}{小时}) - {H（H）}_{米} (\frac{x个 - {x个}_{我}}{小时})} d日 u个 | \\ = | \frac{1}{小时} \int_{{L（左）}_{我}} {{H（H）}_{米} (\frac{x个 - u个}{小时}) - {H（H）}_{米} (\frac{x个 - {x个}_{我}}{小时}) - \frac{u个 - {x个}_{我}}{小时} {H（H）}_{米}^{(1)} (\frac{x个 - {x个}_{我}}{小时})} d日 u个 | \\ \leq | \frac{1}{小时} \int_{{L（左）}_{我}} \frac{{(u个 - {x个}_{我})}^{2}}{2 {小时}^{2}} {H（H）}_{米}^{(2)} (\frac{x个 - {x个}_{我}}{小时}) d日 u个 | + | \frac{1}{小时} \int_{{L（左）}_{我}} {\tilde{H（H）}}_{米} (u个 ， {x个}_{我} ， x个 ， 小时) d日 u个 | \\ \leq \frac{1}{2 {n个}^{2} {小时}^{2}} \int_{{L（左）}_{我}} \frac{1}{小时} | {H（H）}_{米}^{(2)} (\frac{x个 - {x个}_{我}}{小时}) | d日 u个 + O（运行） ({n个}^{- 4} {小时}^{- 4}) . \end{matrix}

(31)

我们同样可以证明不等式(31)在以下情况下保持x个>我/n个现在，有了不平等(30)和(31)，

\begin{matrix} \sum_{我 = 1}^{n个} | \frac{1}{小时} \int_{{L（左）}_{我}} {{H（H）}_{米} (\frac{x个 - u个}{小时}) - {H（H）}_{米} (\frac{x个 - {x个}_{我}}{小时})} d日 u个 | \\ \leq \frac{1}{2 {n个}^{2} {小时}^{2}} \int_{0}^{1} \frac{1}{小时} | {H（H）}_{米}^{(2)} (\frac{x个 - {x个}_{我}}{小时}) | d日 u个 + O（运行） ({n个}^{- 三} {小时}^{- 4}) + O（运行） ({n个}^{- 2} {小时}^{- 2}) ， \end{matrix}

完成了引理。

引理4.术语 $μ_{0} (x个， z)$ 在方程式中定义（25）是 $O（运行） {最大值 ({n个}_{1}^{- 2} {小时}_{n个， 1}^{- 2} ， {n个}_{2}^{- 2} {小时}_{n个， 2}^{- 2})}$ ⁠.

证明。为了简化符号，让

{G公司}_{2} (u个 ， z) = {小时}_{n个 ， 2}^{- 1} \int_{0}^{1} {H（H）}_{米_{2}} {{小时}_{n个 ， 2}^{- 1} (z - v（v）)} μ (u个 ， v（v）) d日 v（v）

和

{G公司}_{1} (u个 ， z) = ({n个}_{2} {小时}_{n个 ， 2})^{- 1} \sum_{j个} {H（H）}_{米_{2}} {{小时}_{n个 ， 2}^{- 1} (z - z_{j个})} μ (u个 ， z_{j个}) - {G公司}_{2} (u个 ， z) .

然后 ${G公司}_{1}$ 是 $O（运行） ({n个}_{2}^{- 2} {小时}_{n个， 2}^{- 2})$ 通过引理3。请注意 $| μ_{0} (x个， z) |$ 由以下项之和限定

| \frac{1}{{n个}_{1} {小时}_{n个 ， 1}} \sum_{我} {H（H）}_{米_{1}} (\frac{x个 - {x个}_{我}}{{小时}_{n个 ， 1}}) {G公司}_{1} ({x个}_{我} ， z) |

（32）

和

| \frac{1}{{n个}_{1} {小时}_{n个 ， 1}} \sum_{j个} {H（H）}_{米_{1}} (\frac{x个 - {x个}_{我}}{{小时}_{n个 ， 1}}) {G公司}_{2} ({x个}_{我} ， z) - \frac{1}{{小时}_{n个 ， 1}} \int {H（H）}_{米_{1}} (\frac{x个 - u个}{{小时}_{n个 ， 1}}) {G公司}_{2} (u个 ， z) d日 u个 | .

(33)

因为 ${G公司}_{1}$ 是 $O（运行） ({n个}_{2}^{- 2} {小时}_{n个， 2}^{- 2})$ ⁠，表达式（32）也是 $O（运行） ({n个}_{2}^{- 2} {小时}_{n个， 2}^{- 2})$ ⁠.根据Durrett附录中的定理9.1(2005), $\partial^{2} {G公司}_{2} / \partial {u个}^{2}$ 存在并且等于 ${小时}_{n个， 2}^{- 1} \int_{0}^{1} {H（H）}_{米_{2}} {{小时}_{n个， 2}^{- 1} (z - v（v）)} \partial^{2} μ (u个， v（v）) / \partial {u个}^{2} d日 v（v）$ ⁠.因此 $\partial^{2} {G公司}_{2} / \partial {u个}^{2}$ 连续且有界。引理3表示(33)是 $O（运行） ({n个}_{1}^{- 2} {小时}_{n个， 1}^{- 2})$ ⁠，这就完成了我们的证明。

B.3节。定理2的证明

表示设计要点 ${{x个}_{我} ， z_{我}}_{我 = 1}^{n个}$ 由(x个，z). 引理2和命题1的证明在装箱数据中的应用 $\tilde{Y（Y）}$ 具有 ${n个}_{1}$ 和 ${n个}_{2}$ 替换为 $我_{1}$ 和 $我_{2}$ ⁠，我们获得

E类 {\hat{μ} (x个 ， z) | (x个 ， z)} = ({I小时}_{n个})^{- 1} \sum_{κ ， 我} E类 {{\tilde{年}}_{κ ， 我} | (x个 ， z)} {G公司}_{κ ， 我} ，

(34)

无功功率，无功功率 {\hat{μ} (x个 ， z) | (x个 ， z)} = ({I小时}_{n个})^{- 2} \sum_{κ ， 我} 无功功率，无功功率 {{\tilde{年}}_{κ ， 我} | (x个 ， z)} {G公司}_{κ ， 我}^{2} ，

(35)

哪里

{G公司}_{κ ， 我} = {H（H）}_{米_{1}} (\frac{x个 - {\tilde{x个}}_{κ}}{{小时}_{n个 ， 1}}) {H（H）}_{米_{2}} (\frac{z - {\tilde{z}}_{我}}{{小时}_{n个 ， 2}}) + {b条}_{κ ， 我} (x个 ， z) ，

和 ${b条}_{κ ，我} (x个， z)$ 定义类似于 ${b条}_{我， j个} (x个， z)$ 在命题1的证明中 ${n个}_{1}$ 和 ${n个}_{2}$ 替换为 $我_{1}$ 和 $我_{2}$ ⁠.让 ${n个}_{κ ，我}$ 是中的数据点数量(κ，我)第个箱子。然后

无功功率，无功功率 {{\tilde{年}}_{κ ， 我} | (x个 ， z)} = {n个}_{κ ， 我}^{- 2} \sum_{我 = 1}^{n个} σ^{2} ({x个}_{我} ， z_{我}) δ_{{| {x个}_{我} - {\tilde{x个}}_{κ} | \leq (2 我_{1})^{- 1} ， | z_{我} - {\tilde{z}}_{我} | \leq (2 我_{2})^{- 1}}} .

所以 $无功功率，无功功率 {{\tilde{年}}_{κ ，我} | (x个， z) \sqrt {n个}_{κ ，我}}$ 是条件方差函数的Nadaraya–Watson核回归估计量 $σ^{2} (x个， z)$ 在 $({\tilde{x个}}_{κ} ， {\tilde{z}}_{我})$ ⁠类似地，我们可以证明 ${n个}_{κ ，我} / (镍^{- 1})$ 是的核密度估计器（f）(x个，z)在 $({\tilde{x个}}_{κ} ， {\tilde{z}}_{我})$ ⁠根据核密度估计量和Nadaraya–Watson核回归估计量的一致收敛理论（例如，参见Hansen(2008)),

\underset{κ ， 我}{啜饮} | {n个}_{κ ， 我} / ({新国际}^{- 1}) - （f） ({\tilde{x个}}_{κ} ， {\tilde{z}}_{我}) | = {O（运行）}_{第页} [\sqrt {我 自然对数 (n个) / n个} + 我^{- 2}] = {o个}_{第页} (1) ，

(36)

和

\underset{κ ， 我}{啜饮} | 无功功率，无功功率 {{\tilde{年}}_{κ ， 我} | (x个 ， z) \sqrt {n个}_{κ ， 我}} - σ^{2} ({\tilde{x个}}_{κ} ， {\tilde{z}}_{我}) | = {O（运行）}_{第页} [\sqrt {我 自然对数 (n个) / n个} + 我^{- 2}] = {o个}_{第页} (1) .

根据以上两个等式

\underset{κ ， 我}{啜饮} | \frac{n个}{我} 无功功率，无功功率 {{\tilde{年}}_{κ ， 我} | (x个 ， z)} - \frac{σ^{2} ({\tilde{x个}}_{κ} ， {\tilde{z}}_{我})}{（f） ({\tilde{x个}}_{κ} ， {\tilde{z}}_{我})} | = {o个}_{第页} (1) .

(37)

对于任何连续函数，通过与命题1的证明类似的论点克(x个，z)超过 $[0 ， 1]^{2}$ ⁠，我们可以推导出

\frac{1}{我 {小时}_{n个}} \sum_{κ ， 我} 克 ({\tilde{x个}}_{κ} ， {\tilde{z}}_{我}) {G公司}_{κ ， 我}^{2} = 克 (x个 ， z) \int {H（H）}_{米_{1}}^{2} (u个) d日 u个 \int {H（H）}_{米_{2}}^{2} (v（v）) d日 v（v） + o个 (1) .

(38)

然后，通过等式(35)和(37)，

| 无功功率，无功功率 {\hat{μ} (x个 ， z) | (x个 ， z)} - \frac{1}{{nh型}_{n个} {I小时}_{n个}} \sum_{κ ， 我} \frac{σ^{2} ({\tilde{x个}}_{κ} ， {\tilde{z}}_{我})}{（f） ({\tilde{x个}}_{κ} ， {\tilde{z}}_{我})} {G公司}_{κ ， 我}^{2} | = \frac{{o个}_{第页} (1)}{{nh型}_{n个} {I小时}_{n个}} \sum_{κ ， 我} {G公司}_{κ ， 我}^{2} = {o个}_{第页} {({nh型}_{n个})^{- 1}} .

(39)

通过出租 $克 (x个， z) = σ^{2} (x个， z) / （f） (x个， z)$ 在方程式中(38)，我们从方程中导出(39)那个

无功功率，无功功率 {\hat{μ} (x个 ， z) | (x个 ， z)} = \frac{1}{{nh型}_{n个}} \frac{五 (x个 ， z)}{（f） (x个 ， z)} + {o个}_{第页} {({nh型}_{n个})^{- 1}} ，

（40）

哪里五(x个，z)在方程式中定义(17).我们可以写 $E类 {{\tilde{年}}_{κ ，我} | (x个， z)}$ 作为

E类 {{\tilde{年}}_{κ ， 我} | (x个 ， z)} = ({n个}_{κ ， 我})^{- 1} \sum_{我 = 1}^{n个} μ ({x个}_{我} ， z_{我}) δ_{{| {x个}_{我} - {\tilde{x个}}_{κ} | \leq (2 我_{1})^{- 1} ， | z_{我} - {\tilde{z}}_{我} | \leq (2 我_{2})^{- 1}}} .

平等(36)意味着每个箱子都是非空的，所以通过泰勒级数展开 $μ ({x个}_{我} ， z_{j个})$ 在 $({\tilde{x个}}_{κ} ， {\tilde{z}}_{我})$ 我们从上面的方程中得出

\underset{κ ， 我}{啜饮} | E类 {{\tilde{年}}_{κ ， 我} | (x个 ， z)} - μ ({\tilde{x个}}_{κ} ， {\tilde{z}}_{我}) | = {O（运行）}_{第页} (我^{- 1 / 2}) .

其次是平等(34)那个

\begin{matrix} | E类 {\hat{μ} (x个 ， z) | (x个 ， z)} - \frac{1}{{I小时}_{n个}} \sum_{κ ， 我} μ ({\tilde{x个}}_{κ} ， {\tilde{z}}_{我}) {G公司}_{κ ， 我} | = {O（运行）}_{第页} (我^{- 1 / 2}) \frac{1}{{I小时}_{n个}} \sum_{κ ， 我} | {G公司}_{κ ， 我} | = {O（运行）}_{第页} (我^{- 1 / 2}) . \end{matrix}

（41）

很容易证明

\frac{1}{{I小时}_{n个}} \sum_{κ ， 我} μ ({\tilde{x个}}_{κ} ， {\tilde{z}}_{我}) {G公司}_{κ ， 我} = μ (x个 ， z) + {n个}^{- 2 米_{1} \times 2 米_{2} / 米_{三}} \tilde{μ} (x个 ， z) + o个 ({n个}^{- 2 米_{1} \times 2 米_{2} / 米_{三}}) ，

哪里 $\tilde{μ} (x个， z)$ 在方程式中定义(16).根据平等原则（41）假设 $我 ˜ {c（c）}_{我} {n个}^{τ}$ 具有 $τ > 4 米_{1} 米_{2} / 米_{三}$ ⁠，

E类 {\hat{μ} (x个 ， z) | (x个 ， z)} = μ (x个 ， z) + {n个}^{- 2 米_{1} \times 2 米_{2} / 米_{三}} \tilde{μ} (x个 ， z) + {o个}_{第页} ({n个}^{- 2 米_{1} \times 2 米_{2} / 米_{三}}) .

(42)

使用方程式（40）和(42)，我们可以证明

{n个}^{2 米_{1} \times 2 米_{2} / 米_{三}} [\hat{μ} (x个 ， z) - E类 {\hat{μ} (x个 ， z) | (x个 ， z)}] \Rightarrow N个 {0 ， 五 (x个 ， z) / （f） (x个 ， z)}

(43)

分配和

{n个}^{2 米_{1} \times 2 米_{2} / 米_{三}} [E类 {\hat{μ} (x个 ， z) | (x个 ， z)} - μ (x个 ， z)] = \tilde{μ} (x个 ， z) + {o个}_{第页} (1) .

(44)

平等(43)和(44)一起证明定理2。

本文根据牛津大学出版社标准期刊出版模式的条款出版和发行(https://academic.oup.com/journals/pages/open_access/funder_policies/chorus/standard_publication_model)

下载所有幻灯片

月份：	总浏览次数：
2023年3月	30
2023年4月	15
2023年5月	4
2023年6月	5
2023年7月	18
2023年8月	21
2023年9月	15
2023年10月	30
2023年11月	15
2023年12月	36
2024年1月	40
2024年2月	29
2024年3月	29
2024年4月	44

文章内容

快速双变量P（P）-样条线：三明治平滑器

总结

1.简介

2.三明治更光滑

2.1. 与E-M估计值的比较

2.2. 快速实施

3.渐近理论

4.不规则间隔的数据

4.1. 实际实施

4.2. 渐近理论

5.仿真研究

5.1. 回归函数估计

5.2. 计算速度

6.应用：协方差函数估计

7.多元P（P）-样条曲线

7.1. 多元的实现P（P）-样条曲线

7.2. 一个例子

致谢

工具书类

附录A：方程推导(11)

附录B：定理证明

B.1、。命题1的证明

B.2节。定理1的证明

B.3节。定理2的证明

引文

意见

海拔高度

电子邮件警报

通过引用文章

最新的

阅读次数最多

被引用次数最多

文章内容

快速双变量P（P）-样条线：三明治平滑器

总结

1.简介

2.三明治更光滑

2.1. 与E-M估计值的比较

2.2. 快速实施

3.渐近理论

4.不规则间隔的数据

4.1. 实际实施

4.2. 渐近理论

5.仿真研究

5.1. 回归函数估计

5.2. 计算速度

6.应用：协方差函数估计

7.多元P（P）-样条曲线

7.1. 多元的实现P（P）-样条曲线

7.2. 一个例子

致谢

工具书类

附录A：方程推导(11)

附录B：定理证明

B.1、。命题1的证明

B.2节。定理1的证明

B.3节。定理2的证明

引文

意见

海拔高度

电子邮件警报

通过引用文章

最新的

阅读次数最多

被引用次数最多

此功能仅对订阅服务器可用