摘要
每|亿美元$|-顶点Cayley图有一个正交本征基,所有本征基的坐标都是|$O(1/\sqrt{n})$|? 虽然阿贝尔群的答案是肯定的,但我们证明它一般是否定的。另一方面,我们表明|n美元$|-顶点Cayley图(更一般地说,顶点传递图)有一个正交基,其坐标都是|$O(\sqrt{\log n/n})$|而这个界限几乎是最好的。我们的研究是由阿萨夫·纳尔(Assaf Naor)的一个问题引发的,他证明了随机阿贝尔Cayley图是小集扩张,推广了Alon–Roichman的一个经典结果。他的证明依赖于阿贝尔Cayley图的有界本征基的存在,我们现在知道这对于一般群是不成立的。另一方面,我们绕过这一障碍,将Naor的结果推广到非贝类群体。
1引言
1.1有界特征基
理解Cayley图的谱分解是一个基本问题。由于Cayley图中的每个顶点都具有相同的度,所以我们讨论的是邻接矩阵还是拉普拉斯矩阵都无关紧要,但为了具体起见,我们将坚持使用邻接矩阵。由于与图的展开性质密切相关,Cayley图的特征值,特别是谱间隙,受到了极大的关注[12,15]. 本文研究了Cayley图的特征向量的互补问题。
我们采用以下标准化。此标准化,查看|x美元$|作为具有平均度量的集或组上的函数,与抽象中使用的归一化不同,在抽象中,我们使用通常的欧几里德距离|${{\mathbb{R}}^n$|.给定一个有限集|美元$|和一个函数|$x\冒号S\到{\mathbb{C}}$|(有时被视为矢量|$x\在{{mathbb{C}}^S中$|),我们表示它|美元L^p$|规范依据Hermitian内积定义为|$\langle x,y\rangle={{mathbb{E}}}_{s\in s}\overline{x(s)}y(s)$|我们这么说|x美元$|是|加元$|-有界的如果|$\左\|x\右\|_{L^\infty(S)}\le C$|,我们说一组函数是|C美元$|-如果其所有元素都是|C美元$|-有界。在酉或正交本征基中,每个本征函数|x美元$|规范化为|$\左\|x\右\|_{L^2(S)}=1$|. 下面是我们研究的主要问题。在这里,我们的凯利图是无权和无向的。有限群上的Cayley图|G美元$|带对称发电机|$S=S^{-1}$|(不包含身份)具有形式的边缘|$(g,sg)$|覆盖所有区域|$g\单位:g$|和|$s\单位:s$|.
问题1.1。最低要求是什么|C(n)美元$|这样每|n美元$|-顶点Cayley图有一个|C(n)美元$|-有界酉(或正交)本征基?
每个阿贝尔-凯利图都有一个|$1$|-有界酉本征基。事实上,给定一个阿贝尔群|G美元$|,傅里叶特征的基础|G美元$|为每个Cayley图形成一个特征基|$克$|特别地,这种傅立叶基的所有坐标都是单位根。有界本征基的存在在某些应用中很有用。事实上,这项工作的最初动机是Naor的结果[16]这证明了随机阿贝尔Cayley图的某种小集展开性质,推广了Alon–Roichman的一个经典结果[1]任意群上的随机Cayley图是扩展器。Naor的论点使用了每个阿贝尔Cayley图都有一个|$1$|-有界特征基。他问自己的研究结果是否也适用于非基督教团体。在这里,我们证明了一般Cayley图并不总是有界本征基,因此对Naor关于非贝拉群的论证存在障碍。另一方面,我们提供了另一种论证,表明Naor定理确实扩展到了一般群。参见定理1.7请参阅下面的详细说明。
我们下面的第一个结果暗示Cayley图并不总是有界酉本征基。它给出了一个下限|$C(n)\gtrsim\sqrt{\log n}/\log \log n$|对于问题1.1对于无限多|n美元$|.(注释:我们写|美元\lesssim B$|和|美元A=O(B)$|意思是说|A\le C B美元$|对于某个常数|$C>0美元$|.)
定理1.2。存在无穷多个Cayley图|G美元$|其邻接矩阵具有其所有特征函数的特征空间|$x\冒号G\到{{mathbb{C}}$|满足|$\left\|x\right\|_{L^\infty(G)}\gec\left\ |x\right\|_{L^2(G){\sqrt{\logn}/\log\logn$|,其中|n美元$|是顶点数|$c>0$|是某个绝对常数。
下一个结果给出了近似匹配的上界|$C(n)\lesssim\sqrt{\log n}$|对于问题1.1.
定理1.3。每个Cayley图都有一个正交法线|$C\sqrt{\log n}$|-有界特征基,其中|n美元$|是顶点数|C美元$|是某个绝对常数。
更一般地,相同的上界适用于顶点传递图。
定理1.4。每个顶点传递图都有一个正交|$C\sqrt{\log n}$|-有界特征基,其中|n美元$|是顶点数|C美元$|是某个绝对常数。
缩小上下限之间的差距仍然是一个有趣的悬而未决的问题。这个问题似乎与格林最近的一个深刻而困难的结果有关[8],他证明了单位球面有限可传递子集的最大可能宽度|${{\mathbb{R}}^d$|按订单|$1/\sqrt{\log d}$|(与无限子集形成鲜明对比,例如,整个球体的宽度为1)。格林定理回答了第三作者的一个问题,而这个问题又是由[5]格林的证明依赖于有限单群的分类。
让我们提几个值得进一步调查的方向。首先,我们的构造证明定理1.2使用递增程度的图形。也能找到没有有界特征基的有界度Cayley图吗?
推测1.5。存在一些|d美元$|这样,对于每一个|C美元$|存在一个|d美元$|-无正交的正则Cayley图|C美元$|-有界特征基。
另一个值得进一步探索的方向是了解什么族的群总是具有有界本征基。扩展阿贝尔群的例子,使用非贝利傅立叶分析不难证明,在每个不可约表示最多都有维数的群中|d美元$|,每个Cayley图都有一个|$\sqrt{d}$|-有界酉本征基。给出这些例子,一个自然的问题是,对于更自然的“近似阿贝尔”群类,每个Cayley图是否都有一个有界特征基。
问题1.6。有界步长幂零群上的Cayley图总是有界特征基吗?仿射群呢?
刻画具有有界特征基性质的群的一般问题有点像Breuillard、Green和Tao对近似群的刻画[4]统一了Freiman关于有界加倍集的经典定理[7]和Gromov关于多项式增长群[10].
让我们提到另一个有界特征基有用的例子是研究Cayley图的差异和特征值之间的关系。Kohayakawa、Rödl和Schacht[13]利用Gowers提出的谱证明,证明了对于阿贝尔Cayley图,具有小差异等价于具有小的第二特征值。证明依赖于阿贝尔Cayley图的有界特征基。阿贝尔假说后来被康隆和赵删除[5]通过Grothendieck不等式的应用。
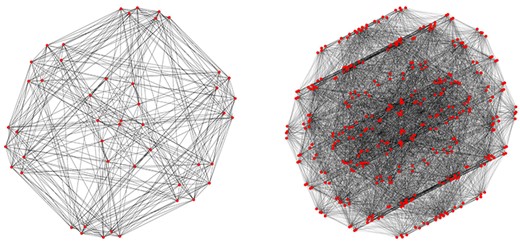
特征函数的有界性有一个吸引人的解释光谱图绘制.霍尔图的光谱图[11](另请参阅Spielman的调查[18],其中包含一些漂亮的图形)放置每个顶点|$v(美元)$|在|{\mathbb{R}}^2中的$(x(v),y(v))$|,其中|x美元$|和|美元$|是对应于拉普拉斯图的第二和第三特征值的特征函数(此处|x美元$|和|美元$|假设正交且适当缩放)。此图形的特性是,它使图中所有图形的平方边长之和最小|${{\mathbb{R}}^2$|顶点位于各向同性位置(因此|x美元$|和|美元$|坐标各有方差1且不相关)。每个阿贝尔Cayley图都有一个所有坐标都有界的谱图。另一方面,定理1.2给出了一个Cayley图的例子,在这个图中,没有谱图可以放在半径为1的圆盘内|$c\sqrt{\log n}/\log \log n$|(前提是定理中的本征空间对应于可以实现的第二和第三本征值;见第节末尾三更多详细信息)。定理证明中Cayley图谱图的几个例子1.2如图所示1.
图1。
定理证明中Cayley图的一些谱图1.2,对应于组|$G=S_d\时间({{\mathbb{Z}}}/2{{\mathbb{Z}})^d$|,为绘制|$d\in\{3,4\}$|这样的光谱图需要一张边长为|$\sqrt{d/\log d}$|,其中顶点不相关|x美元$|和|美元$|每一个具有方差1的坐标。参见本节末尾的备注3.3这些数字是如何产生的。
1.2随机Cayley图是小扩展
Alon和Roichman的经典成绩[1]显示了在群的随机Cayley图中|G美元$|由生成|$k>C\epsilon^{-2}\log\left\lvert G\right\rvert$|独立且均匀的随机群元,除顶部特征值外的所有特征值最多具有绝对值|$k\epsilon美元$|特别是,通过扩展器混合引理,它意味着对于每个|$\空集\neq X\subsetneq G$|,哪里|美元(A,B)$|计算具有一个端点的边数|美元$|另一个在|十亿美元$|. 纳尔[16]发展了一个新的Banach空值Azuma不等式,并在阿贝尔群的随机Cayley图中证明了更精细的小集等周不等式,他问他的结果是否可以推广到所有群。在这里,我们肯定地回答了他的问题。在下面的定理中,通过“Cayley(多重)图关联|千美元$|独立均匀选择的随机群元素“我们的意思是:选择随机|$g_1,\点,g_k$|取生成的Cayley图|$g_1,g_1^{-1},\点,g_k,g_k^{-1{$|,具有多重性。允许多重性使结果更容易表述,这是一个技术性问题,人们可以随意忽略(在许多参数范围内,多重性不太可能发生)。
定理1.7。存在一个通用常数|$C>0$|这样,对于每个正整数|千美元$|和每个组|G美元$|,概率至少为|$1/2$|,关联的Cayley(多重)图|千美元$|独立均匀选择的随机群元具有以下性质:|$X\子条款G$|具有|$1<\left\lvert X\right\rvert\leleft\lfert G\right\ rvert/2美元$|、边数|$e(X,G\设置减去X)$|之间|X美元$|和|$G\设置减去X$|满足 Naor证明定理1.7对于阿贝尔群。他的证明依赖于阿贝尔Cayley图的有界特征基。在节中5我们解释了如何绕过这个障碍,以证明非贝拉群的结果。
2准备工作
2.1非阿贝尔傅立叶变换
我们首先总结非贝叶斯傅里叶分析的一些标准事实(例如[9])。给定一个有限群|G美元$|,让|$\widehat{G}$|表示的不可约幺正表示集|G美元$|对于每个代表|$\rho\in\widehat G$|,称其为维度|$d_\rho(美元)$|,并调用其作用的空间|$W_\rho\cong{{\mathbb{C}}}^{d_\rho}$|。对于任何|$f:G\to\mathbb{C}$|和|$\rho\in\widehat{G}$|,其傅里叶变换计算为|$\rho美元$|由给定它是的自同态|$W_\rho(美元)$|(即。,|$\widehat{f}(\rho)\in\operatorname{结束}W_\ρ$|). 有一个反演公式,即哪里|$\langle A,B\rangle_{\textrm{HS}}=\operatorname{Tr}(A^{\dagger}B)$|是Hilbert–Schmidt内积,它只是矩阵的入门级Hermitian乘积。希尔伯特-施密特规范写成|$\|A\|_{\textrm{HS}}=\sqrt{\operatorname{Tr}(A^{\dagger}A)}$|我们有帕西瓦尔的身份尤其是,最后,我们定义了两个函数的卷积|$f_1,f_2:G\to\mathbb{C}$|通过傅里叶变换将卷积转化为矩阵乘法:为所有人|$\rho\in\widehat{G}$|. 2.2特征组合
给定一个函数|$f:G\to\mathbb{C}$|,我们考虑运算符|M_f美元$|作用于|${{\mathbb{C}}^G$|,功能空间|$G\到{{mathbb{C}}}$|,通过也就是说,|$(M_f x)(g)={{\mathbb{E}}}_{h\在g}f(gh^{-1})x(h)$|为所有人|$x\冒号G\到{\mathbb{C}}}$|和|$g\单位:g$|。同样,也可以查看|M_f美元$|作为矩阵,行和列由索引|G美元$|,其条目已就位|$(g,h)\单位为g\乘以g$|是|$f(gh^{-1})/\left\lvert G\right\rvert$|然后,查看|$x\在{{mathbb{C}}^G中$|作为向量,矩阵乘积|M_f美元x$|与上述定义一致。该矩阵可以被认为是Cayley图的邻接矩阵(经过适当的归一化)。让我们解释一下如何分析|M_f美元$|使用傅里叶变换。 从现在开始假设|$f(g^{-1})=\上划线{f(g)}$|对于每个|$g\单位:g$|.然后是赫密特人。对于任何|$x:G\to\mathbb{C}$|,应用傅里叶变换,我们可以看到|x美元$|是的本征函数|M_f美元$|具有特征值|美元\lambda$|(即。,|$f\ast x=\lambda x$|)当且仅当也就是说,所有的列|$\widehat{x}(\rho)$|(当被视为|$d_\rho\times d_\rho$|矩阵)位于|$\widehat{f}(\rho)$|对应于特征值|美元\lambda$|. 让|$V_\rho(美元)$|是支持傅里叶变换的函数的子空间|$\rho美元$|:对于任何列向量|W_\rho中的$\mathbf{v}\$|,我们定义 特别是,如果|$\widehat f(\rho)\mathbf{v}=\lambda\mathbf{v}$|对一些人来说|{{\mathbb{R}}中的$\lambda\$|,然后|$M_f x=\lambda x$|为所有人|$x\在V_{\rho,\mathbf{V}}中$|(通过傅里叶变换可以看出)。此外,如果|W_\rho中的$\mathbf{v},\mathbf{v}^{prime}\$|具有|$\mathbf{v}^{\dagger}\mathbf{v}^{\prime}=0$|,然后|$\left\langle x,x^{\prime}\right\rangle=0$|为所有人|$x\在V_{\rho,\mathbf{V}}中$|和|$x^{\prime}\在V_{\rho,\mathbf{V}^{\prime}}中$|.
总之,我们有一个正交分解(通过傅里叶变换很容易检查正交性)对于每个|$\rho\in\widehat G$|,让|$\mathbf美元{v} _1个^\rho、\ldots、\mathbf{v}(v)_W_\rho中的{d_\rho}^\rho\$|是…的特征基|$\widehat f(\rho)\in\operator名称{End}W_\rho$|,并调用相应的特征值|$\lambda_{\rho,1},\ldot,\lambda _{\ρ,d_\rho}$|。我们有一个正交分解和|$M_f x=\lambda _j ^\rho x$|对于每个|$x\在V_{\rho,\mathbf中{v} _j(_j)^\ρ}$|因此|M_f美元$|包括|$\lambda _{\rho,j}$|具有多重性|$d_\rho(美元)$|,覆盖所有|$\rho\in\widehat G$|和|$j\在[d_\rho]中$|.的特征空间|M_f美元$|对应于特征值|美元\lambda$|是所有|$V_{\rho,\mathbf{v} _j(_j)^\ρ}$|覆盖所有区域|$\rho\in\widehat G$|和|$j\在[d_\rho]中$|具有|$\lambda_{\rho,j}=\lambda$|. 2.3 Schatten规范
Schatten家族|美元$|-规范|$\l垂直A\r垂直{S_p}$|矩阵的|$A\in{\mathbb{C}}}^{n\times n}$|通过定义哪里|$\σ_1(A),\点,\σ_n(A$|是的奇异值|美元$|. Schatten家族|美元$|-范数满足非交换Hölder不等式(例如[三,推论IV.2.6]):用于|$1\le价格$|具有|$1/p+1/q=1美元$|,我们有 给定一个函数|$f\冒号G\到{\mathbb{C}}$|关于有限群|G美元$|,我们定义其Schatten|美元$|-规范|$\left\lVert f\right\rVert_{S_p}$|成为Schatten|美元$|-关联矩阵的范数|M_f美元$|(给出线性图|$x\mapsto f\ast x$|在|${{\mathbb{C}}^G$|): 3施工
在本节中,我们将证明定理1.2通过在群上构造Cayley图|G美元$|具有所有本征函数都满足的本征空间|$\left\|x\right\|_{L^{\infty(G)}}\gtrsim\left\ |x\right\|_{L^2(G){\sqrt{\log\left\slvert G\right\srvert}/\log\log\leth\lvert G\ right\rvert$|.
为了激励我们的建设,我们首先在第节中解释3.1幺正群会发生什么|$G=U(d)$|,虽然它不是有限的,但分析起来更简单。然后,在第节中3.2,我们解释了如何在|美元(天)$|。然后我们在第节中解释3.3如何通过采样将边缘加权结构转换为未加权结构,并表明特征向量保持其所需的特性。仅部分3.3是定理证明所必需的1.2,前面的小节仅用于激励,但我们希望它们对读者有所帮助。
3.1酉群
让|$G=U(d)$|.让|$\rho美元$|表示|G美元$|在|${{\mathbb{C}}^d$|,这是不可约的。让|$V_\rho(美元)$|表示的子空间|$L^2(G)$|包括所有|$x\单位L^2(G)$|表单的|$x(g)=d\langle\rho(g),范围_{textrm{HS}}$|对一些人来说|$A\在{{mathbb{C}}^{d\times d}中$|也就是傅里叶变换|$\widehat{x}$|在支持|$\rho美元$|和|$\widehat{x}(\rho)=A$|请注意|$V_\rho(美元)$|与我们之前在(2.1)对于有限群。
权利要求3.1。对于任何|$x\以V_\rho表示$|,我们有|$\|x\|_{L^\infty(G)}\ge\sqrt{d}\|x\ |_{L ^2(G){$|.
证明。让|$A\在{{mathbb{C}}^{d\times d}中$|是这样的|$x(g)=d\langle\rho(g),范围_{textrm{HS}}$|.通过傅里叶反演和Parseval,|$\左\|x\右\|_{L^2(G)}=\sqrt{d}\lVertA\rVert_{textrm{HS}}$|因此,我们有根据的定义|$\rho美元$|Schatten规范的二重性。 对于足够通用的|$f\冒号G\到{\mathbb{C}}$|(假设没有不必要的特征值碰撞),子空间|$V_\rho(美元)$|是算子特征空间的直接和|M_f美元$|,通过给出定理的连续模拟1.2.实际构造证明定理1.2将涉及此结构的离散化。
3.2加权结构
在本节中,我们证明了定理的加权类似1.2这是通向整个证明的垫脚石。回想一下前面的函数|$f:G\到{{mathbb{C}}}$|我们有|$M_f(g,h)=f(gh^{-1})/\left\lvert g\right\rvert$|.
定理3.2。存在一些常量|$c>0$|和无限多组|G美元$|和功能|$f:G\到{{mathbb{R}}}$|这样的话|$M_f(百万美元)$|具有其所有元素的特征空间|x美元$|满足 让|$G=S_d\时间({{\mathbb{Z}}}/2{{\mathbb{Z}})^d$|,其中|$S_d(美元)$|作用于|$({{\mathbb{Z}}/2{{\mathbb{Z}})^d$|通过排列坐标。该组具有|d美元$|-上的维度表示|${\mathbb{C}}}^d$|,我们称之为|$\rho美元$|,其中|$S_d(美元)$|排列坐标和|$({{\mathbb{Z}}/2{{\mathbb{Z}})^d$|翻转坐标符号。很容易检查|$\rho美元$|是不可约的。
我们需要一个|G美元$|-单位球面上的轨道|${{\mathbb{C}}^d$|每个方向都有很大的宽度。下一个引理用作Claim的有限类比3.1。此引理也出现在[8]为了方便读者,我们在这里包括了它的证明。
引理3.3。让|$\mathbf{a}$|是以下方向的单位矢量|$(1,1/\sqrt{2},\ldot,1/\sqrt{d})$|.那么对于任何|$\mathbf{v}\in\mathbb{C}^d$|我们有
备注。格林最近的一个艰难成绩[8]证实了赵的猜测,表明有限的,有限的子组|G美元$|属于|美元(天)$|和每个单位向量|$\mathbf{a}\在{{\mathbb{C}}^d中$|,有一些单位向量|$\mathbf{v}$|这样的话|$\sup_{g\in g}\left\lvert\left\langle\mathbf{v},\rho(g)\mathbf{a}\right\rangle\right\rvert\lesssim 1/\sqrt{\log d}$|(即球体的每个有限传递子集的宽度上的紧上界)。相反,球体的无限可传递子集的宽度可以达到|$1$|(例如,整个球体)。最初,有限性假设意味着轨道宽度会急剧减小,这是非常违反直觉的。
证明。首先让我们假设|{{mathbb{R}}^d中的$\mathbf{v}\$|,所以哪里|$\mathbf{w}$|是通过以下坐标获得的向量|$\mathbf{v}$|非负,然后按非递增顺序重新排列。让|$\mathbf{w}=(w_1,\ldot,w_d)$|具有|$w_1\ge\cdots\ge w_d\ge 0$|.然后因此 最后,当|{{mathbb{C}}^d中的$\mathbf{v}\$|,我们可以简化为实际情况。在不丧失一般性的情况下假设(因为|$\rho美元$|是真实的)|$|\operatorname{Re}\mathbf{v}|\ge|\operatorname{Im}\mat血红蛋白{v}|$|.然后
让|$\mathbf{a}$|如引理所示3.3(视为列向量)。定义|$f\冒号G\到{\mathbb{R}}}$|通过因此,通过傅里叶反演,|$\widehat{f}$|在支持|$\rho美元$|和|$\widehat{f}(\rho)=\mathbf{a}\mathbf{a}^插入$|也就是说,|$f\以V_\rho表示$|(如中所示(2.1))。 如中所示(2.2),让|$V_{\rho,\mathbf{a}}$|表示的子空间|$L^2(G)$|包括所有|$x\单位L^2(G)$|表单的|$x(g)=d\langle\rho(g),\mathbf{a}\mathbf{v}^{dagger}\rangle_{textrm{HS}}$|对一些人来说|{{mathbb{C}}^d中的$\mathbf{v}\$|根据第节中的讨论2.2,我们看到了|M_f美元$|只有一个非零特征值,即|$1$|,其特征空间为|$V_{\rho,\mathbf{a}}$|.
我们声称为所有人|$x\在V_{\rho,\mathbf{a}}中$|.出租|$x(g)=d\langle\rho(g),\mathbf{a}\mathbf{v}^{dagger}\rangle_{textrm{HS}}$|,我们有其中最后一个不等式是引理3.3此外,Parseval,自|$\left\lvert G\right\rvert=2^dd$|,我们有|$d=(1+o(1))\log{\left\lvert G\right\rvert}/\log\log{\left\lvert G\right\rvert}$|,这就完成了证明。 3.3未加权施工
让我们首先解释一下整个小节的设置。让|G美元$|是任何有限组(稍后我们将专门研究|$G=S_d\时间({{\mathbb{Z}}}/2{{\mathbb{Z}})^d$|). 让|$\rho\in\widehat G$|是…的真正不可约表示|G美元$|尺寸的|$d=d_\rho$|也就是说,|$\rho\colon G\to O(d)$|是同态。最后,我们假设|$\sqrt{\left\lvert G\right\rvert/\log\left\ lvert G\ right\server}>15天$|.
固定单位向量|$\mathbf{a}\在{{\mathbb{R}}}^d中$|然后让作者:Cauchy–Schwarz,|[0,1]中的$f(g)$|此外,|$f(g^{-1})=f(g)$|自从|$\rho(克)$|包含真实条目。 请注意|$f美元$|与定理证明中给出的示例非常相似3.2但进行了移动和缩放,使其值位于|$[0,1]$|的想法是从|$f美元$|然后其特征值将接近原始值。此外,我们将证明顶部非平凡特征空间(对应于|$\rho美元$|)变化不大,所以估计引理3.3将继续有效。
我们现在对一个随机函数进行采样|$小时$|基于|$f美元$|.让|$G^{\prime}$|是元素集|$g\单位:g$|具有|$g=g^{-1}$|和|$G^{\prime\prime}$|是的子集|$G\设置减去G^{\prime}$|每个集合只包含一个元素|$\{g,g^{-1}\}\在\binom{g}{2}中$|这样的话|$g\neq g^{-1}$|。对于|$g\在g^{\prime}中$|,让|美元小时(克)$|是|$1$|有可能|$f(g)$|否则为零。对于|$g\在g^{\prime\prime}中$|,让|$h(g)=h(g^{-1})=1$|有可能|$f(g)$|和|$0$|否则。这些选择是独立的|$G^{prime}\杯G^{prime\prime}$|。请注意|$f(e)=0$|,所以|$h(e)=0$|.
对于每个|$g\单位:g$|,让|$P_g$|用索引的列和列表示矩阵|$G\乘以G$|带条目|$1/\left\lvert G\right\rvert美元$|在位置|$(gx,x)$|对于每个|$x\单位:G$|其他地方为零。查看|M_f美元$|和|M_h美元$|作为矩阵(如第节所述2.2),我们有我们首先计算|${{\mathbb{E}}[M_h]=M_f$|.
引理3.4。让|$小时$|同上。光谱|$\mathbb{E}[M_h]$|是|$1/2$|具有多重性|$1$|,|$1/(2d)$|具有多重性|d美元$|、和|$0$|具有多重性|$\left\lvert G\right\rvert-d-1$|.
证明。根据期望的线性,|${{\mathbb{E}}[M_h]=M_f$|此外,由于我们看到了|$\widehat{f}(\operatorname{三}_G) = 1/2$|和|$\widehat{f}(\rho)=-\mathbf{a}\mathbf{a}^\internal/(2d)$|通过傅里叶逆变换|$\widehat{f}$|仅支持这两种表示(此处|$\运算符名称{三}_G$|是|$克$|). 第节中的分析2.2因此表明|M_f美元$|具有特征值|$1/2$|具有多重性|$1$|,|$1/(2d)$|具有多重性|d美元$|、和|$0$|为其他人。
为了建立抽样的定量浓度界限,我们使用了Tropp的矩阵Hoeffing不等式[19]. 回忆一下,对于自共轭|A、B美元$|,符号|$A\方案B$|意味着|B-A美元$|是半正定的。
考虑一个有限序列|$\{\mathbf{十} k(_k) \}$|具有维数的独立随机自伴随矩阵|d美元$|,并让|$\{\mathbf{A} k(_k)\}$|是一系列固定的自共轭矩阵。假设每个随机矩阵满足 那么,对于所有人来说|$t\geq 0美元$|,
备注。常量|$8$|可以替换为|$2$|如果|$\mathbf美元{十} k(_k)$|和|$\mathbf美元{A} k(_k)$|通勤几乎是必然的,这在我们的应用程序中是正确的。请参见[19,备注7.4]。
证明。请注意,当|$g=g^{-1}$|我们有这个|$P_g^2=I/\left\lvert g\right\rvert^2$|。否则请注意作为我们正在使用它|$P_g-P_{g^{-1}}$|是反对称的。 使用它|$|h(g)-f(g)|\le 1$|几乎可以肯定,并应用定理3.5到我们发现了为所有人|$t\ge 0美元$|.将相同的不等式应用于|$-M_h(小时)$|产量设置|$t=4\left\lvert G\right\rvert^{-1/2}(\log 6\left\ lvert G\ right\verrt)^{1/2}$|产生引理。 这使我们能够控制|M_h美元$|.
推论3.7。使用|$小时$|如上所述,我们至少有这样的概率|$2/3$|特征值的个数|M_h美元$|在里面|$[-1/d,-1/(3d)]$|确实是|d美元$|.
证明。这是关于特征值偏差的Weyl不等式与引理的直接结果3.4和3.6.
更具体地说,我们有|M_h美元$|和|${{\mathbb{E}}[M_h]$|是自共轭的|$\left\lVert M_h-{{mathbb{E}}[M_h]\right\rVert_{operatorname{op}}\\le4\sqrt{log$|至少有可能|$2/3$|因此,写作|$\nu_1\ge\cdots\ge\nu_{\left\lvert G\right\rvert}$|对于的特征值|${{\mathbb{E}}[M_h]$|(我们知道这一点)|$1/2.0,\ldots,0,-1/(2d),\ldots,-1/(2d)$|具有|$d美元$|的副本|$1/(2d)$|通过引理3.4)和|$\mu_1\ge\cdots\ge\mu_{\left\lvert G\right\rvert}$|对于的特征值|M_h美元$|,我们有为所有人|$1\le j\le\left\lvert G\right\rvert美元$|通过Weyl的不等式。最后一个不等式使用的假设是|$\sqrt{\left\lvert G\right\rvert/\log\left\ lvert G\ right\server}>15天$|. 我们现在展示一下|$\widehat{h}(\rho)$|和|$\widehat{f}(\rho)={{\mathbb{E}}[\wideheat{h}(\ rho)]$|都很接近。
证明。该证明与引理的证明基本相同3.6。请注意,如果|$g=g^{-1}$|然后|$\rho(g)^2=I_d$|。否则作为我们正在使用它|$(g)-\rho(g^{-1})=中间$|是反对称的。 然后,利用矩阵Hoeffing界定理3.5,紧接着就是设置|$t=4\left\lvert G\right\rvert ^{-1/2}(\log 6\left\lvert G\right\rvert)^{1/2}$|产生引理。 我们现在显示|$\widehat{h}(\rho)$|和|$\widehat{f}(\rho)=\mathbb{E}[\wideheat{h}(\ rho)]$|都很接近。这是Davis–Kahan定理的一个特例[6]. 我们包括一个证明(改编自[17,定理5.9])。回想一下|$\widehat{h}(\rho)$|是实的,所以它的特征向量是实的。
引理3.9。让|$h,\rho,\mathbf{a}$|同上。让|$\mathbf{b}$|是的上特征值的实单位特征向量|$\widehat{h}(\rho)$|.至少具有概率|$2/3$|我们有
证明。让和那么我们有了第二个不等式是(2.3),注意到|$\left\lVert\cdot\right\rVert_{\operatorname{op}}=\left\fort\cdot\right\rVert_{\operatorname}}$|。最后一步将其用于矩阵|百万美元$|最多2级,其中一级|$\left\lVert M\right\rVert_{S_1}\le\sqrt{2}\left\ lVert M \right\ rVert_{S_2}=\sqrt{2}\ left\l Vert M\ right\r Vert_{textrm{HS}}$|. 此外,我们还有和所以我们有这个然后否定|$\mathbf{b}$|如有必要,以便|$\mathbf{a}\cdot\mathbf{b}\ge 0$|,我们有按引理3.8,概率至少为|$3/4$|,一个有|$\lVert\Sigma^{\prime}-\Sigma\rVert_{\operatorname{op}}^2\le 16\log(6d)/\left\lVert G\right\rVert$|,引理如下。 我们结合了迄今为止得出的浓度结果。
建议3.10。让|$h,\mathbf{a}$|定义如上。对于|$\左\右\右\右$|足够大,我们至少有可能|$1/3$|以下所有内容均成立:
证明。这是推论的直接应用3.7,引理3.8、和引理3.9请注意,尽管我们对三个语句的失败进行了unin-bounding(最多失败率|$1/3$|每个),引理中使用的事件3.9正是引理3.8.
我们现在可以证明定理了1.2.证明将模仿定理3.2.
如第节所示3.2,让|$G=S_d\times({\mathbb{Z}}}/2{\mathbb{Z}}})^d$|和|$\rho美元$|是其在上的标准表示|${{\mathbb{C}}^d$|(置换和否定坐标),这很容易看出是真实的。此外,让|$\mathbf{a}$|是以下方向的单位矢量|$(1,1/\sqrt{2},\ldot,1/\sqrt{d})$|,作为列查看。
我们取样|$小时$|如本小节开头所述(假设|$\sqrt{\left\lvert G\right\rvert/\log\left\ lvert G\ right\server}>15天$|保持足够大|d美元$|). 让我们的图是带有邻接矩阵的Cayley图|$\left\lvert G\right\rvert M_h$|。由于我们只关心本征空间的尺度不变性质,因此我们将注意力局限于|M_h美元$|,作用于|$V={{\mathbb{C}}}^G$|.
按命题3.10,用于|$\左\右\右\右$|足够大,至少有可能|$2/3$|确实有|d美元$|的特征值|M_h美元$|在里面|$[-1/d,-1/(3d)]$|、和|$\widehat{h}(\rho)$|有一个特征值|美元\lambda$|在这个范围内具有单位特征向量|$\mathbf{b}$|令人满意的 通过Cayley图的特征空间的刻划2.2,我们看到了|$\widehat{h}(\rho)$|贡献一个|d美元$|-维特征空间到|M_h美元$|它的每个特征值。因此,我们看到|d美元$|的特征值|M_h美元$|在里面|$[-1/d,-1/(3d)]$|都是准确的|d美元$|这个特征值的副本|美元\lambda$|.
特别地,|M_h美元$|具有特征值|美元\lambda$|,它具有精确的特征空间|$V_{\rho,\mathbf{b}}$|,从中召回(2.2)是 现在要证明构造满足定理的结论。让|$x\在V_{\rho,\mathbf{b}}中$|我们希望表明(回忆|$\left\lvert G\right\rvert=2^dd$|以便|$d=(1+o(1))\log{left\lvert G\right\rvert}/\log\log{eleft\lvert-G\right\ rvert}$|)如果|$x(g)=d\left\langle\rho(g),\mathbf{b}\mathbf{v}^{\dagger}\right\langle _{\textrm{HS}}}=d\mathbf{v}^{\dagger}\rho(g)\mathbf{b}$|对一些人来说|$\mathbf{v}\ in{\mathbb{C}}}^d$|然后是Parseval,此外,足够大的|d美元$|,通过引理3.3以及(3.2).
备注。生成图中的图形1,我们在上生成一个Cayley图|$G=S_d\时间({{\mathbb{Z}}}/2{{\mathbb{Z}})^d$|每个可能的发电机|$g\neq e(美元)$|包含概率|C美元(1-f(g))$|. (|$C=2/3$|对于第一个数字和|加元=1/7$|对于第二个;这些常量只是为了美学目的而对图形进行稀疏化。)
在定理证明中1.2上面,我们通过类似的过程对一个图进行采样,并推断出它具有正概率的无界维数特征空间|d美元$|事实上,我们可以进一步推断,这个无界特征空间具有负特征值,并且是继平凡特征值之后的最大特征值。因此,一个类似的证明表明,我们上面采样的图具有正概率,具有无界的多重性特征空间|$d\ge 2美元$|,包含第二和第三个特征值。因此,这种图的任何可能的谱图都至少有宽度|$c\sqrt{\log\left\lvert G\right\rvert}/{\log\ log\left \lvert G \right\srvert}$|,根据需要。
最后,在实践中,我们只对较小的值进行采样|$d=3美元$|和|d美元=4$|在这种情况下,对不满足所需特性的图进行采样的概率很高,即第二和第三特征值来自标准表示|$\rho美元$|属于|G美元$|它们的特征空间|d美元$|-维度。生成地物1,我们检查这些属性并重新采样,直到它们保持不变。
4上限
在本节中,我们将证明定理1.3和1.4,显示所有Cayley图(第节4.1)和传递图(第节4.2)上的|n美元$|顶点具有|$O(\sqrt{\log n})$|-有界正交本征基。
4.1凯利图
引理4.1。给定一组|美元$|属于|n美元$|单位向量|$\mathbb{R}^d$|(分别。|${{\mathbb{C}}^d$|)我们可以找到一个正交(对应酉)基|L美元$|属于|$\mathbb{R}^d$|(分别为。|${{\mathbb{C}}^d$|)这样的话此外,当|$S\subseteq{{\mathbb{C}}}^{d}$|,我们可以选择|L美元$|以具有所有实向量。
证明。让我们先做真实的案例。回忆一下高尺寸球形盖体积上的以下标准边界(例如[2,引理2.2]):对于均匀随机单位向量|$\mathbf{w}\在{{mathbb{R}}^d中$|和固定单位向量|{{mathbb{R}}^d中的$\mathbf{v}\$|,一个有 让|$\epsilon=\sqrt{2\log(4dn)/d}$|.然后应用与绑定的并集(4.1),我们发现一个正交基|$L=\{\mathbf{w} _1个,\ldot,\mathbf{w} (_d)\}$|一致随机满足所以有一些|L美元$|这样的话|$\left\langle\mathbf{w},\mathbf{v}\right\rangle<\epsilon\lesssim\sqrt{\log(dn)/d}$|为所有人|$\mathbf{w}\以L表示$|和|S中的$\mathbf{v}\$|. 对于复杂的情况,对于每个|$v\单位:S$|,写入|$\mathbf{v}=\mathbf{v} _1个+i\mathbf{v} _2$|对于|$\mathbf美元{v} _1个,\mathbf{v} 2个\在\mathbb{R}^n中$|.我们将这个引理的实际情况应用于集合获得基础|L美元$|属于|$\mathbb{R}^d\subseteq\mathbb{C}^d$|然后针对每个|$\mathbf{w}\in L$|和|S中的$\mathbf{v}\$|,我们有 现在我们准备证明定理1.3本质上,我们的论证相当于选择一个随机幺正基(通过引理4.1)对于来自群表示理论的每个特征空间|G美元$|Cayley图的。然而,为了选择真实的正交本征基,我们本质上是成对的共轭不可约表示。如果我们只想找到幺正本征基,那么这种技术性是不必要的。
让|美元$|是Cayley图的对称生成集,并且|$\mathbb美元{1} _秒$|是相应的指示函数。召回,来自章节2.2,的正交分解|$V={{\mathbb{C}}}^G$|作为参见第节2.2关于的定义|$V_\rho(美元)$|和|$V_{\rho,{\textbf{V}}$|。这里是向量|${\textbf{v}}_j^\rho$|,|$j\在[d_\rho]中$|,形成的酉本征基|$\widehat{\mathbb{1}\;\;\,}_{\!\!\$|具有各自的特征值|$\lambda_{\rho,j}$|.的特征空间|$M_{\mathbb{1} _秒}$|对应于某个特征值|美元\lambda$|是所有组件的直接总和|$V_{\rho,{\textbf{V}}_j^\rho}$|具有|$\lambda_{\rho,j}=\lambda$|使用这种分解,我们将为算子构造一个实值酉本征基|$M_{\mathbb{1} _秒}$|在|V美元$|如下:对于每个共轭对|$(\rho,\overline\rho)$|和特征向量|$\mathbf{b}$|属于|$\widehat{\mathbb{1} _秒}(\rho)$|,我们将找到一个实值的酉基础|$V{\rho,\mathbf{b}}\oplus V{\overline\rho$|.
对于每个不可约表示|$\rho\in\widehat G$|这样的话|$\rho美元$|和|$\上划线{\rho}$|同构(这种表示称为自对偶的),我们将找到一个特殊的本征基|$\widehat{\mathbb{1} _秒}(\rho)$|,以及给出统一基础的特定结构|$V_\rho(美元)$|这将取决于矩阵|Q美元$|令人满意的|$\rho Q=Q\上划线{\rho}$|对称或反对称。
请注意,第二种情况包括|$\rho美元$|它可以实现为实表示,但并非所有的自对偶表示都是这种形式(例如,四元数群的二维不可约表示|$Q_8$|). 此外,我们将确保所有功能|x美元$|作为上述基本要素的选择满足 作为一个典型案例,我们考虑|$\rho\in\widehat G(大写:$\rho\in\widehat G)$|维数的实不可约表示|$d=d_\rho$|,作用于|${{\mathbb{R}}^d$|严格地说,我们在最后的论证中不需要这种分析,因为我们对自我双重表征的处理更为普遍。让|$\mathbf{b}\在{{mathbb{R}}^d中$|是的实特征向量|$\widehat{\mathbb{1} _秒}(\rho)$|.召回类似于定理证明1.2,正在写入|$x_{mathbf{v}}:G\到{{mathbb{C}}}$|对于函数|$x{\mathbf{v}}(g)=d\langle\rho$|,我们有和根据引理的真实版本4.1应用于|$S=\{\rho(g)\mathbf{b}:g\ in g\}$|,有一个正交基|L美元$|属于|${{\mathbb{R}}^d$|使得(注意|$d^2\le\ left\ lvert G\ right\服务器$|)然后针对每个|$\mathbf{v}\in L$|我们有根据帕西瓦尔的身份,我们可以看到|$\{x_{\mathbf{v}}/\ sqrt{d}:\ mathbf{v}\在L\}中$|形成一个统一的基础|$V_{\rho,\mathbf{b}}$|。还要注意|$x_{\mathbf{v}}$|每个都是实值的|{{mathbb{R}}^d中的$\mathbf{v}\$|。这就完成了真实情况|$\rho美元$|. 接下来,让我们|$(\rho,\overline{\rho})$|是不可约表示的共轭对|$\rho美元$|和|$\上划线{\rho}$|彼此不同构。再次让|$d=d_\rho$|.对于每个特征向量|$\mathbf{b}\在{{mathbb{C}}^d中$|属于|$\widehat{\mathbb{1} _秒}(\rho)$|,通过复杂版本的引理4.1,我们找到了一个酉基|L美元$|属于|${{\mathbb{C}}^d$|以便|L中的$\sup_{\mathbf{v},g中的g}\left\lvert\left\tangle\mathbf{v},\rho(g)\mathbf1{b}\right\rangle\right\srvert\lesssim\sqrt{(\log\left\ lvertG\right\ rvert)/d}$|.再次书写|$x{\mathbf{v}}(g)=d\langle\rho(g),\mathbf{b}\mathbf1{v}^{\dagger}\rangle$|,我们发现|$\{x_{\mathbf{v}}/\sqrt{d}:\mathbf{v}\在L\}中$|是统一的基础|$V_{\rho,\mathbf{b}}$|和同样,以共轭物为例,我们可以看到|$\{上划线{x_{\mathbf{v}}/\sqrt{d}:\mathbf{v}\在L\}中$|是统一的基础|$V_{\overline\rho,\overline{\mathbf{b}}}$|回忆一下,如果|$M_{\mathbb}{1} _秒}x{\mathbf{v}}=\lambda x{\mathbf{v}}$|然后|$M_{\mathbb{1} _秒}上划线{x{mathbf{v}}=\lambda\$|作为|$M_{\mathbb{1} _秒}$|对称,因此|美元\lambda$|是真实的。 收集|2d美元$|向量作为|$\mathbf{v}$|范围超过|L美元$|,形成了实际价值的单一基础|$V{\rho,\mathbf{b}}\oplus V{\overline\rho$|此外,和类似的|$y_{\mathbf{v}}^1$|这就完成了非自对偶复杂不可约表示的情况。 最后,让|$\rho美元$|是一个自对偶不可约表示。再次让|$d=d_\rho$|。请注意|$\widehat{\mathbb{1} _秒}(\rho)$|是厄米特矩阵,因此我们可以选择表示上的坐标,使其成为真正的对角矩阵。完成此操作后,我们现在注意到|$g\mapsto\rho(g)$|和|$g\mapsto\上划线{\rho(g)}$|是同一空间上的同构表示,因为|$\rho美元$|是自对偶的(其中复数共轭是以自然的方式相对于空间上选择的坐标进行的)。因此存在一个酉算子|Q美元$|以便为所有人|$g\单位:g$|.因此为所有人|$g\单位:g$|.通过Schur引理,我们推断对一些人来说|$\omega\in\mathbb{C}$|.自|Q美元$|是单一的,|$QQ^{\dagger}=我$|(我们使用|${}^{\匕首}$|表示Hermitian转置和|${}^\插入$|对于转置),它产生自|Q美元$|是可逆的,我们推断|$\omega^2=1$|,因此|$\omega\in\{\pm 1\}$|. 发件人|$\widehat{\mathbb{1} _秒}(\rho)=\sum_{g\in S}\rho(g)/\left\lvert g\right\rvert$|和|$\rho(g)Q=Q\上划线{\rho$|我们获得自从|$\widehat{\mathbb{1} _秒}(\rho)$|如前所述,是一个真正的对角矩阵。因此|Q美元$|和|$\widehat{\mathbb{1} _秒}(\rho)$|通勤。现在选择一个酉同时本征基|Q美元$|和|$\widehat{\mathbb{1} _秒}(\rho)$|,这可以通过谱定理来实现,因为这两个算子都是正规的。 实际上,我们将采用更具结构的特定基础。首先,注意如果|$\mathbf{b}$|是的特征向量|Q美元$|具有特征值|美元\lambda$|然后因此|$\上划线{\mathbf{b}}$|是的特征向量|Q美元$|具有特征值|$(\omega^{-1}\上划线{\lambda})^{-1{=\omega\lambda$|,使用|$|\lambda|=1$|自从|Q美元$|是单一的。现在我们根据|$\omega\in\{\pm 1\}$|. 如果|$\omega=-1$|,然后我们看到我们的酉同时本征基|Q美元$|和|$\widehat{\mathbb{1} _秒}(\rho)$|可以选择,以便如果|$\mathbf{b}$|就在里面,那么就在里面|$\上划线{\mathbf{b}}$|,自|$\mathbf{b}$|和|$\上划线{\mathbf{b}}$|位于不同的正交特征空间|Q美元$|.对于这样的特征向量|$\mathbf{b}$|,如前所述,我们可以应用引理4.1获得统一基础|L美元$|属于|${{\mathbb{C}}^d$|以便|L中的$\sup_{\mathbf{v},g中的g}\left\lvert\left\tangle\mathbf{v},\rho(g)\mathbf1{b}\right\rangle\right\srvert\lesssim\sqrt{(\log\left\ lvertG\right\ rvert)/d}$|.再次书写|$x{\mathbf{v}}(g)=d\langle\rho(g),\mathbf{b}\mathbf1{v}^{\dagger}\rangle$|,我们发现|$\{x_{\mathbf{v}}/\sqrt{d}:\mathbf{v}\在L\}中$|是统一的基础|$V_{\rho,\mathbf{b}}$|和|$\|x_{\mathbf{v}}\|_{L^\infty(G)}\lesssim\sqrt{\log\left\lvert G\right\rvert}\|x_{\mathbf{v{}}$|.
请注意|$\上划线{x{mathbf{v}}\在v{rho中,\上划线$|自从这表明|$\上划线{V_{\rho,\mathbf{b}}=V_{\ rho,\上划线$|此外,作为|$M_{\mathbb{1} _秒}x{\mathbf{v}}=\lambda x{\mathbf{v}}$|,我们有|$M_{\mathbb{1} _秒}上划线{x{mathbf{v}}=\lambda\$|自从|美元\lambda$|是真实的。然后,作为|$\mathbf{v}$|不同于|L美元$|、功能形成实值的单一基础|$V_{\rho,\mathbf{b}}\oplus V_{\ rho,\上划线{\mathbf{b}{}}$|这就完成了案件的证明|$\omega=-1$|. 如果|$\omega=1$|,然后针对每个特征向量|$\mathbf{b}$|属于|Q美元$|具有特征值|美元\lambda$|,|$\上划线{\mathbf{b}}$|是的另一个特征向量|Q美元$|也具有相同的特征值|美元\lambda$|因此,每个特征空间|美元$|属于|Q美元$|满足|$U=上一行U$|.A型|${{\mathbb{C}}$|-向量空间|美元$|令人满意的|$U=上一行U$|总是|${{\mathbb{C}}$|-扩展|${{\mathbb{R}}$|-向量空间|${\operatorname{Re}}U=\{$|(自每|$\mathbf{v}\(单位:U)$|可以写为|$\mathbf{x}+i\mathbf{y}$|具有|$\mathbf{x}=(\mathbf{v}+\上划线{\mathbf1{v}})/2$|和|$\mathbf{y}=(\mathbf{v}-\overline{\mathbf1{v}})/(2i)$|都有实际坐标)。因此我们可以选择一个正交基|${{\mathbb{R}}^d$|由实值特征向量组成|$\mathbf{b}$|属于|Q美元$|.
固定这样一个实特征向量|$\mathbf{b}$|属于|Q美元$|。对于任何|{{mathbb{C}}^d中的$\mathbf{v}\$|,设置|$x{\mathbf{v}}(g)=d\langle\rho(g),\mathbf{b}\mathbf1{v}^{\dagger}\rangle$|和以前一样,我们有|在v{\rho,\mathbf{b}}中的$\上划线{x{\mathbf{v}}}$|自从因此|$\上划线{V_{\rho,\mathbf{b}}=V_{\ rho,\ mathbf}}$|,则必须是|${{\mathbb{C}}$|-扩展|d美元$|-维度的|${{\mathbb{R}}$|-向量空间|${\operatorname{Re}}V_{\rho,\mathbf{b}}$|. 我们现在应用引理4.1找到统一基础|L美元$|的|d美元$|-维度的|${{\mathbb{R}}$|-向量空间|$\mathbf{v}\ in{\mathbb{C}}}^d:x_{\mathbf{v}}\ in{\operatorname{Re}}v_{\rho,\mathbf{b}}\}$|令人满意的|$\sup_{\mathbf{v}\ in L,g\ in g}\left\lvert\left\langle\mathbf{v},\rho(g)\mathbf{b}\right\rangle\right\rvert\lesssim\sqrt{(\log\left\lvertG\right\rvert)/d}$|.然后|$\{x_{\textbf{v}}/\ sqrt{d}:\ mathbf{v}\在L\}中$|是实际值的单一基础|$V_{\rho,\mathbf{b}}$|具有|$\|x_{\mathbf{v}}\|_{L^\infty(G)}\lesssim\sqrt{\log\left\lvert G\right\rvert}\|x_{\mathbf{v{}}$|.
4.2点传递图
我们现在推广定理1.3到顶点传递图;这个想法和以前一样,只是我们首先提升到自同构群上的Cayley图|G美元$|原件的副本。这个技巧与证明[5,定理2.2]。
让|G美元$|表示给定顶点传递图的自同构群,作用于从右起的顶点集。将顶点固定为图形的根。让|H美元$|表示根的稳定剂。然后图的顶点由右陪集给出|美元汞柱$|,|$g\在H\反斜杠g中$|,根对应于平凡陪集|$小时$|.因此|$|H\反斜杠G|=n$|.
让|$f\冒号H\反斜杠G\到{{mathbb{C}}}$|表示从图的根到其他顶点的边权重。自|G美元$|诱导图上的自同构|美元(高、汞)$|等于|$(高,高)=(高,高)$|为所有人|$h\单位:h$|.因此|$f(gh)=f(g)$|为所有人|$g\单位:g$|和|$h\单位:h$|。这样我们可以查看|$f美元$|作为函数|$f\冒号G\到{\mathbb{C}}$|那就是|H美元$|-左右不变。
顶点集上的函数表示为|$x\冒号H\反斜杠G\到{{mathbb{C}}}$|,我们将其视为左侧-|H美元$|-不变量|$x\冒号G\到{{mathbb{C}}$|也就是说,|$x(hg)=x(g)$|为所有人|$g\单位:g$|和|$h\单位:h$|.
A函数|$x\冒号G\到{{mathbb{C}}$|满足|$x(hg)=x(g)$|为所有人|$g\单位:g$|和|$h\单位:h$|(即,它是左边的-|H美元$|-不变量)当且仅当|$\widehat x(\rho)=\rho(h)\wideha x(\ρ)$|为所有人|$\rho\in\widehat{G}$|和|$h\单位:h$|后一个条件相当于|$\widehat x(\rho)$|位于|$U_\rho(美元)$|,的|$1$|-的特征空间|$\rho|_H$|:傅里叶变换公式的正向含义|$\widehat x(\rho)={{\mathbb{E}}}_{g\in g}x(g)\rho(g)$|,而反向含义则来自反向公式|$x(g)=\sum_\rho d_\rho\operatorname{tr}(\rho(g)^{\dagger}\widehat x(\rho))$|. 让|$m_\rho=\dim U_\rho$|.通过计算所有左侧空间的尺寸-|H美元$|-不变函数,我们得到事实上,条件是|$\widehat{x}(\rho)$|包含列空间|$U_\rho(美元)$|限制|$\widehat{x}(\rho)$|到|$d_\rho m_\rho$|-维子空间|$\operatorname{End}W_\rho$|. 自|$f\冒号G\到{\mathbb{C}}$|既向左又向右-|H美元$|-不变量,|$\widehat{f}(\rho)=\rho$|为所有人|$h,h^{prime}\以h表示$|.所以|$\widehat{f}(\rho)$|叶子|$U_\rho美元$|不变量。让|U_\rho中的$v^\rho_1,\点,v^\rro_{m_\rho}\$|是…作用的特征基|$\widehat{f}(\rho)$|在|$U_\rho(美元)$|.
对于每个|$\rho\in\widehat{G}$|,选择单一基础|$a_1^\rho,\点,a_{d_\rho}^\rho$|属于|$W_\rho(美元)$|,对于每个|$j\在[d_\rho]中$|和|$k\英寸[m_\rho]$|,定义|$x^\rho_{j,k}\冒号G\到{\mathbb{C}}}$|通过设置|$\widehat{x^\rho_{j,k}}(\rho)=v^\rho_k(a_j^\rho)^{\dagger}/\sqrt{d_\rho}$|和|$\widehat x(\rho^{\prime})=0$|为所有人|$\rho^{\prime}\ne\rho$|.
功能|$x^\rho_{j,k}$|,使用|$\rho\in\widehat{G}$|,|$j\在[d_\rho]中$|,|$k\英寸[m_\rho]$|满足以下属性。(1)|$x^\rho_{j,k}$|是左边的-|H美元$|-不变量,也就是说,是函数|$H\反斜杠G\到{{mathbb{C}}}$|(由于|$\widehat{x^\rho_{j,k}}$|在中|$U_\rho(美元)$|),
(2)|$x^\rho_{j,k}$|是的特征函数|M_f美元$|(自|$\widehat{f}(\rho)\wideha{x^\rho_{j,k}}(\ rho)$|是的标量倍数|$\widehat{x^\rho _{j,k}}(\rho)$|)
(3) 功能|$x^\rho_{j,k}$|是成对正交的|$\l垂直x^\rho_{j,k}\r垂直_2=1$|事实上,Parseval认为|$\langle x^\rho_{j,k},x^{\rho^{prime}}_{j^{prime},k^{prime}}\rangle_{\textrm{HS}}=0$|如果|$\rho\ne\rho^{\prime}$|、和 (4) 它们是所有功能的基础|$H\反斜杠G\到{{mathbb{C}}}$|(通过正交性和尺寸计算(4.3).
此外,我们每个人都有|$\rho美元$|,|$j\在[d_\rho]中$|、和|$k\英寸[m_\rho]$|那个 对于每个固定|$\rho\in\widehat G$|,套|$S_\rho=\{\rho(g)v_k^\rho:g\在g中,k\在[m_\rho]\}中$|。从现在起|$\rho(h)v_k^\rho=v_k*\rho$|为所有人|$k\英寸[m_\rho]$|(因为|$M_\rho(美元)$|是|$1$|-的特征空间|$\rho|_H$|),我们看到了|$|S|\le|G/H|m_\rho\len^2$|.通过复杂形式的引理4.1,存在单一基础的选择|$a_1^\rho,\点,a_{d_\rho}^\rho$|在定义中|$x^\rho_{j,k}(g)$|更早,以便因此,功能|$x^\rho_{j,k}$|覆盖所有不可约表示|$\rho美元$|和指数|$j\在[d_\rho]中$|和|$k\英寸[m_\rho]$|,形成一个整体|$\sqrt{\log n}$|-有界特征基。 为了得到真正的正交本征基,我们可以重复定理证明中的技术1.3在前一小节中。我们省略了细节。
随机Cayley图的5个小集展开
在本节中,我们将证明定理1.7,推广Naor定理[16]随机Cayley图到非贝拉群的小集展开。回顾Schatten的定义|美元$|-规范|$\left\lVert\cdot\right\rVert_{S_p}$|来自节2.3我们在下面陈述了群体的Hausdorff–Young不等式,这是标准的,尽管我们包括了它的简短证明(参见[14]局部紧幺模群的证明)。
引理5.1(Hausdorff–群的Young不等式)
让|G美元$|是一个有限群|$f\冒号G\到{\mathbb{C}}$|。对于任何|1美元兑2美元$|具有|$1/p+1/q=1美元$|,一个有
证明。根据Riesz–Thorin插值定理,检查不等式就足够了|$(p,q)=(2,2)$|和|$(1,\英寸)$|。对于|$(p,q)=(2,2)$|,我们有|$\|f\|_{S_2}=\|f\ |_2$|由Parseval编写。对于|$(p,q)=(1,\infty)$|我们有作为|$\left\lVert\rho(g)\right\rVert_{\operatorname{op}}=1$|为所有人|$g\单位:g$|.
引理5.2。让|G美元$|成为一个有限群。对于函数|$f,x\冒号G\到{{mathbb{C}}}$|而且是真的|$p\ge 1美元$|,一个有
证明。对于每个|$\rho\in\widehat{G}$|我们有这里不等式步骤使用矩阵Hölder不等式(2.3):|${\operatorname{Tr}}(AB)\le\left\lVert A\right\rVert_{S_p}\left\ lVert B\right\ rVert_{S_p/(p-1)}}$|为所有人|$p\在[1,\infty]中$|。最后一步使用矩阵的奇异值|美元$|是奇异值的平方根|AA美元$|. 因此,将卷积和Parseval恒等式应用于非贝拉傅里叶变换(第2.1),我们有这证明了期望的不等式。 Naor在一致光滑赋范空间中通过一个新的Azuma型集中不等式证明了随机Cayley图Schatten范数的以下一致界。
存在一个通用常数|$C>0$|具有以下属性。对于任何正整数|千美元$|和任何有限群|G美元$|,如果|$g_1,\点,g_k\以g表示$|然后,至少以概率独立一致地随机选择|$1/2$|,函数|$f\冒号G\到{\mathbb{R}}$|由提供满足每个整数同时|$p\ge 2美元$|. 利用这个集中引理,我们现在可以证明定理1.7与中的证明不同[16]对于阿贝尔群,我们不需要依赖于有界本征基。
让|$g_1,\点,g_k\以g表示$|是生成Cayley(多重)图的随机群元素。定义|$f\冒号G\到{\mathbb{R}}$|如中所示(5.2).
让|$X\子项G$|具有|$1<\left\lvert X\right\rvert\leleft\lfert G\right\ rvert/2美元$|.定义函数|$x\冒号G\到{\mathbb{R}}$|通过检查起来很简单我们也有应用不等式|$\left\lvert\left\ langle f\ast x,x\right\rangle\right\servert\left\lvert f\right\ rvert_{S_p}\left\\x\rift\|_{2p/(p+1)}^2$|从引理5.2,并具有上限|$\left\lVert f\right\rVert_{S_p}\lesssim\left\ lVert G\right\服务器^{-1+1/p}\sqrt{pk}$|从引理5.3,我们至少以概率获得|$1/2$|,一个有同时针对所有正整数|美元$|.将两边分开|$2k\left\lvert X\right\rvert\left\ lvert G\设置减去X\rift\rvert/\left\flvert G\right\ rvert$|,我们获得在最后一步中,我们将不等式应用到哪里|$x^t(1-x)^{1-t}+x^{1-t}(1-x$|对于|$x=\left\lvert x\right\rvert/\left\ lvert G\right\ rvert\le 1/2$|和|$t=1/(p+1)\英寸[0,1/2]$|最后,设置|$p=\left\lceil\log\left\lvertX\right\lvert\right\lceil$|,我们看到最终表达式的上限为|$O(\sqrt{(\log\left\lvert X\right\rvert)/k})$|. 基金
这项工作得到了国家科学基金奖[DMS-1764176 to Y.Z.]的支持;斯隆研究奖学金[发给Y.Z.];和麻省理工学院所罗门-布赫斯鲍姆基金[致Y.Z.]。
致谢
赵感谢阿萨夫·纳尔的讨论和鼓励他解决这个问题。我们感谢张圣通指出了一些印刷错误。
工具书类
[1] 阿龙
,N。
、和年。
罗伊赫曼
“
随机Cayley图和扩展器
.”随机结构。算法
5
(1994
):271
–84
. [2] 球
,英国。
“
现代凸几何简介
.“在几何风格
.,卷。31
.1
–58
.剑桥
:剑桥大学出版社
,1997
. [3] 巴蒂亚
,R。
矩阵分析
.数学研究生课程
,卷。169
.纽约
:施普林格
,1997
. [4] 布勒亚尔
,E.公司。
,B。
绿色
、和T。
道
“
近似群的结构
.”出版物。数学。高等科学研究院。
116
(2012
):115
–221
. [5] 康隆
,D。
、和年。
赵
“
拟随机Cayley图
.”离散分析。
纸张编号。6
(2017
):. [6] 戴维斯
,C、。
、和W.M.公司。
卡汉
“
特征向量的扰动旋转。三
.”SIAM J.数字。分析。
7
(1970
):1
–46
. [7] 弗雷先生
,总会计师。
集合加法结构理论的基础
.罗得岛州普罗维登斯
:美国数学学会
,1973
.. [8] 绿色
,B。
“
关于传递集的宽度:有限群矩阵系数的界
.”杜克大学数学。J。
169
(2020
):551
–78
. [9] 绿色
,B。
、和答:。
威格德森
第22届麦吉尔计算复杂性邀请研讨会讲稿
,2010
,. [10] 格罗莫夫
,M。
“
多项式增长和扩张映射组
.”高等科学研究院。出版物。数学。
53
(1981
):53
–73
. [11] 霍尔
,K.M.公司。
“
安|美元$|-二维二次布局算法
.”管理。科学。
17
(1970
):219
–29
. [12] Hoory公司
,美国。
,N。
Linial公司
、和答:。
威格德森
“
扩展图及其应用
.”牛。阿默尔。数学。Soc公司
. 43
(2006
):439
–561
. [13] 小川县
,年。
,五、。
罗德尔
、和M。
沙赫特
“
Cayley图的差异与特征值
.”捷克斯洛伐克数学。J。
66
(2016
):941
–54
. [14] 昆泽
,注册会计师。
“
L(左)|$_p$|局部紧幺模群上的Fourier变换
.”事务处理。阿默尔。数学。Soc公司。
89
(1958
):519
–40
. [15] 卢博茨基
,答:。
“
纯数学和应用数学中的扩张图
.”牛。阿默尔。数学。Soc公司
. 49
(2012
):113
–62
. [16] 纳尔
,答:。
“
关于Alon–Roichman图的Banach空间值Azuma不等式和小集等参性
.”组合概率。计算。
21
(2012
):623
–34
. [17] 里戈莱
,第页。
、和J.-C.公司。
Hütter公司
高维统计(课堂讲稿)
,2019
,, . [18] 斯皮尔曼
,D。
“
谱图论
.“在组合科学计算
.495
–524
.佛罗里达州博卡拉顿
:查普曼和霍尔/CRC计算。科学。序列号。出版社
,2012
. [19] 特罗普
,J.A.公司。
“
随机矩阵和的用户友好尾界
.”找到。计算。数学。
12
(2012
):389
–434
.
©作者2020。牛津大学出版社出版。保留所有权利。有关权限,请发送电子邮件至:journals.permission@oup.com。