- Chinese name
- Fourier series
- Foreign name
- Fourier series
- Presenter
- Fourier
- Applicable fields
- Any periodic function
- Nature
- A special trigonometric series
- Applied discipline
- mathematics
French mathematician J- B.-J. Fourier It is proposed when studying the boundary value problem of partial differential equations. Thus, it greatly promotes the development of partial differential equation theory. in China, Cheng Minde The first systematic study of multivariate trigonometric series and multivariate Fourier series. He first proved the uniqueness theorem of the spherical sum of multivariate trigonometric series, and revealed many characteristics of the Riess Boehner spherical average of multivariate Fourier series. Fourier series has greatly promoted the development of partial differential equation theory. stay mathematical physics And has important applications in engineering. [1] Given a period of T function X (t), then it can be expressed as Infinite series ： (j is imaginary unit) (1) Among them, It can be calculated according to the following formula: be aware; Is a function with period T, so the periodic signals with different values of k have a harmonic relationship (that is, they all have a common period T). When k=0, the corresponding term in formula (1) is called DC component. When k=1, it has fundamental frequency, which is called first harmonic or fundamental wave
Second harmonic, third harmonic, etc.
Fourier series astringency
Convergence of Fourier series: satisfy Dirichlet condition Of Periodic function Fourier series expressed as are convergent. The Dilihuri conditions are as follows: In any period, x (t) must be absolutely integrable; In any limited section Where x (t) can only take a limited number of maximum or minimum values; On any finite interval, x (t) can only have a finite number Type I breakpoint 。 Gibbs phenomenon : On the nondifferentiable points of x (t), if we only take the finite terms in the infinite series on the right of formula (1) as sum x (t), then x (t) will fluctuate on these points. A simple example is the square wave signal. Orthogonality
The so-called two differences vector Orthogonality refers to their inner product 0, which means that there is no correlation between these two vectors. For example, in three-dimensional Euclidean space, vectors perpendicular to each other are orthogonal. In fact, orthogonality is an abstraction and generalization of perpendicularity in mathematics. A group of n mutually orthogonal vectors must be linearly independent, so they must be expanded into an n-dimensional space, that is, any vector in the space can be expressed linearly with them. The orthogonality of trigonometric function family is expressed by the formula: Parity
Odd functions can be expressed as sine series, while even functions can be expressed as cosine series:
As long as we pay attention to Euler's formula:, these formulas can be easily derived from the formula of Fourier series above.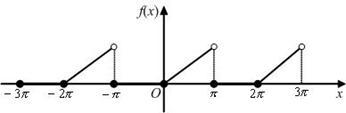 
Fourier series Generalized Fourier series
Similar to the orthogonal decomposition of vector in geometric space, Fourier series of periodic function is the orthogonal decomposition of function in inner product space. Its orthogonal decomposition is derived from The basis is generalized to Legendre (Legendre, 1775-1837) polynomials and Haar (Hal, 1885-1993) wavelet bases, which are called generalized Fourier series. Any orthogonal function system If the function f (x) defined on [a, b] only has a finite number of discontinuity points of the first kind, then if f (x) satisfies the closure equation: Then series
It must converge to f (x), where:
In fact, no matter whether (5) is convergent or not, we always have:
Establishment, which is called Bessel (Bessel） Inequality 。 In addition, Eq. (6) is easily determined by Orthogonality Because for any unit orthogonal basis , vector x in The projection on is always 。 [2] 
