一道古老的几何题落入了新的数学技巧
三位数学家首次展示了如何将面积与圆相同的正方形切割成可以可视化的可互换碎片。
A类公元前450年左右，克拉佐梅纳的阿纳萨戈拉斯有时间思考。这位希腊数学家因声称太阳不是神，而是一块白炽的岩石，像伯罗奔尼撒半岛那么大而入狱。作为一位相信“理性主宰世界”的哲学家，他用自己的监禁来解决一个众所周知的数学问题：用罗盘和直尺，你能得到一个与给定圆面积相等的正方形吗？
令人惊讶的是，数学家仍在研究这个问题。他们正在取得进展。一篇论文在线发布2022年2月初安德拉斯·马瑟和奥列格·皮库尔科沃里克大学和乔纳森·诺埃尔维多利亚大学是最新加入这一古老传统的大学。作者展示了如何通过将一个圆切割成可以可视化和可能绘制的碎片来将其平方。这是一个建立在丰富历史基础上的结果。
1882年，德国数学家费迪南·冯·林德曼证明，将圆平方为不可能的使用经典工具。他证明了pi——半径为1的圆的面积是一种特殊的被归类为超越数的数（这一范畴也包括欧拉数，e（电子）). 因为之前的一个结果已经证明，不可能用罗盘和直尺来构造一个长度等于超越数的长度，所以也不可能用这种方法来确定一个圆的平方。
阿纳萨戈拉斯：希腊克拉佐梅纳的数学家阿纳萨戈拉斯（Anaxagoras of Clazomenae），图中他是一位中世纪学者纽伦堡编年史，是第一个写关于“圆的平方”这一看似困难的问题的人。这可能是故事的结局，但1925年阿尔弗雷德·塔斯基（Alfred Tarski）通过调整规则再次引发了这个问题。他问人们是否可以通过将一个圆切成有限数量的块来完成这项任务，这些块可以在一个平面内移动，并重新组装成面积相等的正方形，这是一种称为等分解的方法。
换言之，如果两个物体可以被分解成大小和形状相同的碎片，或者更准确地说，“如果你能把它们分割成有限的多个部分，使相应的部分相互一致，”皮库尔科说。
1964年的一篇论文首次在塔斯基对这个问题的解释上取得了实质性进展。作者表明，等量分解不能用剪刀完成。如果可能的话，这项任务将需要更复杂的分形碎片，这些碎片上布满了孔洞和错综复杂的锯齿状边缘。
这就是事情的现状，直到1990年，米克洛斯·拉茨科维奇回答了Tarski的问题一个响亮的“是”：一个圆可以重新配置为一个正方形。
要想象拉兹科维奇的成就，想象一个圆形和方形并排在一页上。他证明了如果圆圈最多分成10个50这些碎片都很复杂，形状也很不寻常，甚至可以在不旋转的情况下移动，直到它们完全填满方形。
但为了得到这个结果，拉兹科维奇并没有处理形状。相反，他将几何问题转化为图论问题。他画了一个带有两组独立的顶点的大图形，一组对应于圆，另一组对应于方，然后在一组顶点和另一组顶点之间建立了一对一的对应关系。
斯坦·瓦贡麦克莱斯特学院的数学家拉兹科维奇（Laczkovich）将这一结果描述为“下巴掉下来”。他展示了如何“取一个圆形空间并使其笔直”
然而，有一个陷阱。拉兹科维奇的证明是一种存在性证明，数学家称之为“非构造性”。他证明了这是可以做到的，但他无法说出如何构造这些块，也无法以任何方式描述它们。更糟糕的是，这些碎片是“不可测量的”，这意味着无法确定它们的面积。
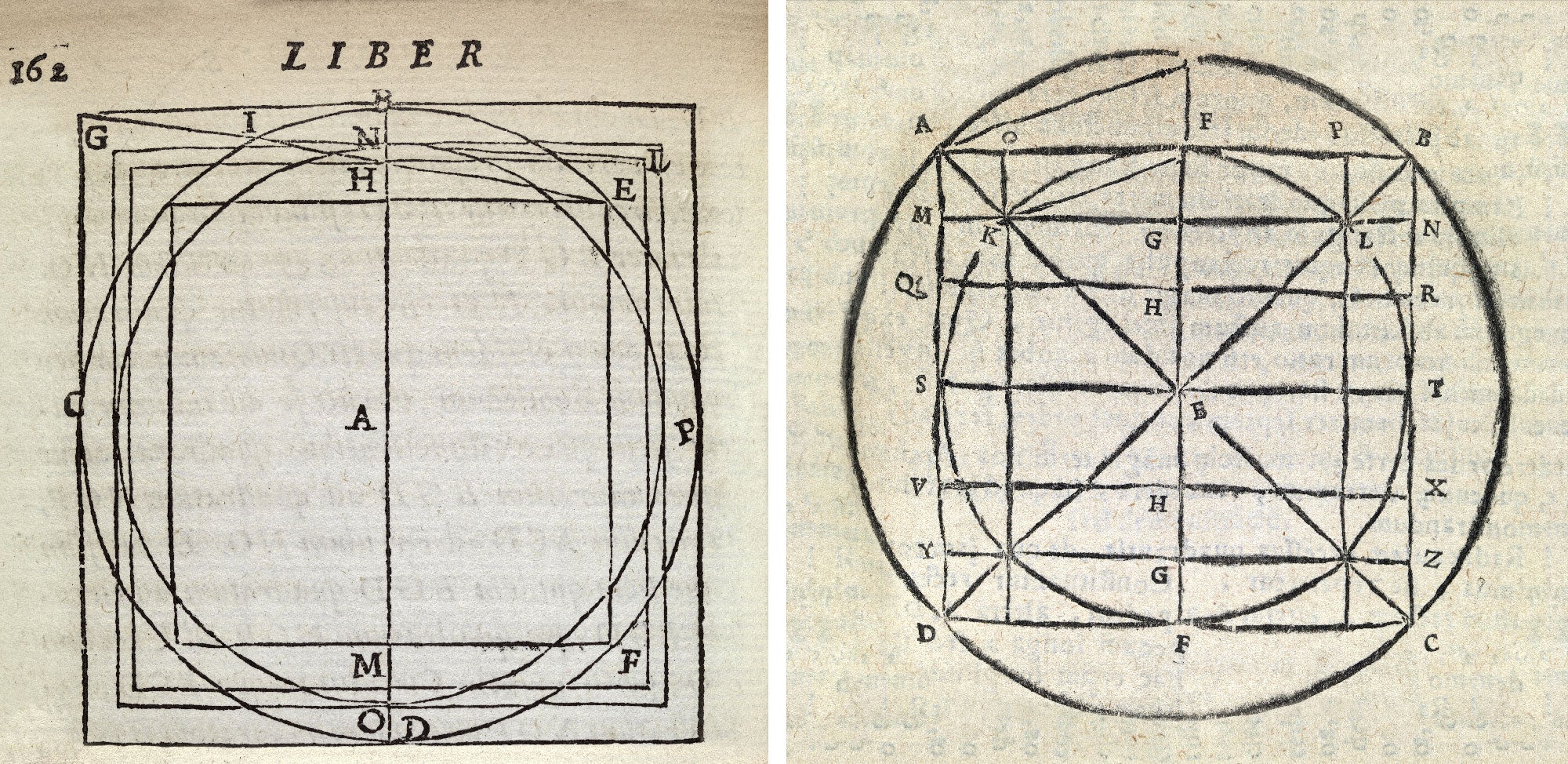摆正圆圈：经过几个世纪的努力，这些图表可以追溯到16世纪和17世纪，费迪南德·冯·林德曼证明，仅用罗盘和直尺就不可能画出一个面积相等的正方形到给定的圆。但如果我们不需要这些工具，问题就有了新的生命。插图由中殿图书馆/科学资源提供.几十年后，又迈出了一大步一篇论文2016年1月由Łukasz Grabowski、Máthé和Pikhurko发布。与拉兹科维奇的证明不同，他们的证明几乎是完全有建设性的，这意味着这些作品大多都有明确的定义。但这里又有一个陷阱：圆圈中定义明确的部分并不能填满整个正方形。为了覆盖正方形的一小部分，仍然需要额外的块。这部分太小了，没有面积，数学家称之为“测量零点集”
“几乎所有的空间都得到了保护，”他说安德鲁·马克斯，洛杉矶加州大学数学家。他说，你甚至不能把缺失的部分画进去，因为这一组看起来是看不见的。
马克斯说，尽管有这些必要的额外部分，但结果是向前迈出了一大步。“他们找到了一种方法来将圆平方，除了一组测量零点之外，这种方法几乎在任何地方都有效。”
一年后，马克斯与现在多伦多大学的斯宾塞·昂格一起取得了重大进步，为无处不在的圆平方定理提供了第一个完全建设性的证据。 他们的论文提供了使圆方正所需的所有部件的完整描述。“他们的棋子更好，”马瑟说。“他们没有这样丑陋的零区设置。”
也就是说，他们的证明涉及更多的片段——大约10个片段200-这些作品仍然相当复杂。“我们论文的缺点是，”Marks说，“尽管这些片段是从数学的角度明确定义的，但很难将它们可视化。”
这留下了一些改进的空间，这就是马瑟、诺埃尔和皮库尔科所做的。他们的作品，又有大约10幅200，形状更简单，数学家更容易想象。
马克斯说：“这里的一大飞跃是，你不能用你容易看到的方式画出斯宾塞和我的作品，但用这些作品你可以。”。
但这并不是故事的结局。对于这个问题，“还有更多的数学要做”，他说亚历山大·凯克里斯他是加州理工学院的数学家。“这是一个过程。”
Pikhurko已经有了进一步简化作品的想法，减少作品总数，减少作品的不均匀性。马克斯做过计算机实验，表明——但并没有证明——等分解可以用22块来完成。他认为最低人数可能更低。
他说：“我敢打赌一杯啤酒，你可以用不到20块的啤酒把圆圈弄平。”。“但我不会赌1000美元。”
史蒂夫·纳迪斯住在马萨诸塞州剑桥市。他的文章出现在许多杂志上，包括发现和天文他最近是《》的合著者生命的形状.
这篇文章是最初出版的上 量子抽象博客。
引导图像：三位数学家发现了迄今为止最有效的圆圈平方方法，或者等效地，通过将形状切割成足够简单的块，以便可视化，然后重新排列它们，来围绕正方形旋转。图片来源：安德烈斯·马瑟
-
史蒂夫·纳迪斯住在马萨诸塞州剑桥市。他的文章出现在许多杂志上，包括发现和天文。最近，他与人合著了生命的形状.
获取Nautilus时事通讯
尖端科学，由最聪明的在世思想家揭开。
