A类算法已经变得无处不在。他们优化了我们的通勤、处理支付和协调互联网流量。似乎对于每一个可以用精确数学术语表达的问题，都有一种算法可以解决它，至少在原则上是这样的。
但情况并非如此，有些看似简单的问题永远无法通过算法解决。先驱计算机科学家阿兰·图灵证明这种“无可争辩”的问题在近一个世纪前就存在了，在同一篇论文中，他阐述了计算的数学模型这开启了现代计算机科学。
图灵用一种违反直觉的策略证明了这一开创性的结果：他定义了一个问题，拒绝任何解决它的尝试。
“我问你在做什么，然后我说，‘不，我要做些不同的事’”拉胡尔·伊兰戈他是麻省理工学院学习理论计算机科学的研究生。
图灵的策略基于一种称为对角化的数学技术，这种技术有着悠久的历史。以下是对他证明背后逻辑的简化说明。
弦论
对角化源于解决一个涉及位串的普通问题的巧妙技巧，每个位串可以是0或1。给定一个长度相等的字符串列表，您能生成一个不在列表中的新字符串吗？
最直接的策略是依次考虑每个可能的字符串。假设您有五个字符串，每个字符串五位长。首先扫描列表00000。如果它不在那里，你可以停下来；如果是，则转到00001并重复该过程。这很简单，但对于长字符串的长列表来说速度很慢。
对角化是另一种方法，它逐位构建缺少的字符串。从列表中第一个字符串的第一位开始，将其反转，这将是新字符串的第一个位。然后反转第二个字符串的第二个位，并将其用作新字符串的第二位，然后重复，直到列表的末尾。翻转的位确保新字符串与原始列表中的每个字符串在至少一个位置上都不同。（它们还通过字符串列表形成一条对角线，为该技术命名。）
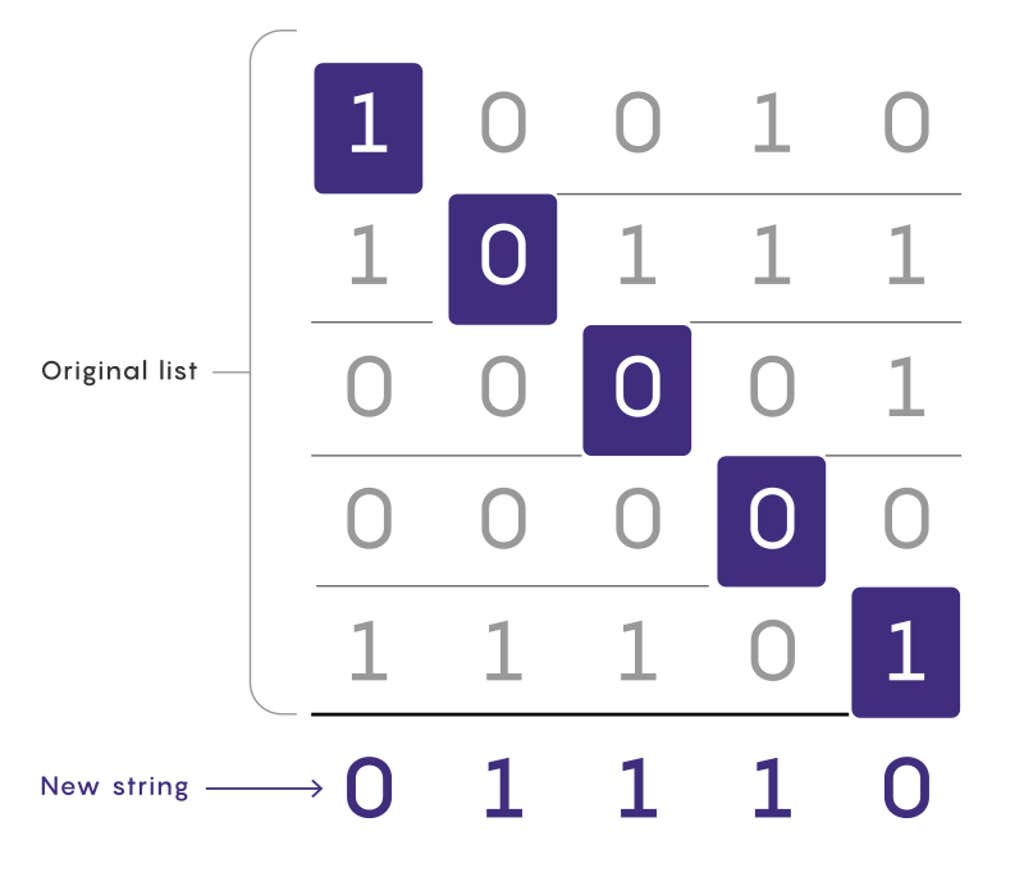信贷：Merrill Sherman/Quanta Magazine对角化只需要检查列表中每个字符串的一个位，因此它通常比其他方法快得多。但它真正的力量在于它能很好地处理无穷大。
“字符串现在可以是无限的；列表可以是无限-它仍然有效，”他说瑞恩·威廉姆斯麻省理工学院的理论计算机科学家。
第一个利用这种力量的人是乔治·坎托，集合论数学子领域的创始人。1873年，康托用对角化证明了一些无穷大是比其他大六十年后，图灵将康托的对角化理论应用到计算理论中，使其具有明显的逆向风格。
限制游戏
图灵想证明没有算法能够解决的数学问题的存在，也就是说，具有定义明确的输入和输出但没有从输入到输出的简单过程的问题。他只关注决策问题，使这项模糊的任务更易于管理，因为决策问题的输入可以是0和1的任何字符串，输出可以是0或1。
判断一个数字是否是素数（只能被1和它本身整除）是一个决策问题的例子——如果输入一个表示数字的字符串，如果数字是素数，正确的输出是1，如果不是，正确的结果是0。另一个例子是检查计算机程序的语法错误（相当于语法错误）。在那里，输入字符串代表不同程序的代码——所有程序都可以这样表示，因为它们是这样在计算机上存储和执行的——目标是如果代码包含语法错误，输出1；如果不包含，输出0。
一个算法只有在为每一个可能的输入生成正确的输出时才能解决问题——如果它即使失败一次，也不是解决该问题的通用算法。通常，你首先要指定要解决的问题，然后尝试找到一个算法来解决它。图灵在寻找无法解决的问题时，将这个逻辑颠倒过来，他想象了一个包含所有可能算法的无限列表，并使用对角化来构造一个顽固的问题，这个问题会阻碍列表上的所有算法。
想象一下，一个由20个问题组成的作弊游戏，答案不是从一个特定的目标开始，而是为每个问题编造一个拒绝的借口。到游戏结束时，他们已经描述了一个完全由其缺乏的品质定义的对象。
图灵的对角化证明是这个游戏的一个版本，在这个版本中，问题遍历无限的可能算法列表，反复问：“这个算法能解决我们想要证明的不可争论的问题吗？”
威廉姆斯说：“这是一种‘无穷大的问题’。”。
为了赢得比赛，图灵需要解决一个问题，每个算法的答案都是否定的。这意味着识别一个特定的输入，使第一个算法输出错误的答案，另一个输入使第二个算法失败，等等。他发现这些特殊的输入使用了一个类似于库尔特·哥德尔最近使用的技巧证明像“这个陈述无法证明”这样的自我参照断言给数学基础带来了麻烦。
关键的见解是，每个算法（或程序）都可以表示为0和1的字符串。这意味着，与错误检查程序的示例一样，一个算法可以将另一个算法的代码作为输入。原则上，算法甚至可以将自己的代码作为输入。
有了这个见解，我们可以定义一个像图灵证明中那样的不可争论的问题：“给定一个表示算法代码的输入字符串，如果该算法在自己的代码是输入时输出0，则输出1；否则输出0。”每一个试图解决这个问题的算法都会在至少一个输入上产生错误的输出，即与自己的代码相对应的输入。这意味着任何算法都无法解决这个反常的问题。
否定不能做什么
计算机科学家还没有完成对角化。1965年，尤里斯·哈特马尼斯（Juris Hartmanis）和理查德·斯坦恩斯（Richard Stearns）将图灵的论点改编为证明并非所有可计算的问题都是等式生成的，这在本质上比其他问题更难。这一结果开创了计算复杂性理论领域，该领域研究计算问题的难度。
但复杂性理论也揭示了图灵相反方法的局限性。1975年，西奥多·贝克、约翰·吉尔和罗伯特·索洛维证明复杂性理论中的许多悬而未决的问题永远不可能仅仅通过对角化来解决。其中最主要的是著名的P对NP问题，它询问所有具有容易检查的解决方案的问题是否也容易用正确巧妙的算法解决。
对角化的盲点是高度抽象的直接结果，这使得它如此强大。图灵的证明并没有涉及到实际中可能出现的任何无可争辩的问题，相反，它在动态中捏造了这样一个问题。其他对角化证明同样远离现实世界，因此它们无法解决现实世界细节重要的问题。
威廉姆斯说：“他们远距离处理计算。”。“我想象一个人正在处理病毒，并通过手套箱访问它们。”
对角化的失败是解决P对NP问题的早期迹象长途旅行尽管有其局限性，对角化仍然是复杂性理论家武库中的关键工具之一。2011年，威廉姆斯将其与一系列其他技术一起用于证明某种有限的计算模型无法解决一些非常困难的问题&这是25年来研究人员一直回避的结果。这与解决P与NP的问题相去甚远，但它仍然代表着重大进展。
如果你想证明某些事情是不可能的，不要低估说“不”的力量。
这篇文章是最初出版的在上 量子抽象博客。
主要图片：Kristina Armitage/Quanta Magazine
-
Ben Brubaker是一名自由科学记者，他的作品出现在Quanta杂志,科学美国人、和对话以及他的博客《反思中的测量》。他拥有耶鲁大学物理学博士学位，并在科罗拉多大学博尔德分校进行博士后研究。
获取Nautilus时事通讯
尖端科学，由最聪明的在世思想家揭开。
