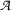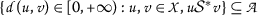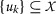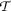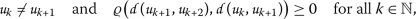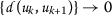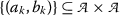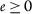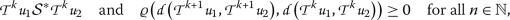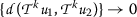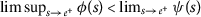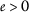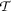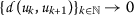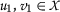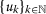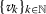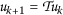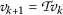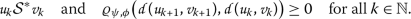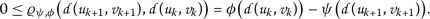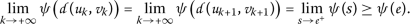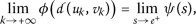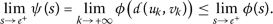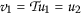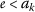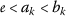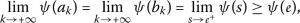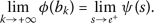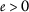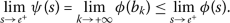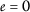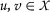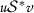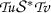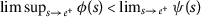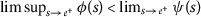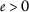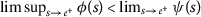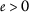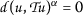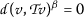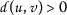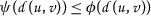摘要
1 介绍




2 前期工作
2.1 代数背景













提议1









引理1










2.2 Roldán–Shahzad大量频谱收缩






定义1



定义2



\((\mathcal) {乙}_ {1} ) \) 以下为: -
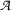
非空且 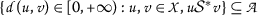
。 \((\mathcal) {乙}_ {2} ) \) 以下为: -
如果 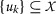
是皮卡车吗 \(\数学{S}\) -非递减序列 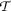
这样的话 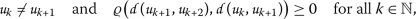
然后 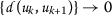
。 \((\mathcal) {乙}_ {3} ) \) 以下为: -
如果 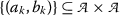
是一个 \(((T,\mathcal{S}^{ast})\) -顺序如下 \({a{k}) 和 \({b{k}) 收敛到相同的极限 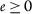
并验证 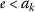
和 \(\varrho(a{k},b{k})\geq0\) 为所有人 \(k\in\mathbb{N}\) ,然后 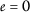
。 \((\mathcal) {乙}_ {4} ) \) 以下为: -
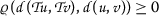
为所有人 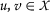
这样的话 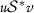
和 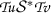
。

\((\mathcal) {乙}_ {2} ^{\prime})\) 以下为: -
如果 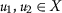
是这样的两点 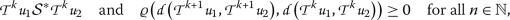
然后 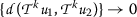
。 \((\mathcal) {乙}_ {5} ) \) 以下为: -
如果 \((a{k},b{k}) 是一个 \(((T,\mathcal{S}^{ast})\) -顺序如下 \(\{b_{k}\}\右箭头0\) 和 \(\varrho(a_{k},b_{k})\geq 0\) 为所有人 \(k\in\mathbb{N}\) ,然后 \(\{a_{k}\}\rightarrow0\) 。
定理1
证明
2.3
ω -插入性宫缩-Reich-Rus型宫缩














定理2






2.4 Proinov收缩
定理3



( \({1}\) ): -
ψ 不会减少 ; ( \(a_{2}\) ): -
\(φ<psi) 对于任何 \(s>0\) ; ( \(a{3}\) ): -
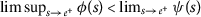
对于任何 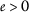
。





三
\((α,β,psi,φ)) -内插收缩



定义3












定理4


-
二元关系 \(\mathcal {宋体}_ {十} \) 在 X(X) 由提供 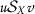
为所有人 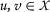
, -
\(A=(0,+\输入)\) , -
\(\varrho_{\psi,\phi}:(0,+\infty)\次(0,+/infty,\rightarrow\mathbb{R}\) , $$\begin{aligned}&\varrho_{\psi,\phi}(t,s)=\phi(s)-\psi(t)\quad\textit{代表所有}t,s\in(0,+\infty)。 \结束{对齐}$$

证明
\((\mathcal) {乙}_ {1} ) \) 以下为: -
这是微不足道的,因为 \(A=(0,+\输入)\) 。 \((\mathcal) {乙}_ {2} ) \) 以下为: -
让 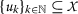
成为皮卡德 \(\数学{S}\) -非递减序列 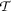
这样的话 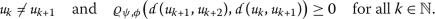
然后引理 2 意味着 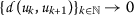
。 \((\mathcal) {乙}_ {2} ^{\prime})\) 以下为: -
让 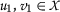
是两个初始点,这样Picard序列 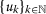
和 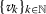
,由定义 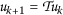
和 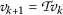
为所有人 \(k\in\mathbb{N}\) ,满足 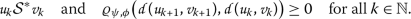
因此,对于所有人来说 \(k\in\mathbb{N}\) , 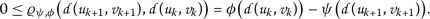
考虑到条件 \((a{2})\) 事实上 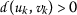
,前面的不等式意味着 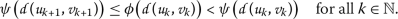
(3.2) 自从函数 ψ 那么就不会减少了 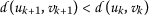
为所有人 \(k\in\mathbb{N}\) .让 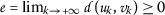
。请注意 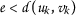
为所有人 \(k\in\mathbb{N}\) .证明这一点 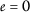
,假设 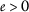
在这种情况下,以下限值相等: 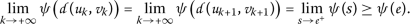
然后( 3.2 )导致 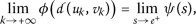
这与之相矛盾( \(a{3}\) )因为 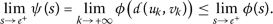
因此, 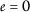
也就是说, 
。 \((\mathcal) {乙}_ {2} ) \) 以下为: -
它直接从 \((\mathcal) {乙}_ {2} ^{\prime})\) 通过选择任意点 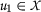
和使用 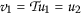
在里面 \((\mathcal) {乙}_ {2} ^{\prime})\) 。 \((\mathcal) {乙}_ {3} ) \) 以下为: -
让 \((a_{k},b_{k{) 成为 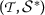
-顺序如下 \({a{k}) 和 \({b{k}) 收敛到相同的极限 
并验证 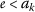
和 \(\varrho{psi,\phi}(a{k},b{k})\geq0\) 为所有人 \(k\in\mathbb{N}\) 因此,对于所有人来说 \(k\in\mathbb{N}\) , \(0\leq\varrho{psi,\phi}(a{k},b{k})=\phi(b{k{)-\psi(a{k})) ,所以 \(psi(a{k}) .自 \(a{k}>0\) 和 \(b{k}>0\) ,然后( \(a_{2}\) )意味着 $$\psi(a_{k})\leq\phi(b_{k})<\psi(b_{k})\quad\text{for all}k\in\mathbb{N}$$ (3.3) 作为 ψ 不会减少, \(a{k}<b{k}\) ,所以 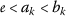
为所有人 \(k\in\mathbb{N}\) .考虑到 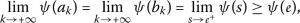
财产( 3.3 )导致 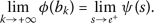
但是,如果 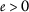
,我们推断出一个矛盾( \(a{3}\) )因为 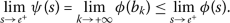
因此, 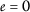
。 \((\mathcal) {乙}_ {4} ) \) 以下为: -
让 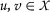
是这样的 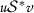
和 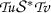
也就是说, 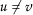
和 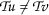
因此收缩性条件( 2.1 )意味着 
\((\mathcal) {乙}_ {5} ) \) 以下为: -
让 \((a{k},b{k}) 成为 \(((T,\mathcal{S}^{ast})\) -顺序如下 \(\{b_{k}\}\rightarrow 0\) 和 \(\varrho{psi,\phi}(a{k},b{k})\geq0\) 为所有人 \(k\in\mathbb{N}\) 。我们可以重复( 3.3 ),所以我们推断 \(a{k}<b{k}\) 为所有人 \(k\in\mathbb{N}\) .因此 \(\{a_{k}\}\rightarrow0\) . □
推论1
推论2
4 的不动点定理 \((α,β,psi,φ)) -内插收缩
引理2


( \(\mathbb{A}\) ): -
它可以容纳 , 同时 , ( \({1}\) ): -
ψ 不会减少 , ( \(a{2}\) ): -
\(φ(s)<\psi(s)\) 为所有人 \(s>0\) , ( \(a{3}\) ): -
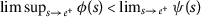
为所有人 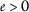
。
( \(\mathbb{B}\) ): -
如果 \({s_{n}\}\子集(0,+\infty)\) 是这样一个序列 \(psi(s{k+1})\leq\phi(s{k}^{1-\beta}s{k+1}^{\beta{)\) 为所有人 \(k\in\mathbb{N}\) , 然后 \(\{s_{k}\}\rightarrow 0\) 。

证明
































备注1
-
1 请注意,前面的结果表明,条件(ii)在[ 23 ,引理3.2]当我们假设(iii)成立时。 -
2 我们包括假设( \(\mathbb{B}\) )因为它可以很容易地在实际例子中检查。 例如,如果有 \([0,1)中的\lambda\) 这样的话 \(磅/平方英寸=秒) 和 \(φ=λs) 为所有人 \(在(0,+\infty)中为\) ,然后( \(\mathbb{B}\) )通常保持不变,我们不需要检查中给出的属性( \(\mathbb{A}\) ).
定理5


( \({1}\) ): -
ψ 不会减少 , ( \(a{2}\) ): -
\(φ<psi) 为所有人 \(s>0\) , ( \(a{3}\) ): -
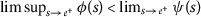
为所有人 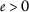
。




证明






























































定理6









( \({1}\) ): -
ψ 不会减少 \((0,+\infty)\) ; ( \(a{2}\) ): -
\(φ<psi) 为所有人 \(s>0\) ; ( \(a{3}\) ): -
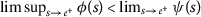
为所有人 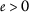
; ( \(a{4}\) ): -
如果 \(s_{0}\在[0,+\infty中)\) 验证 \(磅/平方英寸(s_{0})\leq\phi(0)\) , 然后 \(s_{0}=0\) 。




证明









-
如果 \(阿尔法>0) ,然后 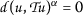
,如果 \(β>0\) ,然后 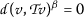
在这两种情况下, 
然而,假设( \(a{4}\) )意味着 
,这与事实相矛盾 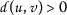
。 -
如果 \(阿尔法=贝塔=0) ,然后( 4.7 )意味着 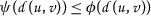
,这与( \(a{2}\) )因为 
。

推论3







证明

推论4







证明
推论5







证明
推论6


( \(a{2}\) ): -
\(\phi(s)<s\) 为所有人 \(s>0\) ; ( \(a{3}\) ): -
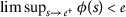
为所有人 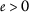
。





证明
推论7


( \({1}\) ): -
ψ 不会减少 \((0,+\输入)\) ; ( \(a{2}\) ): -
\(s<\psi(s)\) 为所有人 \(s>0\) 。





证明


推论8








证明

5 结论和展望工作
数据和材料的可用性
笔记
注意,这位作者忘记在他的主要结果中包括度量空间的完整性[ 23 ].
工具书类
Boyd,D.W.,Wong,J.S.W.:关于非线性收缩。 程序。 美国数学。 Soc公司。 20 ,458–464(1969年) Geraghty,M.:关于压缩映射。 程序。 美国数学。 Soc公司。 40 , 604–608 (1973) Amini-Harandi,A.,Petrušel,A.:完全度量空间中通过改变距离技术的不动点定理。 Miskolc数学。 笔记 14 , 11–17 (2013) Jleli,M.,Samet,B.:巴拿赫压缩原理的新推广。 J.不平等。 申请。 2014 , 38 (2014) Wardowski,D.:完备度量空间中一类新型压缩映射的不动点。 不动点理论应用。 2012 ,文章ID 94(2012) 巴纳赫,S.:《综合集成抽象与应用辅助方程》(Sur les opérations dans les ensemblies abstraits et leur application auxéquations integales)。 芬丹。 数学。 三 (1), 133–181 (1922) Al-Mezel,S.A.、Alsulami,H.H.、Karapñnar,E.、Roldán López de Hierro,A.F.:通过最近的出版物讨论“多维巧合点”。 文章摘要。 申请。 分析。 2014 ,文章ID 287492(2014) Roldán López de Hierro,A.F.,Karapñnar,E.,Manro,S.:模糊度量空间中的一些新的不动点定理。 J.因特尔。 模糊系统。 27 (5), 2257–2264 (2014) Roldán,A.,Martínez-Moreno,J.,Roldan,C.:关于模糊度量结构之间的相互关系。 伊朗。 J.模糊系统。 10 (2), 133–150 (2013) Khojasteh,F.,Shukla,S.,Radenović,S.:通过模拟函数研究不动点定理的新方法。 菲洛马 29 (6), 1189–1194 (2015) Roldán López de Hierro,A.F.,Karapñnar,E.,Roldá的López de Hirro,C.,Martínez-Moreno,J.:度量空间上通过模拟函数的重合点定理。 J.计算。 申请。 数学。 275 , 345–355 (2015) Roldán López de Hierro,A.F.,Shahzad,n.:新的不动点定理 对 -收缩。 不动点理论应用。 2015 ,文章ID 345(2015) Roldán López de Hierro,A.F.,Shahzad,n.:公共不动点定理 \((\mathcal{R},\mathcal{S})\) -收缩性条件。 不动点理论应用。 2016 ,文章ID 55(2016) Shahzad,N.,RoldáN López de Hierro,A.F.,Khojasteh,F.:一些新的不动点定理 \((\mathcal{A},\mathcal{S})\) -收缩性条件。 Rev.R.学术版。 中国。 精确到Fís。 Nat.,Ser。 一块垫子。 111 (2), 307–324 (2017) Roldán López de Hierro,A.F.,Shahzad,n.:振幅谱压缩和相关不动点定理。 数学 7 , 1033 (2019) Kannan,R.:关于不动点的一些结果。 牛市。 加尔各答数学。 Soc公司。 60 , 71–76 (1968) Kannan,R.:关于不动点的一些结果II。 美国数学。 周一。 76 , 405–408 (1969) Roldán López de Hierro,A.F.,Karapñnar,E.,Fulga,A.:多参数压缩和相关的Hardy–Roger型不动点定理。 数学 8 (6) ,文章ID 957(2020) Krein,S.G.、Petunin,J.I.、Semenov,E.M.:线性算子的插值。 美国数学。 普罗维登斯学会(1978年) Karapñnar,E.:通过插值重新审视Kannan型收缩。 高级理论非线性分析。 申请。 2 (2), 85–87 (2018) Agarwal,R.P.,Karapñnar,E.:通过模拟函数实现的插值Rus–Reich–crc irić型收缩。 安提因。 康斯坦·奥维迪乌斯大学 27 (3), 137–152 (2019) Aydi,H.,Karapñnar,E.,Roldán López de Hierro,A.F.: ω -插补性宫缩-Reich-Rus型宫缩。 数学 7 (1) ,文章ID 57(2019) Proinov,P.D.:度量空间中广义压缩映射的不动点定理。 J.不动点理论应用。 22 , 21 (2020) Roldán López de Hierro,A.F.,Shahzad,n.:结合Jleli和Samet的不动点定理,以及Brancari不等式。 非线性科学杂志。 申请。 9 , 3822–3849 (2016) Agarwal,R.P.,Karapñnar,E.,O'Regan,D.,Roldán López de Hierro,A.F.:度量型空间中的不动点理论。 柏林施普林格出版社(2015) Karapánar,E.,Roldán,A.,Martínez-Moreno,J.,Roldín,C.:偏序度量空间中的Meir–Keeler型多维不动点定理。 文章摘要。 申请。 分析。 2013 ,文章ID 406026(2013) Popescu,O.:一些新的不动点定理 α -度量空间中的Geraghty收缩类型映射。 不动点理论应用。 2014 ,文章ID 190(2014)