这个小星状十二面体由12个五角星或五角星,每个顶点有5个五角星。它是四个非凸多面体之一,面为正多边形或星形,称为开普勒–Poinsot多面体.
开普勒研究了小星状十二面体。它出现在他的和谐蒙迪1619年出版。然而,它也可以在威尼斯圣马克大教堂的地面马赛克中找到,似乎是由保罗·乌切洛早在1430年。

威尼斯圣马克大教堂地面马赛克——保罗·乌切洛
后来埃舍尔在他的两幅版画中使用了它:Constrast:秩序与混乱和引力.
小型星状十二面体和其他开普勒-蓬索特固体对早期地形学家提出了挑战。如果我们将小的星状十二面体视为有12个五面体,每条边上有两个面,那么它应该有(12乘以5/2=30)个边。由于它也有12个顶点,其Euler特征应该是
$$\chi\,=\,V–E+F,=\、12–30+12,=\;–6 $$
由于表面的属(g)与其欧拉特征有关,因此小星状十二面体应该有属(4)!Poinsot首先注意到了这一点,它引起了人们对欧拉公式(V–E+F=2\)有效性的一些困惑,我们现在意识到它只适用于凸多面体。
然而,事实上,我们可以将小的星状十二面体视为从亏格4的表面\(\西格玛\)到三维空间的连续映射的图像。这张地图在每个五角星的中心都有2级的分支点,在图片中隐藏起来了!
事实上,如果我们认为星状十二面体定义了球体的分支覆盖层,那么这个分支覆盖层就变成了黎曼曲面。二十面体的方向保持对称性显然充当了这个黎曼曲面的保角变换。因此,它至少具有交替群{A} _5个\)对称性。
这是克莱因在1877年观察到的:
•Felix Klein、Weitere Untersuchungenüber das Ikosaeder、,数学。安纳伦 12(1877), 321–384.
黎曼曲面(Sigma)可以由12个五边形平铺,每个角5个相交。这些对应于小星形十二面体的12个五角形。由于这种平铺,\(\Sigma \)也可以被认为是双曲线平面\(\mathbb{H}^2)由作为等距线的离散群\(\Gamma\)执行。该组通过规则双曲五边形保留双曲线平面的平铺,每个角5个相交:
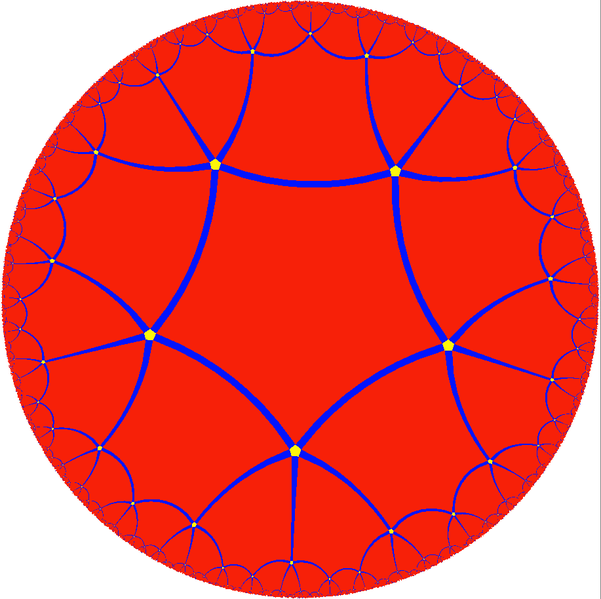
{5,5}瓷砖–Jeff Weeks
这种双曲线平面的平铺称为{5,5}瓷砖.
小星状十二面体是从黎曼曲面(Sigma)到(mathbb{R}^3)的某个映射的图像。但这个曲面也可以以不同的方式映射到\(\mathbb{R}^3),从而得到另一个开普勒-蓬索特多面体,即大十二面体:
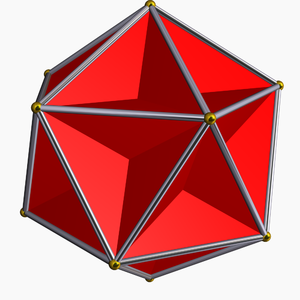
伟大的十二面体–Robert Webb的Stella软件
这并不奇怪,因为大十二面体有12个五边形面,每个顶点有5个面。然而,最终的解释是,大十二面体是二重的在小的星形十二面体中,一个面的顶点位于另一个面的中心,而{5,5}瓷砖是它自己的对偶!
有关大十二面体的更多信息,请参阅此帖子,其中解释了它与异常对称代码的联系:
•Golay代码.
黎曼曲面(Sigma)与五次方程也有着有趣的联系。黎曼曲面也称为“复曲线”,因为其上的点可以用单个复数局部描述。Klein表明,(Sigma)与这些齐次方程所描述的复杂曲线同构:
$$\sum_{i=1}^5 z_i=0,\qquad\sum_{i=1}^5 z_i^2=0,\ qquad_sum_}i=1}^5 z_ i^3=0$$
这三个方程在五个复变量中选取了一组复维2,但当我们“投影化”,识别出相差一个复倍数的解时,我们得到了嵌入在投影空间(mathbb{C}\mathrm{P}^4)中的复曲线。
这称为Bring曲线,并且它是著名的,因为它具有亏格4的任何复曲线(或黎曼曲面)中最大可能的对称群。事实上,这个群体不仅仅是{A} _5个\)但对称群{S} _5个\).
我们可以看到\(\mathrm{S} _5个\)通过将Bring曲面与五次方程关联,起到对称的作用。考虑形式的五次方
$$Q(z)=(z-z_1)\cdots(z–z_5)$$
如果这三个方程
$$\sum_{i=1}^5 z_i=0,\qquad\sum_{i=1}^5 z_i^2=0,\ qquad_sum_}i=1}^5 z_ i^3=0$$
hold,然后\(Q \)采用特殊形式
$$Q(z)=z^5+pz+Q$$
相反,如果(Q)采用这种特殊形式,则其根(z_1,dots,z_5)服从所列的三个方程。因此,布林曲线是一组有序的5元组((z_1,dots,z_5))、模标量因子,它们是形式为(z^5+pz+q)的某些五次曲线的根。
有关这些主题的更多信息,请参阅:
•马蒂亚斯·韦伯,开普勒小星状十二面体作为黎曼曲面,太平洋数学杂志。 220(2005), 167–182.
摘要。我们提供了与小型星状十二面体相关联的亏格4黎曼曲面的雅可比矩阵的一个新的几何计算。从Threlfall的描述开始,我们在这个曲面上引入了其他与全纯1-形式相关的平面共形几何。它们使我们能够证明,雅可比矩阵与一条椭圆曲线的四重乘积是同根的,该椭圆曲线的晶格常数可以用两种不同的方法确定,从而在超几何积分之间产生了一种意想不到的关系。我们还获得了一个新的柏拉图式曲面镶嵌。

小型星形十二面体–Cyp
这张小型星形十二面体的特色图片是用罗伯特·韦伯的Stella软件并放置在Wikicommons上. The same is true of the picture of the大十二面体Robert Webb允许任何人出于任何目的使用这些图片,前提是版权持有人的身份得到了适当的确认。圣马克大教堂(Basilica of St Mark)地面马赛克的图片来自本页:
•乔治·哈特,保罗·乌切洛的多面体.
但可用在Wikicommons上,其中它被列为公共领域。{5,5}瓷砖的图片由绘制汤姆·阮使用Jeff Week的KaleidoTile软件并置于公共领域在Wikicommons上小星形十二面体的旋转图像由塞浦路斯并放置在Wikicommons上在a下Creative Commons Attribution-Share Alike 3.0未导出许可证。
视觉洞察力是一个分享有助于解释高等数学主题的醒目图像的地方。我一直在寻找真正美丽的图像,所以如果你知道,请留言在这里让我知道!









