摘要
介绍
模型描述和准备工作










-
(a) 然后 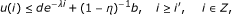
(3)


-
(b) 然后 
(6)






主要成果








































例子








结论
工具书类
Kolmanovskii VB,谢赫LE: 后效系统控制。 在 数学专著的翻译 . 第157卷 美国数学学会,普罗维登斯,RI; 1996 库奇基纳N,谢赫特L: Volterra型随机差分方程的最优控制。 计算数学应用程序 1998, 36 (10-12):251-259. 10.1016/S0898-1221(98)80026-6 谷口T: 随机差分方程的稳定性定理。 数学分析应用杂志 1990, 147 (1):81-96. 10.1016/0022-247X(90)90386-T Ma F,Caughey TK公司: 随机差分系统的平均稳定性。 国际J非线性力学 1982, 17 (2):69-84. 10.1016/0020-7462(82)90040-3 艾哈迈迪G: 关于线性差分方程的均方稳定性。 应用数学计算 1979, 5 (3):233-241. 10.1016/0096-3003(79)90015-8 何志明、张XM: 一阶脉冲差分方程周期边界条件的单调迭代法。 应用数学计算 2004, 156: 605-620. 10.1016/j.amc.2003.08.013 张QQ: 关于具有脉冲的线性时滞差分方程。 Ann Diff Equ公司 2002, 18 (2):197-204. 朱伟、徐岱、杨振聪: 脉冲时滞差分方程的全局指数稳定性。 应用数学计算 2006, 181: 65-72之间。 2016年10月10日/j.amc.2006.01.015 杨志刚、徐岱: 脉冲随机差分方程的均方指数稳定性。 应用数学Lett 2007, 20: 938-945. 2016年10月10日/j.aml.2006.09.006 徐德勇: 非线性时滞差分方程的渐近性。 计算数学应用程序 2001, 42: 393-398之间。 10.1016/S0898-1221(01)00164-X 塞弗特G: 时滞微分方程组的正不变闭集。 J差异Equ 1976, 22: 292-304. 10.1016/0022-0396(76)90029-2 徐岱、杨振聪: 一类脉冲泛函微分方程的吸引集和不变集。 数学分析应用杂志 2007, 329: 1036-1044. 2016年10月10日/j.jmaa.2006.05.072 Liz E,Ferreiro JB: 关于广义差分方程全局稳定性的注记。 应用数学Lett 2002, 15: 655-659. 10.1016/S0893-9659(02)00024-1 Meyn SP,Tweedie R: 马尔可夫链和随机稳定性。 Springer-Verlag,伦敦; 1993