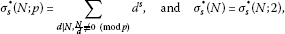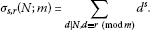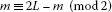跳到主要内容
科学与工程不动点理论与算法
下载PDF

扭曲艾森斯坦级数和扭曲因子函数的卷积恒等式

不动点理论及其应用 体积 2013，物品编号：81(2013)引用这篇文章

摘要

我们的动机是Ramanujan关于两个Eisenstein级数乘积和的递推公式（Berndt in Ramanujian’s Notebook，Part II，1989，Entry 14，p.332）及其证明，以及普通除数函数的Besge-Liouville卷积恒等式 σ k个 − 1 (n个)（威廉姆斯在《刘维尔精神中的数论》，第76卷，2011年，定理12.3）。本文的目的是引入并证明扭曲因子函数的卷积恒等式 σ k个 − 1 * (n个)以及扭曲的艾森斯坦系列 S公司 2 k个 + 2 ， χ 0 和 S公司 2 k个 + 2 ， χ 1 ， S公司 2 k个 + 2 * ， S公司 2 k个 + 2 ， χ 0 * 、和 S公司 2 k个 + 2 ， χ 1 * 作为基于主要结果的应用，我们为金字塔、三角形、梅森和完美数建立了许多有趣的恒等式。此外，我们还展示了如何使用我们的主要结果来获得整数表示数的算术公式n个作为以下各项的总和秒方块。

1主要成果介绍及说明

在本文中，让小时={τ∈C类|伊姆河τ>0}是复杂的上半平面。让 S公司 k个 表示归一化Eisenstein加权级数k个定义于ℌ通过

S公司 k个 := S公司 k个 (τ)=− B类 k个 2 k个 + ∑ n个 = 1 ∞ σ k个 − 1 (n个) q个 n个 ，
(1)

哪里 σ k个 − 1 (n个)= ∑ d日 | n个 d日 k个 − 1 ，q个= e（电子） 2 π 我 τ 、和 B类 k个 是k个第个伯努利数。

让 S公司 k个 * ， S公司 k个 ， χ 0 * 、和 S公司 k个 ， χ 1 * 是由

S公司 k个 * : = S公司 k个 * ( τ ) = S公司 k个 ( τ ) − S公司 k个 ( 2 τ ) = ∑ n个 = 1 ∞ ( σ k个 − 1 ( n个 ) − σ k个 − 1 ( n个 2 ) ) q个 n个 = ∑ n个 = 1 ∞ σ k个 − 1 * ( n个 ) q个 n个 .
(2)

对于我=0，1，我们将扭曲的艾森斯坦级数定义为

S公司 k个 ， χ 我 (τ):= ∑ n个 = 1 ∞ χ 我 (n个) σ k个 − 1 (n个)， S公司 k个 ， χ 我 * (τ):= ∑ n个 = 1 ∞ χ 我 (n个) σ k个 − 1 * (n个) q个 n个 ，
(3)

哪里 σ k个 − 1 * (n个)是扭曲除数函数，由

σ k个 − 1 * ( n个 ) = ∑ d日 | n个 ， n个 d日 古怪的 d日 k个 − 1 ， χ 1 ( n个 ) = { 1 ， 如果 n个 很奇怪 ， 0 ， 否则 和 χ 0 ( n个 ) = { 1 ， 如果 n个 是偶数 ， 0 ， 否则 .

考虑微分算子D类= 1 2 π 我 d日 d日 τ =q个 d日 d日 q个 这样的话

D类 ( ∑ n个 = 1 ∞ 一 n个 q个 n个 ) = ∑ n个 = 1 ∞ n个 一 n个 q个 n个 .

我们的动机是Ramanujan的递归公式 S公司 2 n个 + 2 [[1]，条目14，p.332]及其证明，以及除数函数的Besge-Liouville卷积恒等式 σ k个 − 1 (n个)[[2]，定理12.3]。受这些恒等式的启发，我们证明了各种除数函数卷积和的新恒等式 σ k个 − 1 (n个)， σ k个 − 1 * (n个)以及扭曲艾森斯坦级数的递推公式 S公司 2 k个 + 2 * ， S公司 2 k个 + 2 ， χ 0 * 、和 S公司 2 k个 + 2 ， χ 1 * 给出了基于我们的结果的几个算术应用。

除数函数的卷积和问题 σ 1 (n个)随着准模工具的出现，艾森斯坦级数理论最近引起了人们的极大兴趣。更多细节，我们可以参考罗耶的作品[三]、罗摩克里希南和萨胡[4]、阿拉卡和威廉姆斯[5，6]以及其中的参考文献。关于经典雅可比θ和欧拉函数，函数的其他方面 σ 1 (n个)阿迪加在[7]和Simsek在[8]. 在本文中，我们证明了以下结果。首先，我们将除数函数卷积和的最重要恒等式表述如下。

定理1.1 让 k个∈N个 和 N个∈N个，哪里 k个，N个≥2.我们在表中有身份1.

表1除数函数的恒等式
全尺寸桌子

我们的下一个结果来自定理1.1中的恒等式。因此，我们获得了Eisenstein级数的以下恒等式。

定理1.2 让 k个∈N个 和 n个∈N个，哪里 k个，n个≥2.我们在表中有身份2.

表2除数函数的恒等式
全尺寸桌子

让对是一个质数，让我为任意正整数。我们引入了扭曲除数函数

我们定义

[ n个 米 ] { 对 ， 我 } := ( 对 我 n个 − 1 对 n个 − 1 ) ( 对 我 米 − 1 对 米 − 1 ) ( 对 我 ( n个 − 米 ) − 1 对 n个 − 米 − 1 ) ( n个 米 ) .
(4)

在第3.2节中，我们得出了以下不太确定的结果。

定理1.3 让 k个≥1 和 N个，我≥2.

∑ 秒 = 0 k个 − 1 [ 2 k个 2 秒 + 1 ] { 2 ， 我 } ∑ 米 = 1 N个 − 1 σ 2 k个 − 2 秒 − 1 * ( 2 我 米 ； 2 我 ) σ 2 秒 + 1 * ( 2 我 ( N个 − 米 ) ； 2 我 ) = 1 2 ( 1 2 我 σ 2 k个 + 1 * ( 2 我 N个 ； 2 我 ) − 2 我 N个 σ 2 k个 − 1 * ( 2 我 N个 ； 2 我 ) + ∑ 我 = 1 我 − 1 1 2 我 + 1 σ 2 k个 + 1 * ( 2 我 N个 ； 2 我 ) + N个 ∑ 我 = 1 我 − 1 2 我 σ 2 k个 − 1 * ( 2 我 N个 ； 2 我 ) ) .

最后，在最后的第4节中，我们展示了如何应用我们的主要结果来研究与这个著名问题相关的一些问题

σ 1 (n个)= σ 1 (n个+1)

及其变体。此外，我们考虑了关于算术函数的类似问题 σ 1 * (n个)。建立了许多评论和结果。

2、 对 秒 第个标量乘法函数

让对是一个质数，让我为非负整数。一个函数（f）:N个→C类称为 对 我 第个标量函数如果（f）(对x)= 对 我 （f）(x)对于所有整数x.

此外，a 对 我 第个标量函数（f）(x)称为 对 我 第个标量乘法函数当且仅当（f）(x年)=（f）(x)（f）(年)对于所有正整数x，年这样的话(x，年)=1.

示例2.1

  1. 1

    让（f）(x)=x.然后（f）(x)是一个对第个标量乘法函数。

  2. 2

    让秒为非负整数；我们记得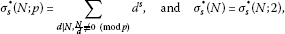

    我们定义了函数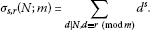

    然后是函数 σ ¯ 秒 (N个；对):= ∑ 第页 = 1 对 − 1 σ 秒 ， 第页 (N个；对)是一个 对 0 第个标量乘法函数。

  3. 三。

    功能 σ 1 ， 1 (N个；2)是20第个标量乘法函数。

定理2.2 除数函数 σ 秒 * (N个；对) 是一个 对 秒 第个标量乘法函数.

证明让第页我= 对 米 N个和对一些人来说第页，我∈N个和素数对.自我不可分割对，我们可以写第页= 对 米 d日对一些人来说d日∈N个因此，我们有

(5)

我们声称 σ 秒 * (M（M）N个；对)= σ 秒 * (M（M）；对) σ 秒 * (N个；对)，其中(M（M），N个)=1.如果对∤M（M）N个，然后

σ 秒 * (M（M）N个；对)= σ 秒 (M（M）N个)= σ 秒 (M（M）) σ 秒 (N个)= σ 秒 * (M（M）；对) σ 秒 * (N个；对).

假设对|M（M）和对∤N个和M（M）= 对 我 M（M） ′ 因此，我们有

σ 秒 * ( M（M） N个 ； 对 ) = σ 秒 * ( 对 我 M（M） ′ N个 ； 对 ) = 对 我 σ 秒 * ( M（M） ′ N个 ； 对 ) = 对 我 σ 秒 * ( M（M） ′ ； 对 ) σ 秒 * ( N个 ； 对 ) = σ 秒 * ( 对 我 M（M） ′ ； 对 ) σ 秒 * ( N个 ； 对 ) .
(6)

因此 σ 秒 * (M（M）N个；对)= σ 秒 * (M（M）；对) σ 秒 * (N个；对)。然后我们得到定理。 □

提议2.3 让 N个∈N个.对于非负整数 米 和 n个，我们有

∑ k个 = 1 N个 − 1 σ 我 * ( 对 米 k个 ； 对 米 ) σ j个 * ( 对 n个 ( N个 − k个 ) ； 对 n个 ) = 对 我 + j个 ( 对 我 米 − 1 ) ( 对 j个 n个 − 1 ) ( 对 我 − 1 ) ( 对 j个 − 1 ) ∑ k个 = 1 N个 − 1 σ 我 * (k个；对) σ j个 * (N个−k个；对).

证明

我们可以看到

∑ k个 = 1 N个 − 1 σ 我 * ( 对 米 k个 ； 对 米 ) σ j个 * ( 对 n个 ( N个 − k个 ) ； 对 n个 ) = ∑ k个 = 1 N个 − 1 { σ 我 ( 对 米 k个 ) − σ 我 ( k个 ) } { σ j个 ( 对 n个 ( N个 − k个 ) ) − σ j个 ( N个 − k个 ) } .
(7)

然后，根据定理2.2，我们得到

σ 我 ( 对 米 k个 ) − σ 我 ( k个 ) = ( σ 我 ( 对 米 k个 ) − σ 我 ( 对 米 − 1 k个 ) ) + ( σ 我 ( 对 米 − 1 k个 ) − σ 我 ( 对 米 − 2 k个 ) ) + ( σ 我 ( 对 米 − 2 k个 ) − σ 我 ( 对 米 − 三 k个 ) ) + ⋯ + ( σ 我 ( 对 2 k个 ) − σ 我 ( 对 k个 ) ) + ( σ 我 ( 对 k个 ) − σ 我 ( k个 ) ) = σ 我 * ( 对 米 k个 ； 对 ) + σ 我 * ( 对 米 − 1 k个 ； 对 ) + σ 我 * ( 对 米 − 2 k个 ； 对 ) + ⋯ + σ 我 * ( 对 2 k个 ； 对 ) + σ 我 * ( 对 k个 ； 对 ) = ( 对 米 我 + 对 ( 米 − 1 ) 我 + 对 ( 米 − 2 ) 我 + ⋯ + 对 2 我 + 对 我 ) σ 我 * ( k个 ； 对 ) = 对 我 对 米 我 − 1 对 我 − 1 σ 我 * ( k个 ； 对 ) .
(8)

因此，使用（8），我们可以将（7）写成

∑ k个 = 1 N个 − 1 σ 我 * ( 对 米 k个 ； 对 米 ) σ j个 * ( 对 n个 ( N个 − k个 ) ； 对 n个 ) = ∑ k个 = 1 N个 − 1 { 对 我 对 米 我 − 1 对 我 − 1 σ 我 * ( k个 ； 对 ) } { 对 j个 对 n个 j个 − 1 对 j个 − 1 σ j个 * ( N个 − k个 ； 对 ) } .

 □

扭曲Eisenstein级数的卷积关系及其应用

3.1扭曲Eisenstein级数的卷积关系 S公司 2 n个 + 2 * (τ)

我们引用以下引理[[2]第10章，第113页]。

引理3.1 让 （f）:Z轴→C类 是偶数函数.让 n个∈N个.然后

∑ ( 一 ， b条 ， x ， 年 ) ∈ N个 4 一 x + b条 年 = n个 x ， 年 古怪的 ( （f） ( 一 − b条 ) − （f） ( 一 + b条 ) ) = （f） ( 0 ) σ 1 ( n个 / 2 ) + ∑ d日 ∈ N个 d日 | n个 ( n个 d日 − d日 ) （f） ( d日 ) − ∑ d日 ∈ N个 d日 | n个 / 2 ( n个 d日 − d日 ) （f） ( d日 ) .

利用上述引理，我们可以证明下一个结果。

定理3.2 让 n个>1.然后

S公司 2 n个 + 2 * (τ)=D类 ( S公司 2 n个 * ( τ ) ) +2 ∑ 秒 = 0 n个 − 1 ( 2 n个 2 秒 + 1 ) S公司 2 n个 − 2 秒 * (τ) S公司 2 秒 + 2 * (τ).
(9)

证明我们接受（f）(x)= x 2 k个 在引理3.1中。引理3.1的左侧是

∑ ( 一 ， x ， b条 ， 年 ) ∈ N个 4 一 x + b条 年 = n个 x ， 年 古怪的 ( ( 一 − b条 ) 2 k个 − ( 一 + b条 ) 2 k个 ) = ∑ ( 一 ， x ， b条 ， 年 ) ∈ N个 4 一 x + b条 年 = n个 x ， 年 古怪的 ( ∑ 第页 = 0 2 k个 ( 2 k个 第页 ) ( − 1 ) 第页 一 2 k个 − 第页 b条 第页 − ∑ 第页 = 0 2 k个 ( 2 k个 第页 ) 一 2 k个 − 第页 b条 第页 ) = − 2 ∑ ( 一 ， x ， b条 ， 年 ) ∈ N个 4 一 x + b条 年 = n个 x ， 年 古怪的 ∑ 第页 = 0 第页 古怪的 2 k个 ( 2 k个 第页 ) 一 2 k个 − 第页 b条 第页 = − 2 ∑ 秒 = 0 k个 − 1 ( 2 k个 2 秒 + 1 ) ∑ ( 一 ， x ， b条 ， 年 ) ∈ N个 4 一 x + b条 年 = n个 x ， 年 古怪的 一 2 k个 − 2 秒 − 1 b条 2 秒 + 1 = − 2 ∑ 秒 = 0 k个 − 1 ( 2 k个 2 秒 + 1 ) ∑ 米 = 1 n个 − 1 σ 2 k个 − 2 秒 − 1 * ( 米 ) σ 2 秒 + 1 * ( n个 − 米 ) .

因此，我们推断

∑ 秒 = 0 k个 − 1 ( 2 k个 2 秒 + 1 ) ( ∑ 米 = 1 N个 − 1 σ 2 k个 − 2 秒 − 1 * ( 米 ) σ 2 秒 + 1 * ( N个 − 米 ) ) = 1 2 { σ 2 k个 + 1 * ( N个 ) − N个 σ 2 k个 − 1 * ( N个 ) } .
(10)

从（10）和（2）中，我们得到了定理。 □

3.2定理的证明1.3

从（4）和（10）中，我们得到

∑ 秒 = 0 k个 − 1 [ 2 k个 2 秒 + 1 ] { 2 ， 我 } ∑ 米 = 1 N个 − 1 σ 2 k个 − 2 秒 − 1 * ( 2 我 米 ； 2 我 ) σ 2 秒 + 1 * ( 2 我 ( N个 − 米 ) ； 2 我 ) = ∑ 秒 = 0 k个 − 1 2 2 k个 ( 2 2 我 k个 − 1 ) 2 2 k个 − 1 ∑ 秒 = 0 k个 − 1 ( 2 k个 2 秒 + 1 ) ∑ 米 = 1 N个 − 1 σ 2 k个 − 2 秒 − 1 * ( 米 ) σ 2 秒 + 1 * ( N个 − 米 ) = ∑ 秒 = 0 k个 − 1 2 2 k个 ( 2 2 我 k个 − 1 ) 2 2 k个 − 1 ⋅ 1 2 { σ 2 k个 + 1 * ( N个 ) − N个 σ 2 k个 − 1 * ( N个 ) } = 1 2 [ { 2 2 k个 我 + 2 2 k个 ( 我 − 1 ) + ⋯ + 2 2 ( 2 k个 ) + 2 2 k个 } σ 2 k个 + 1 * ( N个 ) − N个 { 2 2 k个 我 + 2 2 k个 ( 我 − 1 ) + ⋯ + 2 2 ( 2 k个 ) + 2 2 k个 } σ 2 k个 − 1 * ( N个 ) ] .
(11)

然后，（11）右侧的第一项可以写成

{ 2 2 k个 我 + 2 2 k个 ( 我 − 1 ) + ⋯ + 2 2 ( 2 k个 ) + 2 2 k个 } σ 2 k个 + 1 * ( N个 ) = { ( 2 我 ) 2 k个 + 1 2 我 + ( 2 我 − 1 ) 2 k个 + 1 2 我 − 1 + ⋯ + ( 2 2 ) 2 k个 + 1 2 2 + 2 2 k个 + 1 2 } σ 2 k个 + 1 * ( N个 ) = 1 2 我 σ 2 k个 + 1 * ( 2 我 N个 ) + 1 2 我 − 1 σ 2 k个 + 1 * ( 2 我 − 1 N个 ) + ⋯ + 1 2 2 σ 2 k个 + 1 * ( 2 2 N个 ) + 1 2 σ 2 k个 + 1 * ( 2 N个 ) = ( 1 2 我 σ 2 k个 + 1 ( 2 我 N个 ) − 1 2 我 σ 2 k个 + 1 ( 2 我 − 1 N个 ) ) + ( 1 2 我 − 1 σ 2 k个 + 1 ( 2 我 − 1 N个 ) − 1 2 我 − 1 σ 2 k个 + 1 ( 2 我 − 2 N个 ) ) + ⋯ + ( 1 2 2 σ 2 k个 + 1 ( 2 2 N个 ) − 1 2 2 σ 2 k个 + 1 ( 2 N个 ) ) + ( 1 2 σ 2 k个 + 1 ( 2 N个 ) − 1 2 σ 2 k个 + 1 ( N个 ) ) = 1 2 我 ( σ 2 k个 + 1 ( 2 我 N个 ) − σ 2 k个 + 1 ( N个 ) ) + 1 2 我 ( σ 2 k个 + 1 ( 2 我 − 1 N个 ) − σ 2 k个 + 1 ( N个 ) ) + ⋯ + 1 2 2 ( σ 2 k个 + 1 ( 2 N个 ) − σ 2 k个 + 1 ( N个 ) ) = 1 2 我 σ 2 k个 + 1 * ( 2 我 N个 ； 2 我 ) + 1 2 我 σ 2 k个 + 1 * ( 2 我 − 1 N个 ； 2 我 − 1 ) + 1 2 我 − 1 σ 2 k个 + 1 * ( 2 我 − 2 N个 ； 2 我 − 2 ) + ⋯ + 1 2 2 σ 2 k个 + 1 * ( 2 N个 ； 2 ) .

类似地，（11）右侧的第二项为

− N个 { 2 2 k个 我 + 2 2 k个 ( 我 − 1 ) + ⋯ + 2 2 ( 2 k个 ) + 2 2 k个 } σ 2 k个 − 1 * ( N个 ) = − N个 { 2 我 σ 2 k个 − 1 * ( 2 我 N个 ； 2 我 ) − 2 我 − 1 σ 2 k个 − 1 * ( 2 我 − 1 N个 ； 2 我 − 1 ) − ⋯ − 2 σ 2 k个 − 1 * ( 2 N个 ； 2 ) } .

因此，证明已完成。

3.3金字塔数字

让α是一个固定整数α≥三，并让

梨 α (x)= 1 6 x(x+1) ( ( α − 2 ) x + 5 − α )

表示α四阶金字塔数[9]. 这些组合数在数论和离散数学中起着重要作用。使用（10）k个=1，我们推导

∑ 米 = 1 N个 − 1 σ 1 * (米) σ 1 * (N个−米)= 1 4 { σ 三 * ( N个 ) − N个 σ 1 * ( N个 ) } .
(12)

命题2.3是计算总和的一个非常有效的公式

∑ k个 = 1 N个 − 1 σ 我 * ( 对 米 k个 ； 对 米 ) σ j个 * ( 对 n个 ( N个 − k个 ) ； 对 n个 ) .

例如，使用命题2.3和（12），我们得到了表中有趣的公式三.

  1. 1

    金字塔数字 P（P） 5 ， x 与卷积和密切相关

    ∑ 米 = 1 N个 − 1 σ 1 * (米) σ 1 * (N个−米).

    事实上，如果N个=2q个+1是质数，然后从（12）中，我们得到

    1 2 ∑ 米 = 1 q个 σ 1 * (米) σ 1 * (2q个+1−米)= 1 2 q个 2 (q个+1).

    根据定理2.2，我们推断

    ∑ 米 = 1 q个 σ ˆ 1 * (米) σ ˆ 1 * (2q个+1−米)= 1 2 ∑ 米 = 1 q个 σ 1 * (米) σ 1 * (2q个+1−米)= 梨 5 (q个)，
    （13）

    哪里

    σ ˆ 1 * (t吨)={ σ 1 * ( t吨 ) 如果 t吨 很奇怪 ， σ 1 * ( t吨 2 ) 否则 .

    在表中4，我们列出了的前13个值

    P（P） 5 ， x := 1 2 x 2 (x+1)和 P（P） 5 ， x * := ∑ 米 = 1 x σ ˆ 1 * (米) σ ˆ 1 * (2x+1−米).

    根据表4和图1，我们发现如果2x+1是质数，那么 P（P） 5 ， x 与…一致 P（P） 5 ， x * .

    图1
    图1

    P（P） 5 ， x 和 P（P） 5 ， x * .

    全尺寸图像
  2. 2

    我们考虑金字塔数

    P（P） 三 ， x := 梨 三 (x−1)= 1 6 x(x−1)(x+1)

    和卷积和

    P（P） 三 ， x * := ∑ x ≥ 2 k个 σ 1 (k个) σ 1 (2x+1−4k个).

    从（21）（带N个=2q个+1素数），我们得到

    P（P） 三 ， q个 = P（P） 三 ， q个 * = 梨 三 (q个−1).

    我们列出了 P（P） 三 ， x 和 P（P） 三 ， x * 在表中5根据表5和图2，我们发现如果2x+1是质数，那么 P（P） 三 ， x 与…一致 P（P） 三 ， x * 。我们注意到

    E类: 年 2 = P（P） 三 ， x = 1 6 x(x−1)(x+1)

    是一条椭圆曲线P（P）=(2，1)=(2， P（P） 三 ， 2 * )∈E类(问)∖ E类 或 (问)和等级E类(问)≥1从Lutz-Nagell定理[[10]，第240页]，P（P）不能是有限阶的。有关金字塔数和椭圆曲线秩的扩展结果的更多详细信息，可以参考[9]。

    图2
    图2

    P（P） 三 ， x 和 P（P） 三 ， x * .

    全尺寸图像
表3的值 ∑ k个 = 1 N个 − 1 σ 1 * ( 2 米 k个； 2 米 ) σ 1 * ( 2 米 (N个−k个)； 2 米 )
全尺寸桌子
表4的示例 P（P） 5 ， x 和 P（P） 5 ， x *
全尺寸桌子

3.4扭Eisenstein级数的卷积 S公司 2 k个 + 2 ， χ 我 * ，我=0，1

我们证明了以下结果。

引理3.3 让 k个≥1.然后

S公司 2 k个 + 2 ， χ 0 * ( τ ) = 4 ∑ 秒 = 0 k个 − 1 ( 2 k个 2 秒 + 1 ) S公司 2 k个 − 2 秒 ， χ 1 * ( τ ) S公司 2 秒 + 2 ， χ 1 * ( τ ) = 4 ∑ 秒 = 0 k个 − 1 ( 2 k个 2 秒 + 1 ) S公司 2 k个 − 2 秒 ， χ 1 ( τ ) S公司 2 秒 + 2 ， χ 1 ( τ )

和

D类 ( S公司 2 k个 ， χ 0 * ( τ ) ) =2 ∑ 秒 = 0 k个 − 1 ( 2 k个 2 秒 + 1 ) ( S公司 2 k个 − 2 秒 ， χ 1 * ( τ ) − S公司 2 k个 − 2 秒 ， χ 0 * ( τ ) ) S公司 2 秒 + 2 * (τ).

证明让我们把N个=2L（左）在（10）中。然后

∑ 秒 = 0 k个 − 1 ( 2 k个 2 秒 + 1 ) ∑ 米 = 1 2 L（左） − 1 σ 2 k个 − 2 秒 − 1 * ( 米 ) σ 2 秒 + 1 * ( 2 L（左） − 米 ) = ∑ 秒 = 0 k个 − 1 ( 2 k个 2 秒 + 1 ) ( ∑ 米 = 1 L（左） σ 2 k个 − 2 秒 − 1 * ( 2 米 − 1 ) σ 2 秒 + 1 * ( 2 L（左） − 2 米 + 1 ) + ∑ 米 = 1 L（左） − 1 σ 2 k个 − 2 秒 − 1 * ( 2 米 ) σ 2 秒 + 1 * ( 2 L（左） − 2 米 ) ) = 1 2 { σ 2 k个 + 1 * ( 2 L（左） ) − 2 L（左） σ 2 k个 − 1 * ( 2 L（左） ) } .
(14)

根据定理2.2和（14），我们导出

∑ 秒 = 0 k个 − 1 ( 2 k个 2 秒 + 1 ) ( ∑ 米 = 1 L（左） σ 2 k个 − 2 秒 − 1 ( 2 米 − 1 ) σ 2 秒 + 1 ( 2 L（左） − 2 米 + 1 ) ) = ∑ 秒 = 0 k个 − 1 ( 2 k个 2 秒 + 1 ) ( ∑ 米 = 1 L（左） σ 2 k个 − 2 秒 − 1 * ( 2 米 − 1 ) σ 2 秒 + 1 * ( 2 L（左） − 2 米 + 1 ) ) = 1 2 { 2 2 k个 + 1 σ 2 k个 + 1 * ( L（左） ) − 2 L（左） ⋅ 2 2 k个 − 1 σ 2 k个 − 1 * ( L（左） ) } − 1 2 ⋅ 2 2 k个 { σ 2 k个 + 1 * ( L（左） ) − L（左） σ 2 k个 − 1 * ( L（左） ) } = 1 4 σ 2 k个 + 1 * ( 2 L（左） ) .
(15)

从（14）和（15）中，我们发现

∑ 秒 = 0 k个 − 1 ( 2 k个 2 秒 + 1 ) ∑ 米 = 1 2 L（左） − 1 ( − 1 ) 米 + 1 σ 2 k个 − 2 秒 − 1 * (米) σ 2 秒 + 1 * (2L（左）−米)= 1 2 ( 2 L（左） ⋅ σ 2 k个 − 1 * ( 2 L（左） ) ) .
(16)

从（15）和（16），我们推导出引理。 □

我们有以下定理。

定理3.4 让 L（左），M（M），k个 为正整数.让

U型 2 k个 (M（M）):= ∑ 秒 = 0 k个 − 1 ( 2 k个 2 秒 + 1 ) ∑ 米 = 0 M（M） σ 2 k个 − 2 秒 − 1 (2米−1) σ 2 秒 + 1 ( 2 M（M） − ( 2 米 − 1 ) ) .
  1. （a）

    如果 (L（左），M（M）)=1，然后

    U型 2 k个 (L（左）) U型 2 k个 (M（M）)= 2 2 k个 − 1 U型 2 k个 (L（左）M（M）).
  2. （b）

    如果 L（左）= 2 e（电子） 0 对 1 e（电子） 1 ⋯ 对 第页 e（电子） 第页 带有奇数不同素数 对 我 ，然后

    U型 2 k个 (L（左）)= 2 2 第页 − 2 + ( 2 k个 + 1 ) ( e（电子） 0 − e（电子） 1 − ⋯ − e（电子） 第页 ) U型 2 k个 ( 对 1 e（电子） 1 ) ⋯ U型 2 k个 ( 对 第页 e（电子） 第页 ) .

证明

  1. （a）

    自(L（左），M（M）)=1，我们可以选择2|L（左）和2∤M（M）从定义 U型 2 k个 (M（M）)和（15），我们得到

    U型 2 k个 ( L（左） ) U型 2 k个 ( M（M） ) = 1 4 σ 2 k个 + 1 * ( 2 L（左） ) ⋅ 1 4 σ 2 k个 + 1 * ( 2 M（M） ) = 1 4 σ 2 k个 + 1 * ( 2 L（左） ) ⋅ 1 4 ⋅ 2 2 k个 + 1 σ 2 k个 + 1 * ( M（M） ) = 2 2 k个 − 1 ( 1 4 σ 2 k个 + 1 * ( 2 L（左） M（M） ) ) = 2 2 k个 − 1 U型 2 k个 ( L（左） M（M） ) .
  2. （b）

    自L（左）= 2 e（电子） 0 对 1 e（电子） 1 ⋯ 对 第页 e（电子） 第页 带有奇数不同素数 对 我 ，我们有

    U型 2 k个 ( L（左） ) = 1 4 σ 2 k个 + 1 * ( 2 e（电子） 0 对 1 e（电子） 1 ⋯ 对 第页 e（电子） 第页 ) = 1 4 ⋅ 2 ( 2 k个 + 1 ) e（电子） 0 σ 2 k个 + 1 * ( 对 1 e（电子） 1 ⋯ 对 第页 e（电子） 第页 ) = 1 4 ⋅ 2 ( 2 k个 + 1 ) e（电子） 0 σ 2 k个 + 1 * ( 对 1 e（电子） 1 ) ⋯ σ 2 k个 + 1 * ( 对 第页 e（电子） 第页 ) = 1 4 ⋅ 2 ( 2 k个 + 1 ) e（电子） 0 2 − ( 2 k个 + 1 ) e（电子） 1 σ 2 k个 + 1 * ( 2 对 1 e（电子） 1 ) ⋯ 2 − ( 2 k个 + 1 ) e（电子） 第页 σ 2 k个 + 1 * ( 2 对 第页 e（电子） 第页 ) = 1 4 ⋅ 2 ( 2 k个 + 1 ) e（电子） 0 − ( 2 k个 + 1 ) e（电子） 1 − ⋯ − ( 2 k个 + 1 ) e（电子） 第页 ( 1 4 σ 2 k个 + 1 * ( 2 对 1 e（电子） 1 ) ) ⋯ ( 1 4 σ 2 k个 + 1 * ( 2 对 第页 e（电子） 第页 ) ) ⋅ 4 第页 = 2 2 第页 − 2 + ( 2 k个 + 1 ) ( e（电子） 0 − e（电子） 1 − ⋯ − e（电子） 第页 ) U型 2 k个 ( 对 1 e（电子） 1 ) ⋯ U型 2 k个 ( 对 第页 e（电子） 第页 ) .

 □

3.5三角形和扭曲三角形数：结果和备注

  1. (1)

    利用椭圆θ函数理论，Glaisher[[11]，p.300]考虑等式(15).

  2. (2)

    此处关注（15）和（16）的四种特殊情况（见表6).

  3. (3)

    特别是，如果L（左）那么是一个奇素数

    1 2 ∑ 米 = 1 2 L（左） − 1 ( − 1 ) 米 + 1 σ 1 * (米) σ 1 * (2L（左）−米)= L（左） ( L（左） + 1 ) 2 = ∑ k个 = 1 L（左） k个= T型 L（左） ，
    (17)

    哪里 T型 L（左） 是一个三角形数字。我们注意到

    ∑ 米 = 1 L（左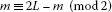） − 1 ( − 1 ) 米 + 1 σ 1 * (米) σ 1 * (2L（左）−米)= σ 1 * ( L（左） ) 2 { L（左） + ( − 1 ) L（左） σ 1 * ( L（左） ) }

    通过使用.如果L（左）那就奇怪了

    ∑ 米 = 1 L（左） − 1 ( − 1 ) 米 σ 1 * (米) σ 1 * (2L（左）−米)= σ 1 * ( L（左） ) 2 { σ 1 * ( L（左） ) − L（左） } .
  4. (4)

    特别是，如果L（左）=2q个−1那么是一个奇素数

    ∑ 米 = 1 L（左） − 1 ( − 1 ) 米 σ 1 * (米) σ 1 * (2L（左）−米)= L（左） + 1 2 = ∑ k个 = 1 q个 k个 0 =q个.
    (18)

    我们引入了扭曲三角数 T型 L（左） * 和 如果 L（左） * 由提供

    T型 L（左） * := 1 2 ∑ 米 = 1 2 L（左） − 1 ( − 1 ) 米 + 1 σ 1 * (米) σ 1 * (2L（左）−米)， 如果 L（左） * := ∑ 米 = 1 2 L（左） − 2 ( − 1 ) 米 σ 1 * (米) σ 1 * (4L（左）−2−米).

    的前16个值

    T型 L（左） ， T型 L（左） * ， 如果 L（左） := ∑ k个 = 1 L（左） k个 0 ， 如果 L（左） *

    表中给出了7.

    我们可以从图中看到三和表7那时候2x−1（分别。x)是质数，数字

    如果 x * = ∑ 米 = 1 2 x − 2 ( − 1 ) 米 σ 1 * (米) σ 1 * (4x−2−米)

    （分别为。 T型 x * := 1 2 ∑ 米 = 1 2 x − 1 ( − 1 ) 米 + 1 σ 1 * (米) σ 1 * (2x−米))和 如果 x = ∑ k个 = 1 x k个 0 （分别为。 T型 x = ∑ k个 = 1 x k个)都是一样的。

  5. (5)

    关于此类卷积公式的类似问题已在前面的[12]：可以找到 第页 1 ， 第页 2 ， 秒 1 ， 秒 2 ，米， α 1 ， β 1 ，β在里面ℤ令人满意的

    ∑ k个 < β 对 / β 1 σ 第页 1 ， 秒 1 ( α 1 k个；米) σ 第页 2 ， 秒 2 (β对− β 1 k个；米)= ∑ k个 = 1 对 − 1 2 k个 u个

    对于固定的u个对于固定奇素数对?

    图3
    图3

    如果 L（左） ， 如果 L（左） * ， T型 L（左） * 、和 T型 L（左） .

    全尺寸图像

    我们认为，这样的问题通常不容易解决。方程式(17)和(18)这个问题有特殊情况吗u个=0和1。类似结果见[[12], (12)].

  6. (6)

    从表格6和7，我们可以很容易地获得 T型 L（左） * 对于任何素数L（左）.

  7. (7)

    在表中8我们比较了三角数的性质 T型 L（左） 和扭曲的三角形数 T型 L（左） * .

备注3.5（申请）

让我们计算一下数量 ∑ k个 = 1 N个 − 1 σ 1 (k个；4) σ 1 (N个−k个；4)，也就是说，

∑ k个 = 1 N个 − 1 σ 1 * ( k个 ； 4 ) σ 1 * ( N个 − k个 ； 4 ) = ∑ k个 = 1 N个 − 1 { σ 1 ( k个 ) − σ 1 ( k个 4 ) } { σ 1 ( N个 − k个 ) − σ 1 ( N个 − k个 4 ) } = ∑ k个 = 1 N个 − 1 σ 1 ( k个 ) σ 1 ( N个 − k个 ) − 2 ∑ k个 < N个 4 σ 1 ( N个 − 4 k个 ) σ 1 ( k个 ) + ∑ k个 < N个 4 σ 1 ( k个 ) σ 1 ( N个 4 − k个 ) = 1 8 { 三 σ 三 * ( N个 ； 4 ) − σ 三 * ( N个 2 ) − 三 N个 σ 1 * ( N个 ； 4 ) } ，
(19)

我们指的是

∑ k个 = 1 N个 − 1 σ 1 (k个) σ 1 (N个−k个)= 1 12 { 5 σ 三 ( N个 ) + ( 1 − 6 N个 ) σ 1 ( N个 ) }
(20)

英寸[[15]，（3.10）]和

∑ k个 < N个 4 σ 1 ( k个 ) σ 1 ( N个 − 4 k个 ) = 1 48 { σ 三 ( N个 ) + ( 2 − 三 N个 ) σ 1 ( N个 ) + 三 σ 三 ( N个 2 ) + 16 σ 三 ( N个 4 ) + ( 2 − 12 N个 ) σ 1 ( N个 4 ) }
(21)

英寸[[15]，定理4]。将（19）和（12）组合在一起，我们得到了表9.

根据定理1.3k个=1，我们推断

∑ k个 = 1 N个 − 1 σ 1 * ( 4 k个 ； 4 ) σ 1 * ( 4 ( N个 − k个 ) ； 4 ) = 9 80 { σ 三 * ( 4 N个 ； 4 ) + σ 三 * ( 2 N个 ) − 16 N个 σ 1 * ( 4 N个 ； 4 ) + 8 N个 σ 1 * ( 2 N个 ) } .
(22)

此外，从（19）和（22）可以看出

∑ k个 = 1 4 ∤ k个 4 N个 − 1 σ 1 ( k个 ) σ 1 ( 4 N个 − k个 ) = ∑ k个 = 1 4 ∤ k个 4 N个 − 1 σ 1 * ( k个 ； 4 ) σ 1 * ( 4 N个 − k个 ； 4 ) = ∑ k个 = 1 4 N个 − 1 σ 1 * ( k个 ； 4 ) σ 1 * ( 4 N个 − k个 ； 4 ) − ∑ k个 = 1 N个 − 1 σ 1 * ( 4 k个 ； 4 ) σ 1 * ( 4 N个 − 4 k个 ； 4 ) = 1 80 { 21 σ 三 ( 4 N个 ) − 19 σ 三 ( 2 N个 ) − 2 σ 三 ( N个 ) + 24 N个 σ 1 ( 4 N个 ) − 72 N个 σ 1 ( 2 N个 ) + 48 N个 σ 1 ( N个 ) } .
(23)

为了完善上述公式，我们使用了以下观察结果。让对成为总理k个，N个∈N个众所周知

σ k个 (对N个)− ( 对 k个 + 1 ) σ k个 (N个)+ 对 k个 σ k个 ( N个 对 ) =0
(24)

来自[[2]，第26页]。现在，如果我们设置对=2并使用（23）和（24），我们得到

∑ k个 = 1 4 ∤ k个 4 N个 − 1 σ 1 (k个) σ 1 (4N个−k个)=17 σ 三 * (N个)= σ 三 * (2N个；4)+ σ 三 * (2N个).
(25)

备注3.6（代表N个作为米三角形数字）我们设置Δ={ T型 k个 |k个=0，1，2，…}。对于米∈N个和N个∈N个∪{0}，我们让

t吨 米 (N个)=卡片 { ( x 1 ， x 2 ， … ， x 米 ) ∈ Δ × Δ × ⋯ × Δ | N个 = x 1 + x 2 + ⋯ + x 米 }

以便 t吨 米 (N个)计算的表示数N个作为米三角形数字。对于N个∈N个∪{0}，我们得到了经典结果

t吨 8 (N个)= σ 三 (N个+1)− σ 三 ( N个 + 1 2 ) = σ 三 * (N个+1)；
(26)

参见[[16]，第55页]。

根据表（26）、（25）、（20）5、和[[17]，p.401]，我们得到表10.

表5的示例 P（P） 三 ， x 和 P（P） 三 ， x *
全尺寸桌子
表6卷积和的特殊情况
全尺寸桌子
表7的示例 T型 L（左） * ， T型 L（左） ， 如果 L（左） 、和 如果 L（左） *
全尺寸桌子
表8三角形和扭曲三角形数
全尺寸桌子
表9卷积和，当 N个 是质数
全尺寸桌子
表10卷积和和三角数
全尺寸桌子

根据定理2.2，我们推导出

t吨 8 (2N个−1)= σ 三 * (2N个)=8 σ 三 * (N个)=8 t吨 8 (N个−1)， t吨 8 ( 2 米 − 1 ) = 8 米 ，

利用定理2.2，我们得到

t吨 8 ( 2 米 对 1 e（电子） 1 ⋯ 对 第页 e（电子） 第页 − 1 ) = σ 三 * ( 2 米 对 1 e（电子） 1 ⋯ 对 第页 e（电子） 第页 ) = 8 米 σ 三 * ( 对 1 e（电子） 1 ) ⋯ σ 三 * ( 对 第页 e（电子） 第页 ) = 8 米 t吨 8 ( 对 1 e（电子） 1 − 1 ) ⋯ t吨 8 ( 对 第页 e（电子） 第页 − 1 )

具有 对 我 奇数不同的素数。

3.6整数的表示N个作为秒正方形

这个秒平方问题是数数 第页 秒 (N个)整数解的( x 1 ，…， x 秒 )丢番图方程

x 1 2 +⋯+ x 秒 2 =N个，
(27)

其中更改了 x 我 ′ 秒给出了不同的解决方案。的显式公式 第页 2 (N个)1798年由勒让德和1801年由高斯给出。1770年，拉格朗日给出了 第页 4 (N个)利用θ函数理论，雅各比得到了 第页 秒 (N个)，其中秒=2，4，6，8Glaisher使用椭圆函数方法而不是模函数来获得 ( 16 N个).公式 第页 24 (n个)拉马努詹证明了这一点。有关更多详细信息，请参阅[18]以及其中的参考。在本小节中，我们为 第页 8 (4N个)依据 σ 三 * 和 σ 三 从我们的主要结果中，我们推导出了这个数的同余公式。根据Jacobi，我们考虑以下方程

ϑ 三 ( 0 ， − q个 ) 秒 :=1+ ∑ N个 = 1 ∞ ( − 1 ) N个 第页 秒 (N个) q个 N个 ，
(28)

哪里 ϑ 三 (0，q个)是z（z）=0θ函数的情况 ϑ 三 (z（z），q个)英寸[19]由提供

ϑ 三 (0，q个)= ∑ j个 = − ∞ ∞ q个 j个 2 .

雅各比[20]已证明

ϑ 三 ( 0 ， − q个 ) 4 = 1 − 8 ∑ 第页 = 1 ∞ ( − 1 ) 第页 − 1 第页 q个 第页 1 + q个 第页 = 1 + 8 ∑ N个 = 1 ∞ ( − 1 ) N个 ( ∑ d日 | N个 ， d日 > 0 4 ∤ d日 d日 ) q个 N个 .
(29)

从（29）和（23）中，我们得到了一个新的公式 第页 8 (4N个)依据 σ 三 * (N个)和 σ 三 (N个)事实上，

第页 8 ( 4 N个 ) = 16 ( σ 1 ( 4 N个 ) − 4 σ 1 ( N个 ) ) + 64 ∑ k个 = 1 4 ∤ k个 4 N个 − 1 σ 1 ( k个 ) σ 1 ( 4 N个 − k个 ) + 64 ∑ k个 = 1 N个 − 1 { σ 1 ( 4 k个 ) − 4 σ 1 ( k个 ) } { σ 1 ( 4 ( N个 − k个 ) ) − 4 σ 1 ( N个 − k个 ) }

然后

第页 8 (4N个)=16 { 56 σ 三 * ( N个 ) + 15 σ 三 ( N个 ) } ，
(30)

它给出了以下定理。在这里，

∑ k个 = 1 N个 − 1 { σ 1 ( 4 k个 ) − 4 σ 1 ( k个 ) } { σ 1 ( 4 ( N个 − k个 ) ) − 4 σ 1 ( N个 − k个 ) } = ∑ k个 = 1 N个 − 1 { 三 σ 1 ( k个 ) − 6 σ ( k个 2 ) } { 三 σ 1 ( N个 − k个 ) − 6 σ ( N个 − k个 2 ) } = 9 ∑ k个 = 1 N个 − 1 σ 1 ( k个 ) σ 1 ( N个 − k个 ) − 36 ∑ k个 < N个 2 σ 1 ( N个 − 2 k个 ) σ 1 ( k个 ) + 36 ∑ k个 < N个 2 σ 1 ( k个 ) σ 1 ( N个 2 − k个 ) = 三 4 ( σ 三 ( N个 ) + 4 σ 三 ( N个 2 ) − σ 1 ( N个 ) + 2 σ 1 ( N个 2 ) ) ，

我们指的是[[15], (3.10), (4.4)].

从上面的计算中，我们得到了一个漂亮的算术结果，我们现在给出了它。

定理3.7 让 N个∈N个.我们有一个公式

第页 8 (4N个)=16 { 56 σ 三 * ( N个 ) + 15 σ 三 ( N个 ) }

如果 是奇数，然后

证明通过使用（30）和，我们得到了定理。 □

备注3.8让M（M）和N个是奇整数(M（M），N个)=1根据定理3.7，我们得出

第页 8 ( 4 M（M） N个 ) = 1 ， 136 σ 三 ( M（M） ) σ 三 ( N个 ) = 1 1 ， 136 ( 1 ， 136 σ 三 ( M（M） ) ) ( 1 ， 136 σ 三 ( N个 ) ) = 1 1 ， 136 第页 8 ( 4 M（M） ) 第页 8 ( 4 N个 )
(31)

和

第页 8 ( 4 对 1 e（电子） 1 ⋯ 对 第页 e（电子） 第页 ) = ( 1 1 ， 136 ) 第页 − 1 第页 8 ( 4 对 1 e（电子） 1 ) ⋯ 第页 8 ( 4 对 第页 e（电子） 第页 ) .
(32)

推论3.9 让 N个= 对 1 e（电子） 1 ⋯ 对 第页 e（电子） 第页 是整数的素分解 N个，如果 为所有人 我=1，…，第页，那么我们有

4问题 σ 1 * (n个)= σ 1 * (n个+1)

西尔宾斯基问 σ 1 (n个)= σ 1 (n个+1)无限频繁。Jud McCranie找到了832个

σ 1 (n个)= σ 1 (n个+1)的n个<4.25× 10 9 ；

参见[[21]，第103页]）。

我们认为 σ 1 * (n个)= σ 1 * (n个+1)和 σ 1 * (n个)= σ 1 * (n个+1)= σ 1 * (n个+2).

4.1进一步结果

首先，我们将比较上述问题 σ 1 (n个)和 σ 1 * (n个).

表的结果11通过组合多台计算机并使用Mathematica 8.0软件实现。我们不可能在这里重现他们的所有细节。根据我们的数值计算，很明显，对上述问题的研究 σ 1 * 比 σ 1 一个。

表11 σ 1 * (n个) 和 σ 1 (n个)
全尺寸桌子

事实上，使用Mathematica 8.0，我们能够获得所有正整数n个<4.25× 10 9 在表中11。请注意 σ 1 (n个)在表中11也显示在[[21]第100页，第103-104页]。

定理4.1

  1. （a）

    如果 2 n个 −1 是奇数质数，然后 σ 1 * ( 2 n个 −1)= σ 1 * ( 2 n个 ).

  2. （b）

    如果 对 和 2对+1 是奇数质数，然后 σ 1 * (2对)= σ 1 * (2对+1).

  3. （c）

    如果 2 n个 −1 是奇数质数，然后我们得到 σ 1 * ( 2 n个 −2)≠ σ 1 * ( 2 n个 −1)= σ 1 * ( 2 n个 ) 具有 n个>三 和 σ 1 * (6)= σ 1 * (7)= σ 1 * (8).

  4. （d）

    如果 n个 和 n个+2 是双质数，然后 σ 1 * (n个+2)= σ 1 * (n个)+2.

  5. （e）

    如果 n个 是正整数，然后我们得到桌子12.

表12表12
全尺寸桌子

证明让对是一个奇数正整数。使用 σ 1 (对)=对+1和 σ 1 * (2米)=2 σ 1 * (米)，我们得到（a）、（b）、（d）和（e）。在（c）中，如果 2 n个 −1是一个带有n个>三，然后n个是奇数。很容易验证

σ 1 * ( 2 n个 − 2 ) =2 σ 1 * ( 2 n个 − 1 − 1 ) =2 σ 1 * ( ( 2 n个 − 1 2 − 1 ) ( 2 n个 − 1 2 + 1 ) ) ≠ 2 n个

和 σ 1 * ( 2 n个 −1)= σ 1 * ( 2 n个 )= 2 n个 很明显 σ 1 * (6)= σ 1 * (7)= σ 1 * (8). □

推论4.2 让 对 是一个奇素数.如果 L（左）= 2 n个 −1 是奇素数或 L（左）=2对，和 2对+1 是质数，然后

σ 1 ( 2 L（左） + 1 ) = 1 2 { σ 1 ( 2 L（左） − 1 ) + 5 σ 1 * ( L（左） ) + ∑ 米 = 1 2 L（左） − 2 ( − 1 ) 米 + 1 σ 1 * ( 米 + 1 ) ( σ 1 * ( 2 L（左） + 1 − 米 ) − σ 1 * ( 2 L（左） − 米 − 1 ) ) } .

证明从表5，我们得到

( L（左） + 1 ) σ 1 * ( L（左） + 1 ) − L（左） σ 1 * ( L（左） ) = ∑ 米 = 1 2 L（左） + 1 ( − 1 ) 米 + 1 σ 1 * ( 米 ) σ 1 * ( 2 L（左） + 2 − 米 ) − ∑ 米 = 1 2 L（左） − 1 ( − 1 ) 米 + 1 σ 1 * ( 米 ) σ 1 * ( 2 L（左） − 米 ) = ∑ 米 = 1 2 L（左） − 1 ( − 1 ) 米 + 1 σ 1 * ( 米 ) { σ 1 * ( 2 L（左） + 2 − 米 ) − σ 1 * ( 2 L（左） − 米 ) } − σ 1 * ( 2 L（左） ) σ 1 * ( 2 ) + σ 1 * ( 2 L（左） + 1 ) = σ 1 * ( 1 ) { σ 1 * ( 2 L（左） + 1 ) − σ 1 * ( 2 L（左） − 1 ) } + ∑ 米 = 2 2 L（左） − 1 ( − 1 ) 米 + 1 σ 1 * ( 米 ) { σ 1 * ( 2 L（左） + 2 − 米 ) − σ 1 * ( 2 L（左） − 米 ) } − 4 σ 1 * ( L（左） ) + σ 1 * ( 2 L（左） + 1 ) .

根据定理4.1（a），（b），我们知道 σ 1 * (L（左）+1)= σ 1 * (L（左）)和 σ 1 * (2L（左）+1)= σ 1 (2L（左）+1); 因此，证明就完成了。 □

引理4.3 让 我 我 :={n个∈N个| σ 1 * (n个)= σ 1 * (n个+我)} 具有 我∈N个.然后 δ 我 ， 2 米 我 : 我 我 → 我 2 米 我 ， δ 我 ， 2 米 我 (n个)= 2 米 n个，是内射映射.特别地，存在一个内射序列 我 2 j个 ，

我 1 ⟶ δ 1 ， 2 我 2 ⟶ δ 2 ， 4 我 4 ⟶ δ 4 ， 8 我 8 →⋯

令人满意的 δ 2 米 ， 2 米 + 1 单射.

证明让n个∈ 我 我 。根据 我 我 ，我们推断 σ 1 * (n个)= σ 1 * (n个+我)根据定理2.2，我们得到 σ 1 * ( 2 米 n个)= σ 1 * ( 2 米 n个+ 2 米 我)和 2 米 n个∈ 我 2 米 我 .然后让n个∈ 我 我 和我∈ 我 我 具有n个≠我，然后 2 米 n个≠ 2 米 我和 σ 1 * ( 2 米 n个)= σ 1 * ( 2 米 n个+我)， σ 1 * ( 2 米 我)= σ 1 * ( 2 米 我+我)因此， δ 我 ， 2 米 我 是内射映射。很明显 δ 2 米 ， 2 米 + 1 是内射映射。 □

通过引理4.3，我们推导出推论。

推论4.4 让 米 是非负整数.如果 ♯{n个| σ 1 * (n个)= σ 1 * (n个+1)}>∞，然后

♯ { n个 | σ 1 * ( n个 ) = σ 1 * ( n个 + 2 米 ) } >∞.

4.2备注和示例

我们列举了以下有趣的评论和例子。

备注4.5

  1. 1

    （Sophie-Germain素数）请注意，如果有无限多的Sophie Germain质数，那么问题 σ 1 * (n个)= σ 1 * (n个+1)有无穷多个解（根据质数）。

  2. 2

    （梅森数）假设 σ 1 * (米)= σ 1 * (米+1)然后，根据定理2.2，我们得到 σ 1 * ( 2 我 米)= σ 1 * ( 2 我 米+ 2 我 )如果梅森素数基数或素数基数对，因此2对+1也是素数，是无限的，那么利用定理4.1（a），（b）米令人满意的 σ 1 * (米)= σ 1 * (米+1)和 σ 1 * (米)= σ 1 * (米+ 2 我 )是无限的。

  3. 三。

    （完美数字）正整数n个称为完美，如果 σ 1 (n个)=2n个欧几里德和欧拉证明了所有的偶数都是这样的形式

    2 对 − 1 ( 2 对 − 1 ) 这样的话 2 对 −1是梅森素数.

    在我们的案例中，我们观察到 σ 1 * ( 2 对 − 1 ( 2 对 −1))≠2⋅ 2 对 − 1 ( 2 对 −1)。如果存在奇数正整数米令人满意的 σ 1 (米)=2米，然后是n个令人满意的 σ 1 * (n个)=2n个是无限的，也就是说， σ 1 * ( 2 我 米)= 2 我 σ 1 * (米)=2( 2 我 米).

4.3截断集的数值计算 我 我 (N个)

让N个是一个正整数并集合 我 我 (N个)= 我 我 ∩{1，2，…，N个}从引理4.3我们可以看到限制映射 δ 我 ， 2 米 我 (n个)= 2 米 n个仍然是内射的 我 我 (N个)和 我 2 米 我 ( 2 米 N个).

在本节中，我们使用Mathematica 8.0计算集合 我 我 (N个)对于N个=100，000= 2 5 ⋅ 5 5 和我=2，4，8，16，32。我们获得了以下列表。

  1. （a）

    我 2 (100，000) = {6、12、14、20、33、44、62、92、116、138、164、212、254、280、308、320、332、356、452、524、572、692、716、764、932、956、1004、1124、1172、1436、1496、1562、1676、1724、1772、1964、2002、2036、2132、2372、2564、2598、2612、2636、2732、2876、2913、2972、3044、3228、3236、3344、3408、3644、3812、4052、407 61424，4，187, 4,196, 4,292, 4,412, 4,728, 4,892, 4,916, 5,156, 5,170, 5,636, 5,756, 5,804, 5,924, 5,996, 6,044, 6,236, 6,332, 6,404, 6,764, 6,932, 7,169, 7,244, 7,424, 7,556, 7,604, 7,724, 7,892, 8,012, 8,050, 8,156, 8,234, 8,252, 8,276, 8,516, 8,564, 8,930, 9,092, 9,356, 9,359, 9,404, 9,572, 9,596, 9,836, 10,172, 10,196, 10,772, 10,796, 10,964, 11,012, 11,276, 11,612, 11,756, 11,852, 11,876, 12,092, 12,212, 12,565, 13,196, 13,316, 13,436, 13,556, 13,652, 13,796, 13,964, 14,156, 14,372, 14,492, 15,044, 15,085, 15,116, 15,212, 15,284, 15,404, 15,452, 15,644, 16,076, 16,120, 16,292, 16,376, 16,382, 16,844, 17,084, 17,396, 17,492, 17,564, 17,636, 17,924, 18,170, 18,932, 19,172, 19,484, 19,676, 19,772, 20,012, 20,156, 20,204, 20,324, 20,684, 20,924, 21,116, 21,212, 21,332, 21,461, 21,518, 21,596, 21,764, 22,004, 22,556, 22,844, 22,964, 23,396, 23,612, 24,212, 24,404, 24,452, 24,524, 24,692, 24,881, 25,019, 25,052, 25,076, 25,292, 25,316, 25,338, 25,796, 25,964, 26,084, 26,204, 26,252, 26,324, 26,609, 27,044, 27,596, 27,932, 28,172, 28,316, 28,412, 28,484, 28,604, 28,772, 28,844, 29,396, 29,696, 29,732, 30,164, 30,572, 30,596, 30,764, 31,292, 31,364, 31,532, 31,604, 32,276, 32,372, 32,444, 32,804, 32,972, 33,092, 33,590, 34,052, 34,652, 34,772, 34,964, 35,358, 35,804, 35,876, 36,116, 36,236, 36,884, 37,172, 37,484, 37,676, 37,892, 37,916, 38,156, 38,516, 38,756, 39,164, 40,244, 40,364, 40,458, 40,652, 41,012, 41,084, 41,252, 41,324, 42,116, 42,356, 42,452, 42,764, 42,836, 42,932, 43,124, 43,196, 43,532, 44,684, 45,078, 45,284, 45,476, 45,572, 45,884, 46,076, 46,196, 46,316, 46,796, 46,863, 47,132, 47,204, 47,252, 47,324, 47,636, 47,756, 47,792, 47,978, 48,044, 48,164, 48,404, 48,476, 48,812, 49,052, 49,225, 49,316, 50,612, 50,684, 51,164, 51,284, 51,596, 51,692, 51,835, 51,836, 52,004, 52,196, 52,916, 53,058, 53,252, 53,804, 53,852, 53,963, 54,212, 54,476, 54,596, 55,052, 55,532, 55,604, 55,652, 55,748, 56,036, 56,324, 56,612, 56,636, 56,996, 57,212, 57,284, 57,956, 58,056, 58,244, 58,484, 58,676, 58,796, 58,964, 59,132, 59,324, 59,516, 59,756, 59,987, 60,404, 60,644, 60,692, 60,932, 61,076, 61,604, 61,832, 62,276, 62,516, 63,092, 63,164, 63,212, 63,692, 64,004, 64,364, 65,012, 65,204, 65,684, 65,972, 66,212, 66,692, 67,244, 67,292, 67,532, 67,724, 68,636, 68,732, 69,164, 69,332, 69,404, 70,316, 70,676, 70,724, 71,756, 71,924, 72,164, 72,524, 72,596, 72,764, 72,836, 72,932, 73,364, 73,772, 73,844, 74,924, 75,092, 75,108, 75,212, 75,596, 76,652, 77,057, 77,204, 77,276, 77,492, 77,564, 77,732, 78,212, 78,236, 78,644, 78,836, 79,004, 79,292, 79,556, 79,652, 79,676, 79,964, 80,252, 80,996, 81,055, 81,476, 81,572, 81,644, 81,764, 82,772, 83,012, 83,036, 83,084, 83,156, 83,516, 83,684, 83,756, 83,852, 84,044, 84,356, 84,596, 84,716, 84,884, 85,364, 85,532, 85,676, 86,170, 86,444, 86,804, 86,852, 87,212, 87,572, 88,052, 88,316, 88,532, 89,036, 89,084, 89,372, 89,396, 89,636, 89,732, 89,876, 89,924, 90,164, 91,004, 91,412, 91,772, 92,396, 93,116, 93,284, 93,356, 93,836, 94,244, 94,412, 94,676, 95,012, 95,276, 95,636, 95,924, 96,812, 96,956, 97,124, 97,892, 98,036, 98,204, 98,444, 98,732, 98,996, 99,638, 99,884 }.

  2. （b）

    我 4 (100，000) = { 12, 24, 28, 40, 51, 66, 88, 115, 124, 184, 232, 276, 319, 328, 424, 508, 560, 616, 640, 664, 712, 904, 1,003, 1,048, 1,144, 1,384, 1,432, 1,528, 1,864, 1,912, 2,008, 2,248, 2,344, 2,585, 2,872, 2,992, 3,124, 3,352, 3,448, 3,544, 3,928, 4,004, 4,072, 4,183, 4,195, 4,264, 4,744, 5,128, 5,196, 5,224, 5,272, 5,464, 5,752, 5,826, 5,944, 5,959, 6,088, 6,456, 6,472, 6,688, 6,816, 7,288, 7,624, 8,104, 8,152, 8,248, 8,374, 8,392, 8,584, 8,824, 9,456, 9,784, 9,832, 10,312, 10,340, 11,272, 11,512, 11,608, 11,659, 11,848, 11,992, 12,088, 12,367, 12,472, 12,561, 12,664, 12,808, 13,528, 13,581, 13,864, 14,338, 14,488, 14,848, 15,112, 15,208, 15,365, 15,448, 15,784, 16,024, 16,100, 16,312, 16,468, 16,504, 16,552, 17,032, 17,128, 17,860, 18,184, 18,712, 18,718, 18,808, 19,144, 19,192, 19,672, 20,344, 20,392, 20,541, 21,544, 21,592, 21,928, 22,024, 22,552, 23,224, 23,512, 23,704, 23,752, 24,184, 24,424, 25,130, 26,392, 26,632, 26,872, 27,112, 27,304, 27,592, 27,928, 28,312, 28,744, 28,984, 29,393, 30,088, 30,170, 30,232, 30,424, 30,568, 30,808, 30,904, 31,288, 32,152, 32,240, 32,584, 32,665, 32,752, 32,764, 33,688, 34,168, 34,792, 34,984, 35,128, 35,272, 35,848, 36,340, 37,864, 38,344, 38,968, 39,352, 39,544, 39,913, 40,024, 40,312, 40,408, 40,648, 41,368, 41,848, 42,232, 42,423, 42,424, 42,664, 42,922, 43,036, 43,192, 43,528, 44,008, 45,112, 45,688, 45,928, 46,792, 47,224, 47,841, 48,424, 48,808, 48,904, 49,048, 49,384, 49,762, 50,038, 50,104, 50,152, 50,435, 50,584, 50,632, 50,676, 51,592, 51,928, 52,168, 52,408, 52,504, 52,648, 53,218, 54,088, 55,192, 55,864, 56,344, 56,632, 56,824, 56,968, 57,208, 57,544, 57,688, 58,792, 59,392, 59,464, 60,328, 61,144, 61,192, 61,528, 62,584, 62,728, 63,064, 63,208, 64,552, 64,744, 64,888, 65,608, 65,944, 66,184, 67,180, 68,104, 69,304, 69,544, 69,928, 70,716, 71,608, 71,752, 72,232, 72,472, 73,768, 74,344, 74,968, 75,352, 75,784, 75,832, 76,312, 77,032, 77,512, 78,328, 80,488, 80,728, 80,916, 81,304, 82,024, 82,168, 82,504, 82,648, 84,232, 84,712, 84,904, 85,528, 85,672, 85,864, 86,248, 86,392, 87,064, 88,303, 89,368, 90,156, 90,568, 90,952, 91,144, 91,768, 92,152, 92,392, 92,599, 92,632, 93,592, 93,726, 94,264, 94,408, 94,504, 94,648, 95,272, 95,512, 95,584, 95,956, 96,088, 96,328, 96,808, 96,952, 97,624, 98,104, 98,450, 98,632}.

  3. （c）

    我 8 (100，000) = { 15, 24, 48, 56, 69, 80, 87, 102, 132, 175, 176, 230, 248, 368, 464, 552, 638, 656, 689, 848, 1,016, 1,120, 1,127, 1,232, 1,280, 1,328, 1,349, 1,424, 1,808, 2,006, 2,096, 2,288, 2,768, 2,864, 3,056, 3,728, 3,824, 4,016, 4,496, 4,688, 5,170, 5,744, 5,984, 6,248, 6,704, 6,896, 7,088, 7,856, 8,008, 8,144, 8,366, 8,390, 8,528, 9,488, 10,256, 10,392, 10,448, 10,544, 10,928, 11,504, 11,652, 11,888, 11,918, 12,176, 12,912, 12,944, 13,376, 13,632, 14,576, 15,248, 16,208, 16,304, 16,496, 16,748, 16,784, 17,168, 17,648, 18,912, 19,511, 19,568, 19,664, 19,829, 20,624, 20,680, 22,544, 23,024, 23,216, 23,318, 23,696, 23,984, 24,176, 24,597, 24,734, 24,944, 25,122, 25,328, 25,616, 27,056, 27,162,27728、28676、28976、29696、30224、30416、30730、30896、31568、32048、32200、32624、32936、33008、33104、34064、34256、35720、36368、37391、37424、37436、37616、37901、38288、38384、39344、40688、40784、41082、43088、43184、43856、44048、45104、45925、4648、47024、47408、47487、47504、48368、48848， 50,260, 52,784, 53,264, 53,744, 54,224, 54,608, 55,184, 55,856, 56,624, 57,488, 57,968, 58,786, 59,125, 60,176, 60,340, 60,464, 60,848, 61,053, 61,136, 61,616, 61,808, 62,576, 64,304, 64,480, 65,168, 65,330, 65,504, 65,528, 67,376, 68,336, 69,584, 69,968, 70,256, 70,544, 71,696, 72,680, 75,728, 76,688, 77,936, 78,704, 79,088, 79,826, 80,048, 80,624, 80,816, 81,296, 81,989, 82,736, 83,696, 84,464, 84,846, 84,848, 85,328, 85,844, 86,072, 86,384, 87,056, 88,016, 90,224, 91,376, 91,856, 93,584, 94,448, 95,682, 96,848, 97,557, 97,616, 97,808, 98,096, 98,768, 99,524, 99,827}.

  4. （d）

    我 16 (100，000) = { 30, 48, 55, 96, 112, 138, 160, 174, 204, 205, 264, 350, 352, 355, 460, 496, 736, 928, 1,104, 1,276, 1,293, 1,312, 1,378, 1,696, 2,032, 2,240, 2,254, 2,464, 2,560, 2,656, 2,698, 2,848, 3,277, 3,616, 3,669, 4,012, 4,192, 4,576, 5,536, 5,728, 6,112, 7,456, 7,648, 8,032, 8,992, 9,376, 9,853, 10,340, 11,488, 11,968, 12,496, 12,549, 13,408, 13,792, 13,899, 14,176, 14,857, 15,712, 16,016, 16,288, 16,732, 16,780, 17,056, 18,976, 20,512, 20,784, 20,896, 21,088, 21,856, 23,008, 23,287, 23,304, 23,776, 23,836, 24,352, 25,824, 25,888, 26,077, 26,752, 27,264, 29,152, 30,496, 32,416, 32,608, 32,992, 33,496, 33,568, 34,336, 35,296, 36,669, 37,824, 39,022, 39,136, 39,187, 39,328, 39,658, 41,248, 41,360, 41,525, 45,088, 46,048, 46,432, 46,636, 47,392, 47,968, 48,352, 49,194, 49,468, 49,888, 50,244, 50,656, 51,232, 54,112, 54,324, 55,456, 56,743, 57,352, 57,952, 59,392, 60,448, 60,832, 61,460, 61,792, 63,136, 64,096, 64,400, 64,963, 65,248, 65,872, 66,016, 66,208, 68,128, 68,512, 71,440, 72,736, 73,321, 74,782, 74,848, 74,872, 75,232, 75,802, 76,576, 76,768, 78,688, 81,376, 81,568, 82,164, 85,839, 86,176, 86,368, 87,712, 88,096, 90,208, 90,637, 91,850, 92,896, 94,048, 94,816, 94,974, 95,008, 95,113, 96,193, 96,736, 97,696}.

  5. （e）

    我 32 (100，000) = { 60, 96, 110, 177, 192, 224, 276, 303, 320, 348, 408, 410, 528, 605, 700, 704, 710, 749, 920, 992, 1,045, 1,157, 1,472, 1,856, 2,208, 2,552, 2,567, 2,586, 2,624, 2,756, 3,392, 4,064, 4,480, 4,508, 4,533, 4,928, 5,120, 5,312, 5,396, 5,696, 6,554, 7,232, 7,338, 7,697, 8,024, 8,384, 9,152, 10,547, 11,072, 11,456, 12,224, 13,199, 14,912, 15,296, 16,064, 16,345, 17,984, 18,752, 19,706, 20,381, 20,680, 21,197, 21,797, 22,976, 23,936, 24,992, 25,075, 25,098, 26,816, 27,584, 27,798, 28,352, 29,321, 29,365, 29,714, 31,424, 32,032, 32,576, 32,849, 33,464, 33,560, 34,112, 37,929, 37,952, 41,024, 41,568, 41,792, 42,176, 43,712, 46,016, 46,574, 46,608, 47,552, 47,672, 48,704, 51,648, 51,776, 52,154,53504、54528、58304、60992、61705、64832、65216、65984、66992、67136、68672、70049、70592、73338、75648、78044、78272、78374、78656、79316、82496、82720、83050、85769、89033、90176、92096、92864、93272、94784、95936、96704、98388、98936、99776｝。

我们通过以下评论来结束本文。

备注4.6根据得到的数值结果，研究集的基数的上下界是很有趣的 我 我 (N个)同样，我们也可以研究这个基数的渐近行为。这样我们就可以知道 我 我 是无限的。

工具书类

  1. 伯恩特BC：Ramanujan的笔记本，第二部分施普林格，柏林；1989

    书 谷歌学者 

  2. 威廉姆斯KS伦敦数学学会学生课文76。在刘维尔精神中的数论剑桥大学出版社，剑桥；2011

    谷歌学者 

  3. Royer E：用拟模形式计算除数函数的卷积和。国际数论2007, 3(2):231–261. 10.1142/S1793042107000924号

    第条 数学科学网 谷歌学者 

  4. Ramakrishnan，B，Sahu，B：卷积和的计算 ∑ 我 + 15 米 = n个 σ(我)σ(米)和 ∑ 三 我 + 5 米 = n个 σ(我)σ(米)和一个应用程序。国际数论杂志（2012年，接受）

  5. Alaca S，Williams KS:卷积和的评估 ∑ 我 + 6 米 = n个 σ(我)σ(米)和 ∑ 2 我 + 三 米 = n个 σ(我)σ(米).J.数论2007, 124(2):491–510. 2016年10月10日/j.jnt.2006.10.004

    第条 数学科学网 谷歌学者 

  6. 阿拉卡A，阿拉卡S，维吾尔F，威廉姆斯KS：限制艾森斯坦级数和某些卷积和。J.库姆。数论2011, 3: 1–14.

    数学科学网 谷歌学者 

  7. Adiga C，Ramaswamy HN：关于某些可除性问题的注释。国际数学杂志。分析。2008, 2(24):1157–1161.

    数学科学网 谷歌学者 

  8. Simsek Y：和椭圆Bernoulli函数相关的Hardy和的椭圆模拟。一般数学。2007, 15(2–3):3–23.

    数学科学网 谷歌学者 

  9. Gyory K，Dujella A，Pinter A：关于金字塔数的幂值，I。《阿里斯学报》。2012, 155: 217–226. 10.4064/aa155-2-9

    第条 数学科学网 谷歌学者 

  10. 西尔弗曼JH：椭圆曲线的算法施普林格，柏林；1986

    书 谷歌学者 

  11. 迪克森LE II。在数论史.切尔西，纽约；1952

    谷歌学者 

  12. Kim A，Kim D，Li Y:除数函数产生的卷积和。J.韩国数学。Soc公司。2013, 50(2):331–360. 10.4134/JKMS.2013.50.2.331

    第条 数学科学网 谷歌学者 

  13. Garge AS，Shirali SA：三角数。共振2012, 17(7):672–681. 10.1007/s12045-012-0074-z

    第条 谷歌学者 

  14. Hoggatt VE Jr.，Bicknell M：三角数。斐波那契Q。1974, 12: 221–230.

    数学科学网 谷歌学者 

  15. Huard JG，Ou ZM，Spearman BK，Williams KS：涉及除数函数的卷积和的初等计算。二、。千年数论2002, 229–274.

    谷歌学者 

  16. Cheng N，Williams KS:一些涉及除数函数和的卷积和的计算。横滨数学。J。2005, 52: 39–57.

    数学科学网 谷歌学者 

  17. Andrew GE，Berndt BC：拉马努扬丢失的笔记本，第一部分施普林格，柏林；2005

    谷歌学者 

  18. Milne S：精确平方和公式、Jacobi椭圆函数和Ramanujanτ函数的新无限族。程序。国家。阿卡德。科学。美国1996, 93: 15004–15008. 10.1073/pnas.93.26.15004

    第条 数学科学网 谷歌学者 

  19. Whittaker ET、Watson GN：现代分析课程第4版。剑桥大学出版社，剑桥；1927:464–498.

    谷歌学者 

  20. Jacobi，CGJ：基础新神学函数Ellipticarum，Sumptibus Fratrum Bornträger。重印于C.G.J.Jacobi，Gesammelte Werke，第1卷，第49-239页。柏林雷默（1881-1891）

  21. 盖伊·RK：数论中尚未解决的问题施普林格，柏林；2004

    书 谷歌学者 

下载参考资料

致谢

献给Hari M Srivastava教授。

这项研究得到了韩国政府资助的国家数学科学研究所（NIMS）拨款（B21303）和埃弗里大学数学系的“装备Ananlyse et Probabilityés”的支持。

作者信息

作者和附属机构

  1. 国家数学科学研究所，韩国大田市裕兴区裕兴谷1689-gil，305-811

    金大中

  2. 埃弗里·瓦尔德埃松大学数学系，法国埃弗里·塞德克斯法国大道23号3èmeétage，邮编91037

    阿卜杜勒梅吉德·巴亚德

作者
  1. 大约尔·金
    查看作者出版物

    您还可以在中搜索此作者公共医学 谷歌学者

  2. 阿卜杜勒梅吉德·巴亚德
    查看作者出版物

    您还可以在中搜索此作者公共医学 谷歌学者

通讯作者

与的通信阿卜杜勒梅吉德·巴亚德.

其他信息

竞争性利益

作者声明，他们没有相互竞争的利益。

作者的贡献

所有作者阅读并批准了最终手稿。

作者提交的原始图像文件

权利和权限

开放式访问本文根据Creative Commons Attribution 2.0 International License的条款分发(https://creativecommons.org/licenses/by/2.0)它允许在任何介质中不受限制地使用、分发和复制原始作品，前提是正确引用了原始作品。

转载和许可

关于本文

引用这篇文章

Kim，D.，Bayad，A.扭曲Eisenstein级数和扭曲因子函数的卷积恒等式。不动点理论应用 2013, 81 (2013). https://doi.org/10.1186/1687-1812-2013-81

下载引文

  • 收到:

  • 认可的:

  • 出版:

  • 内政部:https://doi.org/10.1186/1687-1812-2013-81

关键词