主机名：page-component-8448b6f56d-jr42d总加载时间：0渲染日期：2024-04-19T02:36:58.444Z有数据问题：falsehasContentIssue为false
  • 英语
  • 法国

基于周围结构扰动的振荡流同步降相

剑桥大学出版社在线出版：2021年2月1日

无辜A.Loe 打开Innocentio A.Loe的ORCID记录 [在新窗口中打开] ,
中尾博彦（Hiroya Nakao） ,
Yasuhiko Jimbo先生 和
Kiyoshi Kotani公司
无辜A.Loe*
附属：
日本东京大学精密工程系，东京113-0032
中尾博彦（Hiroya Nakao）
附属：
日本东京理工大学系统与控制工程系，东京152-8552
Yasuhiko Jimbo先生
附属：
日本东京大学精密工程系，东京113-0032
Kiyoshi Kotani公司
附属：
日本东京大学先进科学技术研究中心153-8904
*
†通信电子邮件地址：loe@neuron.t.u-tokyo.ac.jp
权限和权限 [在新窗口中打开]

摘要

在许多自然和人工系统中，例如在心血管系统中，可以观察到周围弹性结构的变形对流体流动的调节。作为研究振荡流动规律的第一步，我们考虑了在正弦外力作用下，弹性结构中圆柱绕流涡旋脱落的同步性。我们使用相还原理论来评估振荡流-结构耦合动力学的同步特性。我们发现，对于固定的模型配置和雷诺数，表征振荡相位响应的相敏函数受到柯西数的显著影响，而受到结构材料的流体-结构密度比和泊松比的轻微影响。预测的同步特性与直接数值模拟的结果非常吻合。当在圆柱下游端附近施加正弦扰动时，同步区域最大化。这些发现为利用相还原理论表征其他表现出流体-结构耦合动力学的实际问题中的同步性提供了进一步的可能性，例如在生物系统和微流体控制中。

JFM分类

非线性动力系统：非线性动力系统非线性动力系统：低维模型涡流：涡流脱落
类型
JFM急流
问询处
流体力学杂志 ,911卷 2021年3月25日 ，R2
检查更新
知识共享
创意通用许可证-CC创意通用许可证-BY
这是一篇开放存取文章，根据知识共享署名许可证的条款分发(http://creativecommons.org/licenses/by/4.0/)它允许在任何介质中无限制地重复使用、分发和复制原始作品，前提是正确引用了原始作品。
版权
©作者，2021年。剑桥大学出版社出版。

1介绍

在许多自然现象中都可以观察到自持振荡，例如振荡化学反应（Kuramoto参考Kuramoto1984)、尖峰神经元（Ermentrout和Terman参考Ermentrout和Terman2010)、心肌细胞（小岛、神户和安田参考小岛、神户和安田2006)和涡流脱落（Zdravkovich参考Zdravkovich1996). 这样的系统可以解释为极限循环振荡器。在振荡动力学中观察到的一个有趣现象是同步（Kuramoto参考Kuramoto1984; Pikovsky、Rosenblum和Kurths参考Pikovsky、Rosenblum和Kurths2001; Ermentrout&Terman公司参考Ermentrout和Terman2010). 虽然这种动力系统通常是非线性的，并且可以是无限维的，但其周期性允许使用相还原理论以简化的方式来表示动力学，相还原理论是一种强大的工具，它允许仅考虑系统的相动力学来分析同步特性（Kuramoto参考Kuramoto1984; 皮科夫斯基等。 参考Pikovsky、Rosenblum和Kurths2001; Ermentrout&Terman公司参考Ermentrout和Terman2010; Nakao公司参考Nakao2016).

相位还原理论已被扩展到许多不同类型的振荡动力学，例如时滞系统和混合系统（Kotani等。 参考Kotani、Yamaguchi、Ogawa、Jimbo、Nakao和Ermentrout2012; 诺维琴科和皮拉加斯参考Novičenko和Pyragas2012; Shirasaka、Kurebayashi和Nakao参考Shirasaka、Kurebayashi和Nakao2017). 在流体力学领域，川村和中尾康夫最近的工作(参考川村和中尾岛2013,参考川村和中尾岛2015)考虑了周期时空模式相还原理论的扩展，以分析海勒-肖流。最近，Taira&Nakao的工作中考虑了涡脱落锁定振荡驱动的计算研究(参考Taira和Nakao2018)和Khodkar&Taira(参考Khodkar和Taira2020).

在振荡流体流与弹性结构接触的情况下，需要将动力学视为流体-结构相互作用（FSI）的问题。周围结构的位移将导致流体边界的移动。相反，流体流在流体-结构界面上施加力，导致结构位移（Richter参考Richter2017). 涉及FSI的振动现象的一个常见例子是旋涡脱落内的振动柔性结构（Gomes&Lienhart参考Gomes和Lienhart2013). 在研究微电子机械系统（Ducloux等。 参考Ducloux、Talbi、Gimeno、Viard、Pernod、Preobrazhensky和Merlen2007). 在生物系统中，众所周知，血管平滑肌上交感神经系统的传出活动会改变血管的收缩性，进而调节周期性血流（Kotani等。 参考Kotani、Struzik、Takamasu、Stanley和Yamamoto2005; Shiogai、Stefanovska和McClintock参考资料Shiogai、Stefanovska和McClintock2010). Kawamura和Tsubaki的工作考虑了利用相位还原实现鞭毛跳动的弹流动力学同步的理论公式(参考河村和Tsubaki2018). 然而，关于流体-结构耦合动力学中的振荡和同步问题，仍有许多未知之处。

在这项工作中，我们将相位还原用于FSI动力学，作为理解振荡流如何通过周围结构上的弱扰动进行调节的第一步。我们在§2相位响应特性对材料类型、扰动位置以及同步特性的依赖性在§三最后，§4通过将其简化为单标量相动力学，本文提出的方法可以被视为分析复杂动力学系统（如FSI）的一种简化但强大的方法。

2方法

2.1.模型定义

在这项研究中，我们定义了一个二维层流不可压缩流模型，该模型通过由弹性结构包围的通道内的圆柱体，如所示图1.圆柱体本身被视为具有直径的静态刚体$d=0.1\\textrm{m}$居中于$（x，y）=（0.2\\text{m}，0.1\\text{m}）$流体和结构完全耦合（Horn&Turek参考喇叭和图雷克2006; 里希特参考Richter2017). 基于有限元方法，使用COMSOL Multiphysics 5.5进行了数值模拟。

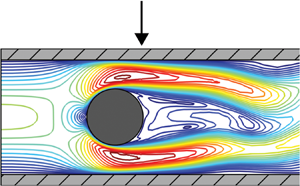
图1。本研究中使用的模型。流体域周围的弹性结构域由阴影图案标记。气缸中心位于$（x，y）=（0.2\\textrm{m}，0.1\\textrm}）$.

流体流动由任意拉格朗日-欧拉（ALE）公式（Quarteroni、Tuveri和Veneziani）中的不可压缩Navier–Stokes方程控制参考季刊、Tuveri和Veneziani2000; 霍恩和图雷克参考喇叭和图雷克2006)这样的话

（2.1）一,b条)\开始｛align｝\rho_f\left\｛\dfrac｛\partial\boldsymbol{u} f（_f）}{\部分t}+[（\粗体符号{u} _（f）-\粗体符号{u} _米)\boldsymbol{\cdot}\boldsymbol{\nabla}]\boldsembol{u} _（f）\right\}=\boldsymbol{nabla}\boldsymbol{\cdot}\left\{-p{\boldsimbol{\tathsf{I}}+\mu\left[\boldsembol{\nabla}\bolsymbol{u} _（f）+（粗体符号{\nabla}\boldsymbol{u} _（f）)^\text{T}\right]\right\}\quad\text{和}\qua2\boldsymbol{\nabla}\boldsympol{\cdot}\bolsymbol{u} _（f）=0，\结束{align}

哪里$\rho _f$,$\亩$,美元$,$\粗体符号{u} _（f）$,$\粗体符号{u} _米$和${\boldsymbol{\mathsf{I}}}$表示流体密度、动态粘度、压力、流体流速、空间坐标速度和单位矩阵。假设外部体积力为零。流体在通道内从左向右流动。出口规定为零压力边界条件。在流体-结构界面和气缸壁周围规定了无滑移边界条件。在入口处规定了抛物线速度剖面，以便$\boldsymbol{u}（0，y）=\bar{U}（U）_{f} {6y（H-y）}/{H^2}$，其中美元\bar{U}（U）_{f}$是平均入口速度$H=0.2\\textrm{m}$是通道宽度。

周围的结构被建模为各向同性的线性弹性材料。动力学由

(2.2)\开始｛方程｝\rho_s\left（\dfrac｛\partial ^2 \粗体符号{w} _秒}{\部分t^2}+\alpha\dfrac{\部分\boldsymbol{w} _秒}{\partial t}\right）=\boldsymbol{\nabla}\boldsymbol{\ cdot}\left（{\boldsimbol{\mathsf{P}}^\text{t}+\beta\dfrac{\partical{\bolsymbol{\mathsf{P}{^\text{t}}{\partitle t}\ right）+\varepsilon\boldsembol{\tata}_s（\boldcymbol{x}，t），\end{方程式}

哪里美元\rho _s$,$\粗体符号{w} _秒$,$\阿尔法$,$\测试版$和${\boldsymbol{\mathsf{P}}}$表示结构密度、位移、质量阻尼系数、刚度阻尼系数和第一个Piola–Kirchoff应力张量（Formato等。 参考Formato、Romano、Formato，Sorvari、Koiranen、Pellegrino和Villeco2019). 应力张量${\boldsymbol{\mathsf{P}}}$以杨氏模量为特征E美元$和泊松比$\nu美元$根据胡克定律的结构材料。在这项工作中，我们定义$\alpha=0.2\\textrm{s}^{-1}$和$\beta=0.1\\textrm{s}$.弹性结构的顶部和底部宽度均设置为0.02m。零位移规定在结构的左右边缘。扰动$\varepsilon\boldsymbol{\eta}_s（\boldsymbol{x}，t）$定义为结构上边界处的局部力，如图1，使得

(2.3一,b条)\开始{align}\varepsilon\boldsymbol{\eta}_s（\boldsymbol{x}，t）=-\varepsilon\delta\left（\bolsymbol{x}-\粗体符号{x} _0（0）\right）\eta（t）\hat{\boldsymbol{e}}_y\quad\text{和}\quad\\delta\left（\boldsymbol{x}-\粗体符号{x} _0（0）\right）=\dfrac{1}{\sqrt{2{\rm\pi}}\sigma_x}\exp\left[-\dfrac}{2}\left（\dfrac{\boldsymbol{x}-\粗体符号{x} 0}｛\sigma_x｝\right）^2 \right]，\结束｛align｝

哪里$\粗体符号{x}$是空间坐标，$\增量（\粗体符号{x}-\粗体符号{x} _0（0） )$描述了空间脉冲分布和$\hat{\boldsymbol{e}}_y$是单位向量美元$方向，而负号表示在结构域的方向上施加扰动。时变分量$\eta（吨）$定义为

(2.4)\begin{方程}\eta（t）=\begin{cases}\dfrac{1}{\sqrt{2{\rm\pi}}\sigma_t}\exp\left[-\dfrac{1}{2}\left（\dfrac[t-t0}{\sigma_t}\right）^2\right]，&\text{表示脉冲扰动}，\\sin（\omega_f t），\\text{表示正弦扰动}。\结束{cases}\结束{equation}

空间和时间脉冲分布均近似为高斯函数$\sigma_x=0.01\\textrm{m}$和$\sigma_t=0.01\\textrm{s}$我们使用脉冲扰动来评估振荡流的相敏函数，这在相还原分析中是必要的，使用正弦扰动来评估振动流的同步性（详见§2.2). 扰动振幅的选择应确保$\varepsilon=0.001 \\textrm{N}$对于脉冲扰动和$\varepsilon\in[0,25]\\textrm{N}中$对于周期扰动的情况。

流体-结构界面满足运动学和动力学耦合条件美元\varOmega$（里希特参考Richter2017)也就是说，

（2.5）一,b条)\开始{等式}\boldsymbol{u} _（f）\bigg|_\varOmega=\boldsymbol{u} _秒\bigg|_\varOmega=\dfrac{\partial\boldsymbol{w} _秒}｛\partial t｝\bigg|_\varOmega\fquad\text｛and｝\fquad\boldsymbol{F} n个\bigg|_\varOmega=\hat｛\boldsymbol｛e｝｝_n\boldsymbol｛\cdot｝\｛-p｛\boldsymbol｛\mathsf｛I｝｝｝+\mu｛\boldsymbol｛nabla｝\boldsymbol{u} _（f）+（粗体符号{\nabla}\boldsymbol{u} _（f）)^\text{T}]\}\bigg|_\varOmega，\end{方程式}

哪里$\粗体符号{u} _秒$是结构位移的速度，$\粗体符号{F} _n（n）$是流体施加在结构上的单位面积法向力$\hat{\boldsymbol{e}}_n$是垂直于流体-结构界面的单位向量。

我们通过基于圆柱直径的雷诺数来表征模型问题$再保险$，柯西数美元C_Y$和流体结构密度比$\mathcal{M}$（德纳耶等。 参考文献DeNayer、Apostolatos、Wood、Bletzinger、Wüchner和Breuer2018)，定义为

(2.6一——c（c）)\开始{方程式}Re=\dfrac{\rho_f\bar{U} _（f）d}{\mu}，\quad C_Y=\dfrac{\rho_f\bar{U} _（f）^2} {E}\quad\text{和}\quae\mathcal{M}=\dfrac{\rho_f}{\rhoS}。\结束{方程式}

表1显示了本研究中考虑的材料属性。使用材质类型1的属性，但通过修改$\亩$，发现极限循环振荡发生于90美元Re 300$。对于定义的所有材料类型，流体属性的选择应确保$Re=100$。材料类型1用作比较的基础值。对于类型2和3$年（_C）$通过更改进行修改E美元$比率为基础值的1.25倍。对于类型4和5$\mathcal{M}$通过更改进行修改美元\rho _s$比率为基础值的1.25倍。对于类型6和7，$\nu美元$按基础值的1.2倍进行修改，以使其保持在各向同性线弹性材料的范围内($1.0<\nu<0.5$). 对于类型8，在保持$再保险$,美元C_Y$,$\mathcal{M}$和$\nu美元$等于基本值。

表1。本研究中考虑的流体类型和结构材料属性。

计算域使用一个总单元数为2864的分布式四边形网格进行离散。气缸和流体-结构界面周围的元件更加精细，最大尺寸限制为$6.72\乘以10^{-3}\\textrm{m}$最小尺寸限制为9.6美元乘以10^{-5}\\textrm{m}$。使用隐式时间步进，模拟输出每$\增量t=0.0005\\textrm{s}$.

2.2.相位还原

在这里，我们简要描述了相位还原理论及其在分析同步特性（Nakao参考Nakao2016; 泰拉和中高参考Taira和Nakao2018). 让我们把受外力扰动的振荡FSI动力学的控制动力学写成

(2.7)\开始{等式}\dfrac{\partial}{\parialt}\boldsymbol{X}（\boldsymbol{X}，t）=\boldsimbol{F}\{\boldsembol{X}\}+\varepsilon\boldcymbol{\eta}

哪里$\boldsymbol｛X｝=[\boldssymbol{u} f（_f），\粗体符号{w} _秒]$是系统状态，$\boldsymbol{F}\{\boldsymbol{X}\}$是系统动力学和扰动$\varepsilon\boldsymbol{\eta}（\boldsymbol{x}，t）$足够小。我们假设系统具有指数稳定的极限环解$\粗体符号{十} _0（0）$具有频率$\ω_n$，使得$\粗体符号{十} _0（0）（\boldsymbol{x}，t+2{\rm\pi}/\omega _n）=\boldsymbol{十} _0（0）（\粗体符号{x}，t）$感到满意。A相功能$\varTheta[\boldsymbol{X}]$将系统状态映射到标量相位值$\θ\ in[0,2{\rm\pi}）$可以引进（中尾府、柳城和川村参考Nakao、Yanagita和Kawamura2014)，以便系统的阶段$\theta=\varTheta[\boldsymbol{X}]$始终以恒定频率增加$\dot{\theta}（t）=\int（\delta\varTheta/\delta\ boldsymbol{X}）\boldsympol{\cdot}\boldsymbol{F}\{\boldsembol{X}\}\，\textrm{d}\bolsymol{X{=\omega_n$当不存在扰动时，在极限环的流域中，其中$\delta\varTheta/\delta\粗体符号{X}$是的函数导数$\varTheta[\boldsymbol{X}]$在$\boldsymbol{X}=\boldsymbol{X}（\boldsimbol{X}，t）$.在最低阶近似下（忽略高阶项），$\delta\varTheta/\delta\粗体符号{X}$可以近似地在$\boldsymbol{X}=\boldsymbol{X} 0（\boldsymbol｛x｝，\theta/\omega _n）$关于极限环和弱扰动下的相位动力学，可以找到

(2.8)\开始{方程式}\dot{theta}（t）=\omega_n+\varepsilon\int\boldsymbol{Z}

哪里$\boldsymbol{Z}（\boldsymbol{x}，\theta）=[\boldsimbol{Z}（Z）_{f} （粗体符号{x}，θ），粗体符号{Z}（Z）_{s} （\boldsymbol{x}，\theta）]=\delta\varTheta/\delta\ boldsympol{x}|_{\boldsymbol{x{=\boldsimbol{十} _0（0）（粗体符号{x}，θ/\omega _n）}$称为相敏函数。如果$\boldsymbol{Z}（\boldsymbol{x}，\theta）$已知，任何扰动函数的影响$\varepsilon\boldsymbol{\eta}（\boldsymbol{x}，t）$可以通过以下方式确定(2.8). 特别是，如果结构上的扰动在空间上以形式局部化$\boldsymbol{\eta}（\boldsymbol{x}，t）=[\boldsimbol{\ta}_f（\bolsymbol{x}，t{x} _0（0）)\eta（t）\hat{\boldsymbol{e}}_y]$，相位方程为$\dot{\theta}（t）=\omega_n+\varepsilon Z_y（\theta）\eta（t）$，其中$Z_y（θ）=int\boldsymbol{Z}（Z）_{s} （\粗体符号{x} _0（0），\theta）\boldsymbol{\cdot}[-\delta（\boldsymbol{x}-$ $\粗体符号{x} _0（0）)\hat{\boldsymbol{e}}_y]\，\textrm{d}\boldsymbol{x}$.

在这项工作中，我们评估$Z_y（θ）$使用直接脉冲扰动法（Ermentrout&Terman参考Ermentrout和Terman2010; Nakao公司参考Nakao2016)，使用摄动函数$\varepsilon\boldsymbol{\eta}_s（\boldsymbol{x}，t）$定义于(2.3一,b条)和(2.4). 通过引入特定相位的脉冲$\θ$（由t_0美元$)相位动力学将受到影响，其中沿极限循环轨道将观察到相移。这种渐近相移称为相位响应函数$g（\theta；\varepsilon\hat{\boldsymbol{e}}_y）$这取决于引入它的振幅、位置、方向和相位。因此，相位的相敏函数$\θ$可以评估为

(2.9)\开始{方程式}Z_y（θ）=\lim_{\varepsilon\到0}\dfrac{g（θ；\varepsilon\hat{\boldsymbol{e}}_y）}{\varesilon}\approx\dfrac}（θ。\结束{方程式}

因此，我们可以评估$Z_y（θ）$通过在整个范围内引入脉冲扰动$\θ$.通过评估$g（\theta；\varepsilon\hat{\boldsymbol{e}}_y）$使用显示周期振荡的适当观测值，$Z_y（θ）$可以使用有限数量的测量来确定。在本研究中，我们考虑了振荡升力系数C_L美元$以圆柱体边界为观察点。相对相位值$\θ=\{0,2{\rm\pi}\}$定义为最小值C_L美元$振荡。

相位动力学的表示允许进一步分析，以确定原始动力学与周期扰动同步的条件$T_f（美元）$和频率$\omega_f=2{\rm\pi}/T_f$.我们考虑相位差$\phi（吨）$在原始振荡动力学的相位之间$θ（t）$和周期扰动$\ω_f t$这样的话

（2.10）\开始｛方程｝\ phi（t）\ equiv \ theta（t）-\omega_f t.\结束｛方程｝

与组合(2.8)在结构上施加扰动的情况下，通过应用平均近似值（Ermentrout&Terman参考Ermentrout和Terman2010)，我们可以评估$\phi（吨）$这样的话

(2.11一,b条)\开始{align}\dot{\phi}（t）=\omega_n-\omega_f+\varepsilon\varGamma

哪里$\varGamma（\phi）$称为相位耦合函数，即$2{\rm\pi}$-定期，以及$\psi=ω_f t$.

通过对中的相位动力学进行稳定性分析(2.11一)，我们可以确定原始振荡动力学将同步到周期扰动的标准，即$\vert\dot{\phi}\vert\转换为0$和$\ω_n$收敛到$\ω_f$在这种情况下，原始的极限循环振荡在一个稳定的不动点渐近地对周期扰动表现出锁相美元\斐$.通过观察(2.11一)，我们可以发现，如果

(2.12)\开始{等式}\varepsilon\min{\varGamma（\phi）}。\结束{方程式}

使用这个稳定性准则，我们可以确定$（\omega _f/\omega _n）$——$\varepsilon美元$空间。这些同步边界也称为阿诺德舌（皮科夫斯基等。 参考Pikovsky、Rosenblum和Kurths2001)稍后将在§中讨论三.

相反，如果$\vert\dot{\phi}\vert>0$和相位差$\phi（吨）$将随时间不断增加（Nakao参考Nakao2016). 我们可以将这种周期性相位滑移的频率定义为$f_{slip}=1/T_{slip}$，其中$T_｛单｝$是周期性相位滑移的间隔，它是作为频率差的函数计算的$\omega _n-\omega _f$当原始振荡动力学与周期扰动锁相时，振荡的平均频率等于$\ω_f$和$f_{slip}\约为0$在锁相区外，会发生相位滑移$f_{slip}$可以计算为

(2.13一,b条)\开始{方程式}f_{slip}=\dfrac{1}{T_{slip{}}\quad\text{和}\quad T_{slip}=\int_{0}^{2{\rm\pi}}\dfrac{\textrm{d}\phi}{\omega_n-\omega_f+\varepsilon\varGamma（\phi）}。\结束{方程式}

根据频率差$f_{slip}$可以是正的也可以是负的。The characteristics of the$f_{slip}$跨距曲线$\omega _n-\omega _f$可以与实际直接数值模拟（DNS）的结果进行比较，如§三.

三。结果和讨论

3.1.相敏性分析

在下文中，我们比较了相敏函数$Z_y（θ）$对于不同的材料类型，假设(2.3一,b条)和(2.4)介绍了。本节的研究结果可进一步用于评估相位耦合功能和分析同步特性。对于每种材料类型，在相同的相位间隔下进行了11次实际模拟$\θ$（由中的标记显示图2和三)利用MATLAB对Akima插值法进行了改进，得到了中间值。

图2。(美元$)定期C_L美元$材料类型1和8的振动。(十亿美元$)的比较$Z_y（θ）$对于不同的扰动位置。实线和虚线分别显示材质类型1和8的结果。

图3。(一)比较$Z_y（θ）$对于的不同值美元C_Y$（单位为$1\乘以10^{-8}$). (b条)的比较$Z_y（θ）$对于不同的值$\mathcal{M}$. (c（c）)的比较$Z_y（θ）$对于不同的值$\nu美元$.

图2(一)显示了C_L美元$材料类型1和8之间的振荡，其中流体和结构属性都发生了变化，但所有特征数保持相等。The period of theC_L美元$振荡出现在$T_n=0.403$s表示材料类型1至7，而对于材料类型8，周期位于$T_n=0.323$s、 表明振荡的主要特征是流体性质（参见表1). 对于所有材料类型，涡旋脱落频率都是结构主谐波频率的3.5倍或更高，因此不会因涡旋脱落而发生大的结构共振。注意，在本研究中，阻尼项包含在结构动力学中，因此随着时间趋于无穷大，结构谐波模式对极限循环振动的影响可以忽略不计。

我们确认，本研究中使用的所选特征数通过以下结果确定了相位动力学图2(b条)可以看出$Z_y（θ）$评估材料类型1和8（分别显示为实线和虚线）。如所示图2(一)C_L美元$由于平均入口速度不同，1类和8类材料的振荡周期不同。然而，当$再保险$,美元C_Y$,$\mathcal｛M｝$和$\u美元$匹配（请参见表1)，得到的相敏函数非常一致。这表明，对于相同的模型配置，相位动力学的特征是$再保险$,美元C_Y$,$\mathcal{M}$和$\nu美元$.

图2(b条)还显示了相敏函数$Z_y（θ）$受扰动位置的显著影响。我们比较了上下游侧相对于圆柱中心的扰动结果$x美元$轴位于$x=0.2\\textrm{m}$对于上游侧施加的扰动，观察到较小的平均值和峰-峰值($x_0<0.2\\textrm{m}$)而在下游侧施加扰动的情况下，观察到较大的值($x_0>0.2\\textrm{m}$). 在上游区域，流动分离尚未发生，因此振荡流尚未完全形成。因此，对于相同的脉冲扰动振幅，相位响应比扰动作用于开始形成涡流的下游侧的情况小得多。这些还表明，实现同步所需的周期扰动幅度和频率，如(2.12)也取决于摄动位置，将在下一小节中进行研究。

我们通过比较在$x_0=0.25$m.如§所述2.1，我们修改了柯西数美元C_Y$以及流体与结构物的密度比$\mathcal{M}$通过改变杨氏模量E美元$和结构密度美元\rho _s$分别是。图3(一)显示了材料类型1、2和3的比较，其中$Z_y（θ）$比较不同的值$年（_C）$. The mean and peak-to-peak values of$Z_y（θ）$随着的价值增加美元C_Y$增加。图3(b条)显示了材料类型1、4和5的比较，其中$Z_y（θ）$比较不同的值$\mathcal{M}$.的峰峰值$Z_y（θ）$随着$\mathcal{M}$增加，而平均值不受影响。图3(c（c）)显示了材料类型1、6和7的比较，其中$Z_y（θ）$比较泊松比的不同值$\nu美元$.的平均值和峰间值$Z_y（θ）$随着的价值增加$\nu美元$减少。

结构材料和流固耦合特征数的影响比较表明$\mathcal{M}$和$\nu美元$对相敏函数的影响小于美元C_Y$即使考虑到$\nu美元$由于参数限制。中的变化美元C_Y$显著影响相敏函数的平均值，而不是其波形。虽然美元C_Y$,$\mathcal{M}$和$\nu美元$不同，这些值表征了弹性结构对扰动的整体相位响应。

观察图2和三表明对于所有选定的材料类型和扰动位置，脉冲扰动导致振荡流的相位提前。所有得到的相位灵敏度函数都具有正的非零平均值。类似的相反应通常在I类神经元中发现（Ermentrout和Terman参考Ermentrout和Terman2010). 这表明，如果我们定期推动结构的上边界，那么扰动频率必须高于振荡流的固有频率才能实现同步。如果我们考虑到扰动是上边界上周期性推拉作用的形式，则可以避免这种限制，本工作将上边界定义为零米正弦函数，如(2.4).

3.2.同步分析

我们考虑材料类型1和定义在(2.3一,b条)和(2.4)用于以下同步分析。假设相敏函数$Z_y（θ）$可以确定，我们可以计算相位耦合函数$\varGamma（\phi）$使用(2.11b条)对于给定的摄动函数。在不同扰动位置评估的相位耦合函数$x_0美元$如所示图4(一). 可以从$Z_y（θ）$如所示图2(b条)，评估的相位耦合函数显示出最大的变化美元\斐$当扰动作用于$x_0=0.25\\textrm{m}$.变更$\varGamma（\phi）$过负和过正表明，低于振荡流固有频率的扰动频率也可以导致同步。

图4。(一)相位耦合函数的比较$\varGamma（\phi）$对于几个扰动位置。(b条)变更$\varGamma（\phi）$扰动位置上方。(c（c）)的同步边界$x_0=0.25\\textrm{m}$用实线表示。来自DNS的同步和非同步情况的结果标记为$\bigcirc美元$和$\次$分别是。(d日)比较$f_{slip}$特性计算方法(2.13一,b条)对于$x_0=0.25\\textrm{m}$和$\varepsilon=10\\textrm{N}$从DNS获得的结果分别用实线和标记显示。

扰动位置的其他几个数值模拟$x_0\英寸[0.1,0.4]\\textrm{m}$进行比较其同步区域，如所示图4(b条). 标记指示实际执行模拟的位置。根据同步标准(2.12)，变化较大$\varGamma（\phi）$将导致更宽的同步区域。对于给定的模型问题，我们发现最宽的同步区域是在$0.30<x_0<0.35 \\textrm{m}$一般来说，由于扰动作用在充分发展涡流的圆柱体下游端附近，因此可以获得更宽的同步区域。随着扰动位置从圆柱体下游移得更远，随着涡流开始衰减，同步区域缩小。

在下面的例子中，我们考虑在$x_0=0.25\\textrm{m}$。在中使用同步标准(2.12)，我们可以以阿诺德舌的形式构造同步区域的表示，如所示图4(c（c）). 我们将近似的同步区域与从DNS获得的结果进行了比较。对于实际模拟C_L美元$当相位差时，振荡和周期扰动被认为是同步的美元\斐$停止增长并在某个值附近出现小波动（即发生锁相）。可以看出，近似的同步区域与非线性FSI动力学的实际模拟结果吻合得很好，特别是对于较小的扰动幅值$\varepsilon美元$。非线性的影响对于$\varepsilon\ge 15\\textrm{N}$其中实际动力学开始偏离使用相还原理论获得的近似值。正如Taira和Nakao的工作中所指出的那样(参考Taira和Nakao2018)，通过相位耦合函数识别Arnold舌状物是有吸引力的，因为我们只需要对相位进行少量的数值模拟$\θ\ in[0,2{\rm\pi}）$以确定同步区域。

弹性结构中的位移振荡美元$方向位于$x=0.25\\textrm{m}$平均值为$-2.77\乘以10^{-6}\\textrm{m}$和峰-峰值$0.54\乘以10^{-6}\\textrm{m}$当不应用周期摄动时。对于具有振幅的周期扰动的同步情况$\varepsilon=25\\textrm{N}$则位移的平均值为$-7.97\乘以10^{-6}\\textrm{m}$峰间值为0.004 m。还观察到美元$由于流固耦合，底部弹性结构的方向与周期摄动同步。

我们比较了近似值$f_{slip}$使用评估的特性(2.13一,b条)使用从DNS获得的结果，如所示图4(d日). 在这项工作中$f_{slip}$比较了扰动幅度的特性$\varepsilon=10\\textrm{N}$。但是，可以对以下任何值进行比较$\varepsilon美元$。近似锁相区域显示在虚线垂直线之间。我们可以看到$f_{slip}$从DNS获得的特征（用标记显示）与从计算中获得的近似特征非常一致。然而，实际锁相区域略微偏向较低的扰动频率。这也与图4(c（c）)其中实际同步区域被偏向于较低的扰动频率、尤其是对于较大的扰动幅度。这些发现进一步证实了使用相位减少的线性近似捕捉到了原始非线性振荡动力学的同步特性。

据我们所知，这是第一项使用相位减少理论来确定FSI动力学中振荡流同步特性的研究。在这里，我们提出了如何在振荡流和对周围弹性结构的周期性作用力之间实现同步的想法，以及如何使用相还原理论来确定同步区域。

微流体领域的最新研究（Sun等。 参考Sun、Lin、Rau和Chiu2017)提出了一种微流体振荡器的设计，其中包括由冲击射流在钝体上引起的自持流动振荡，用于流体混合。众所周知，流体混合可以由流体容器壁上的振动引起（Carlsson、Sen和Löfdahl参考Carlsson、Sen和Löfdahl2005). 这两个概念的结合可能揭示了一种提高混合性能的替代方法，而相还原理论可用于估计获得所需流量调节所需的参数，如本研究中所述。了解弹性结构运动对周期性流体流量的调节，对于研究交感神经系统（Kotani等。 参考Kotani、Struzik、Takamasu、Stanley和Yamamoto2005).

当然，还有其他可以考虑的同步情况，例如对淹没在振荡流体流中的结构施加周期性扰动。此外，使用相还原理论的方法也可以扩展到分析谐波频率附近的同步。最近的实验工作和数学建模（Barros等。 参考Barros、Borée、Noack和Spohn2016; 赫尔曼等。 参考Herrmann、Oswald、Semaan和Brunton2020)说明对称强迫如何导致次谐波同步，而反对称强迫如何导致谐波同步。这些现象也可以在FSI动力学中观察到，相位还原理论也可以用于揭示对称和反对称强迫下的同步特性。

4结论

我们应用相还原理论，通过对周围弹性结构的周期扰动，发现了涡旋脱落的同步特性。我们进行了参数研究，以观察FSI动力学中已知的几个无量纲参数如何影响极限循环振荡的相位动力学。研究发现，在雷诺数定义的模型构型和流体流动特性相等的情况下，相敏函数受柯西数的影响显著，而受流固密度比和泊松比的影响很小。弹性结构上的摄动位置也显著影响相敏函数。此外，通过比较同步区域和周期相位滑移特性，证实了估计的同步特性与DNS获得的结果非常吻合。考虑到在圆柱体下游端附近施加正弦扰动，同步区域最大化。我们的发现为利用相还原理论在其他实际问题中进行同步分析提供了进一步的可能性，这些实际问题涉及由流体-结构相互作用控制的动力学振荡，例如在生物系统和微流体控制中，只需使用有限数量的实验或模拟。

基金

I.A.L.感谢岩谷直系基金会的支持。K.K.感谢朝日玻璃基金会和JSPS KAKENHI（拨款18H04122）的支持。H.N.感谢JSPS KAKENHI（授予JP17H03279）和JST CREST（授予JPMJCR1913）的支持。

利益声明

作者报告没有利益冲突。

工具书类

参考文献

巴罗斯,D。,博雷,J。,诺亚克,业务风险管理。&斯波恩,答：。 2016 三维钝体受迫湍流尾迹中的共振.物理。流体 28,065104.交叉参考谷歌学者
卡尔森,F、。,森,M。&洛夫达尔,L。 2005 振动壁引起的流体混合.欧洲力学杂志。B/液体 24(三),366——378.交叉参考谷歌学者
德纳耶,G.公司。,阿波斯托拉托斯,答：。,木材,J.N.公司。,布莱廷格,英国。,瓦什内尔,R。&布鲁尔,M。 2018 湍流中充气柔性膜瞬态流固耦合的数值研究.J.流体结构。 82,577——609.交叉参考谷歌学者
迪克卢,O。,塔勒比,答：。,希梅诺,L。,维雅德,R。,保乐多,第页。,普列奥布拉任斯基,五、。&梅伦,答：。 2007 微机械阀门中流体-结构相互作用引起的自振模式.申请。物理。莱特。 91(三),034101.交叉参考谷歌学者
Ermentrout公司,通用电气公司。&特曼,D.H.公司。 2010 神经科学的数学基础.施普林格.交叉参考谷歌学者
福尔马托,G.公司。,罗马诺语,R。,福尔马托,答：。,索尔瓦里,J。,科伊拉宁,T。,佩莱格里诺,答：。&维莱科,F、。 2019 用于蠕动泵流动模拟的流固耦合模型.机器 7(三),50.交叉参考谷歌学者
戈麦斯,J。P。&林哈特,H。 2013 层流和紊流中柔性结构的流固耦合振动.J.流体力学。 715,537——572.交叉参考谷歌学者
赫尔曼,B。,奥斯瓦尔德,第页。,塞曼,R。&布伦顿,S.L.公司。 2020 受迫湍流振子流的同步建模.Commun公司。物理。 三,195.交叉参考谷歌学者
喇叭,J。&图雷克,美国。 2006流体-结构相互作用ALE公式的整体FEM/多重网格求解器，用于生物力学应用。在流体-结构相互作用：建模、仿真、优化（编辑H.J.Bungartz和M.Schäfer），《计算科学与工程讲义》，第53卷，第146-170页。斯普林格。交叉参考谷歌学者
川村,年。&Nakao公司,H。 2013 振荡对流的集体相位描述.混乱 23,043129.交叉参考谷歌学者公共医学
川村,年。&Nakao公司,H。 2015 具有空间平移模式的振荡对流的相位描述.物理天 295–296,11——29.交叉参考谷歌学者
川村,年。&津贝吉,R。 2018 拍鞭毛弹流同步的相位缩减方法.物理。版次。E类 97(2),022212.交叉参考谷歌学者公共医学
科德卡尔,文学硕士。&泰拉牌手表,K。 2020 周期外力作用下层流圆柱尾迹的相位同步特性.J.流体力学。 904,R1级.交叉参考谷歌学者
小岛,K。,金子,T。&安田,K。 2006 心肌细胞的群落效应在稳定搏动节律的携带和重建中的作用.生物化学。生物物理学。Res.Commun公司。 351(1),209——215.交叉参考谷歌学者公共医学
小谷,K。,斯特鲁齐克,Z.R.公司。,隆益,K。,赤柱,尊敬的。&山本,年。 2005 健康和疾病中的复杂心率动力学模型.物理。版次。E类 72(4),041904.交叉参考谷歌学者公共医学
小谷,K。,山口,一、。,小川,年。,Jimbo公司,年。,Nakao公司,H。&Ermentrout公司,通用电气公司。 2012 伴随法为延迟诱导振荡提供相位响应函数.物理。修订版Lett。 109(4),044101.交叉参考谷歌学者公共医学
库拉莫托,年。 1984 化学振荡、波浪和湍流.施普林格.交叉参考谷歌学者
Nakao公司,H。 2016 非线性振荡器同步的相位减缩方法.康斯坦普。物理。 57(2),188——214.交叉参考谷歌学者
Nakao公司,H。,柳城县,T。&川村,年。 2014 反应扩散系统时空节律同步的相位约简方法.物理。版次。X（X） 4(2),021032.谷歌学者
诺维琴科,五、。&皮拉加斯,K。 2012 时滞系统中弱摄动极限环振动的相位约简.物理天 241(12),1090——1098.交叉参考谷歌学者
皮科夫斯基,答：。,罗森布拉姆,M。&库思,J。 2001 同步：非线性科学中的一个普遍概念.剑桥大学出版社.交叉参考谷歌学者
Quarteroni公司,答：。,图韦里,M。&威尼斯,答：。 2000 计算血管流体动力学：问题、模型和方法.计算。视觉。科学。 2,163——197.交叉参考谷歌学者
里希特,T。 2017 流体-结构相互作用。模型、分析和有限元.施普林格.交叉参考谷歌学者
盐贝,年。,斯特凡诺夫斯卡,答：。&麦克林托克,第五页。 2010 心血管老化的非线性动力学.物理。代表。 488,51——110.交叉参考谷歌学者公共医学
白坂,美国。,Kurebayashi村,西。&Nakao公司,H。 2017 混合非线性振荡器的相位约简理论.物理。版次。E类 95(1),012212.交叉参考谷歌学者公共医学
太阳,C、。,林,杨杰（Y.J.）。,劳,C、。&邱,美国。 2017 微流体振荡器中弱稀薄流体的流动特性和混合性能.J.非牛顿流体力学。 239,1——12.交叉参考谷歌学者
泰拉牌手表,K。&Nakao公司,H。 2018 周期流同步的相位响应分析.J.流体力学。 846,R2级.交叉参考谷歌学者
兹德拉夫科维奇,医学硕士。 1996 涡流脱落的不同模式：综述.J.流体结构。 10(5),427——437.交叉参考谷歌学者
图0

图1。 本研究中使用的模型。流体域周围的弹性结构域由阴影图案标记。气缸中心位于$（x，y）=（0.2\\textrm{m}，0.1\\textrm}）$.

图1

表1。 本研究中考虑的流体类型和结构材料属性。

图2

图2。 (美元$)定期C_L美元$材料类型1和8的振动。(十亿美元$)的比较$Z_y（θ）$对于不同的扰动位置。实线和虚线分别显示材质类型1和8的结果。

图3

图3。 (一)的比较$Z_y（θ）$对于不同的值美元C_Y$（单位为$1\乘以10^{-8}$). (b条)的比较$Z_y（θ）$对于不同的值$\mathcal｛M｝$. (c（c）)比较$Z_y（θ）$对于不同的值$\nu美元$.

图4

图4。 (一)相位耦合函数的比较$\varGamma（\phi）$对于几个扰动位置。(b条)变更$\varGamma（\phi）$扰动位置上方。(c（c）)的同步边界$x_0=0.25\\textrm{m}$用实线表示。来自DNS的同步和非同步案例的结果标记为$\bigcirc$和$\次$分别是。(d日)比较$f_{slip}$通过（2.13）计算的特性一,b条)对于$x_0=0.25\\textrm{m}$和$\varepsilon=10\\textrm{N}$从DNS获得的结果分别用实线和标记显示。