5分钟问题到五年问题

周六，我在曼哈顿MATHCOUNTS比赛。很长一段时间以来，我在做数学演讲时没有这么开心了！

我在数学竞赛中从来都不例外，但我喜欢它们。我认为他们是有趣的挑战，他们创造了一个充满活力的社区；它们在数学教育中是一个很好的工具。然而，大多数比赛也会助长坏习惯。他们引导学生专注于速度和赢得深入思考。他们鼓励学生学好一些技巧，记住无用的事实。他们进一步延续了数学是关于速度的神话，尽管现实世界的问题需要几天、几个月或几年才能解决。因此，我的演讲是关于过渡到解决“大”问题。下面是我所说的话以及我如何组织这次谈话的日志，供我以后参考，也供任何感兴趣的人参考。

设置舞台

我首先要求房间里的人举手，如果他们在一道数学题上花了一分钟以上的时间，所有人都举手。“五分钟多？”“一个多小时？”现在许多人都举手投降了。“超过一天？”几乎没有人举手。“一个多月？一年多？五年多？”

我解释说，世界上真正的问题需要很长时间。证明一个定理，建立一座桥梁，创建脸书或谷歌——这些都需要几年的时间！所以我鼓励他们用不同的方式思考数学。不要像“我能以多快的速度解决这些问题”、“我能记住30-60-90直角三角形的边吗”或“我知道25平方以内的完美正方形吗”之类的竞赛思维，而是练习深入思考数学。

我告诉他们关于玛丽亚姆·米尔扎哈尼的事。她是我们这个时代最好的数学家之一，菲尔兹奖（数学“诺贝尔奖”）获得者。对我来说，让一个女人学习最高水平的数学是很重要的，我也想和一个现在还活着的人一起学习。我决定努力证明她的资格，并多次说“她”，但我非常小心不她是第一位赢得菲尔兹奖章的女性。

在演讲之前，我就这个选择争论了很长时间。最终，我希望一个赢得菲尔兹奖章的女性看起来很正常。有一段时间，数学界的女性必须考虑到她们的代表性不足，但拥有相对较多女孩的MATHCOUNTS并不是那个时候。我也对爱因斯坦奇怪地赞扬埃米·诺特（20世纪最杰出的数学家之一）讣告他写道：“这是自女性高等教育开始以来，迄今为止最具创造力的数学天才。”这句话的后半部分对埃米·诺特来说完全没有必要。同样，说Mirzakhani是第一菲尔兹奖的女性得主将性别动力学置于首位，而不是她的原始数学成就。（同时，根据历史记录，爱因斯坦是诺伊特的忠实支持者，也是她获得带薪大学职位的原因！）

无论如何，我提到米尔扎哈尼是因为我想分享一个Quanta文章:

米扎哈尼喜欢形容自己动作迟缓。与一些用水银般的才智解决问题的数学家不同，她更倾向于深思熟虑多年的问题。她说：“几个月或几年后，你会看到问题的不同方面。”。她思考了十多年的问题。她说：“但我还是无能为力。”。

简而言之，如果一位如此重要的学者认为速度不重要，那么你为什么要这样做？深入思考，而不是快速思考。

有了这些，是时候讲述一个强化这一想法的故事了。

双素数猜想

最近在孪生质数猜想这是一个非常平易近人的话题。这是我进入的途径，通过这一点数学文化，我可以传达出真正的突破需要很长时间。我首先谈到了它自1860年以来是如何开放的；我想展示一下数学结果是如何相互建立的，以及许多数学家多年来的工作和进步所产生的部分结果。

关于双素数猜想的早期结果之一是，双素数的倒数之和收敛，但我需要为可能没有见过它们的中学生介绍无穷和。我谈到了二次幂的倒数之和是如何收敛的，但正整数的倒数总和却不收敛；我还解释说，已经证明素数的倒数之和发散，而孪生素数的倒数之和收敛。

这让我可以指出，我们证明了关于双素数倒数之和的一些东西，而不知道有多少个或它们收敛到什么，这暗示了非构造性的证明。一个类比有助于解释这个结果的重要性：孪生素数比素数少很多；它们在某种程度上是“稀疏的”，就像2的幂是稀疏的一样。我还指出，我们可能会认为收敛结果是一个“糟糕”的结果，因为我们希望证明存在无穷多个孪生素数，而收敛留下了它们是有限的可能性。然而，任何结果都不应被视为糟糕的，因为一切都能带来洞察力。

在那里，我概述了2005年之前的一些结果，以证明这个猜想。这个想法是讲一个故事。看看数学的稳步发展。我能够谈论我们如何在其他成果的基础上取得成果，并证明这些真正的进展需要时间，回到我的主题，即缓慢而深入地思考是很好的。

然后我带着张怡婷的结果跳到了今天，我笑了起来，说他通过显示有无限多对素数取得了很大进步……它们之间的距离在7000000以内！（考虑到我们的目标是无限多的“2”，这似乎还很遥远，但再次强调，部分结果是关键！）从这里，我谈到了数学家之间奇妙的在线合作，将7000000缩小到246。

最后，为了结束这个话题，我给学生们一个他们可以带回家的挑战：确定有多少个“素数三元组”，即三个素数的集合，每个素数与前一个素数相差2。

到最后，我觉得我已经传达了数学文化的一个强大组成部分，以及如何取得进步。我觉得自己做得很好，向学生们解释说，他们必须深入思考，慢慢来。简而言之，我觉得我已经将他们从典型的竞赛心态中重新调整了过来。

现在的挑战是转向数学。即使他们承认深入思考和花时间的价值，他们仍然没有权利这样做。问题是，在一次45分钟的演讲中，一半已经结束，学生根本没有时间自己解决“大”问题。（事实上，我很早就开玩笑说他们不应该害怕，我的演讲不会持续一年！）

过渡到问题

我认为，才华横溢的外表让许多学生难以接近数学。别误会我，我不怀疑存在才华横溢。然而，似乎证明方法和思想“无处不在”，只有天才才能发现它们。我决定如果我们不能事实上在某个地方解决问题，我至少可以消除这个神话。看似武断但有效的行动实际上来自于观察模式、经验和构建一系列（通常无效）想法。

问题是要把一个轮子分成6个部分。可以根据需要多次向任意两个相邻扇区添加1，如下所示：

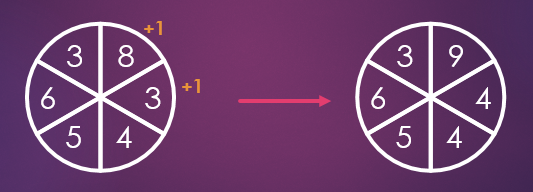
通过这些动作，有可能从起跑轮上下来吗

 

到最后一个所有数字都相等的轮子？

欢迎您在继续之前亲自尝试！

我提出了一个热身问题（很容易找到通向目标轮的动作），然后我们开始回答这个问题。我告诉学生们，如果他们要解决这个问题，他们可能会做一段时间的实验，并对它有所了解。然后，他们会看看他们所有的尝试，看看这是如何运作的。

为了节省演讲时间，我给学生们提供了一个由15种不同状态组成的网格，这些状态是可以实现的，可能是他们实验的结果。然后我给了他们两分钟的时间，让他们自己寻找模式，看看他们能发现什么。我没想到他们会解决这个问题：毕竟，这是一个他们可能要花几个小时解决的问题！相反，他们应该寻求见解，推动他们的想法向前发展。

学生们想出了一些好主意。一名学生建议，也许每个可实现的车轮都会出现两个相等的数字。尽管在我的所有例子中都是这样，但进一步的实验表明情况并非如此。我们为自己设定了一个目标，即找到一个具有所有不同数字的车轮（我们做到了）。另一位学生提出了车轮上最高值和最低值之间的最大差异（无界）。尽管这些想法不起作用，但它们为我们提供了关于车轮的良好结果是我希望学生们认识到，即使他们没有解决问题，这些结果也是有价值的。这就像证明双素数的倒数之和收敛一样。

然后一个学生做了一个有趣的观察：每个轮子上都有两个奇数。太神奇了！我问道，这一直是真的吗？

我们很快发现了一个零奇数的轮子。然而，有趣的是，我们发现了0个奇数，而我们发现了2个奇数。你能只有一个奇数吗？不，你不能！

这让你意识到所有车轮上的数字之和是偶数；这很容易证明，因为每一步都会使总数增加2。这部分结果仍然这并不妨碍找到一个所有六个数字都相等的可实现车轮，因为这样的车轮也会有一个偶数和。 阿盖恩我们没有解决问题，但这仍然是一个巨大的进步！我们现在有一个定理，排除了许多其他的轮子。

也许我们应该后退一步。使用所有数字的总和只是使用游戏工作方式的一部分。即使你被允许在任何两个部门。我们需要找到一个利用两个1必须相邻这一事实的想法。我向他们提出挑战，看看他们是否能想出点什么。

一个学生做到了（尽管我认为他以前见过类似的情况），我们很快缩小了范围，创建轮盘中数字的交替总和，如下所示：

现在，将两个相邻的1相加将使总数保持不变！所有数字相等的轮子的交替和为0，但我们的起始位置的交替和是2！因此，我们知道我们不可能使所有的数字都相等。

想象一下，我告诉学生们，你还没有解决这个问题，有人用交替求和的方法向他们提出了这个证明。他们可能会看一眼说：“那个人太棒了！我永远也不会想到那个。”这忽略了所有这些片面的工作和想法是如何建立在一起的；“聪明”的人并不是从交替求和开始的！（除非他们以前见过类似的问题。）玩弄它让我们开始计算奇数，这导致了求和；然后，寻找一种思考邻接关系的方法使我们得到了交替求和。在深入思考这个问题的背景下，每一步都是有意义的。

很容易想象在这个问题上花了很长时间。也许有一天，你想到了计算奇数的想法，你猜测在一个可实现的轮子里总是有2个奇数。然而，当你发现一个车轮上有0个奇数时，你会得出结论，你的猜测是错误的。你可能会觉得不值得看奇数。但也许一两天后你又回来了，沮丧地，你又想起了奇数——然后你意识到没有一个轮子正好有一个奇数条目，你又在进步了！这需要时间和毅力，这就是我希望学生们学习的。

总结性想法

最后，我说了数学证明是如何凭空产生的。它来自于一个对这个问题进行了深入思考并找到解决方法的人。我谈到了“追随你的鼻子”的想法，并寻找看起来有吸引力的策略，即使你不确定它们是否有效。我还指出，下次出现类似问题时，在奇数/偶数起作用或交替求和有用的情况下，这是他们工具箱中的一个工具。

简言之，培养良好的思维习惯、毅力和尝试很多东西这是我给学生们的结论，他们将在下一步解决大问题。