我收到了压倒性的回应介绍性博客帖子关于图的代数；谢谢大家的评论、问题和建议！在本系列的第二部分中，我将说明代数不仅限于有向图，而且可以扩展到公理地表示无向图、可达图和依赖图（即预序和偏序）、它们的各种组合，甚至超图。

更新：这一系列博客文章是作为功能性珍珠在2017年哈斯克尔研讨会上。

为什么是代数？

在我们继续之前，我想注意到用于表示图形的任何数据结构（例如，边缘列表、基于矩阵的表示、fgl库，GHC标准数据。图表等）可以满足代数公理的适当定义空的,顶点,覆盖 和连接，我不打算将这些实现相互比较。我更感兴趣的是我们可以编写和重用的实现依赖（多态）函数，以及使用代数定律证明这些函数的属性。这就是为什么我认为代数值得学习的原因。

作为一个热身练习，让我们再看几个此类多态图函数的示例。其中一个线程在reddit中的讨论是关于路径图 P（P）₄：即在链中连接4个顶点的图。这里有一个函数可以构造这样的路径图在给定的顶点列表上：

路径 :: 图表 克 =>[顶点 克]-> 克路径[]  =空的路径[x]=顶点x路径xs=从边缘列表$ 拉链X轴(尾X轴）第4页 ::(图表 克,顶点 克~烧焦)=> 克第4页=路径[“a”, “b”, “c”, “d”]

请注意该图第4页也是多态的：我们还没有致力于任何特定的数据表示，但我们知道第4页具有类型烧焦.

如果将路径的最后一个顶点连接到第一个顶点，则会得到电路图，或a周期。让我们用路径功能：

电路 :: 图表 克 =>[顶点 克]-> 克电路[]     =空的电路（x:X轴）=路径$【x】++X轴++【x】五角形 ::(图表 克,顶点 克~国际)=> 克五角形=电路[1..5]

根据定义，我们期望路径是相应电路的子图。我们能在代数中表达这个性质吗？对！对于幂等元+，将a≤b定义为a+b=b是相当标准的，结果表明这个定义对应于子图关系在图形上：

是SubgraphOf ::(图表 克,等式 克)=> 克 -> 克 -> 布尔是x y的子图=覆盖x y==年

我们可以使用QuickCheck测试我们的实现是否满足以下属性：

λ>快速检查$ \X轴->路径xs`是的子图`（电路xs:: 基本 国际)+++ 好 啊,通过100测验.

QuickCheck只能测试特定实例的属性，在本例中，我们选择了基本Int，但使用代数，我们可以证明它适用于以下所有守法实例图表（我将此留作读者练习）。

作为最后一个示例，我们将实现笛卡尔图乘积，通常表示为GH，其中顶点集为V_G公司×V_H（H）如果x=x'且y连接到H中的y'，或y=y'且x连接到G中的x'，则顶点（x，y）连接到顶点（x'，y'）：

箱 ::(Functor（仿真器） （f）,可折叠的 （f）,图表(（f）(一,b条)))=> （f） 一 -> （f） b条 -> （f）(一,b条)方框x y= 文件夹覆盖为空$X轴++年哪里X轴= 地图(\b条-> 功能性维修计划(,b） x）$到列表y年= 地图(\一-> 功能性维修计划（a）,)年）$toList x（目录x）

笛卡尔积GH通过创建|V组装_H（H）|图G的副本并用|V覆盖它们_G公司|图H的副本。我们使用到列表来自可折叠的实例并通过功能性维修计划来自Functor（仿真器）实例。

如您所见，代码仍然是implementation-independent，尽管它要求图形数据类型是Functor（仿真器）和a可折叠的。就像列表、树和其他容器一样，大多数图形数据结构都有Functor（仿真器）,可折叠的,适用的和莫纳德实例（例如我们的基本数据类型包含所有内容）。以下是如何 五边形`box `p4看：

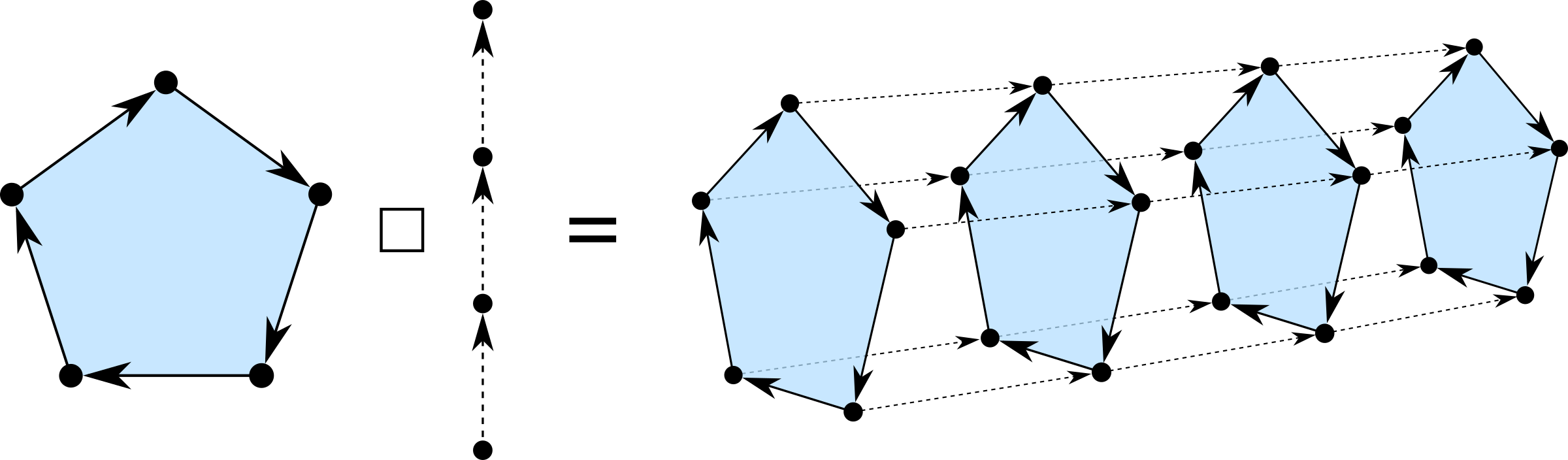
（旁注：箱让我想起此博客帖子作者Edward Yang，让我怀疑Functor（仿真器）,可折叠的加幂等和交换单体一起暗示单体，因为我似乎只需要使用空的和覆盖来自图表类型类。这似乎很奇怪。）

无向图

正如我在前一篇博客文章中所暗示的，要从有向图切换到无向图，只需为连接操作员。对于无向图，表示连接由↔ 或-，因此：

• x个↔ y=y↔ x。

奇怪的是，随着这个公理的引入↔ 遵循（左关联版本）分解公理和+的交换性：

（x）↔ 年）↔ z（z）	=	x个↔ y+x年↔ z+y↔ z（z）	（左分解）
	=	年↔ z+y↔ x+z↔ x个	（+和的交换性↔)
	=	（年↔ z）↔ x个	（左分解）
	=	x个↔（年）↔ z）	（交换性↔)

的交换性连接运算符将仅在边的方向上不同的图表达式强制放到同一等价类中。可以通过对称闭包基本连接性关系：

新类型 无方向性一= 无方向性{来自未定向:: 基本一个}推导(任意的,Functor（仿真器）,可折叠的,号码,显示)实例 订单 一 => 等式(无方向性 一)哪里x个==年=to对称x==到对称y到对称 :: 订单 一 => 无方向性 一 -> 关系 一到对称=对称闭合.到关系.来自Undirected

如您所见，我们只需将基本使用自定义的newtype实现等式实例来处理↔.我们知道结果无方向性数据类型满足所有要求图表法律，因为我们只让一些先前不同的表达相等，而不是相反。

部分订单

在许多应用程序中，图满足及物性属性：如果顶点x连接到y，而y连接到z，那么可以在不改变图的语义的情况下添加或删除x和z之间的边。一个常见的例子是依赖图这种图的语义通常是部分订单在顶点集上。为了用代数方法描述这类图，我们可以添加以下内容关闭公理：

• y≠ε⇒ x个→ 年+年→ z+x（z+x）→ z=x→ 年+年→ z（z）

通过使用公理，人们总是可以将图表达式重写为传递闭包或者，也可以将其转换为可传递性约简因此，所有只存在某些传递边的不同图都被强制归入相同的等价类。注：前提条件（y≠ε）是必要的，否则+和→ 无法再区分：

x个→ z=x→ ε → z=x→ ε + ε → z+x（z+x）→ z=x→ ε + ε → z=x+z

有趣的是+和→ 对部分订单有一个简单的含义：它们对应于并行和顺序组合部分订单。这使得我们可以用代数的方法描述并发系统——我将在另一篇博客上专门讨论这个主题。

我们可以实现部分订单包装实例基本在一个新类型中，通过底层关系的传递闭包提供自定义等式测试，就像我们对无向图所做的那样：

新类型 部分订单一= 部分订单｛来自PartialOrder:: 基本一个}衍生(任意的,Functor（仿真器）,可折叠的,号码,显示)实例 订单 一 => 等式(部分订单 一)哪里x个==年=到传递x==到传递y到可传递 :: 订单 一 => 部分订单 一 -> 关系 一到可传递=传递闭包.to关系.来自部分订单

让我们测试一下，我们的实现正确地识别了这样一个事实，即当路径图被解释为部分顺序时，它等价于团：

λ>快速检查$ \X轴->路径xs==（集团xs:: 部分订单 国际)+++ 好 啊,通过100测验.

实际上，如果我们有一系列n个任务，其中每个任务（除了任务1）都依赖于前一个任务（如路径[1..n])，则任务1是所有后续任务的先决条件，任务2是任务[3..n]等的前提条件，可以表示为集团[1..n].

自反图形

部分订单是反射的（也称为虚弱的)如果每个元素都与自身相关。自反偏序的一个例子是是SubgraphOf如上所述：的确， x`isSubgraphOf`x==真对于所有图x。表示自反图在代数上，我们可以引入以下公理：

• 顶点x=顶点x→ 顶点x

这强制每个顶点都有一个自循环。实施反射式 数据类型与无方向性 和部分订单 所以我不在这里展示它（它是基于底层关系的自反闭包）。

注：循环自反偏序对应于预售，例如：

(1 + 2 + 3) → (2 + 3 + 4)

是顶点2和3构成等价类的一个预序。我们可以找到强连接组件并推导出以下公式凝结:

｛1｝→ {2, 3} → {4}

将此预订单解释为依赖关系图的一种方法是，任务2和3作为步同时，它们都依赖于任务1。

混合图形风味

我们可以将上述三个新公理以不同的组合方式组合在一起。例如，无向图、自反图和传递闭图的代数描述了等价关系。值得注意的是，没有必要保留此类图中所有边的信息，并且基于不相交集数据结构。如果您对此类图的潜在应用感兴趣，请查看这篇论文我用它们来模拟交换网络。更准确地说，我建模家庭交换网络；这需要代数的另一个扩展：一元条件运营商，我将在未来的博客文章中介绍。

Hypergraphs（Hypergraph）

这个线程在《黑客新闻》的讨论中，我又遇到了一个代数难题。让我们将分解公理替换为3分解:

• w个→ x个→ 年→ z=w→ x个→ 年+周→ x个→ z+w（z+w）→ 年→ z+x（z+x）→ 年→ z（z）

简而言之，不像我们对二维分解那样，将所有表达式塌陷为顶点和边（顶点对），而是现在将所有表达式坍塌为顶点、边和三元组（或秩为3的超边）。我还没有弄清楚结果代数是否特别有用，但也许读者可以提供一个见解？

为了更清楚地看到2-分解和3-分解之间的区别，让我们用ε代替3-分解中的w并简化：

x个→ 年→ z=x→ y+x年→ z+y→ z+x（z+x）→ 年→ z（z）

看起来很熟悉吗？它是几乎2分解公理！然而，没有办法摆脱术语x→ 年→ 右边的z：实际上，在这个代数中，三元组是不可破坏的，并且只能提取嵌入其中的对（边）。事实上，我们可以更进一步，重写上面的表达式，以显示嵌入的顶点：

x个→ 年→ z=x+y+z+x→ y+x年→ z+y→ z+x（z+x）→ 年→ z（z）

通过2分解，我们可以实现类似的功能：

x个→ y=x+y+x→ 年

我称之为吸收定理它说边x→ y中嵌入了顶点x和y（其端点）。这看起来很有趣，但我不知道它会指向何处，我想我们会一起找出答案！

注：以上所有代码片段都可以在藻类存储库。看我们可以多么好地测试这个库多亏了代数API！