|
[这篇文章用西班牙语]
[这篇文章用法语]
[这篇文章用中文]
在一个古老的笑话中,两位贵族争相说出更大的数字。第一次,之后沉思了几个小时,得意洋洋地宣布“八十三!”,“你赢了。”
当参赛者参加时,最大数字竞赛显然毫无意义转弯。但是,如果参赛者同时写下他们的数字,都不知道其他人?为了介绍关于“大数字”的演讲,我邀请了两位观众自愿尝试这样做。我告诉他们规则:
你有十五秒钟的时间。使用标准数学符号、英语单词或两者都是,在空白索引卡上说出一个整数,而不是无穷大。Be公司精确到足以让任何理性的现代数学家精确地确定您所指定的号码,只需查看您的卡,如有必要,还可以查看出版的文献。
所以参赛者不能说出“撒哈拉沙漠的沙粒数量”,因为沙粒定期进出撒哈拉沙漠。他们也不能说“我的对手数字加一,“或”任何人都曾想过的最大数字加一“再一次,考虑到我们理性的数学家所拥有的,这些都是不确定的可用。在规则范围内,名字较大的选手获胜。
你准备好了吗?做好准备。去吧。
比赛的结果从来都不是我希望的那样。一次,七年级这个男孩在卡片上连续写了9秒。像许多其他大数字一样提洛斯,他试图通过在每个位值中填入9来最大化他的数字。如果他选择了易于书写的1s而不是曲线优美的9s,他的数字可以已经大了几百万倍。不过,他仍然会被他遇到的女孩写了一个9秒的字符串,后跟上标999啊哈!指数:一个乘以自身的数字999次。注意到这一创新,我宣布女孩的胜利费心数卡片上的9。
然而,如果女孩叠起来的话,她的数字可能会更大强大的指数不止一次。Take(获取)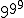 例如。这个庞然大物,等于9387420489个,有369693100个数字。由相比之下,可观测宇宙中基本粒子的数量只有区区85个数字,给或取。当以指数形式叠加时,三个9已经提升了我们令人费解的是,我们所能观察到的事物的因子约为10369,693,015我们什么也没说 例如。这个庞然大物,等于9387420489个,有369693100个数字。由相比之下,可观测宇宙中基本粒子的数量只有区区85个数字,给或取。当以指数形式叠加时,三个9已经提升了我们令人费解的是,我们所能观察到的事物的因子约为10369,693,015我们什么也没说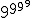 或 或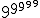 . .
位值、指数、堆叠指数:每个都可以无限地表示大数字,在这个意义上,它们都是等价的。但是符号系统可以表达的数字差异很大简明扼要地.这就是15秒的时间限制所说明的。它需要同样的数量写入时间9999,9999、和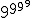 然而第一次数字是日常的,第二个是天文数字,第三个是超兆天文学的。最大数字竞赛的关键不是快速书写,而是这是一个有力的范例,可以简洁地捕捉到巨大的数据。 然而第一次数字是日常的,第二个是天文数字,第三个是超兆天文学的。最大数字竞赛的关键不是快速书写,而是这是一个有力的范例,可以简洁地捕捉到巨大的数据。
这种范式在历史上是罕见的。我们发现古代有一股狂潮,二十世纪的又一场骚乱,其间没有什么。但当简洁地表达大数字的新方法确实出现了,它通常是重大科学革命:系统化数学、形式逻辑、计算机科学。任何库尼安人都会告诉你,这种重大的革命只会发生在正确的社会条件下。大数字的故事就是这样的人类进步。
这与另一个数学故事类似。在他的非凡和未被重视的书π的历史,皮特贝克曼认为周长与直径的比值“有点奇怪”人类历史的镜子在早期的雅典的阿那克萨哥拉斯和希庇亚,亚历山大埃拉托斯梯尼和欧几里得,17世纪英国的牛顿和瓦利斯数学家在计算π方面取得了巨大进步。相比之下,在罗马和中世纪的欧洲π停滞。粗略的近似值,如巴比伦人占主导地位。
我认为,同样的模式也适用于大数字。好奇和开放导致对大数字的迷恋,以及对无数量的乐观看法,无论是星系中的恒星数量还是可能的桥梁数量手,太大了,心灵无法一一列举。相反,无知和非理性导致了关于大数字的宿命论。历史学家伊兰·瓦尔迪引用古希腊语学期砂钻的,口语意义无数; 以及品达的一段话奥林匹克颂歌II声称“沙子不需要计数。”
¨
但正如阿基米德在第三篇文章中所说,沙子无法逃脱计数公元前世纪,他是这样开始的采砂工,一种流行科学致锡拉丘兹国王的文章:
有一些。。。谁认为沙子的数量是无限的众多。。。还有一些人,虽然不认为它是无限的,但想一想,还没有一个数字被命名为足以超过它的众多。。。但我会尽力向你们展示【数字】不仅超过沙的质量等于地球的数量。。。也包括与宇宙大小相等的质量。
阿基米德继续这样做,基本上是使用古希腊术语无数的,表示一万,作为指数的基数。采用阿里斯塔克斯有先见之明的宇宙学模型,其中“固定的球体恒星”比地球围绕地球旋转的球体大得多太阳,阿基米德得到了10的上界63关于沙子的数量填充宇宙所需的颗粒。(假设1063是最大的带有词典编纂标准美国名称的数字:灯盏花.但是守夜最好保持守夜,以免被侵占名字更古怪古尔、或10100、和googolplex公司,或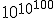 ()当然,虽然它是10个63并没有成为有史以来最大的数字。六个世纪后,迪奥芬图斯发明了一种更简单的指数符号,使他能够超越 ()当然,虽然它是10个63并没有成为有史以来最大的数字。六个世纪后,迪奥芬图斯发明了一种更简单的指数符号,使他能够超越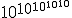 然后,在中世纪,阿拉伯语兴起数字和位值使指数更容易堆叠。但是阿基米德表达大数字的范式并未被根本超越直到二十世纪。即使在今天,指数仍占据主流对巨大事物的讨论。 然后,在中世纪,阿拉伯语兴起数字和位值使指数更容易堆叠。但是阿基米德表达大数字的范式并未被根本超越直到二十世纪。即使在今天,指数仍占据主流对巨大事物的讨论。
举个例子,想想经常被重复的波斯大维齐尔的传说他发明了国际象棋。传说中,国王对新的游戏,并邀请Vizier说出自己的奖励。这位大臣回答说:,作为一个谦逊的人,他只想要一粒小麦棋盘,第二个两粒,第三个四粒,依此类推,两次每个方块上的颗粒数与最后一个方块上的一样多。无数的国王同意了,但没有意识到所有64个正方形上的颗粒总数将是264-1,或相当于世界现有小麦的186亿分之一生产了150年。
恰当地说,正是这种指数增长使国际象棋本身如此困难。每一步棋只有大约35个合法的选择,但选择成倍增加,得到10个左右50可能的董事会位置太多,即使是计算机也无法进行彻底搜索。这就是为什么直到1997年,一台名为“深蓝”的计算机才击败了人类世界的国际象棋冠军。还有围棋,它有一个19乘19的棋盘,超过10150可能的位置,即使是业余爱好者也能击败世界顶尖选手计算机程序。指数级增长也以其他形式困扰着计算机。旅行推销员问题要求连接一组城市之间的距离。问题是可能的路线数量随着城市数量呈指数级增长。什么时候?比如说,有一百个城市,大约有十个158可能的路线,尽管有各种快捷方式,但没有已知的计算机该算法从根本上优于逐条检查每条路径。这个旅行推销员问题属于NP-complete类,它包括数百个其他实际感兴趣的问题。(NP代表技术术语不确定性多项式时间。)众所周知,如果任何NP-完全问题的算法,那么就有高效的算法所有这些。这里,高效意味着使用与at成比例的时间量大多数问题的大小被提高到某个固定幂,例如城市成倍增长。然而,据推测,对于存在NP-完整问题。证明这个猜想,称为P¹NP一直是计算机科学中一个尚未解决的重大问题三十年了。
虽然计算机可能永远无法解决NP完全问题有效地,人们对另一个计算机科学的圣杯有更多的希望:复制人类智能。人脑大约有1000亿由100万亿个突触连接的神经元。虽然单个神经元只被部分理解,人们认为每个神经元根据相对简单的规则发射电脉冲,最多可达1000次每秒几次。所以我们拥有一台高度互联的计算机可能有10个14每秒操作数;相比之下,世界最快的并行超级计算机,位于Sandia的9200 Pentium Pro teraflops机器国家实验室,可以执行10次12每秒操作数。与…相反流行的观点是,灰色缪斯不仅在智力上刻苦追求:它超越了其他人硅甚至在原始计算能力方面。但这不太可能持续下去长。原因是摩尔定律,该定律在20世纪90年代的表述中指出硅芯片上可存储的信息量呈指数级增长,大约每两年翻一番。摩尔定律最终将发挥作用微芯片组件达到原子级和常规光刻步履蹒跚。但是激进的新技术,如光学计算机、DNA计算机、,甚至量子计算机,都有可能取代硅的地位。指数计算能力的增长不可能永远持续,但可能会持续很长时间至少在处理能力上足以让计算机超越人脑。
对于人工智能的预言家来说,摩尔定律是一条光荣的定律指数增长的预兆。但指数也有更令人沮丧的一面。这个人口最近超过60亿,并且大约每增加一倍四十年了。按照这个指数率,如果一个人平均体重为70公斤,那么到3750年,整个地球将由人类组成肉体。但在你投资除臭剂之前,要意识到人口会停止增长很久以前,由于饥荒、流行病、全球变暖、大量物种灭绝、无法呼吸的空气,或进入投机领域,计划生育。不难理解为什么物理学家阿尔伯特巴特利特断言“人类最大的缺点”是“我们的无法理解指数函数。“或者为什么卡尔·萨根建议我们“永远不要低估指数”十亿&十亿,萨根给出了指数的其他一些令人沮丧的结果增长。以每年5%的通货膨胀率计算,一美元只值二十年后的三十七美分。如果铀原子核发射两个中子,两者都与其他铀核相撞,导致他们发出两个中子等等,我有没有提到核毁灭可能是一个结局人口增长?
¨
指数是熟悉的、相关的、与物理密切相关的世界和人类的希望和恐惧。使用我将讨论的符号系统接下来,我们可以简明地命名使指数皮卡尤恩化的数字比较,即主观上超越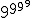 与后者超过9。但这些新系统似乎比指数。道格拉斯·霍夫斯塔特(Douglas Hofstadter)在他的论文《论数字麻木》(On Number Numbness)中读者看到了这些系统的悬崖,但随后又断言: 与后者超过9。但这些新系统似乎比指数。道格拉斯·霍夫斯塔特(Douglas Hofstadter)在他的论文《论数字麻木》(On Number Numbness)中读者看到了这些系统的悬崖,但随后又断言:
如果我们再继续讨论一秒钟,我们就会发现自己处于递归函数理论和算法复杂性,这太抽象了。所以让我们放弃这个话题就在这里。
但放弃这个话题就是放弃,不仅是最大的数字竞赛,而且希望了解更强的范式如何导致更大的数字。所以我们在二十世纪初来到这里,当时一所数学家学校形式主义者试图将所有数学置于严格的公理基础上。形式主义者的一个关键问题是computable这个词的意思是什么。那就是,我们如何判断一个数字序列是否可以由一个确定的,机械程序?一些数学家认为可计算性巧合使用一个称为原始递归的技术概念。但在1928年威廉阿克曼通过构造一个清晰的数字序列来反驳这些观点可计算,但增长太快,无法实现基本递归。
阿克曼的想法是创造一个无止境的算术过程每一次操作都比上一次强大。首先是添加。第二个来了乘法,我们可以将其视为重复加法:例如,5´3表示5与自身相加3次,或5+5+5=15。第三求幂,我们可以把它看作是重复的乘法。第四来。。。什么?我们必须发明一种奇怪的新手术指数运算。数学家鲁迪·拉克称之为四分体。例如,5四分之一到3意味着5提升到自身功率3倍,或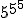 ,一个2185位数的数字。我们可以继续。第五个重复出现四分音符:我们可以称之为五分音符吗?第六个是重复五音:六边形?这些操作将无限持续,每一个操作都站在它的前任将目光投向更高的数字领域。 ,一个2185位数的数字。我们可以继续。第五个重复出现四分音符:我们可以称之为五分音符吗?第六个是重复五音:六边形?这些操作将无限持续,每一个操作都站在它的前任将目光投向更高的数字领域。
如果每个操作都是糖果味的,那么阿克曼序列将是取样器包装,每种口味混合一个数量。序列中的第一个是1+1,或者(不要屏住呼吸)2。第二个是2´2,或4.第三是3提高到3第个功率,或27。嘿,这些数字不是那么大!
费用。Fi.Fo.Fum(消防)。
第四个是4对4,或者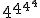 ,具有10154数字。如果你打算写出这个数字,最好现在就开始。第五个是5对应于5,或者 ,具有10154数字。如果你打算写出这个数字,最好现在就开始。第五个是5对应于5,或者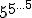 带有5个五角堆栈中的4个数字。这个数字太庞大了,无法用任何语言来描述普通条款。从那时起,数字会越来越大。 带有5个五角堆栈中的4个数字。这个数字太庞大了,无法用任何语言来描述普通条款。从那时起,数字会越来越大。
利用阿克曼序列,我们可以在规模最大的比赛。但我们需要小心,因为有几个阿克曼序列的定义并不完全相同。在15秒的时限内,我可能会写以下内容以避免模糊性:
A(111)Ackermann序列A(1)=1+1,A(2)=2´2,A(3)=3三,等
虽然看起来需要重新编辑,但阿克曼序列确实有一些应用。A类Ramsey理论中的一个问题要求满足某种性质的超立方体。真正的维度被认为是6,但任何人所能证明的最低维度都是如此巨大,以至于它只能使用与阿克曼相同的奇怪算法来表达顺序。事实上吉尼斯世界纪录大全一旦列出这个维数是数学证明中使用过的最大数字。(另一个曾经的冠军争夺者是Skewes数字,大约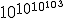 ,这是在素数如何分布的研究中产生的。著名的数学家G.H.哈迪打趣说,斯凯韦斯是“拥有在数学上曾有过明确的目的。“)还有,阿克曼疾驰的骑兵队偶尔会在计算机科学领域表演一段客串。对于例如,在分析名为Union-Find的数据结构时,一个术语得到乘以阿克曼序列的倒数,表示每个整体数字X,第一个数字N,这样N第个阿克曼编号为大于X。逆序列的增长速度与Ackermann的原始序列一样慢生长迅速;就所有实际目的而言,倒数最多为4。 ,这是在素数如何分布的研究中产生的。著名的数学家G.H.哈迪打趣说,斯凯韦斯是“拥有在数学上曾有过明确的目的。“)还有,阿克曼疾驰的骑兵队偶尔会在计算机科学领域表演一段客串。对于例如,在分析名为Union-Find的数据结构时,一个术语得到乘以阿克曼序列的倒数,表示每个整体数字X,第一个数字N,这样N第个阿克曼编号为大于X。逆序列的增长速度与Ackermann的原始序列一样慢生长迅速;就所有实际目的而言,倒数最多为4。
¨
阿克曼的数字相当大,但还不够大。追求因为更大的数字让我们回到了形式主义。阿克曼之后证明了原始递归不是我们所说的可计算的问题仍然存在:什么做我们指的是可计算的?1936年,阿隆佐丘奇和阿兰·图灵独立回答了这个问题。While Church教堂图灵用一种称为lambda演算的逻辑形式来回答使用理想化的计算机器——图灵机,本质上是相当于现代世界上所有的康柏、戴尔、麦金塔和克雷。图灵描述他的机器的论文“关于可计算数字”是正确的被誉为计算机科学的奠基文件。
图灵说:“计算机”,
通常通过在纸上书写某些符号来完成。我们可以这样假设像孩子的算术书一样把纸分成方块。在基本方面有时会用到纸的二维特征。但是这样使用总是可以避免的,我认为人们会同意二维纸的性质不是计算的本质。那么我认为计算是在一维纸上进行的,在一个分为方块。
图灵继续用巧妙的推理解释他的机器第一原则。图灵说,胶带在两个方向上无限延伸,因为理论机器不应该受到物理限制资源。此外,胶带的每个方块上都写着一个符号,就像现代计算机内存中的1s和0s。但是这些符号怎么样操纵?有一个磁带头在磁带上前后移动,一次检查一个正方形,根据明确的规则。规则是磁带头的程序:更改它们改变磁头的作用。
图灵8月的见解是,我们可以对磁带头进行编程,以实现任何计算。图灵机可以加、乘、提取立方根,排序,搜索,拼写检查,解析,玩抖音,列出阿克曼序列。如果我们将键盘输入、显示器输出等表示为磁带,我们甚至可以在图灵机器上运行Windows。但有一个问题。设置一个磁带头在一系列符号上松动,最终可能会停止,或者可能永远像传说中的程序员那样在淋浴时卡住了因为洗发水瓶上的说明是“起泡,冲洗,重复”。如果机器将永远运行,提前知道这一点很好,所以我们不会花太多时间等待它的完成。但我们怎么能确定在有限的时间内,某件事是否会持续下去?如果你和朋友打赌你的手表永远不会停止滴答声,你什么时候能做到宣布胜利?但也许有一些巧妙的程序可以检查其他程序并告诉我们它们是否会停止运行。我们只是还没想过。
不。图灵证明了这个叫做暂停问题的问题是图灵机器无法解决。这个证明是一个很好的例子自我参考。它正式化了一个关于为什么你永远不能拥有完美的内省:因为如果你可以,那么你可以决定你从现在开始,我们要做十秒钟,然后做其他事情。图灵想象有一种特殊的机器可以解决停车问题。然后他向我们展示了如何让这台机器进行自我分析如果它一直运行,它就必须停止;如果它停止,它就永远运行。像只猎犬最后抓住尾巴吞食自己,神秘的机器消失了在激烈的矛盾中。(这是你在研究论文。)
¨
“很好,”你说(或者你可能会说,“一点都不好”)。“但是什么是所有这些都与大数字有关?“啊哈!连接没有发布直到1962年5月。然后,在贝尔系统技术期刊,依偎着关于“多端口结构”和“波导”的务实论文压力密封,”出现了标题适中的“关于非可计算函数”蒂博·拉多。在这篇文章中,Rado介绍了有史以来最大的数字想象。
他的想法很简单。就像我们可以根据单词的字母数来分类一样包含,我们可以根据图灵机器在磁带中有多少规则对其进行分类头部。一些机器只有一条规则,其他机器有两条规则,还有一些机器有三个规则,等等。但对于每个固定的整数N,正如只有有限多个带有N个字母的不同单词,所以也只有有限多的不同单词具有N个规则的机器。在这些机器中,有些机器会停止运行,而另一些则会永远运行从一盘空白磁带开始。停下来的人中,拉多问,是什么任何机器执行的最大步数之前它停下来了吗?(实际上,Rado主要问的是任何机器可以使用的最大符号数停下来之前在磁带上写下。但最大步数,Rado名为S(n),具有相同的基本属性,更容易推理。)
Rado称这个最大值为N第个“忙碌的海狸”号码。(啊,是的,20世纪60年代初是一个更加天真的时代。)他把每台图灵机器想象成一只海狸在磁带上忙碌着,写着又擦着符号。这个那么,挑战是找到最繁忙的有N条规则的海狸,尽管不是无限繁忙。我们可以将此挑战解释为找到“最复杂”的计算机程序N位长:数量最多,但不是无限量。
现在,假设我们知道N第个繁忙的海狸号码,我们将拨打BB(否)。然后我们可以决定任何具有N个规则的图灵机是否停在空白磁带。我们只需要开动机器:如果它停下来,那没关系;但如果它不会在BB(N)步内停止,那么我们就知道它永远不会停止将停止,因为BB(N)是它在停止之前可以进行的最大步数。类似地,如果你知道所有人都在200岁之前死亡,如果萨利活到200岁,你可以断定莎莉是不朽的。因此,没有图灵机可以列出繁忙的海狸号,如果可能的话,它可以解决停机问题我们已经知道这是不可能的。
但这里有一个奇怪的事实。假设我们能说出一个数字更大的比N第个忙碌的海狸编号BB(N)。把这个数字叫做D代表大坝,因为就像海狸坝一样,它是下面忙碌的海狸的屋顶。手里拿着D,计算BB(N)本身变得很容易:我们只需要模拟所有的图灵具有N个规则的机器。那些没有在D内停下来的人会走上那些对大坝顶部的猛击永远不会停止。所以我们可以准确列出机器停止,其中,任何机器的最大步数在它停止之前需要的是BB(N)。
结论?Busy Beaver编号的顺序,BB(1)、BB(2)等,增长速度超过任何可计算序列。比指数更快,堆叠指数,阿克曼序列,你可以命名它。因为如果图灵机器可以计算出一个比Busy Beaver增长更快的序列可以使用该序列获得海狸水坝的D。有了这些D,它可以列出Busy Beaver的号码,这(听起来很熟悉吗?)我们已经知道了是不可能的。Busy Beaver序列是不可计算的,仅仅因为它增长速度快得惊人,任何计算机都无法跟上它,即使在原则。
这意味着没有一个计算机程序可以通过一个。这并不意味着特定的忙碌海狸需要永远存在不可知。事实上,将它们固定下来一直是计算机科学的消遣自从Rado发表了他的文章。很容易验证BB(1),第一个忙碌的海狸号是1。这是因为如果一个单规则图灵机不第一步完成后就停下来,它会一直沿着磁带不停地移动。没有更复杂的行为空间了。有了两条规则,我们可以做得更多,再做一点繁琐的工作就能确定BB(2)是6。六个步骤。关于第三只忙碌的海狸?1965年,Rado和Shen Lin证明了BB(3)是21。这是一项艰巨的任务,需要对许多机器进行人工分析证明它们不会停止,因为没有列出繁忙的海狸号码。接下来,在1983年,Allan Brady证明了BB(4)是107。到目前为止没有压力?好吧,就像Ackermann序列一样,不要被前几个数字。
1984年,A.K.Dewdney致力于科学美国人列设置为Busy海狸,这激发了业余数学家乔治·尤因(George Uhing)建造模拟图灵机器的专用装置。设备,成本Uhing不到100美元,发现了一台运行2133492步的五规则机器在停止确定BB(5)必须至少同样高之前。然后,在1989年,Heiner Marxen和Jürgen Buntrock发现BB(5)至少为47176870。直到今天,BB(5)还没有被精确地固定下来,它可能会变成还要高得多。至于BB(6),Marxen和Buntrock在1997年,证明其至少为8690333381690951。令人生畏的成就,然而Marxen、Buntrock和其他忙碌的海狸猎人只是沿着未知的海岸涉水前行。人类可能永远不会知道BB(6)的值是确定的,更不用说BB(7)的值或顺序。
事实上,前五名和前六名规则竞争者已经躲过了我们:我们不能解释他们如何用人性化的术语工作。如果创意渗透到他们的设计中不是因为人类把它放在那里。理解这一点的一种方法是,即使很小图灵机可以对深刻的数学问题进行编码。拿哥德巴赫的假设每个偶数4或更高的数都是两个质数的和:10=7+3, 18=13+5. 自1742年以来,这一推测一直没有得到证实。然而我们可以设计一个图灵机器,假设有100条规则,可以测试每一条规则数字,查看它是否是两个素数的和,并在找到这个猜想的反例。然后知道BB(100),我们原则上可以运行此机器对于BB(100)步,决定是否停止,从而解决哥德巴赫猜想。我们不需要冒险进入巢穴巴西利斯克。
但正如Rado强调的那样,即使我们无法列出Busy Beaver的数字数学上定义完美。如果你向朋友挑战最大的数字竞赛,我建议你写这样的东西:
BB(11111)Busy Beaver班次#1、6、21等
如果你的朋友不知道图灵机器或类似的东西,但是比方说,只有大约阿克曼数字,你才能赢得比赛。你还是会即使你给你的朋友一个障碍,也要赢,让他终身受益写下他的数字。最大数字竞赛的关键是强有力的范式,而图灵的计算理论确实是强有力的。
¨
但如果你的朋友也知道图灵机器呢?是否有大数字的符号系统甚至比忙碌的海狸还要强大?
假设我们可以赋予图灵机一种神奇的能力来解决暂停问题。我们会得到什么?我们将得到一台超级图灵机器:一台带有超越任何普通机器的能力。但现在,要做到这一点有多难决定是否超级的机器停止?嗯,事实证明甚至没有超级机器可以解决这个超级停机问题,原因与普通机器无法解决普通的停机问题。解决停工问题超级机器的问题,我们需要一个偶数更多强大的机器:超级复制机。并解决超级复制者的暂停问题机器,我们需要一台超级翻跟头机器。等等,没完没了。这个越来越强大的机器的无限层次结构被逻辑学家形式化了1943年,斯蒂芬·克莱恩(Stephen Kleene)(尽管他没有使用“超级笨蛋”这个词)。
想象一下,一部小说嵌入了一部较长的小说中,而小说本身就是嵌入偶数比较长的小说等等。在每个小说中,人物可以讨论任何子小说的文学价值。但是,与不能自我分析的机器类相比人物永远不能评论他们的小说他们自己在中。(我认为,这与我们通常的小说经历不谋而合。)了解一些现实,我们需要走出现实。这是Kleene层次结构的本质:解决某类的暂停问题在机器方面,我们需要一种功能更强大的机器。
而且没有逃脱的余地。假设图灵机器具有神奇的能力解决停车问题,和超级停车问题,和这个超级复制暂停问题,和超级傻瓜大便器停止问题,等等。这肯定会是图灵机器的女王吗?不是相当不错。一旦我们想决定图灵女王机器是否停止,我们需要一台更强大的机器:图灵女皇机器。而且克莱恩的等级制度仍在继续。
但这与大数字有什么关系呢?好吧,每一层克莱恩层次结构生成了一个比所有之前的级别。事实上,每个级别的序列增长如此迅速,以至于它只能由更高级别计算。例如,定义BB2(N) 成为具有N个规则的超级计算机在停止之前可以执行的最大步数。如果这个超级忙碌的海狸序列可以由超级机器计算,然后机器可以解决超级停机问题,我们知道这是不可能的。所以超级繁忙的海狸数量增长太快,无法计算,即使如果我们可以计算出普通的Busy Beaver数字。
你可能认为现在,在最大数字竞赛中,你可以抹杀甚至是一个使用Busy Beaver序列的对手这个:
BB公司2(11111).
但不完全如此。问题是,我从未见过这些“高级忙碌”海狸”在任何地方都有定义,可能是因为,对懂得计算能力的人来说从理论上讲,它们是普通Busy Beaver数字的一个相当明显的扩展。所以我们理性的现代数学家不会知道你是什么数字命名。如果你想在最大数量中使用高级Busy Beavers比赛,这是我的建议。首先,发表一篇论文,将概念形式化在一些晦涩低调的杂志上。然后,在比赛中引用论文在你的索引卡上。
为了超越更高级别的忙碌海狸,我们可能需要一些新的计算模型甚至超过了图灵机。我无法想象这样的模型应该是这样的。然而不知为何,我怀疑符号系统的故事因为大数字已经过去了。也许有一天人类将能够简明扼要地命名这些数字使得Busy Beaver 100看起来和我们的一样幼稚有趣贵族的八十三岁。或者如果我们永远不会说出这样的数字,也许其他文明会。银河系正在进行一场规模最大的数字竞赛吗?
¨
你可能想知道为什么我们不能超越整个范例游行,以及通过包含并超越所有数字的系统命名数字。假设你在最大的数字竞赛中写下了以下内容:
可命名的最大整数,1000个英文字符文本
这个数字肯定存在。使用1000个字符,我们只能有限地命名很多数字,其中必须有一个最大的数字。然而我们没有提及这些数字是如何命名的。英文文本可以调用Ackermann数字,或Busy Beavers,或更高级别的Busy Beaves,甚至一些更广泛的概念还没有人想到。所以除非我们的对手用同样的手法,我们把他打了。多棒的主意!为什么我们没有早点想想这个?
不幸的是,它不起作用。我们不妨写下
一加上可命名的最大整数,1000个英文字符文本
此数字至少需要1001个字符才能命名。然而我们刚刚命名了它只有80个字符!就像一条蛇把自己整个吞下,我们的庞然大物数字在矛盾的喧嚣中消解。什么给你?
我刚才描述的悖论最初是由伯特兰·罗素(Bertrand Russell)发表的,他把它归功于一位名叫G·G·贝里的图书管理员。贝里悖论没有出现来自数学,但来自英语中固有的歧义。没有可靠的方法可以将英语短语转换为它所命名的数字(或者决定它是否命名一个数字),这就是我调用“理性的现代数学家”在规则中进行了最大的数字竞赛。为了避免贝里悖论,我们需要使用精确的,数学符号系统,如图灵机《忙碌的海狸》系列背后的想法。总之,没有狡猾的语言超越阿基米德、阿克曼、图灵和拉多的诀窍,绝非王道大数字。
你可能还想知道为什么我们不能在比赛中使用无穷大。答案因为同样的原因,我们不能在自行车比赛中使用火箭车。无限是迷人而优雅的,但它不是一个整数。我们也不能减法从无穷大到整数。无穷减去17仍然是无穷大,然而无限减去无限是未定义的:它可以是0、38或甚至又是无穷大。实际上我应该说无限,复数。因为最近十九世纪,乔治·坎托证明了无穷大:例如,直线上点的无穷大大于整数的无穷大。而且,正如没有最大的数字一样,所以也没有最大的无限。但对大无穷的追求更多比追求大数字更深奥。它涉及的不是一系列范式,但本质上是一个:康托斯。
¨
所以我们现在处于大数知识的前沿。作为欧几里得的门徒应该会问:“什么是使用所有这些?“我们已经看到了这一进展大数符号系统反映了更广泛领域的进展:数学、逻辑、计算机科学。然而,尽管镜子反映了现实,它并不一定会影响它。即使在数学中,大数字也是他们的学习通常被认为是琐碎的事情,是一种无聊的消遣,没有更广泛的内容启示。我想反驳一个相反的观点:理解大数字了解世界的钥匙。
想象一下,试图向阿基米德解释图灵机器。天才雪城耐心聆听你讨论无限延伸的纸草卷在两个方向上,时间步长、状态、输入和输出序列。最后他爆炸了。
“愚蠢!”他宣称(或古希腊的对等词)。“你所拥有的给我的是一个详尽的定义,没有任何价值。"
你如何回应?阿基米德从未听说过计算机从他那个时代算起,23个世纪后,将处理的棘手的装置世界事务。所以你不能要求实际应用。你也不能呼吁希尔伯特和形式主义程序,因为阿基米德还没有听说这些都是。但是,它击中了你:繁忙的海狸序列。您可以定义阿基米德的序列,说服他BB(1000)比他的1063沙粒填满了宇宙,比1063自力更生1063次。你敢违抗他在不调用图灵机器或其他等效机器的情况下,命名一个更大的数字。作为他思考着这个挑战,图灵机器概念的力量开始显现。虽然他的直觉可能永远不会理解繁忙的海狸数字,但他的理由迫使他承认他们的巨大。大数字有一种灌输方式抽象概念与现实。
事实上,人们可以将科学定义为理性试图补偿我们无法感知大量数据。如果我们能以每小时280000000米的速度奔跑其次,不需要狭义相对论:这是显而易见的对每个人来说,我们走得越快,就越重,越蹲世界上其他地方时间过得更快。如果我们能活700万多年来,没有进化论当然无创造论:我们可以用眼睛观察物种形成和适应,而不是费力地观察从化石和DNA重建事件。如果我们能以20000000英镑的价格烤面包开尔文度数,核聚变将不是物理学家的神秘领域而是普通的家庭知识。但我们不能做这些事情,所以我们拥有科学,用我们的无穷小推断出我们的庞大官能,永远不会有意义。如果人们害怕大数字,这有什么奇怪吗他们也害怕科学,转而寻求安慰神秘主义?
但是做人们害怕大数字?当然有。我见过一些人不知道一百万和十亿之间的区别,也不在乎。我们玩六合彩!,忽略2000万种方法失败。我们打呵欠每年向大气排放60亿吨二氧化碳,以及在指数增长的夹缝中谈论可持续发展。这样的在我看来,案例超越了对算术的无知,代表了一个基本的不愿意与巨人搏斗。
那么,在大数字面前畏缩的原因是什么?它有生物活性吗原产地?1999年,一个由神经心理学家领导的小组Stanislas Dehaene在年报告了证据科学类两个独立的大脑系统数学思维。该小组训练俄英双语者解决问题一组问题,包括两位数加法、右基数加法、立方体根和对数。一些科目是用俄语培训的,另一些科目是用英语培训的。当受试者被要求大致解决问题以选择在两种估计中,比较接近的一种,他们在两种语言中都表现得同样好。但什么时候当被要求准确地解决问题时,他们的语言表现更好培训。此外,脑成像证据表明,受试者的大脑皮层参与空间推理的脑叶在近似过程中更为活跃问题;而左下额叶参与言语推理,在精确计算问题中更加活跃。对患者的研究大脑病变描绘出同样的画面:有时有顶叶病变无法决定9是接近10还是接近5,但请记住乘法表格;而那些有左半球病变的患者有时无法决定2+2是3还是4,但要知道答案更接近3而不是9。Dehaene等人推测人类用两种方式表示数字。对于近似计算我们使用的是一条心算线,这条线在很久以前就已经发展了我们可能与其他动物分享。但为了精确计算,我们使用数字符号是最近发展起来的,它依赖于语言,是人类独有的。这个假设巧妙地解释了实验的发现:受试者在训练语言中表现更好的原因计算而非近似问题是前者调用以语言为导向的左下额叶,后者位于空间定向的顶叶。
如果Dehaene等人的假设是正确的,那么我们该用哪种表示法呢用于大数字?毫无疑问,这是一个象征性的数字线可能足够长,可以容纳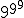 ,5对应于5,或BB(1000)。我想问题就在这里。当考虑3、4或7时,我们以我们的空间直觉为指导,经过数百万年的磨练看到3只瞪羚,4只配偶,7个敌对氏族成员。但在思考时关于BB(1000),我们只有语言,那个进化中的新手,可以依赖。通常用于表示数字的神经通路会导致死胡同。而这个,也许,这就是人们害怕大数字的原因。 ,5对应于5,或BB(1000)。我想问题就在这里。当考虑3、4或7时,我们以我们的空间直觉为指导,经过数百万年的磨练看到3只瞪羚,4只配偶,7个敌对氏族成员。但在思考时关于BB(1000),我们只有语言,那个进化中的新手,可以依赖。通常用于表示数字的神经通路会导致死胡同。而这个,也许,这就是人们害怕大数字的原因。
早期干预能减轻我们对数字的恐惧吗?如果二年级怎么办数学老师在枯燥的繁忙工作中花了一个小时的时间问他们学生们,“你到底怎么命名,真正地大数字?“然后告诉关于指数和叠加指数、四分位数和阿克曼序列,甚至可能是忙碌的海狸:一个比任何数字都大的聚宝盆他们曾经怀过孕,想法超越了他们的界限想象力。
谁能说出更大的数字?谁拥有更深层的范式。你是吗准备好了吗?做好准备。去吧。
工具书类
彼得·贝克曼,圆周率的历史《魔像出版社》,1971年。
Allan H.Brady,“不可计算半径值的确定四状态图灵机的功能Sigma(k),”数学计算,第40卷,第162号,1983年4月,第647页-665
格雷戈里·查廷(Gregory J.Chaitin),“贝里悖论”复杂性,第1卷,第1号,1995年,第26页-30.时间http://www.umcs.maine.edu/~chaitin/unm2.html.
A.K.Dewdney,新图灵综合:66次计算机之旅科学类W.H.Freeman,1993年。
S.Dehaene、E.Spelke、P.Pinel、R.Stanescu和S.Tsivkin,“数学思维的来源:行为和大脑成像证据”科学类,第284卷,第5416号,1999年5月7日,第970页-974
道格拉斯·霍夫斯塔特,元魔法主题:探寻心灵的本质和图案,《基础书籍》,1985年。第6章,“关于数字的无数字性”,pp。115-135
罗伯特·卡尼格尔,知道无限的人:天才的一生拉马努詹华盛顿广场出版社,1991年。
Stephen C.Kleene,“递归谓词和量词”的事务处理美国数学学会第53卷,1943年,第41页-74
Donald E.Knuth,计算机科学论文选、CSLI出版物,1996年。第2章,“数学和计算机科学:应对有限性”,第31页-57
德克斯特·C·科曾,自动机和可计算性、斯普林格-Verlag、,1997
,算法的设计与分析斯普林格·弗拉格,1991年。
Shen Lin和Tibor Rado,“图灵机器问题的计算机研究”计算机协会杂志,第12卷,第2期,4月1965年,第196页-212
Heiner Marxen,Busy Beaver,地址:网址:http://www.drb.insel.de/~海纳/BB/.
和Jürgen Buntrock,“攻击忙碌的海狸5”Bulletin of the欧洲理论计算机科学协会,编号40,2月1990年,第247页-251
Tibor Rado,“关于非可计算函数”贝尔系统技术日记账第四十一卷第2期,1962年5月,第877页-884
鲁迪·拉克,无限与心灵普林斯顿大学出版社,1995
卡尔·萨根,数十亿美元,兰登书屋,1997年。
迈克尔·索莫斯(Michael Somos),《繁忙的海狸图灵机》http://grail.cba.csuohio.edu/~somos/bb.html.
Alan Turing,“关于可计算数字,以及对Entscheidungsproblem,“伦敦数学学会会刊,系列2,第42卷,第230页-265, 1936. 重印于马丁·戴维斯(编辑),不确定因素《乌鸦》,1965年。
伊兰·瓦尔迪(Ilan Vardi),“阿基米德,沙推算师”,网址:网址:http://www.ihes.fr/~ilan/sand_reckoner.ps.
Eric W.Weisstein,CRC简明数学百科全书,CRC出版社,1999.在http://www.treasure-troves.com/math/LargeNumber.html.
|