2015年11月,我想分享我对各种不同的多维连分式算法从用它们进行的各种实验通常涉及组合学和数字几何,但也包括前两个的计算Lyapunov指数。
由于连分式与Sturmian的组合数学有着深刻的联系序列,可以看作是grid\(\mathbb{Z}^2),多维连分数算法与直线和超平面的数字化有关\(\mathbb{Z}^d\)。
这就是为什么我在我称之为三维连续分数算法作弊表因为它的格式受到启发从网上找到的典型备忘单。所有实验都可以使用可选的SageMath包复制板球我在那里分享我的研究代码。人们问我是否会尝试发表这些作弊表,但我担心这种格式会改变每个页面上都有信息和数据,因此,最终我从未提交过这些随时随地作弊。
这里我应该说,(d)代表相关矩阵的作用,并且(d-1)是算法作用的投影空间。
骗局的后果之一是它让我们意识到Julien Cassaigne提出的算法具有相同的前两个Lyapunov指数与Selmer算法相同(前3个有效数字相同)。然后朱利安发现了这个解释,因为它的算法与一些Selmer算法的半排序版本。这个结果是共享在期间WORDS 2017会议。朱利安·勒罗伊(Julien Leroy)、朱利安·卡萨因(Julien-Cassaigne)和我仍在工作在论文的扩展版本上。这需要更长的时间,主要是因为我因为我一直在努力研究不定期的Wang瓷砖前2年。
2019年7月,沃尔夫冈、瓦莱里和约格要求我进行计算(d)维多维的前两个Lyapunov指数大于3的\(d\)的连续分数算法。主要问题是感兴趣的是第二个李亚普诺夫指数是否保持为负尺寸增加。这个属性与强的概念有关同时diopantine逼近的几乎处处收敛性由实数的固定向量算法提供。它没有带走我自从我开始将代码推广到2017年秋季,尺寸更大。事实证明,作为尺寸增加,所有已知的MCF算法的第二个Lyapunov指数变为积极的。我的计算结果证实了他们最终公布的结果在他们的预印本2019年11月。
我分享结果的动机是会议多维连分式与欧几里德动力学本周举行(本应于2020年3月23日至27日在洛伦兹中心举行因电晕病毒而取消)视频中的一些讨论会议与这个主题有关。
下面进行的计算可以总结为一个图形,其中显示了对于各种情况,关于(d)的\(1-\theta_2/\theta_1\)值\(d)维MCF算法。似乎(theta_2)是负数Brun达到尺寸10,Selmer达到尺寸4,以及尺寸5用于ARP。
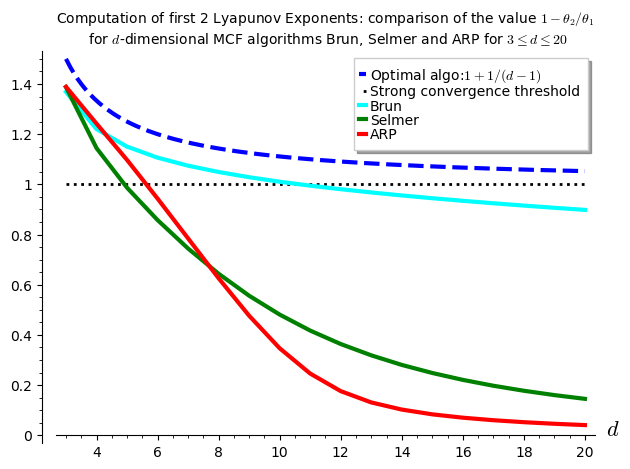
我不得不说,我对结果感到失望,因为算法瓦莱里和我的阿诺克斯-劳兹-波因卡雷(ARP)介绍没有这样做以及它的第二个Lyapunov指数似乎在维度上为正\(第6页)。我对ARP有很好的期望,因为它达到了最高水平在作弊中执行的计算中,(1-\theta_2/\theta_1)的值床单,因此比Brun好,比Selmer好(d=3)。
计算前两个Lyapunov指数的算法是由文森特·德莱克索瓦提供给我。它应用了算法\((v,w)\mapsto(M)^{-1}v,M^T w)\)数百万次。The evolution of the向量(v)的大小给出了第一个Lyapunov指数。进化向量(w)的大小给出了第二个Lyapunov指数。自计算在64位上执行双重的浮点数,它们的是需要处理的数字问题。这就是为什么一些Gramma Shimdts操作是每次将向量重正化为保持向量(w)与(v)正交。否则,数值误差累积量和\(theta_2)的计算值变为相同\(\theta_1)。您可以从以下位置开始在线查看算法第1723行文件的多个cont_frac_pyx.pyx从我的可选软件包。
我不知道文森特从哪里得到了这个算法。所以,我不知道该怎么做确实如此,是否存在上下界的证明正在执行的计算。我能说的是,它在is反复返回相同的值(我的意思是3个常见的最高有效数字)具有任何固定输入(数量迭代)。
下面,我将展示如何重现结果的代码。
版本0.6(2019年11月)板球包括处理某些(d)维多维的必要代码(续)分数(MCF)算法。它文档在线提供。这是一个PIP包,因此可以按如下方式安装:
回想一下,下面的尺寸\(d\)是线性的,\(d-1\)是对应投影算法的空间维度。
从可选软件包中导入Brun、Selmer和Arnoux-Rauzy-PoincaréMCF算法:
圣人: 从 slabbe.mult_cont_frac 进口 布伦, 塞尔默, ARP协议
在单个轨道上计算前两个Lyapunov指数:
圣人: 布伦(昏暗的=3).lyapunov指数(n次迭代=10^7)
(0.30473782969922547, -0.11220958022368056, 1.3682167728713919)
起点是随机的,但结果是三元组的形式\((theta_1,theta_2,1-\theta_2/\theta_1)大致相同:
圣人: 布伦(昏暗的=3).lyapunov指数(n次迭代=10^7)
(0.30345018206132324, -0.11171509867725296, 1.3681497170915415)
增加维度\(d\)将产生:
圣人: 布伦(昏暗的=4).lyapunov指数(n次迭代=10^7)
(0.32639514522732005, -0.07191456560115839, 1.2203297648654456)
圣人: 布伦(昏暗的=5).lyapunov指数(n次迭代=10^7)
(0.30918877340506756, -0.0463930802132972, 1.1500477514185734)
它在大约0.5秒内执行长度为10 ^7的轨道\(10^8)大约5秒,长度大约50秒:
圣人: %时间 布伦(昏暗的=3).lyapunov指数(n次迭代=10^7)
中央处理器 次: 用户 540 毫秒, 系统: 0 纳秒, 全部的: 540 毫秒
墙壁 时间: 539 毫秒
(0.30488799356325225, -0.11234354880132114, 1.3684748208296182)
圣人: %时间 布伦(昏暗的=3).lyapunov指数(n次迭代=10^8)
中央处理器 次: 用户 5.09 秒, 系统: 0 纳秒, 全部的: 5.09 秒
墙壁 时间: 5.08 秒
(0.30455473631148755, -0.11217550411862384, 1.3683262505689446)
圣人: %时间 布伦(昏暗的=3).lyapunov指数(n次迭代=10^9)
中央处理器 次: 用户 51.2 秒, 系统: 0 纳秒, 全部的: 51.2 秒
墙壁 时间: 51.2 秒
(0.30438755982577026, -0.11211562816821799, 1.368331834035505)
下面,我必须承认我需要对我的包,因此下面的代码在版本中不起作用0.6我会的在接下来的几天里更新我的包,以便下面的计算可以复制:
圣人: 从 斯拉贝·利亚普诺夫 进口 利亚普诺夫比较表
对于每一个\(3\leq d\leq 20\),我计算30个轨道,并显示最多有效数字和计算出的30个值的标准偏差。
对于Brun算法:
圣人: 阿尔戈(algos) = [布伦(d日) 对于 d日 在里面 范围(3,21)]
圣人: %时间 lyapunov比较表(阿尔戈(algos), n轨道=30, n次迭代=10^7, ncpus公司=8)
中央处理器 次: 用户 190 毫秒, 系统: 2.8 秒, 全部的: 2.99 秒
墙壁 时间: 6最小值 31秒
算法\#环绕$\theta_1$(std)$\theta _2$(std)$1-\theta _2/\theta _1$(std)
+-------------+----------+--------------------+---------------------+-----------------------------+
布伦 (d日=3) 30 0.3045 (0.00040) -0.1122 (0.00017) 1.3683 (0.00022)
布伦 (d日=4) 30 0.32632 (0.000055) -0.07188 (0.000051) 1.2203 (0.00014)
布伦 (d日=5) 30 0.30919 (0.000032) -0.04647 (0.000041) 1.1503 (0.00013)
布伦 (d日=6) 30 0.28626 (0.000027) -0.03043 (0.000035) 1.1063 (0.00012)
布伦 (d日=7) 30 0.26441 (0.000024) -0.01966 (0.000027) 1.0743 (0.00010)
布伦 (d日=8) 30 0.24504 (0.000027) -0.01207 (0.000024) 1.04926 (0.000096)
布伦 (d日=9) 30 0.22824 (0.000021) -0.00649 (0.000026) 1.0284 (0.00012)
布伦 (d日=10) 30 0.2138 (0.00098) -0.0022 (0.00015) 1.0104 (0.00074)
布伦 (d日=11) 30 0.20085 (0.000015) 0.00106 (0.000022) 0.9947 (0.00011)
布伦 (d日=12) 30 0.18962 (0.000017) 0.00368 (0.000021) 0.9806 (0.00011)
布伦 (d日=13) 30 0.17967 (0.000011) 0.00580 (0.000020) 0.9677 (0.00011)
布伦 (d日=14) 30 0.17077 (0.000011) 0.00755 (0.000021) 0.9558 (0.00012)
布伦 (d日=15) 30 0.16278 (0.000012) 0.00900 (0.000017) 0.9447 (0.00010)
布伦 (d日=16) 30 0.15556 (0.000011) 0.01022 (0.000013) 0.93433 (0.000086)
布伦 (d日=17) 30 0.149002 (9.5e-6号机组) 0.01124 (0.000015) 0.9246 (0.00010)
布伦 (d日=18) 30 0.14303 (0.000010) 0.01211 (0.000019) 0.9153 (0.00014)
布伦 (d日=19) 30 0.13755 (0.000012) 0.01285 (0.000018) 0.9065 (0.00013)
布伦 (d日=20) 30 0.13251 (0.000011) 0.01349 (0.000019) 0.8982 (0.00014)
对于Selmer算法:
圣人: 阿尔戈(algos) = [塞尔默(d日) 对于 d日 在里面 范围(3,21)]
圣人: %时间 lyapunov比较表(阿尔戈(algos), n轨道=30, n次迭代=10^7, ncpus公司=8)
中央处理器 次: 用户 203 毫秒, 系统: 2.78 秒, 全部的: 2.98 秒
墙壁 时间: 6最小值 27秒
算法\#轨道$\teta_1$(标准)$\teta_2$(标准)$1-\theta_2/\theta_1$(标准)
+---------------+----------+--------------------+---------------------+-----------------------------+
塞尔默 (d日=3) 30 0.1827 (0.00041) -0.0707 (0.00017) 1.3871 (0.00029)
塞尔默 (d日=4) 30 0.15808 (0.000058) -0.02282 (0.000036) 1.1444 (0.00023)
塞尔默 (d日=5) 30 0.13199 (0.000033) 0.00176 (0.000034) 0.9866 (0.00026)
塞尔默 (d日=6) 30 0.11205 (0.000017) 0.01595 (0.000036) 0.8577 (0.00031)
塞尔默 (d日=7) 30 0.09697 (0.000012) 0.02481 (0.000030) 0.7442 (0.00032)
塞尔默 (d日=8) 30 0.085340 (8.5电子-6) 0.03041 (0.000032) 0.6437 (0.00036)
塞尔默 (d日=9) 30 0.076136 (5.9e-6条) 0.03379 (0.000032) 0.5561 (0.00041)
塞尔默 (d日=10) 30 0.068690 (5.5电子-6) 0.03565 (0.000023) 0.4810 (0.00032)
塞尔默 (d日=11) 30 0.062557 (4.4e-6段) 0.03646 (0.000021) 0.4172 (0.00031)
塞尔默 (d日=12) 30 0.057417 (3.6电子-6) 0.03654 (0.000017) 0.3636 (0.00028)
塞尔默 (d日=13) 30 0.05305 (0.000011) 0.03615 (0.000018) 0.3186 (0.00032)
塞尔默 (d日=14) 30 0.04928 (0.000060) 0.03546 (0.000051) 0.2804 (0.00040)
塞尔默 (d日=15) 30 0.046040 (2.0e-6页) 0.03462 (0.000013) 0.2482 (0.00027)
塞尔默 (d日=16) 30 0.04318 (0.000011) 0.03365 (0.000014) 0.2208 (0.00028)
塞尔默 (d日=17) 30 0.040658 (3.3电子-6) 0.03263 (0.000013) 0.1974 (0.00030)
塞尔默 (d日=18) 30 0.038411 (2.7e-6条) 0.031596 (9.8e-6段) 0.1774 (0.00022)
塞尔默 (d日=19) 30 0.036399 (2.2e-6页) 0.030571 (8.0e-6段) 0.1601 (0.00019)
塞尔默 (d日=20) 30 0.0346 (0.00011) 0.02955 (0.000093) 0.1452 (0.00019)
对于Arnoux-Rauzy-Poincaré算法:
鼠尾草: 阿尔戈(algos) = [ARP协议(d日) 对于 d日 在里面 范围(3,21)]
圣人: %时间 lyapunov比较表(阿尔戈(algos), n轨道=30, n次迭代=10^7, ncpus公司=8)
中央处理器 次: 用户 226 毫秒, 系统: 2.76 秒, 全部的: 2.99 秒
墙壁 时间: 13最小值 20秒
算法\#环绕$\theta_1$(std)$\theta _2$(std)$1-\theta _2/\theta _1$(std)
+--------------------------------+----------+--------------------+---------------------+-----------------------------+
阿诺克斯-劳西-庞加莱\e(d=3)30 0.4428(0.00056)-0.1722(0.00025)1.3888(0.00016)
阿诺克斯-劳西-庞加莱\e(d=4)30 0.6811(0.00020)-0.16480(0.000085)1.24198(0.000093)
阿诺克斯-劳西-庞加莱\'e(d=5)30 0.7982(0.00012)-0.0776(0.00010)1.0972(0.00013)
阿诺克斯-劳西-庞加莱\e(d=6)30 0.83563(0.000091)0.0475(0.00010)0.9432(0.00012)
阿诺克斯-劳西-庞加莱\e(d=7)30 0.8363(0.00011)0.1802(0.00016)0.7845(0.00020)
阿诺克斯-劳西-庞加莱\e(d=8)30 0.8213(0.00013)0.3074(0.00023)0.6257(0.00028)
阿诺克斯-劳兹-庞加莱\e(d=9)30 0.8030(0.00012)0.4205(0.00017)0.4763(0.00022)
阿诺克斯-劳西-庞加莱\e(d=10)30 0.7899(0.00011)0.5160(0.00016)0.3467(0.00020)
阿诺克斯-劳西-庞加莱\e(d=11)30 0.7856(0.00014)0.5924(0.00020)0.2459(0.00022)
阿诺克斯-劳西-庞加莱\e(d=12)30 0.7883(0.00010)0.6497(0.00012)0.1759(0.00014)
阿诺克斯-劳西-庞加莱\e(d=13)30 0.7930(0.00010)0.6892(0.00014)0.1309(0.00019)
阿诺克斯-劳西-庞加莱\e(d=14)30 0.7962(0.00012)0.7147(0.00015)0.10239(0.000077)
阿努-劳兹-庞加莱\e(d=15)30 0.7974(0.00012)0.7309(0.00014)0.08340(0.000074)
阿诺克斯-劳西-庞加莱\e(d=16)30 0.7969(0.00015)0.7411(0.00014)0.07010(0.000048)
阿诺克斯-劳西-庞加莱\'e(d=17)30 0.7960(0.00014)0.7482(0.00019)0.06005(0.000050)
阿诺克斯-劳西-庞加莱\'e(d=18)30 0.7952(0.00013)0.7537(0.00014)0.05218(0.000046)
阿诺克斯-劳西-庞加莱\e(d=19)30 0.7949(0.00012)0.7584(0.00013)0.04582(0.000035)
阿诺克斯-劳西-庞加莱\e(d=20)30 0.7948(0.00014)0.7626(0.00013)0.04058(0.000025)
使用以下代码计算上图:
圣人: brun_列表 = [1.3683, 1.2203, 1.1503, 1.1063, 1.0743, 1.04926, 1.0284, 1.0104, 0.9947, 0.9806, 0.9677, 0.9558, 0.9447, 0.93433, 0.9246, 0.9153, 0.9065, 0.8982]
圣人: 销售商列表 = [ 1.3871, 1.1444, 0.9866, 0.8577, 0.7442, 0.6437, 0.5561, 0.4810, 0.4172, 0.3636, 0.3186, 0.2804, 0.2482, 0.2208, 0.1974, 0.1774, 0.1601, 0.1452]
圣人: arp_列表 = [1.3888, 1.24198, 1.0972, 0.9432, 0.7845, 0.6257, 0.4763, 0.3467, 0.2459, 0.1759, 0.1309, 0.10239, 0.08340, 0.07010, 0.06005, 0.05218, 0.04582, 0.04058]
圣人: brun_points(深色点) = 列表(列举(brun_列表, 开始=3))
圣人: 销售点(_P) = 列表(列举(销售商列表, 开始=3))
鼠尾草: arp点 = 列表(列举(arp_列表, 开始=3))
圣人: G公司 = 绘图()
圣人: G公司 += 情节(1+1/(x个-1), x个, 3, 20, 图例_标签='最佳算法:$1+1/(d-1)$', 线型=“虚线”, 颜色=“蓝色”, 厚度=3)
圣人: G公司 += 线([(3,1), (20,1)], 颜色=“黑色”, 图例_标签=“强收敛阈值”, 线型=“虚线”, 厚度=2)
圣人: G公司 += 线(brun_points(深色点), 图例标签=“布鲁恩”, 颜色=“青色”, 厚度=3)
圣人: G公司 += 线(销售点(_P), 图例_标签=“塞尔默”, 颜色=“绿色”, 厚度=3)
圣人: G公司 += 线(arp点, 图例_标签=“ARP”, 颜色=“红色”, 厚度=3)
圣人: G公司.伊敏(0)
圣人: G公司.轴_标签([“$d$”,''])
圣人: G公司.显示(标题='前2个Lyapunov指数的计算:值$1的比较-\\θ_2/\\θ_1$\n个对于$d$-维MCF算法,Brun、Selmer和ARP只需$3\\leq d(发光二极管)\\leq 20美元)