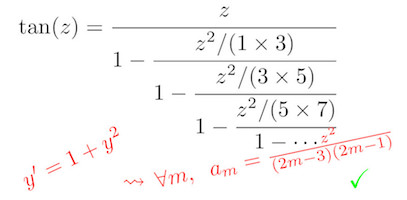我是一个Inria公司研究人员阿里克团队，它是LIP公司实验室里昂高等师范学院我的研究领域是计算机代数。这是对有效数学及其复杂性的研究：一台计算机能完成多少数学，速度有多快？在这方面，我最感兴趣的是经典分析（渐近、特殊函数）和组合学的应用。查看菜单“软件“和”出版物“了解更多信息。
书
2017年，我们出版了本书版本的课程笔记关于计算机代数的有效算法，我们已经给出了10多年。点击封面进入免费下载或订购便宜的纸质版。
最近的工作
将幂级数作为具有适当初始条件的线性微分方程的解，极小化包括找到一个具有该幂级数作为解的最小阶非平凡线性微分方程。这个问题存在于同质和非同质变体中；它不同于微分算子因式分解的经典问题，但与之相关。最近，最小化在先验数论中得到了应用，特别是在计算Siegel（E）函数取代数值的非零代数点时。我们提出了这些问题的算法，并讨论了实现和实验。
A.Bostan、T.Rivoal和B.Salvy，“微分方程和E函数代数值的最小化”计算数学第93卷，第347号，第1427–1472页，2024年。
我们为两个多项式的合成设计了一个新的算法（拉斯维加斯类型）对任意域上的第三个1取模。当这些度多项式由\（n）限定，算法使用\（O（n^{1.43}）字段操作，突破了第一个指数中的“3/2”障碍时间。1978年布伦特和孔提出了以前最快的代数算法，通常需要\（O（n^{1.63}）\）字段操作，以及\（{n^{3/2+O（1）}}\）字段在足够大的场上幂级数的特殊情况下的运算特性。如果使用立方时间矩阵乘法，则新算法在\（{n^{5/3+o（1）}}\）操作中运行，而以前的操作在\（o（n^2）\）中运行操作。
我们的方法依赖于代数关系矩阵的计算这通常是小尺寸的。随机化用于减少随意性对这一有利形势的投入。
V.Neiger，B.Salvy，爱沙尼亚。Schost和G.Villard，“更快的模块化组合”美国计算机学会期刊，第71卷，第2期，2024年。
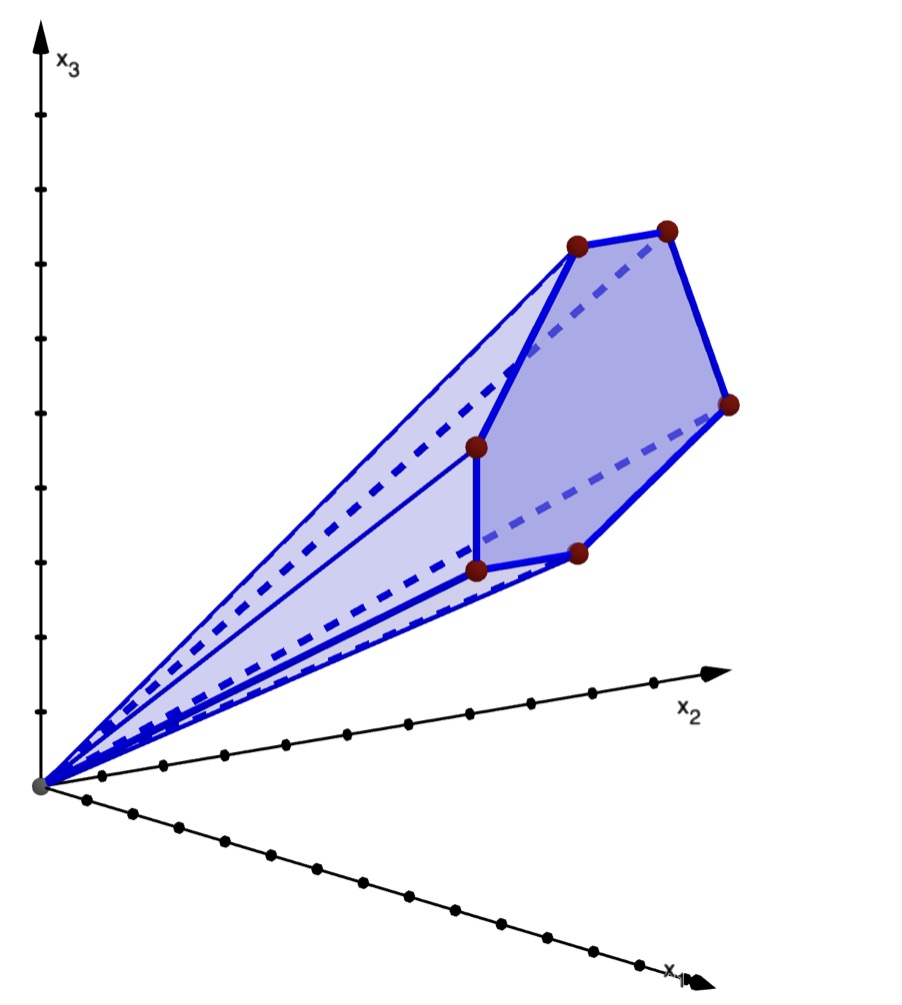
图中的圆锥体包含（n）的所有向量（（u_n，u_{n+1}，u_{n+2}）^t），其中（n）已知，其中（（u _n）_{n\mathbb n}）是由二阶线性递归定义的序列，具有多项式系数。这个圆锥体是证明序列为正的一种方法：首先检查第一个值，直到\（n=n\），然后证明序列没有离开圆锥体。在这项工作中，我们证明了这种方法适用于具有任意阶多项式系数的线性递归解，只要它们是Poincaré型且具有唯一的简单主特征值。在这种情况下，确定正性简化为以精确定义的方式确定初始条件的一般性。我们给出了一个算法，该算法产生一个正性证书，这是一个用于归纳证明的数据结构。这个归纳法的工作原理是，通过递归计算出的圆锥被迭代收缩。
A.Ibrahim和B.Salvy，“线性复发的阳性证明”2024年度ACM-SIAM离散算法（SODA）研讨会论文集2024年，第982-994页。
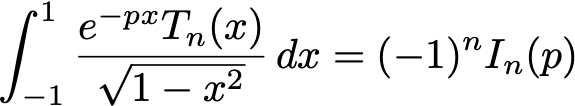涉及特殊函数和序列的定和和积分可以是使用计算机代数技术自动处理创造性伸缩经典算法依赖于计算称为证书的中间对象的大小可以是而且计算量大。事实证明，对于大类和和积分，这部分计算可以避免，加快整个过程。
H.Brochet和B.Salvy，“用于D-有限函数的定和的基于约简的创造性伸缩”，arXiv，2307.072162023年7月。,A.Bostan、F.Chyzak、P.Lairez和B.Salvy，《D有限函数的广义Hermite约化、创造性伸缩和定积分》ISSAC’18-2018年ACM符号和代数计算国际研讨会论文集2018年，第95–102页。
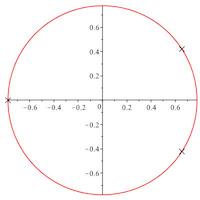
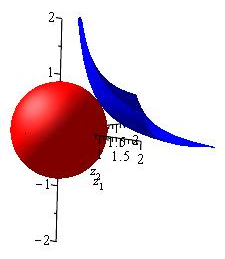
多项式的三个复数根\（17x^3-9x^2-7x+8\），画中所描绘的，位于两个不同的圆圈上，相隔一定距离小于0.000015，因此在图片上无法区分。边界是已知的整数多项式根的绝对值之间的距离系数。我们改进了已知的边界并进行了扩展小范围的实验，以保证其质量界限，这似乎相当悲观。
Y.Bugeaud、A.Dujella、W.Fang、T.Pejković和B.Salvy，“绝对根分离”实验数学第31卷，第3期，第805–812页，2022年。
Y.Bugeaud、A.Dujella、T.Pejkovic和B.Salvy，“绝对实根分离”《美国数学月刊》，第124卷，第10期，第930-936页，2017年12月。
许多超几何级数族（但并非全部）都具有经典正交多项式所熟知的性质。我们考虑了变量（x）中六个超几何级数的一般族，这些超几何级数以整数（n）为索引，并且具有任意数量的参数。对于它们中的每一个，我们给出了递归算子在（n）中的显式因式分解，它们关于（x）的导数及其乘（x）所满足的条件。
N.Brisebarre和B.Salvy，“超几何级数的微分-微分性质”美国数学学会会刊第151卷，第6期，第2603-2617页，2023年。
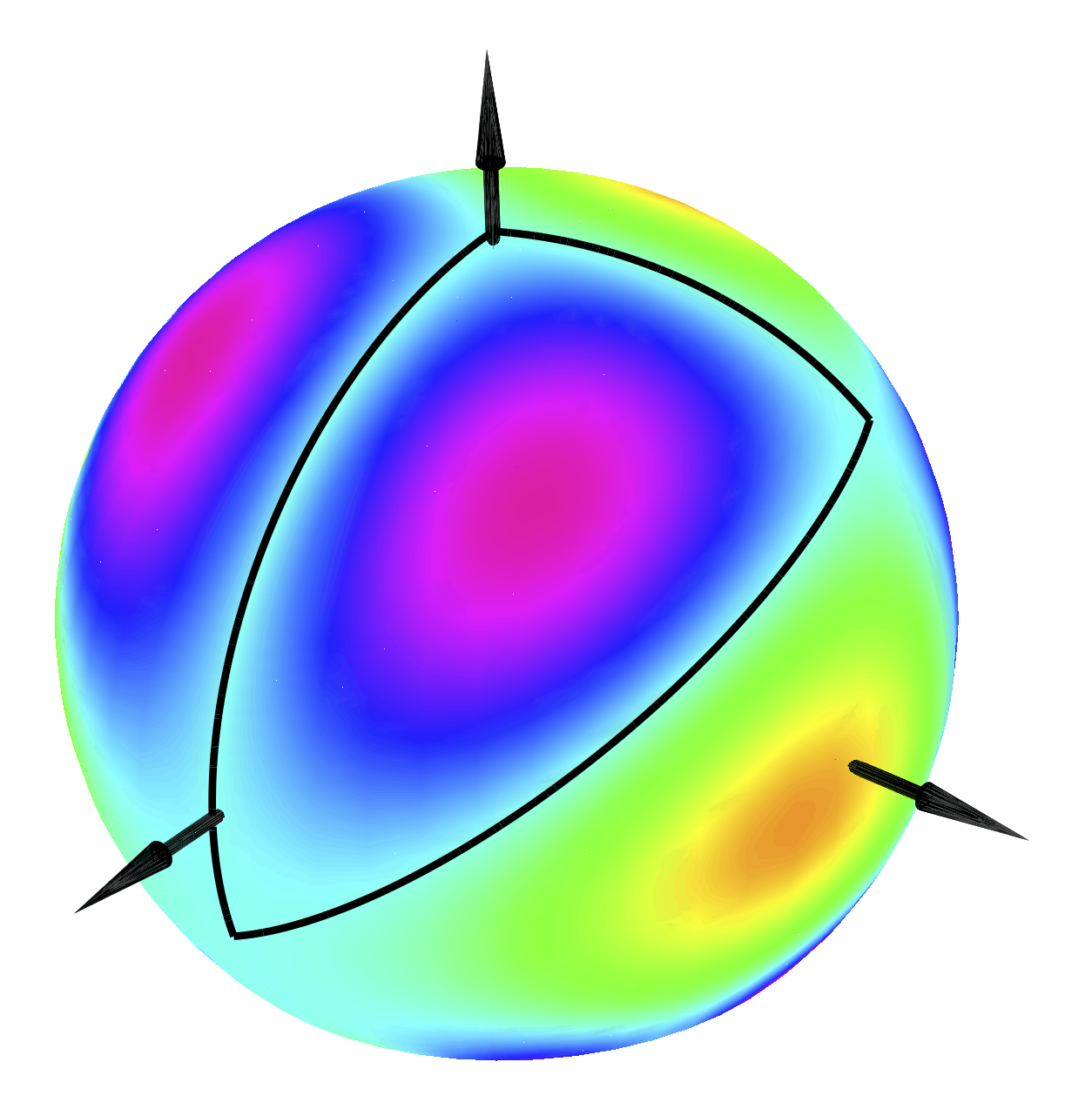
基本特征值的本征函数图这个拉普拉斯算子带角的球面三角形最初来自于研究中的一个问题使用限制步长集在\（\mathbb{N}^3\）中随机行走。每个步长集可以与球面三角形和渐近例如，步数为（n）的行走次数的行为来自\(（0,0,0）\）到自身是格式为\（C\rho^n^\alpha\），其中\（\rho\）很容易根据步骤集进行计算，并且\（\alpha\）与之相关基本特征值。序列\（（e_n）_n\不能是如果指数（α）不是理性。这推动了对认证高精度的研究球面三角形基本特征值的近似。我们通过结合经典方法特殊解、区间算法、泰勒模型和其他工具可以让我们特别获得3D Kreweras模型的基本特征值。从那里连续分数展开让我们得出结论：如果相应的指数（α）是有理的，它的分母将至少为\（10^{51}\）。
J.Dahne和B.Salvy，“拉普拉斯特征值的紧密封闭计算”SIAM J.科学。计算。，第42卷，第5期，A3210–A3232020页。
多变量分析组合学旨在发现对角系数序列的渐近性多元分析函数。计算的起点是集的最小临界点集的确定奇点。这些是该集合最接近原产地。在非负有理函数的情况下系数，这可以有效地实现。一般来说，这种情况仍然可以处理，计算复杂度更高。
S.Melczer和B.Salvy，“多项式系统半数值算法下多元有理函数的有效系数渐近性”符号计算杂志第103卷，第234–279页，2021年。
S.Melczer和B.Salvy，“多变量分析组合数学的符号-数字工具”，inISSAC’16：2016 ACM符号和代数计算国际研讨会论文集，美国纽约州纽约市，2016年，第333–340页。
线性微分算子在许多情况下表现为多项式操作，但不用于因子分解。特别是，系数的阶数线性微分算子的因子可以非常大然而，可以给出这些度的界限，这些界限只取决于关于系数的阶、次和整数的大小算子的系数。
A.Bostan、T.Rivoal和B.Salvy，“线性微分算子右因子的显式度界”《伦敦数学学会通报》，第53卷，第1期，第53–62页，2021年。
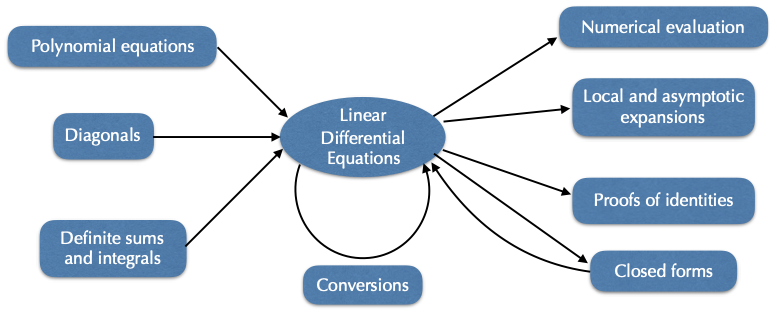线性微分方程解的许多信息可以直接从方程中计算出来。因此，很自然地将这些方程视为一种数据结构，从中可以计算数学特性。因此，近年来设计了各种算法，这些算法的目的不是“求解”，而是用这种表示进行计算。本文对其中许多结果进行了调查。
B.Salvy，“线性微分方程作为数据结构”计算数学基础，第19卷，第5期，第1071-1112页，2019年。
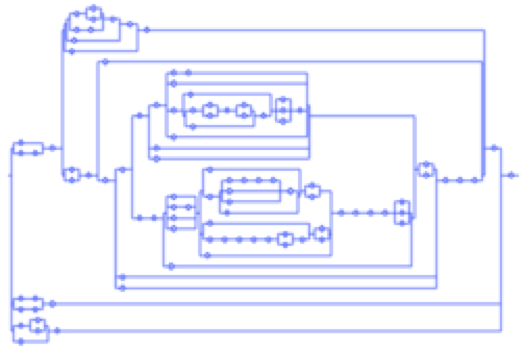
正如Flajolet和Sedgewick在书中所描述的那样，由于分析组合学提供的一组高级工具，许多数据结构的概率行为，如图中的系列平行图，可以进行非常精确的分析。在这个框架中，递归组合定义导致生成函数方程，从中可以设计有效的算法用于枚举、随机生成和某种程度上的渐近分析。在STACS上提供的本教程侧重于随机生成，首先涵盖了分析组合数学的基础知识，然后描述了波尔兹曼采样的思想及其实现。本教程面向广泛的TCS受众，不期望有关于分析组合学的特定先验知识。
B.Salvy，“递归组合结构：枚举、概率分析和随机生成”，in第35届计算机科学理论研讨会（STACS 2018），德国达格斯图尔，2018年，第96卷，第1:1–1:5页。
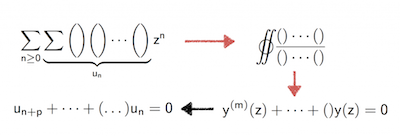
多重二项式和是有理幂级数的对角线。这可以有效地实现，从而得到一个积分表示，从中可以导出生成函数的线性微分方程，并最终得到总和的线性递推。这是一种非常有效的方法，可以避免计算大型证书。
A.Bostan、P.Lairez和B.Salvy，“多重二项式和”符号计算杂志第80卷，第351-386页，2017年。
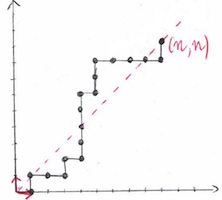
多元有理函数的对角线编码了许多组合序列的枚举序列。在二元情况下，这些对角线是代数幂级数，另一种表示是它们的最小多项式。还有一种可能性是使用他们所满足的线性微分方程。可以计算出这些方程的大小和获得它们的复杂性的精确估计，这表明微分方程通常是更好的选择。
A.Bostan、L.Dumont和B.Salvy，“代数对角线和行走：算法、界限、复杂性”符号计算杂志第83卷，第68–92页，2017年。
A.Bostan、L.Dumont和B.Salvy，《代数对角线和行走》，inISSAC’15：2015 ACM符号和代数计算国际研讨会论文集，美国纽约州纽约市，2015年，第77–84页。
右边的图片来自肯尼思·陈（Kenneth Chan）关于“航天器碰撞概率”（Spacecraft collection probability）一书的封面，它说明了围绕地球轨道运行的碎片数量以及预测碰撞的重要性。我们描述了一种评估此类碰撞概率的方法，该方法使用拉普拉斯变换的闭合形式、泰勒系数的显式递推以及以数值稳定的方式评估这些系数的技术。与其他现有技术相比，该方法具有优势。
R.Serra、D.Arzelier、M.Joldes、J.-B.Lasserre、A.Rondepierre和B.Salvy，“短期碰撞轨道碰撞概率的快速准确计算，”制导、控制与动力学杂志，第39卷，第5期，第1009-1021页，2016年。
R.Serra、D.Arzelier、M.Joldes、J.-B.Lasserre、A.Rondepierre和B.Salvy，《计算短期空间碰撞概率的新方法》AIAA/AAS天体动力学专家会议2014年，第1-7页。
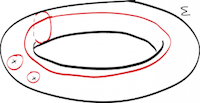
有理函数在多个变量中的定积分通过其生成函数为大量特殊函数或组合序列提供了初等表示。这些积分满足线性微分方程，从中可以很容易地提取有关它们的大量信息。这些积分的计算是一个经典话题，至少可以追溯到埃米尔·皮卡德最近基于创造性伸缩的进展。
A.Bostan、L.Dumont和B.Salvy，“混合创造性望远镜的高效算法”，inISSAC’16-2016年ACM符号和代数计算国际研讨会论文集，2016年，第127-134页。
A.Bostan、P.Lairez和B.Salvy，《使用Griffiths-Dwork方法对有理函数进行创造性伸缩》ISSAC’13：第38届符号和代数计算国际研讨会论文集2013年，第93–100页。
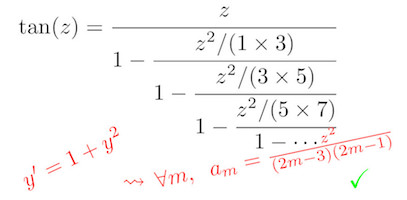
连分式以级数展开式或无穷乘积的相同方式提供了一系列对数字或函数的近似。对于大量特殊函数，这些连分式的系数由指数的显式有理函数给出。这些公式在很大程度上可以用计算机代数来发现和证明。
S.Maulat和B.Salvy，“连分式的公式：自动猜测和证明方法”，inISSAC’15：2015 ACM符号和代数计算国际研讨会论文集，美国纽约州纽约市，2015年，第275-282页。
我最近（和不是最近）的论文集是在这里.
地址
LIP-ENS里昂
46岁，全意大利
69364里昂Cedex 07
法国
电子邮件：名字.Lastname@inria.fr
电话：（+33）（0）4 72 72 89 01
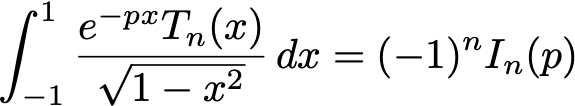
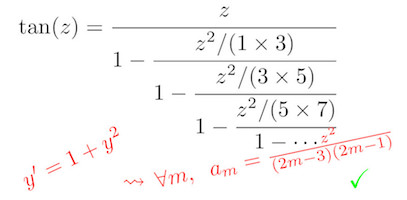
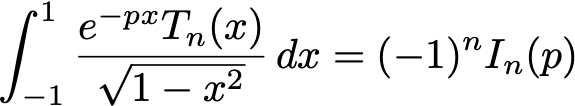