关于0.999…=1的友好聊天

999…=1吗？这个问题激起了学生们的好奇心和学究们的愤怒。一个著名的笑话说明了我的观点：

一个人坐在热气球里在海上迷路了。他看见一座灯塔在雾中逼近。“我在哪里？”他在风中绝望地喊道。“你在气球里！”当他漂向远方时，他听到了。

回答是正确的，但没有帮助。当人们问0.999时……他们不是在说“嘿，你能在实数系统的公理下找到收敛级数的极限吗？”（真的吗？是的，真的！）

不，还有一个更广泛、更有趣的潜台词：当一个数字无限接近另一个数字时会发生什么？

当人们对数学感到好奇时，这是一件罕见的事情：让我们利用这个机会！与其直截了当地提供技术定义来满足某些严格性需求，不如让我们自己来探讨这个问题。

以下是我的简要总结：

0.999的含义……取决于我们对数字行为的假设。
一个普通的假设数字不能“无限接近”在一起-它们要么相同，要么不同。根据这些规则，0.999…=1，因为我们无法表示差异。
如果我们允许“无限接近数”的概念，那么是的，0.999……可以小于1。

数学可以是关于质疑假设、突破界限和思考“如果……会怎么样？”。让我们潜入水中。

无穷小数存在吗？

0.999的含义……是一个复杂的概念，取决于我们允许数字是什么。这里有一个例子：“3-4”对你有什么意义吗？

当然，它是-1。杜。但问题很简单，因为你已经接受了否定的先进思想：你可以接受数字少于零在18世纪，当底片是全新的时候，如果允许的话，“3-4”的概念会引起极大的怀疑。（时间天才在你超越无穷大后会认为消极因素“缠绕”在你周围。）

如今，无穷小的数字面临着类似的困境：它们是新的，挑战了一些长期以来的假设，被认为是“非标准的”。

那么，无穷小存在吗？

那么，负数存在吗？如果你允许使用否定词，并且有一致的使用规则，那么否定词就存在。

我们当前的数字系统假定阿基米德性质：如果一个数字比其他数字都小，那么它必须是零。更简单地说，无穷小的数字不存在.

这个想法应该是有道理的：数字应该是零或者不是零，对吗？好吧，这是“真的”，就像数字必须存在（正）或不存在（零）一样——这是真的，因为我们已经隐式地排除了其他可能性。

但是，这没关系，让我们看看阿基米德性质将把我们带到哪里。

传统方法：0.999…=1

如果我们假设无穷小数不存在，我们可以证明0.999…=1。

首先，我们需要弄清楚0.999…意味着什么。大多数数学家都是这样看待这个问题的：

0.999…代表一系列数字：0.9、0.99、0.999、0.9999，依此类推
问题是：这个系列得到了吗如此接近（收敛）到一个我们无法区分的结果？

这就是背后的原因限制：我们要检查的东西这么近啊到了另一个无论我们多么努力都无法区分的数字？

“好吧，”你说，“你是如何区分数字的？”。问得好。最简单的比较方法是减去：

如果a–b=0，它们是相同的
如果a–b不为零，则它们不同

极限背后的想法是找到“a–b”变为零（小于任何数字）的点；也就是说，我们不能说“要测试的数字”和“结果”不同。

误差容限

当项目采取如此不同的形式（如无限系列）时，仍然很难进行比较。限制背后的下一个聪明想法：定义误差容限:

你给我你对误差/准确度的容忍度（称之为“e”）
我会看看我是否能让这两件事都在允许范围内
如果是这样，他们是平等的！如果我们不能把它们区分开来，无论我们多么努力，它们一定是一样的。

假设我卖给你一块葡萄干燕麦卷，声称是100克。你把它带回家，检查一下未经FDA批准的包装纸，看看我是否在撒谎。你把零食放在秤上，它显示100克。刻度精确到1克。我骗过你了吗？

你不知道：据你所知，在你的准确度范围内，格兰诺拉麦片棒确实是100克。我们目前的问题是类似的：我卖给你一块1克重的“格兰诺拉麦片棒”，但鬼鬼祟祟的是，我实际上给了你一块0.999…克重的。你能说出区别吗？

好吧，让我们解决这个问题。假设您的误差容限为0.1克。那么如果你要求1，我给你0.99，差异是0.01（百分之一），你不知道自己被欺骗了！1和.99在你看来是一样的。

但这是孩子的游戏。比方说你的体重秤精确到1e-9（0.00000001，十亿分之一克）。那么，我会卖给你一个糖块，是999999999999（只有一个第一兆然后你会再次被愚弄！哈！

事实上，与其选择0.01这样的特定公差，不如使用一个通用公差（e）：

误差容限：e
差异：假设e有“n”个精度数字。让0.999…展开，直到我们有一个需要n+1要检测的精度位数。
因此，公差始终可以小于e！差异似乎为零。

看到窍门了吗？以下是一种直观的表达方式：

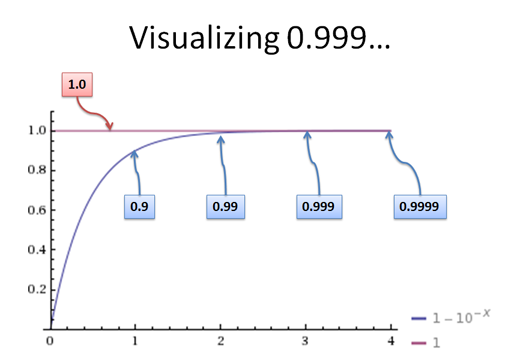
直线正是你所期望的：1.0，完美的格兰诺拉麦片棒。曲线是我们将0.999…扩展到的位数。想法是扩展0.999…，直到它落在“e”内，即您的公差：

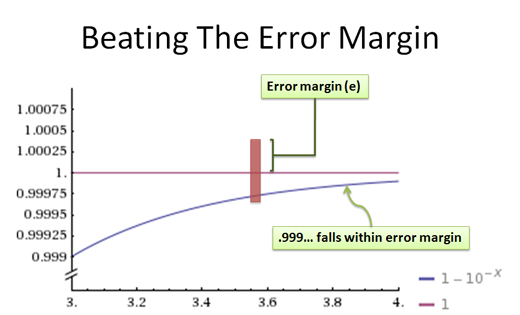
在某种程度上，不管你选什么，0.999……将足够接近以满足我们的数学要求。

（顺便说一下，0.999……不是生长过程，这本身就是一个最终结果。曲线代表了这样一种想法，即我们可以以越来越高的精度逼近0.999……这是另一篇文章的素材）。

有限制，如果两件事之间的差异小于我们能想象到的任何差距，那么它们一定是相同的。

假设无穷小存在

这个第一个结论可能不会让你满意——你可能会觉得被欺骗了。没关系！当我们说0.999…等于1时，我们似乎忽略了一些重要的东西，因为我们以我们有限的精度，无法区分差异。

新的数字系统发展了无穷小存在的思想。明确地：

无限小的数字可以存在：它们不是零，但在我们看来像零。

这似乎是一个令人困惑的想法，但我是这样看的：原子对穴居人来说是不存在的。一旦他们把岩石切割成沙粒，他们就无法再继续了：这是他们能想象的最小单位。事物要么是谷物，要么不存在。他们不能想象原子对于肉眼来说太小的概念。

与其他数字系统相比，我们是穴居人。我们所说的“微小数字”实际上是巨大的。事实上，可能还有另一个“维度”的数字太小，我们无法检测到，即不同的数字只有在这个微小的维度上，我们看起来是一样的，但在一个无限强大的显微镜下却是不同的。

我对0.999的解释是这样的：在这个新的、无限小的维度上，我们能让一个数字小于1吗？

超实数

超实数是一种使用这个“微小维度”来检验无限小数字的系统。在这里，无穷小通常被称为“h”，并被认为是1/h（其中大h是无穷大）。

所以，想法是：

0.999…<1[我们假设允许它更小，并且存在无穷小的数字]
0.999…+h=1[h是构成间隙的无穷小数值]
0.999…=1–h[等价地，我们可以从1中减去无穷小量]

所以，0.999……只是一个微小的位小于1，差值为h！

回到我们的数字

问题是，“h”在我们的宏观世界中并不存在。或者更确切地说，在我们看来，h和零是一样的——我们不能断定它是一个很小的原子，而不是完全缺少任何物质。这里有一种可视化方法：

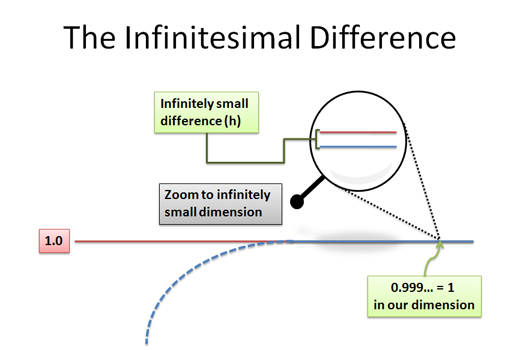
当我们切换回我们的世界时，它被称为取数字的“标准部分”。这实际上意味着我们扔掉所有的h，并将它们转换为零。所以，

0.999…=1–h[存在无穷小的差异]
St（0.999…）=St（1–h）=St（1）–St（h）=1–0=1[对我们来说，0.999…=1]

令人满意的折衷是：更精确的尺寸、0.999…和1不同。但是，当我们以有限的精确度试图描述差异时，我们无法做到：0.999……和1看起来完全相同。

吸取的教训

让我们跳回到我们的世界。“0.999…等于1吗？”的目的是不反驳一个极限问题的答案。这就是将查询解释为“嘿，在我们的系统内0.999…代表什么？”

问题是关于探索。这真的是，“嘿，我想知道数字之间无限接近（.999…和1）。我们如何处理它们？”

我的回答是：

我们对数字的概念经过数千年的发展，包括了新的概念（整数、小数、有理数、实数、负数、虚数……）。
在我们目前的制度中，我们不允许无限小的数字。因此，0.999…=1，因为我们不允许它们之间存在间隙（因此它们必须相同）。
在其他数字系统中（如超实数)，0.999…小于1。这里，允许存在无穷小的数字，这个微小的差异（h）就是0.999……与1的区别。

这里有人生的教训：我们能扩展我们对世界的思维模式吗？否定给了我们这样一个概念：每个数字都可以有相反的数字。你知道吗？事实证明，物质也可能有相反的一面（物质和反物质接触时会相互湮灭，就像3+（-3）=0一样）。

让我们想想无穷小，一个超出我们精度的微小维度：

一些物理理论参考了嵌入到我们自身的微小“卷曲”维度。与我们自己的维度相比，这些维度可能是无限小的——我们从未注意到它们。对我来说，“无限小的维度”是一种描述存在但我们无法检测到的事物的方式。
物理科学使用“有效数字”和误差幅度来说明我们计算的固有误差。我们知道这个现实与我们实际测量的不同：无穷小有助于明确这种区别。
制作模型：无限小的尺寸可以帮助我们创造简单但准确的模型解决世界上的问题。“简单但足够准确”的理念是微积分.

数学不仅仅是解方程。用奇怪的新想法扩展我们的视角有助于不同主题的点击。不要害怕好奇“如果……会怎么样？”。

附录：严酷在哪里？

在写作时，我喜欢想象一个超级学生，他更关心的是满足（和展示）他的严谨性，而不是教育读者。这个神话般的报应激励我专注于直觉。我真的应该给里格尔先生起个名字。

但是，严谨也有用处：它有助于我们画出铅笔线。我不是数学家，但其他人有写下了细节解释0.999…和1或小于1：

“只要没有指定数字系统，学生们的预感999……可能会无限小地小于1，这可以用数学上严格的方式来证明。”

我的目标是教育、娱乐和传播对数学的兴趣。你能想出一种更显著的方法让非数学专业的学生对分析背后的想法感兴趣吗？限额不会自行营销。