Implementation of binary tree storage mode, traversal deletion and other functions

The storage mode of a binary tree can be continuous (array) or random (linked list).

1、 Continuous stored binary tree

When using the continuous storage mode, for a complete binary tree, the child nodes are numbered 2 * n, 2 * n+1, so you can find a node only by using the subscript. But for ordinary binary trees, in order to find nodes using array subscripts, you need to complete them as a complete binary tree, so you need to add a 5 node with an empty value, which will undoubtedly waste space.

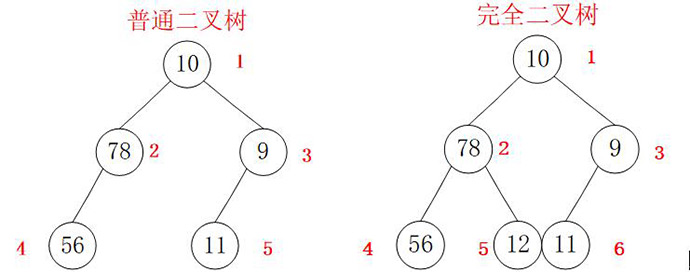
1. Declare a complete binary tree class

This class contains an array to store binary tree nodes.

 class BTreeArray<T> { private T[] bTree; private int count; public BTreeArray(int _number) { count = 0; bTree = new T[_number]; } public bool Add(T _item) { //Storage full if (count >= bTree.Length) { ShowInfo ("storage space is full"); return false; } //Store data bTree[count++] = _item; return true; } private void ShowInfo(string _str) { StringBuilder sb = new StringBuilder(); sb.Append("BTree:"); sb.Append(_str); Console.WriteLine(sb.ToString()); } }

At this time, you can open up a space and store the nodes of the binary tree.

2. Complete binary tree traversal

A Preorder traversal (DLR)

DLR traverses the root node first, then the left node, and finally the right node. Therefore, the traversal order is:

The traversal result should be (10, 78, 56, 12, 9, 11). The idea of writing code is to analyze repeated operations: first access this node, then access the left child node, and finally access the right child node. The operation when accessing the left child node is the same as the previous three steps, so recursion can be used. The codes are as follows:

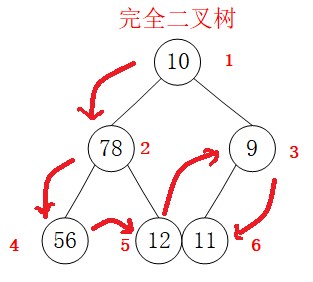
 private void BTreeDLR(int _index) { //Node number is 1 greater than array index int index = _index - 1; //When the index is greater than the total number, the node does not exist if (index >= count) { return; } //Access yourself first Console.WriteLine(bTree[index]); //Access the left child node BTreeDLR(_index * 2); //Access the right child node BTreeDLR(_index * 2 + 1); } public void BTreeDLR() { BTreeDLR(1); }

Test code:

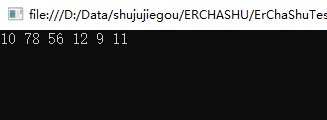
 int[] data = {10,78,9,56,12,11}; BTreeArray<int> bTree = new BTreeArray<int>(data.Length); for (int i = 0; i < data.Length; i++) { bTree.Add(data[i]); } bTree.BTreeDLR(); Console.ReadKey();

Output results:

B Middle order traversal (LDR)

The access sequence is shown as follows:

The traversal result is (56, 78, 12, 10, 11, 9). The idea for LDR to write code is to first access the left child node, then the root node, and finally the right child node, and repeat recursion. Therefore, you only need to change the order of accessing itself, the left child node, and the right child node in the method. The code is as follows:

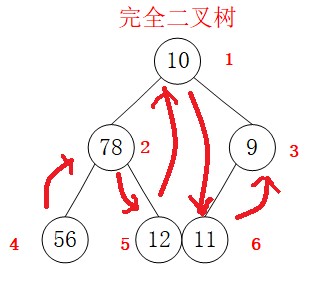
 private void BTreeLDR(int _index) { //Node number is 1 greater than array index int index = _index - 1; //When the index is greater than the total number, it indicates that the end of the road has been reached if (index >= count) { return; } //Access the left child node BTreeLDR(_index * 2); //Access self Console.Write(bTree[index] + " "); //Access the right child node BTreeLDR(_index * 2 + 1); } public void BTreeLDR() { BTreeLDR(1); }

Test code:

 bTree.BTreeLDR();

Operation results:

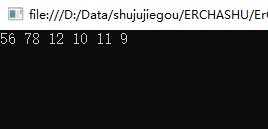
C Post order traversal (LRD)

LRD traversal is the same as above. When writing code, you only need to change the access order.

The traversal result is 56, 12, 78, 11, 9, 10, and the code is as follows:

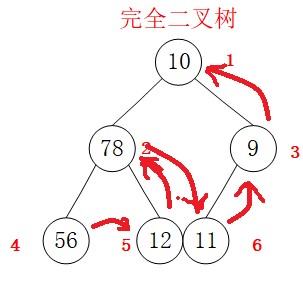
 private void BTreeLRD(int _index) { int index = _index - 1; if (index >= count) { return; } BTreeLRD(_index * 2); BTreeLRD(_index * 2 + 1); Console.Write(bTree[index] + " "); } public void BTreeLRD() { BTreeLRD(1); }

Test code:

 bTree.LRD();

Operation results:

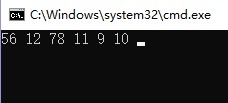
2、 Binary tree stored in linked list

The advantage of using linked list storage is that it does not need to consider whether the binary tree to be stored is a complete binary tree. At the same time, there will be no empty placeholder nodes, which can save some memory. However, we are all familiar with the disadvantages of linked lists. The pointer field of the previous node points to the next node. If the previous node hangs, the whole linked list GG. We look for a node in the array: directly find it through the memory offset represented by the subscript. When searching for a node in the linked list, you can only search by the head node level by level.

A sorted binary tree is a binary tree in which the left child node is smaller than the root node and the right child node is larger than the root node. Here we take a sorted binary tree as an example to implement deletion, addition, modification and traversal respectively.

1. Declare sorting binary tree

It contains a binary tree node class and a binary tree class.

 class BTreeLink    { private BTreeLinkNode<int> headNode; public BTreeLink(BTreeLinkNode<int> _root) { headNode = _root; } } class BTreeLinkNode<T> where T:struct { public BTreeLinkNode<T> Parent { get; set; } public BTreeLinkNode<T> LChild { get; set; } public BTreeLinkNode<T> RChild { get; set; } public T Data { get; set; } public BTreeLinkNode(T _data) { Data = _data; } }

2. Sort Binary Tree Add Node

Because the structure of the sorted binary tree requires sorting when inserting.

 public bool Add(int _data) { Console. WriteLine ("to add"+_data); BTreeLinkNode<int> node = new BTreeLinkNode<int>(_data); if (headNode == null) { headNode = node; return true; } if (node == null) { return false; } BTreeLinkNode<int> temp = headNode; while (true) { if (node.Data <= temp.Data) { Console. WriteLine ("Check, the added value is less than"+temp. Data); //Less than, placed at the left node if (temp.LChild == null) { Console. WriteLine ("The current node has no left child node"); //Left node is empty temp.LChild = node; node.Parent = temp; break; }else { temp = temp.LChild; } } else if (node.Data > temp.Data) { Console. WriteLine ("Check, the added value is greater than"+temp. Data); if (temp.RChild == null) { Console. WriteLine ("The current node has no right child node"); //The right node is empty temp.RChild = node; node.Parent = temp; break; }else { temp = temp.RChild; } } } return true; }

The running result is omitted.

3. Sort the binary tree to find the node

 public BTreeLinkNode<int> Find(int _data) { BTreeLinkNode<int> temp = headNode; while (true) { if (temp == null) { //Not found return null; } if (temp.Data == _data) { //Find return temp; } if (_data > temp.Data) { //Find Right temp = temp.RChild; }else { //Find Left temp = temp.LChild; } } }

Recursive replacement can also be used for the endless loop of the above search operation.

 public BTreeLinkNode<int> Find(int _data,BTreeLinkNode<int> _node) { if (_node == null) { //Jump out Console. WriteLine ("BTree: no node with the value of"+_data+"was found"); return null; } if (_data == _node.Data) { return _node; } else if (_data < _node.Data) { _node = _node.LChild; }else { _node = _node.RChild; } //Recursion return Find(_data, _node); }

Test code:

 BTreeLinkNode testNode = bTreeLink.Find(19); BTreeLinkNode testNode1 = bTreeLink.Find(15, root); if (testNode != null && testNode1 != null) { Console. WriteLine ("Found"+testNode. Data); Console. WriteLine ("Found"+testNode1. Data); }

Operation results:

4. Sort Binary Tree Delete Node

Because this is a sorted binary tree stored in the linked list, the deletion operation is somewhat troublesome. For example, if node 2 is deleted, its sub nodes 7 and 9 need to be reconnected to the binary tree. Idea: Modify the value of node 2 to the maximum node value (14) in the left child node or the minimum node value (16) in the right child node.

How to find the largest node or the smallest node under a node? This is the advantage of sorting binary trees. The smallest node must be the leftmost leaf node under this node, and the largest node must be the rightmost leaf node under this node. Since the minimum value and maximum value must be on the leaf node in the sorted binary tree, the leaf can be deleted after the assignment is completed.

code:

 public bool Del(int _data) { BTreeLinkNode<int> temp = Find(_data); if (temp == null) { Console. WriteLine ("BTree:: Del: deletion failed, no node with the value of"+_data+"exists); return false; } return Del(temp); } public bool Del(BTreeLinkNode<int> _node) { BTreeLinkNode<int> temp; if (_node.LChild == null && _node.RChild == null) { //Leaf node, delete directly if (_node.Data > _node.Parent.Data) { _node.Parent.RChild = null; } else { _node.Parent.LChild = null; } _node.Parent = null; return true; } else if (_node.LChild != null) { temp = _node.LChild; while (temp.RChild != null) { temp = temp.RChild; } //Find the maximum value on the left and place it at this position _node.Data = temp.Data; Del(temp); } else if (_node.RChild != null) { temp = _node.RChild; while (temp.LChild != null) { temp = temp.LChild; } //Find the minimum value on the right and place it here _node.Data = temp.Data; Del(temp); } return true; }

Test code:

 bTreeLink.Del(20); if (bTreeLink.Find(20) == null) { Console. WriteLine ("20 GG"); }

result:

5. Modify the sorting binary tree node

Find the node and change the value.

6. Sort binary tree traversal

Taking DLR preorder traversal as an example, the code is:

 private void DLR(BTreeLinkNode<int> _node) { if (_node == null) { return; } Console.Write(_node.Data +" "); DLR(_node.LChild); DLR(_node.RChild); } public void DLR() { DLR(headNode); }

Test code:

 bTreeLink.DLR();

Operation results:

summary

Continuous storage is fast to read and easy to modify, but it wastes storage space and inserts and deletes GG. Linked list storage is slow to read and needs to look down from the beginning node, and one node damages the data GG behind, but it is convenient to insert and delete, which saves more storage space.

References

1. [Head picture] [HC360] Taotaole Department Store, Taoyuan Town, Rugao City Christmas and New Year Happy Wall Sticker Wholesale