What is a pyramid
Geometry, cone It is one of the four triangles, also called tetrahedron. Its four faces (one is called the bottom, the other is called the side) are all triangles. The polygon on the plane has at least three sides, and the geometry in space has at least four faces, so the tetrahedron is the simplest geometry in space. Tetrahedron is also called triangular pyramid. There are six triangular pyramids Arris length , four vertices, four faces. The base is an equilateral triangle, and the vertex is on the base Projective projection The triangular pyramid at the center of the triangle at the bottom is called Regular pyramid ； And four Congruent The tetrahedron composed of equilateral triangles is called Regular tetrahedron 。 [1] A pyramid is a simple polyhedron. It refers to the closed polyhedron cut out in space by four planes that intersect and are not collinear. It has four faces, four vertices, six edges, four trihedral angles, six dihedral angles and twelve face angles. If the four vertices are A, B, C, D., it can be recorded as tetrahedron ABCD. When it is regarded as a triangular pyramid with A as the vertex, it can also be recorded as triangular pyramid A-BCD. Each vertex of a tetrahedron has a unique face that does not pass through it, which is called the opposite of the vertex, and the original vertex is called the opposite vertex of the face. Of the six edges of a tetrahedron, the two that have no common endpoint are called opposite edges. The tetrahedron has three pairs of opposite edges. And the line segments (three lines) connected by the midpoint of the opposite edge are equally divided at the same point, that is, the center of gravity of the tetrahedron, also known as the centroid of the tetrahedron. The four vertices of the tetrahedron must intersect the line (four line segments) connecting the center of gravity of the opposite (triangle) at the same point, that is, the center of gravity of the tetrahedron. If the centroids with the same weight are placed at the four vertices of the tetrahedron, the centroids of the particle system are located at the center of gravity of the tetrahedron. Or when a tetrahedron is composed of homogeneous matter, its center of mass is at the center of gravity of the tetrahedron. The center of gravity of the tetrahedron bisects the midpoint line of each pair of edges of the tetrahedron. The line segment connecting the vertex of the tetrahedron and the opposite center of gravity is divided into 3:1 (measured from the vertex) by the center of gravity of the tetrahedron. Make a pair of parallel planes through each pair of edges of the tetrahedron, and these three pairs of parallel planes form a Parallelepiped Is the external parallelepiped of the original tetrahedron, and the edges of the tetrahedron are the faces of the external parallelepiped（ parallelogram ）The center of gravity of the tetrahedron bisects each diagonal of its external parallelepiped. In addition to the center of gravity, the tetrahedron has the following properties: 1. Each edge of the tetrahedron and the midpoint of its opposite edge determine a plane, and such six planes share the same point.
2. The edges of the tetrahedron connected to the parallelepiped are parallel and equal to the line segments connecting the midpoints of the pairs of edges in the tetrahedron.
3. The six vertical planes of the six edges of the tetrahedron are at the same point, which is the center of the tetrahedron's outer catch. Each tetrahedron has a unique outer catch.
give an example
The bow and arrow heads, three edged scrapers, and actually all the corners cut from cuboid objects are triangular pyramids.
Correlation calculation
h Is the base height (normal length), A Is the bottom area, V Is the volume, L is the slope height, C is the perimeter of the pyramid bottom, with: [2]
The side unfolded view of a triangular pyramid is composed of four triangles. The area of the unfolded view is the side area of the pyramid S i , i =1,2 is the area of the ith side)
S whole =S Pyramidal side +S bottom
S Regular pyramid =1/2CL+S bottom
V=S (bottom area) · H (height) ÷ 3
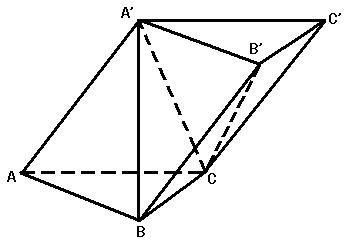Three equal volume triangular pyramids in a triangular prism The volume of a triangular pyramid is obtained by multiplying the bottom area S of the triangular pyramid by the area 0 of vertex A 'divided by the average area of 2 1/2S and the height h:
V=1/2（S+0）h=1/2Sh
S area triangle AC times h 'divided by 2
Example
This is a general triangular prism ABC-A'B'C ', whose volume can be divided into three equal volume triangular pyramids, namely, triangular pyramid C-A'AB, triangular pyramid C-A'B'B, triangular pyramid A' - CB'C '.
Since the side A 'ABB' of the triangular prism is a parallelogram, the area of △ A'AB=the area of △ A'BB ', that is, the bottom areas of the triangular pyramid C-A'AB and the triangular pyramid C-A'B'B are equal, and their two vertices are C, that is, the distance from C to their bottom is equal, so the volume of the triangular pyramid C-A'AB and the triangular pyramid C-A'B'B is equal. The triangular pyramid C-A'B'B can also be regarded as a triangular pyramid A '- BCB', and three edges, etc.), and their two vertices are A ', that is, the distance from A' to their bottom is equal, so the volume of triangular pyramid A '- CB'C' is equal to that of triangular pyramid A '- BCB', so the volume of triangular pyramid C-A'AB, triangular pyramid C-A'B'B, triangular pyramid A '- CB'C' is equal.
Volume formula
Theorem 1: If the length of two opposite edges of a tetrahedron is a and b respectively, their distance is d, and the angle formed is θ, then its volume is 。 Theorem 2: If all sides of a tetrahedron are congruent triangles with side lengths of a, b, and c , then its volume is 。 [5] Inscribed spherical center
The center of the inscribed sphere of the regular pyramid is 1/4 from the bottom of the line between the vertex and the center of gravity of the bottom.
Related calculation: because Regular pyramid The bottom is an equilateral triangle, so the high line is located on the line between any vertex and the midpoint of the bottom Three wires in one , so the center of gravity is located at 2/3 of the height line from the vertex, which can calculate the distance between the vertex and the center of gravity, and also know the side length of the pyramid, which can be based on Pythagorean theorem Calculate the length of the line where the center of the circle is located (that is, the line connecting the vertex and the center of gravity of the bottom surface), and then calculate the distance between the bottom surface and the center of the sphere (that is Inscribed ball Radius). [3] The projection of the inscribed spherical center of a general triangular pyramid on the four faces coincides with the center of gravity of the four faces, according to which the position of the spherical center can be determined.
Externally connected ball center
The circumscribed spherical center of the regular pyramid is 1/4 from the bottom at the line between the vertex and the bottom center of gravity.
Related calculation: calculate the length of the straight line where the center of the circle is located (that is, the line connecting the center of gravity of the vertex and the bottom surface) as the calculation of the inscribed center of the sphere, and then calculate the distance between the vertex and the center of the sphere (that is, the radius of the circumscribed sphere).
The projection of the circumscribed spherical center of a general triangular pyramid on the four faces coincides with the circumscribed center of the four faces, according to which the position of the spherical center can be determined.
Fig. 1 Pyramid Where R is the radius of the outer ball, a, A and B are as shown in Figure 1, It is the dihedral angle of A and B. If the dihedral angle is 90 °, that is, when the two sides are vertical, the formula is simplified as Spherical center tangent to edge
The spherical center tangent to the edge of the regular pyramid is 1/4 away from the bottom at the line between the vertex and the bottom center of gravity (the three centers of the regular pyramid coincide)
The projection of the spherical center of a general triangular pyramid tangent to all four edges on the four faces coincides with the center of the four faces, and thus the position of the spherical center can be determined.
The Vertex Projection of a Pyramid and the "Center" of a Bottom Triangle
With triangular pyramid P-ABC, P on plane ABC Projective projection It is O, when the triangular pyramid meets what conditions, O is the outer center, inner center, side center, center of gravity and perpendicular center of △ ABC（ Triangle five centers ）。 [4] Exocentric
If O is the outer center of △ ABC, OA=OB=OC. Since OP ∨ plane ABC (definition of projection) OP⊥OB、OP⊥OC。 Pythagorean theorem PA=PB=PC. And tanPAO=OP/OA, tanPBO=OP/OB，tanPCO=OP/OC， It can be seen that ∠ PAO=∠ PBO=∠ PCO. In conclusion, the following theorems can be obtained:
- one
When the three sides of the pyramid are equal, the projection of the vertex on the bottom is the outer center of the bottom triangle.
- two
When the angles between the three sides of the pyramid and the bottom are equal, the projection of the vertex on the bottom is the outer center of the bottom triangle. [4]
heart
If O is the heart of △ ABC, then the distance between O and the three sides is equal, and O is within △ ABC. If the vertical segments from O to BC, AC and AB are OD, OE and OF respectively, then OD=OE=OF. According to Pythagorean theorem, PD=PE=PF. TanPDO=OP/OD, tanPEO=OP/OE，tanPFO=OP/OF， Therefore ∠ PDO=∠ PEO=∠ PFO. And by Three perpendicular theorem It can be seen that PD ∨ BC PE⊥AC、PF⊥AB， That is, ∠ PDO, ∠ PEO and ∠ PFO are plane angles of dihedral angles P-BC-A, P-AC-B and P-AB-C respectively. In conclusion, the following theorems can be obtained:
- one
When the distance between the vertices of the pyramid and the three sides of the base triangle is equal, and the projection of the vertex on the base is inside the base triangle, then the projection is the heart.
- two
When the dihedral angles formed by each side of the pyramid and the bottom are equal, and the projection of the vertex on the bottom is inside the bottom triangle, then the projection is the heart.
Bystander
Since the nature of the side center and the heart are the same, they are all points with equal distance to the three sides of the triangle. But the heart is inside the triangle and the side is outside. So the thinking of the discussion is the same as that of the heart, and the difference lies in the positional relationship between O and △ ABC. Therefore, the following theorem is directly obtained:
- one
When the distance between the vertex of the pyramid and the three sides of the base triangle is equal, and the projection of the vertex on the base is outside the base triangle, then the projection is circumscribed.
- two
When the dihedral angles formed by each side of the pyramid and the bottom are equal, and the projection of the vertex on the bottom is outside the bottom triangle, the projection is the side center.
orthocenter
If O is the perpendicularity of △ ABC, there is OA ∨ BC, OB⊥AC，OC⊥AB。 And because O is the projection of P, we can know PA ∨ BC from the three perpendicular theorem, PB⊥AC，PC⊥AB。 From the perspective of promotion, PA ∨ BC can be associated with PA ∨ plane PBC, and according to Line face vertical According to the decision theorem of, the condition of PA ∨ plane PBC is PA ∨ PB, PA ∨ PC. Similarly, PB⊥PA，PB⊥PC；PC⊥PA，PC⊥PB。 That is, PA, PB and PC are vertical. [4] In conclusion, the following theorems can be obtained:
- one
When the three sides of the pyramid are perpendicular (or each side is perpendicular to the opposite side), the projection of the vertex on the bottom is the perpendicular center of the bottom triangle.
- two
When two side edges of a triangular pyramid are perpendicular to the corresponding opposite side, the third group of side edges are also perpendicular to the opposite side, and the projection of the vertex on the bottom is the perpendicular center of the bottom triangle.
focus
Theorem:
- one
When the sum of three times the square of any side edge and the square of its opposite edge of a pyramid is a fixed value, the projection of the apex of the pyramid on the bottom surface is the center of gravity of the bottom surface.
