人性化多计算过程
多重计算是Wolfram物理项目-尤其是我们的核心对量子力学的新理解但如何才能对最初相当抽象的事物获得直觉多计算思想? 我认为,一个好的方法是在熟悉的系统和情况下看到它的作用。我在这里探索一个似乎特别好的例子:游戏和谜题。
人们可能无法想象,像众所周知的游戏和谜题这样的日常活动会与量子力学之类的形式主义有任何联系。但多计算的思想提供了一个链接。事实上,人们可以将“有趣”的游戏和谜题视为与多计算的核心现象有关:多重计算不可约性。
在普通的计算系统中,系统的每个状态都有一个唯一的后继状态,并且最终有一个时间线程来定义计算过程。但在多计算系统中,关键思想是状态可以有多个后继,跟踪它们的行为定义了时间分支和合并线程的整个多路图。关键是,这与人们如何思考典型的游戏和谜题直接相关。
给定游戏或谜题的特定状态,玩家通常必须决定下一步要做什么。多计算的概念来源于他们通常可以做出几个选择。在游戏的任何特定情况下,他们都会做出特定的选择。但是,多计算范式的重点是全局地看待所有可能选择的结果,并生成一个多路图代表他们的。
制作我们称之为多路图的概念实际上已经存在——通常以“游戏图”的名义——用于游戏和谜题一百多年了但随着多计算范式的出现,现在有一些更通用的概念可以应用于这些结构。反过来,理解游戏和谜题之间的关系,有可能提供对多路图的新的直觉和熟悉程度。
我在这里的特别目标是使用我们为研究多计算系统开发的通用方法,系统地研究一系列著名的游戏和谜题。在与日常事物相关的调查中,我们会遇到各种具体细节。虽然这些可能不会立即与大规模讨论相关,但对于我们努力提供真实、相关的实际游戏和谜题图片以及让我们与多计算的联系建立在坚实的基础上来说,它们是很重要的。
值得一提的是,如果没有我们的物理项目,将游戏和谜题与物理联系起来的可能性基本上是没有意义的。因为游戏和谜题通常在一些基本层面上是离散的,特别是在涉及可能性的离散分支的方式上。如果假设物理学基本上是连续的,那么就没有理由期望两者之间存在联系。但我们物理项目的一个关键理念是,物理世界处于最低水平,就像游戏和谜题一样是离散的。更重要的是,我们的物理项目假设,像游戏和谜题这样的物理有着离散的探索可能性。
一开始,我在这里讨论的每一个游戏和谜题在结构和操作上可能都有很大不同。但我们将看到,当以多计算的方式来看时,我们的不同示例之间存在显著且几乎单调的一致性。在结束之前,我不会对我们所看到的内容的重要性发表太多评论,届时我将开始讨论各种重要的多计算现象如何在游戏和谜题的背景下发挥作用。用简单易懂的人类术语来概念化多计算是多么困难,这从根本上导致了游戏和谜题的迷人特性。
Tic-Tac-Toe公司
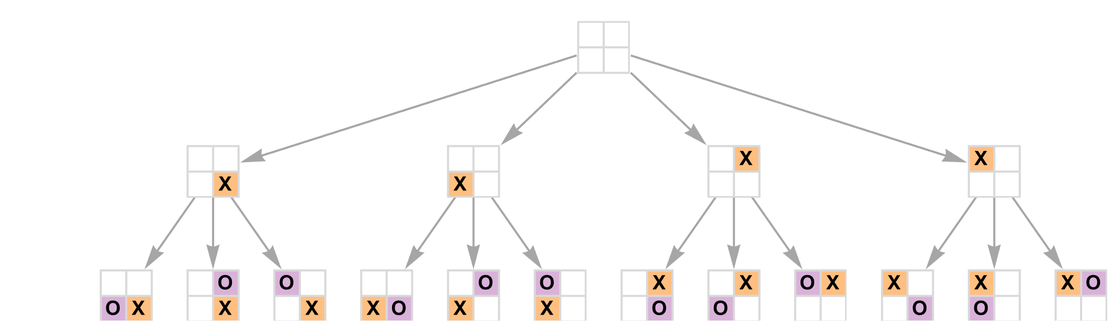
考虑一个简化版本的tic-tac-toe(AKA“noughts and cross”),在2×2的板上玩。假设X先播放。然后可以表示图中可能的移动:
在下一个转弯处,你会得到:
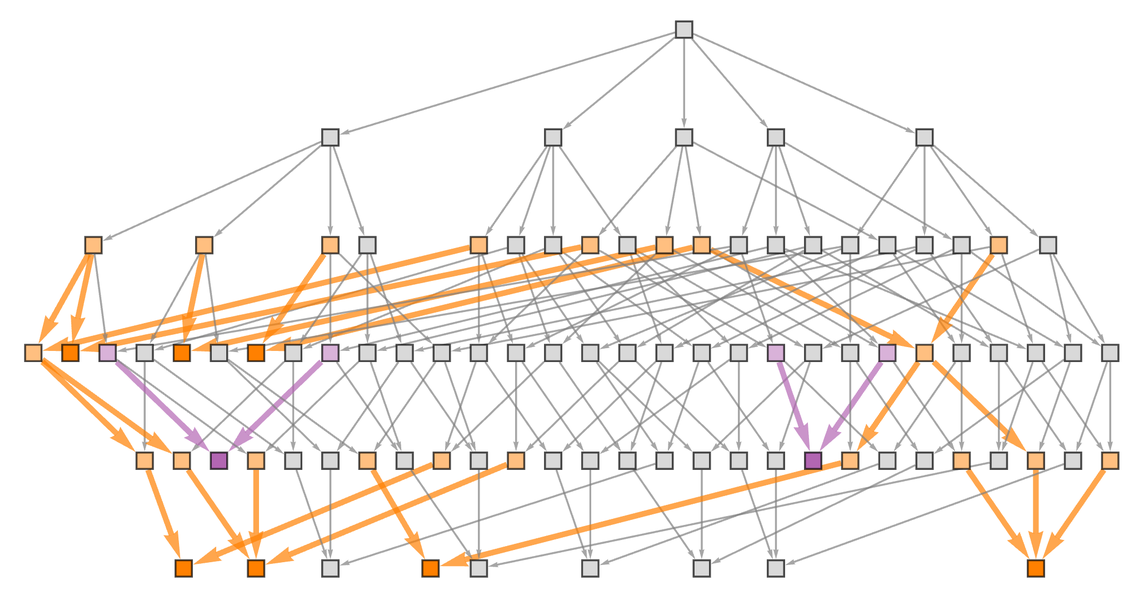
到目前为止,这个图是一个简单的树。但如果我们再进行一次回合,我们将看到不同的分支可以合并,并且“一直玩到棋盘满为止”,我们会得到一个多向图或“游戏图”,其形式如下:
通过此图的每条路径代表一个可能的完整游戏:
在我们目前的设置中,任何游戏中都可以达到的板配置总数(即图中节点的总数)是35,而可能完成的游戏总数(即从图的根开始的可能路径数)是24。
如果用3D渲染图形,可以看到它具有非常规则的结构:
现在,如果我们将“取胜”2×2 tic-tac-toe定义为在水平行中有两个相同的元素,那么我们可以对多路图进行注释,以指示“游戏已经结束”的取胜情况:
多向图的许多核心结构实际上已经很明显了,即使是在“单人tic-tac-toe”这种看似微不足道的情况下,其中一个人只是在逐步填充棋盘上的方块:
但是,使这一点不完全微不足道的是,存在导致等效状态的不同路径。以不同方式渲染图形(其中有2个4=16个节点和4个!=24“游戏路径”)具有明显的4D超立方体形式(现在我们在每个单元格中删除了显式X):
对于3×3板,图是具有2的9D超立方体9=512个节点和9个!=362880“游戏路径”,或“移动分层”形式:
这种基本结构已经在“1人1D tic-tac-toe”中可见,其中“长度”的多路图-n个“板只对应于n个-多维超立方体:
在这种情况下,不同的板配置总数只有2个n个,不同“游戏”的数量为n个!. 移动时吨不同板配置(即状态)的数量为二项式【n,t】。
如果有两名球员,图表会变得稍微复杂一些:
这个州总数在这些图中是
它是渐近的 (请注意,对于n个=4,结果与上面讨论的2×2板相同。)移动时吨不同状态的数量由下式给出
(请注意,对于n个=4,结果与上面讨论的2×2板相同。)移动时吨不同状态的数量由下式给出
好的,那么标准的2人3×3 tic-tac-toe怎么样?它的多路图开始于:
经过两步(即一步按X移动,一步按O移动),图形仍然是一棵树(初始状态现在位于中心):
三步之后,开始合并:
对于所有9个动作,6046个状态的完整分层图是:
在这个图的层次上,结果与总共有9个方块的2人1D版本完全相同。但对于实际的2D 3×3 tic-tac-to,故事中还有一个额外的元素:赢得游戏的概念,从而终止游戏。按照通常的规则,当玩家获得三个正方形的水平、垂直或对角线时,就认为游戏获胜,例如:
每当达到这样的“获胜状态”时,游戏就被认为结束了,因此多路图中的后续状态被修剪,而之前的6046节点图变成了5478节点图
以568个被删减的州为例,其中包括(终止游戏的“胜利”被标记):
胜利可能发生在不同的步骤:从5到9。不同胜利的总数如下
(对于X,在任何步骤中产生626个胜利,对于O,产生316个胜利)。
在每个方块都填满之前,人们无法明确地判断游戏是否以平局告终,最终只能达到16个最终“平局配置”:
我们可以注释完整的(“game-over-pruned”)多路图,指示赢和抽状态:
为了进一步研究这一点,让我们从一个子图开始,该子图只包含“结束游戏”,从已经填充了4个方块的棋盘开始:
我们在这里看到,从我们最初的董事会
X和O都有可能获得最终胜利:
但在许多情况下,结果基本上是在实际获胜之前一步或更长时间内确定的,即除非某个特定的玩家“犯了错误”,否则他们总是能够取得胜利。
例如,如果轮到X,状态为
那么如果他们按照以下方式比赛,X肯定会赢:
我们可以通过给多向图中的子图(或实际上的“光锥”)着色来表示胜利的“预强制”:
在游戏开始的时候,当X第一次移动时,还没有任何强迫。但只需一步,就有可能实现X总是能够取得胜利的配置:
从一个步骤后获得的状态开始,我们可以看到,在两个步骤后,存在O可以强制获胜的配置:
采取更多行动将导致更多的“强制赢”配置:
注释我们得到的整个多路图:
我们可以将此图视为游戏“解决方案”的表示:给定任何状态,图中的着色都会告诉我们哪些玩家可以从该状态中获得胜利,而图定义了他们可以采取哪些行动来实现这一点。
以下是每次移动时可能的游戏状态摘要:
在这里,我们只是计算每一步中各种可能状态的数量。但是,有没有一种方法可以认为这些状态以某种方式被布置在“游戏状态空间”中?分支图提供一种潜在的方法来实现这一点。特定步骤的基本鳃图是通过连接前一步骤中共享同一祖先的状态对获得的。对于2人2×2 tic-tac-toe的情况,我们在连续步骤上得到的鳃图如下:
对于普通的3×3井字游戏来说,事情变得更加复杂。但由于前两个步骤的多路图是一棵纯树,因此这些步骤的鳃图仍然具有相当简单的结构:
通常,连续步骤中连接的组件数量如下
这些被分解为不同的图形结构,如下所示:
这里更详细地介绍了在特定步骤中实现的鳃裂图的一些典型组成部分的形式:
在特定步骤的鳃裂图中,不同部分中可能有不同的获胜次数:
值得注意的是,胜利在鳃部图中分布得相当广泛。这就是为什么tic-tac-toe不是(更)微不足道的原因。如果仅仅通过了解一个人的鳃裂图的组成部分就能立即知道结果,那么游戏中的“悬念”就更少了。但随着鳃部空间的广泛分布,“大致知道你在哪里”对决定你是否会赢没有多大帮助。
到目前为止,我们一直在讨论可以到达哪些州,但没有讨论“多久到达一次”。想象一下,我们不是在玩一个特定的游戏,而是在每一步都以相同的概率做出每一个可能的动作。tic-tac-toe的设置是对称的,对于大多数游戏来说,在给定的步骤中每个可能配置的概率都是相等的。但一旦开始出现“胜利”,并且出现“游戏过度渲染”状态的“圆锥体”,那么其余状态的概率就不再相等。
对于标准的3×3 tic-tac-toe,这会在7次移动后发生,其中有两类状态,发生的概率略有不同:
游戏结束时,有几种不同概率的最终状态:
这意味着游戏不同结果的概率如下:
毫不奇怪,先上场的球员在获胜方面有优势。也许更令人惊讶的是,在这种“无策略”游戏中,平局相对来说是不寻常的,尽管如果一方积极阻止另一方,他们往往会迫使平局。
我们已经了解了“经典tic-tac-toe”和一些特定的变体。但最终有各种可能的变体。对于任何tic-tac-to类游戏来说,表示“棋盘”的一种方便的通用方法就是给出一个“扁平”的值列表,其中0表示空白位置我表示玩家添加的符号我。
在标准的“2D表示”中,可能会有一块类似木板的
平面形式为:
然后可以表示典型的获胜模式
其中,在每种情况下,我们都将相关的“获胜符号”框起来,然后给出它们在扁平列表中的位置。在普通的井字游戏中,很明显,“获胜符号”的位置必须始终形成算术级数。似乎推广tic-tac-toe的一个好方法总是定义一个胜利我与我构成一定长度算术级数的位置符号秒.对于普通tic-tac-toe秒=3,但对于泛化,它可以有其他值。
现在考虑长度为5的列表(即5位置“1D板”)。完整的多路图如下所示,其中“获胜状态”包含长度的算术级数秒=3突出显示:
在更对称的渲染中,这是:
以下是7位棋盘和2名玩家的类似结果:
对于每种尺寸的板n个,我们可以计算任何给定玩家的获胜状态总数,以及状态总数。获胜时的结果基于长度为3的算术级数(即。秒=3)为:
双人游戏n个=9(=3×3)的情况与普通井字类似,但不相同。特别是,像这样的州
在扁平化设置中,被认为是X的胜利,但在普通tic-tac-toe中则不然。
如果我们增加了宣布胜利所需的进程长度秒=4,我们得到:
游戏状态的总数没有改变,但正如预期的那样,“取胜的方式越来越少”。
但假设我们有完全填满的棋盘。对于较小的棋盘尺寸,任何球员的位置都可能没有算术级数,因此游戏必须被视为平局n个=5种情况:
但这是一个结果和拉姆齐理论有关那是为了n个≥9分时,至少有一名球员将不可避免地获得“算术级数胜利”,因此,这些例子说明,永远不会出现平局:
游动及其多重图
像tic-tac-toe这样的游戏在每一步都有效地涉及到几种可能的新板配置中的一种,我们可以将其视为“游戏状态空间”中的不同“位置”。但是,如果我们不考虑板的配置,而是将我们的状态视为晶格上的位置,比如
然后我们看看可能的步行,在这种情况下,每一步可以朝四个方向中的任何一个方向走一个单位?
从特定点开始,1步后的多路图就是
在这里,我们布置了这个图,以便“状态”被放置在晶格上的几何位置。
经过两步,我们得到:
通常,多路图的结构只是“重述”了晶格的结构:
我们可以把多路图中的路径看作是表示晶格中一定长度的所有可能的随机游动。我们可以用3D的方式布置图形,垂直位置代表到达给定点的第一步:
我们也可以像为tic-tac-toe设计多路图那样设计图形:
这些“随机遍历”多向图的一个特点是,它们包含循环,记录“返回到已经去过的地方”的可能性。这与tic-tac-toe中发生的情况不同,在tic-tac-toe中,每一步都只是向板中添加一个元素,而且永远不可能返回。
但我们可以通过考虑“自动排空步行“任何已经访问过的点都无法再访问。让我们首先考虑一个非常平凡的晶格:
现在用红点表示“当前我们到达的地方”,用蓝点表示我们以前去过的地方——从一个角开始:
这里只有两种可能的行走方式,一种是顺时针行走,另一种是逆时针行走。允许一个从每个可能的位置开始,会产生一个稍微复杂的多向图:
通过2×3网格,我们得到
而使用3×3网格,我们得到:
从中心开始,使用不同的多路图布局,我们得到:
请注意,存在着大的“洞”,其中每一侧的路径基本上以“相反的方式”“到达相同的位置”。注意,在2304种可能的方法中,有1个红点和最多8个蓝点,这个实际的多路图只有57个。(从角落开始达到75,从所有可能的初始位置开始达到438。)
使用4×4格(从角落里的步行者开始),多路图的形式如下
或在替代布局中
其中,现在最终访问了524288中的1677个状态,每个步骤访问的新状态数(即图中连续层中的节点数)为:
对于5×5电网,达到89961个状态,按以下步骤分布:
(对于带有n个个顶点,共有个n个2n个–1可能的状态,但实际达到的数量总是小得多。)
在谈论步行时,一个显而易见的问题是关于迷宫。考虑迷宫:
就穿越这个迷宫而言,它相当于在图上“行走”
在另一个嵌入中
但和之前一样,表示所有可能行走的多路图基本上只是“重述”该图。这意味着,在某种意义上,“求解”迷宫可以被视为直接在迷宫图或多路图中找到路径:
标志性游戏与一些亲属
我们对自我回避步行的讨论结果与“伊科西亚游戏“威廉·罗文·汉密尔顿(William Rowan Hamilton)于1857年创作的猎狮头象):

“游戏”(或者更确切地说,谜题)的目标是在访问每个节点的二十面体图周围找到一条路径(是的,一条哈密尔顿路径)(并返回到它开始的位置)。我们可以再次构造一个多向图,表示游戏中所有可能的“移动”序列。
让我们从下面一个更简单的四面体图开始:
由此我们得到了多路图:
四面体图上所有可能起始位置的“组合多路图”给出了一个截断立方八面体多路图:
根据这个图,我们可以看到,从任何初始状态都有可能达到四面体图中每个节点都被访问过的状态。事实上,因为四面体图是一个完整的图,它甚至可以保证序列中的最后一个节点将与起始节点“相邻”,这样就形成了一个哈密顿循环并解决了这个难题。
对于立方体图来说,事情不那么简单:
在这种情况下,多路图(从特定状态开始)是:
现在有13种配置,无法进行进一步移动:
在其中一些情况下,用户实际上是“封闭”的,没有可访问的相邻节点。在其他情况下,所有节点都已填充。但只有3个最终实现了真正的哈密顿循环,该循环结束于起始节点附近:
事实证明,从多路图的根开始,可以通过4条不同的路径到达每个状态。此类路径的示例如下:
我们可以将此路径概括为原始立方体图的哈密顿回路:
在多路图中,12条“获胜路径”是
在不同的渲染中,这将变成
并且只保留“获胜路径”,多路图的子图具有对称形式:
通过对应于这些获胜路径的基本立方体图的实际哈密顿电路为:
对于十二面体图(即原始的Icosian游戏),多路图更大、更复杂。它开始了
在11个步骤(总共529个步骤)后进行了第一次合并,最终总共有11093个节点,其中2446个是“结束状态”,无法进一步移动。这显示了每个连续步骤中结束(以下)和非结束(以上)状态的数量:
“在轨成功”状态的连续分数如下所示,这表明在某种意义上,谜题开始时比结束时更难:
有13个“端态”填充了底层十二面体图的每个位置,其中3个对应于哈密顿循环:
从多路图的根到结束状态的路径总数(实际上是试图解决谜题的方法总数)为3120。其中,60个导致3个哈密顿循环结束态。这些“获胜之路”之一的一个例子是:
对应于3个哈密顿循环结束状态中的每一个的潜在哈密顿周期示例如下:
现在,这显示了通过多路图到达哈密顿循环结束状态的所有60条路径,从而对应于谜题的解决方案:
实际上,解决这个难题在于成功地从多路图中的所有可能性中找到这些路径。例如,在实践中,尽管在理论上证明了这一点,但与直接查看多路图中的所有可能性相比,找到“获胜路径”的方法要有效得多(例如。查找哈密顿循环在里面Wolfram语言). 但为了理解多计算框架中的游戏和谜题,了解这个谜题的解决方案在多路图中的布局是很有用的。
汉密尔顿的伊科西安游戏是在图上推出哈密尔顿圈概念的原因。但早在1736年利昂哈德·尤勒讨论了与哥尼斯堡大桥之谜。用现代术语来说,我们可以将谜题称为寻找一条只访问一次且仅访问一次图中所有边的路径的问题(其中原始谜题中的“双桥”已被额外节点消除歧义):
我们可以创建一个表示从特定顶点开始的所有可能路径的多路图:
但现在我们看到这里的结束状态是
由于他们都没有去过每一个边缘,所以这里没有欧拉电路。为了完全解决这个难题,我们需要制作一个多路图,从所有可能的潜在顶点开始。结果是一个断开的多路图,其结束状态再也不会访问底层图中的每一条边(从每个子图中的“级别”数量小于10这一事实可以看出):
地理游戏
在地理游戏中,一个人有一组单词(比如地名),然后尝试“将单词串在一起”,一个单词的最后一个字母与下一个单词中的第一个字母相同。游戏通常在没有人想出一个有效且以前从未使用过的单词时结束。
通常在实践中,游戏由多个玩家进行。但我们完全可以考虑只有一个玩家的版本。作为一个例子,让我们把“单词”作为美国各州的缩写。然后我们可以绘制一个图表,显示以下内容:
首先,让我们忽略一个状态是否“已被使用”的问题。然后,从马萨诸塞州(MA)开始,我们可以构建一个多向图的开头,给出所有可能的序列:
经过10步后,该图为
或在不同的渲染中:
这显示了该图中路径的总数,作为长度的函数,假设不允许任何状态重复:
路径的最大长度为23,有256条这样的路径,88条以TX结束,168条以AZ结束
所有这些路径都可以用有限状态机来表示:
顺便说一句,通向最长路径的起始状态是MN,它以2336种不同的方式达到长度24,可能的结尾是AZ、DE、KY和TX。一些示例如下:
从MN开始,在多路图的前几个步骤中绘制这些路径,我们得到:
组和(简化)魔方
我们已经讨论了有效地涉及在图形上行走的谜题。可以用这种方式思考的一个特别著名的谜题是魔方。所讨论的图就是可应用于立方体的变换所形成的群的Cayley图。
作为一个非常简单的模拟,我们可以考虑正方形的对称群,D类4基于反射和90°旋转操作。我们生成Cayley图就像生成多路图一样:通过在每个步骤应用每个操作。在这个例子中,Cayley图是:
该图足够小,可以直观地看到如何从任何配置转换到任何其他配置。但是,虽然这个Cayley图有8个节点,从一个节点到另一个节点的最大路径长度为3魔方的凯利图有 节点和最大最短路径长度为20。
节点和最大最短路径长度为20。
为了对这样一个物体的结构有一些了解,我们可以考虑一个非常简化的情况,即“2×2×2立方体”——仅在其角部着色——其中每个面都可以旋转90°:
从上述配置开始的多路图形启动的第一步是这样的(请注意,图形中的边是不定向的,因为底层转换总是可逆的):
再走一步可以:
完整的多路图(这也是组的Cayley图,其结果是S公司8-由转换生成)具有8!=40320个节点(和483840个边)。从状态(即Cayley图中的节点)开始,在连续步骤中达到的新状态数为:
图中最大最短路径由8个步骤组成;例如:
在这两个端点之间,实际上有3216条“测地线”路径,在多路图中分布得很远
仅选取测地线路径,我们可以通过多种方式从立方体的一种配置获得其“对极”之一:
Peg纸牌
虽然像tic-tac-toe这样的游戏需要逐步填充棋盘,但至少在17世纪以来使用的一大类谜题基本上都是从棋盘上取下钉子。典型的规则是,木桩能够跳过单个中间木桩进入洞中,然后将中间木桩拆除。目标是最终只在董事会上钉上一个钉子。
下面是一个基于T形桩排列的简单示例:
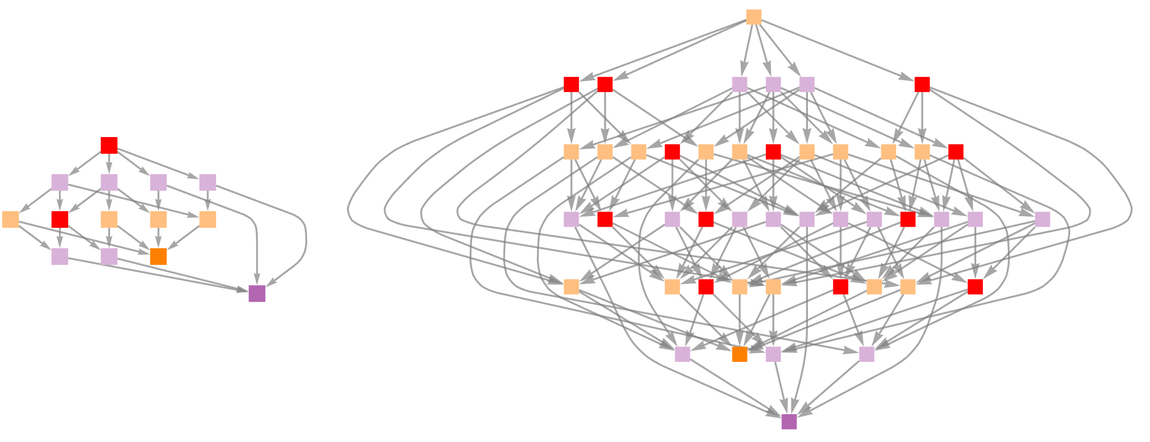
在这种情况下,只有一种方法可以“解决难题”。但总的来说,有一个多向图:
一个更复杂的例子是“Tricky Triangle”(也就是Cracker Barrel拼图”)。其多路图开始于:
再经过几步,它就变成了:
在最终的多路图中,共有3016个状态,其中118个是“无引擎”配置,不可能进一步移动。这些无引擎配置中“最早”的是:
只有4个“获胜州”可以达到,而导致它们的“最终游戏”是:
从初始配置开始,每个步骤中可能达到的状态数如下所示,其中可以导致成功配置的状态以黄色显示:
这显示了完整的多路图,突出显示了“获胜路径”:
在连续的步骤中,可以导致获胜状态的状态的分数如下所示:
鳃部图形高度相连,这意味着在某种意义上,谜题一直“混合”且“不可预测”,直到最后:
方格图案
飞镖单人纸牌是一种单人“游戏”。跳棋(AKA Drawatts)是一款两层游戏,有着类似的设置。“黑色”和“红色”棋子在棋盘上沿对角线方向移动,相邻时通过跳跃来“抓住”对方。
让我们考虑一个相当小的4×4板示例。“黑色”和“红色”的基本移动设置由图表定义(注意,4×4板太小,无法支持“多次跳跃”):
通过此设置,我们可以立即开始生成基于黑色和红色交替移动的多路图:
根据目前定义的规则,完整的161节点多路图为:
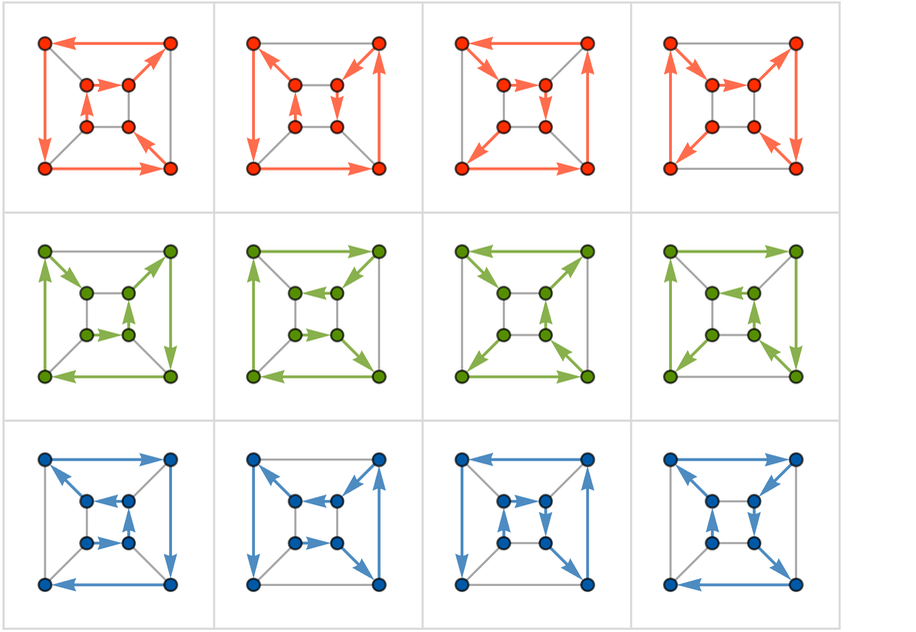
在这个简单的4×4案例中,“赢”意味着什么还不完全清楚。但有一种可能性是,当另一名球员在下一步行动中无法采取任何行动时,就会发生这种情况。这对应于多路图中的“死胡同”。其中有26个,其中只有3个发生在红色的下一个移动时,其余的都发生在黑色的移动时:
如前所述,任何特定的跳棋游戏都对应于多路图中从根到这些结束状态之一的路径。如果我们看一下这种情况下的鳃裂图,我们会发现它们有许多不相连的部分,这表明对于这个简单的游戏来说,有许多基本上独立的“游戏路径”,因此结果没有太多的“混合”:
到目前为止,我们使用的规则并不能说明什么是跳棋的第二级规则:当一块棋子到达棋盘的另一边时,它就变成了一个允许向前和向后移动的“国王”。即使只有一块和一个播放器,现在也已经生成了一个带有循环的多路图形:
或在替代布局中(具有明确的无向边):
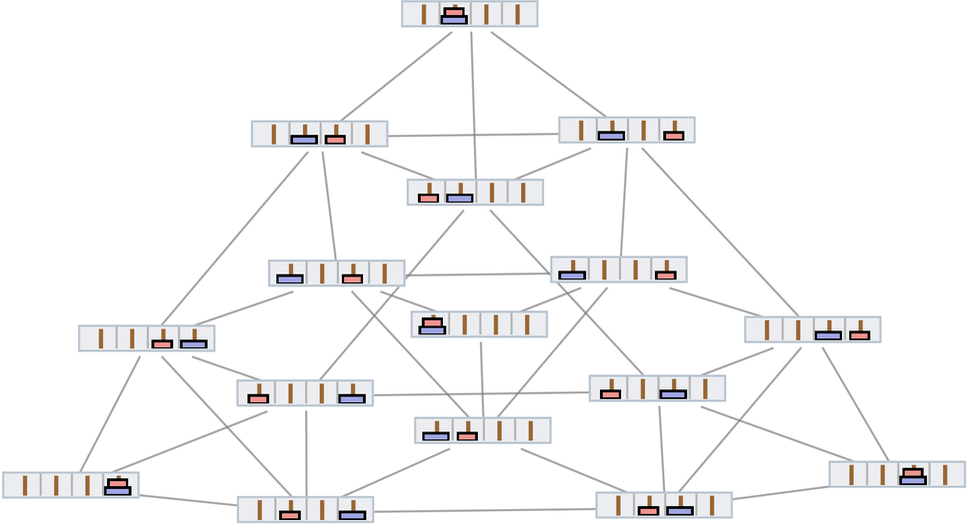
两个棋子(两个玩家轮流)组成“国王”多向图:
有了这个初始配置,但没有反向运动,整个多路图就是:
在这种情况下,完整的“国王”多向图也只有62个节点,但包括各种循环(尽管只有这几个棋子,黑人先下棋,任何胜利都是不可避免的):
从我们最初的初始条件来看,普通的+国王多向图怎么样?组合图有161个来自“预王”阶段的节点,以及4302个来自“后王”阶段,形成最终形式:
(非常简单)开始
围棋的整个游戏都很复杂,在任何现实情况下,它的多向图都太大了,我们根本无法明确生成(尽管人们肯定会怀疑是否存在有意义的“连续极限”结果)。然而,为了获得围棋的一些风味,我们可以考虑一个大大简化的版本,其中黑白“石头”逐步放置在图形的节点上,如果一个玩家成功地包围了另一个玩家的石头的连接集合,则游戏被视为“赢了”。
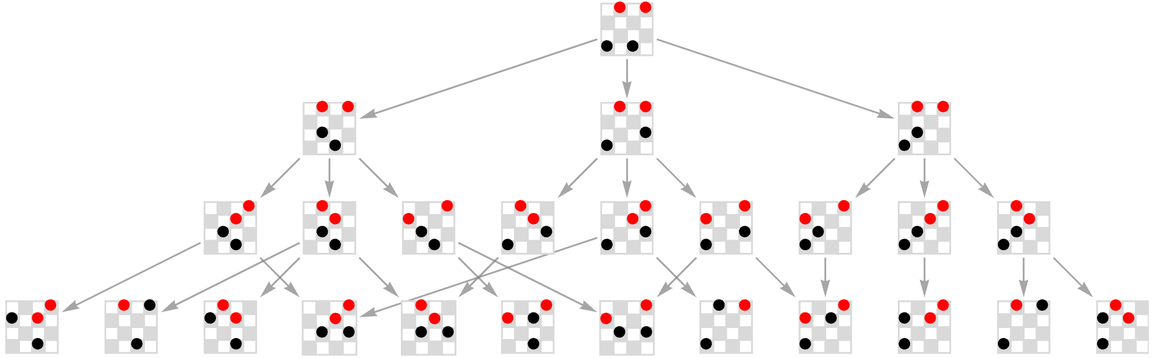
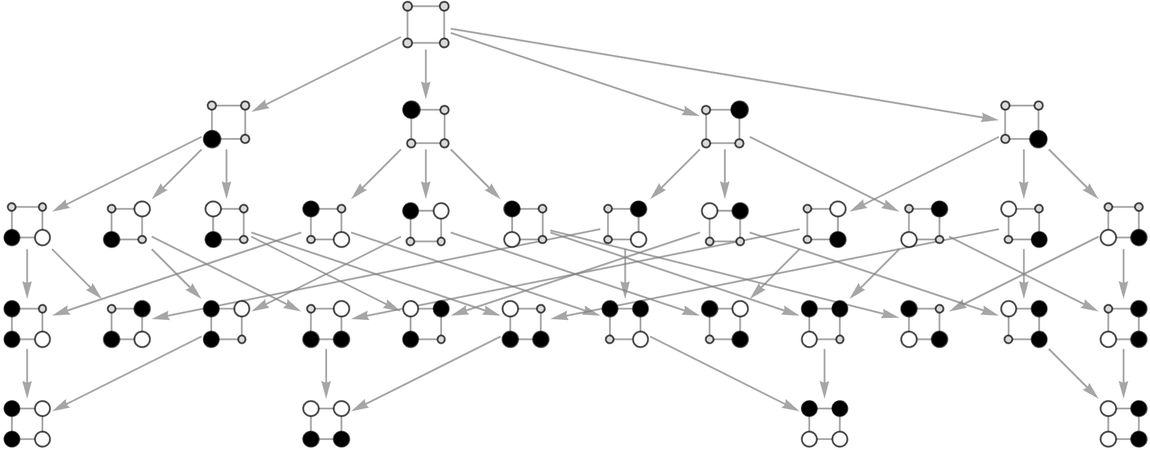
想象一下,我们从一块由2×2个位置组成的空白“板”开始,然后在一系列“旋转”中以所有可能的方式添加黑白石头。生成的多路图为:
每一个没有继任者的州都是黑人或白人的胜利。“黑色胜利”(周围的石头突出显示)是
而“白色胜利”是:
在这个水平上,我们所拥有的基本上等同于2×2 tic-tac-toe,尽管有一个“对角”赢的条件。对于3×2“板”,多路图中的前两个步骤是:
最终的多路图是:
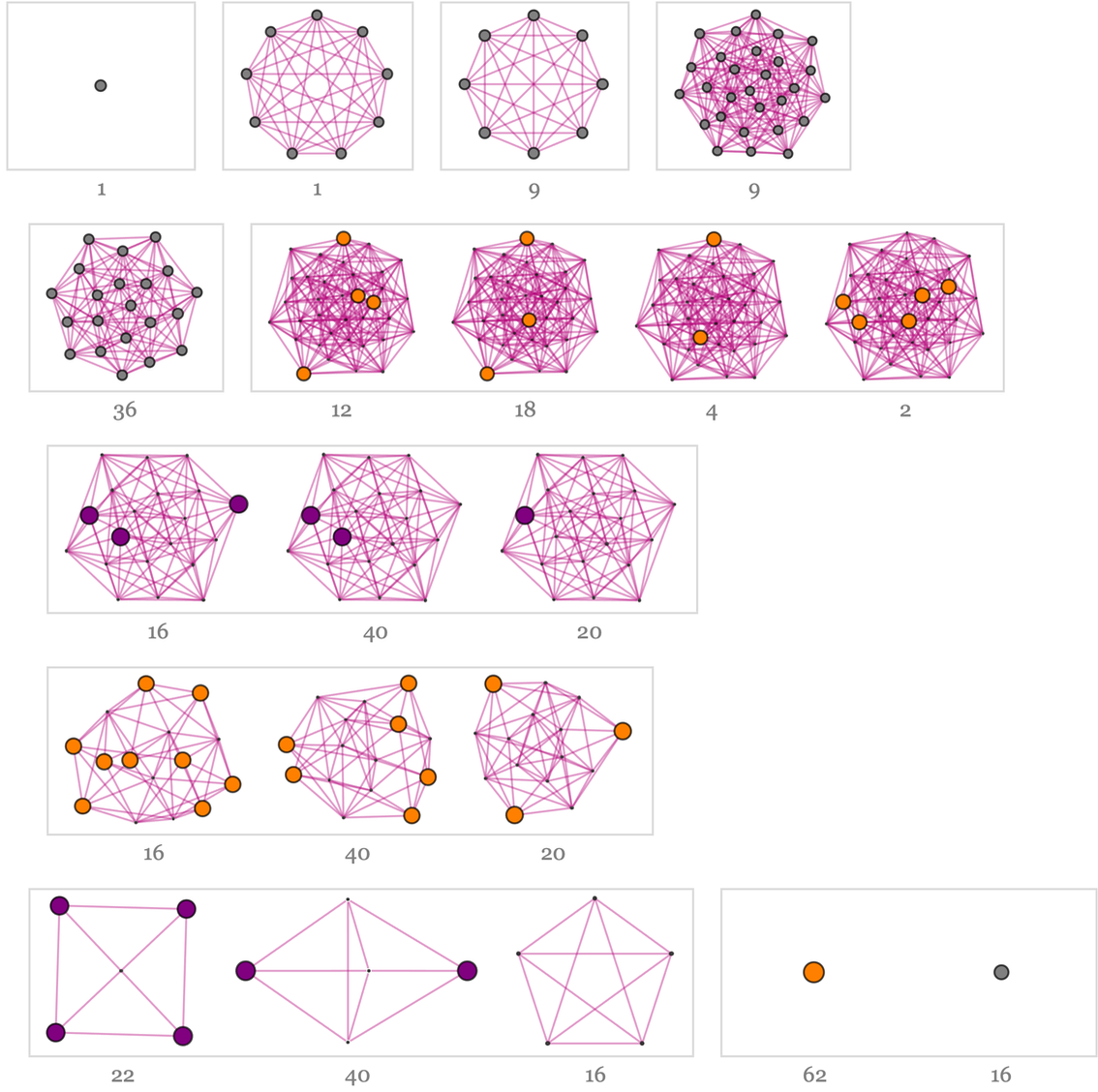
该图有235个节点,其中24个为白色节点,34个为黑色节点:
在这种情况下,连续的鳃裂图是(表示黑白获胜):
对于一个3×3的“棋盘”,多向图有5172个州,其中604个州是白人获胜,684个州则是黑人获胜。
尼姆
作为一个简单游戏的另一个例子,我们现在考虑尼姆。在尼姆,有k个一堆堆物体,每一步第页玩家轮流从他们选择的单堆中取出任意数量的物体。游戏的输家是被迫在所有堆中放置0个物体的玩家。
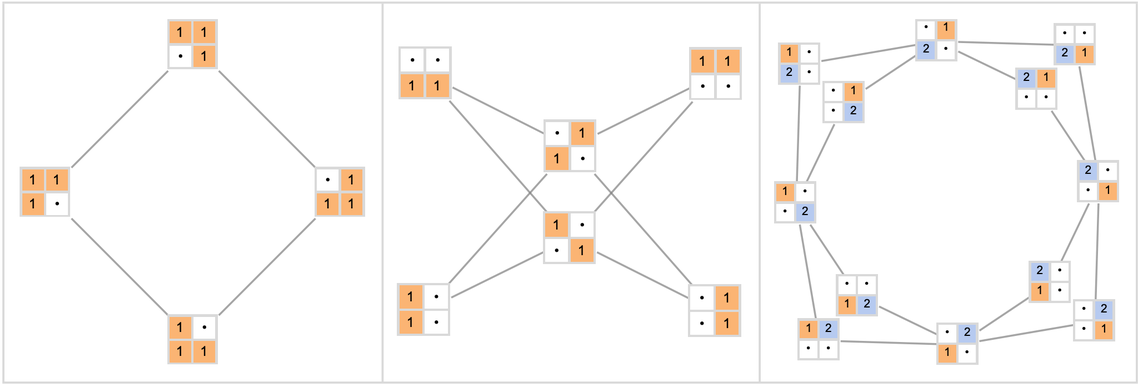
从两个堆开始,每个堆包含两个对象,可以为游戏构建一个多路图:
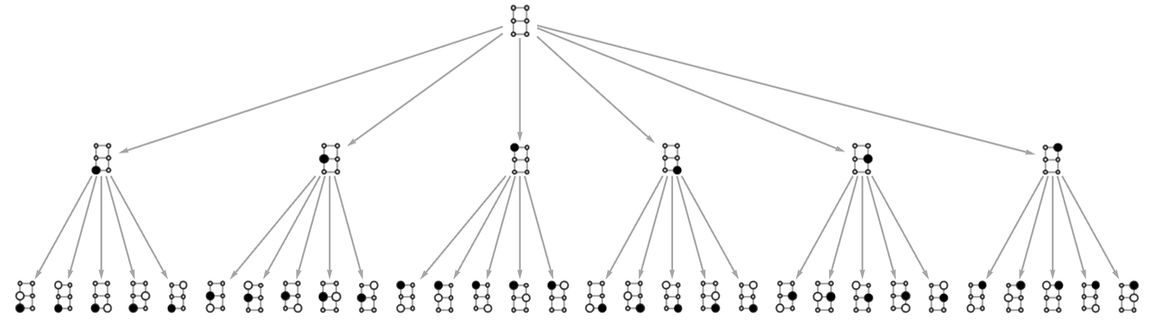
如果使用3个桩,则变为:
这些图表显示了与桩的不同配置相关的所有不同可能移动。然而,它们并没有指明哪个玩家何时移动。加上这一点,我们得到了22个案例
在222例中:
尽管这些图表看起来有点复杂,但事实证明,当一个特定的州具有“对手”可以迫使其输掉比赛的属性时,有一个非常简单的标准:只需获取数字列表,看看是否应用[比特X或,列表]为0。当发生这种情况时,我们会得到:
对于尼姆来说,我们得到的鳃图序列有一个非常规则的结构。在22个案例中,与之前一样突出显示,我们得到:
在222例中,腮腺图的序列变为:
以下是其他一些情况的结果:
滑块拼图
它们有很多名字,有很多不同的主题。但许多谜题最终都是滑块谜题。一个简单的例子可能要求
将滑块滑入空的(较暗的)方块。解决方案是:
可以使用多路图来表示所有可能的转换:
(请注意,这里只显示了块的4!=24个可能配置中的12个;类似于 无法联系。)
无法联系。)
由于块总是可以“双向滑动”的,所以滑动块-模糊多向图中的每条边向前都有一个倒数,所以我们将这些多向图绘制为无向图。
以下是一些简单的例子:
使用3×2板,事情很快变得更复杂:
在3D中渲染,这将变为:
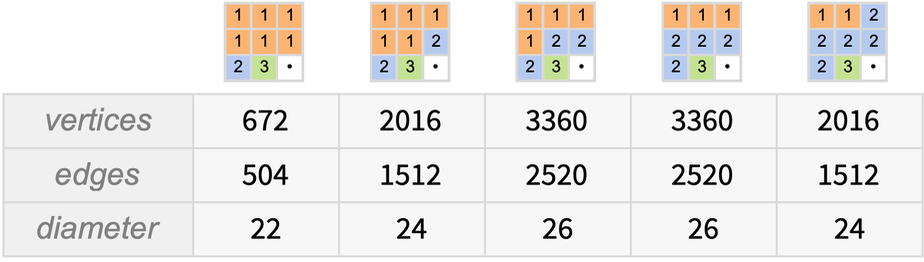
当所有块都不同时,人们往往会得到具有某种球形结构的多路图:
(请注意,在这里的前三种情况下,可以达到块的所有30、120、360个可想象的排列,而在最后一种情况下,只能达到块的“偶数排列”,或720个可想象的排列中的360个。)
这显示了如何从 到
到 :
:
有了许多相同的块,人们往往会建立一个简单的格子:
只需“添加装饰”即可使一块砖与众不同:
当“1”和“2”块的数量接近相等时,结构填充:
快速添加第三种类型的块会导致非常复杂的结构:
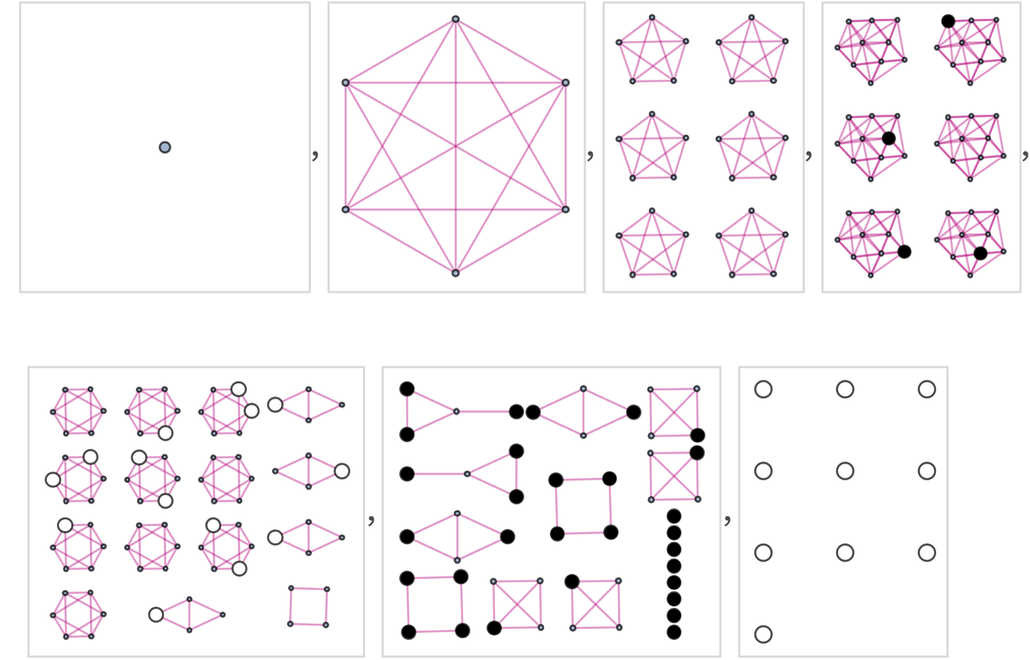
这总结了获得的一些图表:
河内塔等。
另一个著名的谜题是河内塔。再一次,我们可以为它构造一个多路图。从左挂钩上的所有磁盘开始,多路图的第一步是:
通过两个步骤我们可以得到:
然后,完整的多路图是(用无向边代替成对的有向边):
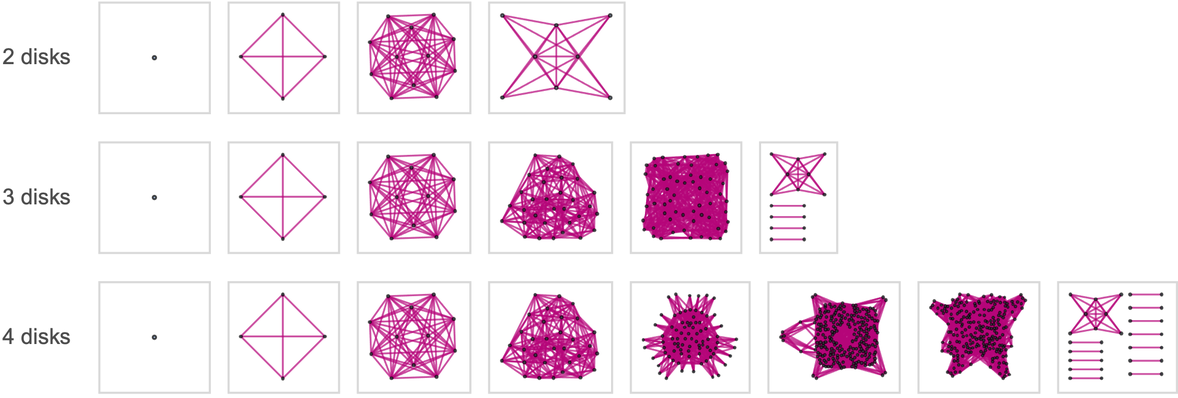
很容易看出这个多路图的递归结构是如何构建的。以下是2个磁盘(和3个销钉)的“基本情况”:
随着每个磁盘的添加,多路图中的节点数增加了3倍,例如使用4个磁盘(仍然使用3个木桩):
有了4个钉子,即使有2个圆盘,事情起初看起来也更加复杂:
在3D渲染中,更多结构开始出现:
下面是3、4和5个磁盘的结果,其中“耳点”对应于所有磁盘都位于一个挂钩上的状态:
使用3个钉,最短的“谜题解决方案”-将所有磁盘从一个钉移动到另一个钉-沿着多路图的“边”n个销钉长度为2n个– 1:
有了4个桩,就不再有唯一的“测地线路径”:
(连续数量桩的路径长度序列为
或略低于 用于大量桩n个.)
用于大量桩n个.)
鳃裂图呢?对于标准的三片式三片式机箱,我们有
其中,假定通过查看上述多路图渲染中的连续垂直级别来获得连续的“时间片”。
对于4个磁盘,基本上可以获得“更多相同的”:
有了4个钉子,事情变得稍微复杂一些:
5个钉住的趋势仍在继续:
多元计算的含义与解释
我们现在已经学习了许多游戏和谜题的例子。在每种情况下,我们都探索了封装其可能行为的整个谱的多路图。那么我们得出什么结论呢?最明显的一点是,当游戏和谜题在我们看来很难,而且可能“有趣”时,这是多向图中明显复杂性的某种反映。或者,换言之,当我们发现多向图在某种程度上“难以解码”时,我们就得到了一个丰富且吸引人的游戏或谜题。
在玩游戏的任何特定情况下,我们基本上都会通过游戏的多路图(或“游戏图”)遵循特定的路径(与物理学类似,我们可以称之为“时间路径”)。在某种程度上,我们可能会做出全局声明,即游戏图代表了所有这些路径。但是多计算范式这表明我们还可以做出更多有用的本地声明。特别是,在时间路径上的每一步,我们都可以在多路图中“横向”查看,并看到“瞬时鳃图”,它表示路径与“邻近路径”的“纠缠”。
在某种意义上,找出“下一步该做什么”就是决定鳃部空间的“方向”。而让游戏变得困难的是,我们无法轻易预测我们将要发生什么”穿越鳃间隙”. 这里有一个与违背了计算不可化归性。沿着某种时间路径从一种状态到另一种状态,计算不可约性意味着,即使我们可能知道潜在的规则,我们也无法轻易预测其结果,因为它可能需要不可约的计算量才能计算出经过许多步骤后的结果。
预测“跨鳃间隙”是一个相关但略有不同的现象,可以描述为“多重计算不可约性”. 这与计算特定路径的难度无关,而是与查看多少纠缠路径相互作用的难度有关。
当一个人玩游戏时,通常会谈论“一个人可以看到多少步”。用我们这里的术语来说,这基本上是关于询问我们能轻易到达“鳃部空间的多远”。作为计算有界实体,我们在鳃间隙有一定的“范围”。如果这个距离不足以达到“制胜位置”,那么这场比赛对我们来说是“困难的”。
不过,这里还有一点。在游戏中,“获胜”通常是指到达多向图中的某些特定位置或区域。但这些地方或区域的定义通常是计算上有界的(“看看是否有一条X线”,等等)。它是对系统的某种“观察”,只提取完整状态的特定(计算上有界的)采样。然后,关键是这种采样无法“解码多计算不可约性”。
这里有一个热力学的类比。在热力学中,我们感知到“热”和“熵增加”,这是因为我们的(粗粒度)测量无法“解码”计算上不可约的过程这导致了系统中产生的特定状态。同样,我们认为“很难弄清楚如何赢得比赛”的事实,是因为我们的获胜标准无法“了解比赛的内部情况”和“解码正在发生的事情”,以至于实际上只能选择一条特定的、直截了当的路径。相反,这是一个涉及到玩游戏的多计算机不可简化过程的问题,实际上,相对于对获胜的观察,“看它落在哪里”。
这里还有一个与量子力学的类比。追踪游戏的许多可能路径,就像遵循量子力学中的许多历史线索,而获胜的标准就像选择某些线索的量子测量。在我们的物理项目我们想象,作为观察者的我们被延伸到鳃的空间,通过我们对自己单一经验线索的信念,“编织”出不同的历史线索。在游戏中,我们对单一经验线索的信念的类比大概是“重要的是谁赢谁输;游戏内部如何进行并不重要”。
要与量子力学进行更紧密的类比,可以开始考虑将“多路游戏”的不同块组合在一起,并尝试计算出这些块是如何组合在一起的。
我们在这里讨论的游戏在某种意义上都是纯粹的“技能游戏”。但在游戏中,如果还有机会因素,我们可以认为这会导致多路图中原本是一条路径的内容“模糊”为一束路径,而鳃空间中原本是单一点的内容则会成为一个完整的扩展区域。
在研究不同的特定游戏和谜题时,我们经常不得不查看相当简化的案例,以获得可管理大小的多路图。但如果我们看非常大的多路图,是否会出现整体规律?游戏图是否存在某种潜在的“连续极限”?
几乎不可避免的是,如果我们仔细观察,就会发现各种各样的多重计算不可约性在起作用。但在我们的物理项目中,实际上在一般的多计算范式中,一个关键问题是相关的观察家没有看到那样的细节。就像热力学或气体定律从基础分子动力学中出现一样,基础计算不可约性的存在必然导致观察者所能感知的简单定律。
那么游戏中的“观察者”是什么样的呢?至少出于某些目的,它基本上可以被认为是“赢”的标准。因此,现在出现了一个问题:如果我们只看这些标准,我们能推导出类似于“物理定律”的东西吗?它对下面所有的多计算不可约细节都不敏感吗?
关于这一点还有很多问题需要解决,但也许有一个地方需要开始,那就是看看鳃部空间的大规模结构,以及各种游戏中的多路图形。在许多不同的游戏中,一个基本的印象是,虽然鳃图的特征可能在游戏的“不同阶段”之间发生变化,但跨一个鳃图往往会有一定的一致性。如果仔细观察细节,可能会发现大量的多重计算不可约性。但在某种“可感知的水平”上,图形的不同部分可能看起来相似。这表明,即使采取了完全不同的行动,“游戏的局部印象”在特定阶段也会趋于相似,这些行动需要一个人到达鳃图定义的“游戏空间”的完全不同的部分。
虽然鳃图的不同部分之间可能存在相似性,但我们已经看到,在一些游戏和谜题中,鳃图分裂成多个不相连的区域。这反映了游戏空间的游戏区域中存在着明显的“保守扇区”,玩家可以进入这些区域,但随后会陷入其中(至少在一定时间内),就像时空中一样事件视界可以阻止传输在物理空间的不同区域之间。
我们在一些游戏和谜题中注意到的另一个(相关的)影响是多路图中的大“洞”:图中两点之间有多条“遥远”路径的地方。当多路图密集连接时,通常总会有一种方法通过重新路由附近的路径来“修复任何错误”。但是,当出现漏洞时,这是一个迹象,表明一个人最终可能会“致力于”一种行动,而不是另一种行动。要达到与其他行动相同的位置,还需要很多步骤。
如果我们假设在某种程度上,我们最终在多路图中“观察到”的是一种对应于评估输赢的粗粒度,那么我们将不可避免地处理可能路径的分布。如果没有“洞”,这些路径可以紧密相连,并且可能看起来很相似。但当有一个洞时,可能会有相隔很远的不同路径。事实上,可能存在“同一分布的一部分”的远距离路径,这可能被认为是量子叠加效应。
游戏中有广义相对论和路径积分的类比吗?为了清晰地表述这一点,我们必须更仔细地定义“游戏空间”的特征。大概会有类似的因果图。大概还会有一个能量模拟在游戏空间中,与游戏空间中不同位置的“活动密度”相关。那么,重力现象的模拟将类似于最佳游戏(即通过游戏图的测地线路径)将因高密度活动的存在而发生偏转。换句话说,如果游戏处于某一状态时有很多事情要做,那么好的游戏往往会被“拉向那个状态”。在某种程度上,这并不奇怪:当游戏图中有高密度的活动时,往往会有更多关于该做什么的选择,所以如果一个人经历了这些,就更有可能“玩得很好”。
到目前为止,我们还没有明确讨论游戏策略但在我们的多计算框架中,策略有一个相当明确的解释:它在规则空间实际上,我们假设了一组关于如何构造多路图的规则。换句话说,给定一个策略,一个是在多路图中选择一些边(或相关多路因果图中的一些可能事件),然后删除其他边。
一般来说,很难谈论“可能策略的空间”,因为这就像谈论“可能程序的空间”。但这正是规则空间让我们谈论的。“战略空间”的确切“几何学”将取决于我们如何选择协调规则空间。但再一次,只看游戏理论中讨论的事物,就会有某种程度的粗粒度。在这个层次上,我们可以预期,各种标准的“结构性”游戏——理论结果通常会成立。
个人备忘
即使是小时候,我也从来没有特别喜欢玩游戏或玩拼图。也许这是一个迹象,我一直有点过于科学家化。因为在我看来,仅仅选择特定的动作总是太武断了。为了引起我的兴趣,我需要一个更大的画面,更连贯的知识故事。但现在,从某种意义上说,这正是我在这里讨论的游戏和谜题的多计算机方法带给我们的。是的,能够思考做出特定动作是非常“人性化”的。但多计算方法立即给了人们一个连贯的全球观点,至少对我来说,这在智力上要令人满意得多。
我在这里讨论的探索可以认为是源于 一种新的科学.英寸第5章属于一种新的科学我有一个我第一次介绍多路系统的部分.而且作为该部分的最后一点我讨论了“游戏系统”:
我在20世纪90年代对此进行了研究,事实上,我现在发现了1998年的一本关于tic-tac-toe的笔记本,其中也有一些相同的结果
以及tic-tac-toe游戏图形的有趣图形表示:
但回到那时,我并没有从我生成的游戏图中得出太多结论;它们看起来又大又复杂。二十年过去了,我没有再想太多。但在2017年我的儿子克里斯托弗正在玩一个名为“尖峰时刻”的益智游戏:

也许是出于家庭倾向,他决定构造其博弈图-在我看来,这是一个非常令人惊讶的结果:
当时我并没有试图理解其中一个的结构,但我仍然“把它归档”,作为游戏图可以具有“可见的大规模结构”的证据。
几年后——2019年末,我们物理项目正在进行中我们意识到量子力学和多路图之间有着深刻的联系。量子力学一直看起来像是某种神秘的东西——纯数学形式主义的抽象结果。但是,看到与多路系统的联系,开始表明人们实际上可能能够“理解量子力学”,因为它可能“机械地产生”于某些具体的底层结构。
我开始思考如何在直观的层面上解释量子力学。为此,我需要一个熟悉的类比:每天都可以连接到多路系统的东西。我立刻想到了游戏。而且在2020年9月我决定看看在游戏中更详细地探索这种类比。我很快分析了tic-tac-toe和Nim等游戏,以及简单的滑块拼图和河内塔。但我想探索更多的游戏和谜题。而我已经其他要做的项目因此,对游戏和谜题的多计算分析被搁置一边。今年早些时候,当我用它作为生成一个证明类多路图的示例,关于我的研究元数学的物理化最后,几周前,我决定是时候写下我目前所知道的关于游戏和谜题的内容,并制作出这里的内容。
谢谢
感谢Brad Klee和Ed Pegg在本文分析的最后阶段提供的广泛帮助,以及Christopher Wolfram在2017年和2020年提供的灵感和帮助。










![]()




















































































![]()



































![]()




![]()
![]()















![]()