思想的动态图像
逻辑图是查尔斯·桑德斯·皮尔斯（Charles Sanders Peirce）为逻辑开发的图形语法风格之一的图形理论结构。
介绍
A类逻辑图是图形语法系统中的一种图形理论结构查尔斯-桑德斯·皮尔斯为逻辑而开发。
在众多关于定性逻辑，实体图、和存在图皮尔士开发了图形形式主义或图形理论形式语言的几个版本，旨在进行逻辑解释。
自皮尔士开创这一发展路线以来的一个世纪里，各种形式系统都从抽象上来说是图形理论结构的相同形式基础上扩展出来。本文从鸟瞰的角度研究了这类形式系统的共同基础，重点讨论了代数、微积分或语言的整个家族共享的形式方面，然而它们碰巧在给定的应用程序中被看到。
抽象观点
所讨论的鸟瞰图更正式地被称为形式对等的视角，从这个角度出发，人们忽略了许多在更具体的环境中显得重要的区别。不同形式中的表达式，其句法结构在代数上或拓扑上同构，在任何重要意义上都不会被认为彼此不同。仔细观察历史细节会顺便注意到，C.S.皮尔士使用了拖缆交叉符号斯宾塞·布朗用木工方记号笔例如，大致相同的形式目的，但纯粹形式层面的主要主题对该顺序的变化漠不关心。
代替开始
考虑以下两个形式方程。
 |
(1) |
 |
（2） |
二重性：逻辑和拓扑
在使用逻辑图时，需要考虑两种对偶类型，逻辑对偶和拓扑对偶。
皮尔斯所考虑的顺序图，那些嵌入到连续流形中的图，如通常由平面纸表示的流形，可以用线性文本表示为所谓的图遍历字符串并解析为指针结构在计算机内存中。
一张空白纸可以用线性文本表示为空白，但这样做往往会令人困惑，除非考虑中的逻辑表达式在单独的显示器上显示出来。
例如，考虑如下所示的公理或初始方程。
 |
(3) |
这可以内嵌为“( ( ) ) = “或在文本显示中显示：
( ( ) ) =
当我们转向在计算机内存中表示相应的表达式时，可以最容易地对其进行操作，我们首先将平面图转换为它们的拓扑对偶。原始图的平面区域对应于对偶图的节点（或点），原始图中平面区域之间的边界对应于对对偶图节点之间的边（或线）。
例如，将相应的对偶图叠加到上面显示的平面嵌入图上，我们得到了以下合成图。
 |
(4) |
虽然它并不存在于事物最抽象的拓扑结构中，但出于各种实用原因，我们发现自己不得不以独特的方式挑出平面的最外层区域，并将其标记为根节点对应的对偶图。在图的当前样式中，根节点由水平贯通标记。
从对偶图的合成矩阵中提取对偶图，我们得到以下方程。
 |
(5) |
很容易看出皮尔士逻辑图的括号表示（简洁地描绘出其形式内容的有序包含）与相应的对偶图之间的关系，对偶图构成了一种有根树，将在下文中进行更详细的描述。
在我们的最后一个例子中，思考一下下面的图片，我们将看到如何从树的根开始，向上爬到树的左侧，直到到达顶部，然后再向上爬回到树的右侧，直到回到根，从而得到相应的括号字符串，在读取符号的同时，在这种情况下(“或”)“，我们在旅行中碰巧遇到。
 |
(6) |
这个仪式叫做穿越树和读取的字符串通常称为遍历字符串在树上。从绳子到树的反向仪式称为解析字符串和构造的树通常称为解析图形这个行话的使用者倾向于松散地使用它，通常使用解析字符串表示解析到关联图形中的字符串。
我们现在已经详细讨论了各种形式的公理或初始方程，它们以字符串形式表示为“( ( ) ) = ”.为了进行比较，让我们将以字符串形式表示的公理的平面形式和对偶形式记录为“( )( ) = ( )”.
首先是平面嵌入地图：
 |
(7) |
接下来，平面图和它们的双树叠加在一起：
 |
(8) |
最后，树木自己生根了：
 |
(9) |
下面是带有遍历字符串的解析树：
 |
(10) |
在这一点上，我们有足够的材料开始思考类比、象似性、隐喻、态射的形式，无论我们怎么称呼它们，这些形式关系到逻辑图在其各种化身中的使用，例如皮尔士所描述的那些实体图和存在图.
计算表示
到目前为止，我们一直在研究的解析图使我们更接近指针图，指针图使上述类型的地图和树保存在计算机内存中，但它们仍有几个步骤过于抽象，无法详细描述我们需要的动态数据结构的具体种类。现在是充实我们到目前为止制定的框架的时候了。
图中的节点表示记录在计算机内存中。记录是可以设想驻留在特定位置的数据集合地址记录的地址类似于指示代词，一个类似于这或那个，程序员将其称为指针符号学家认为它是一种被称为指数.
在下一个具体级别上，指针记录数据结构可以表示如下。
 |
(11) |
这描绘了指数0作为包含以下数据的记录的地址。
资料1，资料2，基准，基准三, …,等等。
将图形理论结构表示为计算机内存中的数据结构是因为地址只是另一个数据，所以我们可能会有如下情况。
 |
(12) |
回到抽象级别，需要三个节点来表示上述三个数据记录：一个根节点连接到两个相邻节点。然后，不指向树上任何位置的数据项被视为它们所在的记录节点上的标签，如下所示。
 |
(13) |
注意，对于像这样的有根树来说，绘制箭头是可选的，因为当根选中一个唯一的节点时，会在树的所有边上产生唯一的方向向上的方向与远离根部.
社区快速游览
这些准备工作使我们能够掌握决定整个逻辑图系统的基本公理或初始方程。
作为符号系统的初级算术
虽然从逻辑上讲，这似乎不太令人兴奋，但有许多理由让自己熟悉由有根树、平衡的括号串和平面上有限组不相交的简单闭合曲线所表示的形式系统，从拓扑上讲，这些形式系统是冷漠的。
- 首先，它为我们提供了一个符号域的非平凡示例，在这个符号域上我们可以切掉我们的符号牙齿，从它包含符号的可数无穷大的意义上来说，这是非平凡的。
- 此外，它还允许我们研究一种简单的计算形式，这种计算可以识别为精神病学或符号转换过程。
这种形式空间，以及将其划分为两个形式等价类的一对公理，就是斯宾塞·布朗所说的初等算术.
主要算法的公理如下所示，它们以图形和字符串的形式出现，以及便于引用公理应用的两个相反方向的成对名称。
让
成为一片生根的树，让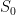
是由根节点和根边组成的2元素子集。简单的直觉，或简单的归纳证明，将确保任何有根树都可以通过基本算法的公理化简为根节点或根边。
例如，考虑如下进行的减少。
 |
(16) |
这被视为一个符号学过程，相当于一系列符号，每一个在第一个符号之后充当解释者它的前身的最后一个符号，可以作为它们共同对象的规范符号，其结果是计算过程的结果。尽管它很简单，但它展示了任何计算的主要特征，即从同一对象的模糊符号到清晰符号的符号过程，其目的和效果是代表澄清的行为。
作为模式微积分的初级代数
经验告诉我们，复杂的物体最好以渐进、分层、模块化的方式处理，一步一层，一次一件，尤其是当这种复杂性是不可简化的，当我们所有的关节和所有的表示都将在与物体本身的结构脱节的关节处分离时，直觉的综合完整性需要一些集合。
这就是为什么要花这么多时间研究零阶逻辑的前半部分的一个很好的原因，在这里，零阶逻辑由基本算术表示，皮尔士在逻辑图方面的工作中，在许多点和时间上都接近于直觉，但斯宾塞·布朗（Spencer Brown）命名了零阶逻辑，并使其更加完整。
在这些原始森林中逗留更长时间的另一个原因是，熟悉“裸树”，即那些没有添加文字或数字标签的树，将为理解“变量的本体论状态”这一经常争论的问题中真正存在的问题奠定基础。
最好以具体的案例来说明这一主题。为了做到这一点，让我们再看一看前面的示例，即在基本算法中发生的约简评估。
|
(16) |
在我们看到了一些大致相同形状的路标变换后，我们很可能会注意到，在靠近一侧的唯一边缘处，其他哪些分支扎根并不重要，最终结果总是相同的。最终，我们会想到通过引入一个标签或变量来表示任何形状的分支，从而总结出许多这样的观察结果，写下如下内容。
 |
(17) |
这样的观察是所有代数的根，它是由各种各样的算术构成的，并由它们的总结而萌芽。
说到代数，刚遇到一个代数定律的例子，我们不妨介绍一下初等代数再次从查尔斯·桑德斯·皮尔斯和乔治·斯宾塞·布朗的作品中分别衍生出它们的实质和名称。
任何形式系统的公理选择在某种程度上都是一个美学问题，因为通常情况下，许多不同的形式规则选择将作为公理，以导出所有其他的定理。碰巧的是，我们首先注意到的一个代数定律的例子，”a（）=（）“，虽然看起来很简单，但根据上述公理，证明了作为一个定理是可以证明的。
在这一点上，我们还可能注意到，如果默认它们各自的公理集，那么在证明理由方面，初级算术和初级代数之间存在着微妙的差异。
算术公理是由菲亚特以准先验的方式引入的，当然，这只是长期以来在实际使用相对发达的几代正式系统方面的经验，而这些系统实际上会促使我们采取这种准原始的行动。相反，代数公理可以从观察和总结算术谱中可见的模式中得出其动机和理由。
正式开发
该主题的讨论继续于逻辑图•形式化开发.
资源
复写的副本：FB|逻辑图•形式法则•马什顿•Academia.edu学院
复写的副本：概念图•控制论•结构建模•系统科学
