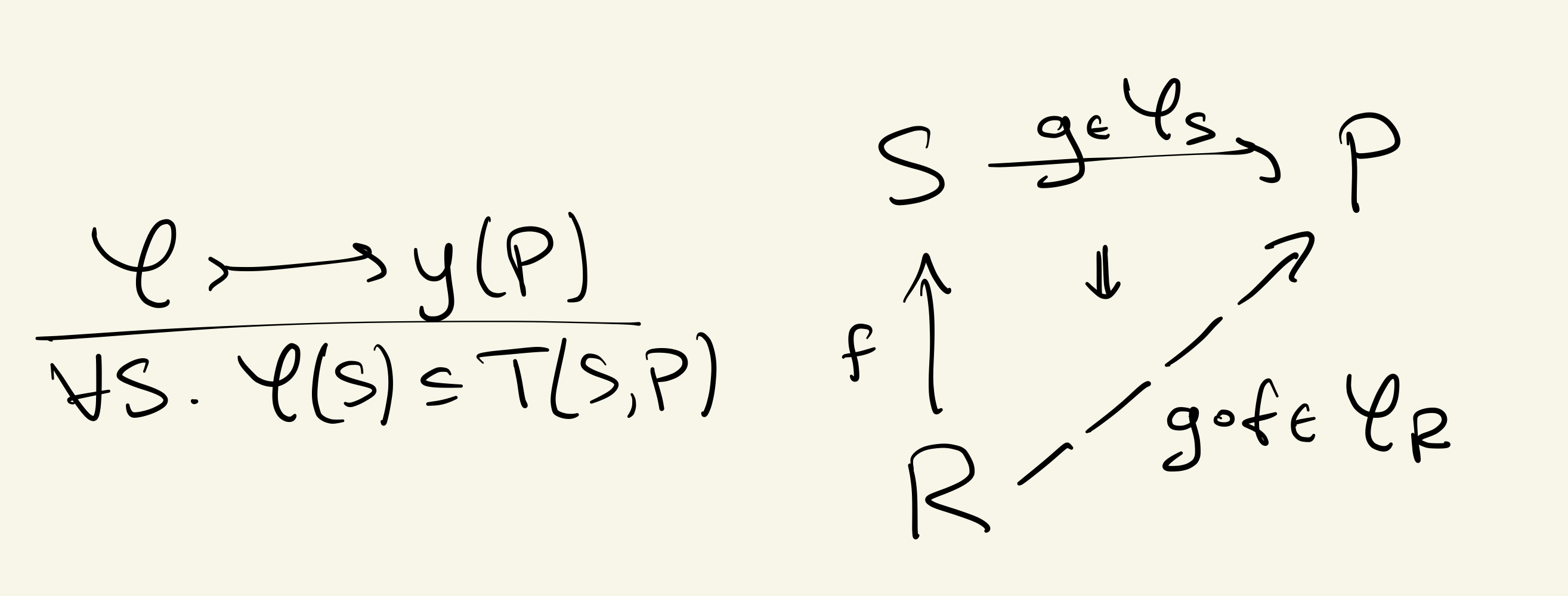每个类别都嵌入到预升地形中
如果是一元封闭的,那么嵌入保持了这种结构:
即使用日卷积,是一元闭合的。因此,我们可以在保护环境的同时进入更丰富的环境高阶代数结构,或语言.
现在,我们使用-微积分作为我们的运行示例。完整的类型系统在报纸,第9页。
代表人
本机类型系统中最简单的对象类型是可代表的 。这是所有排序项的集合,由语言上下文索引。虽然计算机科学中的许多著作要么局限于封闭术语,要么将所有术语集中在一起,但这种索引是自然而有用的。
在-微积分,是所有进程的索引集。
类型系统是通过以下操作从这些基本对象构建的和结构然后我们可以构造谓词、依赖类型、co/limits等,每个构造函数都有相应的推理规则,可供计算机使用。
谓词和类型
拓扑的语言由两个fibration表示:子对象fibration给出谓词逻辑而伴随体纤维形成相依型理论因此,这两个基本实体是谓词和(依赖)类型。类型更为普遍,我们可以将其视为“新型”语言,可以更具表现力。
.png)
谓词对应于可表示的子对象,相当于筛子,筛子:一组变形为,在预压下闭合: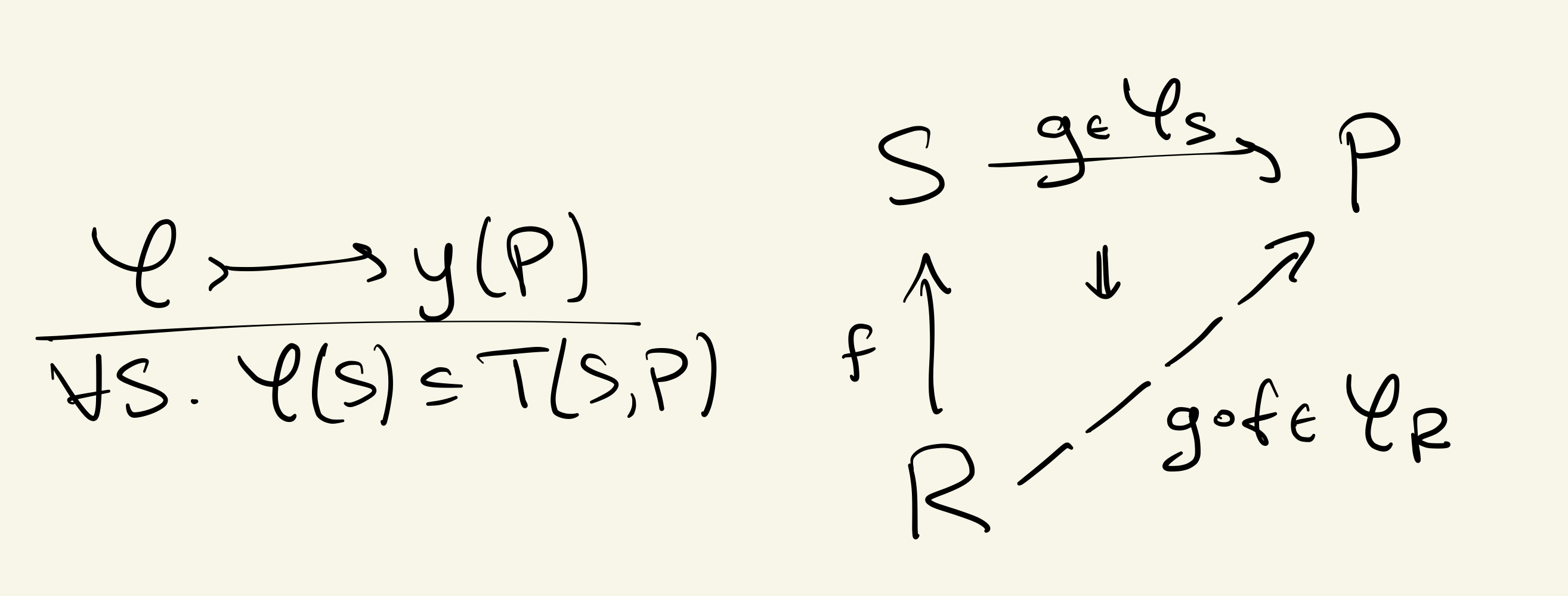
这强调了谓词逻辑超过可表示实际上是在推理抽象语法树:此处是中的一些操作树带有-形洞变量和谓词只关心; 你可以插入任何术语虽然仍然令人满意.
更一般地说,是一个态射被理解为“索引预处理”或从属类型
即针对每个元素,有一根纤维哪个是“类型取决于术语”.
中的类型示例-微积分由输入运算给出,
光纤覆盖的位置是所有频道控制文本对的集合使得.
相依和和乘积
这里我们使用中描述的结构第1部分.谓词函子是一个超学说每个预处理给出了一个完整的Heyting谓词代数,对于每个给出伴随词对于形象,前映像、和安全映像.
类似地,切片函子是带伴随词的共/完全拓扑的超条令。这些是相依和,替代、和从属产品根据这些,我们可以重建谓词逻辑的所有操作,等等。
如(简要)所述第1部分,相依和的概念是指数和泛化乘积; 这里,密码子是一组指数,其纤维是该家族中的一组指数;所以索引和的一个元素是依赖对 双重地,指数积泛化函数:纤维产品的一个元素是元组可以理解为相关函数其中密码子取决于哪个你插上电源。
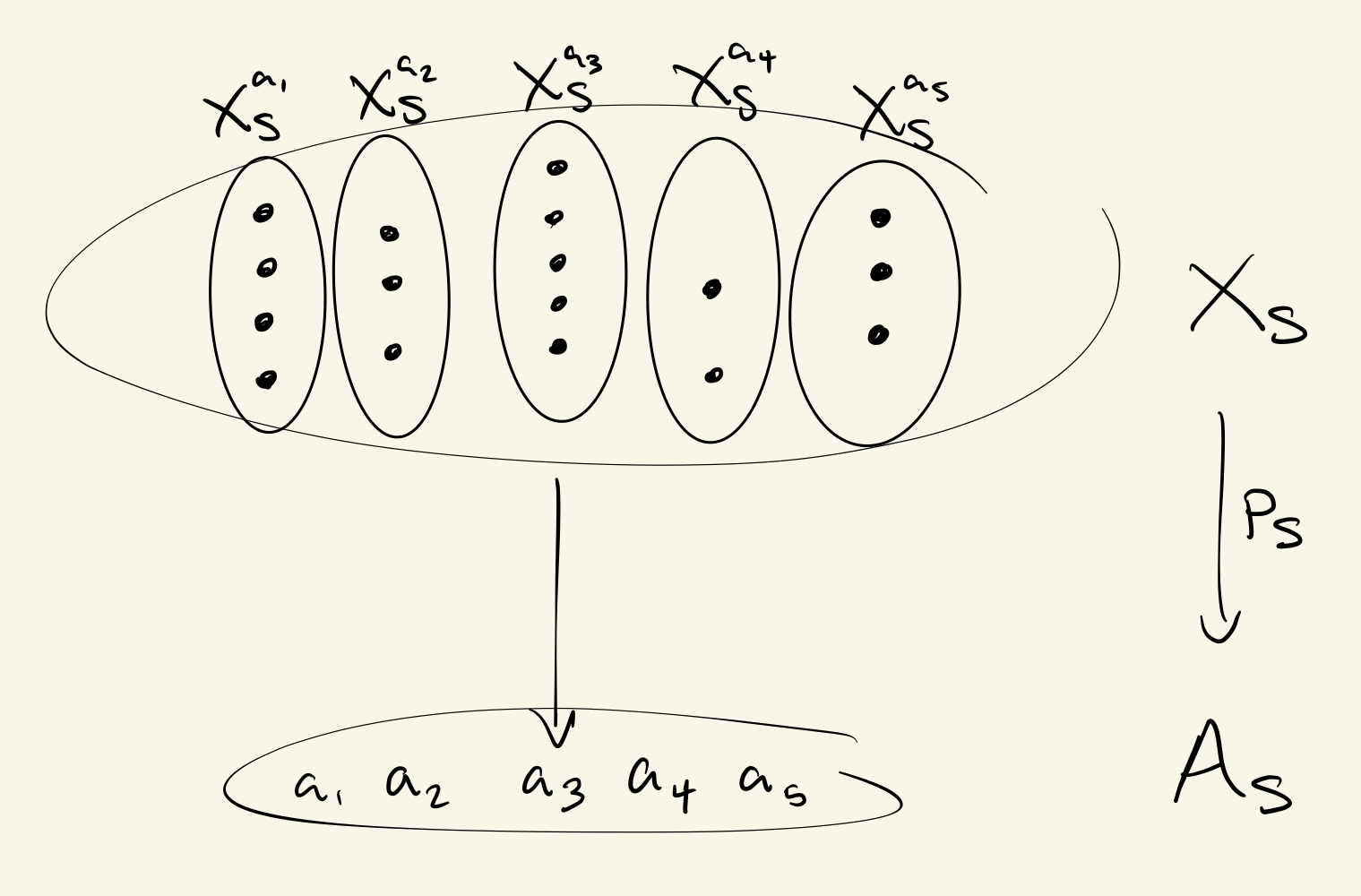
明确地给出和,,我们有和
(1)
(出租和表示光纤). 尽管公式复杂,但直觉基本上与Set中的相同,只是我们需要确保生成的对象仍然是预升的,即在预合成下闭合的。重点是:
主要的例子从理论中的“向前推进”操作开始,使用.给定一个操作,图像接受谓词(筛)并简单地对中的每个术语进行后置运算具有.
因此,一个示例谓词(离开和隐式)是
此谓词确定两个非空进程的并行进程。
例如,从第2部分我们可以使用过程图和重写来模拟计算动力学现在,这些操作在和筛子,为运算符提供“前进或后退”:
虽然“图像”步进给出了所有可能的下一个术语,但“安全”步进提供了可能的术语只有来自。对于安全协议,这可以用于按过去的行为筛选进程.
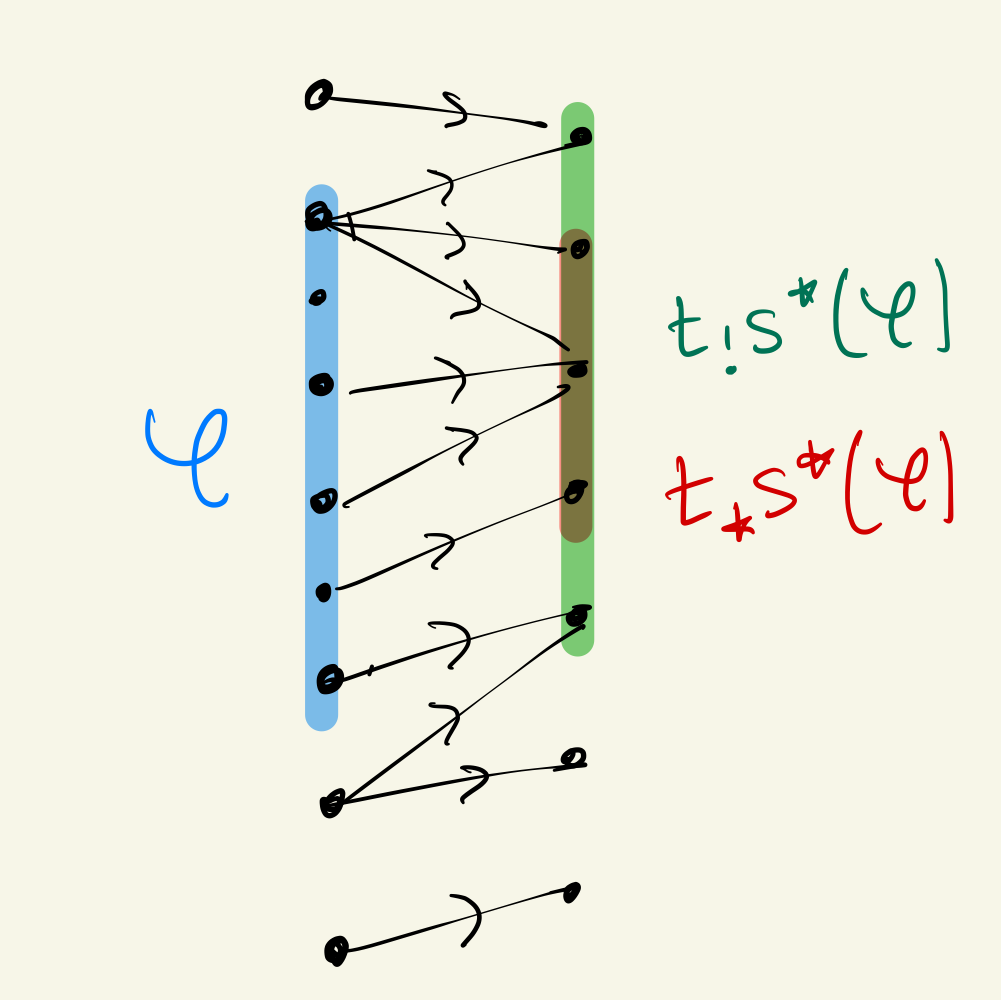
图像/理解和分型
谓词和类型是通过fibrations之间的附加而关联起来的。
转换谓词对于类型,应用理解来构造术语的子对象满足要求的。要转换类型对于谓词,应用图像分解来构造谓词每根光纤是否有人居住。
我们一直隐含地使用理解方向(将谓词视为其子对象);虽然拍摄图像具有更大的破坏性,但为了简化,它肯定是有用的。例如,而不是考虑类型,我们可能只想考虑图像,所有输出进程的集合。
内部Hom和实体化
而格罗森迪克建筑相对来说,人们对地方的索引类别的结构(谓词的完整Heyting代数)通常可以转换为全球的结构总类上对应的纤维。谓词函子的总范畴笛卡尔封闭,允许我们构造谓词homs.
这种结构可以在集合的范畴中理解。鉴于和,我们可以定义
因此,它构建了“确保含义的上下文”。
例如,我们可以构建分离逻辑:让是交换幺半群的理论,带有一组常量作为堆元素邻接的。如果我们定义
然后声称.
有一种更具表现力的方式可以形成homs,我们称之为具体化(第7页);我们不知道它是否被探索过,我们还没有确定它与从属产物的关系。
协同/诱导
同样是协同/完成的,并且可以在总类别上组合成一个全局协同/完成结构。因此,我们可以使用它来构造共归纳类型。
例如,给定名称上的谓词,我们可以在:
哪里表示初始代数,它被构造为一个colimit。这确定流程是否输入,不在上输入,并继续作为满足相同谓词的过程。这可以理解为防火墙.
应用
一旦组合了这些类型构造函数,它们就可以表达关于代码的非常有用和复杂的想法。最好的部分是,这种类型的系统可以从任何包含产品和函数类型的语言,其中包括许多流行编程语言的大块。
要了解更多应用程序,请查看本土类型理论当然,看看论文的其余部分,让我知道你的想法!谢谢你的阅读。
.png)


.png)