哺乳动物网格细胞活动模式下高维对称性的可能性质| eLife

记录的版本: 2015年6月4日
接受的手稿: 2015年4月24日

1. 与相关
三维网格单元的自组织

费德里科·斯特拉（Federico Stella）、亚历山德罗·特雷夫斯（Alessandro Treves）

研究文章 2015年6月4日
进一步阅读

摘要

从矿物的晶体结构到昆虫复眼中小蜂的蜂窝状组织，自然界中存在着丰富的晶格。这些安排为优化打包、高效资源分配和加密协议提供了解决方案。格子在大脑如何表达信息方面也起作用吗？我们将重点放在高维刺激域上，特别强调物理空间的神经表示，并推导出哪些神经元晶格码可以最大限度地提高空间分辨率。对于在水面上航行的哺乳动物，我们表明网格细胞的六边形活动模式是最佳的。对于在三维空间自由移动的物种，以面为中心的立方晶格是最好的。这种预测可以在蝙蝠、树栖猴子或海洋哺乳动物身上进行实验验证。更广泛地说，我们的理论表明，大脑通过网状细胞样神经元的群体来编码高维的感觉或认知变量，这些神经元的活动模式在多个嵌套的尺度上显示出晶格结构。

https://doi.org/10.7554/eLife.05979.001

eLife摘要

哺乳动物的大脑必须存储大量信息。例如，动物在环境中导航的能力取决于它们周围空间的地图，而这些地图是由有限数量的神经元的电活动编码的。2014年，诺贝尔生理学或医学奖授予了对这一过程有深刻见解的神经科学家。其中两位获奖者表示，在对大鼠的实验中，只要大鼠处于空间中的任意一个点，大脑特定区域的神经元就会“放电”。当这些点被绘制成二维图时，它们形成了一个由联锁六边形组成的网格，从而为老鼠提供了一张环境地图。

然而，许多动物，如蝙蝠和猴子，都是在三维空间中导航，而不是在二维空间中导航。目前尚不清楚这些相同的六边形图案是否也用于表示三维空间。Mathis等人现在已经使用数学分析来寻找大脑表示三维空间区域的最有效方法。这项工作表明，神经元需要在大致对应于单个桔子在堆叠时所占据位置的点进行激发。物理学家称这种排列为面心立方晶格。

目前，至少有一组实验神经科学家正在测量自由飞行蝙蝠的神经元放电，因此很快就可以将Mathis等人的预测与实验数据进行比较。

https://doi.org/10.7554/eLife.05979.002

介绍

在哺乳动物中，空间的神经表征依赖于至少两类神经元。”当动物靠近环境中的某个特定位置时，放置细胞放电(O'Keefe和Dostrovsky，1971年). ‘网格单元在跨越覆盖环境的假想六边形晶格的多个位置活跃(Hafting等人，2005年)并在老鼠、爬行蝙蝠和人类身上发现(Hafting等人，2005年;Fyhn等人，2008年;Yartsev等人，2011年;雅各布斯等人，2013年). 这些细胞被认为是建立空间尺度的。

在这些实验中，运动发生在水平面上。理论和数值研究表明，六边形晶格结构最适合表示这样的二维（2D）空间(Guanella和Verschure，2007年;马蒂斯，2012年;Wei等人，2013年). 然而，一般来说，动物的运动是三维的（3D）；鸟类、树栖动物和鱼类尤其如此。他们对3D空间的神经元表征可能由低维斑块的镶嵌组成(Jeffery等人，2013年)攀爬老鼠的记录证明了这一点(Hayman等人，2011年). 另一方面，将细胞放置在飞行蝙蝠中，以均匀且几乎各向同性的方式表示3D空间(雅采夫和乌兰诺夫斯基，2013年).

由于哺乳动物的网格细胞在3D中表示空间的方式可能与在2D中不同，因此我们研究了任意高维空间中的网格细胞表示，并测量了具有周期调谐曲线的神经元群体中此类表示的准确性。我们通过Fisher信息（FI）来测量准确性。尽管细胞之间的激发场重叠，以确保空间的均匀覆盖，但我们展示了如何将群体FI的求解映射到填充问题上不重叠的球体，在其他编码问题和密码学中也扮演着重要角色(香农，1948年;康威和斯隆，1992年;格雷和纽霍夫，1998年). 因此，最佳晶格是具有最高填充率的晶格，最密集的晶格最准确地表示空间。这个非常简单明了的答案意味着六边形晶格对于表示2D空间是最优的。在3D中，我们的理论做出了实验上可测试的预测，即网格单元将具有位于面心立方晶格或其等密度非晶格变体（六角密排结构）上的发射场。

具有单一优先刺激的单峰调谐曲线是视觉皮层位置细胞或方向选择性神经元的特征，已被广泛研究(Paradiso，1988年;Seung和Sompolinsky，1993年;Pouget等人，1999年;Zhang和Sejnowski，1999年;Bethge等人，2002年;尤里奇和威尔克，2000年;Brown和Bäcker，2006年). 这也适用于沿正交刺激轴周期性的多模式调谐曲线，并产生重复的超立方（或超矩形）激活模式(蒙特默罗和装甲，2006年;Fiete等人，2008年;Mathis等人，2012年). 我们的结果扩展了这些研究，将更一般的刺激对称性考虑在内，并使我们假设最优格不仅是物理空间的神经表征的基础，而且也会在其他高维感官或认知空间的表征中发现。

模型

空间人口编码模型

我们认为D类-维度空间 $ℝ^{D类}$ 其中空间位置由坐标表示 $x = (x_{1}, \dots, x_{D类}) \in ℝ^{D类}$ 。动物在这个空间中的位置由编码N个神经元。每个神经元平均放电率的相关性我在x称为神经元的调谐曲线，用Ω表示_我(x). 为了解释神经元放电的试验间变异性，尖峰是根据概率随机产生的 ${P（P）}_{我} ({k个}_{我} | τ Ω_{我} (x))$ 用于神经元我开火k个_我固定时间窗口内的峰值τ.而两个神经元可以有相关的调谐曲线Ω_我(x)，我们假设任意两个神经元的试验间变异性是相互独立的。因此N个统计上独立的神经元激发(k个₁,…,k个_N个)位置处的峰值x总结了编码模型：

P（P） (({k个}_{1}, \dots, {k个}_{N个}) | x) = \prod_{我 = 1}^{N个} {P（P）}_{我} ({k个}_{我} | τ Ω_{我} (x)) .

解码依赖于通过询问来反转这个条件概率：给定尖峰计数向量K（K）= (k个₁,…,k个_N个)，动物在哪里？这样的位置估计将写成 $\hat{x} (K（K）)$ 通过计算解码器的平均均方误差来评估解码的精确度。动物实际位置之间的平均距离x和估计 $\hat{x} (K（K）)$ 是

ε (\hat{x} | x) = {E类}_{P（P） (K（K） | x)} (∥ x - \hat{x} (K（K）) ∥),

给出了人口编码模型 $P（P） (K（K） | x)$ 。此错误称为分辨率(Seung和Sompolinsky，1993年;莱曼，1998年)，其中术语 $∥ . ∥$ 表示欧氏距离， $∥ x ∥ = \sqrt{\sum_{α} x_{α}^{2}}$ 更一般地说，协方差矩阵 $\sum (\hat{x} | x)$ 带系数 $\sum {(\hat{x} | x)}_{α, β} = {E类}_{P（P） (K（K） | x)} ((x_{α} - \hat{x_{α}} (K（K）)) \cdot (x_{β} - \hat{x_{β}} (K（K）)))$ 用于空间标注 $α, β \in {1, \dots, D类}$ ，测量不同误差分量的协方差，以便∑就是决议 $ε (\hat{x} | x)$ 原则上，分辨率取决于特定的解码器和种群编码模型。然而，对于无偏估计量，即平均解码位置的估计量x作为此位置 ${E类}_{P（P） (K（K） | x)} (\hat{x} (K（K）)) = x$ ，FI提供了一种分析方法来评估任何此类解码器的最高可能分辨率(莱曼，1998年).

分辨率和费希尔信息

给出的响应K（K）= (k个₁,…,k个_N个)在人群中，我们问理想的观测者解码刺激的准确度如何xFI衡量一个人辨别附近刺激的能力，并取决于P（P）(x,K（K）)更改为xFI越大，分辨率越高，误差越低 $ε (\hat{x} | x)$ ，因为这两个量是反相关的。更准确地说，FI矩阵的逆矩阵J型(x),

{J型}_{α β} (x) = \int^{​} (\frac{\partial 在 P（P） (K（K）, x)}{\partial x_{α}}) (\frac{\partial 在 P（P） (K（K）, x)}{\partial x_{β}}) P（P） (K（K）, x) d日 K（K）,

限定协方差矩阵 $\sum (\hat{x} | x)$ 估计坐标的x= (x₁,…,x_D类)

\sum (\hat{x} | x) \geq J型 {(x)}^{- 1} .

编码刺激的任何无偏估计器所能达到的分辨率不能大于J型(x)⁻¹这被称为Cramér-Rao边界(莱曼，1998年). 基于这个界限，我们将把金融机构视为解决人口编码问题的一个措施。特别是，我们对空间的各向同性和齐次表示感兴趣。这两个条件确保种群在任何位置和沿任何空间轴具有相同的分辨率。各向同性并不意味着单个神经元Ω的（全局）空间调谐_我(x)，必须是径向对称的，但仅仅是误差根据径向对称分布（局部）分布。例如，具有六边形调谐的网格单元的调谐曲线在场中心周围不是径向对称的（它有三个轴），但其后部在此类网格单元模块的任何给定位置周围是径向对称的。同质性要求金融机构J型(x)渐近独立于x（作为神经元的数量N个变大）；空间各向同性意味着FI矩阵中的所有对角线项J型(x)都是平等的。

周期调谐曲线

网格单元具有周期性调谐曲线，它们在多个位置活跃，称为发射场，这些发射场在环境中呈六边形排列(Hafting等人，2005年). 它们的周期结构由六角晶格给出。调谐曲线Ω的周期结构_我(x)反映其对称性，即将调谐曲线映射到自身的向量集。由于我们想了解周期结构是如何影响人口代码的分辨率的，所以我们将网格单元的概念推广到允许不同的周期结构，而不仅仅是六边形。数学上，周期结构的对称性可以用格子来描述 $L（左）$ ，其构造如下：取一组独立向量(v（v）_α)_{1≤α≤D类}在里面D类-维度空间 $ℝ^{D类}$ ，并考虑这些向量的所有可能组合及其整数倍-每个这样的向量组合指向晶格的一个节点，使得这些向量的并集表示晶格本身。例如，方形格子(图1A，底部）由基向量给出v（v）₁=（1,0）和v（v）₂= (0, 1). 数学上，格子 $L（左） \subset ℝ^{D类}$ 是

\begin{array}{l} L（左） = \sum_{α = 1}^{D类} {k个}_{α} {v（v）}_{α} & 对于 & {k个}_{α} \in ℤ, {v（v）}_{α} \in ℝ^{D类} \end{array},

为此(v（v）_α)_{1≤α≤D类}是 $ℝ^{D类}$ 。我们不考虑退化格。在这项工作中，我们遵循康威和斯隆（1992）。应用字段的术语可能略有不同，尤其是关于包装的命名约定，这是格的泛化(惠塔克，1981年;Nelson，2002年). 我们将在下面讨论格的这些推广。

图1

下载资产未结资产

网格单元和模块。

(A类)网格单元的构造：给定调谐形状Ω和晶格 $L（左）$ ，这里是由*v（v）*₁和*v（v）*₂具有φ=π/2，一个周期表示Ω相对于 $L（左）$ 一个定义了 $Ω^{L（左）} (x)$ 在基本领域*L（左）*作为Ω的值(第页)应用于从零开始的距离，然后在上面重复此地图 $ℝ^{2}$ 喜欢 $L（左）$ 平铺空间。这种构造可以用于晶格 $L（左）$ 任意尺寸(方程式7). (B类)网格模块：三个网格单元（橙色、绿色和蓝色）的发射率由颜色强度表示。电池的调谐相同（Ω和 $L（左）$ 相同），但它们的空间相位不同*c（c）*_我这些具有不同空间相位的相同调谐单元共同定义了一个网格模块。

https://doi.org/10.7554/eLife.05979.003

基于这样的格子 $L（左）$ ，我们构造了周期调谐曲线，如所示图1A.我们从格子开始 $L（左）$ 和调谐形状 $Ω : ℝ^{+} \to [0, 1]$ 从统一到零；Ω(第页)描述了远程周期调谐曲线的发射率第页从任何点阵点开始，应该至少是连续可微的两倍。每个晶格点 $第页 \in L（左）$ 有一个域 ${V（V）}_{第页} \subset ℝ^{D类}$ 称为沃罗诺伊地区，定义为

{V（V）}_{第页} = {x \in ℝ^{D类} | ∥ x - 第页 ∥ < ∥ x - q个 ∥ \forall q个 \in L（左） \land 第页 \neq q个},

包含所有点的x更接近第页比任何其他晶格点q个。请注意V（V）_第页∩V（V）_q个=ϕ如果第页≠q个而这一切 $第页, q个 \in L（左）$ 存在唯一的向量 $v（v） \in L（左）$ 具有V（V）_第页=V（V）_q个+v（v）.

包含null（0）向量的域称为基本域，用L（左）:=V（V）₀对于每个 $x \in ℝ^{D类}$ 有一个唯一的格点 $第页 \in L（左）$ 那张地图x进入基本领域： $x - 第页 \in L（左）$ 。我们将此映射称为 $π_{L（左）}$ 用这个符号可以将Ω周期化为 $L（左）$ 通过将网格单元的调整曲线定义为 $Ω^{L（左）}$ :

Ω^{L（左）} (x) : ℝ^{D类} \to ℝ^{+}, x \mapsto {（f）}_{米 一 x} \cdot Ω ({∥ π_{L（左）} (x) ∥}^{2}),

哪里（f）_最大值是神经元的峰值放电速率。请注意，在整篇论文中，我们设置了（f）_最大值=τ=1，为简单起见。如所示图1A，在基本领域内L（左），调谐曲线 $Ω^{L（左）}$ 上述定义是径向对称的。沿着的节点重复此模式 $L（左）$ 类似于瓷砖。

网格模块定义为M（M）网格单元格 $Ω_{我}^{L（左）}$ , $我 \in {1, \dots, M（M）}$ 具有相同但空间偏移的调谐曲线，即， $Ω_{我}^{L（左）} (x) = Ω^{L（左） + {c（c）}_{我}} (x)$ 和空间相位 ${c（c）}_{我} \in L（左）$ （请参见图1B). 模块内的各种相可以通过它们的相密度进行总结 $ρ (c（c）) = {\sum^{}}_{我 = 1}^{M（M）} δ (c（c） - {c（c）}_{我})$ 这一定义的动机是观察大鼠内嗅皮层空间移位的六边形调谐网格细胞(Hafting等人，2005年;Stensola等人，2012年).

任何网格模块都有其独特的特征 $(Ω, ρ, L（左）)$ 为了研究不同周期结构的作用，我们可以确定调谐形状Ω和密度ρ只改变格子 $L（左）$ 找到产生最高FI的晶格。

结果

确定网格模块的分辨率如何取决于周期结构 $L（左）$ ，我们计算人口FIJ型_ς(x)具有签名的网格单元模块 $ς = (Ω, ρ, L（左）)$ ，它描述了调谐形状、发射场密度和晶格。通过固定调谐形状Ω和数字 $| ρ | = M（M）$ 对于空间相位，我们可以比较不同周期结构的分辨率。(表1包含变量的词汇表。）

表1

首字母缩写词、变量和术语列表

https://doi.org/10.7554/eLife.05979.004

D类	刺激空间的尺寸 $ℝ^{D类}$
金融机构	费希尔信息，通常表示为J型(方程式3)
$L（左）$	描述周期结构的非简并点格(方程式5)
L（左）	的基本域 $L（左）$ ，这是包含0的Voronoi单元格(方程式6)
Ω	调整形状
支持（Ω）	Ω的支持，即Ω不消失的子集
$Ω^{L（左）}$	周期性调整曲线打开 $ℝ^{D类}$ ，其中 $L（左）$ 是一个D类-维晶格和Ω调谐曲线。简单地称为“网格单元”(方程式7)
ρ	栅元相位密度c（c）_我模块内 $ρ (c（c）) = {\sum^{}}_{我 = 1}^{M（M）} δ (c（c） - {c（c）}_{我})$
M（M）	电网模块中的相数 $\int_{L（左）} ρ = M（M）$
$ς = (Ω, ρ, L（左）)$	定义网格模块的签名，该模块是空间相位不同的网格单元的集合c（c）_我，由定义ρ和调谐曲线 $Ω^{L（左）}$
$det（探测） (L（左）)$	格的行列式 $L（左）$ （等于L（左）)
B类_R（右）(0)	的子集 $ℝ^{D类}$ 包含距离小于的所有点R（右）来自0
$Δ (L（左）)$	一个格子的堆积比，即体积最大的 ${B类}_{R（右）} (0)$ 放在里面L（左）除以 $det（探测） (L（左）)$ (方程式15)
$H（H）$ , $问$	单位节点间距的六角形和方形平面晶格(图2)
$F类 C类 C类$ , $B类 C类 C类$ , $C类$	分别以面为中心、以体为中心和以立方晶格为单位的节点到节点距离(图4).
信托收据J型	FI的轨迹，即对角元素的总和
J型_ς	带有签名的网格模块的人口FIς
$信托收据 {J型}_{L（左）}$ , $信托收据 {J型}_{问}$ , $信托收据 {J型}_{H（H）}$	晶格中每个神经元的FI轨迹 $L（左）$ ( $问$ 和 $H（H）$ （分别为）中定义的固定凸形Ω式26
$信托收据 {J型}_{L（左）}^{M（M）}$	晶格的FI轨迹 $L（左）$ 对于M（M）随机分布的相位L（左）对于相同的通气功能

格和嵌套网格代码的缩放

我们的网格结构有一个明显的自由度，即网格的长度尺度或网格大小 $L（左）$ 即基本域的宽度L（左）。对于具有签名的模块 $ς = (Ω, ρ, L（左）)$ 以及任意比例因子λ>0，重新缩放的结构 $λ ς : = (Ω (λ 第页), ρ (λ x), λ \cdot L（左）)$ 也是一个网格模块。相应的调谐曲线满足 ${(Ω \circ λ)}_{λ L（左）} (x) = Ω_{L（左）} (λ x)$ 因此，它只是前者的缩放版本。事实上，正如我们在“材料和方法”部分所示，重新缩放模块的FI为λ⁻² J型_ς(0). Cramér-Rao界(方程式4)这意味着无偏估计器的局部分辨率可以随着网格尺寸的减小而迅速提高，即减小λ.

然而，对于任何网格模块 $ς = (Ω, ρ, L（左）)$ 后验概率，即给定特定峰值计数向量的可能位置的可能性K（K）= (k个₁,…,k个_N个)，也是周期性的。这遵循贝叶斯规则：

P（P） (x | K（K）) = \frac{P（P） (K（K） | x) \cdot P（P） (x)}{P（P） (K（K）)} \propto P（P） (x) \prod_{我 = 1}^{N个} {P（P）}_{我} ({k个}_{我} | τ Ω_{我}^{L（左）} (x)) .

由于右侧在以下操作下是不变的 $L（左）$ 在x上，这个方程的左边也是。因此，解码器无法区分网格单元的多个发射场，因此λ→ 0全局分辨率接近先验不确定性(Mathis等人，2012a,2012年b). 通过组合具有不同空间周期的多个网格模块，可以克服这一基本限制，抵消周期性引起的歧义，并在最小尺度上保持最高分辨率。因此，可以得到网格模块的嵌套种群，其空间周期从粗到细不等。单个模块在一个尺度上的FI决定了下一个模块的最佳长度尺度(Mathis等人，2012a,2012年b). 每个模块的FI越大，后续规模的细化程度就越高(Mathis等人，2012a,2012年b). 这一结果强调了找到赋予网格模块最大FI的格的重要性，但也强调了格的具体规模可以为本研究确定。

带格子的网格模块的FI $L（左）$

我们现在计算带有签名的网格模块的FI $ς = (Ω, ρ, L（左）)$ 对于放电在统计上独立的细胞(方程式1)，联合概率因子；因此，群体FI就是每个神经元对个体FI贡献的总和， ${J型}_{ς} (x) = {\sum^{}}_{我 = 1}^{M（M）} {J型}_{Ω_{我}^{L（左）}} (x)$ 单个神经元仅因空间相位不同而不同c（c）_我，因此 ${J型}_{Ω_{我}^{L（左）}} (x) = {J型}_{Ω^{L（左）}} (x - {c（c）}_{我})$ 因此， ${J型}_{ς} (x) = {\sum^{}}_{我 = 1}^{M（M）} {J型}_{Ω^{L（左）}} (x - {c（c）}_{我})$ ，仅取决于函数 ${J型}_{Ω^{L（左）}} (第页)$ 和偏差x−c（c）_我，其中c（c）_我是最近的晶格点 ${c（c）}_{我} + L（左）$ 到x.如果网格中心密度ρ是均匀的 $L（左）$ 那么，对所有人来说 $x \in ℝ^{D类}$ :J型_ς(x) ≈J型_ς(0). 因此，仅考虑原产地的金融机构就足够了，可以写成：

{J型}_{ς} (0) = \sum_{我 = 1}^{M（M）} {J型}_{Ω^{L（左）}} ({c（c）}_{我}) = \int_{L（左）} {J型}_{Ω^{L（左）}} (c（c）) ρ (c（c）) d日 c（c） .

对于均匀分布的空间相位c（c）_我以及神经元数量的增加M（M），大数定律暗示

\underset{M（M） \to \infty}{林} | \frac{det（探测） (L（左）)}{M（M）} {J型}_{ς} (0) - \int_{L（左）} {J型}_{Ω^{L（左）}} (c（c）) d日 c（c） | = 0 .

在这里， $det（探测） (L（左）)$ 表示基本域的体积。因此，对于大量神经元 $M（M） = \int_{L（左）} ρ (c（c）) d日 c（c）$ 我们获得

{J型}_{ς} (0) \approx \frac{M（M）}{det（探测） (L（左）)} \int_{L（左）} {J型}_{Ω^{L（左）}} (c（c）) d日 c（c） .

这意味着0处的总体FI大约由基本域内的平均FI给出L（左）乘以神经元数量M（M）现在假设supp（Ω）=[0，R（右）]对于某些正半径R（右）在该半径之外，调谐形状为零并且发射速率消失。因此，有助于FI的网格单元的空间相位x=0位于球内B类_R（右）(0). 如果我们现在也假设这个球包含在基本域中， ${B类}_{R（右）} (0) \subset L（左）$ ，我们得到

\int_{L（左）} {J型}_{Ω^{L（左）}} (c（c）) d日 c（c） = \int_{{B类}_{R（右）} (0)} {J型}_{Ω^{L（左）}} (c（c）) d日 c（c） .

这个结果意味着任何网格代码 $ς = (Ω, ρ, L（左）)$ ，带有大型M（M），电源（Ω）=[0，R（右）]、和 ${B类}_{R（右）} (0) \subset L（左）$ ，满足

{J型}_{ς} (0) \approx \frac{M（M）}{det（探测） (L（左）)} \int_{{B类}_{R（右）} (0)} {J型}_{Ω^{L（左）}} (c（c）) d日 c（c） .

因此，原点的FI大约等于R（右）-0周围的球和神经元数量M（M），按R（右）-球到达基本域区域L（左）.由于径向对称 $Ω^{L（左）}$ 、FI矩阵 ${J型}_{Ω^{L（左）}} (c（c）)$ 是对角线，具有相同的条目，保证了空间分辨率的各向同性。每个坐标轴的误差以相同的值为界，即对角线元素1的倒数/J型_ς(0)_ii（ii）对于这样的人群来说。而不是考虑FI矩阵J型_ς（0），因此我们可以考虑J型_ς（0），它是J型_ς(0). 根据方程式4，1/吨J型_ς（0）限定所有维度的均方误差总和 $ε (\hat{x} | x)$ .

对于两个格子 ${L（左）}_{1}$ , ${L（左）}_{2}$ ，使用B类_R（右）(0) ⊂L（左）₁∩L（左）₂我们因此获得

\frac{信托收据 {J型}_{Ω^{{L（左）}_{1}}}}{信托收据 {J型}_{Ω^{{L（左）}_{2}}}} = \frac{det（探测） ({L（左）}_{2})}{det（探测） ({L（左）}_{1})},

这意味着网格模块的分辨率与其基本域的体积成反比。周期性结构 $L（左）$ 从而直接影响网格模块的分辨率。这一结果表明，找到最大FI直接转化为找到具有最高堆积比的晶格。

格子填充率

球形填充问题是数学界普遍感兴趣的问题(康威和斯隆，1992年)并具有从晶体学到信息理论的广泛应用(巴洛，1883年;香农，1948年;惠塔克，1981年;格雷和纽霍夫，1998年;Gruber，2004年). 包装时R（右）-球B类_R（右）在里面 $ℝ^{D类}$ 在非重叠方式下，填料的密度定义为球所覆盖空间的分数。对于晶格 $L（左）$ ，由给出

\frac{体积 ({B类}_{R（右）} (0))}{det（探测） (L（左）)},

也就是包装比 $Δ (L（左）)$ 晶格的。对于给定的晶格，通过选择最大可能的R（右），称为填充半径，定义为包含原点的Voronoi区域的内半径(康威和斯隆，1992年).图2蓝色表示六边形和正方形点阵中半径最大的圆盘，并说明填充比率。

图2

下载资产未结资产

周期化网格-细胞调谐曲线 $Ω^{L（左）}$ 对于两个平面晶格(A类)六边形（等边三角形）晶格 $H（H）$ 和(B类)正方形格子 $问$ ，与基向量一起*v（v）*₁和*v（v）*₂.

这些是π/六角晶格和π/方形格子为2。基本域，即0附近的Voronoi单元，以灰色显示。根据晶格对称性生成的其他几个域用虚线标记。蓝色圆盘表示具有最大半径的圆盘*R（右）*这可以包含在两个基本域中。对于相等且统一的节点到节点距离，即：， $| {v（v）}_{1} | = | {v（v）}_{2} | = 1$ ，两个格子的最大半径均为1/2。填料比Δ为 $Δ (H（H）) = π / \sqrt{12}$ 对于六角形和 $Δ (问) = π / 4$ 对于正方形晶格；六方晶格的密度约为正方形晶格的15.5%。

https://doi.org/10.7554/eLife.05979.005

FI和包装比

我们现在得出了本研究的主要发现：在具有不同晶格的网格模块中，具有最高填充比的晶格导致最高的空间分辨率。

为了得到这个结果，让我们用supp（Ω）=[0固定一个调谐形状Ω，R（右）]，个格子 ${L（左）}_{j}$ 这样的话B类_R（右）(0) ⊂L（左）_j对于1≤j≤K（K）和均匀密度ρ对于每个基数相等的基本域M（M）包装比的任何线性顺序，

Δ ({L（左）}_{1}) \leq \dots \leq Δ ({L（左）}_{j}) \leq \dots \leq Δ ({L（左）}_{K（K）}),

由翻译式14FI痕迹的顺序相同

信托收据 {J型}_{Ω^{{L（左）}_{1}}} \leq \dots \leq 信托收据 {J型}_{Ω^{{L（左）}_{j}}} \leq \dots \leq 信托收据 {J型}_{Ω^{{L（左）}_{K（K）}}},

因此，这些模块的分辨率：封装率越高，网格模块的FI越高。

条件supp（Ω）=[0，R（右）]带有B类_R（右）(0) ⊂L（左）虽然有限制，但与实验观察一致，即网格单元倾向于在网格场之间停止发射，并且场半径和空间周期之间的典型比率远低于1/2(Hafting等人，2005年;Brun等人，2008年;Giocomo等人，2011年). 通常，使FI最大化的调谐宽度不一定满足此条件；看见图3、4，其中调谐曲线的最佳支撑半径θ₂大于内半径R（右）=1/2L（左）同样的观察结果将适用于更高的维度(D类>2），与高斯调谐曲线的最佳调谐宽度随空间维数的增加而增加的结果一致，无论空间是无限的(Zhang和Sejnowski，1999年)或有限(Brown和Bäcker，2006年). 当调谐曲线支架的半径R超过内半径时，最佳晶格可以是不同的我们将用数字表示特定调谐曲线和泊松噪声。然而，像我们刚才演示的那样，对于像实验中观察到的那样分离良好的场，密度最大的晶格为任何调谐形状的Ω提供了最高的分辨率。

图3带1个补充查看所有内容

下载资产未结资产

二维网格单元模块的Fisher信息。

(A类)顶部：周期性凹凸函数Ω和方格 $L（左）$ ，用于各种参数组合θ₁和θ₂.给，θ₁调节衰减θ₂支持。中间：平均轨迹 $信托收据 {J型}_{L（左）}$ 均匀分布网格单元的Fisher信息（FI） $Ω^{L（左）}$ .六边形( $H（H）$ )和正方形( $问$ )格被视为不同的θ₁和θ₂值。当支持完全在基本域内时，六边形网格单元的FI优于二次网格(θ₂<0.5，见正文）。底部：比率 $信托收据 {J型}_{H（H）} / 信托收据 {J型}_{问}$ 作为调谐参数的函数θ₂。对于θ₂<0.5时，六边形布居提供了平方布居的3/2倍的分辨率，这与各自的填充比有关。(B类)平均 $信托收据 {J型}_{L（左）}$ 对于均匀分布在由角度分隔的基向量生成的格子中的网格单元φ（上图所示的基础）。 $信托收据 {J型}_{L（左）}$ 表现得像1/sin(φ)最大值为π/3. (C类)5000变现的分配 $信托收据 {J型}_{L（左）}^{M（M）} / M（M）$ 对于人口为0M（M）=200个随机分布的神经元。对于六角形和方形晶格，参数为θ₁=1/4和θ₂= 0.4. 平均值与(A类). 然而，由于神经元数目有限，不同实现方式的FI差异很大，在大约20%的情况下，方形晶格模块的性能优于六角形晶格。

https://doi.org/10.7554/eLife.05979.006

图4

下载资产未结资产

三维网格单元模块的Fisher信息。

(A类)所考虑的三种晶格：面心立方( $F类 C类 C类$ )，以身体为中心的立方体( $B类 C类 C类$ )、和立方( $C类$ ). (B类) $信托收据 {J型}_{L（左）}$ 对于三个晶格和各种参数组合的周期化bump函数Ωθ₁和θ₂.Fisher信息（FI） $F类 C类 C类$ 当支撑完全在基本域内时，网格单元的性能优于其他网格(θ₂<0.5，见正文）。对于较大的θ₂最佳晶格取决于Voronoi单元边界和调谐曲线之间的关系。(C类)比率 $信托收据 {J型}_{L（左）} / 信托收据 {J型}_{C类}$ 作为的函数θ₂对于 $L（左） \in {F类 C类 C类, B类 C类 C类, C类}$ 。对于θ₂小于0.5时，六角布居的分辨率是平方布居的3/2倍，如填充比所预测的那样。(D类)平均值 $信托收据 {J型}_{{L（左）}_{φ, ψ}}$ 对于网格内均匀分布的网格单元 ${L（左）}_{φ, ψ}$ 由角度分隔的基向量生成φ和ψ（如上所示；θ₁=θ₂= 1/4). $信托收据 {J型}_{{L（左）}_{φ, ψ}}$ 表现为1/（sinφ●正弦ψ)并且对于具有最小体积的晶格具有其最大值。(E类)5000变现的分配 $信托收据 {J型}_{L（左）}^{M（M）} / M（M）$ 对于人口为0M（M）=200个随机分布的神经元。参数：θ₁= 1/4,θ₂= 0.4. 平均值与(B类). 由于神经元数目有限，不同实现方式的FI变化很大。

https://doi.org/10.7554/eLife.05979.008

低维空间中格子的最佳填充比是众所周知的。确立了我们的主要成果后，我们现在可以利用丰富的文献，尤其是康威和斯隆（1992）)，讨论2D和3D环境中网格单元的预期发射场结构。

最佳二维网格单元

包装比为 $π / \sqrt{12}$ ，六角形晶格是平面上密度最大的晶格(拉格朗日，1773年). 根据式14，六边形点阵是平面上栅格发射场的最佳布置。例如，它的性能优于密度为π/4，增加约15.5%（见图2). 因此，沿六边形晶格周期化的网格模块的FI比沿正方形晶格周期化模块的性能好相同的因素。

为了提供一个具体的例子，我们计算了每个神经元的平均FI的轨迹 $信托收据 {J型}_{ς} / \int_{L（左）} ρ$ 供签署 $ς = (Ω, ρ, L（左）)$ 并选择了格子 $L（左）$ 要么是六角形晶格 $H（H）$ 或二次格子 $问$ 。我们将每个神经元的平均FI轨迹表示为： $信托收据 {J型}_{L（左）}$ = $信托收据 {J型}_{ς} / \int_{L（左）} ρ$ ; $信托收据 {J型}_{H（H）}$ 和 $信托收据 {J型}_{问}$ 定义类似。我们考虑了泊松尖峰统计，并使用了一个凹凸不平的调谐形状Ω(式26，“材料和方法”部分）。调谐形状Ω取决于两个参数θ₁和θ₂，其中θ₁以Ω和θ₂定义支撑半径。周期性调整曲线 $Ω^{问}$ 在顶部显示了不同的参数图3A和中图3-图补充1.

图3A描述 $信托收据 {J型}_{H（H）}$ 和 $信托收据 {J型}_{问}$ 对于的各种值θ₁和θ₂通常，对于具有宽调谐（大）的电网模块，FI更大θ₂)和陡峭的调谐坡度（小θ₁).图3A也证明了只要θ₂≤ 1/2, $信托收据 {J型}_{H（H）}$ 持续表现优异 $信托收据 {J型}_{问}$ 但这种影响有多大？正如我们的理论所预测的那样，通过堆积比的关系，六边形晶格的网格模块优于方形晶格 $\sqrt{三} / 2$ ，只要支撑半径θ₂在单位长度的六边形和方形晶格的基本域内，即，θ₂≤1/2（底部图3A). 随着支撑半径的增大，六边形晶格的FI不再一定大于方形晶格的FI；调谐曲线和边界形状的特定相互作用决定了哪个晶格更好：对于θ₁= 1/4, $信托收据 {J型}_{H（H）} / 信托收据 {J型}_{问}$ 迅速下降θ₂=0.5，即使对于θ₁=1，比率保持恒定θ₂= 0.6.

接下来，我们计算了由两个带角度的酉基向量生成的更大平面晶格族的每个神经元的FIφ.图3B显示器 $信托收据 {J型}_{L（左）}$ 对于φ∈ [π/3,π/2] ，斜率参数θ₁=1/4，不同的支撑半径θ₂。对于具有酉长度的晶格，值为φ不能低于π/3 $信托收据 {J型}_{L（左）}$ 随角度增加而衰减φ的确，根据式13，金融机构的情况是 $1 / det（探测） L（左） = 1 / 罪 (φ)$ 因此，六角晶格达到最大值π/3.

金融机构 $信托收据 {J型}_{L（左）}$ 是所有相位的平均值，假设相位密度趋于常数；但这些值是否也指示了小神经群体？为了回答这个问题，我们计算了200个神经元的FI，因为在这种大小的斑块中发现了一些假定的网格细胞(Ray等人，2014年). 对于M（M）=200个随机选择的阶段(图3C)，归一化FI的平均值 $信托收据 {J型}_{L（左）}^{M（M）} / M（M）$ 通过计算每个神经元的FI，可以很好地捕捉到5000多个实现图3A然而，由于FI的波动，在大约20%的情况下，方形晶格优于六角形晶格。

我们的理论表明，对于径向对称调谐曲线，六角晶格在所有平面晶格中提供了最佳分辨率。这一结论与早期的发现一致：Wei等人考虑了分辨率的概念，定义为每最小可分辨尺度的总体代码范围，然后证明了具有六边形调谐的嵌套网格单元的总体对于winner-take-all和Bayesian最大似然译码器是最佳的(Wei等人，2013年). Guanella和Verschure基于最大似然解码对六边形和其他规则格进行了数值比较(Guanella和Verschure，2007年).

三维网格单元的最优网格

高斯证明了任何立方晶格的堆积比都有界于 $π / (三 \sqrt{2})$ 并且对于以面为中心的立方体可以获得该值( $F类 C类 C类$ )晶格(高斯，1831年)如所示图4A这意味着最佳的3D网格中心调整由 $F类 C类 C类$ 格子。为了进行比较，我们还计算了其他两个重要3D晶格的平均布居数FI：立方晶格( $C类$ )和以身体为中心的立方晶格( $B类 C类 C类$ )，均如所示图4A.

在保持bump-like调谐形状Ω和独立泊松噪声的情况下，我们比较了网格模块与此类网格的分辨率(图4B). FI的平均轨迹表示为 $信托收据 {J型}_{F类 C类 C类}$ , $信托收据 {J型}_{B类 C类 C类}$ 、和 $信托收据 {J型}_{C类}$ 分别是。只要支持θ₂Ω小于1/2时，支撑是所有三个格的基本域的子集。因此 $F类 C类 C类$ 表现优于 $B类 C类 C类$ 和 $C类$ 格子。随着人口痕迹的比率，FI随填充比率而缩放(图4C), $F类 C类 C类$ -网格单元为相同数量的神经元提供的分辨率比网格单元高约41% $C类$ -网格单元格。同样， $F类 C类 C类$ -网格单元提供的FI比 $B类 C类 C类$ -网格单元格。

接下来，我们计算了一大类立方晶格的每个神经元的FI ${L（左）}_{φ, ψ}$ 由三个具有跨度角的酉基向量生成φ和ψ.图4D显示器 $信托收据 {J型}_{{L（左）}_{φ, ψ}}$ 对于θ₁=θ₂=1/4和各种φ和ψ.决议 $信托收据 {J型}_{L（左）}$ 随着角度的增加而衰减，并且对于体积最小的晶格，其最大值为式13.

为了研究有限尺寸效应，我们用随机空间相位模拟了5000个由200个网格单元组成的种群。定性而言，结果(图4E)与2D中的匹配(图3C). 尽管模块尺寸较小， $F类 C类 C类$ 优于立方晶格 $C类$ 在所有模拟实现中。

用于网格间调整的等优非晶格解决方案

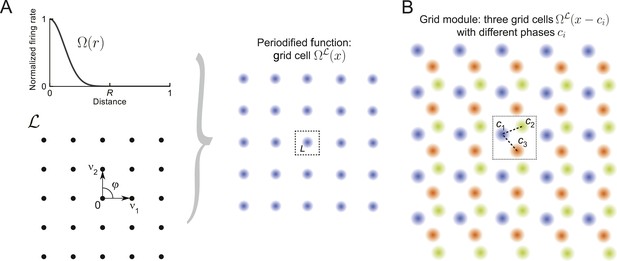
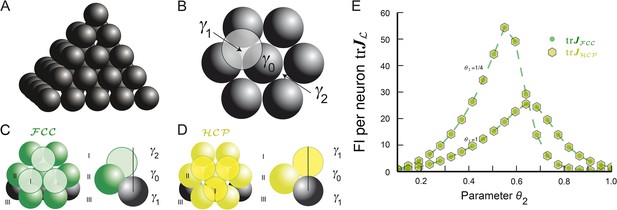
水果通常排列在 $F类 C类 C类$ 形成(图5A). 一个人从一层六边形球体开始到达这个格子。这需要指定两个基向量，这是2D中最密集的填充。为了在3D中最大化填充比，下一层六边形排列的球体必须尽可能紧密地堆叠。第三个基向量和最后一个基向量有两种选择，表示为γ₁和γ₂在里面图5B（模数六角对称）。如果有人选择γ₁，则下面两层没有中心位于该位置的球体γ₁，但却有一个γ₂（反之亦然）。层的堆叠如所示图5C并生成 $F类 C类 C类$ 格子。

图5

下载资产未结资产

3D中的晶格和非晶格解决方案。

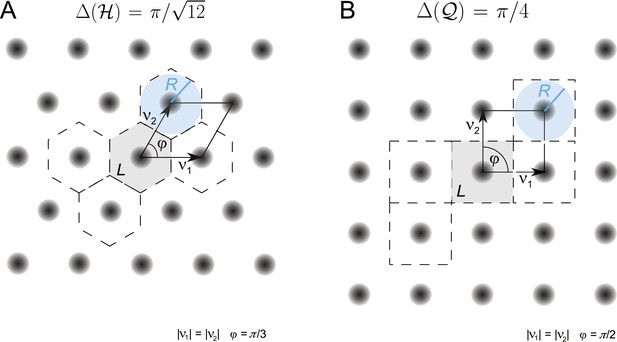
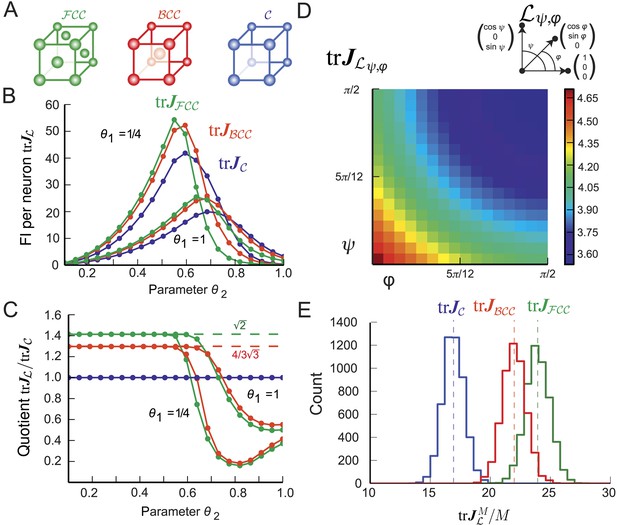
(A类)球体的堆叠，如 $F类 C类 C类$ 格子。在这个3D中密度最大的晶格中，每个球体与其他12个球体接触，每个节点有四个不同的平面六角形晶格。(B类)在以γ₀（黑色）可以从六个位置之一开始放置另一个六边形层，其中两个位置高亮显示，γ₁和γ₂. (C类)如果按照顺序（…，γ₁,γ₀,γ₂，…）获得 $F类 C类 C类$ 注意，层I中的球体与层III中的球体不对齐(D类)按照顺序（…，γ₀,γ₁,γ₀，…）导致六角密封填料 $HCP公司$ 再次，每个球体与其他12个球体接触。然而，通过每个节点只有一个平面，其中球体中心的排列是正六边形晶格。此填料与 $F类 C类 C类$ ，但不是晶格。(E类) $信托收据 {J型}_{L（左）}$ 用于缓冲功能Ω $L（左） = F类 C类 C类$ 和 $HCP公司$ 用于各种参数组合θ₁和θ₂;θ₁调节衰变和θ₂支持。这两种填料具有相同的填充比，对于该调谐曲线，也提供相同的空间分辨率。FI：费希尔信息。

https://doi.org/10.7554/eLife.05979.009

通过选择，可以达到相同的密度γ₁对于顶层和底层以下的层。然而，正如这种排列，称为六角形密排( $HCP公司$ )，不能用三个向量描述，它没有定义晶格（请参见图5D)尽管它和 $F类 C类 C类$ 此类填料，定义为相等的非重叠球的排列(康威和斯隆，1992年;Hales，2012年)，泛化格。

虽然可以为定义网格模块任何格子，如我们上面所示，一个不能由于缺乏对称性，以有意义的方式为任意封装定义网格模块。但对于任何给定的包装 $P（P）$ 属于 $ℝ^{D类}$ 通过球 ${B类}_{1}$ 在半径为1的情况下，可以通过推广格的定义来定义“网格单元”(公式7). 为此，考虑 $ℝ^{D类}$ 通过 $P（P）$ 对于每个位置 $x \in ℝ^{D类}$ 有一个独特的沃罗诺伊细胞V（V）_第页带节点 $第页 \in P（P）$ 一个定义网格单元的调整曲线 $Ω^{P（P）} (x)$ 通过根据 $Ω ({∥ 第页 - x ∥}^{2})$ 用于调节形状Ω和距离 $∥ 第页 - x ∥$ 根据具体的包装，此调整曲线 $Ω^{P（P）}$ 可能是周期性的，也可能不是周期性的。因为包装 $P（P）$ 通常对称性比格子少 $L（左）$ ，任意单元格中的“网格单元格” $P（P）$ 通常不能用于定义“网格模块”。要解释原因，请考虑任意包装和独特的Voronoi电池V（V）₀包含点0的。选择M（M）均匀分布相c（c）₁,…,c（c）_M（M）在内部V（V）₀.内的位置V（V）₀然后将被移位的调谐曲线均匀覆盖 $Ω_{我} (x) : = Ω^{P（P）} (x - {c（c）}_{我})$ 然而，典型地，不同的Voronoi细胞既不一致，也不具有相似的体积。因此，Ω_我通常会不用相同的密度覆盖每个Voronoi单元，因此无法定义合适的网格模块。格子不存在此问题。这里是等价类 ${c（c）}_{我} + L（左）$ 用相同的密度覆盖每个细胞。

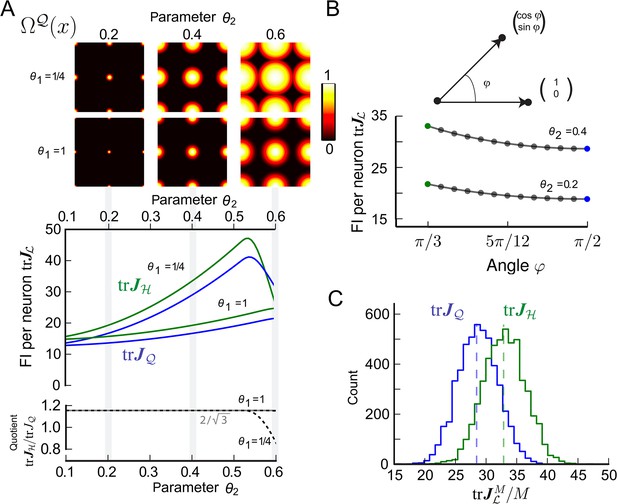
另一方面，高度对称的填料确实允许定义网格模块。例如，六角密封填料 $HCP公司$ 可用于定义网格单元 $Ω^{HCP公司} (x)$ 。使用相同的对称参数方程式9–11，意味着金融机构：

{J型}_{(Ω, ρ, H（H） C类 P（P）)} (x) \approx {J型}_{(Ω, ρ, H（H） C类 P（P）)} (0) \approx \frac{M（M）}{体积 ({V（V）}_{0})} \int_{{V（V）}_{0}} {J型}_{Ω^{H（H） C类 P（P）}} (c（c）) d日 c（c） .

最大内半径R（右）对于 $HCP公司$ 具有网格大小λ=1等于1/2。与晶格一样，我们假设supp（Ω）=[0，R（右）]和B类_R（右）(0) ⊂V（V）₀然后被积函数在距离0大于1/2时消失。因此，我们得到：

{J型}_{(Ω, ρ, H（H） C类 P（P）)} (0) \approx \frac{M（M）}{体积 ({V（V）}_{0})} \int_{{B类}_{1 / 2} (0)} {J型}_{Ω^{H（H） C类 P（P）}} (c（c）) d日 c（c） .

考虑相同的调谐形状Ω和相位数M（M）对于 $F类 C类 C类$ 点阵，其内半径也最大为1/2，式13为 $F类 C类 C类$ 格子：

{J型}_{(Ω, ρ, F类 C类 C类)} (0) \approx \frac{M（M）}{det（探测） (F类 C类 C类)} \int_{{B类}_{1 / 2} (0)} {J型}_{Ω^{F类 C类 C类}} (c（c）) d日 c（c） .

由于两个基本域具有相同的卷，即， $det（探测） (F类 C类 C类) = 体积 ({V（V）}_{0})$ ，并且限制在这些球上的被积函数是相同的，即， ${J型}_{Ω^{F类 C类 C类}} |_{{B类}_{1 / 2} (0)} = {J型}_{Ω^{H（H） C类 P（P）}} |_{{B类}_{1 / 2} (0)}$ ，我们可以得出如下结论：网格模块包括 $F类 C类 C类$ 或 $HCP公司$ -相似的对称性具有相同的FI。我们还数值计算了 $HCP公司$ 网格单元格并将其与 $F类 C类 C类$ 案例。对于凹凸型调谐曲线Ω，两个FI是相同的(图5E)从Ω的径向对称性可以看出。因此，网格单元定义为 $HCP公司$ 或 $F类 C类 C类$ 对称性提供最佳分辨率。

图5D、E显示循环序列(γ₀,γ₁)和(γ₁,γ₀,γ₂)导致 $HCP公司$ 和 $F类 C类 C类$ 分别是。中心γ₀,γ₁、和γ₂也可以用来说明填料的最后一点：有无限多不同的填料具有相同的密度 $π / (三 \sqrt{2})$ 它们可以由不相等的单词构成，这些单词是通过带字母的三角形有限遍历生成的γ₀,γ₁、和γ₂(Hales，2012年)，每个字母代表层的三个方向之一。例如(γ₀,γ₁,γ₀,γ₂)描述了具有相同密度的另一种填料。所有填料都有一个特点：每个球体周围正好有12个球体，排列在其中之一 $HCP公司$ 或 $F类 C类 C类$ 格子式样(Hales，2012年). 这些填料也可用于定义网格模块，因为所有单元中的相密度都是均匀的。此外，在计算FI时 $HCP公司$ 和 $F类 C类 C类$ (方程式18–20)只有本地整合是必要的，这样的混合包装将有与纯 $HCP公司$ 或 $F类 C类 C类$ 填料。

只有在最近几年，才证明没有其他安排比 $F类 C类 C类$ 一个被称为开普勒猜想的问题(Hales，2005年,2012). 根据这些结果和我们对 $信托收据 {J型}_{HCP公司}$ 和 $信托收据 {J型}_{F类 C类 C类}$ (图5E)，我们预测3D网格单元将对应于这些填料之一。虽然在3D中，填料密度与晶格密度相等，但在2D中却不是这样。从而证明了六角形晶格是所有平面填料中密度最大的一种(1910年，星期四); 2D中的网格单元应当具有六边形晶格结构。

讨论

当动物靠近对应于平面六角形晶格顶点的任意多个位置之一时，网格单元处于活动状态(Hafting等人，2005年). 我们概括了网格单元到任意尺寸，使得网格单元的随机活动在 $ℝ^{D类}$ 周期性由底层晶格的对称群捕获 $L（左）$ .A型网格模块由具有相同空间周期但不同空间相位的多个单元组成。然后，利用信息论，我们询问哪个晶格具有最高的空间分辨率。

我们发现网格模块的分辨率与 $L（左）$ -填充率最高的晶格对应于分辨率最高的网格模块。众所周知的数学结果(拉格朗日，1773年;高斯，1831年;康威和斯隆，1992年)然后表明六角形晶格最适合表示2D，而 $F类 C类 C类$ 格子是3D的最佳选择。在3D中，但在2D中，也有与最密集晶格分辨率相同的非晶格填充(1910年，星期四;Hales，2012年). 在3D中，这些高度对称的最佳解决方案的一个共同特征是，每个网格场都被其他12个网格场包围，这些网格场以任意一种方式排列 $F类 C类 C类$ 格子或六角形密排方式。如我们所示，这些解决方案是通过最大化分辨率从所有可能的包装中产生的。然而，FI测量的分辨率并不能区分具有不同对称性的最佳包装溶液。一个现实的神经元解码器，例如基于种群向量平均值的解码器，是否支持一个特定的解决方案，是一个有趣的悬而未决的问题。

如我们所示，使用FI可以找到最佳 $L（左）$ 对所有维度都可解析处理D类并在限制性但与实验测量一致的假设下，挑选出最密集的晶格作为最佳调谐形状(Hafting等人，2005年;Brun等人，2008年;Giocomo等人，2011年). 假设调谐曲线必须在晶格的基本域内有有限的支撑，这对应于栅极单元在发射场外保持沉默。事实上，我们的数值模拟还表明，对于更宽的调谐曲线，具有二次晶格的网格模块可以提供比六角形晶格更多的FI(图3A,θ₂≈0.6和θ₁=1/4）和带有 $C类$ 或 $B类 C类 C类$ 晶格可以提供比 $F类 C类 C类$ (图4B,θ₂>0.65和θ₁= 1/4). 对于平面情况，Guanella和Verschure（2007）数值结果表明，在最大似然译码下，三角形网格的重建误差小于等比的方形网格。补充这一数值分析，Wei等人（2013）提供一个数学论证，证明六边形网格是最佳的。为此，他们将表示2D空间的单个模块的空间分辨率定义为比率R（右）= (λ/我)²，其中λ是网格比例和我是可以确定动物位置的圆的直径。对于固定分辨率R（右），所需的神经元数量为N个=d日罪(φ)R（右）在他们的分析中，其中d日是覆盖空间中每个点的调整曲线数。作为φ∈ [π/3,π/2] 使晶格具有幺正长度(图3B)，最小化N个对于固定分辨率R（右）产量φ=π/3; 因此，六边形晶格应该是最佳的。此外，Wei等人表明，当考虑贝叶斯解码器时，该结果也成立(Wei等人，2013年). Wei等人最小化N个用于固定我，我们最小化我（用符号表示）。与Wei等人一样，我们假设调谐曲线Ω是各向同性的（尽管晶格具有优先方向）；与这些作者不同的是，我们证明了在某些条件下，发射场应该排列在正方形晶格中，而不是六边形。

使用FI给出了任何无偏估计量的局部分辨率的理论界(莱曼，1998年). 特别是，这种局部分辨率没有考虑晶格周期性带来的模糊性。我们的分析仅限于解决动物在基本领域内的位置。对于大量神经元N个和预期峰值峰值计数（f）_最大值τ渐近有效解码器（如最大似然解码器或最小均方估计量）的分辨率确实可以达到FI给定的分辨率界限(Seung和Sompolinsky，1993年;Bethge等人，2002年;Mathis等人，2013年). 因此，对于这些解码器和条件，结果保持不变。相反，对于较小的神经元数量和峰值尖峰计数，最佳代码可能不同，正如过去所示，在这些情况下，FI无法预测最佳调谐宽度(Bethge等人，2002年;Yaeli等人，2010年;Berens等人，2011年;Mathis等人，2012年).

最大化分辨率解释了观察到的二维网格单元的六边形图案，并预测了 $F类 C类 C类$ 网格（或等效填充），用于哺乳动物的网格细胞调谐曲线，可以自由探索其环境的3D性质。定量地，我们证明，对于相同数量的神经元，这些最优种群比具有二次或三次网格单元的网格代码提供了15.5%（2D）和约41%（3D）的分辨率。虽然更好，但这看起来可能不太重要，至少在单个网格模块的级别上是这样。然而，由于内侧内嗅皮层有一个嵌套的网格代码，其中至少有5个模块，可能有10个或更多模块(Stensola等人，2012年)，这转化为更大的收益 ${1.155}^{5 \dots 10} \approx 2.1 \dots 4.2$ 和 ${\sqrt{2}}^{5 \dots 10} \approx 5.7 \dots 32$ 分别为(Mathis等人，2012a,2012年b). 因为具有完美周期调谐曲线的对齐网格格子意味着后部也是周期性的（相比之下方程式8)，不同尺度的信息必须结合起来才能产生明确的读数。嵌套的鳞片是否真的在大脑中以这种方式读出还有待观察(Mathis等人，2012a,2012年b;Wei等人，2013年). 哈夫廷等人首先提出的另一种假设是，太空中的发射场存在轻微但明显持续的不规则性(Hafting等人，2005年;Krupic等人，2015年;Stensola等人，2015年)正在使用。未来的实验应该解决这个关键问题。

我们考虑了完美周期结构（晶格），并询问哪些结构提供了最大的分辨率。然而，网格单元的第一次记录已经表明，这些场并不是完全六边形排列的，不同的场可能具有不同的峰值发射率(Hafting等人，2005年). 最近，六角对称性的偏差得到了相当大的关注(Derdikman等人，2009年;Krupic等人，2013年,2015;Stensola等人，2015年). 这种“缺陷”调节调谐的周期性，从而影响似然函数的对称性。这可能意味着潜在的解码器可能能够区分不同的单元，即使给定单个模块，这对于完美的周期调谐曲线来说是不可能的（比较方程式8). 另一方面，局部分辨率对较小的非相干变化具有鲁棒性，因为FI是具有不同空间相位的许多调谐曲线的统计平均值。在给定的位置，公式9成为

{J型}_{ς} (x) = \sum_{我 = 1}^{M（M）} {J型}_{Ω_{我}^{L（左）}} (x - {c（c）}_{我}) \approx \int_{x - L（左）} {J型}_{\bar{Ω^{L（左）}}} (c（c）) ρ (c（c）) d日 c（c）,

哪里 $\bar{Ω^{L（左）}}$ 是可变调谐曲线的平均值 $Ω_{我}^{L（左）}$ 。因此，峰值速率和栅场的微小变化将平均化，除非这些变化在栅元之间是一致的。因此，FI限定的分辨率对于峰值射速和六边形的微小差异而言是稳健的。类似的论点在更高的维度中成立。

在这项研究中，我们着重于优化各向同性和均匀空间的网格模块，这意味着在空间的每个方向上，分辨率都应该相等。从数学的角度来看，这是最一般的设置，但肯定不是唯一可以想象的场景；未来的研究应该会对其他几何形状有所启发。事实上，洞穴或洞穴等自然栖息地的拓扑结构可能非常复杂。行为相关的空间位置可能需要更高的分辨率。3D空间的神经表示也可以由多个1D和2D面片组成(Jeffery等人，2013年). 然而，仅仅因为这些栖息地涉及复杂的低维几何结构，并不意味着动物无法获得环境的一般地图。庞加莱已经提出，空间的各向同性和均匀表示可以从非欧几里德感知空间中产生，因为人们可以通过学习运动组在物理空间中移动(彭加莱，1913年). 3D空间的各向同性和均匀表示有助于在3D中进行（心理）旋转，并产生独立于环境拓扑的局部坐标。另一方面，有效编码假说(巴洛，1959年;阿迪克，1992年;Simoncelli和Olshausen，2001年)会争辩说，表面结合的动物可能不需要像飞行动物那样，将其有限的神经元资源用于获取空间的完整表示，以便3D空间的表示具有物种特异性(拉斯·乌拉诺夫斯基（Las and Ulanovsky），2014年). 沙漠蚂蚁只把空间表示为对平面空间的投影(Wohlgemuth等人，2001年;Grah等人，2007年). 同样，实验证据表明，大鼠并不以各向同性的方式编码3D空间(Hayman等人，2011年)，但这可能是这些老鼠必须执行特定的各向异性空间导航任务的结果。另一方面，来自飞行蝙蝠的数据表明，至少在这个物种中，位置细胞以均匀且几乎各向同性的方式表示3D空间(雅采夫和乌兰诺夫斯基，2013年). 蝙蝠的3D环形头部定向系统也表明它们可以进入全动作组(Finkelstein等人，2014年). 我们的理论分析假设蝙蝠网格单元也是如此，并且它们具有径向对称的发射场。根据这些假设，我们表明网格单元的发射场应该安排在 $F类 C类 C类$ 格子或包装为 $HCP公司$ 有趣的是，这些解决方案也在3D的自组织网络模型中动态演化(Stella等人，2013年;Stella和Treves，2015年)它扩展了先前呈现六边形网格图案的2D系统(Kropff和Treves，2008年). 在实验上，竞技场的几何形状对网格单元的调谐和锚定的影响也是一个非常有趣的问题(Derdikman等人，2009年;Krupic等人，2013年,2015;Stensola等人，2015年). 首先，让我们注意到，即使环境可能是有限的，网格-细胞表示也不需要受到它的约束，发射场不需要包含在盒子四壁的范围内。实验观察表明，四壁可以与发射场相交（因此只能测量发射场的一部分）。另一方面，边界明显扭曲了2D环境中附近射击场的六边形排列(Stensola等人，2015年)而中央区域则安排得更加完美。当竞技场中只有几个场地时，也会观察到偏差(Krupic等人，2015年). 人们可能会在3D中看到类似的偏差，比如蝙蝠在密闭空间中飞行。我们的数学结果依赖于不包含非周期调谐曲线的对称性参数。考虑到分辨率与格的填充比有关，将该理论推广到一般填充，可以利用最优有限填充的丰富领域(Böröczky，2004年;Toth等人，2004年)从而提供新的假设进行测试。

大鼠内侧内嗅皮层的许多空间调制细胞具有六边形调谐曲线，但有些细胞具有空间周期带的放电场(Krupic等人，2012年). 这些带的方向往往与网格单元的一个晶格矢量一致（因为不同网格单元的晶格共享一个共同的方向），因此带单元可能是布局的“缺陷”。在这种情况下，我们应该指出晶格解不是全局最优的。例如，在2D中，两个嵌套的1D网格代码系统可以产生更高的分辨率，它们与x和年轴，分别比具有相同数量神经元的晶格解。1D细胞的行为类似于带状细胞(Krupic等人，2012年). 类似的反例也可以在更高的维度上给出。攀爬大鼠三维空间编码时网格细胞空间调谐的各向异性(Hayman等人，2011年)可能会利用这一收益(Jeffery等人，2013年). 调谐曲线的径向对称性也可能是非最佳的。例如，两组具有正交短轴的椭圆调谐2D单峰单元通常优于具有径向对称调谐曲线的单峰单元（Wilke和Eurich，2002）。为什么实验观察到的位置场和其他调谐曲线似乎是各向同性调谐的，这是一个悬而未决的问题(O'Keefe和Dostrovsky，1971年;雅采夫和乌兰诺夫斯基，2013年).

表示动物位置的网格单元(Hafting等人，2005年)直到最近才被发现。相比之下，在技术系统中，自20世纪50年代以来，人们就知道2D信号的最佳量化器依赖于六角形晶格(格雷和纽霍夫，1998年). 在这种情况下，我们注意到格码也非常适合覆盖涉及位置以外的感官或认知变量的空间。在高维特征空间中，潜在收益可能是巨大的。例如，最佳八维（8D）晶格的密度大约是正交8D晶格的16倍(康威和斯隆，1992年)因此，将大大提高相应人口代码的分辨率。实验技术的进展，可以同时记录大量神经元(Ahrens等人，2013年;Deisseroth和Schnitzer，2013年)以及自动化刺激传递以实现密集参数映射(布林卡特和康纳，2004年)，现在为在大脑皮层中寻找这种表征铺平了道路。例如，通过参数化卡通人脸的19个度量特征，例如头发长度、虹膜大小或眼睛大小，Freiwald等人表明，面部选择的细胞广泛调整为多个特征维度(Freiwald等人，2009年). 特别是在较高的皮层区域，这种关节特征空间应该是规范而非例外(Rigotti等人，2013年). 虽然在面部选择性细胞的具体案例中没有发现晶格码的证据，但像这样的数据集将成为检验大脑皮层中存在其他嵌套网格状神经表征这一假设的试验台。

材料和方法

我们研究编码D类-考虑FI的维空间J型作为他们解决问题的措施。种群编码模型，将调谐形状Ω周期化到晶格上的构造 $L（左）$ 具有中心密度ρ，以及金融机构的定义，在正文中给出。在本节中，我们将进一步介绍这些方法的背景。

网格单元的缩放及其对J型_ς

请求详细协议

膨胀如何影响网格模块的分辨率？假设我们有一个带有签名的网格模块 $ς = (Ω, ρ, L（左）)$ ，如正文中所定义，并且λ>0是一个比例因子。然后 $λ ς : = (Ω (λ 第页), ρ (λ x), λ \cdot L（左）)$ 也是一个网格模块，以及相应的调整曲线 ${(Ω \circ λ)}_{λ L（左）}$ 满足：

{(Ω \circ λ)}_{λ L（左）} (x) = Ω_{L（左）} (λ x) .

因此，调谐曲线 ${(Ω \circ λ)}_{λ L（左）}$ 是的缩放版本 $Ω_{L（左）}$ 。初始网格模块的FI与重缩放版本之间的关系是什么？让我们修正一下符号： $ρ (c（c）) = {\sum^{}}_{我}^{N个} δ (c（c） - {c（c）}_{我})$ .从人口信息的定义(方程式9)，我们计算

{J型}_{λ ς} (0) = \sum_{我 = 1}^{M（M）} {J型}_{{(Ω \circ λ)}_{λ L（左）}} (λ {c（c）}_{我}) = \sum_{我 = 1}^{M（M）} {J型}_{Ω_{L（左）}} ({c（c）}_{我}) \cdot \frac{1}{λ^{2}} = \frac{1}{λ^{2}} {J型}_{ς} (0),

其中，在第二步中，我们使用了FI的重新参数化公式(莱曼，1998年). 这表明网格模块的FI按系数缩放λ等于初始网格模块的FI乘以1/λ².

径向对称调谐泊松噪声的总体FI

请求详细协议

在“结果”部分，我们给出了泊松噪声和凹凸函数的具体示例。这里我们给出必要的背景。式13声明

{J型}_{ς} (0) \approx \frac{M（M）}{det（探测） (L（左）)} \int_{{B类}_{R（右）} (0)} {J型}_{Ω^{L（左）}} (c（c）) d日 c（c） .

有人想知道 $\int_{{B类}_{R（右）} (0)} {J型}_{Ω^{L（左）}} (c（c）) d日 c（c）$ 对于各种调谐形状Ω，supp（Ω）≤R（右）.

考虑x∈L（左）和α∈ {1,…,D类}. 然后：

{\frac{\partial 自然对数 P（P） (K（K） | x)}{\partial x_{α}} = \frac{\partial 自然对数 P（P） (K（K）, 秒)}{\partial 秒} |}_{秒 = Ω^{L（左）} (x)} \cdot Ω' ({∥ x ∥}^{2}) {（f）}_{米 一 x} τ 2 x_{α} .

连同金融机构的定义式13，这个产量

{J型}_{Ω^{L（左）}} {(x)}_{α β} = 4 x_{α} x_{β} {（f）}_{米 一 x}^{2} τ^{2} Ω' {(∥ x ∥^{2})}^{2} . \underset{= : N个 ({∥ x ∥}^{2})}{\underset{︸}{\sum_{K（K）} {({\frac{\partial}{\partial 秒} 自然对数 P（P） (K（K）, 秒) |}_{秒 = Ω^{L（左）} (x)})}^{2} \cdot P（P） (K（K）, Ω^{L（左）} (x))}} .

请注意，对于α≠β这个函数在x因此，当在对称基本域上平均这些单独贡献时L（左）: $\int_{L（左）} {J型}_{Ω^{L（左）}} {(c（c）)}_{α β} d日 c（c） = 0$ 对于α≠β因此，对角线条目都是相同的。这也适用于任何基本域L（左）什么时候B类_R（右）(0) ⊂L（左），因为B类_R（右）（0）是对称的。

对于泊松峰值 $N个 ({∥ c（c） ∥}^{2})$ 有一个特别简单的形式，即 $N个 ({∥ c（c） ∥}^{2}) = 1 / ({（f）}_{米一 x} τ Ω ({∥ c（c） ∥}^{2}))$ FI矩阵的轨迹变为

信托收据 {J型}_{ς} (0) = 4 {（f）}_{米 一 x} τ \int_{{B类}_{R（右）} (0)} \underset{= : F类 (c（c）)}{\underset{︸}{{∥ c（c） ∥}^{2} \frac{Ω' {(∥ c（c） ∥^{2})}^{2}}{Ω ({∥ c（c） ∥}^{2})}}} d日 c（c） .

因此，轨迹仅取决于调谐形状Ω及其一阶导数。在正文中，我们使用以下特定的调谐形状：

Ω (第页) = {\begin{array}{l} 经验 (\frac{θ_{1}}{θ_{2}^{2}} - \frac{θ_{1}}{θ_{2}^{2} - {第页}^{2}}) & 如果 | 第页 | < θ_{2} \\ 0 & 否则 \end{array} .

这种类型的函数在拓扑中通常称为“凹凸函数”，因为它具有紧凑的支持，但处处光滑（即无限次连续可微）。特别是，此函数的支持是[0，θ₂)，因此由参数控制θ₂.另一个参数θ₁控制凹凸侧面的坡度（请参见的上部面板图3-图补充1).

对于缓冲功能Ω和半径 $第页 = \sqrt{{\sum^{}}_{α}^{D类} x_{α}^{2}}$ FI的被积函数如下所示

F类 (第页) = {\begin{array}{l} \frac{4 θ_{1}^{2} {第页}^{2}}{{(θ_{2}^{2} - {第页}^{2})}^{4}} 经验 (\frac{θ_{1}}{θ_{2}^{2}} - \frac{θ_{1}}{θ_{2}^{2} - {第页}^{2}}) & 如果 | 第页 | < θ_{2} \\ 0 & 否则 \end{array} .

以下面板图3-图补充1刻画的被积函数式25，定义为 $F类 (第页)$ 。此函数显示特定距离的单元格对位置0的影响程度。通过在基本领域整合金融机构L（左）对于晶格 $L（左）$ 一个人得到J型_ς（0），即所有神经元的平均FI贡献（如图3、4、5E).

工具书类

(2013) 使用薄片显微镜以细胞分辨率进行全脑功能成像
自然方法 10:413–420.

https://doi.org/10.1038/nmeth.2434
- 谷歌学者
1. 艾迪克·JJ
(1992) 信息论能提供感官加工的生态学理论吗？
神经系统中的网络计算 三:213–251.

https://doi.org/10.1088/0954-898X/3/2/009
- 谷歌学者
1. 巴洛W
(1883) 晶体内部对称性的可能性质
自然 29:205–207.

https://doi.org/10.1038/029205a0
- 谷歌学者
1. 巴洛HB
(1959)
NPL思维过程机械化研讨会。第10号

535-539，NPL思维过程机械化研讨会。伦敦10号，女王陛下办公大楼。
- 谷歌学者
(2011) 用神经度量函数重新评估最优神经种群码
美国国家科学院院刊 108:4423–4428.

https://doi.org/10.1073/pnas.1015904108
- 谷歌学者
(2002) 最佳短期人口编码：当Fisher信息失效时
神经计算 14:2317–2351.

https://doi.org/10.1162/08997660260293247
- 谷歌学者
书
1. Böröczky K公司
(2004)
有限包装和覆盖（第二版）

剑桥大学出版社。
- 谷歌学者
1. 布林卡特SL
2. 康纳CE
(2004) 后颞下皮质视觉形状选择性的基本原理
自然神经科学 7:880–886.

https://doi.org/10.1038/nn1278
- 谷歌学者
1. 棕色WM
2. 巴克尔A
(2006) 有限刺激空间的最优神经元调谐
神经计算 18:511–1526.

https://doi.org/10.1162/neco.2006.18.7.1511
- 谷歌学者
(2008) 从内嗅皮层背侧到腹侧的网格尺度逐渐增加
海马 18:1200–1212.

https://doi.org/10.1002/hip.20504
- 谷歌学者
书
1. 康威JH
2. 斯隆NJA
(1992)
球形填料、格架和组（第二版）

纽约：Springer-Verlag。
- 谷歌学者
1. 戴塞洛斯K
2. 施尼泽MJ
(2013) 阐明大脑结构和动力学的工程方法
神经元 80:568–577.

https://doi.org/10.1016/j.euron.2013.10.032网址
- 谷歌学者
1. 迪克曼D
2. 惠特洛克JR
3. 曹A
4. Fyhn M公司
5. 盗版T
6. 莫瑟M-B
7. 莫瑟EI
(2009) 多部门环境中网格单元图的碎片化
自然神经科学 12:1325–1332.

https://doi.org/10.1038/nn.2396
- 谷歌学者
1. 尤里奇W
2. 威尔克SD
(2000) 尖峰神经元的多维编码策略
神经计算 12:1519–1529.

https://doi.org/10.1162/089976600300015240
- 谷歌学者
(2008) 网格细胞传达的关于老鼠位置的信息
神经科学杂志 28:6858–6871.

https://doi.org/10.1523/JNEUROSCI.5684-07.2008
- 谷歌学者
(2014) 蝙蝠大脑中的三维头向编码
自然 517:159–164.

https://doi.org/10.1038/nature14031
- 谷歌学者
(2009) 猕猴颞叶的面部特征空间
自然神经科学 12:1187–1196.

https://doi.org/10.1038/nn.2363
- 谷歌学者
(2008) 小鼠的网格细胞
海马 18:1230–1238.

https://doi.org/10.1002/hipo.20472
- 谷歌学者
1. 高斯CF
(1831)
“Untersuchungenüber die Eigenschaften der positiven ternären quadrischen Formen von Ludwig August Seeber”经济衰退

哥廷舍·盖勒赫特·安泽根，7月9日，第1065页；转载于J.Reine Angew。数学。20 (1840)312–320.
- 谷歌学者
(2011) 网格单元使用HCN1通道进行空间缩放
单元格 147:1159–1170.

https://doi.org/10.1016/j.cell.2011.08.051
- 谷歌学者
(2007) 沙漠蚂蚁不会获取和使用三维全球载体
动物学前沿 4:12.

https://doi.org/10.1186/1742-9994-4-12
- 谷歌学者
1. 灰色RM
2. Neuhoff DL公司
(1998) 量化
IEEE信息理论汇刊 44:2325–2383.

https://doi.org/10.109/18.720541
- 谷歌学者
1. Gruber项目经理
(2004) 最优量化及其应用
数学进展 186:456–497.

https://doi.org/10.1016/j.aim.2003.07.017
- 谷歌学者
1. 瓜内拉菌A
2. Verschure PF公司
(2007) 基于网格和位置细胞种群的动物位置预测：一项比较模拟研究
综合神经科学杂志 6:433–446.

https://doi.org/10.1142/S02196352007001556
- 谷歌学者
1. 盗版T
2. Fyhn M公司
3. 莫尔登S
4. 莫瑟MB
5. 莫瑟EI
(2005) 内嗅皮层空间图的微观结构
自然 436:801–806.

https://doi.org/10.1038/nature03721
- 谷歌学者
1. 哈尔斯T
(2005) 开普勒猜想的证明
数学年刊 162:1065–1185.

https://doi.org/10.4007/annals.2005.162.1065
- 谷歌学者
书
1. 哈尔斯T
(2012)
致密球形填料：正式证明的蓝图

剑桥：剑桥大学出版社。
- 谷歌学者
(2011) 基于位置单元和网格单元的三维空间各向异性编码
自然神经科学 14:1182–1188.

https://doi.org/10.1038/nn.2892
- 谷歌学者
1. 雅各布斯J
2. 韦德曼CT
3. 米勒·JF
4. 索尔韦A
5. 伯克JF
6. 魏X-X
7. Suthana N号
8. 斯珀林MR
9. 沙兰AD
10. 油炸I
11. 卡哈娜·乔丹
(2013) 人类空间导航中网格状神经元活动的直接记录
自然神经科学 16:1188–1190.

https://doi.org/10.1038/nn.3466
- 谷歌学者
(2013) 在三维世界中导航
行为与脑科学 36:523–543.

https://doi.org/10.1017/S0140525X12002476
- 谷歌学者
1. 克罗夫E
2. 特列夫斯A
(2008) 网格单元的出现：智能设计还是仅仅适应？
海马 18:1256–1269.

https://doi.org/10.1002/hipo.20520网址
- 谷歌学者
(2012) 由空间周期带组成的位置的神经表示
科学类 337:853–857.

https://doi.org/10.1126/science.1222403
- 谷歌学者
(2015) 网格单元对称性由环境几何形状决定
自然 518:232–235.

https://doi.org/10.1038/nature14153
- 谷歌学者
(2013) 环境几何如何影响网格单元对称性以及我们可以从中学到什么
伦敦皇家学会哲学学报B生物科学 369:20130188.

https://doi.org/10.1098/rstb.2013.0188
- 谷歌学者
1. 拉格朗日JL
(1773)
《算术评论》

693–758，《柏林皇家科学与Belles-Lettres de Berlin，Anneées》，第3期，重印于Oeuvres。
- 谷歌学者
书
1. 拉斯维加斯
2. 乌拉诺夫斯基N
(2014)
跨物种的海马神经生理学

收件人：Derdikman D，Knierim JJ，编辑。海马结构中的空间、时间和记忆施普林格维也纳。第431-461页。
- 谷歌学者
书
1. 莱曼EL
(1998)
点估计理论（第二版）

美国纽约州：斯普林格·弗拉格。
- 谷歌学者
1. 马蒂斯A
(2012)
哺乳动物空间的表示：随机位置码和网格码的解析

路德维希·马克西米利安-慕尼黑大学博士论文。
- 谷歌学者
（2012年a）空间的最佳填充代码：网格单元优于位置单元
神经计算 24:2280–2317.

https://doi.org/10.1162/NECO_a_00319
- 谷歌学者
（2012年b）嵌套神经元表示的分辨率可以是神经元数量的指数
物理审查信函 109:018103.

https://doi.org/10.1103/PhysRevLett.109018103
- 谷歌学者
(2013) 神经系统中的多尺度代码：噪声相关性和周期尺度的模糊性问题
物理评论E，统计，非线性和软物质物理学 88:022713.

https://doi.org/10.1103/PhysRevE.88.022713
- 谷歌学者
1. 马萨诸塞州蒙特默罗
2. 装甲车S
(2006) 周期变量总体编码中的最优调谐宽度
神经计算 18:1555–1576.

https://doi.org/10.1162/neco.2006.18.7.1555
- 谷歌学者
书
1. 尼尔森DR
(2002)
凝聚态物理中的缺陷与几何

剑桥大学出版社。
- 谷歌学者
1. 奥基夫J
2. 多斯特罗夫斯基J
(1971) 海马作为空间地图：自由运动大鼠单位活动的初步证据
大脑研究 34:171–175.

https://doi.org/10.1016/0006-8993(71)90358-1
- 谷歌学者
1. Paradiso马萨诸塞州
(1988) 利用纹状体皮层柱状结构的视觉定向信息使用理论
生物控制论 58:35–49.

https://doi.org/10.1007/BF00363954
- 谷歌学者
书
1. 庞加莱H
(1913)
科学的基础：科学与假设、科学的价值、科学与方法

纽约加里森：科学出版社。
- 谷歌学者
(1999) 窄与宽调谐曲线：人口代码的最佳选择是什么？
神经计算 11:85–90.

https://doi.org/10.1162/089976699300016818
- 谷歌学者
(2014) 内侧内嗅皮质第2层锥体神经元的网格布局和θ调制
科学类 13:987–994.

https://doi.org/10.1126/science.1243028
- 谷歌学者
(2013) 复杂认知任务中混合选择性的重要性
自然 497:585–590.

https://doi.org/10.1038/nature12160
- 谷歌学者
1. 承HS
2. 桑普林斯基H
(1993) 读取神经元群体代码的简单模型
美国国家科学院院刊 90:10749–10753.

https://doi.org/10.1073/pnas.90.22.10749
- 谷歌学者
1. 香农CE
(1948)
传播的数学理论

贝尔系统技术期刊 二十七:379–423.
- 谷歌学者
1. 西蒙塞利EP
2. 奥尔沙森BA
(2001) 自然图像统计和神经表示
神经科学年度回顾 24:1193–1216.

https://doi.org/10.1146/annurev.neuro.24.1.1193
- 谷歌学者
(2013) 太空飞行的网格地图，有人吗？他们是免费的！
行为与脑科学 36:566–567.

https://doi.org/10.1017/S0140525X13000575
- 谷歌学者
1. 斯特拉·F
2. 特列夫斯A
(2015) 三维网格单元的自组织
电子生活 三：e05913。

https://doi.org/10.7554/eLife.05913
- 谷歌学者
(2012) 内鼻网格图被离散化
自然 492:72–78.

https://doi.org/10.1038/nature11649
- 谷歌学者
(2015) 剪切诱导的内嗅网格细胞不对称性
自然 518:207–212.

https://doi.org/10.1038/nature14151
- 谷歌学者
1. 星期四A
(1910)
在埃宾半岛上的尤伯·迪杰斯特·祖萨门斯坦隆·冯·孔格伦滕·克里森（Zusammenstellung von kongruenten Kreisen）

挪威语Videnskabs Selskabets Skrifter 1:1–9.
- 谷歌学者
(2004)
离散和组合数学系列

离散和组合数学系列，第2版，CRC出版社。
- 谷歌学者
(2013)
位置感：大脑中的网格细胞和超越数e

arXiv:1304.0031v1:20。
- 谷歌学者
书
1. 惠特克EJ
(1981)
结晶学：地球（和其他固态）学生入门（第1版）

佩加蒙出版社。
- 谷歌学者
(2001) 三维反里程计
自然 411:795–798.

https://doi.org/10.1038/35081069
- 谷歌学者
1. Yaeli S公司
2. 迈尔R
(2010) 基于错误的最佳调谐函数分析解释了在感觉神经元中观察到的现象
计算神经科学前沿 4:130.

https://doi.org/10.3389/fncom.2010.00130
- 谷歌学者
1. 雅采夫MM
2. 乌拉诺夫斯基N
(2013) 蝙蝠海马的三维空间表征
科学类 340:367–372.

https://doi.org/10.1126/science.1235338
- 谷歌学者
(2011) 蝙蝠内嗅皮层无θ振荡的网格细胞
自然 479:103–107.

https://doi.org/10.1038/nature10583
- 谷歌学者
1. 张凯（Zhang K）
2. Sejnowski TJ公司
(1999) 神经元调谐：锐化还是加宽？
神经计算 11:75–84.

https://doi.org/10.1162/089976699300016809
- 谷歌学者

文章和作者信息

作者详细信息

亚历山大·马蒂斯
1. 美国剑桥哈佛大学分子和细胞生物学系
2. 美国剑桥哈佛大学脑科学中心
贡献
AM，概念和设计，数据分析和解释，起草或修改文章

用于通信
amathis@fas.harvard.edu

竞争性利益
提交人声明，不存在相互竞争的利益。

“此ORCID iD标识了本文的作者：”0000-0002-3777-2202
马丁·B·斯特姆勒
1. 德国伯恩斯坦计算神经科学中心
2. 德国慕尼黑大学路德维希·马克西米利安分校Fakultät für Biologie
贡献
MBS，概念和设计，起草或修改文章

竞争性利益
提交人声明，不存在相互竞争的利益。
安德烈亚斯·VM赫兹
1. 德国伯恩斯坦计算神经科学中心
2. 德国慕尼黑大学路德维希·马克西米利安分校Fakultät für Biologie
贡献
AVMH，概念和设计，起草或修改文章

竞争性利益
提交人声明，不存在相互竞争的利益。

基金

联邦教育与福尚部长（01 GQ 1004A）

马丁·B·斯特姆勒
安德烈亚斯·VM赫兹

Deutsche Forschungsgemeinschaft（马萨诸塞州6176/1-1）

亚历山大·马蒂斯

欧洲委员会（PIOF-GA-2013-622943）

亚历山大·马蒂斯

资助者不参与研究设计、数据收集和解释，也不参与将研究成果提交出版的决定。

致谢

我们感谢Kenneth Blum和Mackenzie Amoroso的讨论。AM感谢Mackenzie Amoroso提供的图形帮助，以及Ashkan Salamat讨论结晶学术语。

版权

本文根据知识共享署名许可协议，它允许不受限制的使用和重新分配，前提是原始作者和来源都是可信的。

韵律学

4,012

意见
727

下载
49

引用

eLife发布的这篇论文的所有版本都聚合了浏览量、下载量和引用量。

下载链接

一个由两部分组成的链接列表，用于以各种格式下载文章或文章的部分。

下载（链接以PDF格式下载文章）

公开引用（在各种在线参考咨询管理服务中打开本文引文的链接）

门德利

引用这篇文章（以与各种reference manager工具兼容的格式下载本文引文的链接）

亚历山大·马蒂斯
马丁·B·斯特姆勒
安德烈亚斯·VM赫兹

(2015)

哺乳动物网格细胞活动模式下高维对称性的可能性质

电子生活 4：e05979。

https://doi.org/10.7554/eLife.05979（网址：https://doi.org/10.7554/eLife.05979）

类别和标签

研究生物

进一步阅读

1. 神经科学
三维网格单元的自组织

费德里科·斯特拉（Federico Stella）、亚历山德罗·特雷夫斯（Alessandro Treves）

研究文章已更新2015年6月4日
我们期望蝙蝠或海豚在探索三维环境时出现周期性的网格细胞吗？要多长时间？我们基于环速率适应的自组织模型指出了一个复杂的答案。数学分析导致类似于面心立方（FCC）和六方紧密堆积（HCP）晶体结构的渐近状态，这两种晶体结构在成本函数方面被计算为彼此非常接近。然而，对整个模型的模拟表明，这种渐近状态的方法涉及不同时间尺度上的几个子过程。观察到，即使在大型3D体量中，单个单元最初不规则的多个场的平滑以及它们在某些最佳平面上排列成六边形网格的速度也相对较快。然而，飞机的正确相互定向和不同装置的协调布置需要更长的时间，网络没有向纯FCC或HCP订购收敛的迹象。
1. 计算与系统生物学
识别生物文献中对色觉障碍患者有问题的图像

哈兰·史蒂文斯（Harlan P Stevens）、卡莉·维尼加（Carly V Winegar）。。。斯蒂芬·皮科洛

研究文章 2024年9月11日
为了帮助最大限度地发挥科学期刊文章的影响，作者必须确保色觉缺陷（CVD）患者能够获得文章数据，色觉缺陷影响高达8%的男性和0.5%的女性。我们评估了2012年至2022年间发表在生物学和医学研究文章中的图像。大多数都包括至少一种颜色对比度，这可能会对最常见的CVD形式的双目失明患者造成问题。然而，空间距离和图像内标签经常可以缓解潜在的问题。最初，我们查看了4964张来自电子生活，将每一个版本与模拟版本进行比较，模拟版本近似于氘核的外观。我们识别出636张（12.8%）图像，我们认为这些图像对氘核来说很难解释。我们的发现表明，随着时间的推移，这个问题的发生频率已经降低，而来自细胞导向学科的文章往往是有问题的。我们使用机器学习自动识别有问题的图像。对于来自的保持测试集电子生活（n=879），卷积神经网络对精度为0.75的图像进行分类。同一网络对PubMed Central（n=1191）的图像进行了分类，精确再调用曲线下的区域为0.39。我们创建了一个Web应用程序(https://bioapps.byu.edu/colorblind_image_tester); 用户可以上传图像、查看模拟版本和获取预测。我们的发现为科学图像的频率和性质提供了新的线索，这些科学图像可能会对双目恐龙造成问题，并激励人们做出更多努力来增加可访问性。
1. 计算与系统生物学
肌张力和阻抗的三丝力学模型

马修·米拉德（Matthew Millard）、大卫·富兰克林（David W Franklin）、沃尔特·赫尔佐格（Walter Herzog）

研究文章 2024年9月10日
主动延长肌肉产生的力量取决于不同长度范围内的不同结构。对于小扰动，肌肉的主动响应可以通过线性时不变（LTI）系统很好地捕捉到：刚性弹簧与轻型阻尼器并联。肌肉对较长拉伸的力反应最好由一个柔顺的弹簧来表示，该弹簧在激活时可以固定其末端。实验工作表明，肌肉对小扰动的刚度和阻尼（阻抗）对运动学习和机械稳定性至关重要，而长时间主动伸展过程中产生的巨大力量对模拟和预测损伤至关重要。除了运动学习和损伤之外，肌肉作为几乎所有陆地运动的一部分都会被积极延长。尽管阻抗和主动延长术在功能上很重要，但没有一种肌肉模型具有所有这些力学特性。在这项工作中，我们提出了粘弹性-跨桥活性肌动蛋白（VEXAT）模型，该模型可以复制肌肉对长度变化大小的响应。为了评估VEXAT模型，我们通过测量肌肉阻抗和长时间主动伸展过程中产生的力的模拟实验，比较其对生物肌肉的响应。此外，我们还比较了VEXAT模型和流行的Hill型肌肉模型的响应。VEXAT模型比Hill型模型更准确地捕捉生物肌肉的阻抗及其对长时间主动拉伸的响应，并且仍然可以再现肌肉的力-速度和力-长度关系。虽然VEXAT模型和生物肌肉之间的比较是有利的，但有一些现象可以改进：模型的低频相位响应，以及支持被动力增强的机制。