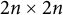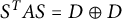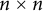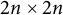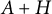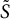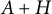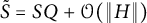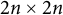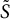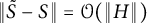Block perturbation of symplectic matrices in Williamson’s theorem

Gajendra Babu; Hemant K. Mishra

doi:10.4153/S0008439523000620

威廉姆森定理中辛矩阵的块扰动

部分：特殊矩阵基本线性代数

剑桥大学出版社在线出版：2023年8月15日

加詹德拉·巴布

和

赫曼特·米什拉

显示作者详细信息

加詹德拉·巴布: 附属：
印度马图拉GLA大学数学系，邮编281406，电子邮件：gajendra0777@gmail.com
赫曼特·米什拉*: 附属：
印度统计研究所理论统计和数学部，印度新德里110016 康奈尔大学电气与计算机工程学院，伊萨卡，NY 14850，美国电子邮件：hemant.mishra@cornell.edu
*: 电子邮件：hemantmishra1124@gmail.com

文章内容

权限和权限

摘要

威廉姆森定理指出，对于任何$2n \乘以2n$实正定矩阵A类，存在一个$2n\乘以2n$实辛矩阵S公司这样的话$S^TAS=D\oplus D$，其中D类是一个$n\次$具有正对角项的对角矩阵称为的辛特征值A类.让H（H）是任何$2n\乘以2n$实对称矩阵，使得扰动矩阵美元A+H$也是正定的。在本文中，我们证明了任何辛矩阵$\波浪线{S}$对角化美元A+H$威廉姆森定理的形式是$\tilde{S}=SQ+\mathcal{O}（\|H\|）$，其中问是一个$2n\乘以2n$实辛矩阵和正交矩阵。此外，问在中辛块对角线具有两倍辛特征值重数的块大小的形式A类因此，我们表明$\波浪线{S}$和S公司可以进行选择，以便$\ | \波浪线{S} -S型\|=\mathcal{O}（\|H\|）$。我们的结果保持不变，即使A类具有重复的辛特征值。这推广了Idel、Gaona和Wolf给出的非重复辛特征值辛矩阵的稳定性结果[线性代数应用。，525:45–58, 2017].

关键词

正定矩阵辛矩阵辛特征值威廉姆森定理扰动，扰动

MSC分类

主要用户： 15B48：正矩阵及其推广；矩阵的锥 15A18：特征值、奇异值和特征向量

类型: 第条
问询处: 加拿大数学通报 ,第67卷 ,第1版，2024年3月第201-214页

内政部：https://doi.org/10.4153/S0008439523000620 [在新窗口中打开]
知识共享: 这是一篇开放存取文章，根据知识共享署名许可证的条款分发(https://creativecommons.org/licenses/by/4.0/)它允许在任何介质中无限制地重复使用、分发和复制原始作品，前提是正确引用了原始作品。
版权: ©作者，2023年。剑桥大学出版社代表加拿大数学学会出版

1介绍

威廉姆森定理与线性代数中的谱定理类似[参考Williamson23]辛线性代数中。它规定，对于任何 $2n \乘以2n$ 实正定矩阵A类，存在一个 $2n\乘以2n$ 真实的辛矩阵S这样的话 $S^TAS=D\oplus D$ ，其中D类是一个 $n\次$ 具有正对角线项的对角线矩阵。对角线条目D类被称为辛特征值属于A类和的列S公司表格a辛特征基属于A类。此结果也称为威廉姆森范式在文学作品中[参考DeGosson7,证明人Dutta、Mukunda和Simon8]. 辛特征值和辛矩阵在许多领域都是普遍存在的，例如经典哈密顿动力学[参考Arnold2]，量子力学[证明人Dutta、Mukunda和Simon8]，和辛拓扑[参考Hofer和森德9]. 最近，它吸引了矩阵分析师的大量关注[参考Bhatia和Jain三–参考Bhatia和Jain5,参考Jain12–参考Mishra14,参考Paradan16,参考Son和Stykel22]和量子物理学家[参考资料Adesso、Serafini和Illuminati1,证明人Chen6,参考香豆、大豆和胡豆10,参考偶像、高娜和沃尔夫11,参考Nicacio15]因为它在连续变量量子信息理论中的重要作用[参考Serafini19]. 例如，任何零平均向量的高斯态都是通过将以辛矩阵为特征的酉映射应用于热态的张量积而获得的[参考Serafini19]高斯态的冯·诺依曼熵是其协方差矩阵辛特征值的光滑函数[参考Parthasarathy17]. 因此，研究威廉姆森定理中辛特征值和辛矩阵的摄动问题具有重要的理论意义和实际意义，二者之间有着密切的联系。的确，两个正定矩阵辛特征值的扰动界A类和B类在中获得[参考Jain和Mishra13]使用辛矩阵对角化导出 $tA+（1-t）B$ 对于 $t\英寸[0,1]$ .英寸[参考偶像、高娜和沃尔夫11]，扰动A类表单的美元+吨$ 考虑了小变量 $t>0$ 和固定实对称矩阵H（H）研究了辛矩阵对角化的稳定性美元+吨$ 在威廉姆森定理中，得到了以下情况的摄动界A类具有不重复的辛特征值。

本文研究了Williamson定理对角化中辛矩阵的稳定性美元A+H$ ，其中H（H）是任意的 $2n \乘以2n$ 实对称矩阵，使得扰动矩阵美元A+H$ 也是正定的。让S公司是固定辛矩阵对角化A类威廉姆森定理。我们证明了任何辛矩阵 $\波浪线{S}$ 对角化美元A+H$ 威廉姆森定理的形式是 $\tilde{S}=SQ+\mathcal{O}（\|H\|）$ 这样的话问是一个 $2n\乘以2n$ 实数辛矩阵以及正交矩阵。此外，问在中辛块对角线具有两倍辛特征值重数的块大小的形式A类因此，我们证明 $\波浪线{S}$ 和S公司可以进行选择，以便 $\ | \波浪线{S} -S型\|=\mathcal{O}（\|H\|）$ 。我们的结果保持不变，即使A类具有重复的辛特征值，推广了中给出的非重复辛特征值情况下辛矩阵的稳定性结果[参考偶像、高娜和沃尔夫11]. 我们不提供任何扰动边界。

论文的其余部分组织如下：第节2，我们回顾了一些定义，集合表示法，并定义了基本的辛运算。在节中三，我们详细介绍了本文的研究结果。这些在提案中给出3.2和3.7和定理3.4和3.6.

2背景和注释

让 $\运算符名称{Sm}（m）$ 表示一组 $m\倍m$ 具有谱范数的实对称矩阵 $\|\cdot（美元）\|$ 也就是说，对于任何人 $X\in\运算符名称｛Sm｝（m）$ , $\|X美元\|$ 是的最大奇异值X。我们也使用相同的符号 $\|\cdot（美元）\|$ 对于欧几里德规范，以及 $\langle\cdot，\cdot\rangle$ 上的欧几里德内积 $\mathbb{R}^{m}$ 或 $\mathbb{C}^m$ .让 $0_{i，j}$ 表示 $i\次j$ 零矩阵，并让 $0_i美元$ 表示 $i\次i$ 零矩阵（即。， $0_i=0_{i，i}$ ). 我们用以下公式表示虚单位数。我们使用Big-O表示法 $Y=\mathcal{O}（\|X\|）$ 表示矩阵Y（Y）作为的函数X其中存在正标量c（c）和美元\ delta$ 这样的话 $\|Y\|\leq c\|X\|$ 为所有人X具有 $\|X\|<\delta$ .

2.1辛矩阵和辛特征值

定义，并让 $J_{2n}=J_2\otimes I_n$ 对于 $n>1$ ，其中美元（_n）$ 是 $n\次n$ 单位矩阵A $2n\乘以2n$ 实矩阵S公司称为辛，如果 $S^TJ（美元）_{2n}秒=J_{2n}$ 这套 $2n\乘以2n$ 辛矩阵，表示为 $\运算符名称｛Sp｝（2n）$ ，在乘法下形成一个组，称为辛群.辛群 $\运算符名称{Sp}（2n）$ 类似于正交组 $\operatorname{Or}（2n）$ 属于 $2n\乘以2n$ 正交矩阵替换矩阵的意义 $J_{2n}$ 具有 $I_{2n}$ 在辛矩阵的定义中，给出了正交矩阵的定义。然而，与正交群相比，辛群是非紧的。此外，每个辛矩阵的行列式等于 $+1$ 这使得辛群成为特殊线性群的子群[证明人Dutta、Mukunda和Simon8]. 让 ${\operatorname{Pd}（2n）\subset\operator name{Sm}（2 n）}$ 表示正定矩阵的集合。威廉姆森定理[参考Williamson23]声明每 $A\in\operatorname{Pd}（2n）$ ，存在 $S\in\operatorname{Sp}（2n）$ 这样的话 $S^TAS=D\oplus D$ ，其中D类是一个 $n\次$ 对角矩阵。对角元素 $d_1（A）\le\cdots\le d_n（A）$ 属于D类独立于S公司，它们被称为的辛特征值A类。表示方式 $\运算符名称{Sp}（2n；A）$ 的子集 $\运算符名称{Sp}（2n）$ 由对角化辛矩阵组成A类威廉姆森定理。威廉姆森定理的几个证明可用基本线性代数（例如[参考DeGosson7,参考Simon、Chaturvedi和Srinivasan20]).

表示一组 $2n\乘以2n$ 正交辛的（正交和辛）矩阵 .任何正交矩阵 $Q\in\operatorname{OrSp}（2n）$ 正是这种形式

(2.1)

$$\begin{align}Q=\begin{pmatrix}X&Y\\-Y&X\end{pmatricx}，\end}对齐$$

哪里 X美元，Y美元$ 是 $n\次$ 这样的实矩阵 $X+\iota年$ 是酉矩阵[参考Bhatia和Jain三]. 对于百万美元$ ，我们表示为 $\operatorname{Sp}（2n，2m）$ 一套 200万美元\乘以200万$ 矩阵M（M）令人满意的 $M^T J_{2n}M=J_{2m}$ 特别是，我们有 $\operatorname{Sp}（2n，2n）=\operator name{Spneneneep（2n）$ .

2.2辛块与辛直和

让米是一个自然数 $\mathcal{I}，\mathcal{J}\subseteq\{1，\ldot，m\}$ .假设M（M）是一个 $m\倍m$ 矩阵。我们表示为 $M_{\mathcal{J}}$ 的子矩阵M（M）由以下列组成M（M）索引位于 $\mathcal{J}（美元）$ 也可以用表示 $M_{\mathcal{I}\mathcal{J}}$ 这个 $|\mathcal{I}|\times|\mathcal{J}|$ 的子矩阵 $M=[M_{ij}]$ 由元素组成 $M_｛ij｝$ 带索引 $i\in\mathcal{i}$ 和 $j\in\mathcal{j}$ .让吨是任何 200万美元\乘以200万$ 块形式的矩阵由

$$\开始{align*}T=\开始{pmatrix}W&X\\Y&Z\end{pmatricx}，\end{align**}$$

哪里 $X、Y、W、Z$ 是有序矩阵 $m\倍m$ .定义辛块属于吨作为形式的子矩阵

$$\begin{align*}\begin{pmatrix}W_{\mathcal{I}\mathcal{J}}&X_{\mathcal{I}\mathcal{J}}\\Y_{\mathcal{I}\ mathcal}}&Z_{\methcal{I}\mathcali{J}}\end{pmartrix}。\结束{align*}$$

此外，定义一个辛对角块属于吨作为形式的子矩阵

$$\begin{align*}\begin{pmatrix}W_{\mathcal{I}\mathcal{I}}&X_{\mathcal{I}\matchcal{I}}\\Y_{\mathcal{I}\ mathcal}I}}&Z_{\methcal{I}\mathcal{I/}}\end{pmartrix}。\结束{align*}$$

下面的示例对此进行了说明。

示例2.1让吨成为 $6\乘以6$ 矩阵由给出

的辛块吨，对应于 $\mathcal{I}=\{3\}$ 和 $\mathcal{J}=\{2\}$ ，由给出

辛对角块，对应于 $\mathcal{I}=\{1,2\}$ ，由给出

让 $T’$ 成为另一个 200万美元\乘以200万$ 矩阵，以块形式给出

$$\开始{align*}T'=\开始{pmatrix}W'&X'\\Y'&Z'\结束{pmatricx}，\结束{align**}$$

在哪里 $W'，X'，Y'，Z'$ 有尺寸 $m'\乘以m'$ .定义辛直和属于吨和 $T’$ 作为

$$\开始{align*}T\oplus^{\operatorname{s}}T'&=\begin{pmatrix}W\oplus W'&X\oplus-X'\\Y\oplu斯·Y'&Z\oplus-Z'\end{pmatricx}。\结束{align*}$$

下面的示例对此进行了说明。

例2.2让

然后我们有

我们知道两个正交矩阵的通常直和也是一个正交矩阵。有趣的是，辛直和也满足类似的性质。如果 $T\in\运算符名称｛Sp｝（2k）$ 和 $T'\in\operatorname{Sp}（2\ell）$ ，然后 $T\oplus^sT'\in\operatorname{Sp}（2（k+\ell））$ 的确，我们已经

$$\开始{align*}&（T\oplus^sT'）^TJ_{2（k+\ell）}（T\oplus^s T'）\\[3pt]&\hspace{0.5cm}=\begin{pmatrix}W\oplus W'&X\oplus-X'\\Y\oplus\Y'&Z\oplu斯·Z'\end{pmatricx}^T\begin}0_{k+\cell}&I_{k+\ell}\\-I_{k+/ell}&0_{k+\ell}\end{pmatrix}\begin{pmartrix}W\oplus W'&X\oplus X'\\Y\oplus-Y'&Z\oplusZ'\end}\\[3pt]&\hspace{0.5cm}=\begin{pmatrix}W^T\oplus W'^T&Y^T\oplus Y'^T\\X^T\oplus X'^T＆Z^T\eplus Z'^T\end{pmatricx}\begin{pmartrix}Y\oplus Y'&Z\oplusZ'\\-W^TY\oplus W'^TY'-Y^TW\oplus Y'^TW'&W^TZ\oplu斯W'^TZ'-Y*TX\oplusY'^TX'^TY'-Z^TW\ oplus Z'^TTW'&X^TZ\ oplusX'^TZ'-Z^ TX\oplus Z'^TX'\end{pmatrix}\\[3pt]&\hspace{0.5cm}=\begin{pmatricx}（W^TY-Y^TW）\oplus.（W'^TY'-Y'^TW'）&！\！\！（W^TZ-Y^TX）\oplus（W'^TZ'-Y'^TX'）\\（X^TY-Z^TW）\opmus（X'^TY'-Z'^TW'）&\！\！（X^TZ-Z^TX）\oplus（X'^TZ'-Z'^TX'Z'^TW'&X'^TZ'-Z'^ TX'\end{pmatrix}\\[3pt]&hspace{0.5cm}=\begin{pmatricx}W^T&Y^T\\X^T&Z^T\end}\begin{pmatrix}Y&Z \\-W&-X\end{pmatricx}\oplus^s \begin{pmatriax}W'^T&Y'^T\\X'^T＆Z'^T\end{pmmatrix}\ begin pmatrix}Y'&Z'\\-W'&-X'\end}\\[3pt]&\hspace{0.5cm}=\begin'{pmatriex}W&X\\Y&Z\end{pmatrix.}k&I_k\\-I_k&0_k\end{pmatrix}\开始{pmatricx}W&X\\Y&Z\end}\oplus^s\begin{pmatrix}W'&X'\\Y'&Z'\end{pmmatrix}^T\begin}0_{\ell}&I_\ell\\-I_\ell&0_{\ ell}\end}{pmartrix}\ begin（开始）{pmatricx}W’&X'\ Y'&Z’\end[3pt]&hsspace{0.5cm}=T^T J_{2k}吨\oplus^sT'^TJ{2\ell}T'\\[3pt]&\hspace{0.5cm}=J{2k}\oplus sJ{2\\ell}\\[3pt]&\h空格{0.5cmneneneep=J{2（k+\ell）}。\结束{align*}$$

2.3辛级联

让 $M=\左（p_1，\ldot，p_{k}，q_1，\ ldot，q_k\右）$ 和 $N=\left（x_1，\ldots，x_{\ell}，y_1，\ ldot，y_\ell\right）$ 是 $2n\乘以2k$ 和 ${2n\乘以2\ell}$ 矩阵。定义辛级联属于M（M）和N个如下所示 $2n\乘以2（k+\ell）$ 矩阵：

这里有一个例子来说明辛级联。

示例2.3让

的辛连接M（M）和N个由提供

假设 $M\in\operatorname{Sp}（2n，2k）$ 和 $N\in\operatorname{Sp}（2n，2\ell）$ .让我们推导一个关于M（M）和N个对于 $k+\ell\leq n$ 这样的话 $M\diamond N\in\operatorname{Sp}（2n，2（k+\ell））$ 。这将在以后有用。我们有

(2.2)

$$开始{align}（M\diamond N）^T J_{2n}_{2n}牛顿\右）\N非数字\\&=\左（M^T J_{2n}^T（M\diamond N）\右）^T \菱形\左（N^TJ_{2\N}^ T（M\ diamond N）\右右）^T\非数字\\&=\左（J_{2k}^T\菱形（M^TJ_{_2n}^TN）\右）^T \菱形\左（（N^TJ_{2n}^TM）\菱形J_{2\ell}^T\右）^T.\结束{align}$$

我们还观察到

(2.3)

$$\开始｛align｝J_｛2（k+\ell）｝&=\left（J_｛2k｝^T\d菱形0_｛2k，2\ell｝\right）^T\d菱形\left（0_｛2\ell，2k｝\d菱形J_｛2\ell｝^T\right）^T。\结束｛align｝$$

通过比较(2.2)和(2.3)，我们推断 $M\diamond N\in\operatorname{Sp}（2n，2（k+\ell））$ 当且仅当 $M^T J_{2n}N=0_{2k，2\ell}$ .

三主要成果

我们在整篇文章中修正了以下注释。让 $A\in\operatorname{Pd}（2n）$ 具有不同的辛特征值 $\mu _1<\cdots<\mu _r$ .面向所有人 $i=1，\ldot，r$ ，定义集合

举例说明这些集合如下。

示例3.1假设 $A\in\operatorname{Pd}（20）$ 具有辛特征值 $1,1,2,3,3,3,4,4,4,5$ .我们有 $\mu_1=1，\\mu_2=2，\\μ_3=3，\\mo_4=4，\\mu_5=5$ 。此外 $\alpha_1=\{1,2\}$ , $\alpha_2=\{3\}，\alpha_3=\{4,5,6\}$ 。请注意 $n=10$ ，所以我们有 $\beta_1=\{11,12\}$ , $\beta_2=\{13\}，\beta_3=\{14,15,16\}$ , $\beta_4=\{17,18,19\}$ , $\β_5=\｛20 \｝$ 。因此，我们也得到 $\gamma_1={1,2,11,12\}$ , $\gamma_2={3,13\}$ , 伽马_3={4,5,6,14,15,16\}$ , $\gamma_4=\{7,8,9,17,18,19\}$ , $\gamma_5=\{10,20\}$ .

提议3.2让 $A\in\operatorname{Pd}（2n）$ 和 $H\in\operatorname{Sm}（2n）$ 这样的话 $A+H\in\operatorname{Pd}（2n）$ 让 ${S\in\operatorname{Sp}（2n；A）}$ 和 $\波浪线{S}\in\operatorname{Sp}（2n；A+H）$ 。对于 1美元$ ，我们有

(3.1)

$$\开始{align}\左（S^{-1}\波浪线{S}\右）_{\gamma_i\gamma-j}&=\mathcal{O}（\|H\|），\quad\qquad\end{align{$$

(3.2)

$$开始{align}\left（S^{-1}\tilde{S}\right）_{\alpha_i\alpha_i}&=\left$$

(3.3)

$$开始{align}\kern-2pt\quad\qquad\q四元\q四元\左（S^{-1}\tilde{S}\right）{\alpha_i\beta_i}&=-\left（S^}\tilde{S}\ right）_{\beta_ i\alpha_ i}+\mathcal{O}（\|H\|），\end{align{$$

(3.4)

$$\开始{align}\\kern1pt\quad\left（S^{-1}\tilde{S}\right）_{\gamma_i\gamma_i}^T\左（S^}\tilde{S}\ right）_{\gamma_i\gamma_i}&=i_{2|\alpha_i|}+\mathcal{O}（\|H\|），\end{align{$$

(3.5)

$$开始{align}\left（S^{-1}\tilde{S}\right）_{\gamma_i\gamma_i}^T J_{2|\alpha_i|}\lert（S^}\tilde{S}\ right）_{\gamma_i\gamma_i}&=J_{2 |\alfa_i|{+\mathcal{O}（\|H\|^2）。\结束{对齐}$$

证明证明以下断言就足够了A类以对角线形式 $A=D\oplus D$ 和 $S=I_{2n}$ 。对于任何 $\波浪线{S}\in\operatorname{Sp}（2n；A+H）$ ，我们有

(3.6)

$$\开始{align}\波浪线{S}^T（A+H）\波浪线}=\波浪线[D}\oplus\tilde{D}，\结束{align{$$

哪里 $\波浪线{D}$ 是带条目的对角线矩阵 $d_1（A+H）\leq\cdots\leq d_n（A+H）$ .根据定理 $3.1$ 第页，共页[参考偶像、高娜和沃尔夫11]，我们得到

(3.7)

$$\开始{align}\tilde{D}=D+\mathcal{O}（\|H\|）。\结束{对齐}$$

由(3.6)和(3.7)，并使用对角线形式 $A=D\oplus D$ ，我们得到

(3.8)

$$\开始{align}\tilde{S}^T（A+H）\tilde}=A+\mathcal{O}（\|H\|）。\结束{对齐}$$

辛矩阵 $\颚化符｛S｝$ 满足

$$\开始{align*}\ | \波浪线{S}\ |^2&=\ |（A+H）^{-1/2}（A+F de{S}\|\\&=2\|（A+H）^{-1}\|d_{1}$$

哪里 $\kappa（T）=\|T\|\|T^{-1}\|$ 是可逆矩阵的条件数吨，我们使用[参考Jain和Mishra13，引理2.2（iii）]。因此，它意味着 $\ | \波浪线{S}\|$ 一致有界美元\|H\|$ 的连续性 $\卡帕$ 。所以，从(3.8)和辛关系 $\波浪线{S}^{-T}=J_{2n}\波浪线{S} J型_{2n}^T$ ，我们得到

(3.9)

$$\开始{align}A\波浪线{S}=J_{2n}\波浪线{S} J型_{2n}^TA+\mathcal{O}（\|H\|）。\结束{对齐}$$

考虑 $\波浪线{S}$ 以块矩阵形式：

$$\begin{align*}\tilde{S}=\begin{pmatrix}\tilde{W}和\tilde}\\tilde{Y}和\ tilde{Z}\end{pmmatrix}，\end}对齐*}$$

其中每个区块 $\波浪线{W}，\波浪线}，\波浪线{Y}，\t波浪线{Z}$ 具有大小 $n\次n$ .来自(3.9)并利用事实 $A=D\oplus D$ ，我们得到

(3.10)

$$\开始{align}\开始{pmatrix}D\波浪线{W}&D\波浪线上{X}\\D\波浪形{Y}&D\波浪形{Z}\end{pmatricx}&=\begin{pmatriax}0_n&I_n\\-I_n&0_n\end{pmatrix{开始{pmmatrix}\波浪形}\\tilde{X}\\tilde}波浪形{Y}&\tilede{Z}\结束{pmattrix}\begin}0_n&-I_n\\I_n&0_n\end{pmatrix}\开始{pmatricx}D&0_n\\0_n&D\end}+\mathcal{O}（\|H\|）\nonnumber\\&=\开始{pmatrix}\波浪线{Z} D类&-\波浪线{Y} D类\\-\波浪线{X} 天&&波浪号{W} D类\end{pmatrix}+\mathcal{O}（\|H\|）。\结束{对齐}$$

现在，使用表示法 $D=\mu_1 I_{|\alpha_1|}\oplus\cdots\oplus\mu_r I_{| \alpha_r|}$ ，并比较中两侧的相应块(3.10)我们得到了 $1\leq i，j\leq r美元$ ,

(3.11)

$$\开始{align}\开始{pmatrix}\mu_i\波浪线{西}_{\字母_i\字母_j}和\ mu_i\波浪线{X}（X）_｛\alpha_i\alpha_j｝\\mu_i\tilde{Y}（Y）_{\字母_i\字母_j}和\ mu_i\波浪线{Z}（Z）_{\alpha_2\alpha_j}\end{pmatrix}&=\begin{pmatricx}\mu_j\波浪线{Z}（Z）_{\字母_i\字母_j}&-\mu_j\波浪线{Y}（Y）_{\字母_i\字母_j}\\-\mu_j\波浪线{X}（X）_{\字母_i\字母_j}和\ mu_j\波浪线{西}_{\alpha_2\alpha_j}\end{pmatrix}+\mathcal{O}（\|H\|）。\结束{对齐}$$

这可以等效地表示为

(3.12)

$$\开始{align}\mu_i\tilde{宋体}_{gamma_i\gamma_j}&=\mu_j j_{2|\alpha_i|}\波浪线{宋体}_{gamma_i\gamma_j}j^T_{2|\alpha_j|}+\mathcal{O}（\|H\|）。\结束{对齐}$$

这也为

(3.13)

$$\开始{align}\mu_j\波浪线{宋体}_{\gamma_2\gamma_j}&=\mu_i j_{2|\alpha_i|}\波浪线{宋体}_{gamma_i\gamma_j}j^T_{2|\alpha_j|}+\mathcal{O}（\|H\|）。\结束{对齐}$$

正在添加(3.12)和(3.13)，然后除以 $\亩_i+\亩_j$ ，给出

(3.14)

$$\开始{align}\波浪线{宋体}_{gamma_i\gamma_j}&=j_{2|\alpha_i|}\波浪线{宋体}_｛\gamma_j\gamma_j｝j^T_｛2|\alpha_j|｝+\mathcal｛O｝（\|H\|）。\结束｛align｝$$

假设我们有 $i\neq j个$ 。这意味着 $\mu _i\neq\mu _ j$ 通过减法(3.13)来自(3.12)，然后除以 $\亩_i-\亩_j$ ，然后我们得到

(3.15)

$$\开始{align}\波浪线{宋体}_{gamma_i\gamma_j}&=-j_{2|\alpha_i|}\波浪线{宋体}_{gamma_i\gamma_j}j^T_{2|\alpha_j|}+\mathcal{O}（\|H\|）。\结束｛align｝$$

通过添加(3.14)和(3.15)，我们得到 $\波浪线{宋体}_{\gamma_i\gamma _j}=\mathcal{O}（\|H\|）$ .这就解决了(3.1).

我们得到了(3.2)和(3.3)直接由于(3.11)通过采取 $i=j$ .

通过辛关系 $\波浪线{S}^TJ_{2n}\波浪线}=J_{3n}$ 我们得到

(3.16)

$$\开始{align}J_{2|\alpha_i|}&=\波浪线{S}^T_{\gamma_i}J_{2n}\波浪线{宋体}_{\gamma_i}\非数字\\&=\sum_{k=1}^r\tilde{宋体}_{\gamma_k\gamma_i}^T J_{2|\alpha_k|}\波浪线{宋体}_{\gamma_k\gamma_i}\n非数字\\&=\波浪线{宋体}_{\gamma_i\gamma_i}^T J_{2|\alpha_i|}\波浪线{宋体}_{\gamma_i\gamma_i}+\sum_{k\neqi，k=1}^r波浪线{宋体}_{\gamma_k\gamma_i}^T J_{2|\alpha_k|}\波浪线{宋体}_{\gamma_k\gamma_i}。\结束{对齐}$$

我们通过了解(3.1)那个 $\波浪线{宋体}_{\gamma_k\gamma _i}=\mathcal{O}（\|H\|）$ 为所有人 $k\neq i$ 。在(3.16)，我们得到

(3.17)

$$\开始{align}J_{2|\alpha_i|}=\波浪线{宋体}_{\gamma_i\gamma_i}^T J_{2|\alpha_i|}\波浪线{宋体}_{\gamma_i\gamma_i}+\mathcal{O}（\|H\|^2）。\结束{对齐}$$

这意味着(3.5). 关系(3.17)还提供

(3.18)

$$\开始{align}\波浪线{宋体}_{\gamma_i\gamma_i}^T J_{2|\alpha_i|}\波浪线{宋体}_｛\gamma_i\gamma_i｝J_｛2|\alpha_i|｝^T=i_｛2|\alpha_i|｝+\mathcal｛O｝（\|H\|^2）。\结束{对齐}$$

这两种关系(3.2)和(3.3)可以组合表示为

(3.19)

$$\开始{align}J_{2|\alpha_i|}\波浪线{宋体}_{\gamma_i\gamma_i}J_{2|\alpha_i|}^T=\波浪线{宋体}_{\gamma_i\gamma_i}+\mathcal{O}（\|H\|）。\结束{对齐}$$

替换(3.19)英寸(3.18)给予

$$\开始{align*}\波浪线{宋体}_{\gamma_2\gamma_i}^T\波浪线{宋体}_{\gamma_i\gamma_i}=i_{2|\alpha_i|}+\mathcal{O}（\|H\|）。\结束{align*}$$

这证明了剩下的断言(3.4).

备注3.3通过采取 $H=0_{2n，2n}$ 在命题中3.2，我们观察到 $\左（S^{-1}\波浪线{S}\右）_{\gamma_i\gamma _j}=0_{2|\alpha_i|，2|\alpha_j|}$ 对于 $i\neq j个$ ，还有那个都是正交辛的我。这意味着 $\波浪线{S}=S Q$ ，其中 $Q=Q_｛[1]｝\oplus ^｛\operatorname｛s｝｝\cdots\oplus ^｛\operatorname｛s｝｝Q_｛[r]｝$ 是正象的。以下结果将此观察推广到任意情况 $H\到0_{2n}$ .

定理3.4让 $A\in\operatorname{Pd}（2n）$ 和 $H\in\operatorname{Sm}（2n）$ 这样的话 $A+H\in\operatorname{Pd}（2n）$ 让 ${S\in\operatorname{Sp}（2n；A）}$ 和 $\波浪线{S}\in\operatorname{Sp}（2n；A+H）$ 随心所欲。然后，存在一个正交矩阵问表单的

$$\开始{align*}Q=Q_{[1]}\oplus^{\operatorname{s}}\cdots\oplus${operatorname{s}{Q_{[r]}，\end{align**}$$

哪里 $Q_{[i]}\in\operatorname{OrSp}（2|\alpha_i|）$ 为所有人 $i=1，\ldots，r$ ，令人满意

$$\开始{align*}\tilde{S}=SQ+\mathcal{O}（\|H\|）。\结束{align*}$$

证明假设这一点不失普遍性A类具有对角线形式 $A=D\oplus D$ 和 $S=I_{2n}$ .有了这个假设，命题3.2给出了以下表示 $\波浪线{S}$ 就辛直和而言：

(3.20)

$$\begin{align}\tilde{S}=\oplus^{\operatorname{S}}_i\begin{pmatrix}\tilde{宋体}_{\字母_i\字母_i}和\波浪线{宋体}_{\alpha_i\beta_i}\\-\波浪线{宋体}_{\alpha_i\beta_i}和\波浪线{宋体}_{\alpha_2\alpha_i}\end{pmatrix}+\mathcal{O}（\|H\|）。\结束{对齐}$$

我们的策略是将Gram–Schmidt正交归一化过程应用于 $\波浪号{宋体}_{\字母_i\字母_i}+\iota\tilde{宋体}_{\α_i\β_i}$ 获得形式为的酉矩阵 $U_{[i]}+\iota V_{[i]}$ ，其中 $U_{[i]}$ 和 $V_｛[i]｝$ 是实矩阵，然后使用表示(2.1)获得正交矩阵 $Q_{[i]}$ .

让 $x_1，\ldot，x_{|\alpha_i|}$ 和 $y_1，\ldot，y_{|\alpha_i|}$ 是的列 $\波浪线{宋体}_{\字母_i\字母_i}$ 和 $\波浪线{宋体}_{\α_i\β_i}$ 分别是。现在，将Gram–Schmidt正交归一化过程应用于复杂向量 $x_1+\iota y_1，\ldots，x_{|\alpha_i|}+\ioda y_{|\ alpha_i |}$ 让 $z_1=x_1+\iota y_1$ 。选择 $w_1=z_1/\|z_1\|\equiv u_1+\iota v_1$ .签署人(3.5)和(3.4)，我们有

$$开始{align*}\|z_1 \|^2&=\|x_1\|^2+\|y_1\||^2 \&=\left\|\begin{pmatrix}x_1\-y_1\end{pmatricx}\right\|^2]（\|H\|）。\结束{align*}$$

这意味着

$$\begin{align*}w_1=z_1+\mathcal{O}（\|H\|）=x_1+\iota y_1+\mathcal{O}（\ |H\|]）。\结束{align*}$$

让 $z{2}=x_2+iota y_2-\langle w_1，x_2+\iota y_2 \rangle w_1$ 。选择 $w{2}=z{2}/\|z{2{2}\|\equivu_2+\iotav_2$ 以便 $\{w_1，w_2\}$ 是一个正交集。由(3.5)和(3.4)，我们有 $\langle x_1+\iota y_1，x_2+\ioda y_2\rangle=\mathcal{O}（\|H\|）$ 。这意味着

$$\begin{align*}z_{2}&=x_2+\iota x_2-\langle w_1，x_2+\ iota y_2\rangle w_1 \\&=y_2+\oota y_2-\langle x_1+\ioata y_1，x2+\ioda y_2\langle w_1+\mathcal{O}（\|H\|）\\&=x_2+\iotay_2+\ mathcal（\|H \|）。\结束{align*}$$

再一次，通过(3.5)和(3.4)，我们有 $\|z_2\|=1+\mathcal{O}（\|H\|）$ ，这意味着 $w_{2}=x_2+\iota y_2+\mathcal{O}（\|H\|）$ .

通过继续Gram–Schmidt过程，我们得到了正交向量 $\{w_1，\ldot，w_{2|\alpha_i|}\}=\{u_1+\iota v_1，\ ldot，u_{|\ alpha_i |}+\iota-v_{|\alfa_i|{}\}$ 这样所有人 $j=1，\ldot，|\alpha_i|$ ,

(3.21)

$$\begin{align}u_j+\iota v_j=x_j+\ iota y_j+\mathcal{O}（\|H\|）。\结束{对齐}$$

让

以便 $U_｛[i]｝+\iota V_｛[i]｝$ 是酉矩阵(2.1)，然后得出以下矩阵：

是正交辛的。关系(3.21)因此给出

$$\开始{align*}Q_{[i]}=\开始{pmatrix}\波浪线{宋体}_{\字母_i\字母_i}和\波浪线{宋体}_{\alpha_i\beta_i}\\-\波浪线{宋体}_{\alpha_i\beta_i}和\波浪线{宋体}_{\alpha_2\alpha_i}\end{pmatrix}+\mathcal{O}（\|H\|）。\结束{align*}$$

这与(3.20)给予 $\tilde{S}=Q+\mathcal{O}（\|H\|）$ 哪里 $Q=Q_{[1]}\oplus^{\operatorname{s}}\cdots\oplus${\operatorname{s{}Q_{[r]}$ ，这就完成了证明。

矩阵平方美元$ 在定理中3.4刻画集合的特征 $\运算符名称{Sp}（2n；A）$ 我们在以下命题中陈述了这一点，其证明直接来自[参考Jain和Mishra13]. 它也被称为定理3.5[参考儿子、Absil、Gao和Stykel21].

提案3.5让 $S\in\operatorname{Sp}（2n；A）$ 被修复。每个辛矩阵 $\hat{S}\in\operatorname{Sp}（2n；A）$ 正是这种形式

$$\开始{align*}\hat{S}=SQ，结束{align**}$$

哪里 $Q=Q_{[1]}\oplus^{\operatorname{s}}\cdots\oplus${\operatorname{s{}Q_{[r]}$ 这样的话 $Q_{[i]}\in\operatorname{OrSp}（2|\alpha_i|）$ 为所有人 $i=1，\ldot，r$ .

在[参考偶像、高娜和沃尔夫11]，表明如果A类没有重复的辛特征值，那么对于任何固定的 $H\in\运算符名称｛Sm｝（2n）$ ，可以选择 $S\in\operatorname{Sp}（2n；A）$ 和 $S（\varepsilon）\in\operatorname{Sp}（2n；A+\varepsilon H）$ 对于小型 $\varepsilon>0$ 这样的话 $\|S（\varepsilon）-S\|=\mathcal{O}（\sqrt{\varepsilon}）$ .我们将他们的结果推广到更一般的情况A类具有重复的辛特征值。此外，我们考虑了A类并加强上述成果。

定理3.6让 $A\in\operatorname{Pd}（2n）$ 和 $H\in\operatorname{Sm}（2n）$ 这样的话 $A+H\in\运算符名称｛Pd｝（2n）$ 给定任何 $\波浪线{S}\in\operatorname{Sp}（2n；A+H）$ ，存在 $S\in\operatorname{Sp}（2n；A）$ 这样的话

(3.22)

$$\开始{align}\|\波浪线{S} -S型\|=\mathcal{O}（\|H\|）。\结束{对齐}$$

证明让 $M\in\operatorname{Sp}（2n；A）$ .根据定理3.4，我们有

$$\begin{align*}\tilde{S}=MQ+\mathcal{O}（\|H\|），\end{aling*}$$

哪里 $Q=Q_{[1]}\oplus^{\operatorname{s}}\cdots\oplus${\operatorname{s{}Q_{[r]}$ 这样的话 $Q_{[i]}\in\operatorname{OrSp}（2|\alpha_i|）$ 为所有人 $i=1，\ldot，r$ .设置以便 $\ | \波浪线{S} -S型\|=\mathcal{O}（\|H\|）$ 。我们也有 $S\in\operatorname{Sp}（2n；A）$ 它来自命题3.5.

我们从定理中知道3.4辛块的距离 $\左（S^{-1}\波浪线{S}\右）_{\gamma_i\gamma-i}$ 从 $\operatorname{OrSp}（2|\alpha_i|）$ 是 $\mathcal{O}（\|H\|）$ 为所有人 $i=1，\ldots，r$ .自 $\运算符名称｛Sp｝（2|\alpha_i|）\supset\运算符名称｛OrSp｝（2|\alpha_i|）$ ，距离 $\左（S^{-1}\波浪线{S}\右）_{\gamma_i\gamma-i}$ 从 $\operatorname{Sp}（2|\alpha_i|）$ 预计将更小。以下结果表明，该距离为 $\mathcal{O}（\|H\|^2）$ .

让 $W=[u，v]$ 成为 $2n\乘以2$ 矩阵，以便 $\operatorname{Range}（W）$ 是非各向同性的即。， $u^TJ美元_{2n}v\neq 0$ 让 $R=\开始{pmatrix}1&0\\0&u^TJ_{2n}v\结束{pmatrix}$ 和 $S=WR^{-1}$ 然后我们有 $S\in\operatorname{Sp}（2n，2）$ .分解 $W=销售代表$ 称为基本SR分解（ESR）。请参见[参考萨拉姆18]用于各种版本的ESR及其在Gram–Schmidt方法辛类似物中的应用。

提议3.7让 $A\in\operatorname{Pd}（2n）$ 和 $H\in\operatorname{Sm}（2n）$ 这样的话 $A+H\in\operatorname{Pd}（2n）$ 让 $S\in\operatorname{Sp}（2n；A）$ 和 $\波浪线{S}\in\operatorname{Sp}（2n；A+H）$ 对于每个 $i=1，\ldot，r$ ，存在 $N_｛[i]｝\in\运算符名称｛Sp｝（2|\alpha_i|）$ 这样的话

$$\begin｛align*｝\left（S^｛-1｝\tilde｛S｝\right）_｛\gamma_i\gamma_i｝=N_｛[i]｝+\mathcal｛O｝（\|H\|^2）。\结束{align*}$$

证明在不失一般性的情况下，我们可以假设A类具有对角线形式 ${A=D\oplus D}$ 和 $S=I_{2n}$ .让 $u_1，\ldot，u_{|\alpha_i|}，v_1，\ ldot，v_{|\ alpha_i |}$ 是的列 $\波浪线{宋体}_{\γ_i\γ_i}$ .设置对于 $j=1，\ldot，|\alpha_i|$ 。我们将数学归纳法应用于j个建造 $N_{[i]}$ 。我们注意到 $\波浪线{宋体}_{\γ_i\γ_i}$ 可以表示为

$$\开始{align*}\波浪线{宋体}_{\gamma_i\gamma_i}=M_{[1]}\diamond\cdots\diamond M_{[|\alpha_i|]}。\结束{align*}$$

选择 $W_{[1]}=M_{[1]}$ 我们从中得知(3.5)那个 $\operatorname{Range}（W_{[1]}）$ 对于较小的美元\|H\|$ 将ESR应用于 $W_{[1]$ 得到 $W_{[1]}=S_{[1]}R_{[1]$ ，其中

(3.23)

$$\开始{align}R_{[1]}&=\开始{pmatrix}1&0\\0&u_1^TJ_{2|\alpha_i|}v_1\end{pmatricx}，\end{align{}$$

和 $S_{[1]}=W_{[1]}R_{[1]{^{-1}\in\operatorname{Sp}（2|\alpha_i|，2）$ .签署人(3.5)，我们有 $u_1^TJ_{2|\alpha_i|}v_1=1+\mathcal{O}（\|H\|^2）$ .将此替换为(3.23)给予

(3.24)

$$\开始{align}R_{[1]}&=I_2+\mathcal{O}（\|H\|^2）。\结束{对齐}$$

替换的值 $R_｛[1]｝$ 来自(3.24)英寸 $W_｛[1]｝=S_｛[1]｝R_｛[1]｝$ 给予

$$\开始{align*}M_{[1]}=W_{[1]}=S_{[1]}+\mathcal{O}（\|H\|^2）。\结束{align*}$$

我们的归纳假设是，对于 $1\leq j<|\alpha _i|$ ，存在 $2|\alpha_i|\乘以2$ 实矩阵 $S_{[1]}，\ldot，S_{[j]}$ 令人满意的 $S_{[1]}\diamond\cdots\diamond S_{[j]}\in\operatorname{Sp}（2|\alpha_i|，2j）$ 和

(3.25)

$$\begin{align}M_{[1]}\diamond\cdots\diamond M_{[j]}&=S_{[1]}\diamend\cdot \diamond S_{[j]}+\mathcal{O}（\|H\|^2）。\结束｛align｝$$

我们选择

(3.26)

$$\begin{align}W_{[j+1]}=M_{[j+1]}-\left（S_{[1]}\diamond\cdots\diamond S_{[j]}\right）j^T_{2j}\left。\结束｛align｝$$

由(3.5)和(3.25)，我们有

(3.27)

$$\begin{align}W_{[j+1]}=M_{[j+1]}+\mathcal{O}（\|H\|^2），\end{alinge}$$

这意味着 $\operatorname{Range}（W_{[j+1]}）$ 对于较小的 $\mathcal{O}（\|H\|）$ 将ESR应用于 $W_{[j+1]}=[W_{j+1}，z_{j+1}]$ 得到 $W_{[j+1]}=S_{[j+1]}R_{[j+1]}$ .给， $S_{[j+1]}\in\operatorname{Sp}（2|\alpha_i|，2）$ 和

(3.28)

$$\开始{align}R_{[j+1]}&=\开始{pmatrix}1&0\\0&w_{j+1}^TJ_{2|\alpha_i|}z_{j+1}\end{pmatricx}。\结束{对齐}$$

发件人(3.5)和(3.27)，我们得到 $w_{j+1}^TJ_{2|\alpha_i|}z_{j+1}=1+\mathcal{O}（\|H\|^2）$ 。在中使用此关系(3.28)暗示 $R_{[j+1]}=I_2+\mathcal{O}（\|H\|^2）$ .将此替换为 $W_{[j+1]}=S_{[j+1]}R_{[j+1]}$ 给予

(3.29)

$$\开始{align}W_{[j+1]}&=S_{[j+1]}+\mathcal{O}（\|H\|^2）。\结束{对齐}$$

组合(3.27)和(3.29)然后给出

$$\开始{align*}M_{[j+1]}=S_{[j+1]}+\mathcal{O}（\|H\|^2）。\结束{align*}$$

因此，我们

$$\开始{align*}M_{[1]}\diamond\cdots\diamond M_{[j+1]}&=S_{[1]{\diamone\cdots\diamond S_{[j+1]}+\mathcal{O}（\|H\|^2）。\结束{align*}$$

为了完成归纳，我们只需要展示一下 $S_{[1]}\diamond\cdots\diamond S_{[j+1]}\in\operatorname{Sp}（2|\alpha_i|，2（j+1））$ .我们有

$$\开始{align*}S_{[1]}\diamond\cdots\diamond S_{[j+1]}&=\left（S_{[1]}\diamend\cdot \ diamond S-{[j]}\right）\diamond S2{[j+1]}。\结束｛align*｝$$

根据以下必要和充分条件 $（S_{[1]}\diamond\cdots\diamond S_{[j]}）\diamond S-{[j+1]}\in\operatorname{Sp}（2|\alpha_i|，2（j+1））$ ，如第节所述2.3，这相当于表明 $（S_{[1]}\diamond\cdots\diamond S_{[j]}）^T j_{2|\alpha_i|}S_{[j+1]}$ 是零矩阵。现在，使用关系 $W_{[j+1]}=S_{[j+1]}R_{[j+1]}$ ，我们得到

(3.30)

$$开始{align}\left（S_{[1]}\diamond\cdots\diamond S_{[j]}\right）^T j_{2|\alpha_i|}S_{[j+1]}&=\left。\结束{对齐}$$

在中替换(3.30)，的值 $W_{[j+1]}$ 来自(3.26)以获得

$$开始{align*}和\左（S_{[1]}\diamond\cdots\diamond S_{[j]}\right）^T j_{2|\alpha_i|}S_{[j+1]}=\左（S{[1]{\diamone\cdots\diamond S-{[j]}\rift）^T j _{2|\ alpha_i |}\\四元\左[M_{[j+1]}-\左（T_{[1]neneneep \金刚石\ cdots\金刚石S_{[j]]}\右）j^T_{2j}\左（S_{[1]}\钻石\cdots\钻石S_{[j]}\左）^TJ_{2|\alpha_i|}M_{[j+1]}\右]R{[j+1]}^{-1}。\结束{align*}$$

应用归纳假设 $S_{[1]}\diamond\cdots\diamond S_{[j]}\in\operatorname{Sp}（2|\alpha_i|，2j）$ 并简化如下：

(3.31)

$$\开始{align}&\左（S_{[1]}\diamond\cdots\diamond S_{[j]}\right）^T j_{2|\alpha_i|}S_{[j+1]}\非数字\\&=\left[\left（S_{[1]}\ diamond\\cdots\damond S_[j]{\right[1]}\diamond\cdots\diamond S_{[j]}\right）^TJ_{2|\alpha_i|}M_{[j+1]}\right]R_{[j+1]}^{-1}\nonumber\\&=\left[\left（S_{[1]}\diamond\cdots\diamond S_{[j]}\right）^T j_{2|\alpha_i|}M_{[j+1]}-\left j，2}。\结束{对齐}$$

因此，我们已经证明 $S_｛[1]｝\d菱形\cdots\diamond S_｛[j+1]｝\in\运算符名称｛Sp｝（2|\alpha_i|，2（j+1））$ 通过归纳，我们得到了所需的矩阵 $N_{[i]}=S_{[1]}\diamond\cdots\diamond S_{[|\alpha_i|]}\in\operatorname{Sp}（2|\alfa_i|）$ ，满足

$$\开始{align*}\波浪线{宋体}_{\gamma_i\gamma_i}=M_{[1]}\diamond\cdots\diamond M_{[|\alpha_i|]}=N_{[i]}+\mathcal{O}（\|H\|^2）\\[-36pt]\结束{align*}$$

4结论

我们工作的主要发现之一是 $S\in\operatorname{Sp}（2n；A）$ 和 $\波浪线{S}\in\operatorname{Sp}（2n；A+H）$ ，存在一个正交矩阵问这样的话 $\tilde{S}=SQ+\mathcal{O}（\|H\|）$ 此外，正辛矩阵问具有结构 $Q=Q_{[1]}\oplus^s\cdots\oplussQ_{[r]}$ ，其中 $Q_{[j]}$ 是一个 $2|\alpha_j|\乘以2|\ alpha_j|$ 正交辛矩阵。这里，第页是不同辛特征值的数目 $\mu _1，\ldot，\mu _r$ 属于A类和 $\α_j$ 是的辛特征值的指数集A类等于 $\亩$ 。我们还证明了 $S\in\operatorname{Sp}（2n；A）$ 和 $\波浪线{S}\in\operatorname{Sp}（2n；A+H）$ 可以进行选择，以便 $\ | \波浪线{S} -S型\|=\mathcal{O}（\|H\|）$ .