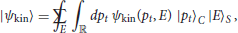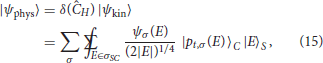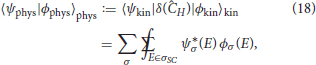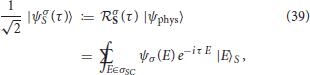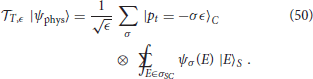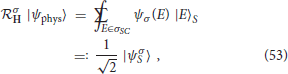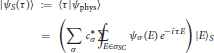Equivalence of Approaches to Relational Quantum Dynamics in Relativistic Settings

Höhn, Philipp A.; Smith, Alexander R. H.; Lock, Maximilian P. E.

doi:10.3389/fphy.2021.587083

原创研究文章

前面。物理。，2021年6月18日
高能和天体粒子物理学
第9卷-2021| https://doi.org/10.3389/fphy.2021.587083

相对论环境下关系量子动力学方法的等价性

菲利普·A·Höhn^1,2^*

亚历山大·史密斯^3,4^*

马克西米利安体育锁⁵^*

¹日本冲绳冲绳科学技术研究生院
²英国伦敦大学学院物理与天文学系
^三美国新罕布什尔州曼彻斯特圣安瑟姆学院物理系
⁴美国新罕布什尔州汉诺威达特茅斯学院物理与天文学系
⁵奥地利科学院量子光学和量子信息研究所，奥地利维也纳

我们之前已经证明了关系量子动力学的三种方法——相对论狄拉克观测，Page-Wootters形式主义和量子去参数化——是等价的。在这里，我们证明了关系量子动力学的这种“三位一体”在相对论环境中每个频率超选择扇区都成立。根据时钟子系统的时间是通过正算子值测度（POVM）定义的，该测度相对于由其（二次）哈密顿量生成的群是协变的。这与通常选择的自共轭时钟观测共轭时钟动量不同。这也解决了库查的批评，即当条件作用于闵可夫斯基时间算符时，Page-Wootters形式主义为相对论粒子产生了不正确的局域化概率。我们表明，条件作用于协变时钟POVM会导致相对论量子力学中常用的Newton-Wigner型局域化概率。通过建立上述等价性，我们还为关系观测值和去参数化指定了一致的条件概率解释。最后，我们扩展了最近一种改变时间参考系的方法，并展示了如何按扇区变换状态和可观测频率。我们使用这种方法讨论了一种间接的时钟自参考效应，并探讨了比较和同步不同量子时钟任务的状态和时间帧依赖性。

1.简介

在广义相对论中，时间所起的作用与经典力学和量子力学或明可夫斯基背景下的量子场论不同。广义协方差省去了时间的首选，而是引入了时间的动力学概念，这取决于爱因斯坦场方程的解。在量子引力的规范方法中，这导致了臭名昭著的时间问题[1–三]. 它最著名的方面是，由于理论的限制，时空的量子态（以及其中包含的任何物质）乍一看似乎没有经历任何时间演化，这似乎与日常经验相矛盾。

这个解决方案来自广义相对论的一个关键见解：任何关于时间的物理概念都是相关的，宇宙的自由度都是相对进化的[4–6]. 这一见解导致了三种主要的时间问题关系方法，每一种方法都试图从量子自由度中提取时间概念，而其他自由度则与之相关：

（i） Dirac量化方案，其中构造了关系观测值，对进化自由度和时钟自由度之间的相关性进行编码[1,2,4,7–38],

（ii）Page-Wootters形式主义，它根据时钟的条件概率和演变的自由度定义了关系动力学[7,25,39–57]、和

（iii）经典或量子去参数化，导致简化的量子理论，只将演化的自由度视为量子[1,2,7,10,30,31,58–65].

这三种方法在很大程度上是独立进行的，它们之间的关系以前是未知的。他们也并非没有批评，尤其是Page-Wootters形式主义。例如，库查[1]对这种方法提出了三个基本批评，即：

（a）在相对论环境中导致错误的定位概率，

（b）与理论约束相冲突，以及

（c）产生错误的传播者。

也有人表示担心，在时钟自由度的选择方面存在固有的模糊性，也称为多项选择问题[1–三,66,67]. 事实上，在一般广义相对论系统中，没有关系时间变量的首选，不同的选择可能导致先验的不同的量子理论。

在我们最近的工作中[7]我们讨论了这三种方法（i）-（iii）与关系量子动力学之间的关系，证明了当时钟哈密顿量具有连续和非简并谱并且与用于描述其动力学的系统解耦时，它们实际上是等价的。具体来说，我们构造了显式变换，将关系量子动力学的每个公式映射到其他公式。这些地图揭示了Page-Wootters形式主义（ii）和量子去参数化（iii）量子对称性约简明显规范不变公式（i）。换句话说，Page-Wootters形式主义（ii）和量子去参数化（iii）可以被视为规范不变量（i）的规范固定公式的量子类似物。相反，关系狄拉克观测值的公式（i）构成了规范固定公式（ii）和（iii）的规范不变扩展的量子模拟。更具体地说，这些转换建立了（i）作为时钟选择-中性（在下文解释的意义上），（ii）作为关系薛定谔，以及（iii）作为动力学的关系海森堡图。由相同量子动力学的三个面组成，我们称之为（i）–（iii）的等价关系量子动力学的三位一体.

这种等价性不仅为关系Dirac观测提供了一致的条件概率解释，还解决了Kucha的批评（b），即Page-Wootters形式主义将与量子约束相冲突。此外，三位一体解决了库查的批评（c），即Page-Wootters形式主义会产生错误的传播者，它表明正确的传播者总是遵循物理希尔伯特空间上明显规范不变的条件概率[7]. 这种批评（c）的解决方案不同于以往依赖理想时钟的解决方案[25,43,68]和辅助辅助系统[43]并且可以被视为[46].

三位一体的（i）-（iii）之间的转换也使我们能够解决Höhn等人的多项选择问题[7]通过扩展量子理论中改变时间参考帧（即时钟）的先前方法[30,31,47]（另请参见[32–34,69]). 问题的解决部分在于认识到，Wheeler-DeWitt方程的解决方案编码了所有子系统之间的关系，包括用作时钟以跟踪其他子系统动力学的子系统间的关系；时钟有多种选择，每种都可以用来定义动力学。因此，我们的建议是将多项选择问题转化为特征通过拥有大量的量子时间选择，我们可以通过量子时间框架转换将其连接起来。这与开发一般协方差的真正量子实现相一致[7,30,31,38,70–74]. 这项提议是目前开发量子参考系变换通用框架（并研究其物理后果）的努力的一部分[75–85])，并应与通过确定时钟的首选来解决多项选择问题的其他尝试进行对比[53]（请参见[7]以进一步讨论本提案）。

我们没有讨论库查的批评（a），即Page-Wootters形式主义在Höhn等人中产生了错误的相对论模型局部化概率[7]因为它们的时钟哈密顿量在动量上是二次的，因此通常具有退化谱，分裂成正负频率扇区。我们以前的结构没有涵盖这种简并。虽然二次时钟哈密顿量是关系观测值[方法（i）]和去参数化[方法（iii）]文献中的标准，参见例如[4,10,11,19,29,31]相对论粒子模型最近才在Page-Wootters形式主义中进行研究[方法（ii）][45,49–51]. 然而，Kuchař的批评（a）认为Page Wootters方法在相对论环境中产生了不正确的局部化概率，这一点尚未得到解决。由于Page-Wootters形式主义在相对论环境中遇到了挑战，考虑到三位一体所暗示的关系方法的等效性，人们可能也会担心关系可观测性和去参数化。

在本文中，我们表明这些挑战是可以克服的，并且可以对关系动力学提供一致的解释。为此，我们将三位一体扩展到二次时钟哈密顿量，从而涵盖了许多相对论设置；我们证明了Höhn等人的所有结果[7]由于由哈密顿约束引起的超选择规则，与时钟相关联的每个频率扇区保持。从频率上看，编码在（i）关系观测值、（ii）Page-Wootters形式主义和（iii）量子去参数化中的关系动力学也完全等价。

我们建设的关键，如Höhn等人[7]，是正算子值测度（POVM）的使用，在此，POVM相对于二次时钟哈密顿量进行协变变换[86–89]作为可观察的时间。这与通常采用与时钟动量共轭的算符（即相对论粒子情况下的Minkowski时间算符）的方法形成了对比。这个协变时钟POVM有助于我们解决Kuchař的批评（a），即Page-Wootters形式主义对相对论系统产生错误的局域化概率。我们证明，当条件作用于这个协变时钟POVM而不是Minkowski时间时，可以获得Newton-Winer型局部化概率[90,91]. 然而，由于Perez-Wilde的相对论局域化no-go定理，Newton-Wigner型局域化是近似的，而不是完全洛伦兹协变的[92]和疾病[93]（另请参见[94,95])，它被普遍认为是相对论量子力学中可能的最佳局部化（在量子场论中，局部化是另一回事[90,94]). 这证明了在关系量子动力学中使用协变时钟POVM的优势[7,44,45,96,97]. 三位一体还扩展了对关系可观测值的概率解释：描述位置算符和协变时钟POVM之间关系的Dirac可观测值对应于相对论环境中的Newton-Wigner型局部化。

最后，我们再次使用（i）和（iii）之间的等价性来构造量子理论中的时间框架变化。由于跨频率扇区的超选择规则，时间帧更改只能将两个频率扇区（一个与每个时钟关联）重叠中包含的信息从一个时钟“透视图”映射到另一个。我们应用这些时间框架变化图来探索间接的时钟自参考以及比较和同步不同量子时钟读数的时间框架和状态依赖性。

在完成这份手稿时，我们意识到了查泰尼耶[38]，这独立地扩展了Höhn et al[7]关于关系观测值的条件概率解释，以及它们与Page-Wootters形式主义的等价性。然而，另一种形式主义[37]在Chataignier中使用[38]，它不使用协变时钟POVM，因此这两种工作相互补充。

在本文中，我们使用的单位是ℏ=1。

2.经典力学和量子力学的钟-中性公式

通俗地说，一般协方差假设物理定律在每个参照系中都是相同的。这通常被解释为意味着物理定律应该采用张量方程的形式。张量可以被视为参照系中性物体：在选择参照系之前，张量定义了物理描述。因此，他们将物理编码为所有参考帧一次“看到”。如果想知道在特定参考坐标系中测量张量会产生的数字，就必须将张量与对应于所选坐标系的向量联系起来。这样，同一张量相对于不同帧的描述看起来不同，但张量就其本身而言，作为一个多线性映射，是引用帧中性的。正是张量的这种参考-框架中立性导致了物理定律的框架依赖性。

参考系作为向量系的概念通常被用来定义一些观察者的局部实验室的方向。在实践中，人们通常会用参考系隐式地标识本地实验室（即，描述剩余物理的参考系）。这是一种理想化，忽略了实验室在时空上的反向反应、与其他物理系统的相互作用和可能的内部动力学，同时假设它足够经典，因此可以忽略方向的叠加。这种理想化适用于广义相对论，其目的是描述时空的大规模结构。然而，在量子引力中，其目标是描述时空的微观结构，这可能不再合适[98]. 更普遍地说，当我们认真对待这样一个事实时，我们可能会问一般协方差的命运，即物理上有意义的参考系在实践中总是与物理系统相关，并且因此由可能与其他系统耦合的动态自由度组成，经历自己的动力学过程，最终将受制于量子理论定律。那么，引用框架中性结构是什么？

关于这个问题，我们注意到，与理想化局部实验室相关的参考框架的一般协方差的经典概念与一般坐标变换下的不变性（即被动微分同态）紧密交织在一起。在转向非理想参考系（或者更确切地说系统）时，我们将焦点从坐标描述转移到动态参考自由度，剩下的物理将与之相对。与此相一致，我们将焦点从被动微分形态转移到主动微分形态，它直接作用于动力学自由度。这对量子引力是有利的，经典时空坐标是先验的不存在。广义协方差的量子版本应该根据动力学参考自由度来表示[7,30,31,38,70–74].

主动对称性意味着物理描述中存在冗余。先验所有自由度都是平等的，因此可以自由选择哪些自由度应被视为多余的自由度。关键思想是将此选择与参考自由度的选择相结合，即与剩余自由度相对的自由度¹因此，选择一个动态参考系等于从描述中删除冗余。因此，我们可以将包含冗余的描述（在经典和量子理论中）解释为透视-中性物理描述，即在选择参考系之前对物理进行全局描述，从参考系的角度描述剩余的自由度[7,30,31,71,72]. 因此，这种透视中性结构被提议作为动态（即非理想化）参考系统的参考系中性结构。

在本文中，我们只关注时间差分，因此关注时间参考帧/系统，或者简单地说时钟。在这种情况下，我们将透视中性结构称为时钟-（选择-）中性结构[7,30,31]，我们在这里简要回顾一下经典和量子理论。它是对物理的描述，在选择一个时间参考系之前，剩余自由度的动力学将被描述。

2.1、。钟-中性经典理论

考虑由动作描述的经典理论 $S公司 = \int_{ℝ} d日 u个我 ({q个}^{一}, d日 {q个}^{一} / d日 u个)$ ，其中q个^一表示由索引的配置变量集合一.这样的理论证明时间微分同构不变性如果行动 $S公司$ 是重矩阵化不变量；也就是说，我(q个^一,数字q^一/杜) ↦我(q个^一,数字q^一/杜'）杜′/杜变换为标量密度u个↦u个′(u个). 这种理论的哈密顿量的形式是H（H）=N个(u个)C类_H（H），其中N个(u个)是一个任意的延时函数，并且

\begin{array}{l} {C类}_{H（H）} = \sum_{一} \frac{d日 {q个}^{一}}{d日 u个} {第页}_{一} - 我 \approx 0, & (1) \end{array}

所谓的哈密顿约束是时间微分同态对称的结果。该等式定义约束曲面 $C类$ 在运动学相空间内 ${P（P）}_{家属}$ ，由标准坐标参数化 ${q个}^{一}, {第页}_{b条}$ ≈表示弱等式，即仅适用于 $C类$ [101,102].

哈密顿量在 $C类$ ，它转换任意相空间函数（f）根据

\begin{array}{l} \frac{d日 （f）}{d日 u个} ≔ {（f）, {C类}_{H（H）}} & (2) \end{array}

并积分为有限变换 $α_{{C类}_{H（H）}}^{u个} \cdot （f）$ ，为简单起见，将失效函数选为统一函数，N个(u个)=1。由于重矩阵化不变性，此流应解释为规范变换而非真正的演化[4,11]因此，对于可观察到的F类要成为物理的，它必须在这种变换下保持不变，即。，

\begin{array}{l} {F类, {C类}_{H（H）}} \approx 0 . & (三) \end{array}

满足方程（3）的观测值称为（弱）狄拉克观测值.

为了获得规范不变的动力学，我们必须选择一个动态的时间参考系统，即时钟函数 $T型 ({q个}^{一}, {第页}_{一})$ ，将约束生成的方程（2）参数化动态流。然后，我们可以描述剩余自由度相对于 $T型 ({q个}^{一}, {第页}_{一})$ 这就产生了所谓的关系狄拉克观测值（又称演化运动常数），它编码了“函数的值是什么”这个问题的答案（f）沿着由C类_H（H）在 $C类$ 当时钟T型读取τ？”[4,7,11–19,19–24,26,30,31]. 我们将通过以下方式来表示这种可观察到的情况F类_{f、 T型}(τ). 如Dittrich所示[21,22]还有Dittrich和Tambornino[23,24]，这些观测值可以通过求解 $α_{{C类}_{H（H）}}^{u个} \cdot T型 = τ$ 对于u个产生解决方案u个=u个_T型（τ）并定义

\begin{array}{l} {F类}_{（f）, T型} (τ) ≔ α_{{C类}_{H（H）}}^{u个} \cdot （f） |_{_{u个 = {u个}_{T型} (τ)}} \\ \approx \sum_{n个 = 0}^{\infty} \frac{{(τ - T型)}^{n个}}{n个!} {（f）, \frac{{C类}_{H（H）}}{{T型, {C类}_{H（H）}}}}_{n个}, & (4) \end{array}

其中{f、克}_n个：={{f、克}_n个−1,克}是n个^第个-嵌套泊松括号受{f、克}₀:=（f）. TheF类_{f、 T型}（τ）满足方程（3），从而构成一系列由τ参数化的Dirac观测值。这种关系观测值就是所谓的规范固定量的规范不变扩展[7,21–24,37,102].

在通用模型中，没有时钟功能的首选T型在自由度之间 ${P（P）}_{家属}$ ，有时也称为多项选择问题[1,2]. 不同的选择T型将导致不同的关系狄拉克观测值，如方程（4）所示。所有这些不同的选择都编码在约束曲面中 $C类$ 然后站起来先验的在平等的基础上。

这引起了对 $C类$ 作为一个时钟-中性结构。时间差分同构对称性导致在描述 $C类$ ：由于哈密顿约束，运动学规范自由度不是独立的，并且由于其规范流，只有 $昏暗的 {P（P）}_{家属} - 2$ 独立的物理相空间自由度。特别是，相对于时钟功能的任何选择T型一个人可以建造 $昏暗的 {P（P）}_{家属} - 2$ 使用方程（4）的独立关系Dirac观测值[101,102]. 因此，关系型狄拉克相对于任何其他时钟选择都能观察到T型'可以从中构造。因此，相对于不同的时钟选择，相关狄拉克观测值之间存在冗余。因此 $C类$ 在选择和固定时钟之前，给出了物理描述，相对于时钟可以描述剩余自由度的计量不变动力学。具体而言，对于哪一个运动学自由度和物理自由度被视为冗余，没有做出任何选择。与张量情况类似， $C类$ 仍然包含关于所有时钟选择及其相关关系动态的信息；它产生了一个时钟中性描述。

具有奇数尺寸 $昏暗的 {P（P）}_{家属} - 1$ , $C类$ 也不是相空间。可以获得适当的相空间描述，例如，通过定规减少相空间[7,30,31,38,58]. 提供时钟功能选择T型，我们可以考虑仪表固定条件T型=常数，可能仅在本地有效 $C类$ .自F类_{f、吨}（τ）是沿每个轨道的常数C类_H（H）对于τ的每一个值，我们不会因为限制为T型=常数并使τ自由。通过限制关系观测值F类_{f、 T型}（τ）相对于时钟T型通过求解这两个条件T型=常数,C类_H（H）=0，我们从运动学和物理自由度中删除冗余。幸存的简化相空间描述不再包含时钟自由度作为动力学变量，可以解释为相对于时钟函数定义的时间参考系的动力学描述T型但现在我们跟踪时间演变，而不是从动力学角度T型，但就代表其“时钟读数”的参数τ而言。特别是，时间参考系没有相对于自身进行描述，例如，人们发现重言式F类_{T、 T型}(τ) ≈ τ. 因此，选择时钟的“透视图”意味着选择相应的时钟自由度作为冗余度并删除它们。然后将理论去参数化：它不再包含计量参数u个，也不是约束，也不是动态时钟变量——只有真正的进化自由度。

2.2. 钟-中性量子理论

遵循Dirac公式量化约束系统[10,11,101,102]，首先提升 ${P（P）}_{家属}$ 到正则位置和动量算符 ${\hat{q个}}^{一}$ 和 ${\hat{第页}}_{一}$ 作用于运动学希尔伯特空间 ${H（H）}_{家属}$ 方程（1）中的哈密顿约束是通过要求量子理论的物理状态被约束函数的量子化所湮灭来实现的

\begin{array}{l} {\hat{C类}}_{H（H）} | ψ_{物理} 〉 = 0 & (5) \end{array}

这个类Wheeler-DeWitt方程的解可以从运动状态构造出来 $| ψ_{家属} 〉 \in {H（H）}_{家属}$ 通过组平均运算[11,103–107]²

\begin{array}{l} | ψ_{物理} 〉 = δ ({\hat{C类}}_{H（H）}) | ψ_{家属} 〉 = \frac{1}{2 π} \int_{G公司} d日 u个 {e（电子）}^{负极 我 {\hat{C类}}_{H（H）} u个} | ψ_{家属} 〉, & (6) \end{array}

哪里G公司是由Ĉ生成的组_H（H）。物理状态在中不可规范化 ${H（H）}_{家属}$ 如果它们是Ĉ的不当本征态_H（H）（即，如果零位于其光谱的连续部分）。然而，它们相对于所谓的物理内积

\begin{array}{l} {〈 ψ_{物理} | ϕ_{物理} 〉}_{物理} ≔ {〈 ψ_{家属} | δ ({\hat{C类}}_{H（H）}) | ϕ_{家属} 〉}_{家属} & (7) \end{array}

其中：_家属是运动学内积 $| ψ_{家属} 〉, | ϕ_{家属} 〉 \in {H（H）}_{家属}$ 位于映射到同一ψ的等价状态类中_物理¦Β，|¦Β_物理〉在方程式（6）的投影下。有了这个内积，方程（5）中Wheeler-DeWitt方程的解空间通常可以由Cauchy完成，形成所谓的物理希尔伯特空间 ${H（H）}_{物理}$ [11,103–107].

可观测的规范不变量（即物理不变量） $\hat{F类}$ 作用于 ${H（H）}_{物理}$ 必须满足方程（2）的量化

\begin{array}{l} [{\hat{C类}}_{H（H）}, \hat{F类}] | ψ_{物理} 〉 = 0 & (8) \end{array}

如此引人注目 $\hat{F类}$ 是一个量子狄拉克可观测.

显然，exp（−i uĈ_H（H）) |ψ_物理〉 = |ψ_物理也就是说，物理状态不会在哈密顿约束产生的动力流下演化。这就是所谓的时间问题在量子引力中[1–三]哈密顿约束定义的量子理论是永恒的。然而，这种理论只是“无背景的”，即物理状态不会随着“外部”规范参数的变化而变化u个参数化哈密顿约束生成的组。相反，将量子理论视为 ${H（H）}_{物理}$ 作为一个时钟-中性量子理论：它是在选择一个内部时钟来描述剩余自由度的动力学之前对物理学的一种全局描述（如[7,30,31]). 就像经典情况一样，通常会有许多可能的时钟选择和“量子约束面” ${H（H）}_{物理}$ 同时包含所有这些选择的信息；因此，它决不是“内在永恒的”

目标是适当量化方程（4）中的关系Dirac观测值，将其提升为算子族 ${\hat{F类}}_{（f）, T型} (τ)$ 在 ${H（H）}_{物理}$ 这涉及时间参考系的量化T型很明显，在量子理论中T型也会导致不同的量子关系狄拉克观测值。这将产生许多规范不变的关系量子动力学，每一个都是根据演化参数τ来表示的，它对应于所选量子钟的读数（因此不仪表参数）。关系观测值的量化是非平凡的，特别是因为方程（4）可能不是全局定义的 $C类$ ，并且在很大程度上取决于所选时钟的特性。已经采取了系统量化相关Dirac观测值的步骤（例如[7,17,20,37,38])本文的一部分致力于为一类相对论模型进一步开发它们。

与经典情况类似，“量子约束面”上的钟-中性描述 ${H（H）}_{物理}$ 冗余：由于满足了约束，并非所有自由度都是独立的。特别地，相对于不同时钟选择的量子关系Dirac可观察性集合以及因此不同的关系量子动力学将是相互依赖的。建议再次将时钟的选择与冗余自由度的选择联系起来；移动到给定时钟的“透视图”意味着将相对于它的量子关系观测值视为独立的观测值，并完全删除（现在冗余的）动态时钟自由度。这通过量子对称性约简过程进行，即相空间约简的量子模拟，相当于量子去参数化并在Höhn和Vanrietvelde开发[30]，Höhn[31]，和Höhn等人[7]并将在第5节中进一步开发。特别是，这个过程是从一个相对于一个量子时钟的描述转变为另一个相对于另一个时钟的描述的核心，我们在第7节中对此进行了详细说明。因此，量子对称性约简是探索广义协方差量子版本提案的关键要素[7,30,31,47,70–72]从而也解决了量子引力和宇宙学中的多重选择问题[1,2]（另请参见[28,32–34,64,65,69,77,108]).

3.二次时钟哈密顿量

在时钟中性讨论的基础上，我们现在假设 ${P（P）}_{家属}$ 和 ${H（H）}_{家属}$ 分裂成时钟C类和一个“不断发展”的系统S公司，它们不相互作用。这将允许我们在下一节中选择一个时间参考系，然后定义经典和量子理论中的关系动力学。

3.1. 经典理论

假设经典理论描述了时钟C类与相空间相关 ${P（P）}_{C类} ≃ {T型}^{*} ℝ ≃ ℝ^{2}$ 和一些感兴趣的系统S公司与相空间相关 ${P（P）}_{S公司}$ ，因此运动学相空间分解为 ${P（P）}_{家属} ≔ {P（P）}_{C类} \times {P（P）}_{S公司}$ .我们假设 ${P（P）}_{C类}$ 被规范对参数化(t、第页_t吨)，但不需要具体说明 ${P（P）}_{S公司}$ （而不是假设它是有限维辛流形）。进一步假设时钟和系统不耦合，导致哈密顿约束函数是它们各自哈密顿量的总和^三

\begin{array}{l} {C类}_{H（H）} = {H（H）}_{C类} + {H（H）}_{S公司} \approx 0, & (9) \end{array}

哪里H（H）_C类是上的函数 ${P（P）}_{C类}$ 和H（H）_S公司是上的函数 ${P（P）}_{S公司}$ .

本文涉及时钟动量为二次的时钟哈密顿量， ${H（H）}_{C类} = 秒 {第页}_{t吨}^{2} / 2$ ，其中秒∈{−1，+1}，使得哈密顿约束变为

\begin{array}{l} {C类}_{H（H）} = 秒 \frac{{第页}_{t吨}^{2}}{2} + {H（H）}_{S公司} \approx 0 . & (10) \end{array}

这类时钟哈密顿量出现在大量（特殊和一般）相对论和非相对论模型中-参见表1例如。它们是双重退化的；的每个值H（H）_C类有两种解决方案第页_t吨，在由定义的行上除外第页_t吨= 0. 请注意第页_t吨是狄拉克观测到的。

表1

表1等式（10）中的形式约束示例。

方程（10）中的约束可以分解为两个约束，每个约束在第页_t吨[30,31,33]:

\begin{array}{l} {C类}_{H（H）} = 秒 {C类}_{+} \cdot {C类}_{-}, 的 {C类}_{σ} ≔ \frac{{第页}_{t吨}}{\sqrt{2}} + σ \sqrt{- 秒 {H（H）}_{S公司}}, & (11) \end{array}

其中我们引入了简并标签σ=±1。注意方程（10）中的力秒H_S公司取非正值 $C类$ 。在秒=-1情况、σ=+1和σ=-1分别定义了量子理论中的正和负频率模式。为了简单起见，我们以后将使用此术语二者都 秒= ±1⁴因此，我们可以将约束曲面分解为正负频率扇区[30,31]

\begin{array}{l} C类 = {C类}_{+} \cup {C类}_{-}, & (12) \end{array}

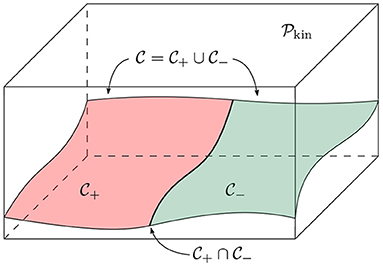
哪里 ${C类}_{σ}$ 是一组解决方案C类_σ=0英寸 ${P（P）}_{家属}$ .十字路口 ${C类}_{+} \cap {C类}_{-}$ 由定义第页_t吨=H（H）_S公司=0（参见图1（如图所示）。

图1

图1所示为表面 ${C类}_{+}$ （红色）和 ${C类}_{-}$ （绿色）由定义C类₊=0和C类_负极分别为0。这些曲面的并集是约束曲面 $C类 = {C类}_{+} \cup {C类}_{-} \subset {P（P）}_{家属}$ ，而他们的十字路口 ${C类}_{+} \cap {C类}_{-}$ 其特点是第页_t吨=H（H）_S公司=0，用粗黑线表示。我们假设H（H）_S公司未退化（见图1[31]对于类似的描述，当H（H）_S公司双重退化）。

3.2. 量子理论

运动相空间的Dirac量子化 ${P（P）}_{家属} = {P（P）}_{C类} \times {P（P）}_{S公司}$ 通向运动学希尔伯特空间 ${H（H）}_{家属} ≃ {H（H）}_{C类} \otimes {H（H）}_{S公司}$ 描述时钟和系统，其中 ${H（H）}_{C类} ≃ 我^{2} (ℝ)$ 和 ${H（H）}_{S公司}$ Hilbert空间与S公司.我们假设系统哈密顿量被提升为自共轭算子Ĥ_S公司在 ${H（H）}_{S公司}$ 。的元素 ${H（H）}_{家属}$ 可以在时钟和系统哈密顿量的本征态中展开为

其中积分和强调了Ĥ_S公司可能具有连续或离散频谱⁵.

理论的物理状态满足方程（5），对于方程（10）中的哈密顿约束，该方程变成

\begin{array}{l} {\hat{C类}}_{H（H）} | ψ_{物理} 〉 = (秒 \frac{{\hat{第页}}_{t吨}^{2}}{2} \otimes 我_{S公司} + 我_{C类} \otimes {\hat{H（H）}}_{S公司}) | ψ_{物理} 〉 = 0 & (13) \end{array}

这里我们假设该约束具有零特征值，即方程（13）的解存在。注意，这需要频谱sĤ_S公司包含非正特征值，与经典情况类似。

量化C类_σ在方程式（11）中，得出[Ĉ₊, Ĉ_负极]=0，因此方程（6）中的组平均投影仪可以表示为

\begin{array}{l} δ ({\hat{C类}}_{H（H）}) = δ (秒 {\hat{C类}}_{+} {\hat{C类}}_{-}) = \frac{1}{2 {(- 秒 {\hat{H（H）}}_{S公司})}^{\frac{1}{2}}} \sum_{σ} δ ({\hat{C类}}_{σ}) . & (14) \end{array}

δ（Ĉ）的形式_H（H）)意味着将物理希尔伯特空间分解为正负频率扇区的直接和 ${H（H）}_{物理} ≃ {H（H）}_{+} \oplus {H（H）}_{-}$ （另请参阅[31,104]). 用投影仪δ（Ĉ_H（H）)任意运动状态产生物理状态

其中ψ_σ(E类)是与正、负频率模式相关联的牛顿-怀特型波函数[90]⁶:

\begin{array}{l} ψ_{σ} (E类) ≔ \frac{ψ_{家属} ({第页}_{t吨, σ} (E类), E类)}{{(2 | E类 |)}^{1 / 4}}, & (16) \end{array}

我们已经定义了函数 ${第页}_{t吨, σ} (E类) ≔ - σ \sqrt{2 | E类 |}$ 和光谱

\begin{array}{l} σ_{S公司 C类} ≔ 规格 ({\hat{H（H）}}_{S公司}) \cap 规格 (- {\hat{H（H）}}_{C类}) \\ = {E类 \in 规格 ({\hat{H（H）}}_{S公司}) | 秒 E类 \leq 0} . & (17) \end{array}

根据方程式（7）中引入的物理内积对物理状态进行归一化

它采用了非相对论性量子力学的通常形式（σ-扇形），符合Newton-Winer-type波函数的性质。在第6节讨论相对论局域化时，这一观察将至关重要。

4.协变时钟

4.1. 具有经典协变时钟的关系动力学

利用自由度分裂为时钟C类（我们的时间参照系）和进化系统S公司，我们现在选择一个时钟功能 T型在 ${P（P）}_{C类}$ 相对而言，我们描述了S公司如第2.1节所述，在关系观测方面。

我们可以简单地选择相空间坐标T型=t吨作为时钟功能。由方程式（2）可知秒=−1种情况t吨在正频率扇区“向前”运行 ${C类}_{+}$ 以及负频率扇区的“倒退” ${C类}_{-}$ 沿着由C类_H（H）; 对于秒=+1相反方向保持不变。请注意 ${C类}_{+} \cap {C类}_{-}$ 对应于静态轨道t吨（自第页_t吨=0），以及t吨因此，是上的最大错误时钟函数 ${C类}_{+} \cap {C类}_{-}$ 这导致在描述与t吨：的逆幂第页_t吨出现在编码系统自由度相对于t吨当规范对打开时 ${P（P）}_{S公司}$ 已使用[18,23,30,31]⁷通过在 ${P（P）}_{S公司}$ 关系可观测值的构造[31]或者在量子理论中，通过仔细地正则化第页_t吨[30].

然而，在本文中，我们将回避这些挑战，并提供一个可以说更优雅的解决方案。我们根据经典协方差条件选择不同的时钟函数：它与H（H）_C类这将导致在第页_t吨=0到时钟函数中（在第4.2节中仍将有意义地量化），并导致相关观测值独立于相位空间坐标的选择 ${P（P）}_{S公司}$ .解决{T、 H（H）_C类}=1，我们发现一个协变时钟函数T型必须采用以下形式T型=科技/第页_t吨+克(第页_t吨)，其中克(第页_t吨)是一个任意函数。从今往后，我们选择克(第页_t吨)=0表示简单，因此我们有

\begin{array}{l} T型 = 秒 \frac{t吨}{{第页}_{t吨}} . & (19) \end{array}

这个时钟功能在任何地方都有明确的定义，除了在线路上第页_t吨=0，其中H（H）_C类是非退化的。很明显T型到处“向前”奔跑 $C类$ 对于两者秒=±1，除 ${C类}_{+} \cap {C类}_{-}$ .

协方差条件与我们的时钟不与系统交互的假设相结合，意味着{T、 C类_H（H）}=1，简化了方程（4）中相关Dirac观测值的形式。例如，与“系统可观测值是什么”问题相对应的关系可观测值（f）_S公司当时钟T型读取τ？”现在采用简单的形式[7,21]

\begin{array}{l} {F类}_{{（f）}_{S公司}, T型} (τ) \approx \sum_{n个 = 0}^{\infty} \frac{{(τ - T型)}^{n个}}{n个!} {{（f）}_{S公司}, {H（H）}_{S公司}}_{n个} . & (20) \end{array}

4.2. 二次哈密顿量的可观测协变量子时间

人们可以尝试通过在时钟希尔伯特空间上直接量化方程（19）中的协变时钟函数来构造量子理论中的时间算符 ${H（H）}_{C类} ≃ 我^{2} (ℝ)$ [86,120,121]. 选择对称排序，这将产生

\begin{array}{l} \hat{T型} = 秒 \frac{1}{2} (\hat{t吨} {\hat{第页}}_{t吨}^{- 1} + {\hat{第页}}_{t吨}^{- 1} \hat{t吨}) . & (21) \end{array}

在这里， ${\hat{第页}}_{t吨}^{- 1}$ 根据谱分解定义，如下所示 $\hat{T型} | {第页}_{t吨} = 0 〉$ 未定义，类似于经典情况。当操作员 $\hat{T型}$ 与时钟哈密顿量正则共轭， $[\hat{T型}, Ĥ_{C类}] = 我$ ，它是一个不允许自伴随扩展的对称算子[86,88]. 自 $\hat{T型}$ 不是自伴的，它的状态似乎是可观察的先验的不清楚的⁸这表明泡利反对量子力学中时间可观测的构造：因为_C类下有界，不存在满足 $[\hat{T型}, Ĥ_{C类}] = 我$ 泡利的结论是，我们被迫将时间视为一个经典参数，这与处理其他观测值（例如位置和动量）的方式不同[122].

然而，后来人们意识到，通过采用POVM提供的更一般的可观察概念协变的可观测时间⁹ E类_T型可以构造其第一矩对应于运算符的 $\hat{T型}$ [86,87,89]. 这种可观测时间由一组效应算子密度定义E类_T型(数据传输时间)≥0归一化为 $\int_{ℝ} {E类}_{T型} (d日 t吨) = 我_{C类}$ ，和自共轭效应运算符 ${E类}_{T型} (X（X）) ≔ \int_{X（X）} {E类}_{T型} (d日 t吨)$ 与概率ψ相关_C类|E类_T型(X（X）)|ψ_C类〉测量E类_T型产生结果t吨∈X（X）⊂ℝ考虑到时钟处于状态 $| ψ_{C类} 〉 \in {H（H）}_{C类}$ 为了能够很好地观察到，它应该满足所谓的协方差条件

\begin{array}{l} {E类}_{T型} (X（X） + t吨) = {U型}_{C类} (t吨) {E类}_{T型} (X（X）) {U型}_{C类}^{†} (t吨), & (23) \end{array}

相对于统一集团诉讼 ${U型}_{C类} (t吨) ≔ {e（电子）}^{- 我 Ĥ_{C类} t吨}$ 由时钟哈密顿量生成。正如我们稍后将看到的，这将导致可观测时间和时钟哈密顿量的正则共轭的推广，并允许我们将该方法扩展到基于协变时钟POVM的关系量子动力学[7]相对论模型。特别地，我们获得了一个有效的可观测量子时间，尽管存在经典的时钟病态。

在本例中，这样一个可观测值可以纯粹从时钟哈密顿量的自共轭量子化中构造出来_C类及其本征态。效应密度可以定义为“投影”的总和

\begin{array}{l} {E类}_{T型} (d日 t吨) = \frac{1}{2 π} \sum_{σ} d日 t吨 | t吨, σ 〉 〈 t吨, σ | & (24) \end{array}

上的时钟状态对应时钟读数t吨∈ℝ在负频率和正频率（即正时钟动量和负时钟动量）扇区¹⁰

\begin{array}{l} | t吨, σ 〉 ≔ \int_{ℝ} d日 {第页}_{t吨} \sqrt{| {第页}_{t吨} |} θ (- σ {第页}_{t吨}) {e（电子）}^{- 我 t吨 秒 {第页}_{t吨}^{2} / 2} | {第页}_{t吨} 〉 . & (25) \end{array}

方程（23）中的协方差条件由时钟状态转换为

\begin{array}{l} | t吨 + {t吨}^{'}, σ 〉 = {U型}_{C类} (t吨) | {t吨}^{'}, σ 〉 . & (26) \end{array}

请注意，时钟状态与病理状态正交|第页_t吨=0Ş，因此可观测的协变时间不支持它。此外，时钟状态不是相互正交的：

\begin{array}{l} 〈 {t吨}^{'}, σ^{'} | t吨, σ 〉 = δ_{σ σ^{'}} [π δ (t吨 - {t吨}^{'}) - 我 P（P） \frac{1}{t吨 - {t吨}^{'}}], & (27) \end{array}

其中P表示柯西主值。因此E类_T型(数据传输时间)不是一个真正的投影仪。然而，以下引理证明了时钟状态|t吨，σ构成的σ-频率扇区的过完备基础 ${H（H）}_{C类}$ ，进而得到可观测到的适当归一化协变时间E类_T型在 ${H（H）}_{家属}$ .

引理1.时钟状态|t吨, σ〉方程式（25）中定义的与投影仪集成 $θ (- σ {\hat{第页}}_{t吨})$ 上的正/负频率扇区 ${H（H）}_{C类}$

\begin{array}{l} \frac{1}{2 π} \int_{ℝ} d日 t吨 | t吨, σ 〉 〈 t吨, σ | = θ (负极 σ {\hat{第页}}_{t吨}) & (28) \end{array}

从而形成如下等式的解析:

\begin{array}{l} \int_{ℝ} E类 (d日 t吨) = \frac{1}{2 π} \sum_{σ} \int_{ℝ} d日 t吨 | t吨, σ 〉 〈 t吨, σ | = 我_{C类} . & (29) \end{array}

证明：证明见补充材料. □

这个n个^第个-可观测时间的矩算子E类_T型定义为

\begin{array}{l} {\hat{T型}}^{(n个)} ≔ \int_{ℝ} {E类}_{T型} (d日 t吨) {t吨}^{n个} = \frac{1}{2 π} \sum_{σ} \int_{ℝ} d日 t吨 {t吨}^{n个} | t吨, σ 〉 〈 t吨, σ | . & (30) \end{array}

虽然时钟POVM的效应算子是自共轭的，但n个≥1不是由于方程（27）中的非正交性。然而，后者是可行的量子可观察性，具有POVM方面的有效概率解释；唯一需要付出的代价是不同的测量结果t吨无法完全区分。

根据这个定义，我们发现第一矩算符 ${\hat{T型}}^{(1)}$ 属于E类_T型实际上等于运算符 $\hat{T型}$ 在方程（21）中。这是之前在Holevo发现的[86]和Busch等人[88]（用于秒=+1箱）。这提供了对可观测时间的具体解释E类_T型根据经典理论-时间算符 ${\hat{T型}}^{(1)}$ ，即可观察到的时间的第一时刻E类_T型，是经典时钟函数的量化T型式（19）中。

引理2.操作员 $\hat{T型}$ 和第一矩算符 ${\hat{T型}}^{(1)}$ 观测到的协变时间 E类_T型 是相等的, $\hat{T型} \equiv {\hat{T型}}^{(1)}$ .

证明：证明见补充材料. □

方程（30）表明时间算符 $\hat{T型}$ 自动分为正频率部分和负频率部分，与之形成对比 $\hat{t吨}$ ，相空间坐标的量化t吨.

接下来，我们发现，虽然时钟状态不是正交的，但它们“几乎”是协变时间算符的本征状态 $\hat{T型}$ 在每个σ-扇区上：

引理3.时钟状态|t吨, σ〉方程（25）中定义的本征态不是 $\hat{T型} = {\hat{T型}}^{(1)}$ .然而，对于所有人来说 $| ψ 〉 \in D类 (\hat{T型})$ ，其中 $D类 (\hat{T型})$ 是的域 $\hat{T型}$ ,他们满意了:

\begin{array}{l} 〈 ψ | \hat{T型} | t吨, σ 〉 = t吨 〈 ψ | t吨, σ 〉, \forall t吨 \in ℝ, σ = \pm 1 . \end{array}

证明：证明见补充材料. □

这导致了另一个结果，它强调了为什么协方差条件方程（23）可以被视为产生正则共轭的推广：

引理4.方程（30）中定义的n阶算子满足 $[{\hat{T型}}^{(n个)}, Ĥ_{C类}] = 我 n个 {\hat{T型}}^{(n个 - 1)}$ .此外, $\forall | ψ 〉 \in D类 ({\hat{T型}}^{n个})$ 我们有 ${\hat{T型}}^{(n个)} | ψ 〉 = {\hat{T型}}^{n个} | ψ 〉$ .

证明：证据见补充材料. □

我们强调引理4的第二个陈述并不适用于所有 ${H（H）}_{C类}$ .

效应密度不与时钟哈密顿量交换[E类_T型(数据传输时间), Ĥ_C类]≠0，表示时钟指示的时间（即测量结果E类_T型)并且不能同时确定时钟能量。然而，重要的是，以下引理表明时钟读数和频率扇区，即σ的值可以同时确定。

引理5.效应密度E_T型(数据传输时间)协变时钟POVM和投影仪到σ-扇区的通勤： $[{E类}_{T型} (d日 t吨), θ (- σ {\hat{第页}}_{t吨})] = 0$ .

证明：证明见补充材料. □

推论1。 由于效应密度与效应和力矩算符相结合，这就需要 $[{E类}_{T型} (X（X）), θ (- σ {\hat{第页}}_{t吨})] = [{\hat{T型}}^{(n个)}, θ (- σ {\hat{第页}}_{t吨})] = 0$ ,对所有人来说 X（X）⊂ ℝ和 n个∈ ℕ.

这个引理和推论的意义在于，它们允许我们同时对时钟和频率扇区所指示的时间进行条件限制。当定义下面的量子约化图时，这将变得至关重要，它将我们从物理希尔伯特空间带到每个σ-扇区存在的关系薛定谔和海森堡图片。因此，这个引理对于扩展Höhn等人的量子约化过程非常重要[7]到这里考虑的模型类别。

5.关系量子动力学的三位一体：二次时钟哈密顿量

在第2节中介绍了经典和量子理论的钟-中性结构后，将运动学自由度自然划分为时钟C类和系统S公司在第3节中，以及可观测的协变时间E类_T型在第4节中，我们现在可以构造一个关系量子动力学，描述了如何S公司相对于C类.

如引言所述，我们在Höhn等人[7]关系量子动力学的三种表述，即（i）量子关系狄拉克观测，（ii）Page-Wootters形式主义的关系薛定谔图，以及（iii）通过量子去参数化获得的关系海森堡图，对于方程（9）中哈密顿约束所描述的模型是等价的当时钟哈密顿量具有连续的非简并谱时；这三种配方构成a三位一体关系量子动力学。在这里，我们证明了这种等价性扩展到方程（13）中的形式约束，涉及双简并时钟哈密顿量¹¹.

由于物理希尔伯特空间的直接和结构 ${H（H）}_{物理} = {H（H）}_{+} \oplus {H（H）}_{-}$ 以及将时钟矩算符（方程30）分离为非退化的正负频率扇区，这是Höhn等人建立等效性所需的所有技术结果[7]对于当前类型的模型，将保持每σ扇区。因此，我们将在没有证据的情况下陈述以下一些结果，让读者适当地参考Höhn等人的相应结果的证据[7]，此处适用于每个σ-扇区。特别是，推论1意味着我们可以同时调节时钟读数和频率扇区。

最后，我们还讨论了通过约化相空间量子化获得的关系量子动力学。在这种情况下，可以根据时钟函数经典地对模型进行去参数化T型，这相当于经典的对称性缩减。虽然由此获得的关系量子动力学产生了类似三位一体动力学（iii）的关系海森堡图，但它并不总是等价的，因此不一定是三位一体的一部分。因此，我们将简化相空间量化的阐述移动到补充材料然而，这有助于理解为什么下面解释的量子对称性约简是通过去参数化经典相空间约简的量子模拟。我们强调对称性减少和量化通常不会相互抵消[7,124–129]. 相对论约束的相关讨论也可以在Kaminski et al[29].

为了帮助读者，我们总结了在三位一体结构中出现的各种希尔伯特空间表2.

表2

表2不同希尔伯特空间的总结。

5.1. 三位一体的三张脸

5.1.1. 动力学（i）：量子关系狄拉克观测

我们现在量化方程（20）中的关系Dirac观测值，证实了第2.2节中关于方程（13）形式哈密顿约束的钟-中性图中的关系量子动力学讨论。当经典时间函数量化时，研究了关系Dirac观测值的量化T型产生自共轭时间算子 $\hat{T型}$ （请参见[4,7,11–20,27–31,35–38,116]以及其中的引用）；然而，当 $\hat{T型}$ 不能自共轭，例如在方程（21）中，需要更一般的量化过程。

Höhn等人介绍了这种程序[7]基于使用协变时间可观察性的等式（20）的量化。将此过程应用于由二次时钟哈密顿量描述的当前类型的模型，我们使用n个方程（30）中定义的矩运算符：

\begin{array}{l} {\hat{F类}}_{{（f）}_{S公司}, T型} (τ) ≔ \int_{ℝ} {E类}_{T型} (d日 t吨) \otimes \sum_{n个 = 0}^{\infty} \frac{我^{n个}}{n个!} {(t吨 - τ)}^{n个} [{\hat{（f）}}_{S公司}, {\hat{H（H）}}_{S公司}]_{n个} \\ = \sum_{σ} \int_{ℝ} \frac{d日 t吨}{2 π} {U型}_{C类 S公司} (t吨) (| τ, σ 〉 〈 τ, σ | \otimes {\hat{（f）}}_{S公司}) {U型}_{C类 S公司}^{†} (t吨) \\ = : \sum_{σ} G公司 (| τ, σ 〉 〈 τ, σ | \otimes {\hat{（f）}}_{S公司}), & (31) \end{array}

哪里 ${[{\hat{（f）}}_{S公司}, Ĥ_{S公司}]}_{n个} ≔ [{[{\hat{（f）}}_{S公司}, Ĥ_{S公司}]}_{n个 - 1}, Ĥ_{S公司}]$ 是n个具有约定的四阶嵌套换向器 ${[{\hat{（f）}}_{S公司}, Ĥ_{S公司}]}_{0} ≔ {\hat{（f）}}_{S公司}$ ,U型_反恐精英(t吨)≔经验（−itĈ_H（H）)，第二行紧随积分变量的变化，并调用方程（26）中的协方差条件。关系狄拉克观测 ${\hat{F类}}_{{（f）}_{S公司}, T型} (τ)$ 因此被揭示为单参数非紧规范群上的非相干平均G公司由约束运算符Ĉ生成_H（H）运动学算子的 $| τ, σ 〉 〈 τ, σ | \otimes {\hat{（f）}}_{S公司}$ 与投影仪配对到时钟读数τ和σ-频率扇区。这种分组平均称为G公司-旋转操作，我们表示它 $G公司$ 如方程式（31）的最后一行。G公司-旋转操作以前主要是在空间量子参考系的背景下进行研究的，例如，参见[130–132]，但也出现在量子狄拉克观测的一些构造中（例如，参见[7,11,37,38,106])¹²如Höhn等人所述[7]，这个G公司-twirl构成了规范固定量的规范不变扩展的量子模拟。

关系Dirac可观察性 ${\hat{F类}}_{{（f）}_{S公司}, T型} (τ)$ 在方程（31）中，构成了强Dirac观测值的单参数族 ${H（H）}_{物理}$ （定理1[7]其证明适用于每个σ扇区）：

\begin{array}{l} [{\hat{F类}}_{{（f）}_{S公司}, T型} (τ), {\hat{C类}}_{H（H）}] = 0, \forall τ \in ℝ . & (32) \end{array}

因此，通过将演化参数τ设为物理期望值，我们获得了规范不变的关系量子动力学 ${〈 ψ_{物理} | {\hat{F类}}_{{（f）}_{S公司}, T型} (τ) | ψ_{物理} 〉}_{物理}$ 运行。

分解 ${\hat{F类}}_{{（f）}_{S公司}, T型} (τ)$ 在方程（31）中，将正负频率扇区划分为两个部分，可以在物理希尔伯特空间上得到狄拉克可观测代数的可约表示。更准确地说，关系Dirac观测值在σ-频率扇区中被替代，因此方程（31）中的σ-和应理解为直接和。要看到这一点，请考虑操作员 $\hat{问} ≔ θ (- {\hat{第页}}_{t吨}) - θ ({\hat{第页}}_{t吨})$ 我们记得 $θ (- σ {\hat{第页}}_{t吨})$ 是对应σ扇区的投影。通过施工 $[\hat{问}, Ĉ_{H（H）}] = 0$ ，这意味着 $\hat{问}$ 是一个强大的狄拉克观测。其特征值为+1和−1的本征空间对应于正频率扇区子空间和负频率扇区子空间 ${H（H）}_{+}$ 和 ${H（H）}_{-}$ 此外， $\hat{问}$ 与任何可观察到的关系狄拉克通勤F类_{（f）_S公司,T型}（τ）根据引理5，在方程（31）中，这意味着问和任何自共轭F类_{（f）_S公司,T型}（τ）可以在相同的特征基中对角化。这又意味着下面的超级选举规则

\begin{array}{l} {\hat{F类}}_{{（f）}_{S公司}, T型} (τ) = {\hat{F类}}_{{（f）}_{S公司}, T型}^{+} (τ) \oplus {\hat{F类}}_{{（f）}_{S公司}, T型}^{-} (τ), & (33) \end{array}

哪里 ${\hat{F类}}_{{（f）}_{S公司}, T型}^{σ} (τ) ≔ G公司 (| τ, σ 〉 〈 τ, σ | \otimes {\hat{（f）}}_{S公司}) \in 我 ({H（H）}_{σ})$ ¹³.

虽然物理希尔伯特空间中确实存在跨σ-频率扇区表现出一致性的状态，例如|ψ_物理〉 ~ |ψ₊〉 + |ψ_负极〉，其中 $| ψ_{σ} 〉 \in {H（H）}_{σ}$ ，由于方程（33）中的分解，这种一致性在物理上是不可获得的，因为它不会影响任何相关Dirac观测值的期望值。换句话说，σ-频率扇区的叠加和经典混合是无法区分的。因此，σ-扇区上物理态的叠加是混合态，而纯物理态是其中之一 ${H（H）}_{+}$ 或 ${H（H）}_{-}$ （另请参见[103,105]讨论组平均中的超选择）。

例如，这种超选择规则表现为相对论粒子情况下正负频率模式之间的超选择，以及FLRW模型中无质量标量场情况下膨胀和收缩解之间的超选举表1[31]. 由于表示的可简化性，通常只限于一个频率扇区（例如，参见[113,114,116,133]). 人们可能会猜测，量子场论中类似的超选择规则将表现为物质和反物质扇区之间的超选择规则。

由G公司-旋转通常被解释为由于缺乏关于参考系的知识，如果使用适当的参考系，则可以取消超选规则[130]. 这种解释在这里似乎不合适。首先，取消超选规则将导致撤消群平均，这违反了规范不变性。其次，这种解释通常与给定群体行动的平均值相关联，该平均值参数化了人们对相对参照系方向的无知。相比之下，这里Dirac观测值的超选择的起源不是由约束生成的群，而是约束属性的结果，即群生成器。事实上，上面的超选规则源于约束的可分解性以及投影仪对约束的分解（方程式14）。这两个属性都依赖于 $\hat{t吨}$ -约束方程（13）中的相关项；如果引入这样一个术语，人们通常会发现[Ĉ₊, Ĉ_负极]≠0，其中Ĉ_σ是经典因子的量化，但我们强调_H（H）≠sĈ₊Ĉ_负极在这种情况下。而这种修改后的约束可能会生成相同的组¹⁴，σ-部门之间不会出现超级选举规则。因此，上述超选规则不能与缺乏共享物理参考框架联系起来。这与将物理希尔伯特空间解释为时钟中性，即时间参考框架中性结构（见第2.2节）相一致。

现在考虑投影仪∏_{σ_{联合国安全理事会}}= θ(−sĤ_S公司)来自 ${H（H）}_{S公司}$ 到由所有系统能量本征态跨越的子空间|E类〉_S公司具有E类∈ σ_{联合国安全理事会}; 即，求解约束方程（13）时允许的值。从今以后，我们将表示这个系统希尔伯特子空间 ${H（H）}_{S公司}^{物理} ≔ Π_{σ_{S公司 C类}} ({H（H）}_{S公司})$ 并称之为物理系统希尔伯特空间。我们将获得物理系统希尔伯特空间的两个副本，每个频率扇区一个副本。与经典情况类似，我们引入量子弱等式在算符之间，表示它们在“量子约束面”上相等 ${H（H）}_{物理}$ :

\begin{array}{l} Ô_{1} \approx Ô_{2} \\ \Leftrightarrow {\hat{O（运行）}}_{1} | ψ_{物理} 〉 = {\hat{O（运行）}}_{2} | ψ_{物理} 〉, \forall | ψ_{物理} 〉 \in {H（H）}_{物理} . & (34) \end{array}

它来自于的引理1[7]，其证明适用于每个σ-扇区，即

\begin{array}{l} {\hat{F类}}_{{（f）}_{S公司}, T型} (τ) \approx {\hat{F类}}_{Π_{σ_{S公司 C类}} {（f）}_{S公司} Π_{σ_{S公司 C类}}, T型} (τ), & (35) \end{array}

是弱相等的关系狄拉克观测值。因此，方程（31）中的关系Dirac观测值在 ${H（H）}_{物理}$ ，其中 ${\hat{F类}}_{{（f）}_{S公司}, T型} (τ) ~ {\hat{F类}}_{克_{S公司}, T型} (τ)$ 如果 $Π_{σ_{S公司 C类}} {\hat{（f）}}_{S公司} Π_{σ_{S公司 C类}} = Π_{σ_{S公司 C类}} ĝ_{S公司} Π_{σ_{S公司 C类}}$ 。这些弱等价类由我们将要表示的内容标记

\begin{array}{l} {\hat{（f）}}_{S公司}^{物理} ≔ Π_{σ_{S公司 C类}} {\hat{（f）}}_{S公司} Π_{σ_{S公司 C类}} \in 我 ({H（H）}_{S公司}^{物理}), & (36) \end{array}

用于任意 ${\hat{（f）}}_{S公司} \in 我 ({H（H）}_{S公司})$ ，其中 $我$ 表示线性运算符集。为了以后的使用，我们注意到物理系统的代数可以观察到 ${\hat{（f）}}_{S公司}^{物理}$ 在 ${H（H）}_{S公司}^{物理}$ 和 ${\hat{F类}}_{{（f）}_{S公司}^{物理}, T型} (τ)$ 在 ${H（H）}_{物理}$ 关于加法、乘法和交换子关系是弱同态的。更准确地说，

\begin{array}{l} {\hat{F类}}_{{（f）}_{S公司}^{物理} + 克_{S公司}^{物理} \cdot {小时}_{S公司}^{物理}, T型} (τ) \approx {\hat{F类}}_{{（f）}_{S公司}^{物理}, T型} (τ) \\ + {\hat{F类}}_{克_{S公司}^{物理}, T型} (τ) \cdot {\hat{F类}}_{{小时}_{S公司}^{物理}, T型} (τ) \end{array}

$\forall {（f）}_{S公司}, 克_{S公司}, {小时}_{S公司} \in 我 ({H（H）}_{S公司})$ 这是Höhn等人定理2的结果[7]（其证明在这里再次适用于每个σ-扇区）。与Höhn等人[7]，这转换了通过Dittrich中的关系观测值定义的弱经典代数同态[21]进入量子理论。

5.1.2. 动力学（ii）：Page-Wootters形式主义

假设我们得到一个量子哈密顿约束方程（5），该方程如方程（9）所示分解为时钟和系统贡献，但目前不一定假设其为方程（13）中的二次型。进一步假设我们得到了在时钟希尔伯特空间上可以观察到的一些（运动学）时间，它不一定是相对于时钟哈密顿量生成的群协变的时钟POVM，而是用来定义时钟读数。Page和Wootters[39,40,134,135]建议从物理状态中提取时钟和系统之间的关系量子动力学，以条件概率表示：可观测的概率是多少 ${\hat{（f）}}_{S公司}$ 与系统关联S公司给出特定结果（f），如果时钟的可观测时间测量值产生时间τ？如果e（电子）_C类（τ）和e（电子）_{（f）_S公司}(（f）)时钟上的投影仪读数τ和系统是否可见 ${\hat{（f）}}_{S公司}$ 获取价值（f），此条件概率假设如下

\begin{array}{l} 探针 (（f） 何时 τ) = \frac{探针 (（f） 和 τ)}{探针 (τ)} \\ = \frac{〈 ψ_{物理} | {e（电子）}_{C类} (τ) \otimes {e（电子）}_{{（f）}_{S公司}} (（f）) {| ψ_{物理} 〉}_{家属}}{〈 ψ_{物理} | {e（电子）}_{C类} (τ) \otimes 我_{S公司} {| ψ_{物理} 〉}_{家属}} . & (37) \end{array}

这个表达式乍一看似乎违反了约束条件，因为它与非狄拉克可观测物理状态上的算符一起作用；这就是Kuchař的批评（b）的基础，即Page Wootters形式主义的条件概率与约束不相容[1]. 然而，对于一类模型，我们在Höhn et al[7]表达式等式（37）是明显规范不变量的规范固定表达式的量子模拟，因此与约束一致。在本节中，我们将此结果推广到相对论设置。

在这里，我们将利用协变时钟POVM将Page-Wootters形式扩展到更一般的哈密顿约束类，形式为方程（13）E类_T型第4.2节¹⁵一方面，这将允许我们证明在关系Dirac观测方面，so-obtained关系量子动力学与明显的规范不变公式完全等价 ${H（H）}_{物理}$ 动力学（i）。顺便说一下，这也将解决Diaz et al中出现的物理状态的规范化问题[50]，其中使用运动学内积而不是物理内积来规范化物理状态，从而产生发散（当用于等质量状态时）。另一方面，协变时钟POVM将允许我们在第6节中处理Kuchař的观察结果[1]在Page-Wootters形式主义中，使用Minkowski可观测时间会导致相对论粒子的定位概率不正确。

Page-Wootters形式通过调节时钟读数τ上的物理状态，在时钟时间τ产生系统状态[39,40,134,135]. 此后，重点讨论由等式（13）中的约束和第4.2节中的协变时钟POVM定义的模型类，并给出了 ${H（H）}_{物理}$ ，由于引理5，我们可以对频率扇区附加条件。在Höhn等人的延伸中[7]，我们可以使用这个条件来定义两个归约图 ${R（右）}_{S公司}^{σ} (τ) : {H（H）}_{物理} \to {H（H）}_{S公司, σ}^{物理}$ ，每个σ-频率扇区一个，

\begin{array}{l} {R（右）}_{S公司}^{σ} (τ) ≔ 〈 τ, σ | \otimes 我_{S公司}, & (38) \end{array}

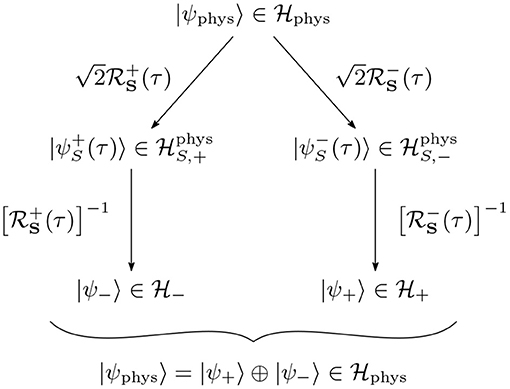
哪里 ${H（H）}_{S公司, σ}^{物理}$ 是的副本 ${H（H）}_{S公司}^{物理} = Π_{σ_{S公司 C类}} ({H（H）}_{S公司})$ 即，求解约束时允许的系统Hilbert空间的子空间，对应于σ-频率扇区。很快就会清楚，标签S公司在缩小图上代表“薛定谔图片”，并将其与斜体区分开来S公司它代表着这个系统，我们从今以后用黑体书写它。由于分解 ${H（H）}_{物理} = {H（H）}_{+} \oplus {H（H）}_{-}$ ，我们装备了这两个副本 ${H（H）}_{S公司, σ}^{物理}$ 用频率标签σ来提醒自己，哪个简化理论对应于哪个正或负频率模式。

简化状态（其归一化因子 $1 / \sqrt{2}$ 稍后将解释），

其中ψ_σ(E类)是方程（16）中定义的Newton-Wigner型波函数，满足关于Ĥ的Schrödinger方程_S公司:

\begin{array}{l} 我 \frac{d日}{d日 τ} | ψ_{S公司}^{σ} (τ) 〉 = {\hat{H（H）}}_{S公司} | ψ_{S公司}^{σ} (τ) 〉 . & (40) \end{array}

我们将其解释为S公司相对于时间参考系C类特别是，这个薛定谔方程对于正负频率扇区看起来是一样的，因为时间是由协变时钟POVM定义的E类_T型在这两个领域都取得了进展。从方程（26）可以清楚地看出，这是早期经典观测的量子模拟，即时钟函数T型在两个频率扇区上“向前”运行 ${C类}_{+}$ 和 ${C类}_{-}$ （与t吨)¹⁶.

由于方程（29）将物理状态分解为正负频率模式，方程（15）也可以写为：

\begin{array}{l} | ψ_{物理} 〉 = \frac{1}{2 \sqrt{2} π} \sum_{σ} \int_{ℝ} d日 t吨 | t吨, σ 〉 | ψ_{S公司}^{σ} (t吨) 〉 . & (41) \end{array}

与引理1一起，这意味着σ扇区左逆 ${H（H）}_{S公司, σ}^{物理} \to {H（H）}_{σ}$ 式（38）中定义的简化图的

\begin{array}{l} \begin{matrix} {({R（右）}_{S公司}^{σ} (τ))}^{负极 1} = \frac{1}{2 π} \int_{ℝ} d日 t吨 | t吨, σ 〉 \otimes {U型}_{S公司} (t吨 负极 τ) \\ = δ ({\hat{C类}}_{H（H）}) (| τ, σ 〉 \otimes 我_{S公司}), \end{matrix} & (42) \end{array}

哪里U型_S公司(t吨)=经验（−iĤ_S公司 t吨)，所以

\begin{array}{l} {({R（右）}_{S公司}^{σ} (τ))}^{- 1} {R（右）}_{S公司}^{σ} (τ) = δ ({\hat{C类}}_{H（H）}) (| τ, σ 〉 〈 τ, σ | \otimes 我_{S公司}) \\ \approx θ (- σ {\hat{第页}}_{t吨}) \otimes 我_{S公司}, & (43) \end{array}

其中≈是量子弱等式，因此

\begin{array}{l} \sum_{σ} {({R（右）}_{S公司}^{σ} (τ))}^{- 1} {R（右）}_{S公司}^{σ} (τ) \approx 我_{物理} . & (44) \end{array}

相反，我们可以在 ${H（H）}_{S公司, σ}^{物理}$ 在表单中

\begin{array}{l} {R（右）}_{S公司}^{σ} (τ) {({R（右）}_{S公司}^{σ} (τ))}^{- 1} = 〈 τ, σ | δ ({\hat{C类}}_{H（H）}) | τ, σ 〉 \\ = Π_{σ_{S公司 C类}} . \end{array}

第二行中的恒等式可以借助于方程式（27）进行检查（也可以遵循中定理2的证明[7]). 这些地图的摘要可以在中找到图2.

图2

图2。Page-Wootters缩减图及其倒数的摘要。量子对称约简映射及其逆映射也存在类似的情况。

使用这些归约图及其逆，我们可以定义编码操作 ${E类}_{S公司}^{τ, σ} : 我 ({H（H）}_{S公司, σ}^{物理}) \to 我 ({H（H）}_{σ})$ ，映射方程（36）中的观测值，作用于物理系统Hilbert空间 ${H（H）}_{S公司, σ}^{物理}$ ，转化为在σ扇区上的Dirac观测值 ${H（H）}_{物理}$ :

\begin{array}{l} {E类}_{S公司}^{τ, σ} ({\hat{（f）}}_{S公司}^{物理}) ≔ {({R（右）}_{S公司}^{σ} (τ))}^{- 1} {\hat{（f）}}_{S公司}^{物理} {R（右）}_{S公司}^{σ} (τ) \\ = δ ({\hat{C类}}_{H（H）}) (| τ, σ 〉 〈 τ, σ | \otimes {\hat{（f）}}_{S公司}^{物理}) . & (45) \end{array}

这些编码的观测值是方程（31）中相关Dirac观测值的σ-扇区部分，如以下定理所述。

定理1.让 ${\hat{（f）}}_{S公司} \in 我 ({H（H）}_{S公司})$ .量子关系狄拉克观测 ${\hat{F类}}_{{（f）}_{S公司}, T型} (τ)$ 作用于 ${H（H）}_{物理}$ ,方程式（31），根据 ${R（右）}_{S公司}^{σ} (τ)$ 对应的投影观测值 ${H（H）}_{S公司, σ}^{物理}$ ,

\begin{array}{l} {R（右）}_{S公司}^{σ} (τ) {\hat{F类}}_{{（f）}_{S公司}, T型} (τ) {({R（右）}_{S公司}^{σ} (τ))}^{- 1} = Π_{σ_{S公司 C类}} {\hat{（f）}}_{S公司} Π_{σ_{S公司 C类}} \equiv {\hat{（f）}}_{S公司}^{物理} . \end{array}

相反，让 ${\hat{（f）}}_{S公司}^{物理} \in 我 ({H（H）}_{S公司, σ}^{物理})$ .方程（45）中系统观测值的编码操作与物理希尔伯特空间一致 ${H（H）}_{物理}$ 方程（31）中的量子关系狄拉克观测值投影到σ扇区:

\begin{array}{l} {E类}_{S公司}^{τ, σ} ({\hat{（f）}}_{S公司}^{物理}) \approx {\hat{F类}}_{{（f）}_{S公司}^{物理}, T型}^{σ} (τ), & (46) \end{array}

哪里 ${\hat{F类}}_{{（f）}_{S公司}^{物理}, T型}^{σ} (τ) = {\hat{F类}}_{{（f）}_{S公司}^{物理}, T型} (τ) (θ (- σ {\hat{第页}}_{t吨}) \otimes 我_{S公司})$ —c.f.方程（33）.

证明：Höhn等人的定理3的证明[7]此处适用于每个σ-扇区。 □

注意，关系狄拉克观测值 ${\hat{F类}}_{{（f）}_{S公司}, T型} (τ)$ 用投影仪通勤 $θ (- σ {\hat{第页}}_{t吨})$ 由于方程（31）中的可简化表示。

除了提供物理希尔伯特空间和物理系统希尔伯特空间上的可观察器之间的σ-扇区字典外，定理1与方程（35）中的弱等价性一起，也暗示了关系Dirac可观察器的全集之间的等价性 ${\hat{F类}}_{{（f）}_{S公司}^{物理}, T型}^{σ} (τ)$ 在 ${H（H）}_{σ}$ 和系统观测 ${H（H）}_{S公司, σ}^{物理}$ .

至关重要的是，物理内积方程（18）中的相关Dirac观测方程（31）的期望值与物理允许系统观测值的期望值σ-扇形一致 ${\hat{（f）}}_{S公司}^{物理}$ 在状态下求解薛定谔方程（40） ${H（H）}_{S公司, σ}^{物理}$ .

定理2.让 ${\hat{（f）}}_{S公司} \in 我 ({H（H）}_{S公司})$ ,并在上表示其关联运算符 ${H（H）}_{S公司}^{物理}$ 通过 ${\hat{（f）}}_{S公司}^{物理} = Π_{σ_{S公司 C类}} {\hat{（f）}}_{S公司} Π_{σ_{S公司 C类}}$ .然后

〈 ψ_{物理} | {\hat{F类}}_{{（f）}_{S公司}, T型}^{σ} (τ) {| ϕ_{物理} 〉}_{物理} = \frac{1}{2} 〈 ψ_{S公司}^{σ} (τ) | {\hat{（f）}}_{S公司}^{物理} | ϕ_{S公司}^{σ} (τ) 〉,

哪里 $| ψ_{S公司}^{σ} (τ) 〉 = \sqrt{2} {R（右）}_{S公司}^{σ} (τ) | ψ_{物理} 〉$ 如方程式（39）所示。因此,

〈 ψ_{物理} | {\hat{F类}}_{{（f）}_{S公司}, T型} (τ) {| ϕ_{物理} 〉}_{物理} = \frac{1}{2} \sum_{σ} 〈 ψ_{S公司}^{σ} (τ) | {\hat{（f）}}_{S公司}^{物理} | ϕ_{S公司}^{σ} (τ) 〉,

证明：Höhn等人对定理4的证明[7]此处适用于每个σ-扇区。 □

因此，关系Schrödinger图（即Page-Wootters形式主义）中的期望值等价于对应关系Dirac观测值的规范不变值 ${H（H）}_{物理}$ 因此，方程式（37）（适用于σ-扇区）等方程式并不违反Kuchař所主张的约束条件[1].

这立即意味着还原图 ${R（右）}_{S公司}^{σ} (τ)$ 按σ部门保存内部产品，如下所示。

推论2.设置 ${\hat{（f）}}_{S公司} = Π_{σ_{S公司 C类}}$ 在定理2中，得出

〈 ψ_{物理} | θ (负极 σ {\hat{第页}}_{t吨}) \otimes 我_{S公司} {| ϕ_{物理} 〉}_{物理} = \frac{1}{2} 〈 ψ_{S公司}^{σ} (τ) | ϕ_{S公司}^{σ} (τ) 〉,

哪里 $| ψ_{S公司}^{σ} (τ) 〉 = \sqrt{2} {R（右）}_{S公司}^{σ} (τ) | ψ_{物理} 〉$ .因此,

\begin{array}{l} \begin{array}{l} {〈 ψ_{物理} | ϕ_{物理} 〉}_{物理} = \frac{1}{2} \sum_{σ} 〈 ψ_{S公司}^{σ} (τ) | ϕ_{S公司}^{σ} (τ) 〉 \\ = \sum_{σ} 〈 ψ_{物理} | (| τ, σ 〉 〈 τ, σ | \otimes 我_{S公司}) {| ϕ_{物理} 〉}_{家属} . \end{array} & (47) \end{array}

引入归一化因子的原因 $1 / \sqrt{2}$ 在方程（39）中现在很清楚：它允许我们处理规范化状态 $〈 ψ_{S公司}^{σ} (τ) | ψ_{S公司}^{σ} (τ) 〉 = 1 = {〈 ψ_{物理} | ψ_{物理} 〉}_{物理}$ 在每个缩减的σ-扇区中，同时在物理希尔伯特空间中。

上述结果表明：

（1）应用Page-Wootters缩减图 ${R（右）}_{S公司}^{σ} (τ)$ 到物理希尔伯特空间 ${H（H）}_{物理}$ 产生a关系薛定谔图关于时钟C类关于物理系统Hilbert空间 ${H（H）}_{S公司, σ}^{物理}$ 对应于σ-频率扇区。

（2） σ-扇区方面，编码在物理希尔伯特空间上的关系狄拉克观测值中的关系量子动力学等价于Page-Wootters形式主义的物理系统希尔伯特空间的关系薛定谔图中的动力学。

（3）给定约化映射的可逆性，定理2形式上表明如果 ${\hat{（f）}}_{S公司}^{物理}$ 是自共轭的 ${H（H）}_{S公司, σ}^{物理}$ ，那么也是 ${\hat{F类}}_{{（f）}_{S公司}, T型}^{σ} (τ)$ 在 ${H（H）}_{σ}$ .

我们注意到，方程（47）第二行中的表达式还定义了Wheeler-DeWitt型约束方程（13）解空间上的内积，它等价于方程（18）中通过群平均获得的物理内积。因此，这两个内积定义了相同的物理希尔伯特空间 ${H（H）}_{物理}$ 方程式（47）第二行中的表达式是对Smith和Ahmadi中引入的Page-Wootters内积的改编[44]与二次时钟哈密顿量哈密顿约束相关的物理希尔伯特空间的可约表示。

5.1.3. 动力学（iii）：量子去参数化

经典地，可以通过规范固定约束的流动来执行时钟中性约束表面的对称性约简。在这种情况下，这产生了两个规范固定的简化相空间副本，每个频率扇区一个副本，每个副本都配备了标准哈密顿动力学，因此产生了一个非参数化理论（参见补充材料). 与经典约束曲面不同，“量子约束曲面” ${H（H）}_{物理}$ 由于对称生成器的求幂运算，它是自动规范不变的_H（H）对所有物理状态和狄拉克观测值的作用微不足道。因此，在解决约束后，量子理论中不再有规范固定。然而，在Höhn和Vanrietvelde之后[30]，Höhn[31]，和Höhn等人[7]，我们现在演示本文中考虑的模型类的经典对称约简过程的量子模拟。因此，这是去参数化的量子模拟，我们以后称之为量子去参数化这种量子对称性简化将时钟-中性狄拉克量子化映射到相对于时钟可观测的海森堡关系图E类_T型、和涉及以下两个步骤。

1约束简化：约束的转换，使其仅作用于选定的参考系（此处为时钟C类)，固定其自由度。经典的模拟是一个正则变换，它将约束转化为动量变量，并将规范变量与规范不变自由度分开[7,71].

2经典轨距固定条件的条件：一个“投影”，用于删除现在冗余的参考框架自由度¹⁷.

我们首先定义约束平凡化映射 ${T型}_{T型, ϵ} : {H（H）}_{物理} \to {T型}_{T型, ϵ} ({H（H）}_{物理})$ 相对于观测到的协变时间E类_T型该映射将物理希尔伯特空间转换为新的希尔伯特空间，同时保留可观测值的内积和代数性质

\begin{array}{l} {T型}_{T型, ϵ} ≔ \sum_{n个 = 0}^{\infty} \frac{我^{n个}}{n个!} {\hat{T型}}^{(n个)} \otimes {({\hat{H（H）}}_{S公司} + 秒 \frac{ϵ^{2}}{2})}^{n个} \\ = \frac{1}{2 π} \sum_{σ} \int_{ℝ} d日 t吨 | t吨, σ 〉 〈 t吨, σ | \otimes {e（电子）}^{我 t吨 ({\hat{H（H）}}_{S公司} + 秒 \in^{2} / 2)} . & (48) \end{array}

与Höhn和Vanrietvelde类似[30]，Höhn[31]，和Höhn等人[7]，我们引入了一个任意的正参数ε>0，使得映射变得可逆。请注意 $秒 ϵ^{2} / 2 \in 规格 (Ĥ_{C类})$ .

引理6.平凡化的左逆 ${T型}_{T型, ¦Β}$ 由提供

{T型}_{T型, \in}^{负极 1} = \frac{1}{2 π} \sum_{σ} \int_{ℝ} d日 t吨 | t吨, σ 〉 〈 t吨, σ | \otimes {e（电子）}^{我 t吨 ({\hat{H（H）}}_{S公司} + 秒 \in^{2} / 2)},

因此，对于任何ϵ> 0, ${T型}_{T型, ϵ}^{- 1} : {T型}_{T型, ϵ} ({H（H）}_{物理}) \to {H（H）}_{物理}$ 和

\begin{array}{l} {T型}_{T型, ϵ}^{- 1} ○ {T型}_{T型, ϵ} \approx 我_{物理} . \end{array}

证明：Höhn等人中引理2的证明[7]此处适用σ-扇区。 □

下面的引理总结了平凡化映射的主要性质。

引理7.地图 ${T型}_{T型, ϵ}$ 简化了方程（13）中对时钟自由度的约束

\begin{array}{l} {T型}_{T型, ϵ} {\hat{C类}}_{H（H）} {T型}_{T型, ¦Β}^{- 1} \overset{*}{\approx} \frac{秒}{2} ({\hat{第页}}_{t吨}^{2} - ϵ^{2}) \otimes 我_{S公司}, & (49) \end{array}

哪里 $\overset{*}{\approx}$ 是平凡的物理希尔伯特空间上的量子弱等式 ${T型}_{T型, ϵ} ({H（H）}_{物理})$ ,并将物理状态转换为两个具有固定和冗余时钟因子的乘积状态之和

证明：Höhn等人中引理2的证明[7]此处适用σ-扇区。 □

因此，每σ-频率扇区，平凡的物理状态是相对于运动学希尔伯特空间的张量积分解的乘积状态。回顾对σ-扇区超选择规则的讨论，方程（50）中的物理状态与包含正负频率模式的可分离混合状态是无法区分的。因此，考虑到方程（15）中的物理状态似乎是纠缠的，我们也可以将平凡化视为σ-扇区方向的解纠缠操作。然而，我们强调，这种纠缠概念是运动学的，而不是规范不变量（参见[7]详细讨论了这一点，以及如何利用琐碎化来阐明纠缠在Page-Wootters形式主义中的作用）。

方程（50）中的时钟因子变得多余，除了区分正负频率扇区。实际上，如果我们得到ϵ=0，那么（忽略发散因子）方程（50）中的负频率项和正频率项都会有一个共同的冗余因子|第页_t吨= 0〉_C类，这样人们就无法在 ${\hat{第页}}_{t吨}$ 和Ĥ_S公司其中状态已经扩展。这说明了为什么 ${T型}_{T型, ϵ = 0}$ 是不作用于物理状态时是可逆的。的确， ${T型}_{T型, ϵ = 0}^{- 1}$ 在窗体的状态上未定义|第页_t吨= 0〉_C类|ψ〉_S公司，自 ${\hat{T型}}^{(n个)}$ 未在上定义|第页_t吨= 0〉_C类这类似于Höhn和Vanrietvelde中平凡化地图的构建[30]和Höhn[31]除此之外，分解为正负频率扇区的过程略有不同。步骤1到此结束。以上。

为了完成对海森堡关系图状态的约简，因此也完成了步骤2。在上面，我们通过投影到经典规范固定条件来“投影”出平凡状态的冗余时钟因子T型=τ（参见补充材料用于讨论经典轨距固定）。也就是说，我们现在按照Page-Wootters约简和琐碎的物理Hilbert空间中的条件状态进行 ${T型}_{T型, ϵ} ({H（H）}_{物理})$ 在时钟读数τ上，分离正频率模式和负频率模式。总之，量子对称性约简图的形式是

\begin{array}{l} {R（右）}_{H（H）}^{σ} ≔ {e（电子）}^{负极 我 τ 秒 \in^{2} / 2} (〈 τ, σ | \otimes 我_{S公司}) {T型}_{T型, \in} . & (51) \end{array}

使用它

\begin{array}{l} 〈 τ, σ | {第页}_{t吨} = - σ^{'} ϵ 〉 = δ_{σ σ^{'}} \sqrt{ϵ} {e（电子）}^{我 τ 秒 ϵ^{2} / 2}, & (52) \end{array}

这是选择ϵ>0的另一个原因，在方程（50）中可以找到τ无关的系统状态

适用于海森堡图片（与等式39相比）。这也是为什么与等式（38）中的Page-Wootters约简相比，尽管后者，我们没有用τ标记量子去参数化映射的原因先验的出现在方程式（51）的右侧，以及为什么我们为其配备H（H）标签。因素 $1 / \sqrt{2}$ 出于规范化目的再次引入。由于波函数

\begin{array}{l} ψ_{S公司}^{σ} (E类) \equiv \sqrt{2} ψ_{σ} (E类), & (54) \end{array}

是平方积分/可和的，很明显 $| ψ_{S公司}^{σ} 〉$ 是物理系统希尔伯特空间的一个元素 ${H（H）}_{S公司, σ}^{物理}$ ，对应于σ-扇区。因此，我们也有 ${R（右）}_{H（H）}^{σ} (τ) : {H（H）}_{物理} \to {H（H）}_{S公司, σ}^{物理}$ ，就像Page-Wootters缩减一样。使用引理6和7，现在还清楚了如何反演量子对称性约化——至少每个σ扇区：

{({R（右）}_{H（H）}^{σ})}^{负极 1} ≔ {T型}_{T型, ¦Β}^{负极 1} (\frac{1}{\sqrt{ϵ}} {| {第页}_{t吨} = 负极 σ ϵ 〉}_{C类} \otimes 我_{S公司})

定义地图 ${H（H）}_{S公司, σ}^{物理} \to {H（H）}_{σ}$ ，所以¹⁸

\begin{array}{l} {({R（右）}_{H（H）}^{σ})}^{负极 1} | ψ_{S公司}^{σ} 〉 = \sqrt{2 θ} (负极 σ {\hat{第页}}_{t吨}) | ψ_{物理} 〉 . & (55) \end{array}

因此，从正/负频率模式的物理系统希尔伯特空间，只能恢复物理希尔伯特空间的正负频率扇区。注意，与Page-Watters情况相比，逆映射与τ无关。

更准确地说，以下观点成立。

引理8.量子对称约简映射弱等于Page-Wootters约简映射和（逆）系统时间演化

\begin{array}{l} {R（右）}_{H（H）}^{σ} \approx 〈 τ, σ | \otimes {U型}_{S公司}^{†} (τ), \\ = {U型}_{S公司}^{†} (τ) {R（右）}_{S公司}^{σ} (τ) . \end{array}

类似地，量子对称性约简的逆等于系统时间演化和Page-Wootters约简的反：

\begin{array}{l} {({R（右）}_{H（H）}^{σ})}^{负极 1} = δ ({\hat{C类}}_{H（H）}) (| τ, σ 〉 \otimes {U型}_{S公司} (τ)) \\ = {({R（右）}_{S公司}^{σ} (τ))}^{负极 1} {U型}_{S公司} (τ) . \end{array}

因此

\begin{array}{l} {({R（右）}_{H（H）}^{σ})}^{- 1} {R（右）}_{H（H）}^{σ} \approx θ (- σ {\hat{第页}}_{t吨}) \otimes 我_{S公司} \end{array}

和

{R（右）}_{H（H）}^{σ} {({R（右）}_{H（H）}^{σ})}^{负极 1} | ψ_{S公司}^{σ} 〉 = | ψ_{S公司}^{σ} 〉 .

证明：Höhn等人中引理3的证明[7]此处适用σ-扇区。 □

考虑到方程（53）中的海森堡型状态，我们可以考虑在 ${H（H）}_{S公司, σ}^{物理}$

\begin{array}{l} {\hat{（f）}}_{S公司}^{物理} (τ) = {U型}_{S公司}^{†} (τ) {\hat{（f）}}_{S公司}^{物理} {U型}_{S公司} (τ) . & (56) \end{array}

事实上，以下定理表明，这些海森堡观测值等价于物理希尔伯特空间σ扇区上的关系狄拉克观测值 ${H（H）}_{σ}$ 从而证明量子对称性约简映射产生了一个关系海森堡图。为此，我们使用这些归约图及其逆来定义另一种编码操作 ${E类}_{H（H）}^{σ} : 我 ({H（H）}_{S公司, σ}^{物理}) \to 我 ({H（H）}_{σ})$ ,

\begin{array}{l} {E类}_{H（H）}^{σ} ({\hat{（f）}}_{S公司}^{物理} (τ)) ≔ {({R（右）}_{H（H）}^{σ})}^{- 1} {\hat{（f）}}_{S公司}^{物理} (τ) {R（右）}_{H（H）}^{σ} . & (57) \end{array}

定理3.让 ${\hat{（f）}}_{S公司} \in 我 ({H（H）}_{S公司})$ .量子关系狄拉克观测 ${\hat{F类}}_{{（f）}_{S公司}, T型} (τ)$ 作用于 ${H（H）}_{物理}$ ,方程式（31），根据 ${R（右）}_{H（H）}^{σ}$ 到海森堡图片中相应的投影演化观测 ${H（H）}_{S公司, σ}^{物理}$ ,方程式（56），即。,

\begin{array}{l} {R（右）}_{H（H）}^{σ} {\hat{F类}}_{{（f）}_{S公司}, T型} (τ) {({R（右）}_{H（H）}^{σ})}^{- 1} = Π_{σ_{S公司 C类}} {\hat{（f）}}_{S公司} (τ) Π_{σ_{S公司 C类}} \\ \equiv {\hat{（f）}}_{S公司}^{物理} (τ) . \end{array}

相反，让 ${\hat{（f）}}_{S公司}^{物理} (τ) \in 我 ({H（H）}_{S公司, σ}^{物理})$ 可以观察到海森堡的任何演变。方程（57）中系统观测值的编码操作与物理希尔伯特空间一致 ${H（H）}_{物理}$ 方程（31）中的量子关系狄拉克观测值投影到σ扇区:

\begin{array}{l} {E类}_{H（H）}^{σ} ({\hat{（f）}}_{S公司}^{物理} (τ)) \approx {\hat{F类}}_{{（f）}_{S公司}^{物理}, T型}^{σ} (τ) . & (58) \end{array}

证明：Höhn等人对定理5的证明[7]此处适用于每个σ-扇区。 □

再一次，该定理建立了相对于时钟的全套关系狄拉克观测值之间的等价性E类_T型在 ${H（H）}_{σ}$ 以及σ-模的物理系统Hilbert空间上的演化海森堡可观察性 ${H（H）}_{S公司, σ}^{物理}$ 因此，人们只能从海森堡观测值中恢复关系狄拉克观测值的σ扇区行为。

引理8和定理2直接意味着我们再次保留了每个σ扇区的期望值，如下定理所示。

定理4.让 ${\hat{（f）}}_{S公司} \in 我 ({H（H）}_{S公司})$ 和 ${\hat{（f）}}_{S公司}^{物理} (τ) = {U型}_{S公司}^{†} (τ) Π_{σ_{S公司 C类}} {\hat{（f）}}_{S公司}$ Π_{σ_{联合国安全理事会}}U型_S公司(τ)是它的相关演化海森堡算子 ${H（H）}_{S公司}^{物理}$ .然后

〈 ψ_{物理} | {\hat{F类}}_{{（f）}_{S公司}, T型}^{σ} (τ) {| ϕ_{物理} 〉}_{物理} = \frac{1}{2} 〈 ψ_{S公司}^{σ} | {\hat{（f）}}_{S公司}^{物理} (τ) | ϕ_{S公司}^{σ} 〉,

哪里 $| ψ_{S公司}^{σ} 〉 = \sqrt{2} {R（右）}_{H（H）}^{σ} | ψ_{物理} 〉$ .

证明：Höhn等人对定理6的证明[7]此处适用于每个σ-扇区。 □

因此，量子对称性约简映射 ${R（右）}_{H（H）}$ 是等距的，正如我们在下面的推论中所述。

推论3。 设置 ${\hat{（f）}}_{S公司} = Π_{σ_{S公司 C类}}$ 在定理4中，得出

〈 ψ_{物理} | θ (负极 σ {\hat{第页}}_{t吨}) \otimes 我_{S公司} {| ϕ_{物理} 〉}_{物理} = \frac{1}{2} 〈 ψ_{S公司}^{σ} | ϕ_{S公司}^{σ} 〉,

哪里 $| ψ_{S公司}^{σ} 〉 = \sqrt{2} {R（右）}_{H（H）}^{σ} | ψ_{物理} 〉$ .因此,

{〈 ψ_{物理} | ϕ_{物理} 〉}_{物理} = \frac{1}{2} \sum_{σ} 〈 ψ_{S公司}^{σ} | ϕ_{S公司}^{σ} 〉 .

因此，我们可以同时处理每个简化σ扇区和物理希尔伯特空间中的归一化状态。

总之：

（1）应用量子对称约简映射 ${R（右）}_{H（H）}^{σ}$ 到物理希尔伯特空间上的时钟-中性图像 ${H（H）}_{物理}$ 产生a海森堡关系图关于时钟C类关于σ-模的物理系统Hilbert空间， ${H（H）}_{S公司, σ}^{物理}$ .

（2） σ-扇区方面，物理希尔伯特空间上关系狄拉克观测值中编码的关系量子动力学等价于物理系统希尔伯特空间中关系海森堡图中的动力学。

（3）给定约化映射的可逆性，定理4形式上表明如果 ${\hat{（f）}}_{S公司}^{物理} (τ)$ 在上是自伴随的 ${H（H）}_{S公司, σ}^{物理}$ ，那么也是 ${\hat{F类}}_{{（f）}_{S公司}, T型}^{σ} (τ)$ 在 ${H（H）}_{σ}$ .

5.1.4. 动力学等效性（ii）和（iii）

前面的小节在关系动力学之间建立了σ-扇区等效性，一方面，在狄拉克量子化的钟-中性图中，另一方面，通过Page-Wootters约简和量子去参数化分别获得的关系薛定谔和海森堡图中。由此可见，薛定谔和海森堡的关系图也确实等价于幺正U型_S公司（τ）他们应该这样做。引理8直接暗示了这一点，它表明Page-Watters和量子对称约简映射（弱）与U型_S公司(τ).

5.2. 规范混合和规范变量扩展的量子模拟

与经典约束曲面不同，“量子约束曲面” ${H（H）}_{物理}$ 由于对称生成器的求幂运算，它是自动规范不变的_H（H）对所有物理状态和狄拉克观测值的作用微不足道。然而，扩展了Höhn et al[7]，我们可以理解量子对称性约简映射 ${R（右）}_{H（H）}$ [并且考虑到它们的幺正关系 ${R（右）}_{S公司}^{σ} (τ)$ ]作为经典相空间缩减的量子模拟，通过规范固定。为了完整起见，后面的过程在补充材料对于本文的模型类。特别是，我们可以考虑物理系统希尔伯特空间 ${H（H）}_{S公司, σ}^{物理}$ 对于σ扇区作为规范的量子模拟，通过施加例如规范获得的固定约化相空间T型经典σ-频率扇区=0 ${C类}_{σ}$ ¹⁹同样，经典地，我们得到了两个外观相同的规范固定约化相空间，每个频率扇区一个。因此，薛定谔和海森堡的关系图都可以被理解为明显规范不变理论的规范固定公式的量子模拟。

因此，定理1和3意味着方程（45）和（57）中系统观测值的编码操作可以理解为计量的量子模拟——不变地扩展计量固定量（另请参见[7]). 同样，方程（47）第二行中的替代物理内积是通过方程（18）中的群平均获得的明显规范不变物理内积的规范固定版本的量子模拟。的确， $\sum_{σ} 〈 ψ_{物理} | (| τ, σ 〉 〈 τ, σ | \otimes 我_{S公司}) {| ϕ_{物理} 〉}_{家属}$ 是物理状态下“投影仪”对时钟时间τ的（运动学）期望值。然而，从薛定谔动力学在 ${H（H）}_{S公司, σ}^{物理}$ 和方程（47），该内积不依赖于τ（“量规”），这与它是明显的量规不变量的量规固定版本的量子模拟的解释一致。

5.3. 插曲：备选路线

顺便提一下，我们提到存在另一种方法来建立钟哈密顿量动量二次型的三位一体。这再次利用了物理希尔伯特空间上的可约表示。σ-扇区 ${H（H）}_{物理}$ 由约束定义 $Ĉ_{σ} = Ĥ_{C类}^{'} + Ĥ_{S公司}^{'}$ ，其中 $Ĥ_{C类}^{'} ≔ \frac{{\hat{第页}}_{t吨}}{\sqrt{2}}$ 和 $Ĥ_{S公司}^{'} ≔ σ \sqrt{- 秒 Ĥ_{S公司}}$ 显然， $Ĥ_{C类}^{'}$ 现在是非简并时钟哈密顿量。在Höhn等人[7]我们建立了非简并时钟哈密顿量和σ扇区的三位一体 $Ĉ_{σ} = Ĥ_{C类}^{'} + Ĥ_{S公司}^{'}$ 产生了一个特殊的情况。然而，这立即意味着每个σ扇区都是三位一体的，现在相对于相对于 $Ĥ_{C类}^{'}$ 很明显，在这种情况下，协变时钟POVM是通过 $\hat{t吨}$ 其中（最大系数为 $\sqrt{2}$ )也是POVM的第一刻。事实上，在Höhn和Vanrietvelde中，对于具有二次时钟哈密顿量的模型，钟-中性狄拉克量子化和关系海森堡图之间的等价性已经被精确地建立起来[30]和Höhn[31]（有关相关讨论，另请参阅[29,38]). 然而，如第4.1节所述，要么必须将关系观测值正规化，要么将它们写成仿射函数，而不是演化自由度的规范对。这是平方根性质的结果 $Ĥ_{S公司}^{'}$ 。在本文的三位一体结构中，这些额外的步骤都不需要，它基于时钟POVM，相对于 $秒 \frac{{\hat{第页}}_{t吨}^{2}}{2}$ ，而不是 ${\hat{第页}}_{t吨} / \sqrt{2}$ .

6.相对论本土化：应对库查的批评

在他对时间问题的开创性评论中，库查对Page-Wootters形式主义提出了三点批评[1]方程（37）（a）中的Page-Wootters条件概率产生了相对论粒子的错误局域化概率，（b）违反了哈密顿约束，（c）产生了错误的跃迁概率。如导言中所述，Höhn等人解决了（b）和（c）项批评[7]-参见定理2，该定理将（b）的分辨率扩展到当前的模型类别。

在这里，我们现在还将讨论Kuchař对相对论局部化的第一次批评（a），这是一个更微妙的问题。主要原因，从佩雷斯-王尔德的定理中可以看出[92]和疾病[93]（另请参阅中的讨论[94,95])，是因为不存在基于相对论协变位置算子的局部化概念，这与相对论因果关系和能量的正性相兼容。这是量子场论的一个关键动机[90,94]-这里有一个挑战，即确定相对论粒子的“正确”局域化概率应该是多少。相反，人们可以求助于牛顿和维格纳提出的近似的相对论非协变局域化概念[90,91]. 我们将通过证明我们基于相对论模型协变时钟的Page-Wootters形式主义公式在这种近似意义上产生了局部化，来解决批评（a）。

为了明确的论证，我们应该像库查一样[1]，只关注自由相对论粒子，其哈密顿约束为（参见。表1)

\begin{array}{l} {\hat{C类}}_{H（H）} = - {\hat{第页}}_{t吨}^{2} + {\hat{第页}}^{2} + 米^{2}, \end{array}

哪里 $\hat{第页}$ 表示空间动量向量。然而，这一论点可以扩展到本手稿中考虑的整个模型类别。在这种情况下，很容易检查物理内积方程（18）的读数[31,104]²⁰

\begin{array}{l} {〈 ϕ_{物理} | ψ_{物理} 〉}_{物理} = \int_{ℝ^{三}} \frac{{d日}^{三} 第页}{2 ε_{第页}} [ϕ_{家属}^{*} (ε_{第页}, 第页) ψ_{家属} (ε_{第页}, 第页) \\ + ϕ_{家属}^{*} (负极 ε_{第页}, 第页) ψ_{家属} (负极 ε_{第页}, 第页)], & (59) \end{array}

哪里 $ε_{第页} = \sqrt{{第页}^{2} + 米^{2}}$ 是粒子的相对论能量，被积函数中的第一项和第二项分别对应于负频率模式和正频率模式。Minkowski空间中Klein-Gordon方程解的Fourier变换

\begin{array}{l} ψ_{物理}^{σ} (t吨, x个) = \frac{1}{{(2 π)}^{三 / 2}} \int_{ℝ^{三}} \frac{{d日}^{三} 第页}{2 ε_{第页}} {e（电子）}^{我 (x个 \cdot 第页 - σ t吨 ε_{第页})} ψ_{家属} (- σ ε_{第页}, 第页), \end{array}

可以进一步检查[31,104]

\begin{array}{l} {〈 ϕ_{物理} | ψ_{物理} 〉}_{物理} = {(ϕ_{物理}^{+}, ψ_{物理}^{+})}_{公斤} 负极 {(ϕ_{物理}^{负极}, ψ_{物理}^{负极})}_{公斤}, & (60) \end{array}

哪里

\begin{array}{l} {(ϕ_{物理}^{σ}, ψ_{物理}^{σ})}_{公斤} = 我 \int_{ℝ^{三}} {d日}^{三} x个 [{(ϕ_{物理}^{σ} (t吨, x个))}^{*} \partial_{t吨} ψ_{物理}^{σ} (t吨, x个) \\ 负极 {(\partial_{t吨} ϕ_{物理}^{σ} (t吨, x个))}^{*} ψ_{物理}^{σ} (t吨, x个)], & (61) \end{array}

是Klein-Gordon内积，其中正频率模式为正半定，负频率模式为负半定，正、负频率模式相互正交。因此，物理内积等价于Klein-Gordon内积（负频率模式具有正确的反转符号），它为自由相对论粒子提供了正确和保守的归一化²¹这就带来了希望，即Page-Wootters形式主义的条件概率可以为相对论粒子产生正确的局域化概率。请注意，到目前为止，我们还没有选择时间运算符。

假设现在Minkowski时间操作符 $\hat{t吨}$ ，量化为上的自共轭算子 ${H（H）}_{家属}$ ，用于定义投影仪到时钟的时间t吨作为e（电子）_C类(t吨) = |t吨〉〈t吨|和e（电子）_x个= |x个〉〈x个|投影仪是否就位x个该时间算符相对于二次时钟哈密顿量不协变。然后，条件概率方程（37）变成

\begin{array}{l} 探针 (x个 何时 t吨) = \frac{| ψ_{物理} (t吨, x个) |^{2}}{\int_{ℝ^{三}} {d日}^{三} {x个}^{'} | ψ_{物理} (t吨, {x个}^{'}) |^{2}}, & (62) \end{array}

其中ψ_物理(t吨,x个) = (〈t吨| ⊗ 〈x个|) |ψ_物理是克莱因-戈登方程的一般解。正如库查指出的那样[1]虽然这是非相对论粒子的正确局域化概率，但对于相对论粒子来说，这是错误的结果。事实上，除了不分离正负频率模式外，这对于概率解释是必要的，例如，如果ψ_物理包含正负频率模式，则方程62中的分母不守恒），方程（62）既不符合方程（61）中Klein-Gordon电流的电荷密度，也不符合Newton-Winer近似局域化概率[90,91]. 特别是，可以不解释解ψ_物理(t吨,x个)以Klein-Gordon方程作为概率振幅来找到相对论粒子的位置x个时间t吨哈格解释的原因[90]，即守恒密度为方程（61）和ψ中的密度_物理和∏_t吨ψ_物理在它内部不仅是依赖的，而且是由非局部卷积关联的

\partial_{t吨} ψ_{物理} (t吨, x个) = \int_{ℝ^{三}} {d日}^{三} {x个}^{'} ε (x个 负极 {x个}^{'}) ψ_{物理} (t吨, {x个}^{'}),

其中ε(x个负极x个′)是−的傅里叶变换iε_第页.

相比之下，现在让我们展示协变时钟POVM的条件概率形式E类_T型第4.2节中给出。我们现在插入 ${e（电子）}_{C类} (τ) = \sum_{σ} | τ, σ 〉 〈 τ, σ |$ 和以前一样，e（电子）_x个条件概率方程（37）。协变时钟POVM之间的关键差异E类_T型和时钟操作员 $\hat{t吨}$ （相对于Ĉ是协变的_σ，但不是Ĉ_H（H）)式（37）的分母等于前者的物理内积（见推论2），但不等于后者²²假设我们使用标准化的物理系统状态 $〈 ψ_{S公司}^{σ} (τ) | ψ_{S公司}^{σ} (τ) 〉 = 1$ ，定理2暗示

\begin{array}{l} 问题 (x个 何时 τ) = 12 \sum_{σ} | ψ_{S公司}^{σ} (τ, x个) |^{2} \\ = {〈 ψ_{物理} | {\hat{F类}}_{{e（电子）}_{x个}, T型} (τ) | ψ_{物理} 〉}_{_{物理}}, & (63) \end{array}

哪里 $ψ_{S公司}^{σ} (τ, x个) ≔ \sqrt{2} (〈 τ, σ | \otimes 〈 x个 |) | ψ_{物理} 〉$ τ现在是不闵可夫斯基时间。具体来说，现在让我们关注正频率模式。使用方程（15）和（25），可以得出

\begin{array}{l} ψ_{S公司}^{+} (τ, x个) = \frac{1}{{(2 π)}^{三 / 2}} \int_{ℝ^{三}} \frac{{d日}^{三} 第页}{\sqrt{2 ε_{第页}}} {e（电子）}^{我 (x个 \cdot 第页 负极 τ ε_{第页}^{2})} ψ_{家属} (负极 ε_{第页}, 第页) . & (64) \end{array}

这是几乎正频率模式的Newton-Wigner位置空间波函数，相对于Minkowski时间读数[90]

\begin{array}{l} ψ_{西北}^{+} (t吨, x个) = \int_{ℝ^{三}} {d日}^{三} x个 K（K） (x个 负极 {x个}^{'}) ψ_{物理}^{+} (t吨, {x个}^{'}) \\ = \frac{1}{{(2 π)}^{三 / 2}} \int_{ℝ^{三}} \frac{{d日}^{三} 第页}{\sqrt{2 ε_{第页}}} {e（电子）}^{我 (x个 \cdot 第页 负极 t吨 ε_{第页})} ψ_{家属} (负极 ε_{第页}, 第页), & (65) \end{array}

哪里K（K）(x个)是的傅里叶变换 $\sqrt{2 ε_{第页}}$ 。的键属性 $| ψ_{西北}^{+} (t吨, x个) |^{2}$ 是的，虽然不是相对共变的，但它做允许对近似定位概率进行解释，精确到康普顿波长的量级，以便在位置上找到粒子x个在闵可夫斯基时间t吨[90,91]. 特别地，

\begin{array}{l} {(ϕ_{物理}^{+}, ψ_{物理}^{+})}_{公斤} = \int_{ℝ^{三}} {d日}^{三} x个 {(ϕ_{西北}^{+} (t吨, x个))}^{*} ψ_{西北}^{+} (t吨, x个), \end{array}

即，Klein-Gordon内积假设Newton-Winer波函数的通常Schrödinger形式。

注意，根据方程式（19），我们可以试探性地将τ视为t吨/ε_第页，与方程（65）相比，我们也可以将方程（64）解释为牛顿-韦格波函数，但相对于不同的时间坐标τ表示。事实上，根据这种解释，我们发现在这种情况下，正频率模式的物理内积方程式（60）也采用了标准薛定谔理论内积的形式

\begin{array}{l} {(ϕ_{物理}^{+}, ψ_{物理}^{+})}_{公斤} = \int_{ℝ^{三}} {d日}^{三} x个 {(ϕ_{S公司}^{+} (τ, x个))}^{*} ψ_{S公司}^{+} (τ, x个) . \end{array}

对于负频率模式，类似的说法是正确的。从这个意义上说，与方程（62）相反，方程（63）确实承认这种解释是每个频率扇区相对论粒子的有效但近似的局域化概率，就像标准的Newton-Wigner情况一样²³.

因此，计算Page-Wootters形式相对于协变时钟POVM的条件概率，而不是非协变Minkowski时间运算符 $\hat{t吨}$ 导致相对论粒子的可接受局域化概率，从而也解决了库查的第一个批评（a）。考虑到Page-Wootters形式主义与通过第5节中的三位一体建立的钟中点图和关系海森堡图的等价性，该结果也适用于量子关系狄拉克观测 ${\hat{F类}}_{x个, T型} (τ)$ 以及不断演化的海森堡观测x个（τ）解释了在Minkowski空间中提供近似的Newton-Winer型局部化。

7.改变量子时钟

到目前为止，我们只使用了一种时钟选择。现在，让我们展示如何从相对于一个时钟选择的进化到相对于另一个时钟的进化。我们的讨论将适用于Page-Wootters形式主义的关系Schrödinger图和通过量子去参数化获得的关系Heisenberg图。

对于具体性，假设我们被给定形式的哈密顿约束

\begin{array}{l} {\hat{C类}}_{H（H）} = 秒_{1} \frac{{\hat{第页}}_{1}^{2}}{2} + 秒_{2} \frac{{\hat{第页}}_{2}^{2}}{2} + {\hat{H（H）}}_{S公司}, & (66) \end{array}

哪里秒_我=±1和 ${\hat{第页}}_{我}$ 表示时钟子系统的动量C类_我,我=1,2，我们用恒等算符压制了张量积。特别是，假设_S公司不依赖于任何一个时钟自由度。对于两种时钟选择，我们将使用第4.2节中的协变时钟POVM。例如，相对论粒子的约束，平面(k个=0）具有无质量标量场的FLRW模型和Bianchi I和II模型表1属于上述形式²⁴。因此，我们随后的讨论将直接适用于这些模型。

由于我们将利用Page-Wootters和对称约简映射作为“量子坐标映射”，从时钟中性图到给定的“时钟透视图”，我们将能够从相对于一个时钟的动力学描述更改为与另一个时钟相关的动力学描述，这与协调流形上的变化非常类似。由于方程（66）中约束的形状，我们现在有Dirac观测值的超选和σ上的物理Hilbert空间₁-时钟的频率扇区C类₁和σ₂-时钟的频率扇区C类₂物理希尔伯特空间的形式

\begin{array}{l} {H（H）}_{物理} = \underset{σ_{1}, σ_{2}}{Ş} {H（H）}_{σ_{1}, σ_{2}}, & (67) \end{array}

哪里 ${H（H）}_{σ_{1}, σ_{2}} ≔ {H（H）}_{σ_{1}} \cap {H（H）}_{σ_{2}}$ 是σ的重叠₁-时钟扇区C类₁和σ₂-时钟扇区C类₂如我们所见，每个频率扇区的简化图都是可逆的。因此，我们只能改变给定的σ₁-扇形到σ的一部分₂-包含在其中的频率扇区。换句话说，“量子坐标变化”仅限于每个重叠 ${H（H）}_{σ_{1}, σ_{2}}$ .

下面展示的改变时间参照系的方法是对之前几部作品的直接延伸：Höhn和Vanrietvelde[30]和Höhn[31]为两个示例模型的方程（66）中类型的哈密顿量的海森堡关系图中的状态和观测值开发了σ-扇形方法，但使用了与时钟动量标准共轭的时钟算符 ${\hat{第页}}_{我}$ （因此，相对于全时钟哈密顿量而言，不是时钟POVM协变）。Höhn和Vanrietvelde证明了将相关观测值从一种时钟描述转换为另一种时钟表示的方法[30]和Höhn[31]然而，对于关系狄拉克观测值的子集，要特别注意到达时间观测值引起的正则化必要性[18,23,117–119]. 我们上一篇文章[7]对Schrödinger和Heisenberg关联图中具有非简并连续谱的时钟哈密顿量的状态和观测值综合发展了方法；具体地说，对应于S公司时钟是为相应类别的模型开发的。在Castro Ruiz等人[47]对于哈密顿量与时钟动量本身重合的理想时钟，在关系薛定谔图中展示了状态变换的时钟变换方法。我们的讨论也可以被视为Bojowald等人半经典方法的完全量子扩展[32,33]和Höhn等人[34]然而，这在半经典阶下是等价的，也适用于非单调的时钟函数，即具有转折点，与所提到的其他作品相比（参见[70–72,74]用于相关的空间量子帧更改）。

特别是，由于我们关注协变时钟POVM，所有的结果和证明[7]将σ-sector-wise应用于本例。然而，我们也将研究新的效应，例如比较时钟读数的时间帧依赖性。

7.1。状态转换

表示方式 ${R（右）}_{我}^{σ_{我}}$ ，其中我∈ {S、 H（H）}，Page-Bootters或量子对称约简映射到σ_我-时钟扇区C类_我为了简化符号，我们去掉了Page-Wootters减少对时钟读数τ的依赖性_我时钟的C类_我目前。时间帧变化（TFC）图 $Λ_{我 \to J型}^{σ_{我} \to σ_{j个}} : {H（H）}_{{C类}_{j个}, σ_{我}}^{物理} \otimes {H（H）}_{S公司, σ_{我}}^{物理} \to {H（H）}_{{C类}_{我}, σ_{j个}}^{物理} \otimes {H（H）}_{S公司, σ_{j个}}^{物理}$ 来自时钟C类_我sσ_我-扇区到时钟C类_j个sσ_j个-扇区然后读取

\begin{array}{l} Λ_{我 \to J型}^{σ_{我} \to σ_{j个}} ≔ {R（右）}_{J型}^{σ_{j个}} \circ {({R（右）}_{我}^{σ_{我}})}^{- 1} . & (68) \end{array}

在这里 ${H（H）}_{{C类}_{j个}, σ_{我}}^{物理}$ 表示物理时钟C类_j个σ对应的希尔伯特空间_我-时钟扇区C类_我，即 ${H（H）}_{{C类}_{j个}}$ 与约束方程（66）的解兼容，与其他希尔伯特空间的解类似。什么时候？我≠J型在方程（68）中，TFC图不仅改变了时间参考框架，还改变了相应的海森堡和薛定谔关系图之间的关系。让我们写 $Λ_{我}^{σ_{我} \to σ_{j个}} ≔ Λ_{我 \to 我}^{σ_{我} \to σ_{j个}}$ 当没有发生关系图变化时。

更明确地说，TFC映射自σ₁-时钟的频率扇区C类₁在与σ相关的Schrödinger图中₂-时钟的频率扇区C类₂在关系Schrödinger图中

\begin{array}{l} Λ_{S公司}^{σ_{1} \to σ_{2}} = (〈 τ_{2}, σ_{2} | \otimes 我_{{C类}_{1} S公司}) δ ({\hat{C类}}_{H（H）}) (| τ_{1}, σ_{1} 〉 \otimes 我_{{C类}_{2} S公司}) . \end{array}

在这里，我们使用了方程（38）和（42）以及两个时钟的协变时钟状态方程（25）。此映射下的简化状态转换如下：

\begin{array}{l} (θ (负极 σ_{1} {\hat{第页}}_{1}) \otimes 我_{S公司}) | ψ_{{C类}_{1} S公司 | {C类}_{2}}^{σ_{2}} (τ_{2}) 〉 = Λ_{S公司}^{σ_{1} \to σ_{2}} | ψ_{{C类}_{2} S公司 | {C类}_{1}}^{σ_{1}} (τ_{1}) 〉, & (69) \end{array}

其中我们使用了方程（43）和 $| ψ_{{C类}_{j个} S公司 | {C类}_{我}}^{σ_{我}} (τ_{我}) 〉$ 是时钟的关系薛定谔图状态C类_j个和系统S公司相对于时钟C类_我，它被选为时间参考框架，在σ中_我-部门。换句话说，l.h.s.上的Heaviside函数强调了我们只能从σ映射₁-时钟扇区C类₁σ的那部分₂-时钟扇区C类₂包含在σ中₁-时钟扇区C类₁这一点很清楚，因为任何约化映射都只能在其关联的σ-扇区上可逆：从σ₁关系Schrödinger图只能恢复σ₁-物理希尔伯特空间的扇区。因此，随后的Page Wootters归约映射到σ₂-时钟扇区C类₂在方程式（68）中，只能得出σ重叠的信息₁-和σ₂-物理Hilbert空间中的扇区（另请参见[30,31]对于关系海森堡图中这种情况的明确示例）。这是σ和σ的超级选举的表现₁-和σ₂-部门。

类似地，σ的TFC映射₁-时钟的频率扇区C类₁在海森堡图与σ的关系中₂-时钟的频率扇区C类₂在海森堡的关系图中

\begin{array}{l} Λ_{H（H）}^{σ_{1} \to σ_{2}} = (〈 τ_{2}, σ_{2} | \otimes {U型}_{{C类}_{1} S公司}^{†} (τ_{2})) \\ \times δ ({\hat{C类}}_{H（H）}) (| τ_{1}, σ_{1} 〉 \otimes {U型}_{{C类}_{2} S公司} (τ_{1})) & (70) \end{array}

其中我们利用了引理8。使用相同的引理，这个映射下的约化态变换与方程（69）完全相似

[θ (负极 σ_{1} {\hat{第页}}_{1}) \otimes 我_{S公司}] | ψ_{{C类}_{1} S公司 | {C类}_{2}}^{σ_{2}} 〉 = Λ_{S公司}^{σ_{1} \to σ_{2}} | ψ_{{C类}_{2} S公司 | {C类}_{1}}^{σ_{1}} 〉,

具有 ${U型}_{{C类}_{j个} S公司} (τ_{我}) ≔ 经验 [- 我 τ_{我} (秒_{j个} \frac{{\hat{第页}}_{j个}^{2}}{2} + Ĥ_{S公司})]$ 复合时钟系统的演化算子C类_j个和系统S公司相对于时钟C类_我.

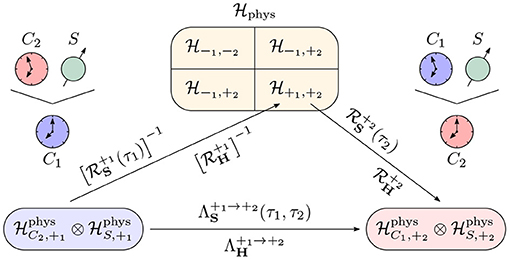
注意，将简化图解释为“量子坐标图”，将一个从时钟中性物理希尔伯特空间到特定的“时钟透视图”，方程（68）中的任何此类TFC图都采用与流形上坐标变化相同的组成形式。特别是，任何这样的时间帧变化都是通过时钟中性物理希尔伯特空间进行映射来进行的，类似于坐标变化总是通过流形进行的（参见图3). 这个观察结果是量子参考系变化的透视-中性方法的核心[7,30,31,71,72]. 这也是为什么我们可以将物理希尔伯特空间解释为时钟-中性结构的原因，在选择与其他自由度演变相关的时间参考框架之前，提供动力学的描述。与此相一致，就关系狄拉克观测的不同单参数族而言，物理希尔伯特空间包含了与所有不同可能的时钟选择相关的动力学的完整信息。

图3

图3时间帧变化的示意图，如等式（68）所定义。该图包含Page-Watters形式主义的关系Schrödinger图和量子去参数化的关系Heisenberg图（以及它们的混合物）。查看缩减图 ${R（右）}_{我}^{+_{我}}$ 作为量子坐标映射，任何这样的时间帧变化都以相对于时钟的描述的量子坐标变换的形式出现C类₁相对于时钟的一个C类₂正如坐标变换通过参考框架中性流形一样，量子坐标变换也通过时钟中性物理Hilbert空间，这与第2节中关于时钟中性结构和量子广义协方差的一般讨论一致。由于双重超选择规则，量子坐标变换必须保持C类₁和C类₂在这里，我们举例说明了两个时钟的正频率扇区的重叠，以便通过相应的帧变换 ${H（H）}_{+_{1}, +_{2}}$ （参见方程式67）。

7.2. 可观测变换

正如我们通过规范不变的物理希尔伯特空间（参见图3)现在，我们通过物理希尔伯特空间上Dirac观测值的规范不变代数，将相对于一个时钟的观测值描述转换为相对于另一个时钟。因此，可观察到的变换将是状态变换的对偶。我们总是这样描述相同的物理，编码在时钟-中性物理希尔伯特空间的规范不变状态和观测值中，但相对于不同的时间帧。再次，我们必须注意时钟-中性物理希尔伯特空间上的两个超选择规则，我们将分别演示关系Schrödinger和Heisenberg图片的可观察变换。

7.2.1. 关系薛定谔图中的可观测变换

假设给我们一个可观察的 $Ô_{{C类}_{2} S公司 | {C类}_{1}}^{物理}$ 描述复合系统的某些性质C类₂S公司在Schrödinger关于时钟的关系图中C类₁在后者的任一频率段²⁵。根据定理1，我们可以将其写成对应关系Dirac观测值的约简 ${H（H）}_{物理}$ :

{R（右）}_{S公司}^{σ_{1}} (τ_{1}) {\hat{F类}}_{{O（运行）}_{{C类}_{2} S公司 | {C类}_{1}}, {T型}_{1}} (τ_{1}) {({R（右）}_{S公司}^{σ_{1}} (τ_{1}))}^{负极 1} = {\hat{O（运行）}}_{{C类}_{2} S公司 | {C类}_{1}}^{物理} .

我们现在还可以将相同的关系Dirac观测值映射到σ₂-钟的薛定谔关系图的扇区C类₂:

\begin{array}{l} {\hat{O（运行）}}_{{C类}_{1} S公司 | {C类}_{2}}^{物理} (τ_{1}, τ_{2}) : = {R（右）}_{S公司}^{σ_{2}} (τ_{2}) {\hat{F类}}_{{O（运行）}_{{C类}_{2} S公司 | {C类}_{1}}, {T型}_{1}} (τ_{1}) {({R（右）}_{S公司}^{σ_{2}} (τ_{2}))}^{负极 1} . & (71) \end{array}

结果将是原始可见光的图像 $Ô_{{C类}_{2} S公司 | {C类}_{1}}^{物理}$ ，描述的属性C类₂S公司相对于C类₁，从时钟的“角度”来看C类₂因此，如果 $Ô_{{C类}_{2} S公司 | {C类}_{1}}^{物理}$ 非私人依赖C类₂，在最后一个等式中出现了间接的自我参照效应[7]. 请注意，虽然在Schrödinger图片中可以观察到C类₁与演化参数τ无关₁Schrödinger图片中关于时钟的相同可观察到的描述C类₁通常取决于两个演化参数τ₁，τ₂.对τ的依赖性₁是它与演化参数τ有关的Dirac观测值减少的结果₁，但进入了C类₂.可能的τ₂依赖性可能是上述间接自我参照的结果。例如，假设 $Ô_{{C类}_{2} S公司 | {C类}_{1}}^{物理} = {\hat{T型}}_{2} \otimes 我_{S公司}$ 所以关系狄拉克观测值是 ${\hat{F类}}_{{O（运行）}_{{C类}_{2} S公司 | {C类}_{1}}, {T型}_{1}} (τ_{1}) = {\hat{F类}}_{{T型}_{2}, {T型}_{1}} (τ_{1})$ 方程（71）中l.h.s.上的观测值描述了第一矩算符 ${\hat{T型}}_{2}$ 与关联C类₂相对于C类₁从C类₂; 这肯定会产生τ₁依赖。我们稍后将对此进行更详细的解释。

考虑到σ₁-和σ₂-扇区，这些观察意味着σ的关系Schrödinger图的可观察变换₁-时钟扇区C类₁σ的关系Schrödinger图₂-时钟扇区C类₂阅读

\begin{array}{l} Λ_{S公司}^{σ_{1} \to σ_{2}} Ô_{{C类}_{2} S公司 | {C类}_{1}}^{物理} {(Λ_{S公司}^{σ_{1} \to σ_{2}})}^{- 1} = {(Λ_{S公司}^{σ_{2} \to σ_{1}})}^{- 1} Ô_{{C类}_{2} S公司 | {C类}_{1}}^{物理} Λ_{S公司}^{σ_{2} \to σ_{1}} \\ = {R（右）}_{S公司}^{σ_{2}} (τ_{2}) \circ {({R（右）}_{S公司}^{σ_{1}} (τ_{1}))}^{- 1} Ô_{{C类}_{2} S公司 | {C类}_{1}}^{物理} {R（右）}_{S公司}^{σ_{1}} (τ_{1}) ∙ {({R（右）}_{S公司}^{σ_{2}} (τ_{2}))}^{- 1} \\ = {R（右）}_{S公司}^{σ_{2}} (τ_{2}) {E类}_{S公司}^{τ_{1}, σ_{1}} (Ô_{{C类}_{2} S公司 | {C类}_{1}}^{物理}) {({R（右）}_{S公司}^{σ_{2}} (τ_{2}))}^{- 1} \\ \approx {R（右）}_{S公司}^{σ_{2}} (τ_{2}) {\hat{F类}}_{{O（运行）}_{{C类}_{2} S公司 | {C类}_{1}}, {T型}_{1}} (τ_{1}) (θ (- σ_{1} {\hat{第页}}_{1}) \otimes 我_{{C类}_{2} S公司}) {({R（右）}_{S公司}^{σ_{2}} (τ_{2}))}^{- 1} \\ = (θ (- σ_{1} {\hat{第页}}_{1}) \otimes 我_{S公司}) Ô_{{C类}_{1} S公司 | {C类}_{2}}^{物理} (τ_{1}, τ_{2}) . & (72) \end{array}

在第二行中，我们使用了方程（45）、定理1的第三行和方程（71）的第四行，事实上 $θ (- σ_{1} {\hat{第页}}_{1})$ 使用C类₂时钟和 ${\hat{F类}}_{{O（运行）}_{{C类}_{2} S公司 | {C类}_{1}}, {T型}_{1}} (τ_{1})$ （参见引理5）。

观察到该转换的结构表明，相对于一个时钟的减少的可观测值将始终通过规范不变的狄拉克可观测代数转换为相对于另一个时钟减少的可观察值。

使用等式（38）、（42）和（45），我们可以将此转换写成

\begin{array}{l} (θ (负极 σ_{1} {\hat{第页}}_{1}) \otimes 我_{S公司}) {\hat{O（运行）}}_{{C类}_{1} S公司 | {C类}_{2}}^{物理} (τ_{1}, τ_{2}) = 〈 τ_{2}, σ_{2} δ ({\hat{C类}}_{H（H）}) \\ (| τ_{1}, σ_{1} ​ 〉 〈 τ_{1}, σ_{1} | \otimes {\hat{O（运行）}}_{{C类}_{2} S公司 | {C类}_{1}}^{物理}) δ ({\hat{C类}}_{H（H）}) | τ_{2}, σ_{2} 〉 . & (73) \end{array}

此转换揭示了期望值以以下方式保存：

\begin{array}{l} 〈 ψ_{{C类}_{1} S公司 | {C类}_{2}}^{σ_{2}} (τ_{2}) | (θ (- σ_{1} {\hat{第页}}_{1}) \otimes 我_{S公司}) Ô_{{C类}_{1} S公司 | {C类}_{2}}^{物理} (τ_{1}, τ_{2}) | ϕ_{{C类}_{1} S公司 | {C类}_{2}}^{σ_{2}} (τ_{2}) 〉 \\ = 〈 ψ_{{C类}_{2} S公司 | {C类}_{1}}^{σ_{1}} (τ_{1}) | (θ (- σ_{2} {\hat{第页}}_{2}) \otimes 我_{S公司}) Ô_{{C类}_{2} S公司 | {C类}_{1}}^{物理} (θ (- σ_{2} {\hat{第页}}_{2}) \otimes 我_{S公司}) | ϕ_{{C类}_{2} S公司 | {C类}_{1}}^{σ_{1}} (τ_{1}) 〉 . & (74) \end{array}

投影仪在σ上₂-r.h.s.上出现扇区是因为C类₂等式（72）中的约化图产生了这样的投影（将其与对偶的状态变换等式（69）进行比较）。换句话说，只有重叠的物理信息σ₁-和σ₂-从相对于时钟的描述更改时保留扇区 C类₁ 相对于时钟的一个 C类₂反之亦然再一次，这是由约束方程（66）的形状引起的双重超选规则的直接结果。

7.2.2. 关系海森堡图中的可观测变换

对海森堡关系图的论证以完全类比的方式进行。因此，我们只引用了前面小节中通过使用引理8得到的结果。当然，在这种情况下，减少的观测值明显依赖于演化参数（方程56）。

σ的关系海森堡图的可观测变换₁-时钟扇区C类₁σ的海森堡关系图₂-时钟扇区C类₂由提供

\begin{array}{l} Λ_{H（H）}^{σ_{1} \to σ_{2}} Ô_{{C类}_{2} S公司 | {C类}_{1}}^{物理} (τ_{1}) {(Λ_{H（H）}^{σ_{1} \to σ_{2}})}^{- 1} \\ \approx {R（右）}_{H（H）}^{σ_{2}} {\hat{F类}}_{{O（运行）}_{{C类}_{2} S公司 | {C类}_{1}}, {T型}_{1}} (τ_{1}) (θ (- σ_{1} {\hat{第页}}_{1}) \otimes 我_{{C类}_{2} S公司}) {({R（右）}_{H（H）}^{σ_{2}})}^{- 1} \\ = (θ (- σ_{1} {\hat{第页}}_{1}) \otimes 我_{S公司}) {U型}_{{C类}_{1} S公司}^{†} (τ_{2}) Ô_{{C类}_{1} S公司 | {C类}_{2}}^{物理} (τ_{1}, τ_{2}) {U型}_{{C类}_{1} S公司} (τ_{2}) \\ =: (θ (- σ_{1} {\hat{第页}}_{1}) \otimes 我_{S公司}) Ô_{{C类}_{1} S公司 | {C类}_{2}}^{H（H）} (τ_{1}, τ_{2}), & (75) \end{array}

哪里 $Ô_{{C类}_{1} S公司 | {C类}_{2}}^{物理} (τ_{1}, τ_{2})$ 由方程式（71）和（73）给出。由于双重超选规则，这种转换再次保留了σ的每个重叠的期望值₁-σ₂-扇区，明显类似于方程式（74）。

7.3. 间接时钟自参考的发生

最后，让我们回到时钟的间接自我参照效应C类₂上面提到过。以下定理改编自Höhn等人[7]对于每对σ，其证明在这里适用₁-和σ₂-部门，揭示了这种间接自我参照发生的必要和充分条件：

定理5.考虑操作员 $Ô_{{C类}_{2} S公司 | {C类}_{1}}^{物理} \in 我 ({H（H）}_{{C类}_{2}}^{物理} \otimes {H（H）}_{S公司}^{物理})$ 复合系统的 C类₂S公司 从时钟的角度描述 C类₁.从时钟的角度 C类₂,此运算符独立于τ₂,以便 $Ô_{{C类}_{1} S公司 | {C类}_{2}}^{物理} (τ_{1}, τ_{2}) = Ô_{{C类}_{1} S公司 | {C类}_{2}}^{物理} (τ_{1}) \in 我 ({H（H）}_{{C类}_{1}}^{物理} \otimes {H（H）}_{S公司}^{物理})$ 当且仅当

\begin{array}{l} Ô_{{C类}_{2} S公司 | {C类}_{1}}^{物理} = \sum_{我} {(Ô_{{C类}_{2} | {C类}_{1}}^{物理})}_{我} \otimes {({\hat{（f）}}_{S公司 | {C类}_{1}}^{物理})}_{我}, \end{array}

哪里 ${({\hat{（f）}}_{S公司 | {C类}_{1}}^{物理})}_{我}$ 是上的操作员 ${H（H）}_{S公司}^{物理}$ 和 ${(Ô_{{C类}_{2} | {C类}_{1}}^{物理})}_{我}$ 是一个运动常数, $[{(Ô_{{C类}_{2} | {C类}_{1}}^{物理})}_{我}, 秒_{2} \frac{{\hat{第页}}_{2}^{2}}{2}] = 0$ .此外，在这种情况下，转换的可观察读数

\begin{array}{l} [θ (负极 σ_{1} {\hat{第页}}_{1}) \otimes 我_{S公司}] Ô_{{C类}_{1} S公司 | {C类}_{2}}^{第页 小时 年 秒} (τ_{1}) \\ = Π_{σ_{{C类}_{1} S公司 {C类}_{2}}} [​ \sum_{我} {G公司}_{{C类}_{1} S公司} ​ (| τ_{1}, σ_{1} 〉 〈 τ_{1}, σ |_{1} \otimes {({\hat{（f）}}_{S公司 | {C类}_{1}}^{第页 小时 年 秒})}_{我}) \\ 〈 {t吨}_{2}, σ_{2} | {({\hat{O（运行）}}_{{C类}_{2} | {C类}_{1}}^{第页 小时 年 秒})}_{我} δ ({\hat{C类}}_{H（H）}) | {t吨}_{2}, σ_{2} 〉] Π_{σ_{{C类}_{1} S公司 {C类}_{2}}}, & (76) \end{array}

哪里 $Π_{σ_{{C类}_{1} S公司 {C类}_{2}}} = θ [- 秒_{2} (秒_{1} \frac{{\hat{第页}}_{1}^{2}}{2} + Ĥ_{S公司})]$ 是投影仪到的物理子空间 ${H（H）}_{{C类}_{1}} \otimes {H（H）}_{S公司}$ , |t吨₂, σ₂〉是任意的σ₂-C的扇区时钟状态₂,和 ${G公司}_{{C类}_{1} S公司}$ 是G-旋转进化生成器生成的组 $秒_{1} \frac{{\hat{第页}}_{1}^{2}}{2} + Ĥ_{S公司}$ 复合系统C的₁S公司.

也就是说，间接自我参照效应，因此τ₂-方程（72）的依赖性不存在当且仅当关系Dirac可观测编码C类₂S公司属性相对于C类₁不包含任何时钟自由度C类₂不断发展。

什么时候？ $Ô_{{C类}_{2} S公司 | {C类}_{1}}^{物理} = 我_{{C类}_{2}} \otimes {\hat{（f）}}_{S公司 | {C类}_{1}}^{物理}$ 即，仅系统自由度相对于C类₁如所述，定理5意味着相对于C类₂简化如下：

\begin{array}{l} (θ (- σ_{1} {\hat{第页}}_{1}) \otimes 我_{S公司}) Ô_{{C类}_{1} S公司 | {C类}_{2}}^{物理} (τ_{1}) = \\ Π_{σ_{{C类}_{1} S公司 {C类}_{2}}} {G公司}_{{C类}_{1} S公司} (| τ_{1}, σ_{1} 〉 〈 τ_{1}, σ_{1} | \otimes {\hat{（f）}}_{S公司 | {C类}_{1}}^{物理}) Π_{σ_{{C类}_{1} S公司 {C类}_{2}}} . \end{array}

特别是，转换后的系统可观测性与视角无关，即其相对于C类₁和C类₂当且仅当它是运动常数时重合（参见[7]为了证明这一说法，这里同样适用于每对σ₁-和σ₂-部门）：

推论4。 C的一个运算符₂S公司 相对于 C类₁

\begin{array}{l} Ô_{{C类}_{2} S公司 | {C类}_{1}}^{物理} = 我_{{C类}_{2}} \otimes {\hat{（f）}}_{S公司 | {C类}_{1}}^{物理} . \end{array}

在时间帧变化映射下转换为C的透视图₂ 如下

\begin{array}{l} Ô_{{C类}_{1} S公司 | {C类}_{2}}^{物理} = 我_{{C类}_{1}} \otimes {\hat{（f）}}_{S公司 | {C类}_{2}}^{物理}, \end{array}

哪里 ${\hat{（f）}}_{S公司 | {C类}_{1}}^{物理} = {\hat{（f）}}_{S公司 | {C类}_{2}}^{物理}$ 当且仅当 ${\hat{（f）}}_{S公司 | {C类}_{1}}^{物理}$ 是一个运动常数, $[{\hat{（f）}}_{S公司 | {C类}_{1}}^{物理}, Ĥ_{S公司}] = 0$ .

定理5转换为关系海森堡图（参见[7]对于这里适用于每对σ的证明₁-和σ₂-部门）：

推论5。 让 $Ô_{{C类}_{2} S公司 | {C类}_{1}}^{物理} (τ_{1}) \in 我 ({H（H）}_{{C类}_{2}}^{物理} \otimes {H（H）}_{S公司}^{物理})$ 是描述复合系统C特性动力学的运算符₂S公司 相对于C₁ 在海森堡的照片中。在时间框架下，将方程（75）更改为C的角度₂,此运算符转换为运算符 $Ô_{{C类}_{1} S公司 | {C类}_{2}}^{H（H）} (τ_{1}, τ_{2})$ 满足时钟C中的海森堡运动方程₂ 时间τ₂ 没有显式τ₂ 从属项,

\begin{array}{l} \frac{d日}{d日 τ_{2}} Ô_{{C类}_{1} S公司 | {C类}_{2}}^{H（H）} (τ_{1}, τ_{2}) = 我 [秒_{2} \frac{{\hat{第页}}_{2}^{2}}{2} + {\hat{H（H）}}_{S公司}, Ô_{{C类}_{1} S公司 | {C类}_{2}}^{H（H）} (τ_{1}, τ_{2})], \end{array}

当且仅当

\begin{array}{l} Ô_{{C类}_{2} S公司 | {C类}_{1}}^{物理} (τ_{1}) = \sum_{我} {(Ô_{{C类}_{2} | {C类}_{1}}^{物理})}_{我} \otimes {({\hat{（f）}}_{S公司 | {C类}_{1}}^{物理} (τ_{1}))}_{我}, \end{array}

和 ${(Ô_{{C类}_{2} | {C类}_{1}}^{物理})}_{我}$ 是一个运动常数, $[秒_{1} \frac{{\hat{第页}}_{1}^{2}}{2}, Ô_{{C类}_{2} | {C类}_{1}}^{物理}] = 0$ .

转换的解释当然完全类似于关系薛定谔图。

7.4. 应用程序：比较时钟读数

上述时间帧改变方法的一个应用是比较不同时钟的读数。这也是发展时钟同步概念的先决条件。

例如，我们可能希望比较一些系统属性的演变 ${\hat{（f）}}_{S公司}$ 相对于时钟C类₁具有 ${\hat{（f）}}_{S公司}$ 相对于时钟C类₂这两个关系演变将被编码在形式的Dirac可观测的两个单参数族中 ${\hat{F类}}_{我_{{C类}_{2}} \otimes {（f）}_{S公司}, {T型}_{1}} (τ_{1})$ 和 ${\hat{F类}}_{我_{{C类}_{1}} \otimes {（f）}_{S公司}, {T型}_{2}} (τ_{2})$ 为了将这两种动力学联系起来，我们需要一种一致的方法来关联不同的时钟读数τ₁，τ₂虽然从经典的角度来看，有一种明确的方法来回答“读数τ的值是多少”的问题₂时钟的C类₂，当时钟C类₁读取τ₁?” 即通过设置τ₂(τ₁) ≔F类_{T型₂,T型₁}(τ₁)在量子理论中并非如此，因为这两个时钟现在都是用量子算符来描述的，它们的关系取决于量子态。事实上，我们将简短地论证，比较时钟读数通常取决于时间帧的选择（这里要么C类₁或C类₂)在量子理论中。

7.4.1. 比较时钟读数的三种方法

为了解决量子理论中的这个难题，让我们回顾方程（37）中的条件概率，并求出C类₂读取τ₂什么时候C类₁读取τ₁（为了简单起见，暂时忽略频率扇区）：

\begin{array}{l} P（P） ({T型}_{2} = τ_{2} | {T型}_{1} = τ_{1}) \\ = 〈 ψ_{物理} | {e（电子）}_{{C类}_{1}} (τ_{1}) \otimes {e（电子）}_{{C类}_{2}} (τ_{2}) \otimes 我_{S公司} {| ψ_{物理} 〉}_{家属} \\ = P（P） ({T型}_{1} = τ_{1} | {T型}_{2} = τ_{2}) . & (77) \end{array}

在这里，我们假设物理状态是标准化的，因此根据推论2，任意一个时钟的薛定谔图中的约化状态也是标准化的。

比较时钟读数.给出条件概率方程(77)，我们可以考虑以下三个通常不同的选项来比较时钟读数.

（A）的时钟读数 C类₂ 什么时候 C类₁ 读取τ₁ 定义为的值τ₂ 最大化条件概率 P（P）(T型₂= τ₂|T型₁=τ₁)。这假设分布具有唯一的最大峰值.

（B）的时钟读数 C类₂ 什么时候 C类₁ 读取τ₁ 定义为期望值

\begin{array}{l} τ_{2} (τ_{1}) ≔ \int_{ℝ} d日 τ^{'} τ^{'} P（P） ({T型}_{2} = τ^{'} | {T型}_{1} = τ_{1}) . & (78) \end{array}

（C）的时钟读数 C类₂ 什么时候 C类₁ 读取τ₁ 定义为 ${(τ_{2}^{(n个)} (τ_{1}))}^{1 / n个}$ 对于 n个> 1，其中

\begin{array}{l} τ_{2}^{(n个)} (τ_{1}) ≔ \int_{ℝ} d日 τ^{'} {(τ^{'})}^{n个} P（P） ({T型}_{2} = τ^{'} | {T型}_{1} = τ_{1}) & (79) \end{array}

是 n个方程中条件概率分布的矩(77).

根据期望值关联不同的时钟读数，如（B）所示，可以说是最自然的选择，最初在Höhn和Vanrietvelde中讨论过[30]，Höhn[31]，Bojowald等人[32,33]，Höhn等人[34]史密斯和艾哈迈迪[45]; 我们在这里展开讨论。

显然，只有当条件概率分布在期望值上达到峰值时，两个定义（A）和（B）才一致。此外，所有三个定义（A）-（C）在特殊情况下都同意 $P（P） ({T型}_{2} = τ^{'} | {T型}_{1} = τ_{1}) = δ (τ^{'} - τ_{1})$ ，即当条件概率分布中没有波动时。

7.4.2. 比较二次时钟哈密顿量的时钟读数

现在，让我们在方程（66）定义的当前模型类别中探讨这些定义，并再次考虑不同的频率扇区。考虑到双重超选规则，我们将方程式（77）替换为

\begin{array}{l} {P（P）}_{σ_{1}, σ_{2}} ({T型}_{2} = τ_{2} | {T型}_{1} = τ_{1}) \\ = 〈 ψ_{物理} | {e（电子）}_{{C类}_{1}}^{σ_{1}} (τ_{1}) \otimes {e（电子）}_{{C类}_{2}}^{σ_{2}} (τ_{2}) \otimes 我_{S公司} {| ψ_{物理} 〉}_{家属} \\ = 〈 ψ_{σ_{1}, σ_{2}} | {e（电子）}_{{C类}_{1}} (τ_{1}) \otimes {e（电子）}_{{C类}_{2}} (τ_{2}) \otimes 我_{S公司} {| ψ_{σ_{1}, σ_{2}} 〉}_{家属}, & (80) \end{array}

哪里 $| ψ_{σ_{1}, σ_{2}} 〉 \in {H（H）}_{σ_{1}, σ_{2}}$ 位于σ的重叠处₁-和σ₂-扇区（见公式67）和 ${e（电子）}_{{C类}_{我}}^{σ_{我}} (τ_{我}) ≔ \frac{1}{2 π} | τ_{我}, σ_{我} 〉 〈 τ_{我}, σ_{我} |$ ,我= 1, 2. 然后我们可以编写n个^第个-方程（78）和（79）中条件概率分布的矩n个∈ℕ，因此考虑到定义（B）和（C），如下所示：

\begin{array}{l} τ_{2}^{(n个)} (τ_{1}) = \int_{ℝ} d日 τ^{'} {(τ^{'})}^{n个} {P（P）}_{σ_{1}, σ_{2}} ({T型}_{2} = τ^{'} | {T型}_{1} = τ_{1}) \\ = 〈 ψ_{{C类}_{2} S公司 | {C类}_{1}}^{σ_{1}} (τ_{1}) | {\hat{T型}}_{2, σ_{2}}^{(n个)} \otimes 我_{S公司} | ψ_{{C类}_{2} S公司 | {C类}_{1}}^{σ_{1}} (τ_{1}) 〉 \\ = 〈 ψ_{σ_{1}, σ_{2}} | {\hat{F类}}_{{T型}_{2}^{(n个)} \otimes 我_{S公司}, {T型}_{1}} (τ_{1})) {| ψ_{σ_{1}, σ_{2}} 〉}_{物理}, & (81) \end{array}

式中（30）

\begin{array}{l} {\hat{T型}}_{2, σ_{2}}^{(n个)} = \frac{1}{2 π} \int_{ℝ} d日 t吨 {t吨}^{n个} | t吨, σ_{2} 〉 〈 t吨, σ_{2} | \\ = θ (负极 σ_{2} {\hat{第页}}_{2}) {\hat{T型}}_{2}^{(n个)} θ (负极 σ_{2} {\hat{第页}}_{2}) \end{array}

是σ₂-部门n个对应于C类₂。在方程（81）的第二行中，我们使用了方程（38）和（80），而在第三行中我们引用了定理2。注意，通过等式（74），等式（81）中的表达式定义了期望值，该期望值在C类₁和C类₂.

由于引理3和4，我们可以写出n个方程式（81）中的th-mement也采用以下形式

\begin{array}{l} τ_{2}^{(n个)} (τ_{1}) = 〈 ψ_{{C类}_{2} S公司 | {C类}_{1}}^{σ_{1}} (τ_{1}) | {\hat{T型}}_{2, σ_{2}}^{n个} \otimes 我_{S公司} | ψ_{{C类}_{2} S公司 | {C类}_{1}}^{σ_{1}} (τ_{1}) 〉 \\ = 〈 ψ_{σ_{1}, σ_{2}} | {\hat{F类}}_{{T型}_{2}^{n个} \otimes 我_{S公司}, {T型}_{1}} (τ_{1})) | {ψ_{σ_{1}, σ_{2}} 〉}_{物理}, \end{array}

只要 $| ψ_{{C类}_{2} S公司 | {C类}_{1}}^{σ_{1}} (τ_{1}) 〉 \in (D类 ({\hat{T型}}_{2}^{n个}) \cap {H（H）}_{{C类}_{2}}^{物理}) \otimes {H（H）}_{S公司}^{物理}$ .自 ${(τ_{2}^{(n个)} (τ_{1}))}^{1 / n个} \neq τ_{2} (τ_{1})$ 对于n个>对于一般状态，定义（B）和（C）通常不相等。在续集中，我们将主要考虑Höhn和Vanrietvelde扩展中的定义（B）[30]，Höhn[31]，Bojowald等人[32,33]，Höhn等人[34]史密斯和艾哈迈迪[45]. 这似乎是物理上最吸引人的一个，特别是如果可以为正在考虑的模型开发一个集成解释的话。只有当条件概率分布具有单个最大峰值且定义（C）在操作上不自然且复杂时，定义（A）才是明确的。也就是说，我们设置了时钟读数的值C类₂什么时候C类₁读取τ₁:

\begin{array}{l} τ_{2} (τ_{1}) ≔ τ_{2}^{(1)} (τ_{1}) . & (82) \end{array}

然而，以下讨论在定性上也适用于定义（C）。

7.4.3. 比较时钟读数取决于时间帧

请注意，定义（A）-（C）处理C类₂作为波动子系统。因此，我们可以将其解释为提供时钟读数的定义C类₂相对于时间参考框架C类₁相反，我们当然可以转换角色C类₁和C类₂并询问时钟读数C类₁相对于C类₂。根据定义（B），这将产生

\begin{array}{l} τ_{1} (τ_{2}) = \int_{ℝ} d日 τ^{'} τ^{'} {P（P）}_{σ_{1}, σ_{2}} ({T型}_{2} = τ_{2} | {T型}_{1} = τ^{'}) . & (83) \end{array}

去掉方程（81）和（83）中参数的标签，这两个方程都涵盖了所有ℝ，重要的是要注意τ₁（τ）和τ₂（τ）通常会不是τ的相同函数。这是因为一般来说 ${P（P）}_{σ_{1}, σ_{2}} ({T型}_{2} = τ^{'} | {T型}_{1} = τ) \neq {P（P）}_{σ_{1}, σ_{2}} ({T型}_{2} = τ | {T型}_{1} = τ^{'})$ 式（80）中。换句话说C类₂从C类₁根据定义（B）可能不同于C类₁相对于C类₂（对于相同的物理状态）。

人们可能想知道函数τ₁(τ₂)式（83）中是τ的反演₂(τ₁)式（81）中，即通过求解τ获得₂(τ₁)对于τ₁经典地说，这当然是一种情况，对于固定的时钟读数来说，这是必然的 $τ_{1}^{*}$ 属于C类₁有人发现 $τ_{1} (τ_{2} (τ_{1}^{*})) = τ_{1}^{*}$ 物理上这意味着两个时间参考框架C类₁和C类₂同意当C类₁读取 $τ_{1}^{*}$ ,C类₂读取值 $τ_{2} (τ_{1}^{*})$ 当定义（a）–（C）完全一致时，即当 ${P（P）}_{σ_{1}, σ_{2}} ({T型}_{2} = τ_{2} (τ_{1}^{*}) | {T型}_{1} = τ^{'}) = δ (τ^{'} - τ_{1}^{*})$ 在方程式（83）中，在这种情况下，期望值、最可能值和通过n个现在大家都同意。虽然这确实发生在具有高度对称性的简单模型中C类₁和C类₂[31]，在更有趣的情况下，情况并非如此，因为物理状态通常沿τ分布不同₁和τ₂轴[30,32–34]. 在我们的例子中，这意味着波函数

ψ_{{C类}_{2} S公司 | {C类}_{1}}^{σ_{1}, σ_{2}} (τ_{1}, τ_{2}) ≔ (〈 τ_{1}, σ_{1} | \otimes 〈 τ_{2}, σ_{2} | \otimes 〈 ϕ_{S公司} |) | ψ_{物理} 〉,

对于某些物理系统状态 $| ϕ_{S公司} 〉 \in {H（H）}_{S公司}^{物理}$ ，可以将其视为C类₁或C类₂关系薛定谔图在τ中可能有不同的扩散₁小于τ₂在这种情况下，我们通常会发现 $τ_{1} (τ_{2} (τ_{1}^{*})) \neq τ_{1}^{*}$ 这种效应将出现在本文所考虑的模型类别中，因为物理状态在第页₁和第页₂（因此τ中没有₁或τ₂)由于系统的存在S公司在Bojowald等人的各种模型中，半经典方法也证明了这种效应[32,33]和Höhn等人[34]如果发现之间的ℏ顺序不一致 $τ_{1}^{*}$ 和 $τ_{1} (τ_{2}^{*} = τ_{2} (τ_{1}^{*}))$ .

总之，这种影响可以解释为根据定义（B）[或（C）]比较时钟读数的时间框架依赖性：如果从时间参考框架的角度来看，由C类₁时钟C类₂读取 $τ_{2} (τ_{1}^{*})$ （根据方程式81计算），当C类₁读取 $τ_{1}^{*}$ 反过来，从定义的时间参考框架的角度来看C类₂时钟C类₁一般不会阅读 $τ_{1}^{*}$ 什么时候C类₂读取值 $τ_{2} (τ_{1}^{*})$ 也就是说，C类₁和C类₂通常会对时钟读数的配对产生分歧。

现在让我们也简要地评论一下量子时钟同步的概念。使用状态依赖关系方程（82），我们可以询问哪个状态会产生 $τ_{2} (τ_{1}^{*}) = τ_{1}^{*}$ 以便C类₁和C类₂阅读相同的值，当C类₁读取值 $τ_{1}^{*}$ 。更强大的是，我们可以问是否存在τ为₂(τ₁) = τ₁+常数，对于所有τ₁∈ℝ，因此，直到恒定偏移，C类₁和C类₂始终同步。方程式（81）告诉我们，如果 ${P（P）}_{σ_{1}, σ_{2}} ({T型}_{2} = τ^{'} | {T型}_{1} = τ_{1}) = δ (τ^{'} - τ_{1} - c（c） o个 n个秒 t吨)$ 同样，虽然这发生在简单模型中[31]，由于上述关于比较时钟读数的帧依赖性的观察结果，我们正在学习的课堂模型一般不会发生这种情况。因此，这种同步概念过于强烈，通常无法实现。此外，它通常也依赖于帧。

7.4.4. 比较系统相对于两个时钟的演化

回到我们最初的目标，因此根据定义（B），使用更通用的（与帧相关的）时钟比较更有用，以便比较S公司关于C类₁和C类₂在关系薛定谔图中工作，如果 $| ψ_{{C类}_{2} S公司 | {C类}_{1}}^{σ_{1}} (τ_{1}^{*}) 〉$ 是的初始状态C类₂S公司从…的角度C类₁，然后根据方程（69）C类₁S公司从…的角度C类₂是

\begin{array}{l} (θ (负极 σ_{1} {\hat{第页}}_{1}) \otimes 我_{S公司}) | ψ_{{C类}_{1} S公司 | {C类}_{2}}^{σ_{2}} (τ_{2} (τ_{1}^{*})) 〉 \\ = {R（右）}_{S公司}^{σ_{2}} (τ_{2} (τ_{1}^{*})) \circ {({R（右）}_{S公司}^{σ_{1}} (τ_{1}^{*}))}^{负极 1} | ψ_{{C类}_{2} S公司 | {C类}_{1}}^{σ_{1}} (τ_{1}^{*}) 〉 . & (84) \end{array}

然后，我们可以评估“相同”的可观测简化系统 $我_{{C类}_{我}} \otimes {\hat{（f）}}_{S公司}^{物理}$ 在这两个州，其中我当相对于进行评估时=1C类₂反之亦然（参见推论4），以便比较属性的演变 ${\hat{（f）}}_{S公司}^{物理}$ 相对于处于不同量子状态的两个时钟（这也相当于时钟的量子状态）。为了避免混淆，我们强调 $我_{{C类}_{我}} \otimes {\hat{（f）}}_{S公司}^{物理}$ ,我=1，2，对应于两个不同的关系Dirac观测值 ${\hat{F类}}_{我_{{C类}_{2}} \otimes {（f）}_{S公司}, {T型}_{1}} (τ_{1})$ 和 ${\hat{F类}}_{我_{{C类}_{1}} \otimes {（f）}_{S公司}, {T型}_{2}} (τ_{2})$ 关于时钟中性物理Hilbert空间 ${H（H）}_{物理}$ ; 特别是，这两个是不由TFC映射关联 $Λ_{S公司}^{σ_{1} \to σ_{2}}$ 因此，通过评估通过TFC映射相关的关系Schrödinger态中这两个减少的观测值 $Λ_{S公司}^{σ_{1} \to σ_{2}}$ 通过方程（84），我们可以比较两种真正不同的关系动力学。海森堡关系图中的结构当然是完全相似的。

在Höhn等人[7]和卡斯特罗·鲁伊斯[47]对于哈密顿量为无界动量算符的理想时钟，显示出与帧相关的时间非定域效应。例如，当时钟C类₂被认为是两个峰值状态的叠加，并且与S公司从…的角度C类₁，然后C类₁S公司通常会被缠住C类₂并经历时间演变的叠加。此效应适用于不同σ的每个重叠₁-和σ₂-部门。研究这种依赖于帧的时间局部性如何影响时钟的（潜在的依赖于帧）比较和同步以及S公司相对于C类₁和C类₂在不同的量子态中，对应着不同的钟-中性物理态的选择。这种探索将出现在其他地方。

最后，这些时间框架变化和时钟同步将与量子宇宙学相关。例如，最近有人指出，量子宇宙学中的奇点分辨率取决于用来定义关系动力学的时钟的选择[77]. Gielen和Menéndez-Pidal中使用的不同关系动力学[77]可以解释为我们的关系薛定谔/海森堡图意义上的简化动力学的不同选择。这里发展的时间框架变化原则上可以用于更系统地研究宇宙奇点命运的时间框架依赖性。

8.结论

在这项工作中，我们证明了三种不同的方法对关系量子动力学的等价性——相对论Dirac观测、Page-Wootters形式主义和量子去参数化——对于由哈密顿约束描述的模型，系统作为时钟的动量以二次形式出现。由于这类模型包含许多相对论设置，因此我们扩展了Höhn等人以前的结果[7]进入相对论的语境。此扩展中的一个关键成分是时钟POVM，它相对于哈密顿约束生成的群是协变的，用于描述时钟定义的时间参考框架。这种选择不同于相对论设置中通常使用的自共轭时钟操作符。

由于正负频率模式之间的哈密顿约束形状所诱导的超选择规则，这种等效性（我们称之为关系量子动力学的三位一体）在频率方面保持扇形。此外，我们进一步发展了时间量子框架变化的方法[7,30–34,47,69]在此设置中解决了多项选择问题。然后，该方法用于探索在时钟透视图之间转换时出现的间接自我参照现象，并揭示比较甚至同步不同量子时钟读数的时间框架和状态依赖性。这一结果增加了量子参考系相关物理性质的不断增加，如纠缠[70,72,74]，旋转[73]，古典[72]或客观性[79,80]子系统的叠加[70,72]，某些量子资源[78]，个测量值[70,76]，因果关系[47,83]，时间位置[7,47]，甚至时空奇点分辨率[77]. 时间框架的变化也可以用来扩展最近关于研究量子钟时间膨胀效应的建议[45,136,137]（另请参见[137–140]). 此外，将时间框架变化扩展到宇宙学微扰理论来研究功率谱的时间框架依赖性是很有意思的[64,65].

重要的是，协变时钟POVM允许我们解决库查的批评，即Page-Wootters形式主义不能为闵可夫斯基空间中的相对论粒子产生正确的局域化概率[1]. 事实上，当调节由惯性Minkowski时间坐标量化定义的时间时，会出现这种不正确的定位概率。我们表明，条件作用于协变时钟POVM令人惊讶地产生了Newton-Wigner型局域化概率，虽然近似而非完全协变，但通常被视为相对论量子力学中局域化的最佳可能概念[90,94]. 这个结果强调了协变时钟POVM在定义一致关系量子动力学方面的好处[7,44,45,96,97].

结合上一篇文章[7]因此，我们解决了Kucha针对Kucha中Page-Wootters形式主义提出的所有三个批评（a）–（c）（见引言）[1]. 因此，Page-Wootters形式主义是关系量子动力学的可行方法。通过三位一体建立的等价性，它还为关系可观测公式和去参数化提供了一致的条件概率解释。特别是，描述位置算符相对于协变时钟POVM演化的关系观测值在相对论环境中产生了Newton-Wigner型局域化。

数据可用性声明

本文中包含了研究中提出的原始贡献/补充材料，可向相应作者进行进一步查询。

作者贡献

所有作者都在PH的引导下为文章的研究和写作做出了巨大贡献。

基金

PH感谢西蒙斯基金会通过It-from-Qubit奖学金和基础问题研究所通过FQXi-RFP-1801A号拨款提供的支持。AS感谢加拿大自然科学与工程研究委员会和达特茅斯研究员协会的支持。ML感谢奥地利科学院ESQ Discovery Grant以及奥地利科学基金会（FWF）通过START项目Y879-N27提供的支持。这项工作得到了冲绳科学技术研究生院的部分资助。该项目的最初阶段是在约翰·邓普顿基金会的资助下得以实现的。

免责声明

本出版物中表达的观点是作者的观点，并不一定反映约翰·邓普顿基金会的观点。

利益冲突

作者声明，该研究是在没有任何可能被解释为潜在利益冲突的商业或金融关系的情况下进行的。

补充材料

本文的补充材料可以在以下网站上找到：https://www.frontiersin.org/articles/10.3389/fphy.2021.587083/full#补充-材料

脚注

1^事实上，为了避免自我参照问题，我们不想描述与自身直接相关的参考自由度[99,100]. 然而，通过透视-中性结构，可以通过时间框架变化构建量子钟的间接自我参照效应，参见Höhn等人[7]第7.3节。

2^与之相反[11,103–107]为了简化符号，我们避免使用更严格的公式来表示希尔伯特空间（稠密子集）的Gel'fand三元组和代数对偶。然而，本文的其余部分可以用这样一种更精确的表述。

三。^时钟和系统不相互作用的假设在一般广义相对论系统中不成立。然而，它在一些常用示例中得到了满足（请参见[7]进行讨论和表1例如）。

4^因此，正频率模式和负频率模式由第页_t吨<0和第页_t吨>分别为0，从设置开始C类_σ= 0.

5^我们书写物理状态的方式隐含地假设了sĤ_S公司非退化。如果不是这样，则需要附加简并标签。然而，这不会影响后续分析。参见Höhn[31]对于具有无质量标量场的平面FLRW模型的显式构造，其哈密顿约束也可以解释为自由相对论粒子，因此具有2倍系统能量简并性。

6^第四个根是因为Newton-Winer波函数通常是为Klein-Gordon系统定义的，我们称之为E类实际上是能量的平方 $ω_{第页} ≔ \sqrt{{\vec{第页}}^{2} + 米^{2}}$ 另请注意，对于Klein-Gordon情况，一个具有双简并系统能量，我们这里不考虑。在这种情况下，使用动量更方便，而不是物理状态的能量表示，以及一种独特的度量。方程（16）可以被解释为通常的牛顿-维纳波函数，用运动状态表示。这将在第6节中进行更详细的讨论（另请参阅[31]).

7^这些挑战与量子力学中到达时间算符的定义有关[18,23,30,117–119].

8^使用交换关系 $[\hat{t吨}, {\hat{第页}}_{t吨}^{- 1}] = - 我 {\hat{第页}}_{t吨}^{- 2}$ ，它来自乘法 $[\hat{t吨}, {\hat{第页}}_{t吨}] = 我$ 来自双方 ${\hat{第页}}_{t吨}^{- 1}$ ，我们也可以将此运算符编写为

\begin{array}{l} \hat{T型} & = & 秒 {\hat{第页}}_{t吨}^{- 1} (\hat{t吨} - \frac{我}{2} {\hat{第页}}_{t吨}^{- 1}) & (22) \end{array}

^我们顺便注意到操作员 $\hat{t吨} - \frac{我}{2} {\hat{第页}}_{t吨}^{- 1}$ 正是在Bojowald等人[32]（另请参见[33,34,77])当为Wheeler-DeWitt型方程构造关系Schrödinger图时，约束形式为方程（13）。

9^我们强调，观测到的协变时间是运动学的可观察到 ${H（H）}_{家属}$ 而不是可观测到的规范不变量狄拉克 ${H（H）}_{物理}$ 就像建筑一样，它的力矩不会与约束相互抵消。特别是，它是一个部分可观察的[123].

10^与Braunstein等人[89]，我们使用简并标签σ的不同定义（这里适用于正负频率模式），稍微改变归一化，固定相对相位，保持动量本征态为能量本征态，并引入秒为了简化符号，我们还在Braunstein等人[89]（考虑到自由选择时钟状态）归零。这是我们在上面所做的经典选择的量子模拟，我们也在这里设置克(第页_t吨)英寸T型=t吨/第页_t吨+克(第页_t吨)至零（另请参阅补充材料第页，共页[7]). 然而，重新插入这个很简单克(第页_t吨)在以下每个表达式中。

11^我们还请读者参考最近的工作[38]我们在完成这份手稿时就意识到了这一点。它扩展了Höhn等人的一些结果[7]同样，尽管使用了查泰尼耶提出的不同形式主义[37]. 在二次时钟哈密顿量的情况下，它也不使用协变时钟。

12^最近[37,38]还基于积分技术而非此处和Höhn等人中使用的求和技术，为相关狄拉克观测值开发了一个系统的量化程序[7]，这也产生了一个类似于方程式（31）第二行中的表达式。Chataignier的施工程序[37,38]它包含了一类更一般的模型（但也隐含地假设了全局单调时钟），它使用了更严格的时钟观测选择，这与这里和Höhn et al.中的协变时钟POVM不同[7]，需要是自共轭的。然而，关系观测值的两个量化过程是兼容的，将它们结合起来将是富有成效的。

13^特别是，当_S公司不包含零G公司-旋转 $G公司$ 可以将每个σ-扇区上的G公司-旋转 ${G公司}_{σ}$ ，即由Ĉ生成的一个_σ，而不是Ĉ_H（H）事实上，很容易看出方程（31）中的观测值满足

{\hat{F类}}_{{（f）}_{S公司}, T型}^{σ} (τ) = G公司 (| τ, σ 〉 〈 τ, σ | \otimes {\hat{（f）}}_{S公司}) \approx δ ({\hat{C类}}_{H（H）}) (| τ, σ 〉 〈 τ, σ | \otimes {\hat{（f）}}_{S公司}),

^其中≈是方程（34）中引入的量子弱等式。现在使用方程（14），注意δ（Ĉ_−σ) |τ, σ〉 ⊗ |E类〉_S公司=0，当零不在Ĥ的频谱中时_S公司。此观察结果产生

\begin{array}{l} {\hat{F类}}_{{（f）}_{S公司}, T型}^{σ} (τ) \approx \frac{1}{2 {(- 秒 {\hat{H（H）}}_{S公司})}^{\frac{1}{2}}} δ ({\hat{C类}}_{σ}) (| τ, σ 〉 〈 τ, σ | \otimes {\hat{（f）}}_{S公司}), \\ \approx \frac{1}{2 {(- 秒 {\hat{H（H）}}_{S公司})}^{\frac{1}{2}}} {G公司}_{σ} (| τ, σ 〉 〈 τ, σ | \otimes {\hat{（f）}}_{S公司}), \end{array}

^最后一个弱等式仅限于 ${H（H）}_{σ}$ 当零确实位于Ĥ谱中时_S公司，分解方程（14）没有明确定义，需要进行正则化。

14^例如，当 ${C类}_{H（H）} = {第页}_{t吨}^{2} - {H（H）}^{2} ({q个}_{我}, {第页}_{我}, t吨)$ 和H（H）²> 0 ∀t吨∈ ℝ.

15^另请参阅最近的[38]用于补充方法。注意，它没有为二次哈密顿量使用协变POVM，因此受到了第1节中描述的Kuchař的批评（a）。

16^注意，我们也可以定义时钟状态的线性组合 $| τ 〉 ≔ \sum_{σ} {c（c）}_{σ} | τ, σ 〉 .$ 显然，我们也会发现

17^我们将投影放在引号中，因为当应用于物理希尔伯特空间时，它不是一个真正的投影，因为它只删除描述中的冗余，即通过约束固定的自由度。没有物理信息丢失，这就是为什么此操作是可逆的。然而，这将是对 ${H（H）}_{家属}$ .

18^这被理解为附加了新的时钟张量因子|第页_t吨= −σϵ〉_C类到简化的系统状态 $| ψ_{S公司}^{σ} 〉$ 然后应用与琐碎化相反的方法（请记住，物理状态对时钟读数的调节不是一个真正的投影，因此是可逆的，请参阅前面的脚注）。注意，将简化的系统状态嵌入回物理希尔伯特空间是先验的高度模糊，因为系统状态本身不再携带任何关于已投射出的时钟状态的信息。然而，这里是对还原态的物理解释，作为对系统的描述S公司相对于时间参考系C类它将嵌入时钟中性点（即时间参考系统中性点） ${H（H）}_{物理}$ 当然，这种物理解释是补充信息，但至关重要。有关此主题的更详细讨论，请参见Vanrietvelde等人[71].

19^然而，请注意，这种经典约化相空间的量子化在某些情况下（但一般情况下）将与量子理论一致 ${H（H）}_{S公司, σ}^{物理}$ 由于Dirac和简化量化之间的普遍不平等（参见补充材料).

20^注意这里我们有一个双简并系统能量 $Ĥ_{S公司} = {\hat{第页}}^{2} + 米^{2}$ 与方程式（18）中的表达式相反，我们忽略了简并性。

21^这也解决了Diaz等人[50]其中物理状态是使用运动学而非物理内积进行归一化的，因此产生了与此处不同的发散归一化（对于等质量状态）。

22^看看这是如何与可观测到的时钟相对于Ĉ的（非）协方差联系起来的，这很有启发性_H（H）.让e（电子）_C类要么是协变的e（电子）_C类（τ）或非协变e（电子）_C类(t吨). 方程式（37）的分母为

〈 ψ_{物理} | {e（电子）}_{C类} \otimes 我_{S公司} {| ψ_{物理} 〉}_{家属} = 〈 ψ_{家属} | δ ({\hat{C类}}_{H（H）}) ({e（电子）}_{C类} \otimes 我_{S公司}) {| ψ_{物理} 〉}_{家属} .

^方程（44）表示δ（Ĉ_H（H）)(e（电子）_C类(τ) ⊗我_S公司) ≈我_物理这利用了协方差，并立即表明分母与物理内积方程（18）一致。相反，非协方差意味着δ（Ĉ_H（H）)(e（电子）_C类(t吨) ⊗我_S公司) ≠我_物理，因此在这种情况下，分母与物理内积不同。

23^正频率解的物理内积 $ψ_{物理}^{+} (t吨, x个)$ 当然，Klein-Gordon方程采用标准的Klein-Cordon（而不是Schrödinger）形式的方程（61）。然而，内核K（K）(x个负极x个′)方程（65）第一行中的非局部卷积随米|x个负极x个′| [90]. 因此，对于大质量粒子，我们甚至可以将方程（62）解释为提供了近似的局部化。

24^事实上，真空Bianchi I和II模型的哈密顿约束可以写成[116]

\begin{array}{l} {\hat{C类}}_{H（H）} = - \frac{{\hat{\bar{第页}}}_{0}^{2}}{2} + \frac{{\hat{\bar{第页}}}_{-}^{2}}{2} + \frac{{\hat{\bar{第页}}}_{+}^{2}}{2} + {k个}_{+} {e（电子）}^{- 4 \sqrt{三} {\hat{\bar{β}}}^{+}} . \end{array}

25^回想一下，标签“phys”强调了可观察到的物质作用于物理C类₂S公司希尔伯特空间，即 $Π_{σ_{{C类}_{2} S公司 {C类}_{1}}} ({H（H）}_{{C类}_{2}} \otimes {H（H）}_{S公司})$ ，其中 $Π_{σ_{{C类}_{2} S公司 {C类}_{1}}} = θ [- 秒_{1} (秒_{2} \frac{{\hat{第页}}_{2}^{2}}{2} + Ĥ_{S公司})]$ 是投影到与光谱相对应的子空间上吗 $σ_{{C类}_{2} S公司 {C类}_{1}} ≔ 规格 (秒_{2} \frac{{\hat{第页}}_{2}^{2}}{2} + Ĥ_{S公司}) \cap 规格 (- 秒_{1} \frac{{\hat{第页}}_{1}^{2}}{2})$ 约束方程（66）允许（参见方程17）。因此，我们也可以将这种可观察的现象理解为投影 $Ô_{{C类}_{2} S公司 | {C类}_{1}}^{物理} ≔ Π_{σ_{{C类}_{2} S公司 {C类}_{1}}} Ô_{{C类}_{2} S公司 | {C类}_{1}} Π_{σ_{{C类}_{2} S公司 {C类}_{1}}}$ 一些可观察到的 $Ô_{{C类}_{2} S公司 | {C类}_{1}} \in 我 ({H（H）}_{{C类}_{2}} \otimes {H（H）}_{S公司})$ ; 参见方程式（36）。

工具书类

1.库车。时间和量子引力的解释。国际J Mod物理D. (2011) 20:3–86. doi:10.1142/S0218271811019347

CrossRef全文|谷歌学者

2.Isham CJ。经典量子引力和时间问题。收录：Ibort LA，Rodríguez MA，编辑。可积系统、量子群和量子场论多德雷赫特：施普林格荷兰（1993）。第157-287页。doi:10.1007/978-94-011-1980-1_6

PubMed摘要|CrossRef全文|谷歌学者

3.安德森·E。时间问题。物理基础理论190卷巴塞尔：施普林格国际出版公司（2017）。

谷歌学者

4.罗维利C。量子引力剑桥：剑桥大学出版社（2004）。

谷歌学者

5.斯莫林L。背景独立性案例牛津：牛津大学出版社（2006）。

谷歌学者

6.Smolin L.时间关系主义。arXiv公司. (2018) 180512468.

谷歌学者

7.霍恩PA、史密斯ARH、洛克MPE。关系量子动力学的三位一体。arXiv公司. (2019) 191200033.

谷歌学者

8.德维特BS.量子引力理论。一、规范理论。物理版次. (1967) 160:1113–48. doi:10.1103/PhysRev.160.113

PubMed摘要|CrossRef全文|谷歌学者

9.罗维利C。广义相对论和标准量子力学中对待时间的方式是否不兼容。收件人：Ashtekar A，Stachel J，编辑。量子引力的概念问题巴塞尔：Birkhauser（1991）。第126-40页。

谷歌学者

10.阿什特卡尔A。非微扰经典引力讲座。物理学与宇宙学第6卷新加坡：《世界科学》（1991）。

谷歌学者

11.蒂曼·T。现代经典量子广义相对论剑桥：剑桥大学出版社（2008）。

谷歌学者

12.罗维利C.没有时间的量子力学：一个模型。物理版次D. (1990) 42:2638–46. doi:10.103/物理版本D.42.2638

CrossRef全文|谷歌学者

13.Rovelli C.量子引力中的时间：薛定谔机制之外的物理学。物理版次D. (1991) 43:442–56. doi:10.1103/PhysRevD.43.442

CrossRef全文|谷歌学者

14.罗维利C.在经典引力和量子引力中可以观察到什么？类量子引力. (1991) 8:297–316. doi:10.1088/0264-9381/8/2011

CrossRef全文|谷歌学者

15.Rovelli C.量子参考系。类量子引力. (1991) 8:317–32. doi:10.1088/0264-9381/8/012

CrossRef全文|谷歌学者

16.马洛夫·D·量子宇宙学中的几乎理想时钟：时间的简短推导。类量子引力. (1995) 12:2469–86. doi:10.1088/0264-9381/12/10/007

CrossRef全文|谷歌学者

17.Marolf D.量子观测和重陷动力学。类量子引力. (1995) 12:1199–220. doi:10.1088/0264-9381/12/5/011

CrossRef全文|谷歌学者

18.佐治亚州波尔图甘比尼R。一般协变量子系统中的关系时间：四个模型。物理版次D. (2001) 63:105014. doi:10.1103/PhysRevD.63.105014

CrossRef全文|谷歌学者

19.Tambornino J.重力关系观测：综述。SIGMA公司. (2012) 8:017. doi:10.3842/SIGMA.2012.017

CrossRef全文|谷歌学者

20.吉丁斯SB、马洛夫D、哈特尔JB。在有效重力下可观察到的物体。物理版次D. (2006) 74:064018. doi:10.1103/PhysRevD.74.064018

CrossRef全文|谷歌学者

21.Dittrich B.哈密顿约束系统的部分和完全可观测性。相对重力发电机. (2007) 39:1891–927. doi:10.1007/s10714-007-0495-2

CrossRef全文|谷歌学者

22.Dittrich B.正则广义相对论的部分和完全可观测性。类量子引力. (2006) 23:6155–84. doi:10.1088/0264-9381/23/22/006

CrossRef全文|谷歌学者

23.Dittrich B，Tambornino J.狄拉克可观测性及其时空代数的微扰方法。类量子引力. (2007) 24:757–84. doi:10.1088/0264-9381/24/4/001

CrossRef全文|谷歌学者

24.Dittrich B，Tambornino J.关于广义相对论对称简化扇区的规范不变扰动：宇宙学应用。类量子引力. (2007) 24:4543–86. doi:10.1088/0264-9381/24/18/001

CrossRef全文|谷歌学者

25.Gambini R，Porto RA，Pullin J，Torterolo S.Dirac观测的条件概率和量子引力中的时间问题。物理版次D. (2009) 79:041501. doi:10.1103/PhysRevD.79.041501

CrossRef全文|谷歌学者

26.Pons JM，Salisbury DC，Sundermeyer KA。根据规范固定方法，重新审视一般协变理论中的观测值。物理版次D. (2009) 80:084015. doi:10.1103/PhysRevD.80.084015

CrossRef全文|谷歌学者

27.Ashtekar A，Pawlowski T，Singh P.大爆炸的量子本质：分析和数值研究。一、。物理版次D. (2006) 73:124038. doi:10.1103/PhysRevD.73.124038

CrossRef全文|谷歌学者

28.Kaminski W、Lewandowski J、Pawlowski T。以LQC为例讨论QG的物理时间和其他概念问题。类量子引力. (2009) 26:035012. doi:10.1088/0264-9381/26/3/3035012

CrossRef全文|谷歌学者

29.卡明斯基W、勒万多夫斯基J、鲍洛夫斯基T。量子约束、狄拉克观测和演化：LQC中的群平均与薛定谔图。类量子引力. (2009) 26:245016. doi:10.1088/0264-9381/26/24/245016

CrossRef全文|谷歌学者

30.Höhn PA，Vanrietvelde A.如何在关系量子时钟之间切换。新J Phy. (2020) 22:123048. 数字对象标识代码：10.1088/1367-2630/abd1ac

CrossRef全文|谷歌学者

31.Höhn PA。转换内部时间和“宇宙波函数”的新观点。宇宙. (2019) 5:116. doi:10.3390/universe5050116

CrossRef全文|谷歌学者

32.Bojowald M，Höhn PA，Tsobanjan A.解决时间问题的有效方法。类量子引力. (2011) 28:035006. doi:10.1088/0264-9381/28/3/035006

CrossRef全文|谷歌学者

33.Bojowald M，Höhn PA，Tsobanjan A.时间问题的有效方法：一般特征和示例。物理版次D.（2011）83:125023。doi:10.1103/PhysRevD.83.125023

CrossRef全文|谷歌学者

34.Höhn PA，Kubalova E，Tsobanjan A.不可积分宇宙模型的有效关系动力学。物理版次D. (2012) 86:065014. doi:10.1103/PhysRevD.86.065014

CrossRef全文|谷歌学者

35.Dittrich B，Höhn PA，Koslowski TA，Nelson MI。在量子引力中可以观察到混沌吗？物理Lett B. (2017) 769:554–60. doi:10.1016/j.physletb.2017.02.038

CrossRef全文|谷歌学者

36.Dittrich B，Höhn PA，Koslowski TA，Nelson MI。混沌，狄拉克观测和约束量化。arXiv公司. (2015) 150801947.

谷歌学者

37.Chataignier L.论量子狄拉克观测的构造和WKB时间的出现。物理版次D. (2020) 101:086001. doi:10.1103/PhysRevD.101.086001

CrossRef全文|谷歌学者

38.Chataignier L.关系观测值、参考框架和条件概率。arXiv公司. (2020) 200605526. doi:10.1103/PhysRevD.103.026013

CrossRef全文|谷歌学者

39.DN页，Wootters WK。没有进化的进化：由静止观测描述的动力学。物理版次D. (1983) 27:2885. doi:10.1103/PhysRevD.27.2885

CrossRef全文|谷歌学者

40.伍特WK。“时间”被量子关联所取代。国际理论物理杂志. (1984) 23:701. doi:10.1007/BF02214098

CrossRef全文|谷歌学者

41.Gambini R，Pullin J.《真实棒子和时钟的关系物理学与量子力学的测量问题》。找到Phy. (2007) 37:1074–92. doi:10.1007/s10701-007-9144-6

CrossRef全文|谷歌学者

42.甘比尼R、波尔图R、普林J.《量子引力的基本消相干：教学综述》。相对重力发电机. (2007) 39:1143–56. doi:10.1007/s10714-007-0451-1

CrossRef全文|谷歌学者

43.Giovannetti V，Lloyd S，Maccone L.量子时间。物理版次D. (2015) 79:945933. doi:10.1103/PhysRevD.92.045033

CrossRef全文|谷歌学者

44.Smith ARH，Ahmadi M.量化时间：相互作用的时钟和系统。量子. (2019) 3:160. doi:10.22331/q-2019-07-08-160

CrossRef全文|谷歌学者

45.Smith ARH，Ahmadi M.量子时钟观察经典和量子时间膨胀。国家公社. (2020) 11:5360. doi:10.1038/s41467-020-18264-4

PubMed摘要|CrossRef全文|谷歌学者

46.杜比CE。哈密顿约束的条件概率解释。arXiv公司. (2004) 0406034.

谷歌学者

47.卡斯特罗·鲁伊斯E、贾科米尼F、贝伦西亚A、布鲁克纳采。量子钟和引力量子系统中事件的时间局部化。国家公社. (2020) 11:2672. doi:10.1038/s41467-020-16013-1

PubMed摘要|CrossRef全文|谷歌学者

48.Boette A，Rossignoli R.系统和操作员的历史状态。物理版次A. (2018) 98:032108. doi:10.1103/PhysRevA.98.032108

CrossRef全文|谷歌学者

49.Diaz NL，Rossignoli R.狄拉克理论的历史状态形式主义。物理版次D. (2019) 99:045008. doi:10.1103/PhysRevD.99.045008

CrossRef全文|谷歌学者

50.Diaz NL，Matera JM，Rossignoli R.标量粒子的历史状态形式主义。物理版次D. (2019) 100:125020. doi:10.1103/PhysRevD.100.125020

CrossRef全文|谷歌学者

51.辛格A.量子空间、量子时间和相对论量子力学。arXiv公司. (2020) 200409139.

谷歌学者

52.Leon J，Maccone L.泡利的反对意见。找到Phy. (2017) 47:1597–608. doi:10.1007/s10701-017-0115-2

CrossRef全文|谷歌学者

53.Marletto C，Vedral V.没有进化也没有歧义的进化。物理版次D. (2017) 95:043510. doi:10.1103/PhysRevD.95.043510

CrossRef全文|谷歌学者

54.Nikolova A、Brennen G、Osborne TJ、Milburn G、Stace TM。任意电子系统中的关系时间。物理版次A. (2018) 97:030101. doi:10.1103/PhysRevA.97.03011

CrossRef全文|谷歌学者

55.Baumann V、Santo FD、Smith ARH、Giacomini F、Castro-Ruiz E、Brukner C。Wigner友情场景的无限公式中的广义概率规则。arXiv公司. (2019) 191109696.

谷歌学者

56.Favalli T，Smerzi A.永恒宇宙中的厄米时间算符。arXiv公司. (2020) 200309042. doi:10.22331/q-2020-10-29-354

CrossRef全文|谷歌学者

57.Foti C、Coppo A、Barni G、Cuccoli A、Verrucchi P。只有一次。arXiv公司. (2020) 200612103.

谷歌学者

58.Thiemann T.减少相空间量化和Dirac观测。类量子引力. (2006) 23:1163–80. doi:10.1088/0264-9381/23/4/006

CrossRef全文|谷歌学者

59.Bojowald M，Tsobanjan A.动力学辛约化的量化。arXiv公司. (2019) 190604792. doi:10.1007/s00220-020-03856-4

CrossRef全文|谷歌学者

60.Giesel K，Thiemann T.代数量子引力（AQG）。四、回路量子引力的简化相空间量子化。类量子引力. (2010) 27:175009. doi:10.1088/0264-9381/27/17/17509

CrossRef全文|谷歌学者

61.Domagala M，Giesel K，Kaminski W，Lewandowski J.引力量子化：带标量场的圈量子引力。物理版次D. (2010) 82:104038. doi:10.1103/PhysRevD.82.104038

CrossRef全文|谷歌学者

62.Husain V，Pawlowski T.时间和量子引力的物理哈密顿量。物理Rev Lett. (2012) 108:141301. doi:10.1103/PhysRevLett.108.141301

PubMed摘要|CrossRef全文|谷歌学者

63.Giesel K，Vetter A.使用四个Klein-Gordon标量场作为参考物的简化循环量化。类量子引力. (2019) 36:145002. doi:10.1088/1361-6382/ab26f4

CrossRef全文|谷歌学者

64.Giesel K，Herold L，Li BF，Singh P.Mukhanov-Sasaki方程，在带有尘埃参考场的明显规范不变线性化宇宙摄动理论中。物理版次D. (2020) 102:023524. doi:10.1103/PhysRevD.102.023524

CrossRef全文|谷歌学者

65.Giesel K，Li BF，Singh P.朝向具有膨胀势的环量子宇宙学中的简化相空间量子化。arXiv公司. (2020) 200706597. doi:10.1103/PhysRevD.102.126024

CrossRef全文|谷歌学者

66.阿尔布雷希特A，伊格莱西亚斯A。时钟的模糊性和物理定律的出现。物理版次D. (2008) 77:063506. doi:10.1103/PhysRevD.77.063506

CrossRef全文|谷歌学者

67.Albrecht A，Iglesias A.时钟模糊性：含义和新发展。收件人：Mersini-Hougton L，Vaas R，编辑。时间之箭。物理基础理论，第172卷。柏林；海德堡：施普林格（2012）。doi:10.1007/978-3-642-23259-6_4

CrossRef全文|谷歌学者

68.新泽西州科尔宾五世。量子力学条件概率解释中的半经典极限和最小退相干。找到Phy. (2009) 39:474. doi:10.1007/s10701-009-9298-5

CrossRef全文|谷歌学者

69.Bojowald M，Halnon T.量子宇宙学中的时间。物理版次D. (2018) 98:066001. doi:10.1103/PhysRevD.98.066001

CrossRef全文|谷歌学者

70.Giacomini F，Castro-Ruiz E，Brukner采。量子力学和量子参考系中物理定律的协方差。国家公社. (2019) 10:494. doi:10.1038/s41467-018-08155-0

PubMed摘要|CrossRef全文|谷歌学者

71.Vanrietvelde A，Höhn PA，Giacomini F，Castro-Ruiz E.视角的改变：通过视角-中性框架切换量子参考框架。量子. (2020) 4:225. doi:10.22331/q-2020-01-27-225

CrossRef全文|谷歌学者

72.Vanrietvelde A，Höhn PA，Giacomini F.在N体问题中切换量子参考框架以及缺乏全局关系视角。arXiv公司. (2018) 180905093.

谷歌学者

73.贾科米尼F，卡斯特罗·鲁伊斯E，布鲁克纳。相对论量子参考系：自旋的操作意义。物理Rev Lett. (2019) 123:090404. doi:10.1103/PhysRevLett.123.090404

PubMed摘要|CrossRef全文|谷歌学者

74.de la Hamette AC，Galley TD.一般对称群的量子参考系。量子. (2020) 4:367. doi:10.22331/q-2020-11-30-367

CrossRef全文|谷歌学者

75.Loveridge L、Miyadera T、Busch P.对称性、参考系和量子力学中的关系量。找到Phy. (2018) 48:135–98. doi:10.1007/s10701-018-0138-3

CrossRef全文|谷歌学者

76.杨继明.为量子测量切换量子参考系。量子. (2020) 4:283. doi:10.22331/q-2020-06-18-283

CrossRef全文|谷歌学者

77.Gielen S，Menéndez-Pidal L.奇点分解取决于时钟。arXiv公司. (2020) 200505357. doi:10.1088/1361-6382/abb14f

CrossRef全文|谷歌学者

78.Savi MF，Angelo RM。量子资源协方差。arXiv公司. (2020) 200509612. doi:10.10103/物理版本A.103.022220

CrossRef全文|谷歌学者

79.Le TP、Mironowicz P、Horodecki P.在量子参考系中模糊了量子达尔文主义。arXiv公司. (2020) 200606364. doi:10.1103/PhysRevA.102.062420

CrossRef全文|谷歌学者

80.Tuziemski J.量子参考系中的退相干和信息编码。arXiv公司. (2020) 200607298.

谷歌学者

81.哈代·L。结构解释：通往量子引力的概念之路。arXiv公司. (2018) 180710980.

谷歌学者

82.Hardy L.量子等效原理的实现。收录人：Finster F、Giulini D、Kleiner J、Tolksdorf J，编辑。引力量子理论的进展与展望：物理学和数学的桥梁基础巴塞尔：Birkhäuser（2020年）。第189-220页。数字对象标识代码：10.1007/978-3-030-38941-38

CrossRef全文|谷歌学者

83.宾夕法尼亚州盖林，布鲁克纳。量子事件的依赖于观测者的局域性。新J Phy. (2018) 20:103031. doi:10.1088/1367-2630/aae742

CrossRef全文|谷歌学者

84.Zych M，Costa F，Ralph TC。量子叠加的相对性。arXiv公司. (2018) 180904999.

谷歌学者

85.Barbado LC、Castro Ruiz E、Apadula L、BruknerČ。加速度叠加时探测器的Unruh效应。arXiv公司. (2020) 200312603. doi:10.1103/PhysRevD.102.045002

CrossRef全文|谷歌学者

86.Holevo公司。量子理论的概率和统计方面。统计学与概率第1卷阿姆斯特丹：North-Holland Publishing Company（1982）。

谷歌学者

87.Busch P、Grabowski M、Lahti PJ。操作量子物理。物理专题讲座笔记第31卷.柏林；海德堡：Springer-Verlag（1995）。

谷歌学者

88.Busch P、Grabowski M、Lahti PJ。量子理论中的时间观测。物理Lett A. (1994) 191:357–61. doi:10.1016/0375-9601（94）90785-4

CrossRef全文|谷歌学者

89.Braunstein SL、Caves CM、Milburn GJ。广义不确定性关系：理论、示例和洛伦兹不变性。安·菲斯. (1996) 247:135–73. doi:10.1006/aphy.1996.040

CrossRef全文|谷歌学者

90.哈格·R。局部量子物理：场、粒子、代数.柏林；海德堡：Springer-Verlag（2012）。

谷歌学者

91.Newton TD，Wigner EP。基本系统的局部状态。修订版Mod Phys. (1949) 21:400–6. doi:10.1103/RevModPhys.21.400

CrossRef全文|谷歌学者

92.费尔南多·佩雷斯J，王尔德IF.相对论量子力学中的局部化和因果关系。物理版次D. (1977) 16:315. doi:10.1103/PhysRevD.16.315

CrossRef全文|谷歌学者

93.Malament数据库。为教条辩护：为什么不可能存在（可定域）粒子的相对论量子力学。作者：Clifton R，编辑。量子现实的观点。西安大略大学科学哲学丛书（科学哲学、方法论、认识论、逻辑、科学史及相关领域丛书），第57卷。多德雷赫特：施普林格（1996）。第1-10页。doi:10.1007/978-94-015-8656-6_1

CrossRef全文|谷歌学者

Yngvason J.相对论量子物理中的局域化和纠缠。Lect Notes物理. (2015) 899:325–48. doi:10.1007/978-3-662-46422-9_15

CrossRef全文|谷歌学者

95.Papageorgiou M，Pye J.相对论对粒子局域化和基态纠缠的影响。物理杂志A. (2019) 52:375304. doi:10.1088/1751-8121/ab3593

CrossRef全文|谷歌学者

96.Brunetti R，Fredenhagen K，Hoge M.量子物理学中的时间：从外部参数到内在可观测。找到Phy. (2010) 40:1368–78. doi:10.1007/s10701-009-9400-z

CrossRef全文|谷歌学者

97.Loveridge L，Miyadera T.相对量子时间。找到Phy. (2019) 49:549–60. doi:10.1007/s10701-019-00268-w

CrossRef全文|谷歌学者

98.Höhn PA。量子和引力物理学中信息范式的思考。J Phys Conf系列. (2017) 880:012014. doi:10.1088/1742-6596/880/1/012014

CrossRef全文|谷歌学者

99.Dalla Chiara ML.逻辑自指，集合理论悖论和量子力学中的测量问题。J Philos逻辑. (1977) 6:331–47. doi:10.1007/BF00262066

CrossRef全文|谷歌学者

100.布鲁尔·T。不可能进行准确的状态自我测量。Philos Sci公司. (1995) 62:197–214. doi:10.1086/289852

CrossRef全文|谷歌学者

101.狄拉克·帕姆。量子力学讲课纽约州纽约市：耶什瓦大学贝尔弗科学研究生院（1964年）。

谷歌学者

102.Henneaux M，Teitelboim C。量规系统的量化新泽西州普林斯顿：普林斯顿大学出版社（1992）。

谷歌学者

103.Marolf D.精化代数量化：具有单个约束的系统。arXiv公司. (1995) 9508015.

谷歌学者

104.Hartle JB，Marolf D.比较重参数化-不变系统的广义量子力学公式。物理版次D. (1997) 56:6247–57. doi:10.1103/PhysRevD.56.6247

CrossRef全文|谷歌学者

105.朱利尼D，马洛夫D。关于精细代数量化的一般性。类量子引力. (1999) 16:2479–88. doi:10.1088/0264-9381/16/7/321

CrossRef全文|谷歌学者

106.Giulini D，Marolf D。约束量化的唯一性定理。类量子引力. (1999) 16:2489–505. doi:10.1088/0264-9381/16/7/322

CrossRef全文|谷歌学者

107.Marolf D.群平均和精细代数量化：我们现在在哪里？arXiv公司. (2000) 0011112.

谷歌学者

108.Pailas T.“时间”-协变薛定谔方程和Reissner-Nordström黑洞的正则量子化。arXiv公司. (2020). doi:10.3390/quantum2030029

CrossRef全文|谷歌学者

109.Blyth WF，Isham CJ。充满标量场的弗里德曼宇宙的量子化。物理版次D. (1975) 11:768–78. doi:10.1103/PhysRevD.11.768

CrossRef全文|谷歌学者

110.霍金西南。量子宇宙学。在：DeWitt BS，Stora R，编辑。相对论、群和拓扑II，Les Houches暑期学校，1983年阿姆斯特丹：North-Holland Publishing Company（1984）。第333页。

谷歌学者

111.哈希切克P.量子引力非均匀性的起源。物理版次D. (1986) 34:1040. doi:10.1103/PhysRevD.34.1040

CrossRef全文|谷歌学者

112.基弗C.超小型空间中的波包。物理版次D. (1988) 38:1761. doi:10.1103/PhysRevD.38.1761

CrossRef全文|谷歌学者

113.Ashtekar A，Singh P.Loop量子宇宙学：现状报告。类量子引力. (2011) 28:213001. doi:10.1088/0264-9381/28/21/213001

CrossRef全文|谷歌学者

114.Ashtekar A，Corichi A，Singh P.环量子宇宙学关键特征的稳健性。物理版次D. (2008) 77:024046. doi:10.103/物理版本D.77.024046

CrossRef全文|谷歌学者

115.博约瓦尔德M。经典引力及其应用：宇宙学、黑洞和量子引力剑桥：剑桥大学出版社（2010）。

谷歌学者

116.Ashtekar A，Tate R，Uggla C.迷你超空间：可观测和量化。国际J Mod物理D. (1993) 2:15–50. doi:10.1142/S0218271893000039

CrossRef全文|谷歌学者

117.格罗特·N，罗维利·C，泰特·RS。量子力学的到达时间。物理版次A. (1996) 54:4676. doi:10.1103/PhysRevA.54.4676

CrossRef全文|谷歌学者

118.Aharonov Y、Oppenheim J、Popescu S、Reznik B、Unruh W。量子力学中到达时间的测量。物理版次A. (1998) 57:4130. doi:10.1103/PhysRevA.57.4130

CrossRef全文|谷歌学者

119.Muga JG，Leavens CR。量子力学中的到达时间。物理代表. (2000) 338:353–438. doi:10.1016/S0370-1573（00）00047-8

CrossRef全文|谷歌学者

120.Aharonov Y，Bohm D.量子理论中的时间以及时间和能量的不确定性关系。Phys修订版. (1961) 122:1649. doi:10.1103/PhysRev.122.1649

CrossRef全文|谷歌学者

121.佩雷斯A.用量子钟测量时间。Am J Phys公司. (1980) 48:552–7. doi:10.119/112061

CrossRef全文|谷歌学者

122.Pauli W.Die allgemeinen prinzipien der wellen mechanik保利·W·德韦伦机械师。Handbuch der Physik公司. (1958) 5:1–168. doi:10.1007/978-3642-80539-4_1

CrossRef全文|谷歌学者

123.Rovelli C.部分观察结果。物理版次D. (2002) 65:124013. doi:10.1103/PhysRevD.65.124013

CrossRef全文|谷歌学者

124.Ashtekar A，Horowitz G.关于量子引力的规范方法。物理版次D. (1982) 26:3342–53. doi:10.1103/PhysRevD.26.3342

CrossRef全文|谷歌学者

125.KuchařKV。仪表系统的协变因子排序。物理版次D. (1986) 34:3044–57. doi:10.1103/PhysRevD.34.3044

PubMed摘要|CrossRef全文|谷歌学者

126.Schleich K.约化相空间量子化等价于狄拉克量子化吗？类量子引力.（1990）7:1529–38。doi:10.1088/0264-9381/7/8/028

CrossRef全文|谷歌学者

127.Romano JD，Tate RS.Dirac与简单约束系统的简化空间量化。类量子引力. (1989) 6:1487. doi:10.1088/0264-9381/6/10/017

CrossRef全文|谷歌学者

约束和量化的非交换性：U（1）规范模型。物理版次D. (1990) 41:3785–91. doi:10.1103/PhysRevD.41.3785

PubMed摘要|CrossRef全文|谷歌学者

129.Kunstatter G.Dirac与简化量化：几何方法。类量子引力. (1992) 9:1469–86. doi:10.1088/0264-9381/9/6/005

CrossRef全文|谷歌学者

130.Bartlett SD、Rudolph T、Spekkens RW。参考框架、超选择规则和量子信息。修订版Mod Phys. (2007) 79:555–609. doi:10.1103/RevModPhys.79.555

CrossRef全文|谷歌学者

131.Smith ARH。在没有共享参考帧的情况下进行通信。物理版次A. (2019) 99:052315. doi:10.1103/PhysRevA.99.052315

CrossRef全文|谷歌学者

132.史密斯·ARH、皮亚尼·M、曼·RB。与非紧群相关的量子参考系：平移和推进的情况以及质量的作用。物理版次A. (2016) 94:012333. doi:10.1103/PhysRevA.94.012333

CrossRef全文|谷歌学者

133.Banerjee K，Calcagni G，Martín-Benito M。环路量子宇宙学导论。SIGMA公司. (2012) 8:016. doi:10.3842/SIGMA.2012.016

CrossRef全文|谷歌学者

134.第DN页。时间是不可观测的NSF-ITP-89-18（1989）。

谷歌学者

135.第DN页。时钟时间和熵。收录人：哈里维尔JJ、佩雷兹·梅卡德J、苏莱克·怀特，编辑。时间不对称的物理根源剑桥：剑桥大学出版社（1994）。第287-98页。

谷歌学者

136.史密斯·ARH。量子时间膨胀：相对论量子理论的新测试。arXiv公司. (2020) 200410810.

谷歌学者

137.Grochowski PT、Smith ARH、Dragan A、Dȩbski K。原子光谱中的量子时间膨胀。物理修订研究. (2021) 3:023053. doi:10.1103/PhysRevResearch.3.023053

CrossRef全文|谷歌学者

138.Zych M，Costa F，Pikovski I，Brukner采。量子干涉可见度作为广义相对论真时间的见证。国家公社. (2011) 2:505. doi:10.1038/ncomms1498

PubMed摘要|CrossRef全文|谷歌学者

139.Khandelwal S，Lock MPE，Woods MP。离域时钟中广义相对论时间膨胀的普遍量子修正。量子. (2020) 4:309. doi:10.22331/q-2020-08-14-309

CrossRef全文|谷歌学者

140.Paige AJ，Plato ADK，Kim MS。量子钟的经典和非经典时间膨胀。物理Rev Lett. (2020) 124:160602. doi:10.1103/PhysRevLett.124.160602

PubMed摘要|CrossRef全文|谷歌学者

关键词：关系量子动力学，时间问题，关系狄拉克观测，Page-Wootters形式主义，量子去参数化，量子钟，量子参考系，相对论量子钟

引文：Höhn PA、Smith ARH和Lock MPE（2021）相对论环境中关系量子动力学方法的等效性。前面。物理学。9:587083。doi:10.3389/fphy.2021.587083

收到：2020年7月24日；认可的：2021年3月22日；
出版：2021年6月18日。

编辑：

丹妮尔·奥里蒂德国慕尼黑路德维希·马克西米利安大学

审核人：

梅赫迪·阿萨尼奥西波兰华沙大学
吴振斌美国芝加哥伊利诺伊大学
斯特芬·吉伦英国谢菲尔德大学

*通信：菲利普·A·Höhn，philipp.hoehn@oist.jp; 亚历山大·史密斯，arhsmith@anselm.edu; 马克西米利安·P·E·洛克，maximilian.lock@eoaw.ac.at

原创研究文章

相对论环境下关系量子动力学方法的等价性

1.简介

2.经典力学和量子力学的钟-中性公式

2.1、。钟-中性经典理论

2.2. 钟-中性量子理论

3.二次时钟哈密顿量

3.1. 经典理论

3.2. 量子理论

4.协变时钟

4.1. 具有经典协变时钟的关系动力学

4.2. 二次哈密顿量的可观测协变量子时间

5.关系量子动力学的三位一体：二次时钟哈密顿量

5.1. 三位一体的三张脸

5.1.1. 动力学（i）：量子关系狄拉克观测

5.1.2. 动力学（ii）：Page-Wootters形式主义

5.1.3. 动力学（iii）：量子去参数化

5.1.4. 动力学等效性（ii）和（iii）

5.2. 规范混合和规范变量扩展的量子模拟

5.3. 插曲：备选路线

6.相对论本土化：应对库查的批评

7.改变量子时钟

7.1。状态转换

7.2. 可观测变换

7.2.1. 关系薛定谔图中的可观测变换

7.2.2. 关系海森堡图中的可观测变换

7.3. 间接时钟自参考的发生

7.4. 应用程序：比较时钟读数

7.4.1. 比较时钟读数的三种方法

7.4.2. 比较二次时钟哈密顿量的时钟读数

7.4.3. 比较时钟读数取决于时间帧

7.4.4. 比较系统相对于两个时钟的演化

8.结论

数据可用性声明

作者贡献

基金

免责声明

利益冲突

补充材料

脚注

工具书类

本文是研究主题的一部分

人们还关注