An Efficient Numerical Technique for Solving Time-Fractional Generalized Fisher's Equation

Majeed, Abdul; Kamran, Mohsin; Abbas, Muhammad; Singh, Jagdev

doi:10.3389/fphy.2020.00293

原创研究文章

前面。物理。，2020年10月8日
统计和计算物理
第8卷-2020| https://doi.org/10.3389/fphy.2020.00293

求解时间分数广义Fisher方程的一种有效的数值方法

¹巴基斯坦拉合尔教育大学数学系科学与技术部
²巴基斯坦萨戈达萨戈达大学数学系
^三印度斋浦尔斋浦尔工程学院和研究中心（JECRC）大学数学系

本文通过增加源项和推广非线性部分的度β，对现有的Fisher方程进行了推广。还研究了使用三次B样条配置格式对不同β值的修正Fisher方程的数值解。基于我1公式，而三次B样条基函数用于插值空间导数。模型中的非线性部分通过修正公式线性化。通过对四个具有不同初始和边界条件的测试实例进行仿真，验证了该方案的有效性。讨论了不同参数的影响，并以表格和图形的形式给出。此外，利用Von Neumann稳定性公式，证明了该方案是无条件稳定的。误差范数的结果表明，该格式适用于非线性时间分数阶微分方程。

1.简介

基于分数阶微积分的模型已被用于工程和科学的不同领域。近几年来，分数阶微分方程得到了广泛的应用。分数阶微分方程的主要优点是在数学建模中具有非局部性。在二十世纪，作者们[1–三]增加了分数微积分领域的大量研究。这些应用可以在不同的科学和工程分支中看到，例如金融[4]、纳米技术[5]，电动力学[6]和粘弹性。费希尔方程常用于流行病和细菌、分支布朗运动、新石器时代过渡和化学动力学[7–9]. Fisher解释了男性基因在无限介质中的时空传播[10]. 应用和分析了Riemann-Liouville和Caputo意义分数阶导数微分方程的几种数值方法[11–13]。

Baranwal et al[14]本文通过两种不同的方式进行了修改：（1）引入源项；（2）推广非线性功率。

时间分数费希尔方程的修正形式为：

\begin{array}{l} \frac{\partial^{α} Z轴 (第页, 吨)}{\partial 吨^{α}} - ν \frac{\partial^{2} Z轴 (第页, 吨)}{\partial {第页}^{2}} - Z轴 (第页, 吨) (1 - {Z轴}^{β} (第页, 吨)) \\ = （f） (第页, 吨), 一 \leq 第页 \leq b条, 0 < α \leq 1, 吨 \geq 0, & (1.1) \end{array}

具有初始条件

\begin{array}{l} Z轴 (第页, 0) = ψ (第页), 一 \leq 第页 \leq b条, & (1.2) \end{array}

和边界条件

\begin{array}{l} Z轴 (一, 吨) = ψ_{1} (吨), Z轴 (b条, 吨) = ψ_{2} (吨), 吨 \geq 0, & (1.3) \end{array}

其中ν是粘度参数。

Caputo和Riemann-Liouville分数导数有广泛的应用[15–17]. 本工作中使用了卡普托导数：

\begin{array}{l} \frac{\partial^{α} Z轴 (第页, 吨)}{\partial 吨^{α}} = {\begin{matrix} \frac{1}{Γ (问 - 一)} \int_{0}^{吨} \frac{\partial^{问} Z轴 (第页, 秒)}{\partial 吨^{问}} {(吨 - 秒)}^{问 - α - 1} d日 秒, & 问 - 1 < α < 问, \\ \frac{\partial^{问} Z轴 (第页, 吨)}{\partial 吨^{问}}, & 问 = α . \end{matrix} \end{array}

Caputo导数由我1个配方[18]以下为：

\begin{array}{l} \frac{\partial^{α} 小时}{\partial 吨^{α}} | 吨_{n个} = \frac{1}{{(Δ 吨)}^{α} Γ (2 - α)} \sum_{k个 = 0}^{n个 - 1} λ_{k个}^{α} [小时 (吨_{n个 - k个}) - 小时 (吨_{n个 - k个 - 1})] + 哦 (Δ 吨), & (1.4) \end{array}

哪里 $λ_{k个} = {(k个 + 1)}^{1 - α} - {k个}^{1 - α}$ .

在本文中，我们推广了在[19]以下为：

\begin{array}{l} {({Z轴}^{β})}_{j个}^{n个 + 1} = β {Z轴}_{j个}^{n个 + 1} {({Z轴}^{β - 1})}_{j个}^{n个} - (β - 1) {({Z轴}^{β})}_{j个}^{n个}, & (1.5) \end{array}

其中β是一个正整数。

分数阶偏微分方程的数值解和解析解在解释日常生活中出现的非线性问题的特征方面起着重要作用。在文献中，研究人员应用了各种技术来求解Fisher方程的数值解。Baranwal等人[14]介绍了一种基于变分迭代法（VIM）和Adomian分解法（ADM）求解非线性时间分数阶反应扩散方程的解析算法。瓦兹瓦兹和戈尔吉斯[20]应用ADM对费希尔方程进行分析研究。Abedle-Rady等人将同伦摄动sumudu变换方法用于求解分数阶非线性色散方程[21]. 古普塔和萨哈·雷[22]实现了两种方法。求解任意阶偏微分方程（如Burger-Fisher方程和广义Fisher方程）数值解的Haar小波方法和最优同伦渐近方法（OHAM）。Cherif等人[23]用经典HPM求解了空间分数阶Fisher方程。卡德尔和萨阿德[24]提出了一种利用切比雪夫谱配置技术求解空间分数阶Fisher方程的数值方法。拉瓦什德[25]引入分数阶自然分解方法（FNDM），求非线性时间分数阶Harry Dym方程和非线性时间分数Fisher方程的解析解和近似解。辛格[26]介绍了一种求解非线性Lane-Emden型方程近似解的有效计算方法。Singh研究了大型薄膜分数阶振动方程的数值解[27]雅可比多项式。中的作者[28]采用三次B样条方法对时间分数Burgers方程和Fisher方程进行了数值模拟。Singh等人[29]构造了求解时空分数耦合Burgers方程的q-homotopy分析变换方法。Najeeb等人[30]用HPM方法求解时间分数反应扩散方程。Majeed等人[28]使用非均匀B样条构造颅面骨折。

本文提出了一种三次B样条（CBS）算法，用于时间分数阶广义Fisher方程的数值模拟。卡普托时间分数导数基于我1格式是用有限差分公式离散的，而空间导数是用CBS函数离散的。目前的方法对于分数阶偏微分方程的数值结果来说是新颖的，据我们所知，时间分数阶广义Fisher方程的任何样条解都还没有研究过。此外，该格式对齐次和非齐次边界条件同样有效。

本文以以下方式呈现。第二节简要介绍了时间离散化、三次B样条函数和空间离散化。第四节讨论了该算法的稳定性。第5节报告了对四个试验问题的数值结果的讨论。第6节给出了这项工作的结论。

2.方法说明

让我们考虑一下间隔[a、 b条]被细分为N个等间距有限元小时由节决定第页_j个,j个= 0, 1, 2, 3.……,N个这样的话一=第页₀<第页₁<第页₂… <第页_N个−1<第页_N个=b条。网格点处的三次B样条基函数定义为

\begin{array}{l} ϕ_{j个} (第页) = \frac{1}{6 {小时}^{三}} {\begin{array}{l} {(第页 - {第页}_{j个})}^{三}, 如果 第页 \in [{第页}_{j个}, {第页}_{j个 + 1}), \\ {小时}^{三} + 三 {小时}^{2} (第页 - {第页}_{j个 + 1}) \\ + 三 小时 {(第页 - {第页}_{j个 + 1})}^{2} - 三 {(第页 - {第页}_{j个 + 1})}^{三}, 如果 第页 \in [{第页}_{j个 + 1}, {第页}_{j个 + 2}], \\ {小时}^{三} + 三 {小时}^{2} ({第页}_{j个 + 三} - 第页) \\ + 三 小时 {({第页}_{j个 + 三} - 第页)}^{2} - 三 {({第页}_{j个 + 三} - 第页)}^{三}, 如果 第页 \in [{第页}_{j个 + 2}, {第页}_{j个 + 三}], \\ {({第页}_{j个 + 4} - 第页)}^{三}, 如果 第页 \in [{第页}_{j个 + 三}, {第页}_{j个 + 4}) . \end{array} & (2.1) \end{array}

根据上述基础，近似解Z轴_N个(r、 t吨)可以用三次B样条基函数的线性组合表示如下

\begin{array}{l} {Z轴}_{N个} (第页, 吨) = \sum_{j个 = - 1}^{N个 + 1} Υ_{j个} (吨) ϕ_{j个} (第页), & (2.2) \end{array}

哪里 $Υ_{j个} {(吨)}^{'} 秒$ 是有待确定的未知因素。使用四个连续的三次B样条来构造每个元素[第页_j个,第页_j个+1]. 三次B样条及其在节点处的导数的值如所示表1. The variation ofZ轴_N个(r、 t吨)在典型组件上[第页_j个,第页_j个+1]由给定

\begin{array}{l} {Z轴}_{N个} ({第页}_{j个}, 吨_{n个}) = \sum_{米 = j个 - 1}^{j个 + 1} Υ_{米} (吨) ϕ_{米} ({第页}_{米}) . & (2.3) \end{array}

表1

表1.节点处CBS及其导数的系数第页_j个.

通过插入中给出的近似值表1在式（2.3）中(第页_j个,吨_n个)，方程（1.1）得出以下分数阶常微分方程组。

\begin{array}{l} [(Υ_{j个 - 1}^{•} (吨) + 4 Υ_{j个}^{•} (吨) + Υ_{j个 + 1}^{•} (吨)) / 6] - \frac{ν}{{小时}^{2}} [Υ_{j个 - 1} - 2 Υ_{j个} + Υ_{j个 + 1}] \\ - [(Υ_{j个 - 1} + 4 γ_{j个} + Υ_{j个 + 1}) / 6] [1 - {((Υ_{j个 - 1} + 4 Υ_{j个} + Υ_{j个 + 1}) / 6)}^{β}] \\ = （f） ({第页}_{j个}, 吨_{n个}) . & (2.4) \end{array}

这里，•表示α第个对时间的分数导数进行排序。经过一些简化后，方程（1.1）β=3的递推关系可以写成

\begin{array}{l} Υ_{j个 - 1}^{n个 + 1} [\frac{γ}{6} - \frac{1}{2 {小时}^{2}} - \frac{1}{12} + \frac{2}{1296} {({T型}_{米})}^{三}] \\ + Υ_{j个}^{n个 + 1} [\frac{4 γ}{6} + \frac{1}{{小时}^{2}} - \frac{1}{三} + \frac{8}{1296} {({T型}_{米})}^{三}] \\ + Υ_{j个 + 1}^{n个 + 1} [\frac{γ}{6} - \frac{1}{2 {小时}^{2}} - \frac{1}{12} + \frac{2}{1296} {({T型}_{米})}^{三}] \\ = Υ_{j个 - 1}^{n个} [\frac{γ}{6} + \frac{1}{2 {小时}^{2}} + \frac{1}{12}] + Υ_{j个}^{n个} [\frac{4 γ}{6} - \frac{1}{{小时}^{2}} + \frac{1}{三}] \\ + Υ_{j个 + 1}^{n个} [\frac{γ}{6} + \frac{1}{2 {小时}^{2}} + \frac{1}{12}] - \frac{1}{1296} {({T型}_{米})}^{4} + （f） ({第页}_{j个}, 吨_{n个}) \\ - (γ \sum_{k个 = 0}^{n个 - 1} λ_{k个} [((Υ_{j个 - 1}^{n个 - k个 - 1} - Υ_{j个 - 1}^{n个 - k个}) + 4 (Υ_{j个}^{n个 - k个 - 1} - Υ_{j个}^{n个 - k个}) \\ + (γ_{j个 + 1}^{n个 - k个 - 1} - Υ_{j个 + 1}^{n个 - k个})) / 6] + ρ_{Δ 吨}^{n个 + 1}), & (2.5) \end{array}

哪里 $λ_{k个} = [{(k个 + 1)}^{1 - α} - {k个}^{1 - α}],$ ${T型}_{米} = Υ_{j个 - 1}^{n个} + 4 γ_{j个}^{n个} + Υ_{j个 + 1}^{n个},$ $γ = \frac{{(Δ 吨)}^{- α}}{Γ (2 - α)}$ 此外，截断误差 $ρ_{Δ 吨}^{n个 + 1}$ 边界为

\begin{array}{l} | ρ_{Δ 吨}^{n个 + 1} | \leq ϖ {(Δ 吨)}^{2 - α}, & (2.6) \end{array}

其中ϖ是一个实际常数。

引理2.1。系数λ_k个 in（2.5）具有以下特征[31]以下为：

• λ_k个>0和λ₀= 1,k个= 1:1:n个,

• λ₀> λ₁>λ₂> … > λ_k个, λ_k个→0作为k个→ ∞,

• $\sum_{k个 = 0}^{n个} (λ_{k个} - λ_{k个 + 1}) + λ_{n个 + 1} = (1 - λ_{1}) + \sum_{k个 = 1}^{n个 - 1} (λ_{k个} - λ_{k个 + 1}) + λ_{n个} = 1$ .

方程式（2.5）修改为

\begin{array}{l} Υ_{j个 - 1}^{n个 + 1} α_{0} + Υ_{j个}^{n个 + 1} α_{1} + Υ_{j个 + 1}^{n个 + 1} α_{0} = Υ_{j个 - 1}^{n个} ({n个}_{1}) + Υ_{j个}^{n个} ({n个}_{2}) \\ + Υ_{j个 + 1}^{n个} ({n个}_{1}) - \frac{1}{1296} {({T型}_{米})}^{4} + （f） ({第页}_{j个}, 吨_{n个}) \\ - (γ \sum_{k个 = 1}^{n个 - 1} λ_{k个} [((Υ_{j个 - 1}^{n个 - k个 - 1} - Υ_{j个 - 1}^{n个 - k个}) + 4 (Υ_{j个}^{n个 - k个 - 1} - Υ_{j个}^{n个 - k个}) \\ + (Υ_{j个 + 1}^{n个 - k个 - 1} - Υ_{j个 + 1}^{n个 - k个})) / 6] + ρ_{Δ 吨}^{n个 + 1}), & (2.7) \end{array}

哪里 $α_{0} = \frac{γ}{6} - \frac{1}{2 {小时}^{2}} - \frac{1}{12} + \frac{2}{1296} {({T型}_{米})}^{三}, α_{1} = \frac{4 γ}{6} + \frac{1}{{小时}^{2}} - \frac{1}{三} + \frac{8}{1296} {({T型}_{米})}^{三},$ ${n个}_{1} = \frac{γ}{6} + \frac{1}{2 {小时}^{2}} + \frac{1}{12}$ 和 ${n个}_{2} = \frac{4 γ}{6} - \frac{1}{{小时}^{2}} + \frac{1}{三}$

从（2.7）开始，系统N个+1线性方程N个+3个未知参数 ${(Υ_{- 1}, Υ_{0}, Υ_{1}, \dots, Υ_{N个 + 1})}^{T型}$ 可以获得。为了获得系统的唯一解，需要两个额外的方程。为此，使用给定的边界条件。因此，表达式（2.7）的线性方程组变成

\begin{array}{l} P（P） {Y（Y）}^{n个 + 1} = 问 {Y（Y）}^{n个} . & (2.8) \end{array}

\begin{array}{l} {Y（Y）}^{n个} = {(Υ_{- 1}^{n个}, Υ_{0}^{n个}, Υ_{1}^{n个}, \dots, Υ_{N个 + 1}^{n个})}^{T型} . \end{array}

哪里

\begin{array}{l} P（P） = [\begin{matrix} \frac{1}{6} & \frac{4}{6} & \frac{1}{6} & 0 & \dots & 0 & 0 & 0 \\ α_{0} & α_{1} & α_{0} & 0 & \dots & 0 & 0 & 0 \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋱ & ⋮ & ⋮ & ⋮ \\ 0 & 0 & 0 & 0 & \dots & α_{0} & α_{1} & α_{0} \\ 0 & 0 & 0 & 0 & \dots & \frac{1}{6} & \frac{4}{6} & \frac{1}{6} \end{matrix}] . & (2.9) \end{array}

3.初始向量

对于初始向量，所考虑问题的初始条件和边界条件将有助于计算初始向量 ${Y（Y）}^{0} = {(Υ_{- 1}^{0}, Υ_{0}^{0}, Υ_{1}^{0}, \dots, Υ_{N个 + 1}^{0})}^{T型}$ 因此，近似值（2.2）变为

\begin{array}{l} {Z轴}_{N个} (第页, 0) = \sum_{j个 = - 1}^{N个 + 1} Υ_{j个} (0) ϕ_{j个} (第页) . \end{array}

确定γ⁰，初始条件和边界条件导数的近似值如下[32]以下为：

• ${({Z轴}_{第页})}_{j个}^{k个} = 克^{'} ({第页}_{j个})$ 对于j个= 0,N个

• ${(Z轴)}_{j个}^{0} = 克 ({第页}_{j个})$ 对于j个= 0, 1, 2, …,N个

这提供了以下内容(N个+ 3) × (N个+3）矩阵系统：

\begin{array}{l} [\begin{matrix} \frac{- 1}{2 小时} & 0 & \frac{1}{2 小时} & 0 & \dots & 0 & 0 & 0 \\ \frac{1}{6} & \frac{4}{6} & \frac{1}{6} & 0 & \dots & 0 & 0 & 0 \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋱ & ⋮ & ⋮ & ⋮ \\ 0 & 0 & 0 & 0 & \dots & \frac{1}{6} & \frac{4}{6} & \frac{1}{6} \\ 0 & 0 & 0 & 0 & \dots & \frac{- 1}{2 小时} & 0 & \frac{1}{2 小时} \end{matrix}] [\begin{matrix} Υ_{- 1}^{0} \\ Υ_{0}^{0} \\ ⋮ \\ Υ_{N个 + 1}^{0} \end{matrix}] = [\begin{matrix} 克^{'} ({第页}_{0}) \\ 克 ({第页}_{0}) \\ ⋮ \\ 克 ({第页}_{N个}) \\ 克^{'} ({第页}_{N个}) \end{matrix}] \end{array}

4.稳定性分析

冯·诺依曼（von Neumann）分析经常用于确定稳定性要求，因为它通常简单易行。单傅里叶模式下的解定义为

\begin{array}{l} Υ_{j个}^{n个} = Υ^{k个} {e（电子）}^{我 η j个 小时}, & (4.1) \end{array}

哪里 $我 = \sqrt{- 1}$ 广义Fisher方程（2.7）的近似解可以写成

\begin{array}{l} Υ_{j个 - 1}^{n个 + 1} (α_{0}) + Υ_{j个}^{n个 + 1} (α_{1}) + γ_{j个 + 1}^{n个 + 1} (α_{0}) = Υ_{j个 - 1}^{n个} ({n个}_{1}) + Υ_{j个}^{n个} ({n个}_{2}) \\ + Υ_{j个 + 1}^{n个} ({n个}_{三}) - \frac{1}{1296} {({T型}_{米})}^{4} \\ + （f） ({第页}_{j个}, 吨_{n个}) - γ \sum_{k个 = 1}^{n个 - 1} λ_{k个}^{α} [((Υ_{j个 - 1}^{n个 - k个 + 1} - Υ_{j个 - 1}^{n个 - k个}) \\ + 4 (Υ_{j个}^{n个 - k个 + 1} - Υ_{j个}^{n个 - k个}) + (Υ_{j个 + 1}^{n个 - k个 + 1} - γ_{j个 + 1}^{n个 - k个})) / 6] . & (4.2) \end{array}

哪里 ${n个}_{1} = \frac{γ}{6} + \frac{1}{2 {小时}^{2}} + \frac{1}{12}, {n个}_{2} = \frac{4 γ}{6} - \frac{1}{{小时}^{2}} + \frac{1}{三}, {n个}_{三} = \frac{γ}{6}$ $+ \frac{1}{2 {小时}^{2}} + \frac{1}{12},$ ${T型}_{米} = Υ_{我 - 1}^{n个} + 4 Υ_{我}^{n个} + Υ_{我 + 1}^{n个} .$

将（4.1）替换为（4.2），我们得到

\begin{array}{l} Υ^{k个 + 1} {e（电子）}^{我 η (j个 - 1) 小时} (α_{0}) + Υ^{k个 + 1} {e（电子）}^{我 η (j个) 小时} (α_{1}) + Υ^{k个 + 1} {e（电子）}^{我 η (j个 + 1) 小时} (α_{0}) \\ = Υ^{k个} {e（电子）}^{我 η (j个 - 1) 小时} ({n个}_{1}) \\ + Υ^{k个} {e（电子）}^{我 η (j个) 小时} ({n个}_{2}) + Υ^{k个} {e（电子）}^{我 η (j个 + 1) 小时} ({n个}_{三}) - \frac{1}{1296} {({T型}_{米})}^{4} + （f） (第页, 吨) \\ - \sum_{k个 = 1}^{n个 - 1} λ_{k个}^{α} [((Υ^{n个 - k个 + 1} {e（电子）}^{我 η (j个 - 1) 小时} \\ - Υ^{n个 - k个} {e（电子）}^{我 η (j个 - 1) 小时}) + 4 (Υ^{n个 - k个 + 1} {e（电子）}^{我 η (j个) 小时} - Υ^{n个 - k个} {e（电子）}^{我 η (j个) 小时}) \\ + (Υ^{n个 - k个 + 1} {e（电子）}^{我 η (j个 + 1) 小时} - Υ^{n个 - k个} {e（电子）}^{我 η (j个 + 1) 小时})) / 6] . \end{array}

\begin{array}{l} Υ^{k个 + 1} [{e（电子）}^{我 η (j个 - 1) 小时} (α_{0}) + {e（电子）}^{我 η (j个) 小时} (α_{1}) + {e（电子）}^{我 η (j个 + 1) 小时} (α_{0})] \\ = Υ^{k个} [{e（电子）}^{我 η (j个 - 1) 小时} ({n个}_{1}) + {e（电子）}^{我 η (j个) 小时} ({n个}_{2}) \\ + {e（电子）}^{我 η (j个 + 1) 小时} ({n个}_{三})] - \frac{1}{1296} {({T型}_{米})}^{4} + （f） (第页, 吨) \\ - \sum_{k个 = 1}^{n个 - 1} λ_{k个}^{α} [(Υ^{n个 - k个 + 1} {e（电子）}^{我 η (j个 - 1) 小时} - γ^{n个 - k个} {e（电子）}^{我 η (j个 - 1) 小时} \\ + 4 Υ^{n个 - k个 + 1} {e（电子）}^{我 η (j个) 小时} - 4 Υ^{n个 - k个} {e（电子）}^{我 η (j个) 小时} + γ^{n个 - k个 + 1} {e（电子）}^{我 η (j个 + 1) 小时} \\ - Υ^{n个 - k个} {e（电子）}^{我 η (j个 + 1) 小时}) / 6] . \end{array}

\begin{array}{l} Υ^{k个 + 1} = \frac{Υ^{k个} {e（电子）}^{我 η (j个) 小时} [{e（电子）}^{- 我 η 小时} ({n个}_{1}) + {n个}_{2} + {e（电子）}^{我 η 小时} ({n个}_{三})] - \frac{1}{1296} {({T型}_{米})}^{4} {e（电子）}^{- 我 η j个 小时} + （f） (第页, 吨) {e（电子）}^{- 我 η j个 小时}}{{e（电子）}^{我 η (j个) 小时} [{e（电子）}^{- 我 η 小时} (α_{0}) + α_{1} + {e（电子）}^{我 η 小时} (α_{0})]} \\ - \frac{\sum_{k个 = 1}^{n个 - 1} λ_{k个}^{α} [Υ^{n个 - k个 + 1} {e（电子）}^{我 η j个 小时} ({e（电子）}^{- 我 η 小时} + 4 + {e（电子）}^{我 η 小时}) - Υ^{n个 - k个} {e（电子）}^{- 我 η j个 小时} ({e（电子）}^{- 我 η 小时} + 4 + {e（电子）}^{我 η 小时})]}{{e（电子）}^{我 η (j个) 小时} [{e（电子）}^{- 我 η 小时} (α_{0}) + α_{1} + {e（电子）}^{我 η 小时} (α_{0})]} . \end{array}

通过插入α值₀, α₁和n个₁,n个₂,n个_三在上面的表达式中，我们有

\begin{array}{l} Υ^{k个 + 1} = \frac{Υ^{k个} [\frac{γ}{三} (余弦 η 小时 + 三) + \frac{1}{6 {小时}^{2}} (余弦 η 小时 - 6) + \frac{1}{6} (余弦 η 小时 + 2)] - \frac{1}{1296} {({T型}_{米})}^{4} {e（电子）}^{- 我 η j个 小时}}{\frac{γ}{三} (余弦 η 小时 + 三) - \frac{1}{6 {小时}^{2}} (余弦 η 小时 - 6) - \frac{1}{6} (余弦 η 小时 + 2) + \frac{三}{216} {({T型}_{米})}^{2} (余弦 η 小时 + 三)} \\ + \frac{（f） (第页, 吨) {e（电子）}^{- 我 η j个 小时} - \sum_{k个 = 1}^{n个 - 1} λ_{k个}^{α} [2 余弦 η 小时 + 4 (γ^{n个 - k个 + 1} - Υ^{n个 - k个})]}{\frac{γ}{三} (余弦 η 小时 + 三) - \frac{1}{6 {小时}^{2}} (余弦 η 小时 - 6) - \frac{1}{6} (余弦 η 小时 + 2) + \frac{三}{216} {({T型}_{米})}^{2} (余弦 η 小时 + 三)} . \end{array}

如果增大因子|γ，应用的方案是稳定的^k个+1|≤1，并且，从上述表达式中，我们可以观察到，对于γ、η、，小时.随着近似值的增大，该方案变得不稳定。

Υ^{k个 + 1} \leq Υ^{k个},

Υ^{k个 + 1} \leq 1 .

因此，上述结果反映了该方案是无条件稳定的。

5.应用和讨论

本节给出了一些具有不同初始和边界条件的示例。数值结果以图形和数字的形式显示在图表中。误差标准我²和我^∞计算以分析建议技术的精度

\begin{array}{l} 我^{2} = ∥ {Z轴}_{e（电子） x个 一 c（c） 吨} - {Z轴}_{一 第页 第页 第页 o个 x个} ∥_{2} ≃ \sqrt{小时 \sum_{j个 = 0}^{n个} | {({Z轴}_{j个})}_{e（电子） x个 一 c（c） 吨} - {({Z轴}_{j个})}_{一 第页 第页 第页 o个 x个} |^{2}}, \end{array}

\begin{array}{l} 我^{\infty} = ∥ {Z轴}_{e（电子） x个 一 c（c） 吨} - {Z轴}_{一 第页 第页 第页 o个 x个} ∥_{\infty} ≃ 米 一 {x个}_{j个} ∣ {({Z轴}_{j个})}_{e（电子） x个 一 c（c） 吨} - {({Z轴}_{j个})}_{一 第页 第页 第页 o个 x个} ∣ . \end{array}

在这份手稿中，我们使用了MATLAB 2015b英特尔^对核心^TM公司我5个CPU，8GB RAM和64位操作系统（窗口7），用于数值模拟。

示例5.1。考虑β=3的分数阶Fisher方程（1.1）

\begin{array}{l} \frac{\partial^{α} Z轴 (第页, 吨)}{\partial 吨^{α}} - ν \frac{\partial^{2} Z轴 (第页, 吨)}{\partial {第页}^{2}} - Z轴 (第页, 吨) (1 - {Z轴}^{三} (第页, 吨)) = （f） (第页, 吨) . & (5.1) \end{array}

\begin{array}{l} 我 C类 : Z轴 (第页, 0) = 0, 0 \leq 第页 \leq 1 . \end{array}

\begin{array}{l} B类 C类 秒 : Z轴 (0, 吨) = 吨^{2 α}, Z轴 (1, 吨) = 0, 吨 \geq 0 . \end{array}

和源项

\begin{array}{l} \begin{array}{r} （f） (第页, 吨) = 经验 (2 第页) (1 - {第页}^{2}) 吨^{α} \frac{Γ (2 α + 1)}{Γ (1 + α)} - 2 ν 吨^{2 α} (1 - 4 第页 - 2 {第页}^{2}) 经验 (2 第页) \\ - [吨^{2 α} (1 - {第页}^{2}) 经验 (2 第页)] [1 - {(吨^{2 α} (1 - {第页}^{2}) 经验 (2 第页))}^{三}] . \end{array} \end{array}

近似解（2.3）可以以分段形式写成：

\begin{array}{l} Z轴 (第页, 吨_{n个}) = Υ_{j个 - 三} ϕ_{三, j个 - 三} (第页) + Υ_{j个 - 2} ϕ_{三, j个 - 2} (第页) \\ + Υ_{j个 - 1} ϕ_{三, j个 - 1} (第页) + Υ_{j个} ϕ_{三, j个} (第页), 第页 \in [{第页}_{j个}, {第页}_{j个 + 1}) . & (5.2) \end{array}

\begin{array}{l} {Z轴}_{N个} (第页, 1) = {\begin{matrix} {第页}^{三} - 0.64 {第页}^{2} - 0.805 第页 + 0.99997, 第页 \in [0, 0.1), \\ 0.56667 {第页}^{三} - 0.51 {第页}^{2} - 0.818 第页 + 1.0004, 第页 \in [0.1, 0.2), \\ 16.75 {第页}^{三} - 10.22 {第页}^{2} + 1.124 第页 + 0.87093, 第页 \in [0.2, 0 . 三), \\ 0.11667 {第页}^{三} - 0.195 {第页}^{2} - 0.8945 第页 + 1.0068, 第页 \in [0 . 三, 0.4), \\ - 0.033333 {第页}^{三} - 0.015 {第页}^{2} - 0.9665 第页 + 1.0165, 第页 \in [0.4, 0.5), \\ - 0.066667 {第页}^{三} + 0.035 {第页}^{2} - 0.9915 第页 + 1.0206, 第页 \in [0.5, 0.6), \\ - 0.05 {第页}^{三} + 0.005 {第页}^{2} - 0.9735 第页 + 1.017, 第页 \in [0.6, 0.7), \\ - 0.033333 {第页}^{三} - 0.03 {第页}^{2} - 0.949 第页 + 1.0113, 第页 \in [0.7, 0.8), \\ - 3546.6 {第页}^{三} + 8511.7 {第页}^{2} - 6810 . 三 第页 + 1816.8, 第页 \in [0.8, 0.9), \\ 10640.0 {第页}^{三} - 29793.0 {第页}^{2} + 27664.0 第页 - 8525.4, 第页 \in [0.9, 1) . \end{matrix} & (5.3) \end{array}

（5.1）的精确解为Z轴(r、 t吨)=吨^2α(1 −第页²)经验（2第页).

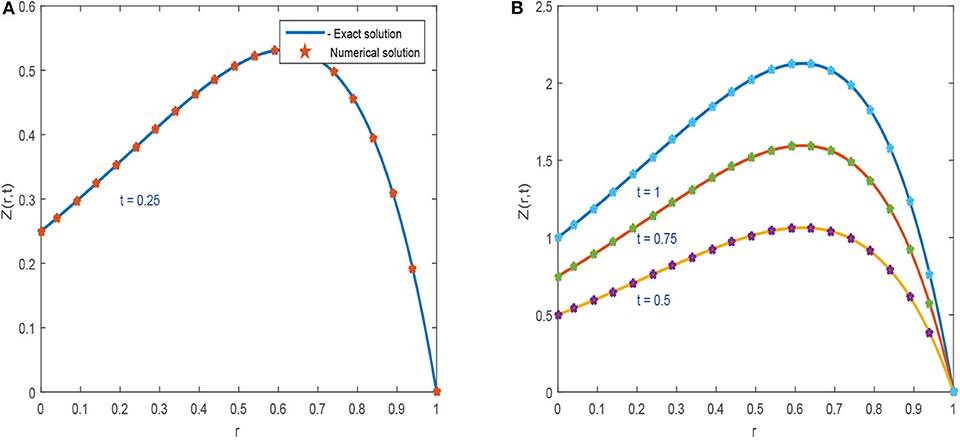
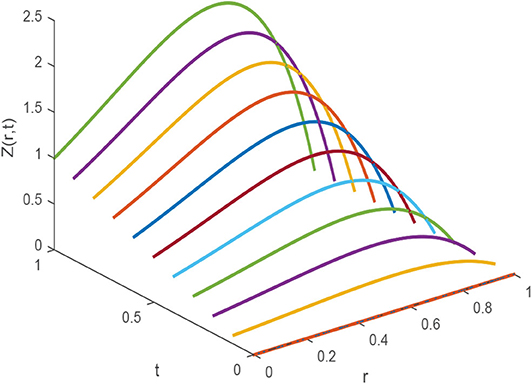
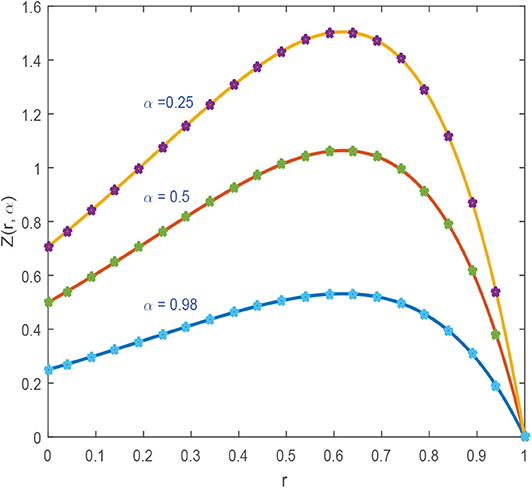
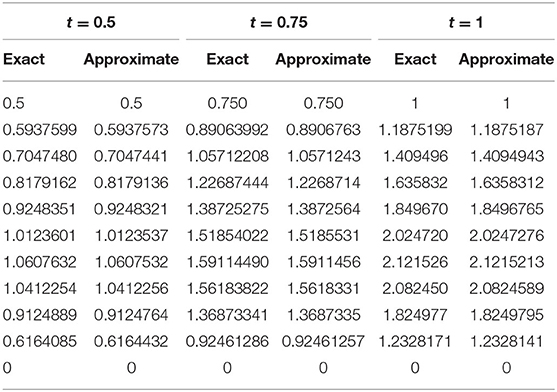
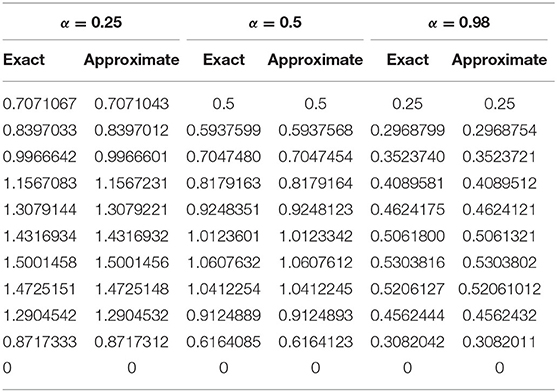
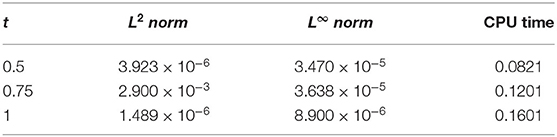
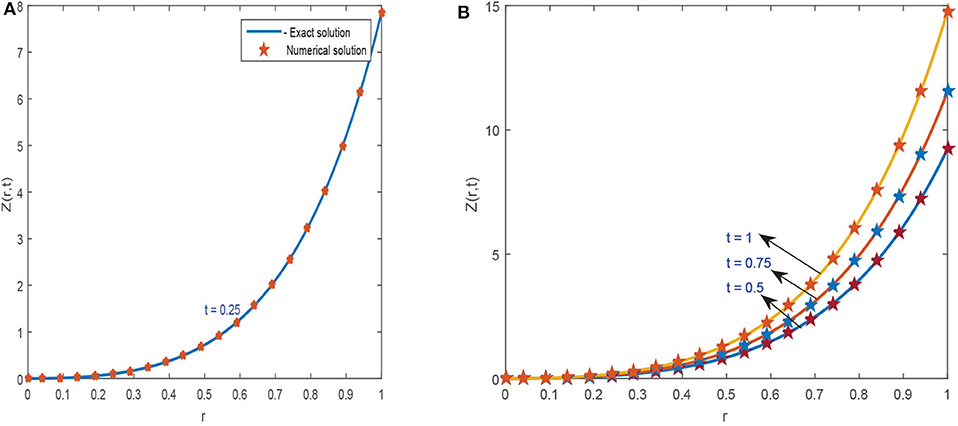
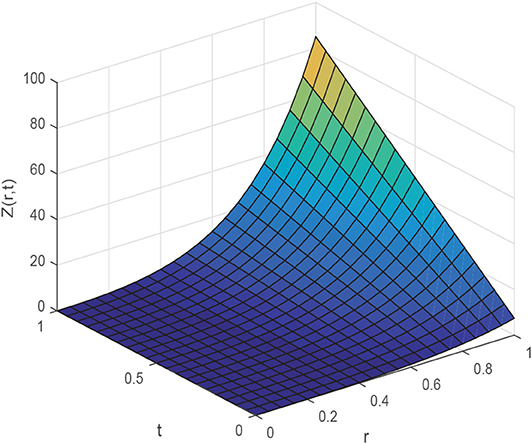
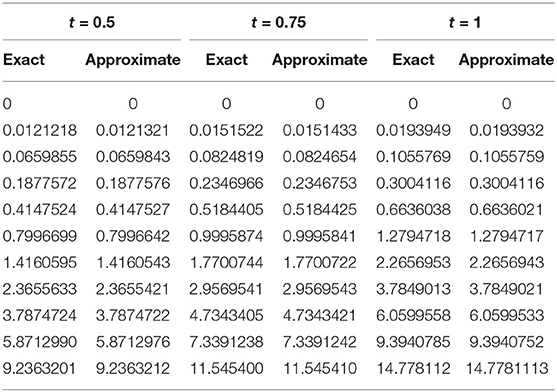
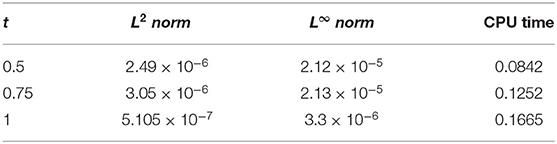
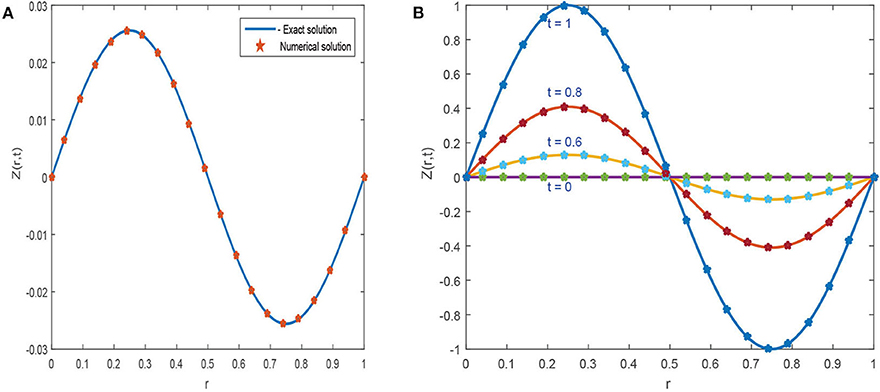
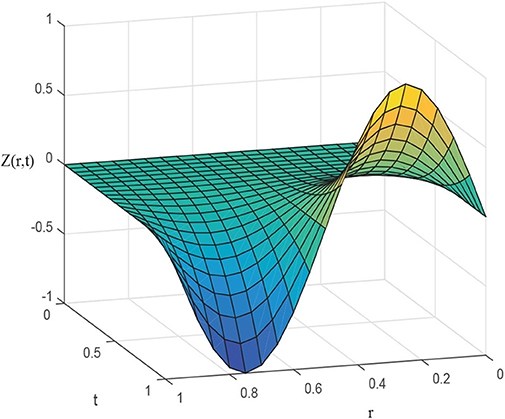
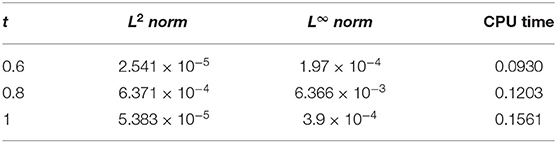
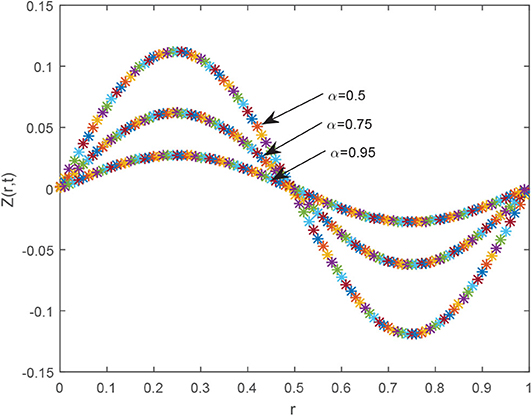
图1,2探索了对于不同参数，CBS解与实施例5.1的精确解的比较。图1A显示了的近似和精确结果的二维预览吨=0.25，α=0.95，小时= 0.01, Δ吨=0.0003和ν=1。该图表明，精确结果和近似结果不分青红皂白地相似。图1B引用方程式（5.1）的解的作用，α=0.95，小时=0.01，ν=1，对于各种时间步长吨=0.5、0.75和1，Δ吨= 0.0003. 从图中可以清楚地看出，这两种解决方案是重叠的。三维预览已在中给出图2虽然已经讨论了α对不同布朗运动的影响，即α=0.25、0.5和0.98 in图3可以观察到，随着α值的增加，解的轮廓减小，并且随着α→1，数值解往往与精确解重叠。数值结果和精确结果的比较表示为表2，这表明两个结果相互一致，精确到小数点后5位。α变化的数值结果如所示表3。从表格数据中可以清楚地看出，两个结果彼此非常一致，并且通过中所示的误差规范检查了方案的准确性表4.

图1

图1.实施例5.1在不同时间水平下α=0.95，ν=1，Δ的近似结果吨=0.0003，以及小时= 0.01.（A）对于吨= 0.25.（B）对于吨=0.5、0.75和1。

图2

图2示例5.1数值解的3D图像tϵ[0, 1], α = 0.25, ν = 1, Δ吨=0.0003，以及小时= 0.01.

图3

图3.对于α=0.25、0.5、，和0.98, ν = 1, Δ吨=0.0003，以及小时= 0.01.

表2

表2示例5.1不同时间水平的结果比较。

表3

表3.实例5.1在不同α和α值下的结果比较吨= 0.5.

表4

表4示例5.1的误差范数的计算。

例5.2。β=3的分数阶Fisher方程（1.1）可以写成：

\begin{array}{l} \frac{\partial^{α} Z轴 (第页, 吨)}{\partial 吨^{α}} - ν \frac{\partial^{2} Z轴 (第页, 吨)}{\partial {第页}^{2}} - Z轴 (第页, 吨) (1 - {Z轴}^{三} (第页, 吨)) = （f） (第页, 吨) . & (5.4) \end{array}

具有

\begin{array}{l} 我 C类 : Z轴 (第页, 0) = {第页}^{2} 经验 (2 第页), 0 \leq 第页 \leq 1 . \end{array}

\begin{array}{l} B类 C类 秒 : Z轴 (0, 吨) = 0, Z轴 (1, 吨) = 经验 (2) (1 + 吨^{2}), 吨 \geq 0 . \end{array}

源项为

\begin{array}{l} \begin{array}{r} （f） (第页, 吨) = \frac{2 {第页}^{2} 吨^{2 - α} 经验 (2 第页)}{Γ (三 - α)} - 2 ν (1 + 吨^{2}) (1 + 4 第页 + 2 {第页}^{2}) 经验 (2 第页) \\ - [(1 + 吨^{2}) {第页}^{2} 经验 (2 第页)] [1 - {((1 + 吨^{2}) {第页}^{2} 经验 (2 第页))}^{三}] . \end{array} \end{array}

例5.2的精确解为Z轴(r、 t吨) = (1 +吨²)第页²经验（2第页).图4,5绘制示例5.2精确和近似解的二维和三维预览。图中所示图4A证明了近似解吨= 0.25, α = 0.95,小时= 0.01, Δ吨=0.0003，且v=1与精确解相容。图4B显示了各种时间步长的效果吨=0.5、0.75和1。从图中可以清楚地看出，对于固定值α=0.95，精确解和数值解具有相同的行为。精确结果和近似结果的比较见表5这清楚地表明，这两个解决方案彼此非常接近，误差可以忽略不计。图5给出近似解的3D预览。为了检验当前技术的准确性，计算了误差范数并显示在表6.

图4

图4.实施例5.2在不同时间水平下α=0.95，ν=1，Δ的近似结果吨=0.0003，以及小时= 0.01.（A）对于吨= 0.25.（B）对于吨=0.5、0.75和1。

图5

图5示例5.2数值解的3D预览tϵ[0, 1], α = 0.95, ν = 1, Δ吨=0.0003，以及小时= 0.01.

表5

表5示例5.2的数值结果。

表6

表6例5.2的误差标准。

近似解（2.3）可以分段书写：

\begin{array}{r} Z轴 (第页, 吨_{n个}) = Υ_{j个 - 三} ϕ_{三, j个 - 三} (第页) + γ_{j个 - 2} ϕ_{三, j个 - 2} (第页) + Υ_{j个 - 1} ϕ_{三, j个 - 1} (第页) \\ + γ_{j个} ϕ_{三, j个} (第页), 第页 \in [{第页}_{j个}, {第页}_{j个 + 1}) . & (5.5) \end{array}

\begin{array}{l} {Z轴}_{N个} (第页, 1) = {\begin{array}{l} - 5.4667 {第页}^{三} + 0.9700 {第页}^{2} + 14.08 第页 + 0.000033333, 第页 \in [0, 0.1), \\ - 4.2667 {第页}^{三} + 0.61 {第页}^{2} + 14.116 第页 - 0.0011667, 第页 \in [0.1, 0.2), \\ - 221.05 {第页}^{三} + 130.68 {第页}^{2} - 11.898 第页 + 1.7331, 第页 \in [0.2, 0 . 三), \\ - 1.4667 {第页}^{三} - 1.395 {第页}^{2} + 14.614 第页 - 0.04415, 第页 \in [0 . 三, 0.4), \\ 5.35 {第页}^{三} - 9.575 {第页}^{2} + 17.887 第页 - 0.48042, 第页 \in [0.4, 0.5), \\ - 1.6333 {第页}^{三} + 0.9 {第页}^{2} + 12.649 第页 + 0.3925, 第页 \in [0.5, 0.6), \\ 56.233 {第页}^{三} - 103.26 {第页}^{2} + 75.145 第页 - 12.107, 第页 \in [0.6, 0.7), \\ - 104.25 {第页}^{三} + 233.76 {第页}^{2} - 160.77 第页 + 42.939, 第页 \in [0.7, 0.8), \\ 587.43 {第页}^{三} - 1426 . 三 {第页}^{2} + 1167 . 三 第页 - 311.2, 第页 \in [0.8, 0.9), \\ - 1846.6 {第页}^{三} + 5145.5 {第页}^{2} - 4747.4 第页 + 1463.2, 第页 \in [0.9, 1) . \end{array} & (5.6) \end{array}

示例5.3。对于β=2，时间分数费希尔方程变为

\begin{array}{l} \frac{\partial^{α} Z轴 (第页, 吨)}{\partial 吨^{α}} - ν \frac{\partial^{2} Z轴 (第页, 吨)}{\partial {第页}^{2}} - Z轴 (第页, 吨) (1 - {Z轴}^{2} (第页, 吨)) = （f） (第页, 吨) . & (5.7) \end{array}

\begin{array}{l} 我 C类 : Z轴 (第页, 0) = 0, 0 < 第页 < 1, \end{array}

\begin{array}{l} B类 C类 秒 : Z轴 (0, 吨) = 0, Z轴 (1, 吨) = 0, 吨 \geq 0 . \end{array}

源项

\begin{array}{r} （f） (第页, 吨) = \frac{24 吨^{4 - α}}{Γ (5 - α)} 罪 (2 π 第页) \\ + 4 π^{2} 吨^{4} 罪 (2 π 第页) - (吨^{4} 罪 (2 π 第页)) (1 - 吨^{4} 罪 (2 π 第页)) . \end{array}

上述条件的精确解为

\begin{array}{l} Z轴 (第页, 吨) = 吨^{4} 罪 (2 π 第页) . \end{array}

因此，近似解（2.3）可以分段书写：

\begin{array}{r} Z轴 (第页, 吨_{n个}) = Υ_{j个 - 三} ϕ_{三, j个 - 三} (第页) + Υ_{j个 - 2} ϕ_{三, j个 - 2} (第页) \\ + Υ_{j个 - 1} ϕ_{三, j个 - 1} (第页) + Υ_{j个} ϕ_{三, j个} (第页), 第页 \in [{第页}_{j个}, {第页}_{j个 + 1}) . & (5.8) \end{array}

\begin{array}{l} {Z轴}_{N个} (第页, 1) = {\begin{array}{l} - 17815.0 {第页}^{三} + 3562.9 {第页}^{2} + 0.008 第页 - 23.753, 第页 \in [0, 0.1), \\ 5938.2 {第页}^{三} - 3562.9 {第页}^{2} + 712.59 第页 - 47.506, 第页 \in [0.1, 0.2), \\ 0.033333 {第页}^{三} - 0.045 {第页}^{2} + 0.0195 第页 - 0.00085, 第页 \in [0.2, 0 . 三), \\ - 0.025 {第页}^{2} + 0.0155 第页 - 0.00058333, 第页 \in [0 . 三, 0.4), \\ 1490 . 三 {第页}^{三} - 1788.4 {第页}^{2} + 715.36 第页 - 95.38, 第页 \in [0.4, 0.5), \\ - 4470.7 {第页}^{三} + 7153.2 {第页}^{2} - 3755.4 第页 + 649.75, 第页 \in [0.5, 0.6), \\ 4470.8 {第页}^{三} - 8941.7 {第页}^{2} + 5901.5 第页 - 1281.6, 第页 \in [0.6, 0.7), \\ - 1490.1 {第页}^{三} + 3576.4 {第页}^{2} - 2861.1 第页 + 762.98, 第页 \in [0.7, 0.8), \\ 0.016667 {第页}^{三} + 0.005 {第页}^{2} - 0.0425 第页 + 0.020917, 第页 \in [0.8, 0.9), \\ - 0.033333 {第页}^{三} + 0.14 {第页}^{2} - 0.164 第页 + 0.057367, 第页 \in [0.9, 1) . \end{array} & (5.9) \end{array}

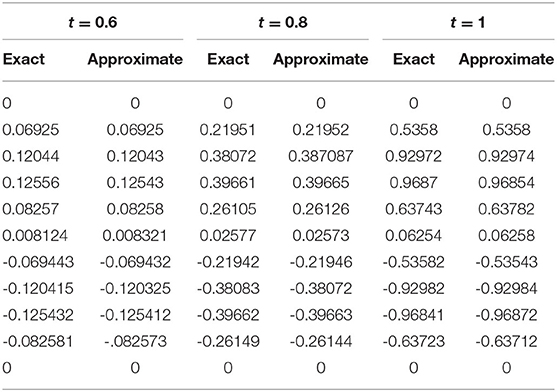
图6A，显示示例5.3的数值和精确解吨= 0.4, α = 0.96,小时=0.01和Δ吨= 0.0001. 这些图形表明，数值解和精确解显然可以不加区分地相互比较。时间浓度的影响吨=0.6、0.8和1在图6B保持其他参数不变。从图中可以看出，这两种解决方案都具有对称的行为，其相应的数值数据显示在表7这表明两个结果都是准确的，误差可以忽略不计。图7图中给出了三维解和误差范数结果表8.

图6

图6.实施例5.3在α=0.96，ν=1时时间变化的数值解，小时= 0.01, Δ吨=0.0001，β=1。（A）对于吨= 0.25.（B）对于吨=0、0.5、0.75和1。

表7

表7在不同时间段比较实施例5.3的准确结果和数值结果。

图7

图7示例5.3近似结果的3D图像tϵ[0,1]，α=0.96，步长小时= 0.01, Δ吨=0.0001，ν=1。

表8

表8实施例5.3的误差标准的比较。

布朗运动（即α=0.25，0.75）对溶液曲线的影响如所示图8解曲线的相同行为表明，对于较小的α值，解轮廓远离精确结果，并且当α→1时，近似解和精确解趋于重叠。

图8

图8.实施例5.3中α=0.5，0.75的近似结果和0.95,小时= 0.01, Δ吨=0.0001，ν=1。

示例5.4。β=1的分数阶Fisher方程（f）(r、 t吨)=0，是

\begin{array}{l} \frac{\partial^{α} Z轴 (第页, 吨)}{\partial 吨^{α}} - ν \frac{\partial^{2} Z轴 (第页, 吨)}{\partial {第页}^{2}} - Z轴 (第页, 吨) (1 - Z轴 (第页, 吨)) = （f） (第页, 吨) . & (5.10) \end{array}

\begin{array}{l} w个 我 吨 小时 我 C类 : Z轴 (第页, 0) = σ^{*}, 0 \leq 第页 \leq 1 . \end{array}

α=1时模型的精确解为，

Z轴 (第页, 吨) = \frac{经验 (吨) σ^{*}}{1 - σ^{*} + σ^{*} 经验 (吨)} .

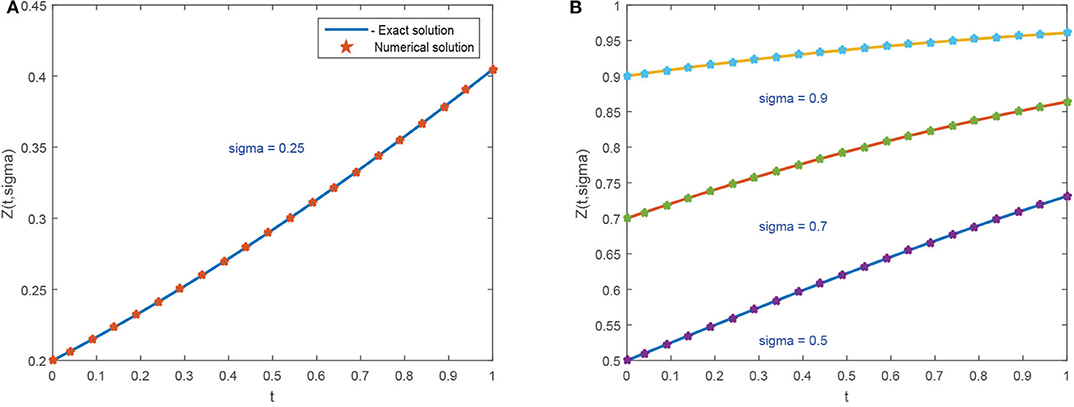
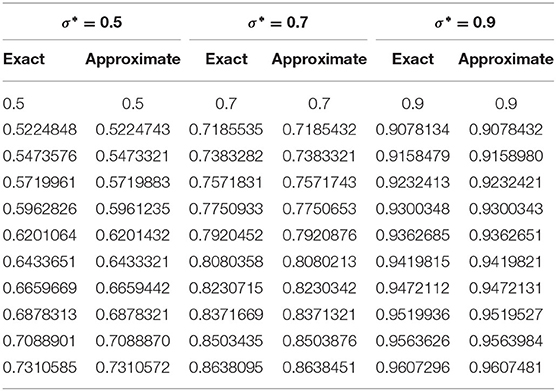
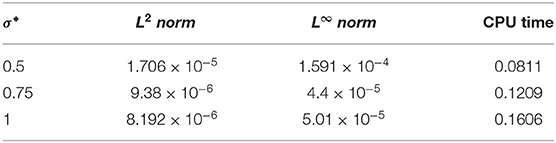
示例5.4的精确和数值解的图解如所示图9.图9A显示精确结果和数值结果的兼容性小时= 0.01, Δ吨=0.02，α=1，σ^*= 0.25. 各种σ值的精确解和数值解的多重曲线^*=0.5、0.7和0.9如所示图9B。建议方案获得的精确解和近似解的比较表示为表9表中数据表明，对于不同的σ值，这两种解决方案彼此兼容^*.表10演示了错误规范。

图9

图9示例5.4中各种σ值的数值结果^*α=1，Δ吨=0.02，以及小时= 0.01.（A）对于σ^*= 0.25.（B）对于σ^*=0.5、0.7和0.9。

表9

表9示例5.4在不同σ值下的精确数值结果^*.

表10

表10.误差标准的比较。

6.结束语

在本研究中，成功地实现了三次B样条（CBS）格式，以获得β=2和3的时间分数修正Fisher方程的数值解。时间导数在卡普托意义下通过以下方式离散化我1公式，而CBS函数用于空间导数。该方案获得的结果以表格和图形的形式呈现。以下是本研究的主要结果。

1.通过增加源项和增加非线性项的整数幂，对现有的Fisher模型进行了修改。

2.研究了不同值下α参数的影响，观察到随着α值的逐渐增加，溶液轮廓Z轴(r、 t吨)倾向于精确解。如图所示，当α接近1时，数值解与精确解重叠。

3.在不同的时间水平上观察了不同初始和边界条件下所提出模型的数值行为。

4.对图形中显示的精确结果和数值结果的比较表明，两个结果都显示出对称行为，表中显示的相应数值数据清楚地说明了结果的一致性。

5.关于所提出方案稳定性的研究结果表明，所提出的方案是无条件稳定的。

此外，通过计算误差范数量化了该方案的精度和效率，数值结果表明该方案适用于非线性时间分数阶广义Fisher方程。

作者贡献

列出的所有作者都对这部作品做出了实质性、直接和智力上的贡献，并批准出版。

利益冲突

作者声明，该研究是在没有任何可能被解释为潜在利益冲突的商业或金融关系的情况下进行的。

审稿人HS向处理编辑宣布，他曾与其中一位作者JS合著。

工具书类

1.卡普托·M。Elasticita e Dissipazione弹性体博洛尼亚：Zanichelli（1969）。

2.米勒·KS，罗斯·B。分数微积分与分数微分方程导论纽约州纽约市：Wiley（1993）。

3.廖SJ。同伦分析法：非线性问题的一种新的分析方法。应用数学力学. (1998)19:957–62. doi:10.1007/BF02457955

CrossRef全文|谷歌学者

4.标量E、Gorenflo R、Mainardi F.分数微积分和连续时间金融。物理A. (2000)284:376–84. doi:10.1016/S0378-4371（00）00255-7

CrossRef全文|谷歌学者

5.West BJ、Turalskal M、Grigolini P。分数阶微积分将复杂网络动力学的微观和宏观尺度联系在一起。新J Phy（2015年）17：045009.网址：10.1088/1367-2630/17/4/045009

CrossRef全文|谷歌学者

6.塔拉索夫VE。分数向量微积分和分数麦克斯韦方程。Ann Phys公司. (2008)323:2756–78. doi:10.1016/j.aop.2008.04.005

CrossRef全文|谷歌学者

7.Rossa J、Villaverdeb AF、Bangab JR、Vazquezc S、Moranc F.广义Fisher方程及其在化学动力学中的应用。《美国科学院院刊》. (2010)107:12777–81. doi:10.1073/pnas.1008257107

PubMed摘要|CrossRef全文|谷歌学者

8.阿默曼AJ，Cavalli-Sforza LL。欧洲新石器时代的变迁与人口遗传学新泽西州普林斯顿：普林斯顿大学出版社（1984）。

PubMed摘要|谷歌学者

9.科克虚拟机。流行病和细菌研究中Fisher方程变体的结果。物理A.（2004年）342:242–8. doi:10.1016/j.physa.2004.04.084

CrossRef全文|谷歌学者

10.费希尔RA。优势基因的发展浪潮。安·尤根. (1937)7:355–69. 文件编号：10.1111/j.1469-1809.1937.tb02153.x

CrossRef全文|谷歌学者

11.波德鲁布尼一世。分数微分方程，科学与工程数学卷198加州圣地亚哥：学术出版社（1999）。

12.Odibat Z.分数积分和caputo分数导数的近似。应用数学计算. (2006)178:527–33. doi:10.1016/j.amc.2005.11.072

CrossRef全文|谷歌学者

13.Baleanu D、Diethelm K、Scalas E、Trujillo JJ。分数阶微积分模型和数值方法，复杂性、非线性和混沌系列丛书第3卷新加坡：《世界科学》（2012）。

谷歌学者

14.Baranwal VK，Pandey RK，Tripathi MP，Singh OP。基于新迭代方法的时间分数阶非线性反应扩散方程的分析算法。Commun Nonlin科学数字模拟. (2012)17：3906–21。doi:10.1016/j.cnsns.2012.02.015

CrossRef全文|谷歌学者

15.Yang XJ，Machado JAT，Baleanu D.扩展Mittag-Lefler型函数核内具有一般分数导数的反常扩散模型。罗马代表Phys（2017年）69：120.网址：http://hdl.handle.net/20.500.12416/1850

谷歌学者

16.杨旭杰。常阶和变阶分数导数应用于传热问题中的反常松弛模型。热科学（2017年）21:116–71. doi:10.2298/TSCI161216326Y

CrossRef全文

17.杨晓杰，马查多·JAT，卡塔尼·C，高飞。关于局部分数阶微积分建模的分形液晶电路。通用非线性科学数字仿真（2017年）47:200–6. doi:10.1016/j.cnsns.2016.11.017

CrossRef全文|谷歌学者

18.Alaatin E，Ucar Y，Yagmurlu N，Tasbozan O。求解分数阶扩散和分数阶扩散波方程的Galerkin有限元方法。数学模型分析. (2013)18:260–73. doi:10.3846/13926292.2013.783884

CrossRef全文|谷歌学者

19.Rubin SG，格拉夫斯RA。流体力学问题的三次样条逼近华盛顿特区：NASA TR R-436（1975）。

谷歌学者

20.Wazwaz AM，Gorguis A.使用Adomian分解方法对Fishers方程进行分析研究。应用数学计算. (2004)154:609–20. doi:10.1016/S0096-3003（03）00738-0

CrossRef全文|谷歌学者

21.Abedle-Rady AS，Rida SZ，Arafa AAM，Adedl-Rahim HR.使用同伦摄动Sumudu变换方法的分数阶非线性色散方程的近似解析解。国际J Innov科技. (2014)19:257–67.

谷歌学者

22.阿拉斯加州古普塔，Ray SS。用两种可靠的方法研究分数阶Burgers-Fisher方程和广义Fishers方程的解。国际数学与数学科学杂志. (2014)2014：682910.doi:10.1155/2014/682910

CrossRef全文|谷歌学者

23.Cherif MH，Belghaba K，Zaine D.求解分数阶Fishers方程的同伦摄动方法。国际分析应用. (2016)101:916.

谷歌学者

24.Khader MM，Saad KM。使用Chebyshev谱配置方法求解分数阶Fisher方程的一种数值方法。混沌孤立分形. (2018)110：169177.doi:10.1016/j.chaos.2018.03.018

CrossRef全文|谷歌学者

25.Rawashdeh MS。分数自然分解法：理论和应用。数学方法应用科学. (2016)40:2362–76. doi:10.1002/mma.4144

CrossRef全文|谷歌学者

26.Singh H.天体物理学中非线性Lane-Emden型方程近似解的一种有效计算方法。天体物理学空间科学. (2018)363：71.doi:10.1007/s10509-018-3286-1

CrossRef全文|谷歌学者

27.Singh H.使用Jacobi多项式近似求解分数阶振动方程。应用数学计算. (2018)317:85–100. doi:10.1016/j.amc.2017年8月17日57

CrossRef全文|谷歌学者

28.Majeed A、Piah ARM、Rafique M、Abdullah JY、Rajion ZA。NURBS曲线与多骨骨折重建的应用。应用数学计算（2017年）315:70–84. doi:10.1016/j.amc.2017.05.061

CrossRef全文|谷歌学者

29.Singh J，Kumar D，Swroop R.利用同伦算法求解时空分数耦合Burgers方程。亚历克斯·恩格·J. (2016)552:1753–63. doi:10.1016/j.aej.2016.03.028

CrossRef全文|谷歌学者

30.Najeeb AK，Ayaz F，Jin L，Ahmet Y。关于Fisher型时间分式反应扩散方程的近似解。国际物理科学杂志. (2011)6:2483–96.

谷歌学者

31.Sayevand K，Yazdani A，Arjang F.三次B样条配置法及其在输运动力学系统中反常分数扩散方程中的应用。J可控震源控制. (2016)22:2173–86. doi:10.1177/10775463166282

CrossRef全文|谷歌学者

32.Dag I，Irk D，Saka B.使用三次B样条曲线对Burgers方程进行数值求解。应用数学计算. (2005)163:199–211. doi:10.1016/j.amc.2004.01.028

CrossRef全文|谷歌学者

关键词：三次B样条（CBS）配置方案，时间分数修正Fisher方程，Caputo导数，稳定性分析，误差范数

引用：Majeed A、Kamran M、Abbas M和Singh J（2020）《求解时间分段广义Fisher方程的高效数值技术》。前面。物理学。8:293. doi:10.3389/fphy.2020.00293

收到：2020年3月17日；认可的：2020年6月29日；
出版：2020年10月8日。

编辑：

杨晓军中国矿业大学

审核人：

哈西·穆罕默德·巴斯科努斯土耳其哈伦大学
哈伦德拉·辛格印度理工大学

*通信：穆罕默德·阿巴斯，muhammad.abbas@uos.edu.pk

原创研究文章

求解时间分数广义Fisher方程的一种有效的数值方法

1.简介

2.方法说明

3.初始向量

4.稳定性分析

5.应用和讨论

6.结束语

作者贡献

利益冲突

工具书类

本文是研究主题的一部分

人们还关注