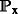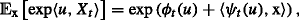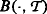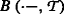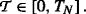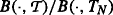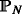具有多条曲线的仿射伦敦银行同业拆借利率模型的连续期限扩展及其在XVA中的应用

摘要

我们考虑一类具有多条曲线的仿射LIBOR模型，这是一类易于分析处理的离散期限模型，很容易适应正利率或负利率和正利差。通过引入插值函数，我们将仿射LIBOR模型推广到连续期限，并推导了瞬时远期利率和短期利率的表达式。我们证明了连续期限模型是无套利的，在即期鞅测度下保持了分析的可跟踪性，并且在温和的条件下可以找到一个插值函数，使得扩展模型适合于任何初始向前曲线。这使我们能够通过求解相应的“预设”BSDE来一致地计算值调整（即XVA）。作为应用，我们计算了基差互换的价格和价值调整，并研究了与不同插值函数相关的模型风险。

介绍

在信贷危机和欧洲主权债务危机之后，一些经典的金融范式不再能够描述新的现实，需要重新设计。一方面，不同期限的利率之间出现了显著的利差，这导致了多曲线利率模型的发展。另一方面，交易对手信用风险与流动性风险、融资约束和交易抵押一起，已成为违约风险的固有形式。因此，在危机后市场中，衍生产品的报价（或者更好地说，其对冲投资组合的成本）计算为产品的“干净”价格，以及反映交易对手信用风险、流动性风险、融资约束等的若干价值调整。在利率衍生产品的背景下，“干净”价格通常是使用（离散期限）伦敦银行同业拆借利率（LIBOR）市场模型在鞅测度下计算的折现预期收益，而价值调整是通过BSDE的解决方案提供的，该解决方案要求存在短期利率来对现金流进行折现。

这项工作的目的是一致地计算价格和价值调整，从这个意义上说，我们只校准了离散期限的伦敦银行同业拆借利率模型，然后从中推断出短期利率的动态，而不是求助于额外的外部短期利率模型。在续集中，我们将使用具有多条曲线的仿射LIBOR模型类。这类模型很容易产生正利率和正息差，以及负利率和正利差。此外，从驱动过程在所有远期措施下保持密切关系的角度来看，这些模型在分析上是可处理的，这允许推导出资本头寸价格的显式表达式和互换期权的半分析表达式。因此，这些模型可以有效地根据市场数据进行校准；囊性纤维变性。Grbac等人（2015）了解更多详细信息。

一旦建立了仿射LIBOR模型，我们引入了一个插值函数，允许将模型从离散期限扩展到连续期限，并导出了瞬时远期利率和短期利率的动力学显式表达式。本部分遵循并延伸Keller Ressel（2009），而最近由Cuchiero等人（2016）此外，我们还证明了所得的连续期限模型是无套利的，并且属于仿射期限结构模型。让我们提一下，相反，“经典”LIBOR市场模型的无套利插值是一项具有挑战性的任务；参见示例。，贝弗里奇和乔希（2012）此外，我们证明了在点鞅测度下，驱动过程仍然是仿射过程，因此在该测度下，短速率也是解析可解的。插值函数的选择并不是无害的，因为它可能会导致短期利率的不良行为；例如，它可能在固定的时间引发跳跃。因此，我们研究了（离散期限）仿射LIBOR模型和插值函数应该具有什么性质才能避免这种情况。特别地，我们证明了在温和的假设下，存在一个插值函数，使得扩展模型可以拟合任何初始正向曲线。

然后，我们可以使用Crépey框架通过“预设”BSDE的解计算价值调整(2015年a,b条). 作为一个例子，我们设计并校准了一个仿射LIBOR模型，并考虑了一个简单的危机后利率衍生品，即基差互换。使用上述方法，我们使用插值函数推导了短期利率和基差互换的动态，并计算了不同规格合同的价值调整。由于插值函数的选择仍然是任意的，我们研究了与不同选择相关的模型风险。

本文组织如下：“上的仿射进程\（{\mathbb{R}}_{\geqslate 0}^{d}\）“审查仿射流程和节”具有多条曲线的仿射LIBOR模型“介绍了多曲线市场和仿射LIBOR模型的概述。章节“仿射LIBOR模型的连续期限扩展重点研究了仿射伦敦银行同业拆借利率模型的连续期限扩展，并研究了插值函数的性质。最后一节”仿射伦敦银行同业拆借利率模型中XVA的计算“概述了仿射LIBOR模型中价值调整的计算，并讨论了与插值函数选择相关的模型风险。这个附录包含关于仿射过程的时间积分的有用结果。

上的仿射进程\（{\mathbb{R}}_{\geqslate 0}^{d}\）

本节简要概述仿射过程的基本概念和属性。有关证据和更多详细信息，请参阅Duffie等人（2003），英寸Keller Ressel（2008）中的、和菲利波维奇（2005）对于时间不均匀的情况。

让表示Jacod和Shiryaev意义上的完全随机基础(2003，Def.I.1.3），其中\（\mathbb F=（\mathcal{F}（F）_{t} ）_{在[0，t]}中\）和T型∈[0,∞)表示时间范围。在续集中，我们将考虑一个过程X（X）满足以下要求：

假设( \（\mathbb{A}\） )

让是一个保守的、时间同质的、随机连续的马尔可夫过程，取值为\（D=\mathbb{右}_{\geqslate 0}^{d}\）即。，是上的概率测度族\（（\Omega，\mathcal{F}）\）和X（X）=(X（X） _t吨 )_{t吨∈[0,T型]}是一个马尔可夫过程，对于每个x∈天它成立X（X）₀=x，-几乎可以肯定。表示方式期望w.r.t.测度和通过〈·，·〉中的内积\（{\mathbb{R}}^{d}\）.设置

我们假设

• （i） \（0\in\mathcal{我}_{T} ^{\circ}\），其中\（\mathcal I_{T}^{circ}\）表示的内部\（\数学I_｛T｝\）;

• （ii） 条件矩母函数X（X） _t吨 在下面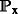对x具有指数依赖性；也就是说，存在函数\（\phi\colon[0，T]\times\mathcal{我}_{T} \rightarrow\mathbb{R}\）和\（\psi\colon[0，T]\times\mathcal{我}_{T} \右箭头{\mathbb{R}}^{d}\）这样的话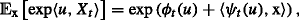

  

  (1)

  为所有人\（（t，u，x）在[0，t]\times\mathcal中{我}_{T} \次D\）。

功能ϕ和ψ满足半流动方程，即，对于所有0≤t吨+秒≤T型和\（u\in\mathcal{我}_{T} \）

$$开始{对齐}\phi{t+s}（u）&=\phi{t}（u）+\phi{s}$$

(2)

具有初始条件

$$\phi_{0}（u）=0\quad\text{和}\quad\\psi_{0{（u$$

使用半流方程，我们可以导出广义Riccati方程

$$\begin{aligned}\frac{\partial}{\partitlet}\phi_{t}（u）&=F（\psi_{tneneneep（u）），\qquad\phi_{0}（u）=0，\\frac{\ partial{{\partict}\psi_{t}[u）&=R（\psi.{t}（u）$$

(3)

对于\（（t，u）\in[0，t]\times\mathcal{我}_{T} \），其中F类和R（右）=(R（右）₁,…,R（右） _d日 )是Lévy–Khintchine形式的函数：

$$\begin{aligned}F（u）&=langle b，u\rangle+\int_{D}\left（\mathrm{e}^{langle\xi，u\rangle}-1\rangle\right）m（\mathrm{D}\xi），\\R{i}（u）&=\langle\beta{i}，u\langle+\left\langleft\frac{\alpha_{i}2u，u\right\rangle+\int_{D}left（\ mathrm m{e}^{langle\xi，u\rangle}-1-\langleu，h{i}（\xi）\rangle\right$$

(4)

同时(b条,米,α _我 ,β _我 ,μ _我 )_{1≤我≤d日}是容许参数-参见中的定义2.6Duffie等人（2003）有关详细信息，以及\（h{i}\colon{\mathbb{右}_{\geqslate 0}}^{d}\rightarrow\mathbb{R}^{d\）是合适的截断函数。满足假设的过程的无穷小生成器(\（\mathbb A\）)由提供

$$\开始｛对齐｝\mathcal{A} （f）（x） &=\left\langle b+\sum\limits_{i=1}^{d}\beta_{i} x个_{i} ，\nabla f（x）\right\rangle+\frac1{2}\sum\limits_{i=1}^{d}\alpha_{i，kl}x_{i} 分形{部分^{2}}{部分x{k}\部分x{l}}f（x）\\&quad+\int_{D}\左（f（x+\xi）-f（x）\右）m（\mathrm{D}\xi gle\right）x{i}\mu{i}（\mathrm{D}\xi），\end{aligned}$$

(5)

为所有人\（C_{0}^{2}（D）中的f\）和x个∈天。

以下引理总结了其他结果。在续集中，不平等必须从组件的角度来理解，即(一₁,一₂)≤(b条₁,b条₂)当且仅当一₁≤b条₁和一₂≤b条₂。

引理1

功能ϕ和ψ满足以下要求：

• 1 ϕ _t吨 (0)=ψ _t吨 （0）=全部为0t吨∈[0,T型].

• 2 \（\mathcal{我}_{T} \）是凸集；此外，对于每个t吨∈[0,T型]、功能u个↦ϕ _t吨 (u个)和u个↦ψ _t吨 (u个)，用于\（u\in\mathcal{我}_{T} \），是（组件）凸的。

• 三。 ϕ _t吨 （·）和ψ _t吨 （·）保序：let\（（t，u），\，（t，v）\在[0，t]\times\mathcal中{我}_{T} \），使用u个≤v（v）.然后

  $$\phi{t}（u）\leq\phi{t}（v）\quad\text{和}\quad_psi{t}-（u）\ leq\psi{t}-（v）$$

  (6)

• 4 ψ _t吨 （·）严格遵守秩序：让\（（t，u），\，（t，v）\在[0，t]\times\mathcal中{我}_{T} ^{\circ}\），使用u个<v（v）.然后ψ _t吨 (u个)<ψ _t吨 (v（v）).

• 5 ϕ和ψ共同持续\（[0，T]\times\mathcal{我}_{T} ^{\circ}\）。

• 6 偏导数

  $$\frac{\部分}{\部分u{i}}\phi{t}（u）\quad\text{和}\quad_frac{\partial}{\局部u{i{}\psi{t}（u），\quadi=1，\dots，d$$

  存在并持续\（\left（t，u\right）\在[0，t]\times\mathcal中{我}_{T} ^{\circ}\）。

证明

参见Keller-Ressel等人(2013，莱姆。4.2）用于报表(1)–(4)和Keller-Ressel(2008，道具。3.16和Lem。3.17）。□

仿射过程具有丰富的结构特性，在金融建模中被证明特别有用。然而，在某些情况下，无法满足时间同质性条件；例如，时间不均匀性可以通过测量的等效变化引入。菲利波维奇（2005）引入了时间非均匀仿射过程，其条件矩母函数的形式为

对于所有0≤秒≤t吨≤T型和\（u\in\mathcal{我}_{T} \）.定理2.7 in菲利波维奇（2005）得出无穷小生成器由

(7)

其中函数F类和R（右）保持与时间同质情况下相同的形式，但是，（允许的）参数现在是与时间相关的。如果过程X（X）是强正则仿射-也就是说，参数满足一些连续性条件，请参见中的定义2.9菲利波维奇（2005）了解更多详细信息ϕ_秒,t吨(u个)和ψ_秒,t吨(u个)满足具有时间相关函数特征的广义Riccati方程F类(秒,u个)和R（右）(秒,u个)，即，对于所有0≤秒≤t吨≤T型

$$\beart｛aligned｝-\frac｛\partial｝｛\partial s｝\ phi_｛s，t｝（u）&=F\left（s，\pis_｛s，t｝（u）\right），\ quad\pis_｛t，t｝（u）=0，\-\frac｛\partial｝｛\pis_｛s，t｝（u）&=R\left（s，\pis_｛s，t｝（u）\right），\ quad\pis_｛t，t｝（u）=u.\end｛aligned｝$$

(8)

具有多条曲线的仿射LIBOR模型

多曲线设置

我们首先介绍了一些基本符号和多曲线LIBOR模型中使用的主要概念，然后介绍了水银（2010）; 另请参见Grbac等人（2015）以获取概述和更多详细信息。

OIS和LIBOR利率之间出现的显著利差取决于投资期限（也称为期限），这意味着我们无法再使用单一期限结构。让\（\mathcal{T}=\{0=T_{0}<T_{1}<\cdots<T_{N}=T\}\）表示离散的等距时间结构，其中T型 _k个 ，用于\（k\in\mathcal{k}=\{1，\点，N\}\），表示相关的市场日期，例如支付日期和交易工具的到期日。这组期限表示为\（\mathcal{X}=\{X_{1}，\dots，X_{n}\}\），我们通常会\（\mathcal{X}=\{1,3,6,12\}\）月。然后，每\（x\ in \ mathcal{x}\）我们考虑相应的期限结构\（\mathcal{T}^{x}=\{0=T_{0}^{x}<T_{1}^{x}<\cdots<T_{N^{x{}}^{x}=T_{N}\}\）具有恒定的男高音长度\（δ_{x}=T_{k}^{x} -T型_{k-1}^{x}\）.我们用表示\（\mathcal{K}^{x}=\{1，\点，N^{x{\}\）与男高音结构相关的所有下标的集合\（\mathcal{T}^{x}\），并假设\（\mathcal{T}^{x}\subseteq\mathcal{T}\）为所有人\（x\ in \ mathcal{x}\）。

隔夜指数掉期（OIS）利率被视为无风险利率的最佳市场代理。此外，目前大多数交易利率衍生品都有抵押，抵押品的报酬基于隔夜利率。因此，折扣因素B类(0,T型)假设从OIS利率中剥离，并为每个可能的到期日定义\（T\in\mathcal{T}\）; 另见Grbac和Runggaldier(2015, §1.3.1).B类(t吨,T型)表示折现系数，即时间-t吨到期零息债券的价格T型假设与相应的基于OIS的零息票债券一致。

让是一个完全随机基础，其中表示最终向前测度，即与基准值相关的鞅测度B类(·,T型 _N个 ). 我们考虑未来的措施与数字相关\（\{B（\cdot，T_{k}^{x}）\}_{x，k}\）每一双(x个,k个)带有\（x\ in \ mathcal{x}\）和\（k\in\mathcal{k}^{x}\）.假设流程\（B（\cdot，T_{k}^{x}）/B（\cdop，T_{N}）\）都是真的-每对鞅(x个,k个)、远期措施在以下方面是绝对连续的并以通常的方式定义，即通过Radon–Nikodym密度

因此，远期措施通过以下方式相互关联

（9）

因此，它们与终端测量有关

(10)

对未来措施的期望以及终端测量表示为和分别为。

接下来，我们定义了多曲线LIBOR设置中的主要建模对象：OIS远期利率、远期LIBOR利率和相应的利差。

定义1

时间-t吨OIS远期利率对于时间间隔\（[T_{k-1}^{x}，T_{k}^{x}]\）由定义

$$F{k}^{x}（t）：=\frac1{\delta{x}}\左（\frac{B\左（t，t_{k-1}^{x}\右）}{B\右（t，t_{k}^{x{右）}-1\右）$$

(11)

定义2

时间-t吨远期伦敦银行同业拆借利率对于时间间隔\（[T_{k-1}^{x}，T_{k}^{x}]\）由定义

(12)

哪里\（左\左（T_{k-1}^{x}，T_{k}^{x}\右）\）表示当时的即期伦敦银行同业拆借利率\（T_{k-1}^{x}\）对于时间间隔\（\左[T_{k-1}^{x}，T_{k}^{x}\右]\）。

远期伦敦银行同业拆借利率是远期利率协议隐含的利率，远期即期伦敦银行同业拆放利率被兑换为固定利率；cf.汞(2009第12-13页）。即期伦敦银行同业拆借利率\（左\左（T_{k-1}^{x}，T_{k}^{x}\右）\）提前设置，因此\（{\mathcal{F}}_{T_{k-1}^{x}}\）-因此，我们认为远期伦敦银行同业拆借利率与相应期限日的即期伦敦银行同业拆放利率一致，即。，

定义3

这个（加性）扩散远期LIBOR利率和OIS远期利率之间的定义如下

$$S_{k}^{x}（t）：=L_{k}^{x{$$

备注1

在单曲线设置中，远期LIBOR利率通过(11)而价差始终等于零。然而，在多曲线模型中，这些速率不再相等，我们通常会这样\（L_{k}^{x}\geqF_{k{^{x{）。\（F_{k}^{x}\）和\（L_{k}^{x}\）也可以解释为分别对应于无风险债券和风险债券的远期利率；参见Crépey等人(2012).

具有多条曲线的仿射LIBOR模型

我们现在将注意力转向由Keller-Ressel等人（2013）并扩展到多曲线设置Grbac等人（2015）一个重要的成分是大于或等于1的鞅。考虑一个过程X（X）满足假设(\（\mathbb{A}\）)从规范值开始1=（1,1，…，1），并设\（u\in\mathcal{我}_{T} \）然后，流程\（{{M^{u}=（M^{u}_{t} ）_{在[0，t]}}中\）由定义

(13)

是鞅。此外，如果\（u\in\mathcal{我}_{T} \cap\mathbb{右}_{\geqslate 0}^{d}\）映射\（u\mapsto M_{t}^{u}\）正在增加并且\（百万）^{u}_{t} 第1页对于每个t吨∈[0,T型]; 参见Keller-Ressel等人(2013，厚度。5.1）和帕帕潘托利翁（2010）。

多曲线仿射LIBOR模型定义如下：

定义4

一个多曲线仿射伦敦银行同业拆借利率模型\（（X，\数学{X}，T_{N}，u，v）\）由以下元素组成：

• 仿射过程X（X）在下面满足假设(\（\mathbb{A}\）)从规范值开始1。

• 一组男高音\（\mathcal{X}\）。

• 最终到期日T型 _N个 。

• 向量序列u个=(u个₁,…,u个 _N个 )带有\（u{l}=：u{k}^{x}\in\mathcal{我}_{T} \cap\mathbb{右}_{\geqslate 0}^{d}\），对于所有人\（l=kT_{1}^{x}/T_{1}\）和\（x\ in \ mathcal{x}\），因此

  $$u{1}\geu{2}\ge\cdots\geu{N}=0$$

  (14)

• 向量序列的集合\（v={\left\{（v_{1}^{x}，\点，v^{x}_{N^{x}}）\right\}}_{x\in\mathcal{x}}\）具有\（v_{k}^{x}\in\mathcal{我}_{T} \cap\mathbb{右}_{\geqslate 0}^{d}\），因此

  $$\开始{aligned}v_{k}^{x}\geu_{k{^{x{quad\text{forall}~k\in\mathcal{k}^{x}，x\in\mathcal{x}。\结束{对齐}$$

  (15)

模型中OIS远期利率和远期伦敦银行同业拆借利率的动态根据

$$1+\delta_{x}F_{k}^{x}（t）=\压裂{M_{t}^{u_{k-1}^{x}}{M_}t}^}{u_}k}^}x}}\quad\text{和}\quad 1+\delta{x}L_{k{^{x{（t ^{u_{k}^{x}}}$$

(16)

为所有人\（位于[0，t_{k}^{x}]\）,\（k\in\mathcal{k}^{x}\）和\（x\ in \ mathcal{x}\）。

多曲线仿射LIBOR模型的定义意味着OIS远期利率和远期LIBOR利率的动态，更准确地说\（1+\增量_{x} F类_{k} ^{x}\）和\（1+\增量_{x} L（左）_{k} ^{x}\），在驱动过程中表现出指数仿射依赖性X（X）; 参见(13)和(16).Glau等人（2016）最近的研究表明，只有表现出这种指数仿射依赖性的模型才能产生结构保持的LIBOR模型；参见其中的建议3.11。中的分母(16)这两种情况都是一样的，因为两种利率都必须是-鞅的定义。另一方面，不同的序列\（（u{l}）{l\in\mathcal{K}}）和\（\左（v_{k}^{x}\右）_{k\in\mathcal{k}^{x}}\）在中的分子中使用(16)为OIS和LIBOR利率产生不同的动态。这些序列用于将多曲线仿射LIBOR模型拟合到OIS和LIBOR利率的给定初始期限结构。特别是，随后的命题表明，通过将模型拟合到初始术语结构，我们可以自动获得序列\（（u{l}）{l\in\mathcal{K}}）和\（（（v_{k}^{x}）_{k\in\mathcal{k}^{x}}）让人满意的(14)和(15)分别为；另见Grbac等人(2015，Rem.4.和4.5），以获得对这些序列的进一步评论。

以下数量衡量了多曲线仿射LIBOR模型拟合给定初始期限结构的能力

(17)

在数学金融学中常用的几种模型中，例如由次级机构驱动的Cox–Ingersoll–Ross模型和Ornstein–Uhlenbeck过程，这个数量等于无穷大。以下命题表明，仿射LIBOR模型定义明确，可以在温和条件下拟合任何初始期限结构。

提议1

考虑时间结构\（\mathcal{T}\），让B类(0,T型 _我 ),\（l \ in \ mathcal{K}\），是OIS贴现因子的初始期限结构，并假设

$$B（0，T_{1}）\geq\cdots\geqB（0、T_{N}）>0$$

(18)

然后，以下内容保持不变：

• 1 如果γ _X（X） >B类(0,T型₁)/B类(0,T型 _N个 )，存在一个序列\（（u{l}）{l\in\mathcal{K}}）在里面\（\mathcal{我}_{T} \cap\mathbb{右}_{\geqslate 0}^{d}\）令人满意的(14)这样的话

  $$M_{0}^{u_{l}}=\frac{B（0，T_{l}）}{B（O，T_{N}）{quad\text{for-all}l\in\mathcal{K}$$

  特别是，如果γ _X（X） =∞则多曲线仿射LIBOR模型可以拟合OIS利率的任何初始期限结构。

• 2 如果X是一维的，那么序列\（（u{l}）{l\in\mathcal{K}}）是独一无二的。

• 三。 如果所有初始OIS率均为正，则序列\（（u{l}）{l\in\mathcal{K}}）正在严格减少。

证明

参见中的命题6.1Keller-Ressel等人（2013）.□

提议2

考虑前一个命题的设置，修复\（x\ in \ mathcal{x}\）以及相应的音高结构\（\mathcal{T}^{x}\）.让\（L_{k}^{x}（0）\）,\（k\in\mathcal{k}^{x}\），是非负远期LIBOR利率的初始期限结构，并假设\（k\in\mathcal{k}^{x}\）

$$L_{k}^{x}（0）\geq\frac1{\delta_{x}}\左（\frac{B\左（0，T_{k-1}^{x}\右）}{B\右（0，T_{k}^{x{右）}-1\右）=F_{k{^{xneneneep（0）$$

(19)

然后，以下内容保持不变：

• 1 如果\（伽马{X}>（1+\delta_{x} L（左）_{k} ^{x}（0））B（0，T_{k}^{x{）/B（0，T_{N}）\）为所有人\（k\in\mathcal{k}^{x}\），则存在一个序列\（（（v_{k}^{x}）_{k\in\mathcal{k}^{x}}）在里面\（{\mathcal{I}}_{T}\cap{\mathbb{右}_{\geqslate 0}}^{d}\）令人满意的(15)这样的话

  $$M_{0}^{v_{k}^{x}}=\左（1+\增量_{x} L（左）_{k+1}^{x}（0）\右）M_{0}^{u_{k+1{x}}，\quad\text{代表所有}~k\in\mathcal{k}^{x}\setminus\{N^{x{}$$

  特别是，如果γ _X（X） =∞则多曲线仿射LIBOR模型可以拟合远期LIBOR利率的任何初始期限结构。

• 2 如果X是一维的，那么序列\（（（v_{k}^{x}）_{k\in\mathcal{k}^{x}}）是独一无二的。

• 三。 如果所有初始LIBOR-OIS利差均为正值（即(19)变得严格），然后\（v{k}^{x}>u{k}^{x{），对于所有人\（k\in\mathcal{k}^{x}\setminus\{N^{x{}\}\）。

证明

参见中的命题4.2Grbac等人（2015）.□

备注2

这些命题的证明是有建设性的，并提供了一个简单的算法，用于将仿射LIBOR模型拟合到给定的OIS和LIBOR利率的初始期限结构。然而，对于d日>1序列u个和v（v）^x个不是唯一的，因此出现了优化问题；参见小节中的讨论“关于插值函数的选择“和”讨论”. 在命题1的证明中，序列\（（u{l}）{l\in\mathcal{K}}）沿直线选择\（\mathcal{我}_{T} \cap\mathbb{R}^｛d｝_{\geqslate 0}\）来自一些\（u\in\mathcal{我}_{T} \）到0，这样u个满足

(20)

然而，其他连续路径u个^′到0，满足(20)并且正在按成分递减，也会起作用。

下一个命题表明，多曲线仿射LIBOR模型在分析上是可处理的，即仿射结构在任何向前测度下都保持不变。

提案3

基本流程X（X）是测度下的时间非均匀仿射过程，每\（x\ in \ mathcal{x}\）和\（k\in\mathcal{k}^{x}\）。力矩产生功能由提供

对于每个w个这样的话\（磅/平方英寸）_{N} -吨}（u{k}^{x}）{我}_{T} \），其中

$$\开始{数组}{@{}rcl@{}}\phi_{t}^{x，k}（w）&=\phi_}t}\left（\psi_{t_{N} -吨}（u_{k}^{x}）+w\右）-\phi_{t}\左（\psi_{t_{N} -吨}（u{k}^{x}）\右），\\psi{t}^{x，k}（w）&=\psi{t}\左（\psi_{t_{N} -吨}（u_{k}^{x}）+w\右）-\psi_{t}\左（\psi_{t_{N} -吨}（u{k}^{x}）\右）。\结束{数组}$$

证明

请参阅中的建议4.6Grbac等人（2015）.□

上述定义的多曲线仿射LIBOR模型满足命题1和命题1的前提条件2是无套利离散期限模型，在这个意义上\（F_{k}^{x}\）和\（L_{k}^{x}\）是-每个的鞅\（k\in\mathcal{k}^{x}\）,\（x\ in \ mathcal{x}\），而利率和利差为正，即。，\（F_{k}^{x}（t）\ge 0\）和\（S_｛k｝^｛x｝（t）=L_｛k｝^｛x｝（t）-F_｛k｝^｛x｝（t）\ge 0\）对于每个\（在[0，t_{k-1}^{x}]中，在mathcal{k}^{x}中）,\（x\ in \ mathcal{x}\）; 请参阅中的命题4.3Grbac等人（2015）。

备注3

具有多条曲线的仿射LIBOR模型可以扩展，以适应负利率和正利差；参见Grbac等人(2015，§4.1）。

备注4

我们可以在仿射LIBOR模型的构建中使用与时间相关的参数，即时间非均匀仿射过程，特别是因为X（X）在正向测量下是时间相关的；见提案3。我们改用仿射过程，以简化模型及其属性的表示，并与相关文献保持一致（参见Keller-Ressel等人。2013和Grbac等人。2015).

仿射LIBOR模型的连续期限扩展

离散到连续期限

本节致力于将仿射LIBOR模型从离散期限结构扩展为连续期限结构，并推导相应瞬时远期利率和短期利率的动力学。主要工具是插值函数，它是在[0上定义的函数，T型 _N个 ]匹配的u个 _我 在每个期限日T型 _我 本小节遵循并延伸Keller Ressel（2009）。

定义5

安插值函数对于多曲线仿射LIBOR模型\（（X，\数学{X}，T_{N}，u，v）\）是一个连续的、分量递减函数具有为所有人t吨∈[0,T型 _N个 ]和有界右导数，这样为所有人\（T_{l}\ in \ mathcal{T}\）。

备注5

自是来自[0的映射，T型 _N个 ]，定义一个元素。可以这样选择这与命题1一致。

插值函数允许导出多曲线仿射伦敦银行同业拆借利率模型中零息债券价格动态的显式表达式。特别是，它们属于仿射项结构模型; 参见例如，Björk(2009, §24.3).

引理2

让是多曲线仿射LIBOR模型的插值函数\（（X，\数学{X}，T_{N}，u，v）\）并定义（OIS零息票）债券价格B类(t吨,T型)由

(21)

对于0≤t吨≤T型≤T型 _N个 ，其中鞅定义为(13). 然后，债券价格满足

(22)

哪里

（23）

证明

使用OIS远期利率的定义(16)以及债券价格的积极性，在离散期限的情况下，

$$B（T_{k}，T_{i}）=\prod\limits_{l=k}^{i-1}\frac{B\左（T_{k}，T_{l+1}\right）}{B（T_{k}，T_{l}{l}}}=\压裂{M_{T_{k}}^{u{i}}}{M__{T{k}{^{u_k}}}$$

对于每个\（T_{k}，T_{i}\在\数学{T}\中）这样的话T型 _k个 ≤T型 _我 ≤T型 _N个 。同样，在连续期限的情况下，使用(21)我们得到0≤t吨≤T型≤T型 _N个 那个

(24)

哪里⌊t吨⌋是这样的T型_⌊t吨⌋是时间结构中最大的元素\（\mathcal{T}\）小于或等于t吨因此，自取决于指数仿射X（X） _t吨 ，我们到达(22)–(23). □

接下来，我们将证明仿射LIBOR模型从离散期限扩展到连续期限是无套利期限结构模型。跟随穆西拉和鲁特考夫斯基(1997定义2.3），我们说债券价格系列满足无仲裁条件如果有措施这样的话是一个-局部鞅和对于任何

定理1

让是多曲线仿射LIBOR模型的插值函数\（（X，\数学{X}，T_{N}，u，v）\）.然后，是一个仿射LIBOR模型的连续期限扩展即，适用于所有到期日的无套利模型，对于所有到期日\（T\in\mathcal{T}\）债券价格与（离散期限）仿射LIBOR模型的价格一致。

证明

插值函数的定义立即得出，连续期限延长中的债券价格与所有到期日的离散期限仿射LIBOR模型的债券价格一致。

据Musiela和Rutkowski介绍(1997，§2.3），为了证明模型是无套利的，只需验证系列的以下条件债券价格：

• （i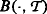） 是一个严格正的特殊半鞅和左极限过程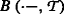也是绝对积极的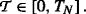

• （ii） 债券价格商数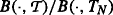是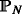-鞅。

• （iii） B类(t吨,S公司)≤B类(t吨,U型)对于所有0≤t吨≤S公司≤U型≤T型 _N个 。

第二个条件紧随其后(21)以及M（M）^u个作为一个-鞅。为了检查第一和第三个条件，我们将使用引理中的债券价格表示2事实上，最后一个条件直接来自表示(22)–(23)，使用函数的单调性和的保序性ϕ和ψ; 参见引理1。此外ϕ和ψ与一起(22)暗示这确保了

最后，是的平滑函数X（X）因此它也是一个半鞅，如果它的关联跳跃过程是特殊的是绝对有界的；参见Jacod和Shiryaev(2003，莱姆。I.4.24）。过程X（X）和X（X）_负极为非负a.s.，同样适用于ΔX（X），因为跳跃测度的补偿器X（X）完全由正半空间支撑；参见Duffie等人(2003，定义2.6）。再次使用引理1（4）和我们明白了和取负半空间中的值。因此，我们可以估计跳跃过程如下：

□

所有到期日的债券价格现在，我们可以计算瞬时正向速率的动力学有到期日当时盛行t吨和短期利率第页 _t吨 当时盛行t吨这些数量通常定义为

连同以下要求我们得到前者相当于

(25)

引理3

让作为插值函数，考虑仿射LIBOR模型的连续期限扩展\（{（X，\mathcal{X}，T_{N}，u，v）}\）。然后，通过以下公式提供瞬时远期汇率和短期汇率

（26）

哪里

(27)

为所有人在这里，一∘b条表示两个向量的分量相乘一和b条具有相同的尺寸。

证明

我们从引理中知道2债券价格是对数函数X（X），尤其是由(22)–(23). 现在的结果是取的右导数水反应堆。，通过定义5和引理1（6）存在。另请注意和都是积极的□

此外，持续复合的银行账户B类^⋆定义如下：

$$B^{\star}=\exp\left（\int_{0}^{\cdot}r_{s}\mathrm{d}s\right）$$

(28)

而相关的现场测量，其中债券价格由

接下来计算。

引理4

让作为插值函数，考虑仿射LIBOR模型的连续期限扩展\（{（X，\mathcal{X}，T_{N}，u，v）}\）然后，现场测量由密度过程决定

哪里和。

证明

现场测量和终端正向测量通过

参看Musiela和Rutkowski(2005, §13.2.2). 然后，上面的表示很容易从(28), (22)–(23)、引理1（1）和备注5，使用以下事实因此□

下一个结果类似于命题3，表明驱动过程X（X）在spot度量下仍然是仿射过程换言之，多曲线仿射LIBOR模型在即期测量下仍然可以进行分析处理。

定理2

让作为插值函数，考虑仿射LIBOR模型的连续期限扩展\（{（X，\mathcal{X}，T_{N}，u，v）}\）然后是基础流程X（X）是在spot测度下的时间非均匀仿射过程特别是，X（X）是强正则仿射和下的函数特征由提供

$$F^{\star}\左（t，w\右）=F\左（w+Q_{t}\右）-F\左（Q_{t\right）\quad\text{和}\quad R^{\sart}\左$$

对于每个w个这样的话\（w+Q_{t}\in\mathcal{我}_{T} \）。

证明

我们首先证明X（X）在下具有指数仿射形式.从的力矩生成函数开始X（X）在下面，并使用引理4中的条件密度过程和(26)–(27)，我们到达

（29）

中的定理4.10Keller Ressel（2008）提供了一种优雅的方法来计算时间积分仿射过程的功能特性。这一结果被证明适用于\（Y_{\cdot}=\int_{0}^{\cdot}X_{u}\mathrm{d}u\）并扩展到\（\widetilde{Y}（Y）_{\cdot}=\big（\int_{0}^{\cdot}\theta_{u}^{i} X（X）_{u} ^{i}\mathrm{d}u\big）{1\lei\led}\）对于确定性、有界性和正性θ在附录的定理3中。然后，我们得到了联合过程的功能特征\（\左（X_{t}，\widetilde{Y}（Y）_{t} \右）\）由提供

$$\widetilde{F}（t，w_{x}，w_}y}）=F（w_{x}）\quad\text{和}\quad_widetilde{R}（t，w_x}、w_{y}$$

插值函数的定义和引理1（6）得出q个英寸(27)有界。因此，应用定理3可以得出B类英寸(29)采取形式

$$B=\exp\left（\widetilde{\phi}_{t-s}（w+Q_{t}，\mathbf1）+left\langle\widetelde{\psi}_{ts}{Y}（Y）_{s} ）\right\rangle\right）$$

哪里\（\widetilde{\phi}\）和\（\widetilde{\psi}\）广义Riccati方程的解定义为\（\widetilde{F}\）和\（\widetilde{R}\）; 参见(三). 的形式\（\widetilde{R}\）意味着\（\widetilde{\psi}\）对应于\（\widetilde{Y}\）满足\（widetilde{\psi}{t-s}（w{x}，w{y}）{y}=w{y{）因此，我们从(29)那个

现在，条件反射X（X） _秒 =x，并取关于秒在t吨=秒，我们到达发电机X（X）在下面以下为：

$$\开始｛对齐｝\mathcal{答}_{t} \mathrm{e}^{left\langlew，x\right\rangle}=\left（F（w+Q{t}）-F；\结束{对齐}$$

(30)

与…相比(7). 仿射过程的半群X（X）在下面在Filipović的意义上是弱规则的(2005，定义2.3），因为该过程X（X）是随机连续的发电机存在并在w个全部=0(t吨,x个)∈[0,T型]×天此外，X（X）是强正则仿射由于弱容许参数(α^⋆(t吨),b条^⋆(t吨),β^⋆(t吨),米^⋆(t吨),μ^⋆(t吨))由暗示(30)是的连续变换(α,b条,β,米,μ). □

利用最后一个命题，我们得到了X（X）在下面由提供

(31)

哪里\（φ{s，t}^{star}\）和\（磅/平方英寸_｛s，t｝^｛\star｝\）是具有函数特征的广义Riccati方程的解F类^⋆和R（右）^⋆; 参见(8). 由于瞬时正向速率和短期速率都是驱动过程的时间相关仿射变换X（X），它们将从继承许多（分布式）属性X（X）事实上，一旦我们计算了驾驶过程的特征X（X）根据现场测量，很容易看出，短期利率第页具有时间非均匀性特征，即仿射w.r.t。X（X）的确，来自(26)和(31)我们得到

(32)

关于插值函数的选择

插值函数的要求非常弱，因此即使在u个 _k个 与到期日相对应T型 _k个 ,\（k\ in\ mathcal k\），可以使用。然而，看看等式(26)–(27)对于短速率过程的动力学第页，我们可以立即观察到跳跃将在固定时间发生，到期日T型 _k个 ，如果不是连续可微的。插值函数的一个更复杂但仍然是任意的选择是三次样条，即三次分段多项式，它们是连续可微的，因此不会导致确定性间断；参见图1以进行说明。

图1

当X（X）是1D CIR过程，以及作为时间函数的平均值（计算超过10⁵路径）。左侧面板：使用三次样条插值(u个 _k个 )以获得。右侧面板：使用线性插值

下一个推论是引理3的直接结果X（X）是随机连续的。

推论1

让是一个连续可微的插值函数，即。，，并考虑仿射LIBOR模型的连续期限扩展\（{（X，\mathcal{X}，T_{N}，u，v）}\）然后是短期流程第页是随机连续的。

然而，即使插值函数是连续可微的，也可能存在从序列继承的短速率的不良行为的来源(u个 _k个 )本身（除非d日=1; cf.备注2). 例如，考虑以下“对角线”结构(u个 _k个 )，与Grbac等人（2015）对不同到期利率之间的独立性进行建模：

(33)

具有\（\bar{u}_{i} \in\mathbb{右}_{\geqslate 0}\），对于1≤我≤N个。在这种情况下，唯一可用于插值的路径是连接元素的路径u个 _k个 和u个_k个+1序列的(u个 _k个 )通过直线，否则插值函数将不会按分量递减。因此，任何插值函数都映射到非光滑流形上。然后，要求插值函数（在时间上）连续可微，将导致在每T型 _k个 ,\（k\in\mathcal{k}\），因为插值函数的导数每次都等于零T型 _k个 ; 再次查看(26)和(27)，以及图2。

图2

由对角结构和连续可微插值函数导出的20条短速率样本路径以及2.5/97.5个百分位

我们希望在续集中提供条件，使仿射LIBOR模型的持续期限延长所产生的短期利率表现出“合理”的行为，即它既不会在固定时间跳跃，也不会在每个到期日降至零。此外，我们想确定一种选择插值函数的方法，这种方法可以消除这种选择的任意性。前者的一个条件是序列\（（u_{k}）_{k\in\mathcal{k}}）位于光滑的歧管上。关于后者，我们可以要求债券价格也要符合连续性。这些共同导致了一个唯一定义的、连续可微的插值函数。

示例1

让\（{（X，\mathcal{X}，T_{N}，u，v）}\）是仿射LIBOR模型，并假设序列\（（u_{k}）_{k\in\mathcal{k}}）接受插值函数\（{{U}}\）映射到平滑流形上的此外，让\（\波浪线{f}（0，\cdot）\冒号[0，T_{N}]\rightarrow\mathbb{右}_{\geqslate 0}\）是一个初始的远期曲线，例如Nelson–Siegel或Svensson家族，与初始债券价格一致，即。，

$$B（0，T_｛k｝）=\exp\left（-\int_｛0｝^｛T_｛k｝｝\tilde f（0，s）\mathrm｛d｝s\right）$$

(34)

然后，我们可以找到一个插值函数这样，连续或扩展仿射LIBOR模型适合给定的初始正向曲线\（\颚化符f \）为了实现这一点，插值函数应满足以下要求：

(35)

为所有人该等式直接遵循以下要求：(34)为所有人保留与一起(22)–(23)以及备注5。此外，瞬时正向速率的动态由以下公式提供(26)–(27)为所有人T型∈[0,T型 _N个 ]，并满足初始条件

中的曲线拟合问题(35)可以类似于拟合序列的问题来解决(u个 _k个 )债券价格的初始期限结构；与中的命题6.1进行比较Keller-Ressel等人（2013）以及相应的证明。所得插值函数就时间而言是可微的，如下结果所示。

提案4

让\（{（X，\mathcal{X}，T_{N}，u，v）}\）是一个多曲线仿射LIBOR模型，假设\（\颚化符f（0，\cdot）：[0，T_{N}]\to\mathbb{右}_{\geqslate 0}\）是连续的\（（u_{k}）_{k\in\mathcal{k}}）允许映射到C类¹-歧管然后，存在唯一的连续可微插值函数令人满意的(35).

证明

这句话是隐函数定理的一个简单推论，其中ϕ和ψ在空间和时间上，以及它们的保序性（参见引理1）被使用。事实上

$$G{左（t，u\right）}=\phi_{t_{N}}{左$$

在中连续可微t吨∈[0,T型 _N个 ]和\（u\in\mathcal{我}_{T} \）.让成为C类¹-歧管，其中是有限索引集，是一个开放的覆盖和\（g_{\alpha}:U_{\alpha}\rightarrow I_{\阿尔pha}\substeq\mathbb{R}\）是一个C类¹-同胚。定义\（G^｛\star｝\colon[0，T_｛N｝]\times I_｛\alpha｝\rightarrow｛\mathbb｛R｝｝\）通过\（{\左（t，x\右）}\mapsto G{\左^{-1}_{\alpha{\左（x\右）}}\右）{）.通过（严格）保序属性ϕ和ψ我们知道偏导数\（\分数{\部分}{\部分x}G^{\星{\左（t，x\右）}}\）不是零，因此通过紧性参数存在唯一的连续可微函数\（x\冒号[0，T_{N}]\rightarrow\mathbb{R}\）这样的话G公司^⋆(t吨,x个(t吨))全部=0t吨∈[0,T型 _N个 ]. 插值函数由下式给出□

备注6

图1揭示了仿射LIBOR模型暗示的短期利率的另一个有趣行为。特别是，短期利率存在一个大于零的下限。实际上，由于驱动仿射过程的状态空间是\（\mathbb{右}_{\geqslate 0}^{d}\），我们有第页 _t吨 ≥第页 _t吨 ，作为ϕ严格遵守秩序u个正在减少。与Keller-Ressel等人相比，在LIBOR利率的离散期限模型中已经观察到类似的现象(2013第6.4段）。

仿射伦敦银行同业拆借利率模型中XVA的计算

危机前市场中衍生产品的报价等于其折现预期回报（根据鞅测度），因为交易对手被视为无违约，市场上流动性充足，其他摩擦也可以忽略不计。然而，在危机后的市场中，这些假设受到了挑战；特别是，交易对手信用风险已成为违约风险的自然形式，金融市场流动性不足，而其他摩擦也越来越重要。因此，报价中必须考虑到这些事实。一种方法是，首先计算衍生品的所谓“干净”价格，该价格等于其折现后的预期回报（在鞅测度下），然后将其相加价值调整，统称为XVA，反映交易对手信用风险、流动性成本等Brigo等人（2013），克雷佩(2015年a，b），Crépey和Bielecki（2014）、和Bichuch等人（2016）以及其他有关XVA的更多详细信息。

清洁估价

本节回顾了基差互换，并在具有多条曲线的仿射LIBOR模型中提供了其净价的公式。这些模型中的上限、掉期期权和基础掉期期权的净估值在Grbac等人（2015）。

利率互换的典型例子是浮动利率兑换为固定利率；参见，例如Musiela和Rutkowski(2005, §9.4). 不同期限利率之间出现的巨大利差导致了一种新的利率互换，称为基差互换，在这种互换中，与不同期限的基础利率相关联的两种浮动支付流被交换。例如，在与伦敦银行同业拆借利率挂钩的300万至600万基差掉期中，3个月的伦敦银行同业拆借利率每季度支付一次，6个月的伦敦银行同业拆借利率每半年收到一次。

让\（\mathcal{T}（T）_{对_{1} q个_{1} ｝^｛x_｛1｝｝＝\left\｛T_｛p_｛1｝｝^｛x_｛1｝｝，\dots，T_｛q_｛1｝｝^｛x_｛1｝｝\ right\｝\）和\（\mathcal{T}（T）_{对_{2} q个_{2} }^{x{2}}=\left\{T_{p_{2}{^{x_2}}，\dots，T_{q_2}}^{x_2}}\right\}\）表示两个期限结构，其中\（T_{p_{1}}^{x_1}}=T_{p_2}}^}x_2}}\）,\（T_{q{1}}^{x{1}=T_{q}2}}^}x{2}}\）、和\（\mathcal{T}（T）_{对_{2} q个_{2} }^{x{2}}\子集\数学{T}（T）_{对_{1} q个_{1} }^{x{1}}\）考虑于启动的基差互换\（T_{p_{1}}^{x_1}}=T_{p_2}}^}x_2}}\），第一笔付款到期日为\（T_{p_{1}+1}^{x{1}}\）和\（T_{p_{2}+1}^{x{2}}\）分别是。为了反映启动时浮动利率之间可能存在的差异\（左（T_{i-1}^{x{1}}，T_{i}^{x1}}\右）对应较短的榫头长度x个₁被替换为\（左（T_{i-1}^{x{1}}，T_{i}^{x1}}\右）+S\）对于固定的S公司这称为基差互换价差。时间-第页名义金额标准化为1的基差掉期价值\（0\ler\leT_{p_{1}}^{x{1}}\），由给出

公允基础互换利差\（S_{r}\left（\mathcal{T}（T）_{对_{1} q个_{1} }^{x{1}}，\mathcal{T}（T）_{对_{2} q个_{2} }^{x{2}}\右）然后进行计算，使掉期开始时的价值为零，即。，\（\mathbb{英国标准}_{r} \左（S，\mathcal{T}（T）_{对_{1} q个_{1} }^{x{1}}，\mathcal{T}（T）_{对_{2} q个_{2} }^{x{2}}\右）=0\）对于\（0\leqr \leqT_{p_{1}}^{x_{1{}}\）因此，公平价差由

$$\开始{aligned}\！S_{r}\！\左（\mathcal{T}（T）_{对_{1} q个_{1} }^{x{1}}，\mathcal{T}（T）_{对_{2} q个_{2} }^{x{2}}\right）=\frac{\sum{i=p{2+1}}^{q{2}{\delta{x{2]}B\left（r，T_{i}^{x{2}\rift）L_{i}T_{i}^{x{1}}\右）L_{i}^{x_1}}（r）}{\sum_{i=p_{1}+1}^{q_1}}\delta_{x_1{}}B（r，T_{i{^{x}}}}）}。\结束{对齐}$$

此外，时间-t吨基差互换的价值\（位于左[t_{p_{1}}^{x{1}，t_{q{2}}^}x{2}{right]\），使用(16)和(24)，采用以下形式：

(36)

哪里\（S_｛r｝=S_｛r｝\left（\mathcal{T}（T）_{对_{1} q个_{1} }^{x{1}}，\mathcal{T}（T）_{对_{2} q个_{2} }^{x{2}}\右），用于\（位于\左[0，T_{p_{1}}^{x_{1{}}\右]\）为成立日期，而\（\lceil t\rceil{i}=\min\left\{k\in\mathcal{k}^{x{i}}:t<t_{k}^{x{i}{right\}\）。

备注7

基差互换是危机后的金融产品，只能在考虑到利率多重曲线性质的模型中进行定价。在单曲线模型中，基差互换的价格为零；参见Crépey等人(2012第181页）

XVA方程

上一小节中的定价公式反映了在没有交易对手信用风险、资金限制和其他市场摩擦的环境下的估值。为了将后者纳入定价框架，引入了几种价值调整：信贷和债务估值调整（CVA和DVA）、资金估值调整（FVA）以及重置成本（RC）等。然而，我们忽略了资本估值调整（KVA），这是由于资本要求及其相关成本的增加而引入的，而保证金估值调整（MVA）是在需要初始保证金的情况下，通过假设银行进行完美套期保值且无初始保证金而产生的。各种估值调整通常缩写为XVA，而我们将其总和称为估价调整（VA），即。，

$$\text{VA}:=\text{CVA}+\text{DVA}+\text{FVA}+\text{RC}$$

我们计算VA的方法与Crépey的工作密切相关(2015年a,b条)，而我们的说明和数值示例基于Crépey等人（2013）和Crépey等人(2015，第5.1节）。

我们考虑两个交易对手，在续集中称为银行和投资者，它们都是可违约的，并表示为τ _b条 银行的默认时间，由τ _我 投资者的默认时间，而我们设置τ=τ _b条 ∧τ _我 ∧T型。的默认强度τ _b条 ,τ _我 、和τ表示为γ _b条 ,γ _我 、和γ分别是。我们还考虑了“全模型”过滤\（\mathbb{G}\），由给出\（\mathbb{F}\）通过默认时间的自然过滤而扩大τ _b条 和τ _我 ，并假设沉浸式假设成立，即\（\mathbb{F}\）-鞅停在τ是一个\（\mathbb{G}\）-鞅。

VA可以被视为银行对投资者债务的股息支付期权的价格，在首次违约时偿还τ在这里，我们含蓄地采纳了银行的观点。从投资者的角度来看，由于不同的融资条件，VA是相似的，但并不完全相同。有效结论克雷佩（2015年b）是可以在“预设”框架中计算上述设置中的VA，其中交易对手的违约风险仅通过违约强度出现；具体见第3节。更具体地说，弗吉尼亚州Θ是以下BSDE在鞅测度下的解

(37)

哪里第页表示短期利率过程，P（P）清洁价格过程，以及克VA系数。银行合同的总价格，换言之，包含各种风险的对冲成本，由净价和VA之间的差额得出：

$$\Pi{t}=P_{t}-\Theta{t}，\quad t\in[0，t]$$

VA系数克具有以下形式：

$$\开始{对齐}&\！\！\！g{t}（r_{t}，P_{t{，\Theta_{tneneneep）+r_{t}\Theta{t}\=\\&-\gamma{t}^i}\左（1-\rho^{i}\右）\左（Q_{t}（t）-\伽马{t}\右）^{-}&\text{CVA}\\&+\Gamma{t}^{b}\左（1-\rho^{b{\右）\左（Q_{t}（t）-\伽玛{t}\右）^{+}&\text{DVA}\\&+b_{t}\Gamma{t}^{+{-\bar{b}_{t} 左（P_{t}（t）-\Theta公司_{t}（t）-\伽玛{t}\右）^{+}-\波浪线\lambda{t}\left（P_{t}（t）-\Theta公司_{t}（t）-\Gamma_｛t｝\right）^｛-｝&&\text｛FVA｝\\&&+\Gamma_｛t｝\left（P_{t}（t）-\Theta公司_{t} -问_{t} \右），&\text{RC}\end{aligned}$$

哪里\（\tilde\lambda_{t}=\bar{\lambda}_{t}（t）-\γ{t}^{b}（1-\mathfrak{r}），而右侧的每一行对应于价值评估的四个组成部分之一。上述等式中的参数具有以下财务解释：

• \（\gamma_{t}^{i}，\，\gamma_t}^{b}\）、和γ _t吨 分别是投资者、银行和第一违约强度。

• ρ^我,ρ^b条是投资者和银行之间的回收率，以及\（\mathfrak{r}\）是银行对其无担保资助者的回收率（当银行的内部资金来源耗尽时，第三方会介入；假定该资助者没有风险）。

• 问 _t吨 是根据信用支持附件（CSA）中规定的某些估价方案得出的合同价值，该附件是场外交易合同中的常见部分。

• \（\Gamma_{t}=\Gamma_2{t}^{+}-\Gamma_t}^{-}\）是银行向投资者提供的抵押品的价值。

• \（b_{t}，\，\bar{b}_{t} \）和\（\lambda{t}，\，\bar{lambda}{t}\）是无风险利率的利差吗第页 _t吨 对应于抵押品和外部借贷（来自无担保投资者）的报酬。

合同的价值问以及抵押品Γ，以及资金系数b条和\（\bar{b}\）在合同的CSA中规定，用于降低交易对手风险。不同的CSA规范将导致VA的不同行为；参见Crépey等人(2013，第3节）和下一小节了解更多详细信息。

备注8

浸入假设意味着合同与相关方违约时间之间存在弱或间接依赖性。因此，并非每个合同都可以在预先设定的VA框架内定价。由于利率合同对违约时间的依赖性较弱，因此这种方法适合我们的设置；另见克雷佩(2015年b，剩余。2.3).

仿射LIBOR模型中的XVA计算

我们现在有兴趣计算利率衍生品的价值调整，并将重点放在基差互换上，作为危机后产品的主要示例。根据具有多条曲线的仿射LIBOR模型，对各期限的OIS远期利率和远期LIBOR利率进行建模，并根据caplet数据对模型进行校准；参见Grbac等人(2015，§8）了解仿射LIBOR模型校准的详细信息。随后选择插值函数，并导出了短速率过程的动力学。之后，值调整的计算是VA BSDE在(37).

这种方法使我们能够一致地计算期权价格和价值调整，因为我们只需校准离散时间或仿射LIBOR模型，而在VA计算中至关重要的短期利率过程的动态是从插值中得出的。特别是，我们不需要像其他方法那样引入和校准（或估计）短期利率的“外生”模型。因此，插值函数在我们的方法中起着至关重要的作用，因为一旦仿射LIBOR模型被校准，这是唯一的“自由”成分。同时，通过插值函数的不同可能选择，引入了模型风险的一个元素。在接下来的部分中，我们将检查不同插值函数对值调整的影响。

我们用于数值实验的数据对应于2013年5月27日的欧元市场，并从彭博社收集；另见Grbac等人(2015，§8.4）了解更多详细信息。带有多条曲线的affne LIBOR模型被校准为10年期的caplet数据，其中期限长度为3个月和6个月。驱动仿射过程由三个独立的CIR过程组成。序列(u个 _k个 )和(v（v） _k个 )其构造使其位于光滑的歧管上\（\mathcal{我}_{T} \cap{\mathbb{R}}^{3}_{\geqslate 0}\）; 参见图三特别是，u个 _k个 位于直线上k个∈{0,…,k个₁}∪{k个₂,…,k个_三}∪{k个₄,…,N个}和在椭圆段上k个∈{k个₁+1,…,k个₂−1}∪{k个_三+1,…,k个₄−1}. 序列u个如下所示：

$$\begin｛array｝｛ccccc｝u_｛N-1｝&=&（0&0&\bar{u}_{N-1}）\\&\vdots&&\\u_{k_{4}}&=&（0&0&\bar{u}_{k{4}}）\\u{k_{4}-1}&=&（0&\颚化符{u}_{克_{4}-1}&\bar（&\bar）{u}_{克_{4}-1})\\u_{k_{4}-2}&=&（0&\颚化符u{k_{4}-2}&\bar（&\bar）{u}_{克_{4}-2})\\&\vdots&&&\\end{数组}$$

哪里\（\bar u{j}，\tilde u{jneneneep \in \mathbb{右}_{\geqslate 0}\）并满足\（\bar u{j}\ge\bar u_{j+1}\）和\（\ tildeu{j}\ge\ tildeu{j+1}\）所有相关信息\（j\in\mathcal K\）; 参见(14)再次。序列的结构v（v）^x个每个期限x个是类似的。换句话说，短期远期伦敦银行同业拆借利率是由驱动过程的所有三个组成部分驱动的X（X），中期利率由两部分组成，而长期利率仅由X（X）。一旦构建了歧管，序列(u个 _k个 )和(v（v） _k个 )通过将模型与同一日期的OIS和EURIBOR数据拟合而获得。（注意，在这个例子中，我们有N个=40，我们选择k个₁=9,k个₂=16,k个_三=21，以及k个₄=28.)

图3

用于拟合序列的平滑流形(u个 _k个 )和(v（v） _k个 )

为了说明不同插值函数对值调整的影响，我们考虑插值函数的三种不同规格U型以下为：

• （如果₁)：通过拟合整个正向曲线进行插值（参见示例1）；

• （如果₂)：之间的线性插值u个 _k个 的；

• （如果_三)：扇区上的样条插值，其中除一个分量外，所有分量都是矢量u个 _k个 在中为常数k个以及这些扇区之间的线性插值（即，当u个 _k个 位于歧管的曲线段上）。

现在让我们将注意力转向价值调整的计算。我们考虑以伦敦银行同业拆借利率（LIBOR）为基础的3M-6M基础掉期，初始日期为t吨=0，10年内到期。我们关注Crépey等人（2013）并考虑五种不同的CSA规范，由

$$\开始{数组}{lcclccl}（\text{CSA}_{1} ）：&&&&\left（\mathfrak｛r｝，\rho^｛b｝，\rho^｛i｝\right）=\left（0.4,0.4,0.4\right），&Q=P，&&\Gamma=0，\\（\text{CSA}_{2} ）：&&&\left（\mathfrak{r}，\rho^{b}，\ rho^}\right）=\ left（1,0.4,0.4\ right），&Q=P，&&\Gamma=0，\\（\text{CSA}_{3} ）：&&&\left（\mathfrak{r}，\rho^{b}，\sho^{i}\right）=\ left（1,1,0.4\ right），&Q=P，&&\Gamma=0，\\（\text{CSA}_{4} ）：&&&\left（\mathfrak{r}，\rho^{b}，\ rho^}\right）=\ left（1,1,0.4\ right），&Q=\Pi，&&\Gamma=0，\\（\text{CSA}_{5} ）：&&&\左（\mathfrak{r}，\rho^{b}，\ rho^}\right）=\左（1,0.4,0.4\右），&Q=P，&&\Gamma=Q=P、\end{array}$$

而默认强度和扩散相等

$$\gamma^{b}=5\%，\\gamma^}i}=7\%，\ gamma=10\%，\b=\bar{b}=\lambda=1.5\%，\squad\text{和}\quad\bar{\lambda}=4.5\%$$

前三个CSA规范对应于无抵押的“干净”恢复方案，因为合同的价值问等于净价，并且没有抵押。第四个规范对应于没有抵押的“预设”恢复方案，而最后一个规范对应的是完全抵押的合同。此外，第一个规范在VA中产生了线性BSDEΘ，允许使用（正向）蒙特卡罗模拟计算VA。

价格P（P） _t吨 基础掉期的(36)对于每个\（位于[t_{p_{1}}^{x{1}，t_{q{2}}^x{2}]\）我们可以观察到P（P） _t吨 是的确定性转换X（X） _t吨 此外，短期利率第页 _t吨 是确定的仿射变换X（X） _t吨 ; 参见(26). 因此，VA系数克 _t吨 (第页 _t吨 ,P（P） _t吨 ,Θ _t吨 )也是X（X） _t吨 ，我们可以定义一个确定性函数\（\帽子\）这样的话

$$\hat g（t，X_{t}，\Theta_{tneneneep）：=g_{t{$$

换句话说，在这种情况下，VA BSDE是马尔可夫的，VA也是由半线性PDE的解提供的。为了数值计算基差互换的VA，我们在点鞅测度下进行了研究使用由10个元素组成的空间网格⁵路径和时间网格n个=步长为200步小时我们在时空网格上应用了向后回归，即。，

并使用米-最近邻估计量米=3.在线性VA系数的情况下，与（正向）蒙特卡罗模拟相比，该选择是最佳的。

讨论

数值实验的结果如图所示4,5和6从图中的顶部面板开始4我们观察到，由于不同的插值函数，短期利率的动力学存在显著的结构差异；这在查看平均值和百分位线时最为明显。同一图中的底部面板显示了不同插值函数的3M-6M基差掉期的价格过程。由于差异不如以前那么明显，我们绘制了价格的绝对差异，这是由于图中不同的插值函数造成的5在这里，我们看到，当使用不同的插值函数时，价格会出现显著差异（请记住，掉期的名义金额等于1，因此价格的偏差不可忽略）。正如预期的那样，第一插值函数与第二插值函数以及第一插值函数和第三插值函数产生的价格之间的最大差异发生在用于构造的流形的曲线部分(u个 _k个 )和(v（v） _k个 ). 相反，流形曲线段上第二个插值函数与第三个插值函数的价格差异为零，因为这两个函数在该段中都是线性插值的。

图4

每个插值函数的短利率（上图）和基差互换价格过程（下图）的二十个样本路径，以及平均值（黑线）和97.5%和2.5%的百分位数，计算范围为10⁵变现

图5

不同插值函数的基差互换价格过程之间的绝对差异

图6

五种不同CSA规范（左面板，从上到下）的基础互换VA过程的二十个样本路径，以及平均值和百分位数，以及不同插值函数的VA过程之间的差异（从左到右）

图6使用五种不同CSA规范（从上到下）的第一个插值函数（左面板）描述了VA过程的样本路径，而其他图显示了由于不同插值函数导致的VA差异。VA的差异比价格差异小一个数量级，然而，VA本身比基差互换价格小一个量级。反映价格情况的是，使用第一个插值函数和其他两个插值函数的VA之间的最大差异发生在流形的弯曲部分周围。然而，歧管扁平部分的VA差异比相应的价格差异更为明显。原因是，插值通过基础掉期价格和用于贴现的短期利率影响价值调整，其影响通过反向回归传播到不同的细分市场。当人们看到使用第二个和第三个插值函数产生的价格和价值调整之间的差异时，这一点就变得清楚了；虽然价格差异为零，但价值调整的差异远远不是零。

上述数值例子表明，插值函数的选择会带来显著的模型风险。我们选择的函数在上确界范数方面相差不太远，因此上述差异可能会更大。事实上，由于插值函数的作用，短期利率的系数可以变得任意大。因此，两个流形上的序列u个和v（v）必须谨慎选择lie和插值函数，因为它们可以从根本上改变模型的行为。

附录A

仿射过程的时间积分

以下结果是中定理4.10的扩展Keller Ressel（2008）。

定理3

让\（\theta\colon[0，T]\rightarrow{\mathbb{R}}^｛d｝_{\geqslate 0}\）是一个有界函数，并且(X（X） _t吨 )_{t吨∈[0,T型]}是上的仿射过程\（\mathbb{R}^｛d｝_{\geqslate 0}\），具有功能特征F类和R（右）.然后\（{\left（X_{t}，\int_{0}^{t}\theta_{u}\circ X_{u{mathrm{d}u\right）}_{t\in[0，t]}\）是上的时间非均匀仿射过程\（{\mathbb{R}}^｛d｝_{\geqsland 0}\times{\mathbb{R}}^｛d｝_{\geqslate 0}\）具有功能特性

$$\widetilde{F}{\left（t，u_{X}，u__{Y}\right）}=F{\ left（u_{X}\rift）}\quad{\text和}\quad\widetildere{R}{\ left（t，u，u，u_Y}\right）}=\ left \右）$$

在这里，∘表示向量之间的分量乘法。

证明

让\（n\in\mathbb{n}\）,k个∈{0,…,n个}，并定义\（s{k}=\压裂{k}{n} 秒\)和\（h=\压裂{s}{n}\），因此秒₀,…,秒 _n个 是[0的等距分区，秒]具有步长小时用黎曼和逼近积分，并利用支配收敛定理，我们得到

下一步使用条件期望塔式定律和的仿射性质X（X）,A类 _n个 可以写成如下

通过迭代此过程，我们得出

$$A{n}=\exp\left（p_{n}{left（u_{X}，u_{Y}\right）}+{left\langleq_{n{{left$$

具有第页₀(u个 _X（X） ,u个 _Y（Y） )=0,q个₀(u个 _X（X） ,u个 _Y（Y） )=u个 _X（X） +小时u个 _Y（Y） ∘θ_t吨+秒和

$$开始{对齐}p_{k+1}{\左（u_{X}，u_{Y}\右）}&=p_{k}{\右（u_}X}、u_{Y}\右{h}{\左（q_{k}{\右（u_{X}，u_{Y}\右）}\right）}+hu{Y}\circ\theta{t+s_{n-（k+1）}}。\结束{对齐}$$

使用广义Riccati方程(三)，我们可以扩展ϕ和ψ围绕原点线性旋转。因此，我们得到

$$开始{对齐}p_{k+1}{\左（u_{X}，u_{Y}\右）}&=p_{k}{\右（u__{X{，u{Y}\右）}+h F{\左右）}&=q_{k}{\左（u_{X}，u_{Y}\右）}+h{\左。\结束{对齐}$$

作为θ是非负且有界的，中定理4.10的证明的第二部分Keller Ressel（2008）保持不变。因此，上面的递归方案是从终端时间开始到ODE的欧拉型近似

$$\begin{aligned}\frac{\partial}{\parial s}p{\left（s，t，u_{X}，u__{Y}\right）}&=F{\left[（s，t，u_}X}、u_{Y{\right{X}，u_{Y}\右）}\右$$

具有初始条件第页(第页,第页,u个 _X（X） ,u个 _Y（Y） )=0和q个(第页,第页,u个 _X（X） ,u个 _Y（Y） )=u个 _X（X） ，对于所有人第页≥0. □