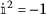具有离散时间和空间变量的草丛-莎草模型中四种机制诱导的时空模式

摘要

本文研究了具有离散时间和空间变量的淡水草丛-莎草模型的时空模式。我们首先分析了动力学系统，并分别给出了flip和Neimark–Sacker分岔的参数条件。利用空间扩散，我们证明了所获得的稳定齐次解在一定条件下可以经历图灵不稳定性。通过数值模拟，我们发现了周期倍增级联、周期窗口、不变循环、混沌行为和一些有趣的空间模式，它们是由四种机制诱导的：纯周期不稳定性、翻转不稳定性、奈马克-萨克-图灵不稳定性和混沌。

1介绍

Tussock莎草是一种常见的北美苔草。它们几乎只生长在草丛顶部，丛生茂密，茎和叶纤细。丛丛之间的空间可以为小动物提供栖息地。苔草在湿地生态系统中起着重要的作用，如堤防加固、护坡和防止水土流失。一般来说，死糠躺在草丛的脚下，聚集在低矮的丛间地带，抑制植物的生长。另一方面，它们激活了残骸。植物和腐烂物之间的相互作用以及两者的不均匀扩散对于时空格局的形成至关重要[1]. 从数学的角度研究时空模式的形成机制，具有重要的理论意义和现实应用价值。在[2]通过设置实验点，研究了草丛苔草的空间格局，发现其规律性与空间尺度有密切关系。他们研究的模型以反应扩散方程为特征。近年来，许多生物和生态现象，特别是空间格局，都以反应扩散方程为特征。不同扩散形式，交叉扩散[三]自我扩散、亚扩散[4]，超扩散[5,6]例如，等被广泛应用于反应扩散方程，这是导致系统发生图灵不稳定性的关键因素[1]形成丰富的图案：斑点、条纹、迷宫、缝隙、螺旋、圆形等[7–10].

近几十年来，围绕连续或半离散反应扩散系统开展了大量关于图灵不稳定性的工作，请参见[11,12]以及其中的参考文献。对于中的一个草丛莎草模型[2]通过连续的时间和空间变量，作者[13]发现了由平衡和极限环生成的分层图灵模式。在[14]研究表明，模式的形成与区域大小、草丛莎草生长速度和土地承载力有关。此外，他们通过计算Leray–Schauder度导出了模式存在的条件。在[15]作者考虑了二维空间中的另一种植物-齿条模型，但在植物生物量方程中具有半抑制性，发现了斑点、迷宫以及带状和斑点共存的模式。在许多情况下，数据采集不是时间连续的，生物种群的分布也是空间不连续的。此外，模拟空间模式的算法是基于连续系统的相应离散形式。基于这些考虑，离散模型或有效的离散化方法对于将实际模型与仿真联系起来也非常重要。因此，在本文中，我们主要集中于研究草丛-莎草模型的模式形成机制[2]但具有离散的时间和空间变量。我们将应用耦合映射格（CML）方法对连续的tussock-sedge模型进行离散化，以得到具有离散时间和空间变量的相应系统。通过CML方法获得的系统通常称为CML模型。令人惊讶的是，与连续系统相比，CML模型的动力学和模式更加丰富。

对于CML模型，一些有效的方法，如用于稳定性分析的雅可比矩阵、中心流形约简[16]，以及空间离散算子的计算[17]，以及关于离散系统Turing不稳定性判据的理论结果[18]已获得并可供研究人员使用[19–23]. CML模型的一个优点是它保留了原始系统的固有特性；同时，它代表了一种数值模拟算法[24,25]. CML方法在许多方面都有广泛的应用，如化学振荡器[26]、生态系统[23]，神经动力学系统[27,28]. 更多相关文学作品请参见[7,29–32]以及其中的参考文献。

对于CML型草丛-莎草模型的动力学行为和模式形成的研究还不多。通过一系列理论分析，我们发现该模型表现出丰富的动力学特性。如果给定合适的参数，CML模型可以同时进行时空分岔，从而产生四种模式形成机制：翻转分岔、奈马克-萨克-图灵分岔、混沌振荡和纯周期分岔。因此，与连续形式相比，这些模式更加丰富。

我们将论文组织如下。在Sect。 2，我们首先在第。 2.1，然后对第节中反应阶段动力学系统的均相稳态动力学进行理论分析。 2.2。在Sect。 三，我们主要考虑均匀定态的分岔行为，包括Sect中的翻转分岔。 3.1，Neimark–教派中的萨克分支。 3.2和图灵分歧。 3.3。在Sect。 4进行了模拟，目的是解释理论结论，并说明动力学和空间模式。最后，我们进一步展示了我们的结论和讨论。

2CML型模型及稳定性分析

我们首先构造了与连续草丛-莎草模型相对应的CML型模型，然后分析了其稳定性。

2.1CML草丛苔草模型的建立

一种连续的草丛莎草模型[2]是

$$\begin{aligned}\textstyle\begin{cases}\frac{\partial P}{\partic t}=P（1-P）-sP-\theta PW+d_{P}\Delta P，\\frac{\ partial W}{\partial t}=sP-bW+d_}\DeltaW，\end{cases}\displaystyle\end{aligned}$$

(1)

哪里\（P（x，y，t）\）和\（W（x，y，t）\）植物和腐生物量t吨和空间\（（x，y）\）分别是，和\（δ=\frac{\partial^{2}}{\paratilx^{2{}+\frac}\partial ^{2neneneep}{\protialy^{2neneneei}\）.术语秒表示叶片衰老的特定速率。腐烂的分解速率表示为b条.植物和腐生物的扩散速率为\（d_{p}\）和\（d_{w}\）分别是，和\（d_{w}>d_{p}\）在这个模型中，腐皮对植物的生长有抑制作用，即线性项\（-θPW），其中θ表示抑制率。有关模型的详细信息(1)，请看[2].

让\（P=\frac{b^{2}}{\thetas}\bar{P}\）,\（W=\frac{b}{\theta}\bar{W}\）,\（t=\压裂{t}{b}\），然后是系统(1)已更改为

$$\开始{aligned}\textstyle\begin{cases}\frac{\partial\bar{P}}{\paratilT}=\bar{s}\bar{P}（P）-｛P｝^｛2｝-\棒{P}\bar{W}+d_{\bar{P}}\Delta\bar{P}，\\frac{partial\bar{W}}{partial T}=\bar｛P｝-\bar{W}+d_{\bar{Wneneneep}\Delta\bar{W}，\end{cases}\displaystyle\end{aligned}$$

(2)

哪里\（\bar{s}=\frac{1-s}{b}\）,\（xi=frac{b}{thetas}\）,\（d_{\bar{P}}=\压裂{d_{P}}{b}\）、和\（d_{\bar{W}}=\压裂{d_{W}}{b}\）。为了保持符号简洁直观，我们去掉了^负极，更换T型具有t吨，并重写系统(2)为以下无量纲形式：

$$\开始{aligned}\textstyle\begin{cases}\frac{\partial P}{\partitle t}=sP-\xi P^{2} -电源+d_{P}\增量P，\\frac{\partial W}{\partitle t}=P-W+d_{W}\增量W.结束{cases}\显示样式\end{aligned}$$

(3)

基于系统(三)，我们建立了CML模型。在二维矩形区域上，我们定义了一些\（n次n次）晶格位置。我们指定了两个数字，植物生物量\（P_{（i，j，t）}\）和腐生物量\（W_{（i，j，t）}\），时间\（位于Z^{+}中）在每个站点上\（（i，j）\）,\（（i，j\in\{1,2,3，\ldots，n\}）在不同地点之间，我们假设存在局部反应和空间扩散[23,25]各站点植物和腐皮的生物量随时间的变化遵循系统动力学。

发件人t吨到\（t+1\）CML模型中植物和腐皮的动力学行为包括两个阶段：“反应”阶段和“扩散”阶段[7,23–25]. 扩散行为发生在反应行为之前。介绍时间步骤τ和空间步长δ并离散系统的空间形式(三)，我们得到了控制扩散过程的方程：

$$\开始{对齐}\textstyle\开始{cases}P'{（i，j，t）}=P_{（i，j，t）}+\frac{\tau}{\delta^{2}}d_{P}\nabla{d}^{2{P}（i、j、t）}，\\W'{\nabla_{d}^{2}W_{（i，j，t）}，\end{cases}\displaystyle\end{aligned}$$

(4)

哪里\（P'_{（i，j，t）}\）和\（W'_{（i，j，t）}\）是参与下一个反应阶段的植物和腐皮的生物量。离散形式的拉普拉斯算子Δ描述为\（纳布拉{d}^{2}\）:

$$\开始{对齐}\textstyle\开始{cases}\nabla_{d}^{2}P_{（i，j，t 1，j，t）}+W{（i，j，t）}+W{。\结束{cases}\displaystyle\end{aligned}$$

(5)

通过离散非空间形式(三)，我们得到了控制反应过程的方程式：

$$\begin{aligned}\textstyle\begin{cases}P_{（i，j，t+1）}=f（P'{（i，j，t$$

(6)

哪里

$$\begin{aligned}\begin{aligned}&{f（P，W）=P+\tau\bigl（sP-\xi P^{2} -电源\较大）}，\\&{g（P，W）=W+\tau（P-W）}。\end{aligned}\end{alinged}$$

(7)

方程式(4)–(7)是系统的CML模型(三). 所有参数均为正值，且\（P_{（i，j，t）}\geq 0\）,\（W_{（i，j，t）}\geq 0）接下来，我们研究了CML模型在以下周期边界条件下的动力学：

$$\begin{aligned}\begin{aligned}&{P_{（i，0，t）}=P_{（i，n，t，t）}=W_{（i，n，t）{，\qquad W_{（i，1，t）｝=W_（i，n+1，t）\end{aligned}\end{alinged}$$

(8)

离散的时间和空间草丛-苔草模型具有空间上的均匀性和异质性行为。对于所有人我,j个、和t吨，齐次行为满足

$$\开始{aligned}\nabla^{2}_{d} P（P）_{（i，j，t）}=0，\qquad\nabla^{2}_{d} 周_{（i，j，t）}=0。\结束{对齐}$$

(9)

连同方程式(4)——(7)，忽略空间站点索引的均匀动力学受以下因素控制

$$\begin｛aligned｝\textstyle\begin｛cases｝｛P_｛t+1｝=P_｛t｝+\tau（sP_{t}（t）-\xi P_{t}^{2} -P_{t} W公司_{t} ）}，\\{W{t+1}=W{t}+\tau（P_{t} -西_{t} ）}，\end{cases}\displaystyle\end{aligned}$$

可以写入以下地图：

$$\开始{aligned}\开始{pmatrix}P\\W\结束{pmatricx}\mapsto\begin{pmatriax}P+\tau（sP-\xi P^{2} -电源)\\W+\tau（P-W）\end{pmatrix}。\结束{对齐}$$

(10)

CML模型的齐次动力学(4)–(7)然后可以通过分析地图得到(10). 对于异构行为，它需要至少一组我,j个、和t吨制造\（纳布拉^{2}_{d} P（P）_{（i，j，t）}\neq 0\）和\（纳布拉^{2}_{d} W公司_{（i，j，t）}\neq 0\）.

2.2均匀定态动力学

在本小节中，我们试图得到使齐次稳态稳定的参数条件。自从地图的定点(10)与CML模型的均匀稳态完全等价(4)–(7)，我们可以分析地图不动点的动力学(10)而不是分析CML模型的均匀稳态。通过求解以下方程：

$$\begin{aligned}\textstyle\begin}cases}{P=f（P，w），}\\{w=g（P，w），}\end{cases}\displaystyle\end{aligned}$$

我们得到地图的两个不动点(10):\（（P_{1}，W_{1{）=（0,0）\）和\（（P_{2}，W_2}）=（压裂{s}{1+\xi}，压裂{s{1+\ xi}）对于两个不动点的稳定性，下面的定理给出了一系列精确的参数条件。

定理1

固定点 \（（P_{1}，W_{1{）\） 的地图(10)是一个马鞍.对于固定点 \（（P_{2}，W_{2{）\）:

• (1) 如果其中之一 \（（H_{1}）\） 和 \（（H_{2}）\） 持有,它是一个马鞍,哪里

  $$\begin{aligned}（H_{1}）\quad\textstyle\begin{cases}0<s<s_{1{，\\tau{1}<\tau<\tau{2}，\end{cases}\displaystyle\qquad；\结束{cases}\displaystyle\end{aligned}$$

• (2) 如果其中之一 \（（序号{1}）\） 和 \（（序号{2}）\） 持有,它是一个稳定的节点,如果其中一个 \（（UN_{1}）\） 和 \（（UN_{2}）\） 持有,它是一个不稳定的节点,哪里

  $$\begin{aligned}&（SN_{1}）\quad\textstyle\begin{cases}0<s<s_{1{，\\0<\tau<\tau_{1neneneep，\end{cases}\displaystyle\qquad（SN_2}）\ quad\ textstyle\begin{cases}s>s_{2}，\\0<\tau<\tau_1}，\ end{cases}\disposystyle \\&（UN_{1neneneei）\quae\textstyle\ begin cases{0<s<s_{1}，\\tau>\tau_2}，\end{cases}\displaystyle\qquad（UN_{2}）\quad\textstyle\begin{cases}s>s{2}，\\tau>\tau{2}。\结束{cases}\displaystyle\end{aligned}$$

  此外,如果其中之一 \（（H_{3}）\） 和 \（（H_{4}）\） 持有,它是一个稳定的退化节点,如果其中一个 \（（H_{5}）\） 和 \（（H_{6}）\） 持有,它不稳定,哪里

  $$\begin{aligned}&（H_{3}）\quad\textstyle\begin{cases}s=s_{1}，\\0<\tau<\tau_{*}，\end{cases}\displaystyle\qquad（H_}4}）\ quad\ textstyle\begin{cases}s=s_{2}，\ \0<\tau{{*}，\ end{案例}\disposystyle\\&（H_2{5}1}，\\tau>\tau_{*}，结束{cases}\displaystyle\qquad（H_{6}）\quad\textstyle\begin{cases}s=s{2}，\\tau>\tau{*}；\结束{cases}\displaystyle\end{aligned}$$

• (3) 如果 \（平方英尺） 持有,这是一个稳定的焦点,如果 \（（UF）\） 持有,这是一个不稳定的焦点,哪里

  $$\begin{aligned}（SF）\quad\textstyle\begin{cases}s_{1}<s<s_{2}，\\0<tau<tau_{*}，\end{cases}\displaystyle\qquad（UF）\qua2\textstyle\ begin}s_1}<s<s_{2]，\\tau>\tau_{*{}$$

哪里 \（s{1}=frac{（1+xi）（1-\sqrt{1+xi}）^{2}{xi^{2{}）,\（s_｛2｝=\frac｛（1+\xi）（1+\sqrt｛1+\xi｝）^｛2｝｝｛xi ^｛2｝｝）,\（τ{1}=frac{1+\xi+s\xi-\xi\sqrt{（s-s{1}）（s-s}2}）}{s（1+\xi）}）,\（τ{2}=frac{1+\xi+s\xi+\xi\sqrt{（s-s{1}）（s-s}2}）}{s（1+\xi）}）,\（\tau _｛*｝=\frac｛1+\xi+s\xi｝｛s（1+\xi）｝\）.

证明

通过计算映射雅可比矩阵的特征值(10)分别在关联的不动点上，我们可以确定不动点的稳定性条件。对于固定点\（（P_{1}，W_{1{）=（0,0）\），雅可比矩阵为

$$\begin{aligned}J（P_{1}，W_{1{）=\begin{pmatrix}1+\tau s&0\\tau&1-\tau\end{pmatricx}。\结束{对齐}$$

显然\（J（P_{1}，W_{1{）\）是\（1+\tau s>1）和\（1-\tau<1）.根据[33]，固定点\（（P_{1}，W_{1{）\）是一个马鞍。对于固定点\（（P_{2}，W_{2{）\），相应的雅可比矩阵为

$$开始{对齐}J（P_{2}，W_2}）=\begin{pmatrix}1-\frac{\xi-s\tau}{1+\xi}&-\frac{s\tau}{1+/xi}\\tau&1-\tau\end{pmatricx}。\结束{对齐}$$

这两个特征值是

$$\开始{aligned}\lambda_{1,2}=\frac{1}{2}\bigl[\operatorname{tr}日本（P_{2}，W_2}）\pm\sqrt{\bigl[\operatorname{tr}日本（P_｛2｝，W_｛2｝）\bigr]^{2}-4\操作员姓名{检测}J（P_{2}，W_2}）}\bigr]，\end{对齐}$$

哪里

$$\开始{aligned}&\operatorname{tr}日本（P_{2}，W_2}）=2-\tau-\frac{xi-s\tau}{1+\xi}，\\&\operatorname{检测}J（P_｛2｝，W_｛2｝）=\frac｛1+\xi-\xi s\tau｝｛1+1+一，的的。\结束{对齐}$$

根据[33]，我们可以通过直接计算获得结果。□

在后继部分中，不动点附近的分岔行为和模式形成机制\（（P_｛2｝，W_｛2｝）\）因为不动点$(0,0)$总是不稳定的。为了便于描述，我们称之为地图的不动点(10)CML模型的齐次稳态(4)–(7).

三均匀定态的分岔分析

在本节中，我们处理τ作为主要的分岔参数，分别研究了齐次稳态的分岔行为，如翻转分岔、内马克-萨克分岔和图灵分岔。基于这一理论分析，我们得到了支持空间模式形成的参数条件。

3.1翻转分岔分析

翻转分岔可以导致稳定节点\（（P_{2}，W_{2{）\）成为一个不稳定的人。与此同时，出现了新的周期-2点。出现翻转分岔的第一个要求是\（λ{1}）或\（λ{2}）雅可比矩阵\（J（P_{2}，W_{2{）\）在翻转分岔的临界值为-1时，另一个既不是-1也不是1。以下条件可满足此要求：

$$\begin{aligned}\textstyle\begin{cases}{4+（-2-\frac{2s\xi}{1+\xi}）\tau+s\tau^{2}=0}，\\{\tau（1+\frac{xis}{1+/xi}，）\neq 2,4}。\结束{cases}\displaystyle\end{aligned}$$

求解上述条件，我们可以得到翻转分岔的临界值，并得出以下结论。

提议2

假设 \（\xi>0\） 和其中一个条件 \（（C_{1}）：0<s<s_{1{） 和 \（（C_{2}）：s>s_{2{） 持有,然后是固定点 \（（P_{2}，W_{2{）\） 在临界值处经历翻转分岔 \（\tau=\tau _｛1｝\）,哪里 \（τ{1}）,\（s{1}\）,和 \（s_｛2｝\） 在定理中定义1.

当发生翻转分叉时，新的周期2轨道分叉。接下来，我们利用翻转分岔定理和中心流形约化进一步分析了周期2点的稳定性。我们首先考虑τ作为自变量，并让\（w=P-P_{2}\）,\（z=W-W_{2}\）,\（波浪线{\tau}=\tau-\tau_{1}）为了便于以后的分析。地图(10)表示如下：

$$\开始{对齐}\开始{pmatrix}w\\z\\tilde{\tau}\end{pmatriax}=\begin{pmatricx}a{1}&a{2}&0\\b{1}&b{2}&0\\0&0&1\end{pmmatrix}\begin}pmatrix}w\ \z\\tilde{\tau}\end}+\begin{pmattrix}f{1}（w，z，\tiled{\tau}）\\f{2}（w，z，\tilde{\tau{）\\f2}（w，z，\ tilde{tau}）\end{pmatrix}，\end{aligned}$$

(11)

具有

$$\开始{aligned}\开始{arigned}&f{1}（w，z，\tilde{tau}）=\frac{1}{2} 一个_{3} w个^{2} +a个_{4} 瓦茨+一个_{5} w个\波浪线{\tau}+a_{6} z（z）\波浪线{\tau}+\frac{1}{2} 一个_{7} w个^{2} \波浪线{\tau}+a_{8} 瓦茨tilde{tau}+O（4），\\&f_{2}（w，z，tilde{tau}）=b_{3} w个\波浪线{\tau}+b_{4} z（z）\波浪线{\tau}+O（4），\\&f_{3}（w，z，\tilde{\tau{）=0，\end{aligned}\end{arigned}$$

其中，术语\（O（4）\）表示变量中阶数至少为4的多项式函数w个,z（z）,τ̃、和

$$\begon｛aligned｝\begon｛aligned｝&a_｛1｝=1-\frac｛s\到的要求的下的一，他一个的一个于的、型的一他的一一个个的到的活动的的一到到到的到一的的到到的的一份，（针对制定和所的一，｛s｝｛1+\xi｝，\cuad a_｛7｝=-2\xi，\cuad a_｛8｝以来的的的时，就，《一，的一了一目的制个的了了的情况，天。\end{aligned}\end{alinged}$$

(12)

应用逆变换\（w=a{2}（波浪号{w}+波浪号{z}）和\（z=（-1-a_｛1｝）\波浪号｛w｝+（\λ_{2} -a个_{1} ）\波浪号｛z｝\）具有\（λ{2}=1+a{1}+b{2}），我们可以编写系统(11)作为

$$\begin{aligned}\begin{aligned}&{\波浪线{w}\mapsto-\tilde{w}+\frac{1}{a{2}（1+\lambda{2}）}F{1}（波浪线{w}，波浪线{z}，波形线{tau}lambda_2}）}F_2}（\波浪线{w}，\波浪线}z}，\波浪线{tau}）$$

(13)

哪里

$$\开始{对齐}F{1}（\波浪线{w}，\波浪线}，\波浪线{tau}）={}&（\lambda_{2} -a个_{1} ）f{1}\bigl（a{2}（波浪线{w}+\波浪线{z}），（-1-a{1}）波浪线{w}+（lambda_{2} -a个_{1} ）\波浪线{z}，\波浪线}\tau}\bigr）\\&{}-a_{2} （f）_{2} \bigl（a{2}（\tilde{w}+\ tilde{z}），（-1-a{1}）\tilde}w}+（\lambda_{2} -a个_{1} ）\波浪线{z}，\波浪线\\tau}\bigr），\\F{2}（波浪线{w}，波浪线{z}，波线{tau}）={}&（1+a{1}）F{1}\bigl_{2} -一个_{1} ）\波浪线{z}，\波浪线}\tau}\bigr）\\&{}+a_{2} （f）_{2} \bigl（a{2}（\tilde{w}+\ tilde{z}），（-1-a{1}）\tilde}w}+（\lambda_{2} -a个_{1} ）\波浪线{z}，\波浪线}\陶}\大）。\结束{对齐}$$

为了获得关于分岔周期2轨道稳定性的一些信息，我们需要推导中心流形上的控制方程。假设中央歧管\（W^{c}（0,0,0）\）系统的(13)是

$$\begin{aligned}W^{c}（0,0,0）=\bigl\{（\tilde{W}，\tilde}，\ tilde{tau}）\in R^{3}\vert\tilde{z}=h^{*}（\utide{W{，\titde{\tau}），h^{**}（0，0）=0，Dh^{*.}（0.0）=0\bigr\}\end aligned{}$$

(14)

具有\（h^{*}（\tilde{w}，\tilde}\tau}）=e_{1}\ tilde{w}^{2}+e_{2}\ tilder{w}\ tilde{\tau}+e_{3}\ tiled{\tau}^{2}+O（3）\）.采取\（波浪线{z}=h^{*}（波浪线}，波浪线{tau}）到地图中(13)，我们有

$$\开始{aligned}&\lambda_{2} 小时^{*}（波浪线{w}，波浪线{tau}）+\frac{F{2}{*}（波浪线{w}，波浪线{\tau}）}{a{2}，\tilde{\tau}）}{a{2}（1+\lambda{2}）}\biggr]\ tilde{\t au}+e_{3}\ tilde}\tau}^{2}+O（3）。\结束{对齐}$$

比较\（\波浪线{w}^{2}\）,w̃τ\771],\（\tude｛\tau｝^｛2｝\）在每一边，我们都有

$$\开始｛对齐｝\开始｛对齐｝&｛e_｛1｝=\frac｛（1+a_｛1｝）[a_{2} 一个_{3}-2（1+a{1}）a{4}]}{2（1-\lambda^{2}_{2} ）}}，\\&{e{2}=\frac{（1+a{1}）^{2} 一个_{6} -a个_{2}^{2} b条_{3}-（1+a{1}）a{2}（a_{5} -b个_{4} （1+\lambda{2}）^{2}}，\\&{e{3}=0}。\end{aligned}\end{alinged}$$

（15）

相应地，限制在中央歧管上，映射(13)已更改为

$$开始{对齐}\波浪线{w}\mapsto-\tilde{w}+\mu_{1}\波浪线上{w}^{2}+\mu_{2}\波浪线宽{w}\波浪带{tau}+\mo_{3}\波浪形{w}^{2{\波浪形}+\mu_{4}\波浪状{w}\\tilde{tau{2}+\mu_波浪形{5}\波浪式{w}#{3}+O（4），\结束{对齐}$$

(16)

哪里

$$\begin{aligned}\mu_{1}={}&\frac{1}{2（1+\lambda{2}）}（\lambda_{2} -a个_{1} ）\bigl[a_{2} 一个_{3} -2a个_{4} （1+a{1}）\bigr]，\\mu{2}={}&\frac{1}{a{2}（1+\lambda{2]）}\bigl（a{2neneneep \bigl[-a_{2} b条_{3} +（1+a{1}）b{4}\bigr]+\bigl[a_{2} 一个_{5}-（1+a{1}）a{6}\bigr]（\lambda_{2} -a个_{1} ），\\mu{3}={}&\压裂{1}{a{2}（1+\lambda{2}）}\biggl（-\frac{1}{2} 一个_{2} （a）_｛2｝-\lambda_{2}）\bigl[a_{2} 一个_{7}-2（1+a_｛1｝）a_｛8｝\bigr]+e_{2} 一个_{2} （a）_{1}-\λ_｛2｝）\\&｛｝\times\bigl[-a_{2} 一个_{3} +a_{4}（1+2a）_{1}-\lambda_{2}）\bigr]+e_{1}\bigl[（\lambda_{2} -a个_{1} ）\bigl（a）_{2} 一个_{5} +a_{6}（\lambda_{2} -a个_{1} ）\bigr）\\&{}-a{2}\bigl（a_{2} 一个_{3} +b_{4}（\lambda_{2} -a个_{1} ）\biger）\bigr]\biggr），\\mu_{4}=&\frac{e_{2}}{a{2}（1+\lambda{2}）}\bigl（（\lambda_{2} -a个_{1} ）\bigl[a_{2} 一个_{5} +a_{6}（\lambda_{2} -a个_{1} ）\bigr]-a{2}\bigl[a_{2} b条_{3} +b_{4}（\lambda_{2} -a个_{1} ），\\mu_{5}={}&\frac{e_{1}（a_{1}-\λ{2}）}{1+\lambda{2}}\bigl[-a_{2} 一个_{3} +a{4}（1+2a_{1}-\lambda_{2}）\bigr]。\结束{对齐}$$

对于地图(16)，发生翻转分岔需要另外两个非零选项[16]:

$$\开始{aligned}\开始{arigned}&{\eta_{1}=\biggl（\frac{\partial^{2} F类}{\partial\tilde{w}\partial/tilde{\tau}}+\frac{1}{2}\frac{\particf}{\paratil\tilder{\tau{}}\cdot\frac{\ partial^{2} 如果}{\partial\tilde{w}^{2}}\biggr）\bigg|{（\tilde}w}，\tilde\\tau}）=（0,0）}=\mu{2}\neq0}，\\&{\eta{2}=\biggl（\frac{1}{6}\frac}\partial^{3} F类}｛\partial \ tilde｛w｝^｛3｝｝+\ biggl（\ frac｛1｝｛2｝\ frac｛\partial ^｛2｝F｝｛\partial \ tilde｛w｝^｛2｝｝\ biggr）^｛2｝\ biggr）\ bigg | _｛（\ tilde｛w｝，\ tilde｛\tau｝）=（0,0）｝=\ mu _｛5｝+\ mu _｛1｝^｛2｝\ neq 0｝。\end{aligned}\end{alinged}$$

基于上述分析和计算，我们可以得出如下结论：(10)如果适当地给出参数，则可能发生翻转分叉。因此，对于CML模型(4)–(7)我们可以得出以下结论。

定理3

如果条件之一 \（（C_{1}）\） 和 \（（C_{2}）\） 感到满意,那么CML模型(4)–(7)如果发生翻转分叉 \（\eta_{1}\neq 0\）,\（\eta_{2}\neq 0\）,和 \（τ=τ{1}）.此外,如果 \（\eta_{2}>0\）,然后是稳定期-2轨道从均匀定态分叉 \（（P_{2}，W_{2{）\）,while if（如果） \（\eta_{2}<0\）,然后是分岔期-2轨道不稳定.

如果重新缩放的转换率秒满足\（0<s<s{1}\）或\（s>s{2}\），作为τ从小于\（τ{1}）超过\（τ{1}），正齐次定态\（（P_{2}，W_{2{）\）从稳定节点到不稳定节点的变化。考虑\（\eta_{1}\neq 0\）和\（\eta_{2}>0\），CML模型(4)–(7)在\（（P_{2}，W_{2{）\）在翻转分岔临界值的右侧分岔出一个稳定的周期2轨道\（τ{1}）这意味着植物和腐生物量可能在周期2点之间以振荡状态共存。

3.2Neimark–Sacker分岔分析

参考[16]，如果一个不动点经历了Neimark–Sacker分岔，则围绕该不动点的一个不变环被分岔。Neimark–Sacker分岔的出现需要两个特征值\（λ{1,2}）相应雅可比矩阵的\（J（P_{2}，W_{2{）\）是一对共轭复数，并且\（\vert\lambda_{1,2}\vert=1\）。这意味着\（[\operatorname{tr}日本（P_{2}，W_{2{）]^{2}-4\操作员姓名{检测}J（P_{2}，W_{2{）<0\）和\（\操作员姓名{检测}J（P_{2}，W_2}）=1\），即

$$\begin{aligned}\textstyle\begin}cases}s_{1}<s<s_{2}，\\tau=\tau_{*}，\end{cases}\displaystyle\end{aligned}$$

(17)

哪里\（s{1}\）,\（s{2}\）、和\（tau_{*}\）在定理中定义1.

在条件下(17)，我们进行转换\（w=P-P_{2}\）,\（z=W-W_｛2｝\）转换固定点\（（P_{2}，W_{2{）\）到原点$(0,0)$，这可以简化后面的描述和分析。在这个坐标变换中，映射(10)可以写为：

$$\begin{aligned}\begin{aligned}&{w\mapstoa{1}w+a_{2} z（z）+\压裂{1}{2} 一个_{3} w个^{2} +a个_{4} 瓦茨+O\bigl（\bigl-（\vert w\vert+\vert z\vert\bigr）^{4}\bigr，\\&{z\mapsto b_{1}w+b_{2} z（z）+O\bigl（\bigl-（\vert w\vert+\vert z\vert\bigr）^{4}\bigr。\end{aligned}\end{alinged}$$

(18)

系数\（{1}\）,\（a{2}\）,\（a{3}\）,\（a{4}\）,\（b{1}\）,\（b{2}\）如前所述(12)，但有\（τ{1}）替换为\（tau_{*}\）由于逆平移不会改变不动点的定性行为，因此映射雅可比矩阵的特征值(18)在$(0,0)$也是共轭复数，模为1。为了便于记法，我们将这两个特征值表示为\（\lambda（\tau_{*}）\）和\（\bar{\lambda}（\tau_{*}）、和

哪里\（J（τ{*}）=J（P_{2}，W_{2{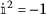）,和\（\vert\lambda（\tau_{*}）\vert=\vert\bar{\lambda}（\tau_{*neneneep）\vert=1\）.

除了条件(17)，Neimark–Sacker分岔也需要特征值来满足非零横截条件\（\frac{d\vert\lambda（\tau_{*}）\vert}{d\tau}\neq0\）直接计算表明

$$\begin{aligned}{\frac{d\vert\lambda（\tau_{*}）\vert}{d\tau}=\frac{1+\xi+\xis}{2（1+\xi）}>0}。\结束{对齐}$$

(19)

此外，Neimark–Sacker分岔要求这两个特征值既不是实特征值，也不是虚特征值。这一要求可以通过以下条件得到保证：

$$\begin{aligned}{\bigl（\lambda（\tau_{*}）\bigr）^{\theta}}\neq 1，\quad\theta=1，2，3，4，\end{alinged}$$

(20)

即，

$$\begin｛aligned｝｛\tau｛*｝\biggl（1+\frac｛\xi s｝｛1+\xi｝\biggr）\neq 2,3.｝\end｛aligned｝$$

(21)

为了实现Neimark–Sacker分岔，我们还需要获得映射的正规形式(18)通过对中心歧管进行还原，得到最后一个判据。让\（w=a_｛2｝\波浪号｛w｝\）,\（z=（\alpha-a{1}）\波浪线{w}-\β\颚化符｛z｝\），此可逆变换引导映射(18)至

$$\开始{aligned}\开始{arigned}&{\tilde{w}\mapsto\alpha\tilde{w}-\beta\tilde{z}+\frac{1}{a{2}\beta}G{1}（\tilde}w}，\tilde\z}）}，\\&{\tilde>z}\mapsto\beta\ tilde{w}+\alpha\tilde<z}+\frac{1}}{a}2}\beta}G{2}$$

(22)

哪里

$$\begin{aligned}&G{1}（\tilde{w}，\tilde}）=a{2}\beta\tau{*}（a_{1}-\西安_｛2｝-\alpha）\tilde{w}+a{2}\beta\tau_{*}\tilde}w}\tilder{z}+O\bigl（\bigle（\vert w\vert+\vert z\vert\bigr）^{4}\biger），\\&G{2}（\ tilde{w}，\ tilde}）=\frac{\alpha-a{1}{\beta}G{1}。\结束{对齐}$$

确保地图出现Neimark–Sacker分歧(22)，我们要求确定数量σ令人满意的

$$\begin{aligned}\sigma=-\operatorname{Re}\biggl（\frac{（1-2\lambda）\bar{\lambda}^{2}}{1-\lambda}\xi_{11}\xi_20}\bigr）-\frac}{2}\vert\xi_11}\vert^｛2｝-\vert\xi_{02}\vert^{2}+\operatorname{Re}（\bar{\lambda}\xi_{21}）\neq 0，\end{aligned}$$

(23)

哪里

根据上述分析和计算，我们得出以下结论。

定理4

假设 \（s_｛1｝＜s＜s_｛2｝\） 和条件(21)持有.如果 \（\sigma\neq 0）,然后CML模型(4)–(7)在均匀稳态下经历Neimark–Sacker分岔 \（（P_{2}，W_{2{）\） 什么时候 \（τ=τ{*}）.此外,如果 \（σ>0）,当 \（0<\tau<\tau_{*}\）；如果 \（σ<0）,当 \（tau>tau_{*}\）.

如果重新缩放的转换率秒满足\（s{1}<s<s{2}\），作为\（0<\tau<\tau_{*}\），均匀静止状态\（（P_{2}，W_{2{）\）是一个稳定的焦点，当\（\tau>\tau_｛*｝\），这是一个不稳定的焦点。动态转变暗示了内马克-萨克尔分叉发生的可能性。考虑到\（\sigma\neq 0），这表明当\（τ=τ{*}）.如果\（σ<0），分叉循环是稳定的。这意味着植物和腐皮以均匀准周期振荡的形式共存。

3.3图灵分岔分析

空间对称性的破坏是图灵分岔发生的主要原因。如果发生图灵不稳定性，由于不均匀的空间扩散，CML模型的稳定均匀定态将变得不稳定。这导致了空间模式的形成。对于图灵分岔的发生，两个条件是必要的[7,8,34]. 首先，我们需要非平凡的均匀定态在时间上保持稳定。其次，我们需要稳定的非平凡均匀定态在一种或多种空间异质扰动下是不稳定的。来自定理1，我们知道如果其中一个条件\（（序号{1}）\）,\（（序号{2}）\）,\（平方英尺）,\（（H_{3}）\）、和\（（H_{4}）\）保持，然后\（（P_{2}，W_{2{）\）在时间上是稳定的。

在本小节中，我们假设\（（序号{1}）\）,\（（SN_｛2｝）\）,\（平方英尺）,\（（H_{3}）\）、和\（（H｛4｝）\）保持，并探索均匀定态的图灵分岔。为了得到支持图灵不稳定性的条件，我们首先讨论了离散拉普拉斯算子的特征值问题\（纳布拉^{2}_{d} \）.考虑以下方程式：

$$\开始{aligned}\nabla^{2}_{d} X^{ij}+\lambda X^{ij}=0，\end{对齐}$$

(24)

适应周期性边界条件

$$\开始{对齐}X^{i，0}=X^{i，n}，\qquad X^{i，1}=X#{i，n+1}，\ qquad X ^{0，j}=X ^{n，j}，\squad X#{1，j}=X^{n+1，j}。\结束{对齐}$$

如中所示[17]，我们有这个特征值\（λ{kl}）属于\（纳布拉^{2}_{d} \）满足

$$开始{对齐}\lambda_{kl}=4\biggl[\sin^{2}\frac{（k-1）\pi}{n}+\sin^}\frac{（l-1）\p}{n{\biggr]：=4\bigl（\sin^2}\phi_{k}+\sins^{2{\phi_}\bigr），\end{aligned}$$

(25)

哪里\（k，l \ in \｛1,2,3，\ldots，n \｝\）.对应于特征值\（λ{kl}），本征函数表示为\（X）^{ij}_{kl}\）即，\（纳布拉^{2}_{d} X（X）^{ij}_{kl}+\lambda_{klneneneep X^{ij}_{kl}=0\）.

在后续部分中，我们研究了\（（P_{2}，W_{2{）\）在小的空间非均匀扰动下。让\（\波浪号{P}（P）_{（i，j，t）}=P_{（i，j，t）}-P_{2}\）,\（\波浪号{西}_{（i，j，t）}=W{（i，j，t）}-W{2}\），并将扰动纳入CML模型(4)–(7)，自\（纳布拉^{2}_{d} \波浪线{P}（P）_｛（i，j，t）｝=\nabla^{2}_{d} P（P）_｛（i，j，t）｝\）,\（纳布拉^{2}_{d} \波浪线{西}_{（i，j，t）}=\纳布拉^{2}_{d} W公司_{（i，j，t）}\），我们有

$$\开始{aligned}\开始{arigned}\tilde{P}（P）_{（i，j，t+1）}={}&a{1}\biggl（\波浪线{P}（P）_{（i，j，t）}+\压裂{\τ}{\δ^{2}}d_{P}^{2}_{d} \波浪线{P}（P）_{（i，j，t）}\biggr）\\&{}+a{2}\bigl（\波浪线{西}_{（i，j，t）}+\压裂{\τ}{\δ^{2}}d_{W}^{2}_{d} \波浪线{西}_{（i，j，t）}\biggr）+O\bigl（\bigl-（\vert\tilde{P}（P）_{（i，j，t）}\vert+\vert\tilde{西}_{（i，j，t）}\vert\biger）^{2}\biger），\\波浪号{西}_{（i，j，t+1）}={}&b{1}\biggl（\波浪线{P}（P）_{（i，j，t）}+\压裂{\τ}{\δ^{2}}d_{P}^{2}_{d} \波浪线{P}（P）_{（i，j，t）}\biggr）\\&{}+b{2}\bigl（\波浪线{西}_{（i，j，t）}+\压裂{\τ}{\δ^{2}}d_{W}^{2}_{d} \波浪线{西}_{（i，j，t）}\biggr）+O\bigl（\bigl-（\vert\tilde{P}（P）_{（i，j，t）}\vert+\vert\tilde{西}_{（i，j，t）}\vert\bigr）^{2}\bigr$$

(26)

哪里\（{1}\）,\（a{2}\）,\（b{1}\）、和\（b{2}\）在中给出(12). 当扰动较小时，线性项支配系统的动力学(26). 乘法\（X）^{ij}_{kl}\）在方程式的两端(26)，我们获得

$$\开始｛对齐｝\开始｛对齐｝X^{ij}_{kl}\波浪线{P}（P）_{（i，j，t+1）}={}&X^{ij}_｛kl｝（a_｛1｝\波浪{P}（P）_{（i，j，t）}+a{2}\波浪线{西}_｛（i，j，t）｝）\\&｛｝+\frac｛\tau｝｛\delta^｛2｝｝X^{ij}_{kl}\bigl（a_{1} d日_{P} \nabla（纳布拉）^{2}_{d} \波浪线{P}（P）_{（i，j，t）}+a_{2} d日_{W} \nabla（纳布拉）^{2}_{d} \波浪线{西}_{（i，j，t）}\较大），\\X^{ij}_{kl}\波浪线{西}_{（i，j，t+1）}={}&X^{ij}_{kl}（b{1}\波浪线{P}（P）_{（i，j，t）}+b{2}\波浪线{西}_{（i，j，t）}）\\&{}+\frac{\tau}{\delta^{2}}X^{ij}_{kl}\bigl（b_{1} d日_{P} \nabla（纳布拉）^{2}_{d} \波浪线{P}（P）_{（i，j，t）}+b_{2} d日_{W} \nabla（纳布拉）^{2}_{d} \波浪线{西}_{（i，j，t）}\较大）。\end{aligned}\end{alinged}$$

(27)

对于方程(27)，我们将所有我和j个共同形成以下系统：

$$\开始{aligned}\开始{arigned}\sum_{i，j=1}^{n}X^{ij}_{kl}\波浪线{P}（P）_{（i，j，t+1）}={}&a{1}\和{i，j=1}^{n} X（X）^{ij}_{kl}\波浪线{P}（P）_｛（i，j，t）｝+a_｛2｝\sum_｛i，j=1｝^{n} X（X）^{ij}_｛kl｝\波浪{西}_{（i，j，t）}\\&{}+\frac{\tau}{delta^{2}}_{1} 天_{P} \sum_{i，j=1}^{n} X（X）^{ij}_{kl}纳布拉^{2}_{d} \波浪线{P}（P）_{（i，j，t）}+\frac{\tau}{\delta^{2}}a_{2} d日_{W} \sum_{i，j=1}^{n} X（X）^{ij}_{kl}纳布拉^{2}_{d} \波浪线{西}_{（i，j，t）}，\\sum_{i，j=1}^{n}X^{ij}_{kl}\波浪线{西}_{（i，j，t+1）}={}&b{1}\sum{i，j=1}^{n} X（X）^{ij}_{kl}\波浪线{P}（P）_{（i，j，t）}+b{2}\求{i，j=1}^{n} X（X）^{ij}_{kl}\波浪线{西}_{（i，j，t）}\\&{}+\压裂{\tau}{\增量^{2}}b_{1} d日_{P} \sum_{i，j=1}^{n} X（X）^{ij}_{kl}纳布拉^{2}_{d} \波浪线{P}（P）_{（i，j，t）}+\frac{\tau}{\delta^{2}}b_{2} d日_{W} \sum_{i，j=1}^{n} X^{ij}_{kl}纳布拉^{2}_{d} \波浪号{西}_{（i，j，t）}。\end{aligned}\end{alinged}$$

(28)

让\（\bar{P}（P）_｛t+1｝=\sum_｛i，j=1｝^{n} X（X）_{kl}^{ij}\波浪线{P}（P）_{（i，j，t）}\）,\（\bar{西}_{t+1}=\sum{i，j=1}^{n} X（X）_{kl}^{ij}\波浪线{西}_{（i，j，t）}\），系统(28)可以写为：

$$\开始{aligned}\开始{arigned}&\bar{P}（P）_{t+1}=a_{1}\biggl（1-\frac{\tau}{\delta^{2}}d_{P}\lambda_{kl}\bigr）\bar{P}（P）_{t} +a{2}\biggl（1-\frac{\tau}{\delta^{2}}d_{W}\lambda{kl}\bigr）\bar{西}_{t} ，\\&\bar{西}_{t+1}=b_{1}\biggl（1-\frac{\tau}{\delta^{2}}d_{P}\lambda_{kl}\bigr）\bar{P}（P）_{t} +b_{2}\biggl（1-\frac{\tau}{\delta^{2}}d_{W}\lambda_{kl}\bigr）\bar{西}_{t} ●●●●。\end{aligned}\end{alinged}$$

(29)

在所有晶格中，空间异质扰动的动力学都由系统控制(29). 如果固定点$(0,0)$系统的(29)是稳定的，然后是空间同质定态\（（P_{2}，W_{2{）\）CML模型的(4)–(7)是稳定的。否则，国家\（（P_{2}，W_{2{）\）不稳定。在后一种情况下，图灵模式将形成。下面，我们计算系统雅可比矩阵的特征值(29)在$(0,0)$。我们非常感兴趣的是找到使至少一个特征值的模大于1的参数条件。

系统的雅可比矩阵(29)在$(0,0)$是

$$\开始{对齐}\开始{pmatrix}a{1}（1-\frac{\tau}{\delta^{2}}d_{P}\lambda{kl}）&a{2}（1-\ frac{\tau}{\delta^{2}}d_{W}\lampda{kl}）\\b_1}&b{2}（1-\frac{\tau}{\delta^{2}}d_{W}\lambda{kl}）\end{pmatrix}。\结束{对齐}$$

相应的特征值为

$$\begin｛aligned｝\lambda _｛\pm｝（k，l，\tau）=\frac｛1｝{2} R（右）（k，l，τ）\pm\frac{1}{2}\sqrt{R^{2}（k，1，τ$$

(30)

哪里

$$\begin｛aligned｝\begin｛aligned｝&R（k，l，\tau）=a_｛1｝+b_｛2｝-\frac{\tau}{\delta^{2}}\lambda_{kl}（a_{1} 天_{P} +b个_{2} d日_{W} ），\\&Q（k，l，\tau）=（a_{1} b条_{2} -a个_{2} b条_{1} ）\biggl（1-\frac{\tau}{\delta^{2}}d_{P}\lambda_{kl}\biggr）\bigl（1-\frac{\tao}{\delta^{2]}d_{W}\lampda_{kl}\biggr）。\end{aligned}\end{alinged}$$

(31)

让

$$\begin{aligned}\begin{aligned}&Z（k，l，\tau）=最大值^{n} Z轴（k，l，\tau），\bigl（（k，1）\neq（1,1）\bigr）。\end{aligned}\end{alinged}$$

（32）

通过求解\（Z_{m}（τ）=1），我们可以得到图灵分岔的临界值\（头饰）。更准确地说，当τ接近\（头饰），如果\（R^{2}（k，l，τ）>4Q（k，1，τ是满意的，那么\（头饰）满足

$$\开始{aligned}\max^{无}_{k=1，l=1}\bigl\{\bigl\ vert R\bigl（k，l，\tau'\bigr）\bigr\vert-Q\bigl。\结束{对齐}$$

(33)

如果\（R^｛2｝（k，l，\tau）\leq 4Q（k，l，\tau）\）保持，然后\（头饰）满足

$$\begin{aligned}Q\bigl（k，l，\tau'\bigr）=1。\结束{对齐}$$

(34)

上述计算表明了以下定理。

定理5

假设其中一个条件 \（（序号{1}）\）,\（（序号{2}）\）,\（平方英尺）,\（（H｛3｝）\）,和 \（（H_{4}）\） 持有,和 τ 在附近 \（\tau'\）.均匀定态 \（（P_｛2｝，W_｛2｝）\） CML模型的(4)–(7)限于周期边界条件(8)经历图灵分岔，如果 \（Z_{m}（τ）>1）.因此,图灵图案开始成形.同质定态 \（（P_{2}，W_{2{）\） 是稳定的，如果 \（Z_{m}（τ）<1）,因此,没有图案会成形.

总结整个分析和计算，我们得出结论：如果齐次稳态\（（P_{2}，W_{2{）\）只有经历图灵不稳定性，模式才由纯周期分岔诱导。如果翻转分岔和图灵不稳定性同时发生，则模式是由翻转不稳定性引起的。如果内马克-萨克分岔和图灵不稳定性同时发生，则空间模式是由内马克-萨克-图灵不稳定引起的。

4数值模拟

我们进行了数值模拟，以说明翻转、Neimark–Sacker分岔和图灵不稳定性的动态演化以及本节中的相关时空模式。

4.1翻转分岔及其图灵模式

我们首先解释在命题中获得的理论结果2和定理三然后，我们将翻转分岔与图灵分岔相结合，分别给出了纯翻转不稳定性、翻转不稳定性和混沌机制诱导的一些空间模式。在本小节中，我们设置\（xi=5.58）,\（s=5\），计算矩形网格为\（n=150）.

固定点的位置\（（P_{2}，W_2}）=（压裂{s}{1+\xi}，压裂{s{1+\ xi}）独立于τ，但其稳定性与τ.固定点为\（（P_2}，W_2}）=（0.7599,0.7599）\）进一步直接计算表明\（s{1}=0.51769）,\（s_｛2｝=2.68605\）显然，条件\（（C_{2}）：s>s_{2{）在命题中2感到满意。翻转分岔的临界值为\（τ_｛1｝=0.501806\）.设置\（τ=τ{1}），则特征值为−1和0.370478，以及\（eta{1}=-3.98561<0）,\（eta{2}=0.989406>0）.如定理所述三，当τ就在附近\（τ_｛1｝\）。我们用\（陶氏[0.4,0.7]\），请参见图1（a） ●●●●。翻转分岔仿真的初始值为\（（P_{2}+0.0001，W_{2{+0.0015）\）从图1（a） 我们可以清楚地看到糠秕生物量的周期性双重级联W公司为了从周期窗口获得一些详细信息，我们在图中绘制了局部放大图1（b） 带有\（陶氏[0.656,0.66]\）在这个周期窗口中，我们看到一个周期为6的轨道。

图1

(一)映射的翻转分支图(10)带有\（陶氏[0.4,0.7]\）；(b条)图的局部放大1(一)带有\（陶氏[0.656,0.66]\）

对应于翻转分岔图，我们绘制了图中的最大Lyapunov指数2这可以帮助我们定量地确定混沌和非混沌行为。从图2（b） ，我们可以看到，当τ约为0.659。这意味着可能会发生混沌行为。

图2

(一)图中对应的最大Lyapunov指数1(一)；(b条)图的局部放大2(一)

根据翻转分支图和最大Lyapunov指数，我们展示了映射的动态演化(10). 我们首先说明了不同给定条件下植物和糠秕生物量随时间变化的动态τ值。然后我们绘制相位肖像来说明地图的动态过渡(10).

设置\（τ=0.45则特征值分别为-0.793523和0.435469。我们选择初始状态\（（P_{2}+0.0001，W_{2}-0.0015)\)并演示植物的生物量对和腐烂W公司图中随时间变化三（a） ●●●●。我们可以看到不动点\（（P_2}，W_2}）=（0.7599,0.7599）\）是一个稳定的节点。设置\（τ=0.502）则特征值分别为−1.00078和0.370234。固定点\（（P_{2}，W_{2{）\）是不稳定的节点。节点失稳导致出现稳定周期-2点$(0.7491,0.7633)$和$(0.7704,0.7562)$.从相同的初始状态开始\（（P_{2}+0.0001，W_{2}-0.0015)\)，植物的生物量对和腐烂W公司收敛到周期-2点。植物的生物量对最终在0.7491和0.7704之间振荡。请参见图中的红点三（b） ●●●●。植物的生物量W公司最后在0.7633和0.7562之间振荡，请参见图中的蓝点三（b） ●●●●。这意味着分叉周期2轨道是稳定的，植物和腐烂的生物量最终在周期2点之间振荡：$(0.7491,0.7633)$和$(0.7704,0.7562)$。继续增加的值τ，我们观察到周期加倍的行为。例如，让\（τ=0.61），我们可以看到周期-4点$(0.4451,0.8203)$,\（（0.9506,0.5941）\）,$(0.5495,0.7831)$、和$(0.9352,0.6406)$如图所示三（c） 。相应地，随时间变化的动力学如图所示三（d） ●●●●。我们可以看到植物的生物量对（用红点表示）从\（P_{2}+0.0001\）收敛到周期4轨道，最后在四个交替状态0.4451、0.9506、0.5495、0.9352之间振荡。腐生物量W公司（用蓝点表示）从\（W_{2}-0.0015\)收敛到周期4轨道，最后在四个交替状态0.8203、0.5941、0.7831、0.6406之间振荡。这四种状态之间的动态过程如下。例如，如果从状态开始$(0.5495,0.7831)$然后是植物的生物量对和腐烂W公司到达该州$(0.9352,0.6406)$然后去州政府$(0.4451,0.8203)$然后去州政府$(0.9056,0.0.5914)$，然后返回$(0.5495,0.7831)$.进一步适当增加τ，周期将进一步翻倍。例如，set\（τ=0.6252），我们看到一个稳定的8周期轨道，请参见图4（a） ●●●●。植物和腐生物量\（P，W）\）将收敛到周期8点，并最终在八个交替状态之间振荡。由于动力学类似于图三（b） 和图三（d） ，我们没有显示动态随时间变化。

图3

不同参数值下植物和腐皮生物量随时间变化的动态τ

图4

各种参数值的相图τ

在下面，我们集中讨论地图的动态转换(10)作为的值τ增加。在图中4（a） ，我们看到一个8周期轨道\（τ=0.6302）和\（τ=0.632），我们得到另外两个不同的周期轨道。请参见图4（b） –（c）。接下来，我们设置\（τ=0.6575），然后我们到达与图中周期窗口相对应的周期-6轨道1（b） ，请参见图4（d） ●●●●。最后，我们展示了一个混沌吸引子\（τ=0.659）在图中4（e） ●●●●。图的局部放大4（e） 如图所示4（f） 给出关于混沌吸引子的一些详细信息。

来自图三和4，我们可以清楚地看到从稳定不动点到混沌的路径上的动态变化，如翻转分岔图所示τ值。

在后续部分中，我们首先演示了图灵分岔图，以确定相应的临界值\（头饰）然后我们画出图案形成区域。根据不同的地区，我们展示了模式的转变。

设置\（d_{P}=0.3\）,\（d_{W}=0.6）,\（δ=10\），我们绘制\（Z）_{米}-\tau\）图，请参见图5（a） ●●●●。通过这些给定的参数值，我们得到了图灵分岔的临界值\（陶氏大约0.5018062）.结合翻转分叉曲线\（τ=τ{1}）带图灵分岔曲线\（τ=τ’），我们在图中显示了图案形成区域5（b） 作为\（d_{W}\）从0到8不等。得到了三个区域：均匀稳态区域、纯瞬态不稳定区域和翻转瞬态不稳定区。

图5

(一)\（Z）_{米}-\陶\）图灵分岔图；(b条)\（τ-d_{W}）显示图案形成区域的图表

在下文中，我们模拟了重定标的腐生物量的空间模式W公司这是由图中的纯扭转、翻转不稳定性和混沌机制引起的6对应于图中的情况三和图4。所有显示的关于空间模式的图形都被视为CML模型的空间分布\（t=100{，}000\）初始状态是均匀稳态的随机扰动\（（P_{2}，W_{2{）\）.

图6

重组濑鱼生物量的空间格局W公司纯周期不稳定性、翻转周期不稳定性和混沌条件下的自组织\（150乘以150）格子

设置\（d_{W}=0.6），用于\（τ=0.45\）则既不会发生图灵分岔，也不会发生翻转分岔，稳定的齐次稳态是局部一致稳定的。因此，不会形成空间模式。生物量W公司投影到\（150次150次）矩形网格，请参见图6（a） ●●●●。对于\（τ=0.502），CML模型(4)–(7)同时经历图灵分岔和翻转分岔。此时，CML模型将形成由翻转不稳定性机制诱导的空间异质模式，请参见图6（b） ●●●●。糠秕的空间分布主要集中在两种可选状态（用两种不同的颜色表示：黄色（糠秕生物量\（宽=0.7633）)和蓝色（腐生物量\（宽=0.7562）))即周期-2点。让\（τ=0.61），然后我们发现W公司相互交织，如图6（c） 。事实上，图案由四种颜色组成，代表周期4点。

对于\（τ=0.6252），我们观察到一个包含八种状态的空间模式W公司（图6（d） ），以周期8点为主。类似地，我们可以想象当\（τ=0.6032）。因此，我们不在此处介绍它们。对于\（τ=0.632），我们看到更多碎片图案，请参见图6（e） ●●●●。对于\（τ=0.659），来自图三（h） ，我们知道CML模型的动力学是混沌的。同时，相关模式也表现出混沌特征。图案为马赛克式。我们无法说出图案中有多少种颜色。从上述模拟中，我们可以看到图案逐渐过渡到碎片类型，最后是混沌τ变化范围为0.45至0.659。在过渡过程中，图案在空间上也表现出周期加倍的现象。

4.2Neimark–Sacker分歧和图灵模式

在本小节中，我们首先对定理中得到的Neimark–Sacker分歧的结果进行了数值说明4然后结合图灵分岔，我们展示了相关的模式。在本小节中，参数ξ和秒固定为\（xi=5.58）,\（s=0.9）。计算网格为\（n次n=200次200次）.

自\（xi=5.58）,\（s=0.9），然后\（s{1}=0.51769<s<s{2}=2.68605）直接计算表明，不动点为\（（P_{2}，W_{2{）=（0.1368,0.1368）\）.根据定理4，地图(10)经历Neimark–Sacker分歧\（τ=τ{*}=1.959135）Neimark–Sacker分岔图如图所示7（a） 初始状态设置为\（（P_{2}+0.02，W_{2{+0.002）\）.区别数量σ为−4.95574。因此，对于\（tau>tau_{*}\），将出现一个吸引不变的循环。奈马克-萨克分歧可能导致混乱的出现。为了定量确定混沌和非混沌行为，我们绘制了最大Lyapunov指数（如图所示）7（b） ）对应于图7（a） ●●●●。

图7

Neimark–Sacker分岔和相应的最大Lyapunov指数图

从图的局部放大图7（b） ，如图所示8，我们发现当适当地选择τ值，例如\（τ=2.151）和2.21，最大Lyapunov指数可以在零以上，这意味着可能发生混沌行为。

图8

对应于图的最大李亚普诺夫指数的局部放大7(b条)

在下面，我们首先模拟map的动态行为(10)以获得稳定的焦点。然后我们利用相图展示了与Neimark–Sacker分岔图相关的从不动点到混沌行为的动态转变。

让\（τ=1.95），然后\（τ<τ{*}）.我们计算雅可比矩阵的特征值\（J（P_{2}，W_{2{）\）并获得和\（vert\lambda_{1,2}\vert=0.9919<1）因此，均匀定态\（（P_{2}，W_{2{）=（0.1368,0.1368）\）地图的(10)是一个稳定的焦点。选择初始状态\（（P_{2}+0.02，W_{2{+0.002）\）（图中的绿点9)，我们得到了一条带有离散点序列的轨迹（图中的蓝点9). 为了解释从初始状态到焦点的动态演变，我们将这些点按顺序连接到线段，并使用箭头指示从一个状态到下一个状态的方向。请参见图9。除了初始状态外，我们用\（ST_{1}\模拟ST_{15}\）并为前15个点指定两个箭头。一个箭头表示前一个状态，另一个箭头指示下一个状态。从初始状态开始的轨迹继续到\（ST_{1}\），然后到\（ST_{2}\），至\（ST_{3}\），至\（ST_{4}\）等等。从前15个点的演化可以得出结论，轨迹收敛到稳定焦点\（（P_{2}，W_{2{）\）逆时针方向。

图9

具有离散映射点序列的轨迹(10)带有\（τ=1.95）收敛到稳定焦点\（（P_{2}，W_{2}）=（0.1368,0.1368）\）

在续集中，与Neimark–Sacker分岔图相关的图7（a） ，我们使用相位肖像来明确地展示从稳定焦点到混沌行为的动态转变τ增加。请参见图10。在图中10（a） ，我们显示了稳定的焦点\（τ=1.95）.增加τ到1.9592，然后\（tau>tau_{*}\），定理4和Neimark–Sacker分岔图7（a） 暗示\（（P_{2}，W_{2{）\）失去稳定性成为不稳定焦点。一个吸引不变的圆是分叉的，请参见图10（b） ●●●●。此外，让\（τ=2.055），2.1，2.12，我们得到了一些其他振幅较大的不变环，如图所示10（c） （e）和（f）。继续增加τ，例如\（τ=2.07）,\（τ=2.14）、和\（套=2.19），我们得到了与图7（a） 分别出现周期8、周期11和周期6轨道，请参见图10（d） 和图11（a） 和（c）。根据图中的最大Lyapunov指数8，让\（τ=2.151）和2.21，我们得到了两个不同的混沌吸引子，请参见图11（b） 和（d）。从图10和图11，作为τ增加，映射(10)演示了从焦点到不变循环的动态转换，中间经历周期窗口，最后到混沌吸引子。

图10

不同参数值的相位图τ对应于图7指示地图的动态过渡(10)

图11

图的续10

在下面，我们将说明\（n次n=200次200次）具有空间步长的格\（增量=10）初始状态是均匀稳态的随机扰动\（（P_{2}，W_{2{）\）。所有显示的关于空间模式的图形都被视为CML模型的空间分布\（t=150{，}000-250{，{000\）.

在图中12（a） ，我们绘制\（Z_{m}\）与τ图并得到图灵不稳定性的临界值，即\（套=1.95912137）。在图中12（b） ，我们分别绘制了Neimark–Sacker分岔曲线和Turing分岔曲线。然后我们得到了两个模式形成区域：纯蒂林不稳定区域和奈马克-萨克-图灵不稳定区域。右边的两个区域都是无模式形成区域，一个是均匀定态区域，另一个是纯Neimark–Sacker分岔区域。

图12

(一)\（Z）_{米}-\陶\）图显示图灵分岔；(b条)\（τ-d_{W}）显示空间模式形成区域的图形

设置\（d_{P}=0.02\）,\（d_{W}=1.0\），我们展示了在纯时间和奈马克-萨克-图灵分岔和混沌下自组织的空间模式。

什么时候？\（τ=1.95），对应图10（a） ，然后\（τ<τ{*}）和\（\tau<\tau'\）此时，既不会发生Neimark–Saker分岔，也不会发生Turing分岔。从图13（a） ，我们看到了海壳生物量在均匀水平上的均匀分布。在\（τ=1.959125），然后\（τ’<τ<τ{*}）CML模型经历了纯周期不稳定性。从图13（b） ，我们可以看到斑点图案。让\（τ=1.9592），然后\（\tau>\tau'\）和\（tau>tau_{*}\）CML模型经历了Neimark–Sacker–Turing不稳定性。从图13（c） ，我们可以看到斑点图案变形了。光斑半径增加。继续更改的值τ，我们可以看到其他类型的图案，如圆形和螺旋形，如图所示13（d） –（f）和图14（a） –（b）。最后，当τ在2点151分左右，模式开始变得支离破碎。提出了镶嵌型图案。作为τ增加，图案最终呈现完全无序和混乱，请参见图14（c） –（e）。在空间模式的转换过程中，我们发现斑点模式先分裂为条纹，然后分裂为螺旋，最后分裂为镶嵌型。不规则性增加。请注意，在周期窗口中，空间模式与\（τ=2.14）（螺旋）和\（套=2.19）（马赛克）。对于这两种不同的混沌吸引子，空间模式都是镶嵌型的，但具有较大的值τ，空间格局更加零散。此外，在模拟过程中，我们发现图案也有一个周期。周期可能与由于Neimark–Sacker分叉而从不动点分叉的不变循环的周期有关。

图13

的空间模式W公司纯固化和Neimark–Sacker–Turing不稳定性下的自组织\（200\乘以200\）格子

图14

图的续13

5结论和讨论

在本文中，我们研究了具有离散时间和空间变量的草丛-莎草模型的齐次和非齐次动力学。首先，我们利用耦合映象格子方法开发了我们的系统。其次，通过一系列理论分析，我们分别给出了支持稳定齐次稳态、翻转分岔、Neimark–Sacker分岔和Turing不稳定性出现的参数的精确条件。最后，我们给出了一些数值例子来说明理论结果，并给出了丰富的空间模式。

值得注意的是，CML模型的动力学更加丰富。对于齐次行为，CMLs-tussock-sedge模型可能会经历翻转分岔和混沌，这在相应的连续系统中是不可能发生的。因此，tussock-sedge模型离散形式的齐次动力学更加丰富，尤其是混沌行为。值得注意的是，对于不动点，还有其他分岔类型，例如鞍节点分岔。这是我们下一步的研究工作。对于异质行为，图灵模式可以由四种机制生成：纯图灵不稳定性、翻转不稳定性、奈马克-萨克-图灵不稳定和混沌。一般来说，由翻转不稳定性引起的模式呈现出碎片在空间加倍的现象。当不动点是焦点时，纯周期不稳定性引起的模式可以是斑点型。此外，斑点图案显示出关于时间的周期性变形。如果CML模型经历Neimark–Sacker–Turing不稳定性，则诱导模式具有螺旋特征。在空间模式的转换中，我们观察到τ值影响图案中斑点的大小，请参见图13（b） –（c）。混沌引起的图案在时间和空间上都呈现无序行为。我们选择两个不同的值τ看看图案是否相同。事实上，这两种图案都呈现出不规则的图案。对于较大的τ，模式更为复杂和零散。

离散系统齐次动力学的丰富性，例如由翻转分岔和Neimark–Sacker分岔生成的多周期轨道、不变环和混沌吸引子，增强了组合机制下生成的模式的复杂性和多样性。不同的模式意味着离散系统可以呈现更丰富的时空自组织结构。