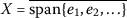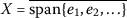方程的关联能量泛函(1.1)是
$$J(u)=\frac{1}{p}\hat{M}\bigl(\Vertu\Vert^{p}\ bigr)-\frac}\lambda}{q}\int_{{mathbb{R}}^{N}}g\vertu\Vert^{q}\,dx-\frac[1}{R}\int_{mathbb{R}{N}h\Vert u\Vert ^{R},dx$$
(2.1)
对于任何\(C_{0}^{\infty}({\mathbb{R}}^{N})中的v\),我们有
$$\begin{aligned}\bigl\langle J'(u),v\bigr\rangle={}&\bigl[M\bigl(\Vert u\Vert^{p}\bigr)\bigr]^{p-1}\int_{{\mathbb{R}}^{N}\bigle(\Vert\nabla u\Vert^{p-2}\nabla u \cdot\nablav+v\Vert u\Vert^{p-2}紫外\biger)\,dx\\&{}-\lambda\int_{{\mathbb{R}}^{N}}g\vert u\vert^{q-2}紫外\,dx-\int_{{\mathbb{R}}^{N}}h\vert u\vert^{r-2}紫外线\,dx。\结束{对齐}$$
(2.2)
我们这么说\({u}n}\}\)是一个\((PS)_{c}\)功能的顺序J型如果
$$\开始{对齐}J(u_{n})\到c\quad\text{和}\quad J'(u_})\to0\quad_text{in}X^{*},结束{对齐{$$
(2.3)
哪里\(X^{*}\)表示的对偶空间X(X)。如果每\((PS){c}\)序列J型有一个强收敛的子序列,那么我们说J型满足\((PS)\)条件。
定理的证明1.3主要依赖于以下山口引理[22](另请参见[23]).
引理2.1
让
电子
成为一个真正的巴拿赫空间
\(C^{1}(E,\mathbb{R})中的J)
具有
\(J(0)=0).假设
\((\mathrm{高}_{1})\)
有
\(\rho,\alpha>0\)
这样的话
\(J(u)\ge\alpha\)
对于
\(\|u\|_{E}=\rho\);
\((\mathrm{高}_{2})\)
有
\(e中的e),\({e}>\rho\)
这样的话
\(J(e)<0).定义
$$\Gamma=\bigl\{\Gamma\在C^{1}\bigl([0,1],E\bigr)|\Gamma(0)=0,\Gamma(1)=E\bigr\}中$$
然后
$$c=\inf_{\gamma\in\gamma}\max_{0\let\le1}J\bigl(\gamma(t)\bigr)\ge\alpha$$
是有限的,并且
\(J(\cdot)\)
拥有
\((PS){c}\)
水平顺序
c(c).此外,如果J满足
\((PS)\)
条件,则c是J的临界值.
在以下内容中,我们将进行验证J型满足山口引理的所有条件。
引理2.2
假设
\((\mathrm{A})\), (\(\mathrm){米}_{1}\))和(\(\mathrm{米}_{2}\))或(\(\mathrm{米}_{3}\)).还假设
\(p<\sigma r).然后是任何
\((PS){c}\)
J序列有界.
证明
让\({u}n}\}\)是任何\((PS){c}\)序列J型并满足(2.3).
由(\(\mathrm{米}_{1}\))和\((\mathrm{A})\),我们有
$$开始{对齐}c+1+\Vert u_{n}\Vert\ge{}&J(u_{n})-\frac{1}{r}\bigl\langle J'(u_}n}),u_{n}\bigr\rangle\\={}&\frac}1}{p}\hat{M}\bigle(\Vert u{n}\Vert^{p}\bigr)-\frac{1}\r}\bigl[M\bigl(\Vert u_{n}\Vert ^{p}\bigr)\bigr]^{p-1}\ Vert u_{n}\垂直^{p}-\lambda\biggl(\frac{1}{q}-\frac{1}{r}\biggr)\int_{{\mathbb{r}}^{N}}g\vertu{N}\vert^{q}\,dx\\ge{}&\biggl(\frac{\sigma}{p}-\压裂{1}{r}\biggr)\bigl[M\bigl(\Vertu_{n}\Vert^{p}\biger)\bigr]^{p-1}\Vertu_n}\Vert^{p}-\lambda\biggl(\frac{1}{q}-\frac{1}{r}\biggr)S_{q}^{-q/p}\Vertu{n}\Vert^{q}。\结束{对齐}$$
(2.4)
案例1.如果(\(\mathrm{M}_{2}\))持有。然后我们从(2.4)那个
$$\开始{aligned}c+1+\Vertu_{n}\Vert\ge\biggl(\frac{\sigma}{p}-\压裂{1}{r}\biggr)m_{0}^{p-1}\垂直u_{n}\垂直^{p}-\lambda\biggl(\frac{1}{q}-\压裂{1}{r}\biggr)S_{q}^{-q/p}\Vertu{n}\Vert^{q}。\结束{对齐}$$
(2.5)
因此\({u}n}\}\)有界。
案例2.如果(\(\mathrm{米}_{3}\))持有。让\(tau_{0}>0\)被修复。如果\(u{n}p}ge\tau{0}),然后
$$\开始{aligned}c+1+\Vertu_{n}\Vert\ge\biggl(\frac{\sigma}{p}-\frac{1}{r}\biggr)\bigl[M(\tau_{0})\bigr]^{p-1}\Vertu_{n}\Vert^{p}-\lambda\biggl(\frac{1}{q}-\frac{1}{r}\biggr)S_{q}^{-q/p}\Vertu{n}\Vert^{q},\end{aligned}$$
(2.6)
这意味着\({u}n}\}\)有界。□
引理2.3
假设
\((\mathrm{A})\), (\(\mathrm{米}_{1}\))和(\(\mathrm{米}_{2}\))或(\(\mathrm{米}_{4}\)).那么就有了
\(\rho,\alpha>0\)
这样的话
\(J(u)\ge\alpha\)
对于
\(\|u\|=\rho\).
证明
案例1. (\(\mathrm{M}_{2}\))感到满意。它源自(1.11), (2.1),以及(\(\mathrm{米}_{1}\))–(\(\mathrm{M}_{2}\))那个
$$\开始{对齐}J(u)&\ge\frac{\sigma}{p}m_{0}^{p-1}\Vert-u\Vert^{p}-\压裂{\lambda}{q} S公司_{q} ^{-q/p}\垂直u\垂直^{q}-\压裂{1}{r} S公司_{r} ^{-r/p}\垂直u\垂直^{r}\\&=\垂直u\Vert^{q}\biggl(\frac{\sigma}{p}m_{0}^{p-1}\Vertu\Vert^{p-q}-\压裂{\lambda}{q} S公司_{q} ^{-q/p}-\压裂{1}{r} S公司_{r} ^{-r/p}\Vert u\Vert ^{r-q}\biggr)。\结束{对齐}$$
(2.7)
表示\(φ(t)=在^{p-q}-B\λ-Ct ^{r-q}\)具有
$$\begin{aligned}A=\sigma m_{0}^{p-1}/p,\qquad B=S_{q}^{-q/p}/q,\qquad C=S_{r}^{-r/p}/r.\end{alinged}$$
(2.8)
显然,\(φ(t))达到最大值
$$\phi(t_{0})=\frac{r-p}{r-q}在_{0}^{p-q}-B\λ$$
在
$$t=t_{0}=\biggl(\frac{A(p-q)}{C(r-q)}\biggr)^{1/(r-p)}$$
让\(\lambda_{0}=\压裂{A(r-p)}{B(r-q)}t_{0}^{p-q}\),\(\rho=t_{0}\)、和\(α=t{0}^{q}\phi(t{0{)\).然后\(J(u)\ge\alpha>0)对于\(\|u\|=\rho\)和\([0,\lambda_{0}中的\lambda)\).
案例2. (\(\mathrm){米}_{4}\))已实现。让\(\|u\|=\rho\)然后,通过(1.11), (2.1),以及(\(\mathrm{米}_{1}\)),等一下
$$\开始{对齐}J(u)&\ge\frac{\sigma}{p}\bigl[M\bigl(\Vert u\Vert^{p}\bigr)\bigr]^{p-1}\Vert u \Vert^{p}-\压裂{\lambda}{q} S公司_{q} ^{-q/p}\垂直u\垂直^{q}-\压裂{1}{r} S公司_{r} ^{-r/p}\垂直u\垂直^{r}\\&=\rho^{q}\bigl(A(\rho)\rho^{p-q}-B\lambda-C\rho^{r-q}\biger),\end{对齐}$$
(2.9)
哪里\(A(\rho)=压裂{\sigma}{p}[M(\rho^{p})]^{p-1}\)和\(B、C)由定义(2.8). 鉴于(\(\mathrm{米}_{4}\)),\(J(u)\ge\alpha>0)为所有人\(0<\lambda<\lampda_{0}=\frac{1}{B}[A(\rho)\rho^{p-q}-C\rho^{r-q}]\). □
引理2.4
假设
\((\mathrm{A})\), (\(\mathrm{米}_{1}\))和
\(p<\sigma r).然后就有了
\(X中的e)
具有
\(\|e\|>\rho\)
这样的话
\(J(e)<0).
证明
通过集成(\(\mathrm{米}_{1}\)),我们获得
$$\beart{aligned}\hat{M}(t)\le\hat{M}(t_{1})\bigl(\frac{t}{t_{1}}\biggr)^{1/{\sigma}}quad\text{for all}t\ ge t_{1}>0。\结束{对齐}$$
(2.10)
因此,对于\(图{p}图{1}),
$$\开始{对齐}J(tu)\le\frac{1}{p}\hat{M}(t_{1})\biggl(\frac}\Vertu\Vert^{p}}{t{1}}\biggr)^{1/{\sigma}}t^{\frac{p}{\simma}}-t^{a{p}-t^{q}\ frac{\lambda}{q}\int_{\mathbb{R}}}^{N}}g \Vert u\Vert^{q}\,dx-t^{R}\ frac{1}{R}\int_{{\mathbb{R}}^{N}}h\Vert u \vertqu{R},dx。\结束{对齐}$$
(2.11)
因此,\(J(tu)<0)如果\(t \ge R)对一些人来说\(R>0)足够大。□
引理2.5
假设
\((\mathrm{A})\), (\(\mathrm{米}_{1}\))和(\(\mathrm{米}_{2}\))或(\(\mathrm{米}_{3}\)).然后是任何
\((PS){c}\)
J序列具有强收敛子序列.
证明
让\({u}n}\}\)是任何\((PS){c}\)序列J型并满足(2.3). 按引理2.2,\({u}n}\}\)有界。如有必要,传递到子序列
$$开始{对齐}和u_{n}\rightharpoonup u\quad\text{in}X,\\&u_{n}\to u\qua2\text{in}L^{q}\bigl({\mathbb{R}}^{n},g\bigr)\text{和}\text{in}L^{R}\bigle}{\mathbb{R}}^{n}。\结束{对齐}$$
表示\(P_{n}=langle J'(u_{n{),u_{n} -u个\范围\)和
$$Q_{n}=\bigl[M\bigl(\Vert u_{nneneneep \Vert ^{p}\bigr)\bigr]^{p-1}\int_{{mathbb{R}}^{n}}\bigle(\Vert\nabla-u\Vert^{p-2}\nabla-u \nabla(u_{n} -u个)+V\垂直u\垂直^{p-2}铀(u)_{n} -u个)\bigr)\,dx$$
我们很容易得到
$$开始{对齐}&\lim_{n\to\infty}P_{n}=0,\qquad\lim_}n\to\infty}Q_{n{=0,\\&\lim{n\to\ infty{int_{{mathbb{R}}^{n}}g(x)\vert u{n}\vert^{q-2}u_{n} (u)_{n} -u个)\,dx=0,\\&\lim_{n\to\infty}\int_{{\mathbb{R}}^{n}}h(x)\vert u_{n}\vert^{r-2}铀_{n} (u)_{n} -u个)\,dx=0。\结束{对齐}$$
自
$$\开始{对齐}P_{n} -问_{n} ={}&\bigl[M\bigl(\Vertu_{n}\Vert^{p}\bigr)\bigr]^{p-1}\int_{{\mathbb{R}}^{n}}\bigl-(\Vert\nabla-u_{nneneneep \Vert^{p-2}\nabla-u_{无}-\vert\nabla u\vert^{p-2}\nabla u\bigr)\nabla(u_{n} -u个)\,dx\\&{}+\bigl[M\bigl(\Vertu_{n}\Vert^{p}\bigr)\bigr]^{p-1}\int_{{mathbb{R}}^{n}}V\bigl(\vertu_{nC}\Vert^{p-2}铀_{n} -\vert u\vert^{p-2}铀\较大)(u_{n} -u个)\,dx\\&{}-\lambda\int_{{\mathbb{R}}^{N}g(x)\vert u_{N}\vert^{q-2}u_{n} (u)_{n} -u个)\,dx-\int_{{\mathbb{R}}^{N}}h(x)\vert u_{N}\vert^{r-2}铀_{n} (u)_{n} -u个)\,dx,\结束{对齐}$$
我们可以推断
$$开始{对齐}&\lim_{n\to\infty}\biggl\{\bigl[M\bigl(\Vertu_{n}\Vert^{p}\bigr)\bigr]^{p-1}\int_{{mathbb{R}}^{n}}\bigle(\Vert\nabla-u_{n{Vert^{p-2}\nabla-u_{无}-\vert\nabla u\vert^{p-2}\nabla u\bigr)\nabla(u_{n} -u个)\,dx\\&\quad{}+\bigl[M\bigl(\Vert u_{n}\Vert^{p}\bigr)\bigr]^{p-1}\int_{{mathbb{R}}^{n}}V\bigle(\Vert u_}\Vert^{p-2}铀_{n} -\vert u\vert^{p-2}铀\较大)(u_{n} -u个)\,dx\biggr\}=0。\结束{对齐}$$
(2.12)
案例1. (\(\mathrm{米}_{2}\))持有。使用中的标准不等式\({\mathbb{R}}^{N}\)由提供
$$\开始{aligned}\bigl\langle\vert x\vert^{p-2}x-\vert y\vert^{p-2}年,x-y\bigr\rangle\ge C_{p}\vert x-y\vert^{p}\squad\text{if}p\ge2\end{aligned}$$
(2.13)
或
$$\开始{aligned}\bigl\langle\vert x\vert^{p-2}x-\vert y\vert^{p-2}年,x-y\biger\rangle\ge\frac{C_{p}\vert x-y\vert^{2}}{(\vert x\vert+\vert y\vert)^{2-p}}\quad\text{if}2>p>1,\end{aligned}$$
(2.14)
我们从(2.12)那个\(\|u_{n} -u个\|\到0\)作为\(到英寸).
案例2.如果(\(\mathrm{米}_{3}\))保持,然后由于(1.1),必须考虑两种情况:\(\inf{n}\|u{n}\|>0\)或\(\inf{n}\|u{n}\|=0\).
案例2-1:\(\inf{n}\|u{n}\|>0\)然后我们可以从(2.12)–(2.14)那个\(\|u_{n} -u个\|\到0\)如情况1。
案例2-2:\(\inf_{n}\|u_{n}\|=0\)。如果0是序列的累加点\({\|u{n}\|\}\),则有一个子序列\({u}n}\}\)(未重新标记)\(u{n}\to0).因此\(0=J(0)=lim_{n\to\infty}J(u_{n})=c\).莱玛2.3,\(c>0)。这是不可能的。因此,0是\({\|u{n}\|\}\)。因此,存在以下子序列\({u}n}\}\)(未重新标记)\(\inf{n}\|u{n}\|>0\),我们可以像以前一样继续。
这就完成了证明。□
结论由引理得出2.2–2.5立即。□
得到问题的多重性结果(1.1),我们需要以下喷泉定理。
引理2.6
(喷泉定理[24])
让
X(X)
是具有规范的巴拿赫空间
\(\|\cdot\|\),然后让
\(X_{i}\)
是的子空间序列
X(X)
具有
\(\dim X_{i}<\infty\)
对于每个
\(i\in\mathbb{N}\).进一步,设置
$$X=\overline{\bigoplus_{i=1}^{\infty}X_{i}},\qquad Y_{k}=\bigoblus_{i=1}^{k} X(X)_{i} ,\qquad Z_{k}=\上划线{\bigoplus_{i=k}^{\infty}X_{i}}$$
考虑一个偶数函数
\(C^{1}中的\Phi\(X,\mathbb{R})\).假设,对于每个
\(k\in\mathbb{N}\),存在
\(\rho{k}>\gamma{k}>0)
这样的话
-
\((\Phi_{1})\):
-
\(a_{k}:=\max_{u\在Y_{k}中,\|u\|=\rho_{k}}\Phi(u)\le0\);
-
\((\Phi_{2})\):
-
\(b_{k}:=\inf_{u\in Z_{k},\|u\|=\gamma_{k}}\Phi(u)\to+\infty,k\to+\infty\);
-
\((\Phi_{3})\):
-
Φ满足
\((PS){c}\)
每个的条件
\(c>0\).
然后Φ具有无界的临界值序列.
显然,功能J型是均匀的。还有待验证J型满足\((\Phi_{1})\)–\((\Phi_{3})\)在引理中2.6.
它源自(2.10)那个
$$\开始{aligned}\hat{M}(t)\le C_{1} t吨^{1/\sigma}+C_{2}\结束{对齐}$$
对于正常数\(C_{1},C_{2}\)以及所有人\(第0页).因此
$$开始{对齐}J(u)\le\frac{1}{p}\bigl{N}}h\Vert u\Vert ^{R}\,dx。\结束{对齐}$$
(2.15)
因为所有范数在有限维空间上都是等价的\(Y_{k}\),我们都有\(Y_{k}中的u),
$$开始{对齐}J(u)\le\frac{1}{p}\bigl(C_{1}\Vert-u\Vert^{frac{p}{\sigma}}+C_{2}\bigr)-\lambda C_{3}\Vert u\Vert^{q} -C_{4} \垂直u\垂直^{r},\结束{对齐}$$
(2.16)
哪里\(C_{3},C_{4}\)为正常数。因此\(在Y{k}中a{k}:=max{u\,\|u\|=\rho{k}}J(u)<0\)对于\(\|u\|=\rho{k}\)足够大。这给\((\Phi_{1})\).
表示\(Z_{k}中的\beta{k}=\sup{u\,\|u\|=1}(\int_{{mathbb{R}}^{N}}h|u|^{R}\,dx)^{1/R}\).自\(Z_{k+1}\子集Z_{k}\),我们推断\(0\le\beta{k+1}\le\beta{k}\).因此\(\beta{k}\to\beta_{0}\ge0\)作为\(k到+infty)根据的定义\(β_{k}\),存在\(在Z{k}中为u{k}\)具有\(\|u_{k}\|=1\)这样的话
$$-\frac{1}{k}\le\beta_{k}-\biggl(\int_{{mathbb{R}}^{N}}h\vert u_{k}\vert^{R}\,dx\biggr)^{1/R}\le0$$
为所有人\(k\ge1)因此,存在一个子序列\({u{k})(未重新标记)\(u{k}\rightharpoonup u\)在里面X(X)和\(语言u,e_{j}^{*}\rangle=\lim_{k\to\infty}\langleu{k},e_}^{**}\range=0\)为所有人\(第1页)。因此,\(u=0)。这意味着\(u_{k}\右箭头框0\)在里面X(X)等等\(u{k}\to0)在里面\(L^{r}({\mathbb{r}}^{N},h)\).因此\(\beta_{0}=0\).证明\((\Phi_{2})\)分为以下两种情况。
案例1: (\(\mathrm{米}_{2}\))持有。对于任何\(u\在Z_{k}\中),有个保持
$$\开始{对齐}J(u)\ge\frac{\sigma}{p}m_{0}^{p-1}\Vert-u\Vert^{p}-\压裂{\lambda}{q} S公司_{q} ^{-q/p}\垂直u\垂直^{q}-\裂缝{1}{r}\beta_{k}^{r}\垂直u\Vert^{r{。\结束{对齐}$$
(2.17)
设置
$$\gamma_{k}=\biggl(\frac{\sigma m{0}^{p-1}r}{4p\beta{k}^{r}}\biggr)^{\frac{1}{r-p}},\qquad\lambda{1}=\frac{\sigmaqm{0}^{p-1}}{2p}\gamma{1}^{p-q}S_{q} ^{q/p}$$
然后
$$开始{对齐}J(u)\ge\frac{\sigma}{4p}m_{0}^{p-1}\gamma{k}^{p}\end{aligned}$$
(2.18)
为所有人\(\lambda\in(0,\lambda_{1})\)和\(u=gamma{k}).因此\((\Phi_{2})\)已实现。
案例2: (\(\mathrm){米}_{3}\)), (\(\mathrm{米}_{5}\))保持。对于\(\|u\|=\rho\),我们有
$$\开始{对齐}J(u)和\ge\frac{\sigma}{p}\bigl[M\bigl(\rho^{p}\ bigr)\bigr]^{p-1}\rho^{p}-\压裂{\lambda}{q} S公司_{q} ^{-q/p}\rho^{q}-\压裂{1}{r} S公司_{r} ^{-r/p}\rho^{r}。\结束{对齐}$$
(2.19)
设置
$$\widetilde{\gamma}_{k}=\biggl(\frac{\sigma[M(\gamma_1}^{p})]^{p-1}r}{4p\beta{k}^{r}}\biggr)^{\frac{1}{r-p}},\qquad\widetilde{\lambda}{1}=\frac}\sigmaq[M(\gamma{1}^{p})]^{p-1}}{2p}\gamma_{1}^{p-q}S_{q} ^{q/p}$$
然后由(\(\mathrm{米}_{5}\))
$$开始{对齐}J(u)\ge\frac{\sigma}{4p}\bigl[M\bigl(\widetilde{\gamma}_{1}^{p}\bigr)\bigr]^{p-1}\gamma_{k}^{p}\end{aligned}$$
(2.20)
为所有人\((0,\widetilde{\lambda}_{1})中的\lambda)和\(u=widetilde{gamma}_{k}\).因此\((\Phi_{2})\)已实现。
按引理2.5,我们获得\((\Phi_{3})\)因此,结论遵循喷泉定理。□