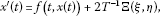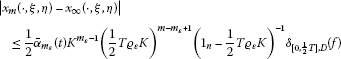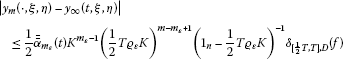摘要
介绍
1问题设置和基本假设


2符号和符号
-
1 是维度的单位矩阵 n个 . -
2 是矩阵的最大模特征值 K(K) . -
三。 给定一个闭合区间 ,我们定义向量 通过设置 (2.1) -
4 , :见(10.5)。 -
5 ∂ Ω是域Ω的边界。 -
6 :见定义10.1。
三 对 -周期逐次逼近


-
1 顺序 (3.4) 收敛到极限函数 (3.7)
-
2 极限函数 (3.7) 满足 对 - 周期边界条件 -
三。 功能 是柯西问题的唯一解决方案 
(3.8)

-
4 给定任意小的正数 ε , 人们可以选择一个数字 这样估计
-
1 给定一个 , 函数 是解决 对 - 周期边值问题 (3.2), (3.3) 当且仅当 z(z) 是方程的根 (3.15) -
2 对于任何解决方案 问题的 (3.2), (3.3) 具有 , 存在一个 这样的话 .
4间隔减半、参数化和粘合




5半程迭代





6逐次逼近及其收敛性


-
1 制服 , 在里面 , 限制 (6.6)
-
2 功能 是柯西问题的唯一解决方案 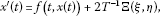
(6.8)

-
三。 给定任意小的正数 ε , 人们可以指定一个数字 这样的话 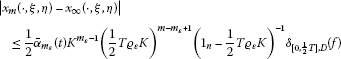
(6.11)
-
1 制服 , 在里面 , 限制 (6.13)
-
2 功能 是柯西问题的唯一解决方案 
(6.15)

-
三。 对于任意小的正值 ε , 人们可以找到一个数字 这样的话 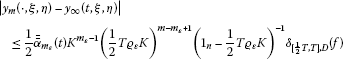
(6.18)


7辅助语句
-
1 对于 , (7.2) -
2 对于 , (7.3)

8极限函数和确定方程
-
1 功能 由定义 (8.1) 是周期边值问题的解 (1.3), (1.4) 当且仅当这对 满足系统 2 n个 方程式 (8.2) -
2 对于每个解决方案 问题的 (1.3), (1.4) 具有 , 存在一对 这样的话 .
9近似确定方程



10基于近似的可解性分析
11解的近似
12示例




13条评论
13.1实际近似方案
13.2其他问题的扩展
13.3可变子区间长度
13.4小间隔的适用性
13.5与其他方法相比的优势
13.6重复间隔减半
13.7与其他方法的结合
13.8高阶近似的非退化条件
13.9与延拓定理的关系


参考文献
RontóA,Rontó)M:周期连续逼近和区间减半。 Miskolc数学。 笔记 2012, 13(2):459-482. 尼伦伯格L: 非线性泛函分析主题 纽约大学数学科学学院,纽约; 1974年。(E.Zehnder的一章,R.a.Artino的笔记,演讲笔记,1973-1974) Gaines RE,Mawhin JL数学课堂笔记568。 在 重合度与非线性微分方程 施普林格,柏林; 1977 Cesari L Ergebnisse der Mathematik and Ihrer Grenzgebiete,N.F.第16页。 在 常微分方程的渐近性与稳定性问题 第二版。 纽约学术出版社; 1963 海尔JK: 非线性系统的振动 McGraw-Hill,纽约; 1963 Samoilnko AM:研究常微分方程周期系统的数值分析方法。 一、。 乌克兰。 数学。 J。 1965, 17(4):82-93. 2007年10月10日/BF02526569 Samoilnko AM:研究常微分方程周期系统的数值分析方法。 二、。 乌克兰。 数学。 J。 1966, 18(2):50-59. 2007年10月10日/BF02537778 Samoilenko AM:关于多项式序列及其Abel-Poisson和的收敛半径。 乌克兰。 数学。 J。 2003, 55(7):1119-1130. doi:10.1023/B:UKMA.000010610.69570.13 Samoilenko AM,Ronto NI: 研究周期解的数值分析方法 .米尔,莫斯科; 1979年(由Yu.a.Mitropolskii作前言) Samoilenko AM,Ronto NI: 边值问题研究的数值分析方法 .基辅Naukova Dumka; 1986年。(俄语,英文摘要,由Yu.a.Mitropolskii编辑并附有前言) Samoilenko AM,Ronto NI: 常微分方程边值问题理论中的数值分析方法 .基辅Naukova Dumka; 1992年。(俄语,Yu.a.Mitroposkii编辑并作序) RontóA,Rontó)M:常微分方程非线性边值问题中的逐次逼近技术。 把手b。 不同。 埃克。 在 微分方程手册:常微分方程。 第四卷 爱思唯尔/荷兰北部,阿姆斯特丹; 2008:441-592. RontóA,RontoóM:具有特殊变元偏差的微分方程某些线性边值问题的逐次逼近方法。 Miskolc数学。 笔记 2009年,10:69-95。 RontóA,RontoóM:关于具有变元偏差的线性微分方程的Cauchy-Nicoletti型三点边值问题。 Miskolc数学。 笔记 2009, 10(2):173-205. RontóA,Rontó)M:关于线性泛函微分方程的非分离三点边值问题。 文章摘要。 申请。 分析。 2011年、2011年:文章ID 326052。 doi:10.1155/2011/326052 Ronto A,RontóM:关于非线性两点边值问题的数值分析方法的一个注记。 非线性Oscil。 2001, 4: 112-128. 朗托A,朗托M:关于周期解的一些对称性质。 非线性Oscil。 2003, 6: 82-107. doi:10.1023/A:1024827821289 10.1023/A:1024827821289 RontóM,Shchobak N:关于非线性边界条件参数化问题的数值分析研究。 非线性Oscil。 2003, 6(4):469-496. doi:10.1023/B:NONO.000028586.11256.d7 RontóM,Shchobak N:关于分离条件下非线性边值问题的参数化。 电子。 J.资格。 理论不同。 埃克。 2007, 18: 1-16. Ronto AN,Ronto M,Shchobak NM:关于三点非线性边值问题的参数化。 非线性Oscil。 2004, 7(3):384-402. 2007年10月10日/11072-005-0019-5 Ronto AN,RontóM,Samoilnko AM,Trofimchuk SI:关于自治差分方程的周期解。 格鲁吉亚数学。 J。 2001, 8: 135-164. RontóM,Mészáros J:关于连续逼近的数值分析方法收敛性的一些评论。 乌克兰。 数学。 J。 1996, 48: 101-107. doi:10.1007/BF02390987 10.1007/BF02 390987 RontóM,Samoilenko上午: 边值问题理论中的数值分析方法 《世界科学》,River Edge; 2000年。(Yu.a.Mitroposky作序,作者和S.I.Trofimchuk附录) RontóA,Rontó》:线性泛函微分方程组三点边值问题的存在性结果。 卡帕斯。 数学杂志。 2012, 28: 163-182. Kwapisz M:关于Samoilnko解边值问题的数值分析方法积分方程的修正。 数学。 纳克里斯。 1992, 157: 125-135. Kwapisz M:关于Samoilnko求解差分方程边值问题的数值分析方法的修正。 申请。 数学。 1993年,38(2):133-144。 RontóA,RontoóM,HolubováG,Nečesal P:研究具有Dirichlet条件的非线性方程解的数值分析技术。 已绑定。 价值问题。 2011年、2011年:文章ID 58。 doi:10.1186/1687-2770-2011-58 Mawhin J CBMS数学区域会议系列40。 在 非线性边值问题的拓扑度方法 美国数学。 普罗维登斯; 1979年。(1977年6月9日至15日在加利福尼亚州克莱蒙特哈维·穆德学院举行的CBMS地区会议上的公开讲座)