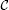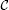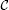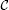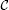引理3.1 对于任何 ,三者的独特解决方案-点边值问题
(6)
由提供
证明对于,通过引理2.1,我们知道方程的一般解可以写为
(7)
哪里是任意常数。自,,,我们有
使用边界条件,我们得到
因此,我们有
替换的值,在(7)中,我们得到了结果。这就完成了证明。□
从引理3.1的证明中,我们注意到当,也就是说,(4)中的不分离特征比(1)中的更为明显。
让和是所有连续实函数的Banach空间J进入之内ℝ配备标准.鉴于引理3.1,我们定义了一个算子如下
请注意,当且仅当操作员具有固定点。我们表示为,其中
这里是常数和由提供
现在,我们可以展示我们的主要成果。
定理3.1
假设
连续且满足
对于 ,,和 .如果
(8)
然后是问题(4)有独特的解决方案,哪里
证明表示。对于任何和每个,我们有
因此,我们有
这与(8)一起意味着ℱ是收缩映射。收缩映射原理得出ℱ具有唯一不动点,这是问题(4)的唯一解。这就完成了证明。□
推论3.1
假设
连续且满足
对于 ,,和 .然后是问题(4)有独特的解决方案,假如
定理3.2 让 是连续函数.假设
对于每个 ,,, 和 .然后是问题(4)至少有一个解决方案.
证明让,,其中
请注意是Banach空间的封闭有界凸子集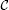 .
.
首先,我们证明。对于任何,我们有
因此,我们有
这意味着.
其次,我们证明ℱ将有界集映射为等连续集。让B类是任意有界集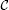 。请注意(f)持续打开J因此,在不失一般性的情况下,我们可以假设N个这样的话
。请注意(f)持续打开J因此,在不失一般性的情况下,我们可以假设N个这样的话
对于任何和现在,我们让然后针对每个,我们有
和
因此,我们有
并且该极限与因此,操作员是等连续且一致有界的。Arzela-Ascoli定理意味着相对紧凑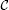 根据定理2.1,我们知道问题(4)至少有一个解。证明已完成。□
根据定理2.1,我们知道问题(4)至少有一个解。证明已完成。□
推论3.2 假设 对于 , 具有 .然后是问题(4)至少有一个解决方案.
定理3.3 让 是连续函数.假设
-
(1)
存在一个函数 和一个非-递减函数 这样的话
哪里 ,;
-
(2)
存在一个常数
这样的话
哪里
然后是问题(4)至少有一个解决方案.
证明首先,我们证明ℱ将有界集映射为中的有界集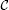 .让B类是的有界子集
.让B类是的有界子集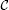 和对于任何.在定理3.2的证明中,我们有
和对于任何.在定理3.2的证明中,我们有
因此,
其次,我们声称ℱ是等连续的。该权利要求的证明与定理3.2的证明相同。
最后,我们让对一些人来说。然后针对每个,我们有
这意味着
根据假设,我们知道存在K(K)这样的话.让
操作员是连续的和完全连续的。结合以下选项O(运行)和定理2.2,我们可以推断ℱ在中有一个固定点,这是问题(4)的解决方案。□