摘要







2.基本概念





























































































































3.主要成果


























































































































































































































































参考文献
穆斯塔法Z,西姆斯B: 广义度量空间的一种新方法。 非线性与凸分析杂志 2006, 7 (2):289–297. Mustafa Z,Obiedat H,Awawdeh F:完备映射的不动点定理 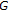
-度量空间 不动点理论及其应用 2008, 2008: -12. 穆斯塔法Z,西姆斯B: 关于-度量空间的一些注记。 在 不动点理论和应用国际会议记录,2004年,日本横滨 .横滨; 189–198之间。 Mustafa Z,Sims B:完全压缩映射的不动点定理 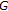
-度量空间 不动点理论及其应用 2009, 2009: -10. Mustafa Z,Shatanawi W,Bataineh M:不动点的存在导致 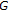
-度量空间 国际数学与数学科学杂志 2009, 2009: -10. 马可夫斯基J: 点上具有压缩迭代的映射的不动点定理。 美国数学学会会刊 1977, 62 (2):344–348. 10.1090/S0002-9939-1977-0436113-5 穆斯塔法Z: 广义度量空间的一种新结构及其在不动点理论中的应用,博士论文 .英国纽卡斯尔纽卡斯尔大学; 2005