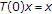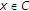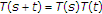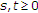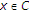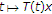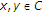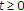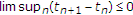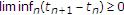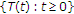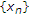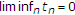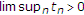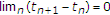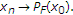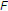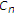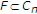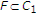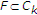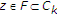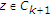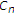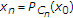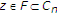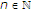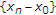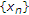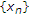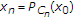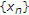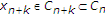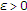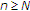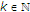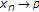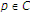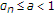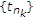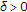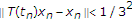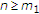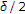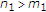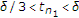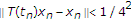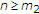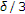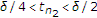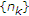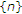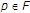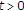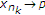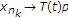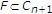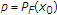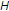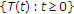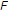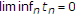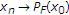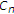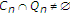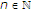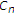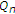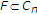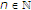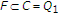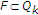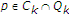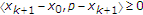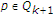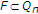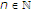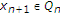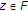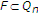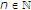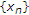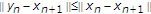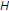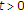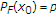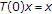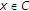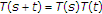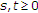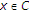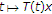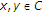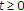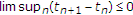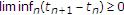2.1. 收缩投影法
以下方法由Takahashi等人在[5]. 我们使用此方法来近似不含Bochner积分的非扩张半群的公共不动点,如[5,定理4.4]。
定理2.1。
让 是实Hilbert空间的闭凸子集
是实Hilbert空间的闭凸子集 .让
.让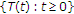 是上的非扩张半群
是上的非扩张半群 具有非空公共不动点
具有非空公共不动点 也就是说,
也就是说, 。假设
。假设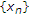 是由以下方案迭代生成的序列:
是由以下方案迭代生成的序列:
哪里 ,
,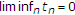 ,
,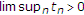 、和
、和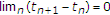 .然后
.然后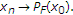
证明。
众所周知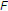 是封闭和凸的。我们首先证明了迭代格式的定义。看看每个
是封闭和凸的。我们首先证明了迭代格式的定义。看看每个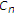 是非空的,这足以表明
是非空的,这足以表明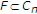 .通过归纳法进行证明。显然,
.通过归纳法进行证明。显然,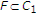 。假设
。假设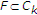 然后,对于
然后,对于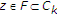 ,
,
那就是,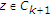 根据需要。
根据需要。
请注意
是凸的,因为
这意味着每个子集 是凸的。很明显
是凸的。很明显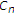 已关闭。因此,第一个主张得到了证明。
已关闭。因此,第一个主张得到了证明。
接下来,我们证明 有界。作为
有界。作为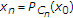 ,
,
特别是,对于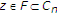 为所有人
为所有人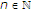 ,序列
,序列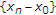 是有界的,因此也是
是有界的,因此也是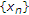 .
.
接下来,我们展示一下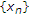 是一个柯西序列。作为
是一个柯西序列。作为 和
和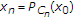 ,
,
此外,由于序列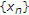 有界,
有界,
请注意
特别是,因为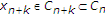 为所有人
为所有人 ,
,
然后,它是由 那个
那个 是一个柯西序列。事实上,对于
是一个柯西序列。事实上,对于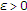 ,存在一个自然数
,存在一个自然数 这样,对所有人来说
这样,对所有人来说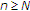 ,
,
哪里 特别是,如果
特别是,如果 和
和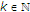 ,然后
,然后
此外,
我们现在假设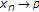 对一些人来说
对一些人来说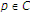 。从现在起
。从现在起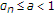 为所有人
为所有人 和
和 ,
,
最后一个收敛点来自(2.12)。我们选择一个序列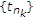 正实数的
正实数的
我们现在展示如何构造这样一个特殊的子序列。首先我们修复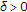 这样的话
这样的话
从(2.13),存在 这样的话
这样的话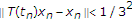 为所有人
为所有人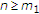 .根据引理1.1,
.根据引理1.1,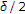 是的群集点
是的群集点 特别是
特别是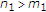 这样的话
这样的话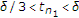 。接下来,我们选择
。接下来,我们选择 这样的话
这样的话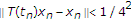 为所有人
为所有人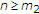 再次通过引理1.1,
再次通过引理1.1,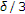 是的群集点
是的群集点 这意味着存在
这意味着存在 这样的话
这样的话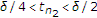 继续这样,我们得到了一个子序列
继续这样,我们得到了一个子序列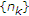 属于
属于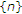 令人满意的
令人满意的
因此,满足(2.14)。
我们接下来会展示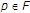 。为了看到这一点,我们修复
。为了看到这一点,我们修复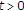 ,
,
作为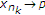 (2.14),我们有
(2.14),我们有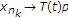 等等
等等 .
.
最后,我们证明 .自
.自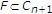 和
和 ,
,
但是 ; 我们有
; 我们有
因此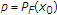 根据需要。这就完成了证明。
根据需要。这就完成了证明。
2.2. 混合方法
我们考虑使用混合方法(一些作者称之为CQ方法)进行迭代方案计算。He和Chen证明了以下结果[三]. 然而,证据的重要部分似乎被忽视了。这里我们给出了在参数的一些附加限制下的修正 .
.
定理2.2。
让 是实Hilbert空间的闭凸子集
是实Hilbert空间的闭凸子集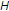 .让
.让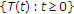 是上的非扩张半群
是上的非扩张半群 具有非空公共不动点
具有非空公共不动点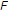 也就是说,
也就是说, 。假设
。假设 是由以下方案迭代生成的序列:
是由以下方案迭代生成的序列:
哪里 ,
,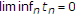 ,
, 、和
、和 .然后
.然后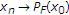 .
.
证明。
为了清晰起见,我们给出了整个草图的证明,即使证明的某些部分与[三]. 为了确保方案得到了很好的定义,只需表明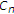 和
和 是封闭和凸的,并且
是封闭和凸的,并且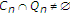 为所有人
为所有人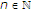 从定义中很容易得出以下结论:
从定义中很容易得出以下结论: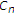 和
和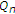 只是…的交叉点
只是…的交叉点 和半空间,
和半空间,
与前面定理的证明一样,我们有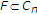 为所有人
为所有人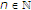 显然,
显然,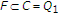 。假设
。假设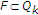 对一些人来说
对一些人来说 ,我们有
,我们有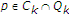 特别是,
特别是,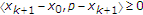 也就是说,
也就是说,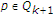 根据归纳法
根据归纳法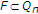 为所有人
为所有人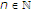 这证明了这一说法。
这证明了这一说法。
我们接下来会展示 为了看到这一点,我们首先证明
为了看到这一点,我们首先证明
作为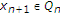 和
和 ,
,
对于固定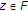 。它源自
。它源自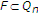 为所有人
为所有人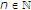 那个
那个
这意味着序列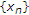 有界且
有界且
请注意
这意味着
然后根据 那个
那个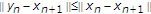 因此
因此
如定理2.1所示,我们可以选择子序列 属于
属于 这样的话
这样的话
因此,对于任何 ,
,
这意味着
根据Opial的情况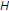 ,我们有
,我们有 为所有人
为所有人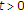 也就是说,
也就是说, 接下来,我们观察到
接下来,我们观察到
这意味着
因此,
因此,整个序列必须收敛到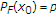 ,根据需要。
,根据需要。