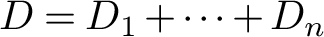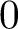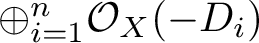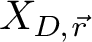THE LOCAL-ORBIFOLD CORRESPONDENCE FOR SIMPLE NORMAL CROSSING PAIRS

Luca Battistella; Navid Nabijou; Hsian-Hua Tseng; Fenglong You

doi:10.1017/S1474748022000172

简单正规交叉对的局部对数对应

部分：射影几何和枚举几何曲线

剑桥大学出版社在线出版：2022年3月25日

卢卡·巴蒂斯特拉 ,

纳维德·纳比茹 ,

谢华曾

和

丰隆优

显示作者详细信息

卢卡·巴蒂斯特拉: 附属：
德国海德堡纽恩海默费尔德205号鲁普列支卡尔斯大学海德堡数学研究所，邮编：69120(lbattestella@mathi.uni-heidelberg.de)
纳维德·纳比茹: 附属：
剑桥大学纯粹数学和数学统计系，英国剑桥CB3 0WB威尔伯福斯路数学科学中心(nn333@cam.ac.uk)
谢华曾*: 附属：
俄亥俄州立大学数学系，美国俄亥俄州哥伦布市西18大道231号100号数学大厦，邮编：43210
凤龙游: 附属：
奥斯陆大学数学系，Niels Henrik Abels hus，Moltke Moes vei 35，0851 Oslo，Norway(youf@math.uio.no)
*: hhtseng@math.ohio-state.edu

文章内容

权限和权限

摘要

对于X（X）一个光滑投影簇和$D=D_1+\dotsb+D_n$作为一个简单的正规交叉因子，我们在属之间建立了精确的循环级对应$0$局部Gromov–维滕束理论$\oplus_{i=1}^n\mathcal{O} X（_X）（-D_i）$以及多根堆栈的最大接触Gromov–Witten理论$X_{D，\vec r}$证明是降阶策略的实施。我们用这个观点来阐明对数不变量和球形不变量之间的关系。

关键词

Gromov–Witten不变量眼眶局部Gromov–Witten不变量产品配方等级降低

MSC分类

主要用户： 14N35:Gromov成文不变量、量子上同调、Gopakumar-Vafa不变量、Donaldson-Thomas不变量

次要： 14H10：模族（代数）

类型: 研究文章
问询处: Jussieu数学研究所期刊 ,第22卷 ,第5期 2023年9月第2515-2531页

内政部：https://doi.org/10.1017/S1474748022000172 [在新窗口中打开]
知识共享: 这是一篇开放存取文章，根据知识共享署名许可证的条款分发(https://creativecommons.org/licenses/by/4.0)允许不受限制地重复使用、分发和复制，前提是正确引用了原始文章。
版权: ©作者，2022年。剑桥大学出版社出版

1介绍

让X（X）是一个光滑的投影变体 $D=D_1+\dotsb+D_n$ 一个带nef分量的简单正规交叉因子 $D_i（美元）$ .我们研究了该属之间的关系 $0$ 当地格罗莫夫-维滕理论 $\oplus_{i=1}^n\mathcal O_X（-D_i）$ 和属 $0$ orbifold Gromov–Witten多根堆栈理论 $X_{D，\vec r}$ 我们的主要结果是对[推荐曾和你27，推测1.8]：

定理A（定理2.1）

让 $\测试版$ 成为曲线类X（X）具有 $d_i:=d_i\cdot\beta>0$ 对于 $i\in\{1，\dotsc，n\}$ 。对于美元_i$ 两两互质且足够大，以下恒等式在模空间上成立 $\mathsf美元{克}_｛0，m｝（X，\β）$ 的稳定映射到X（X）:

$$\开始{align*}\rho_\star\left[\mathsf{K}^{max}_{0，\left（I_1，\dotsc，I_m\right）}\left j^\星\左（\cup_{I\在I_j}D_I\右）\右）\\&\quad\cap\left[\mathsf{克}_{0，m}\左（\oplus_{i=1}^n\mathcal{O} X（_X）（-D-i），\beta\right）\right]^{\operatorname{virt}}，\end{align*}$$

哪里 $I_j\substeq\｛1，\dotsc，n\｝$ 记录标记的除数集 $x_j$ 与相切（参见§2.1详细信息），以及 $\rho美元$ 是忘了球形结构的态射。

这推广了光滑除数局部算术对应[参考van Garrel、Graber和Ruddat29]将多根堆栈的orbifold理论解释为对数理论的替代，从而实现简单的正交点设置[推荐曾和你26].

什么时候？D类平滑，定理A类根据先前的结果，将局部不变量和球形不变量与相对不变量等同[参考阿布拉莫维奇、卡德曼和怀斯1,参考van Garrel、Graber和Ruddat29,推荐曾和你28]. 对于一般情况D类，关键观察是局部和orbifold理论都满足稳定映射空间上的乘积公式X（X）.定理A类紧接着，通过从平滑除数情况引导。这是Gromov–Witten理论中“降阶”技术的另一种表现[参考Abramovich和Chen2,参考Nabijou和Ranganathan22].

1.1对数Gromov–Witten理论

与局部和orbifold理论不同，对数理论不满足稳定映射空间上朴素的乘积公式X（X）。该观察结果用于[参考Nabijou和Ranganathan22]给出局部算术猜想的反例。同样的推理表明，球形不变量也不同于对数不变量（并且很容易找到最大接触设置以外的反例）。事实上，推论3.4将orbifold不变量与所谓的朴素不变量，引入于[参考Nabijou21，§3]，并在[参考Nabijou和Ranganathan22]:

定理B（推论3.4）

多根堆栈的球状不变量与朴素不变量一致，因此与对数不变量不同。这适用于任意选择联系顺序。

总之，有四个属 $0$ 与简单正交点对相关的最大接触理论：对数、orbifold、naive和local。它们之间的关系如下：

球形、局部和朴素的理论都与组合因素相吻合。对数理论在更本质的方面有所不同，尽管有一个原则上的程序将其与其他三个理论联系起来。

尽管循环级局部-算术对应失败，但仍有许多目标和插入的选择，这些对应在数值级上保持不变。当插入终止中描述的校正项时，会发生这种情况[参考Nabijou和Ranganathan22，定理3.4]。在[参考Bousseau、Brini和van Garrel7,参考Bousseau、Brini和van Garrel8,参考Bousseau、Brini和van Garrel9]建立了大量的数值局部算术对应实例：对于复曲面品种，对数Calabi–Yau曲面和orbifold对数Calabi-Yau曲面；英寸[参考Nabijou和Ranganathan22，§5]，建立了产品几何的数字对应关系。作为定理的推论A类，所有这些对数不变量都与相应的球形不变量相一致。

这些不同的理论是用非常不同的技术来处理的。圆环定位以各种形式应用于计算球面不变量和局部不变量[参考Klemm和Pandharipande18,参考Coates、Corti、Iritani和Tseng11,范、曾和尤的参考资料12]; 另一方面，对数不变量通常使用热带对应定理和散射图计算[参考Nishinou和Siebert23,参考Gross、Pandharipande和Siebert15]. 根据上下文，一种技术可能比另一种更有效。这些通信在不同技术之间架起了桥梁，从而增加了Gromov–Witten理论中可用的计算工具。

1.2与以往工作的关系

定理的光滑除子情形A类然后结合轨道对数对应关系[参考阿布拉莫维奇、卡德曼和怀斯1,推荐曾和你28]以强有力的形式[参考范和武13,推荐曾和你27]局部算术对应[参考van Garrel、Graber和Ruddat29]. 定理的几个例子A类对于正常交叉因子，在中进行了数值验证[推荐曾和你27，§5.2]，通过计算J型-双方的职能。

1.3用户指南

我们提供了两种降秩方法。第一个（§2)使用根堆栈的迭代构造和投影公式，并依赖于某些光滑球面对的局部或局部对应（定理2.2). 第二个（§三)在稳定映射到粗模空间的空间上使用球面不变量的乘积公式（定理3.1). 这适用于任意相切阶，但需要一个正假设。球形不变量和朴素不变量的识别（推论3.4)是一个直接的后果。

2降阶一：投影公式

2.1几何设置

固定一个光滑投影簇X（X）和一个简单的正规交叉因子 $D=D_1+\dotsb+D_n\substeq X$ .对于两两互素和足够大的整数组成的元组 $\vec r=（r_1，\dotsc，r_n）$ ，我们形成关联的多根堆栈

$$\begin{align*}\mathcal{X}=X_{D，\vec r}。\结束{align*}$$

考虑米标记的点 $x_1，\dotsc，x_m$ 并修复索引集的有序分区 $\{1，\dotsc，n\}$ 成为不相交的子集 $I_1，\dotsc，I_m$ 这样的话 i_j}D_i中的$\cap_{i\$ 每个都不是空的 $j\in\{1，\dotsc，m\}$ .修复曲线类 H_2^+（X）中的$\beta\$ 这样的话 $d_i:=d_i\cdot\beta>0$ 为所有人我.

我们考虑亏格的模问题 $0$ 相对于的稳定映射美元（X，D）$ ，使得标记 $x_j$ 具有最大联系顺序 $d_i（美元）$ 每个除数 $D_i（美元）$ 具有 i_j中的$i\$ 。请注意美元（_j）$ 可能为空，对应于无相切条件的标记。一些标记可能沿几个除数同时具有正的接触顺序，这特别意味着它们应该映射到交点。

这个模问题决定了多根堆栈的orbifold稳定映射的模问题的相关离散数据 $\mathcal{X}$ ，通过进行每个标记 $x_j$ 有扭转指数

$$\开始{align*}s_j=\prod_{i\在i_j}r_i.\end{align**}$$

扭曲扇区插入

$$\begin{align*}\mu_{s_j}=\prod_{i\ in i_j}\mu_{r_i}\end{aling*}$$

由于源和目标的扭曲指数相同，因此与切线阶元组一致[参考Cadman和Chen10, §2.1]. 我们将相关模空间表示为

$$\开始{align*}\mathsf{K}^{max}_{0，\left（I_1，\dotsc，I_m\right）}（\mathcal{X}，\beta）\end{align**}$$

然后让 $\rho美元$ 表示忘记球形结构的态射：

$$\开始{align*}\rho\colon\mathsf{K}^{max}_{0，\left（I_1，\dotsc，I_m\right）}（\mathcal{X}，\beta）\to\mathsf{克}_{0，m}（X，\beta）。\结束{align*}$$

2.2本地-本地通信

我们的主要结果是多根轨道理论和相关分裂向量束的局部理论之间的循环级对应，证明[推荐曾和你27，推测1.8]：

定理2.1。对于美元_i$ 足够大，我们有

$$开始{align*}\rho_\star\left[\mathsf{K}^{max}_{0，\left（I_1，\dotsc，I_m\right）}（\mathcal{X}，\beta）\right]^{\operatorname{virt}}&=\left \cup_{I\in I_j}d_I\right）\right（右）\&\quad\cap\left[\mathsf｛K｝_｛0，m｝\left（oplus_｛i=1｝^n\mathcal{O} X（_X）（-D-i），\beta\right）\right]^{\operatorname{virt}}。\结束{align*}$$

案例 $n=1$ 然后组合平滑除数局部算术对应[参考van Garrel、Graber和Ruddat29]以其强大的形式（参见[参考范和武13，简介]或[推荐曾和你27，方程（2）]），以及光滑除数对数-双折对应[参考阿布拉莫维奇、卡德曼和怀斯1,推荐曾和你28].

证明。我们通过归纳法n个.基本情况 $n=1$ 已经讨论过了。对于归纳步骤，考虑根堆栈

$$\begin{align*}\mathcal{Z}=X_{left（D_1，\dotsc，D_{n-1}\right），\left（r_1，\ dotsc、r_{n-1\right）}。\结束{align*}$$

出租 $p\colon\mathcal{Z}\到X$ 是粗模空间的同构 $\mathcal美元{D} _n（n）=p^{-1}D_n$ ，我们有

$$\开始{align*}\mathcal{X}=\mathcal{Z}（Z）_{\马塔尔{D} _n（n），序号}。\结束{align*}$$

有序分区 $（I_1，\dotsc，I_m）$ 属于 $\{1，\dotsc，n\}$ 引入分区 $（J_1，\dotsc，J_m）$ 属于 $｛\｛1，\dotsc，n-1｝｝$ 通过设置 $J_J=I_J\设置减号\{n\}$ 考虑模空间的塔

归纳假说给出了

(1)

$$开始{align}\varphi_\star\left[\mathsf{K}^{max}_{0，\left（J_1，\dotsc，J_m\right）}（\mathcal{Z}，\beta）\right]^{operatorname{virt}}&=\left星形\左（\cup_{i\in J_J}d_i\right）\右）\nonumber\\&\quad\cap\left[\mathsf{克}_｛0，m｝\left（\oplus_｛i=1｝^｛n-1｝\mathcal{O} _X（X）（-D-i），\beta\right）\right]^{\operatorname{virt}}，\end{align}$$

和定理2.2建立光滑orbifold对的局部或双对应 $（\mathcal{Z}，\mathcal{D} _n（n）)$ ，给予

(2)

$$开始{align}&\psi_{star}\left[\mathsf{K}^{max}_{0，\left（I_1，\dotsc，I_m\right）}（\mathcal{X}，\beta）\right]^{operatorname{virt}}=（-1）^{d_n-1}\operatorname{mathrm{ev}{j_n}^\star\mathcal{D} _n（n）\cap\left[\mathsf{克}_{0，\left（J_1，\dotsc，J_m\right）}^{\max}（\mathcal{O}（O）_{\mathcal{Z}}（-\mathcal{D} _n（n）)，\beta）\right]^{\operatorname{virt}}\nonumber\\&\quad=（-1）^{dn-1}\operator name{\mathrm{ev}}_{j_n}^\star\mathcal{D} _n（n）\cdot\mathrm{e}\left（\mathrm{R}^1\pi_\star f^\star\mathcal{O}（O）_{\mathcal{Z}}（-\mathcal{D} _n（n）)\右）\cap\left[\mathsf{克}_{0，\left（J_1，\dotsc，J_m\right）}^{\max}（\mathcal{Z}，\beta）\right]^{\operatorname{virt}}，\ end{align}$$

哪里 $j_n\in\{1，\dotsc，m\}$ 是唯一索引，因此 $n\在I_{j_n}中$ .自 $\mathcal美元{D} _n（n）=p^\star D_n$ 被从X（X），我们有

$$\开始{align*}\operatorname{\mathrm{ev}}_{j_n}^\star\mathcal{D} _n（n）&=\varphi^\star\operatorname{\mathrm{ev}}_{j_n}^\star D_n\\mathrm}e\left（\mathrm{R}^1\pi_\star f^\star\mathcal{O}（O）_{\mathcal{Z}}（-\mathcal{D} _n（n）)\右）&=\varphi^\star\mathrm{e}\left（\mathrm{R}^1\pi_\star f^\star\ mathcal{O} X（_X）（-D_n）\右）。\结束｛align*｝$$

后一个方程来自投影公式和以下事实。拉回 $\varphi^\star C$ 通用曲线的 $\mathsf美元{克}_｛0，m｝（X，\β）$ 与通用曲线的粗化一致

$$\开始{align*}\mathcal C\to\mathsf{克}_{0，\left（J_1，\dotsc，J_m\right）}^{\max}（\mathcal{Z}，\beta），\end{align*}$$

这使得合成通用地图 $\mathcal C\to\mathcall Z\toX$ 具有代表性。因此，通用曲线的结构滑轮通过前推保持不变[参考文献阿布拉莫维奇、奥尔森和维斯托利4，定理3.1]。然后根据方程式得出结果(1)和(2)，的投影公式美元\varphi$ 以及局部理论中障碍束的分裂 $\oplus_{i=1}^n\mathcal{O} X（_X）（-D_i）$ .

2.3光滑球面对的局部-正交对应

仍需建立光滑球面对的局部或双球面对应 $（\mathcal{Z}，\mathcal{D} _n（n）)$ ，用于前面的证明。

定理2.2。在定理证明中使用符号2.1，我们有

$$开始{align*}\psi_\star\left[\mathsf{K}^{max}_{0，\left（I_1，\dotsc，I_m\right）}（\mathcal{X}，\beta）\right]^{operatorname{virt}}=（-1）^{d_n-1}\operatorname{\mathrm{ev}{j_n}^\star\mathcal{D} _n（n）\cap\left[\mathsf{克}_{0，\left（J_1，\dotsc，J_m\right）}^{\max}（\mathcal{O}（O）_{\mathcal{Z}}（-\mathcal{D} _n（n）)，β）\right]^｛\operatorname｛virt｝｝。\结束{align*}$$

我们仅在我们需要的设置中建立此结果，即当 $\mathcal{Z}$ 是一个多根堆栈，并且 $\mathcal美元{D} _n（n）$ 是从粗模空间拉回来的除数。该证明适用于[参考van Garrel、Graber和Ruddat29]，但由于 $\mathcal{Z}$ ，对除数的切线进行编码 $D_1，\dotsc，D_{n-1}$ 这些使证明中的关键维度计数复杂化（§2.3.3)也会影响最终的多重性计算（§2.3.4).

备注2.3。目前尚不清楚这些信件是否具有更大的普遍性。如果除数有通用稳定器，则维度计数（§2.3.3)可能会失败，因此最好必须通过其他方法建立结果。此外，在这种情况下，特殊图（§2.3.4)不同的是，这暗示了对通信的任何概括实际上都需要一个新的公式。

2.3.1建立退化公式

让 $\mathfrak{X}$ 是正常锥体的退化 $\mathcal美元{D} _n（n）\subseteq\mathcal{Z}$ ，并让M（M）是正常锥体的退化 $D_n\subseteq X$ .

引理2.4。 $\mathfrak{X}$ 是的根堆栈M（M）沿着除数的严格（相当于完全）变换 $D_i\times\mathbb{A}^1$ 对于 $i\in\{1，\dotsc，n-1\}$ .

证明。除数 $D_i\times\mathbb{A}^1$ 与爆破中心相交 $D_n\次\{0\}$ 横向上，因此严格变换和总变换是一致的。用表示 $T_i\子项M$ .每个 $T_i$ 承认根 $\mathfrak{X}$ ，即根除数的拉回 $\mathcal美元{D} i（_i）\substeq\mathcal｛Z｝$ 沿着构图 $\mathfrak{X}\to\mathcal{Z}\times\mathbb{A}^1\to\mathcal{Z}$ .通过根堆栈的普适性，我们得到了一个态射

$$\开始{align*}\mathfrak{X}\到M_{left（T_1，\dotsc，T_{n-1}\right），\left（r_1，\dotcc，r_{n-1{\right$$

局部计算表明这是一个同构。

家庭的一般纤维 $\mathfrak{X}\to\mathbb{A}^1$ 是

$$\begin{align*}\mathcal{Z}=X_{left（D_1，\dotsc，D_{n-1}\right），\left（r_1，\ dotsc、r_{n-1\right）}。\结束{align*}$$

中央光纤由两部分组成 $\mathcal{Z}$ 和 $\mathcal{Y}$ 一起开会 $\mathcal美元{D} _n（n）$ .在这里 $\mathcal{Y}$ 通过将束生根获得 $Y=\mathbb{P}（P）_{D_n}\左（\mathrm{无}_{D_n\mid X}\oplus\mathcal{O}（O）_{D_n}\右）$ 沿着除数 $\pi^{-1}（D_i\cap D_n）$ 对于 $i\in\{1，\dotsc，n-1\}$ .有一个笛卡尔正方形

我们注意到 $\mathcal美元{D} _n（n）$ 本身是一个沿着简单的法向交叉除数的多根堆栈

$$\开始{align*}\mathcal{D} _n（n）=（D_n）_{左（E_1，\dotsc，E_{n-1}\右），\左（r_1，\dots，r{n-1{\右）}，\结束{align*}$$

哪里 $E_i=D_i\cap D_n\substeq D_n$ .我们让 $\mathcal美元{E} _ i=E_i/r_i\subseteq\mathcal{D} _n（n）$ 是相应的gerby除数。

刚性惯性堆的每个连接部件 $\overline｛\mathcal｛I｝｝（\mathcal{D} _n（n）)$ 是封闭地层的硬化 $\bigcap_{i\inI}\mathcal{E} _ i$ 除数的 $\mathcal美元{E} _1个+\dotsb+\mathcal{电子}_{n-1}\subseteq\mathcal{D} _n（n）$ （包括地层 $\mathcal美元{D} _n（n）$ 对应于空十字路口）。这种刚性化是从 $\bigcap_{i\在i}E_i中$ 通过在十字路口生根 $E_j（美元）$ 为所有人 $j\n不在I中$ 对扭曲扇区的描述对于理解退化公式的结构至关重要。

最后， $\mathcal美元{D} _0（0）\substeq\数学{Y}$ 表示由其与 $\mathcal{Z}$ 、和 $\mathcal美元{D}（D）_\infty\subseteq\mathcal{Y}$ 表示 $\mathfrak{X}$ 经过严格的转换 $\mathfrak{D}$ 属于 $\mathcal美元{D} _n（n）\times\mathbb｛A｝^1$ .

考虑 $\mathfrak L=\operatorname{Tot}\mathcal O_{\mathfrak X}（-\mathflak D）$ 。这形成了一系列（非正确）目标 $\mathbb{A}^1$ .一般光纤为 $\operatorname{Tot}\mathcal O_{mathcal Z}（-\mathcar{D} _n（n）)$ 中心纤维是 $\mathcal｛Z｝\times\mathbb A^1$ 和 $\operatorname{Tot}\mathcal O_{mathcal Y}（-\mathcar{D}（D）_\infty）$ .

我们应用退化公式[参考Abramovich和Fantechi三]至 $\mathfrak{L}$ 中心纤维的成分用二分图表示 $\伽马射线$ .顶点 $v\英寸\Gamma$ 被划分为 $\mathcal{Z}$ -顶点和 $\mathcal{Y}$ -顶点和相关的模空间 $\mathsf美元{K} _v（_v）$ 是根对展开式的映射空间

$$\开始{align*}\left（\mathcal{Z}\times\mathbb{A}^1，\mathcal{D} _n（n）\times\mathbb{A}^1\right）\qquad\text{和}\qqua2\left（\mathcal{O}（O）_{\mathcal{Y}}（-\mathcal{D}（D）_\infty），\mathcal（信息）{D} _0（0）\times\mathbb{A}^1\right），\end{align*}$$

分别定义为[参考Abramovich和Fantechi三, §3]. 使用扩展是无关紧要的，因为虚拟类的前推与对应根堆栈的映射空间的前推相匹配，而不使用扩展[参考阿布拉莫维奇、卡德曼和怀斯1，定理2.2]。我们用以下公式表示扭转指数 r_n美元$ .在原始配方中[参考Abramovich和Fantechi三, §3.4], $r_n美元$ 被要求可被粘合节点处的所有接触顺序整除，但被[推荐曾和你28]可以在不影响不变量的情况下删除此条件。因此，我们假设 r_n美元$ 大且与每个 $r_1，\dotsc，r_{n-1}$ .

组件 $\mathsf美元{克}_{\伽马}$ 关联到 $\伽马射线$ 映射到光纤产品

(3)

关于求值映射到连接因子的刚性惯性堆栈。的虚拟类 $\mathsf美元{克}_\伽马射线$ 向前推到虚拟类的倍数 $\mathsf美元{F}（F）_\伽马射线$ 通过此图进行赋值；态射的虚度美元\菲律宾比索$ 很容易理解[参考Abramovich和Fantechi三，提议5.9.1]。每个空间 $\mathsf美元{K} _v（_v）$ 分解为子堆栈的不相交并集，这些子堆栈作为惯性堆栈连接组件的预图像获得。

在推进到稳定映射的空间之后 $\mathcal{Z}$ ，退化公式给出了类的等式

(4)

$$\开始{align}\left[\mathsf{K}^{max}_{0，\left（J_1，\dotsc，J_m\right）}（\mathcal{O}（O）_{\mathcal{Z}}（-\mathcal{D} _n（n）)，β）\right]^｛\operatorname｛virt｝｝=\sum_｛\Gamma｝\dfrac｛1｝｛\lvert E（\Gamma）\rvert！｝\cdot\Psi_\star[\mathsf｛K｝_{\Gamma}]^{\operatorname{virt}}，\end{align}$$

哪里美元\磅/平方英寸$ 是作文

$$\开始{align*}\mathsf{克}_{\Gamma}\to\mathsf{K}（\mathfrak{L} 0)\to\mathsf{K}（\mathcal{Z}）。\结束{align*}$$

让 $j=j_n$ 是我们希望与之相切的标记的索引 $D_n$ （如定理证明2.1)，并覆盖方程式的两边(4)带有 $\operatorname{\mathrm{ev}}_j^\star\mathfrak{D}$ 。左侧给出了的局部不变量 $\mathcal美元{O}（O）_{\mathcal{Z}}（-\mathcal{D} _n（n）)$ 用…封顶 $\operatorname{\mathrm{ev}}_j^\star\mathcal{D} _n（n）$ 。我们的目标是显示除右侧的一个项外，其余项都消失。

2.3.2第一次消失： $\mathcal{Z}$ -顶点

首先假设有一个 $\mathcal{Z}$ -顶点 $v\英寸\Gamma$ 具有 $k>1$ 相邻边。对于每个相邻边缘e（电子），对应的评估图因子（局部）通过刚性惯性堆栈的特定组件。这样一个分量是通过严格化除数的交集（可能为空）而获得的 $\mathcal美元{E} _ i$ 在里面 $\mathcal美元{D} _n（n）$ 。我们将其表示为 $\数学{E} （_E）$ 因此，评估图的产品采用以下形式

$$\开始{align*}\mathsf{K} _v（_v）\to\prod_e\left（\mathcal{E} （_E）\times\mathbb{A}^1\right）。\结束{align*}$$

然而，由于源曲线是正确的，因此到仿射空间的映射是恒定的。这确保了所有点评估一致，即通过闭合子堆栈的地图因子

$$\开始{align*}\left（\prod_e\mathcal{E} （_E）\right）\times\mathbb{A}^1\hookrightarrow\prod_e\left（\mathcal{E} （_E）\times\mathbb{A}^1\right）。\结束{align*}$$

我们现在遵循以下论点[参考van Garrel、Graber和Ruddat29，引理3.1]。有一个笛卡尔图

多余交集公式[参考Fulton14，定理6.3]给出

$$\开始{align*}\Delta^=\操作员姓名{c}_{k-1}（E）\cap\widetilde\Delta^！，\结束{align*}$$

哪里E类是多余的捆，在这种情况下[参考Fulton14，例6.3.2]等于

$$\开始{align*}E=\widetilde\Delta^\star\mathrm{无}_{\iota^\prime}/\mathrm｛N｝_{\iota}，\end{align*}$$

如果 $k>1$ 。由此可见 $\增量^=0$ 因此 $\伽玛$ 消失。

2.3.3第二次消失： $\mathcal{Y}$ -顶点

我们的结论是，只有那些只有一个 $\mathcal{Y}$ -顶点。让 $v\英寸\Gamma$ 成为这样一个顶点。这对应于根对的扩展映射空间 $\左（\mathcal{O}（O）_{\mathcal{Y}}（-\mathcal{D}（D）_\infty），\mathcal（信息）{D} _0（0）\times\mathbb{A}^1\right）$ 回忆一下 $\mathcal{Y}$ 是除数上的投影束 $\mathcal美元{D} _n（n）$ 。假设在离散数据中 $\mathsf美元{K} _v（_v）$ ，或者

•曲线等级不是纤维等级的倍数，或者
•至少有三个特殊点。

这确保了稳定映射的相应模空间 $\mathsf美元{K} _v（_v）（\mathcal{D} _n（n）)$ 到束的底部定义良好。有一个投影

(5)

$$\开始{align}\mathsf{K} _v（_v）\to\mathsf{K} _v（_v）（\mathcal{D} _n（n）)，\结束{align}$$

我们声称虚拟类沿着这个态射向前推进到零。由于在中的扭曲扇区之间存在自然双射 $\mathcal｛Y｝$ 和扭曲的扇区 $\mathcal美元{D} _n（n）$ ，年龄对虚拟维度的贡献是一致的。从中可以推断出

$$\开始{align*}\operatorname{\mathrm{vdim}}\mathsf{K} _v（_v）=\operatorname{\mathrm{vdim}}\mathsf{K} _v（_v）（\mathcal{D} _n（n）)+2，\结束{align*}$$

因此，如果我们给出这个公式，这个主张就成立了(5)满足虚拟前推属性[参考Manolache20，定义3.1]（我们注意到，如果 $\mathcal美元{D} _n（n）$ 允许使用通用稳定剂）。由[参考阿布拉莫维奇、卡德曼和怀斯1，定理2.2]，它等价于表明

$$\开始{align*}\mathsf{K} _v（_v）\左（\mathcal{Y}（Y）_{\马塔尔{D} _0（0），r_n}\right）\to\mathsf{K} _v（_v）（\mathcal{D} _n（n）)\结束{align*}$$

满足虚拟推送属性。为此，我们调整了[参考van Garrel、Graber和Ruddat29, §4]. 让

$$\开始{align*}s=\Pi_{i=1}^{n}r_i，\qquad t=\Pi_{i=1{^{n-1}r_i=s/r_n.\end{align**}$$

通过可表示性，任何稳定的源曲线的稳定群映射到 $\mathcal美元{Y}（Y）_{\马塔尔{D} 0，r_n｝$ （分别为。， $\mathcal美元{D} _n（n）$ )必须有顺序划分秒（分别为。，t吨). 我们用以下公式表示有效曲线类的幺半群

$$\开始{align*}A=H_2^+\left（\mathcal{Y}（Y）_{\马塔尔{D} _0（0），r_n}\right），\qquad B=H_2^+（\mathcal{D} _n（n）). \结束{align*}$$

现在考虑下图，其中涉及具有同源权重的预稳定扭曲曲线的模量堆栈：

(6)

其中的态射 $\nu美元$ 用垂直同源类压缩不稳定曲线分量并粗化 r_n美元$ –扭曲（这种变形是由一个e tale cover和一个root结构组成）。

从与光滑投影相关的相对切线束的短精确序列 $\mathcal美元{Y}（Y）_{\马塔尔{D} _0（0），r_n}到mathcal{D} _n（n）$ ，我们得到了图中三角形的相容三元组(6). 我们注意到，与目标是多样性时不同，我们可能有

$$\开始{align*}H^1\left（\mathcal{C}，f^\star\mathrm{T}（T）_{\马塔尔{Y}（Y）_{\马塔尔{D} _0（0），r_n｝/\数学{D} _n（n）}\右）\neq 0\end{align*}$$

if组件 $\mathcal{C}$ 映射到根除数。因此，态射 $\upsilon（美元）$ 通常不是平滑的，但实际上总是平滑的，这就足够了。中给出的参数[参考van Garrel、Graber和Ruddat29，引理5.1和命题5.3]然后逐字应用，表明虚拟前推特性成立，并且 $\伽马射线$ 消失了。

2.3.4特殊图形的贡献

我们得出结论，只有图 $\伽马射线$ 有贡献的是那些单身的 $\mathcal{Y}$ -顶点 $v_1$ 最多有两个特殊点，曲线类是纤维类的倍数F类.自 $v_1$ 必须包含至少一个节点和标记 $x{j}$ ，我们只剩下一个图 $\伽马射线$ ，包括

•一 $\mathcal{Z}$ -顶点 $v_0（美元）$ 支持除 $x{j}$ 和曲线类 $\beta_0=\beta$ ; 和
•一 $\mathcal{Y}$ -顶点 $v_1$ 支持标记 $x_｛j｝$ 和曲线类 $\beta_1=d_n\cdot F$ 对于 $d_n=\数学{D} _n（n）\cdot\测试版$ .

它们沿单边连接e（电子）、和图表(三)减少到以下内容：

回想一下该部件 $\mathsf美元{克}_{\伽马}$ 中心纤维的长度实际上在纤维产品上是有限的 $\mathsf美元{F}（F）_{\伽马}$ .让

$$\开始{align*}J_J\subseteq\{1，\dotsc，n-1\}\end{align**}$$

是记录除数的子集 $D_1，\dotsc，D_{n-1}$ 哪个标记 $x{j}$ 相切。此相切编码为加于普通光纤和中央光纤上的扭曲扇区插入。在 $\mathsf美元{克}_{v_1}$ 这些对应于包的年龄限制

$$\开始{align*}\mathcal{O}（O）_{\mathcal{Y}}\左（\pi^{-1}\mathcal{E} _ i\右）=\pi^\star\mathcal{O}（O）_{\马塔尔{D} _n（n）}（\mathcal{E} _ i). \结束{align*}$$

由于曲线类是光纤的倍数，因此当拉回到源曲线时，这些束的阶数为零。根据平价考虑 $\mathsf美元{克}_{v_1}$ 为空，除非节点标记q个与边缘相对应e（电子）也有扭曲的扇区插入，与 $x{j}$ .这意味着我们必须

$$\开始{align*}\operatorname{年龄}_{q} \pi^\star\mathcal{O}（O）_｛\数学{D} _n（n）}（\数学{E} _ i)=1-\操作员姓名{年龄}_{x_j}\pi^\star\mathcal{O}（O）_{\马塔尔{D} _n（n）}（\mathcal{E} _ i)\结束{align*}$$

为所有人 J_{J}中的$i\$ 通过对评估图中带的反演，我们得到了节点标记的相反年龄q个在 $\mathsf美元{克}_{v0}$ 。因此，顶点 $v_0（美元）$ 提供根堆栈的orbifold不变量 $\mathcal美元{Z}（Z）_{\马塔尔{D} _n（n），r_n}=\mathcal{X}$ 扭曲扇形插入，使单个标记具有最大相切性q个关于所有除数 $D_i（美元）$ 对于 i_j中的$i=j_j\杯\{n\}$ ，根据需要。

对于 $v_1$ ，请注意 $\operatorname{\mathrm{ev}}_q$ 采用的组件中的值 $\overline｛\mathcal｛I｝｝（\mathcal{D} _n（n）)$ 这与

$$\在J_J}\mathcal中开始{align*}\bigcap_{i\{E} _i。\结束{align*}$$

我们将这种僵化表示为 $\数学{电子}_｛J_J｝$ 直接计算表明

$$\开始{align*}\operatorname{\mathrm{vdim}}\mathsf{克}_{v_1}=\dim\mathcal{电子}_{J_J}+1。\结束{align*}$$

有一个除法插入 $\operatorname{\mathrm{ev}}_j^\star\mathcal{D}（D）_\英菲$ 在 $\mathsf美元{克}_{v_1}$ 以及 $v_1$ 可以表示为唯一的 $m\in\mathbb{Q}$ 这样的话

$$\开始{align*}（\operatorname{\mathrm{ev}}_q）_\star\left（\operatorname{\mathrm{ev}}_j^\star\mathcal{D}（D）_\infty\cap\left[\mathsf{克}_{v_1}\right]^{\operatorname{virt}}\right）=m\cdot\left[\mathcal{电子}_{J_J}\右]。\结束{align*}$$

这可以通过将光纤限制在 $\mathcal美元{电子}_{J_J}$ .围绕这一点在当地开展工作 $\mathcal美元{E} _ i$ 变得微不足道，因此我们获得了一个映射空间

$$\boot｛align*｝\mathbb｛P｝（r_n，1）\times\prod_｛i \ in J_J｝\mathcal｛B｝\mau_｛r_i｝。\结束{align*}$$

映射到 $\mathcal{B}\mu_{r_i}$ 是唯一确定的，每个都有一个自同构因子 1美元/r_i$ 这与连接因子惯性堆栈上Chen–Ruan交集对产生的自同构因子抵消[参考Abramovich和Fantechi三, §5.2.3].

留给我们的是一个计算 $\mathbb{P}（r_n，1）$ 。贡献是一个局部不变量，带有 $\operatorname{\mathrm{ev}}_{j}^\star（\infty）$ 后一种插入可以通过除数公理进行分解；局部理论的障碍束沿着地图被拉回，忘记了一个标记，因为通用曲线的结构滑轮是通过沿稳定方向的前推保持的。剩余的局部不变量可以通过定位来计算。最终结果[推荐人：约翰逊、潘哈里潘德和曾17，（21）]是

$$开始{align*}（d_n）\left（\dfrac{（-1）^{d_n-1}}{d_n^2}\right）=\dfrac{（-1-）^{dn-1}}{d_n}，结束{align**}$$

与粘合因子结合 d_n美元$ 出现在退化公式中完成定理证明2.2.□

三降阶二：相对积公式

确立了主要定理2.1，我们现在提出了另一种方法，也是基于秩约简哲学的。虽然这种方法不太通用，需要一个积极的假设，但我们选择包括它，因为它使用的“相对乘积公式”提供了对映射到多根堆栈的几何结构的有价值的见解，并澄清了与对数不变量的关系。此外，主要结果不需要最大接触假设。

3.1凸面嵌入

如前所述，固定一个平滑投影变化X（X）和一个简单的正规交叉因子 $D=D_1+\dotsb+D_n\substeq X$ 。为了简化符号，我们将从现在开始假设 $n=2$ ; 归纳法是对一般情况的扩展。

我们将在本节中假设存在一个简单的正态交叉对 $（P，H=H_1+H_2）$ 具有P（P）凸嵌入与闭嵌入 $X\hook右箭头P$ 这样的话 $D_i=X\cap H_i$ 对于每个我。在这种情况下，我们打电话给美元（X，D）$ 一凸嵌入该定义包含的两个重要案例是

(1) X（X）凸面和 $D_i美元$ 任意性；
(2) X（X）武断和 $D_i（美元）$ 非常充足。

在本案例中，首先给出所有定义和证明，其中X（X）它本身是凸的，然后通过虚拟拉回扩展到凸嵌入。

3.2根堆栈的相对乘积公式

如§2，我们修正了亏格模问题的离散数据 $0$ 相对稳定映射到美元（X，D）$ ：曲线类 H_2^+（X）中的$\beta\$ ，多个标记点米和指定的相切顺序 $1美元$ 和 D_2美元$ 在标记点。请注意，我们不要求此时的联系订单最大。

选择大互质整数 r_1美元$ 和 r_2美元$ 并考虑根堆栈

$$\开始{align*}\mathcal{十} _1个=X_{D_1，r_1}，\qquad\mathcal{十} _2=X_{D_2，r_2}。\结束{align*}$$

这两个都有X（X）作为它们的粗模空间。对于每个 $\数学{十} _ i$ 通过使每个标记都具有扭曲指数，我们可以为orbifold稳定映射的模空间建立数据美元_i$ .扭曲扇区插入 $\mu_{r_i}$ 由于源和目标的扭曲指数相同，因此与切线顺序一致[参考Cadman和Chen10, §2.1]. 现在考虑多根堆栈

$$\开始{align*}\mathcal{X}=\mathcal{十} _1个\times_X\mathcal{十} 2。\结束{align*}$$

如前所述，我们可以为一个orbifold稳定映射空间构造离散数据 $\mathcal{X}$ .标记与两者相切 $1美元$ 和 D_2美元$ 将具有扭曲指数 r_1r_2美元$ ，而扭曲扇区插入是 $\亩{r_1r_2}$ 它映射到规范同构下的正确切线对 $\mu_{r1r2}=\mu__{r1\times\mu_{R2}$ 。从现在起，离散数据将从符号中消除。

在本节中，我们证明了orbiold稳定映射的理论在粗模空间的映射空间上满足一个相对乘积公式。更准确地说，我们有以下几点：

定理3.1。存在一个图表

(7)

这样，当X（X）是凸的，我们有

(8)

$$\开始{align}\nu_*[\mathsf{K}（\mathcal{X}）]^{\operatorname{virt}}=\Delta_{\mathsf{K}（X）}^！\左（[\mathsf{K}（\mathcal{十} _1个)]^{\operatorname{virt}}\times[\mathsf{K}（\mathcal{十} _2)]^｛\operatorname｛virt｝｝\right）\！。\结束{对齐}$$

证明。形态 $\nu\colon\mathsf{K}（\mathcal{X}）\to\mathcal{P}$ 通过取相对粗模空间（参见[参考阿布拉莫维奇和维斯托利5，§9]和[参考Abramovich、Olsson和Vistoli4，定理3.1]）。对于每个我，部分粗化 $\mathcal{C}\to\mathcar{C} _ i$ 是地图中的初始值 $\mathcal{C}\to\mathcal{Y}$ 通过它可以看到地图 $\mathcal{C}\to\mathcar{十} _ i$ 并具有代表性。

我们称扭曲曲线为阻力曲线（对于某些正整数第页)如果每个稳定器组的顺序不同第页.由于地图稳定 $\mathcal美元{C} _ i\到\马塔尔{十} _ i$ 必须具有代表性，因此 $\mathcal美元{C} _ i$ 是一个美元_i$ -曲线。

纤维产品的一点 $\mathcal价格$ 由两个稳定映射的数据组成 $\mathcal美元{C} _1个\到\马塔尔{X} 1个$ 和 $\mathcal美元{C} _2\到\马塔尔{十} _2$ 这导致了相同的底层映射 $C\到X$ 关于粗模量。

引理3.2。假设 r_1美元$ 和 r_2美元$ 是互质的，让 $\mathcal美元{C} _1个，\mathcal{C} _2$ 是 r_1美元$ -, r_2美元$ -具有相同粗曲线的曲线C类然后进行归一化

(9)

$$\begin{align}\mathcal{C}=\left（\mathcal{C} _1个\times_C\mathcal{C} _2\右）^{\sim}\end{align}$$

是一条扭曲的曲线。

证明。如果 $p\单位：C$ 是带有局部方程的粗曲线上的标记z，然后为每个 $\mathcal美元{C} _ i$ 由提供

$$\开始{align*}\mathcal{C} _ i=\left[\left（x_i^{ri}=z\right）/\mu_{ri}\right]。\结束{align*}$$

因此，纤维产品 $\左[\左（x_1^{r_1}=x_2^{r_2}\右）/\mu_{r_1r_2}\right]$ 注意，这不是扭曲曲线（除非 $r_1=1$ 或 $r_2=1$ ). 另一方面，因为 r_1美元$ 和 r_2美元$ 是互质的，纤维产品的归一化由下式给出

$$\开始{align*}\left[\mathbb A^1_y/\mu_{r_1r_2}\right]，结束{align**}$$

哪里 $y^{r_1}=x_2，y^{r_2}=x_1$ 围绕节点的计算是完全类似的，除了基底也必须被归一化，围绕节点持续存在的除数。

备注3.3。这种现象与对数几何中的饱和问题有关，通过扭曲曲线和对数结构延伸之间的对应关系[参考Olsson24]. 的确，幺半群 $\mathbb{N}e_1\oplus_{r_1，\mathbb2{N}，r_2}\mathbb{N}e_2$ 未饱和：在集团化中 $\mathbb{Z}^2/（r_1，-r_2）\cong\mathbb{Z}$ ，发电机的图像美元e_1$ 可除以 r_2美元$ :

$$开始{align*}e_1=（a_1r_1+a_2r_2）e_1=a_1r_2e_2+a_2r_2e_1=r_2（a_1e_2+a_2e_1），结束{align**}$$

哪里 $a_1，a_2\in\mathbb{Z}$ 是这样的 $a_1r_1+a_2r_2=1$ 类似地 $e_2（美元）$ 可除以 r_1美元$ .

扭曲的曲线 $\mathcal{C}$ 携带自然地图 $\mathcal{X}$ 这是显而易见的。因此我们有一个笛卡尔图

(10)

其中底态射是归一化。形态美元\varphi$ 带有自然完美的障碍理论。我们现在将为美元\psi$ .图表

是笛卡尔。使用凸性假设，对于美元\ Delta$ 由提供

(11)

$$\开始{align}\left（\pi_{0\star}f_0^{star}\mathrm{T} X（_X）\右）^\vee[1]，\end{align}$$

哪里 $\pi_0$ 是通用粗曲线。这又回到了一个完美的障碍理论 $\mathcal｛P｝\到\mathsf｛K｝（\mathcal{十} _1个)\时间{\mathfrak{M}}\mathsf{K}（\mathcal{十} _2)$ 后一个空间承载着完美的障碍理论 $\mathfrak{M}^{r_1-\operatorname{tw}}\times_{\mathfrak{M}}\mathbrak{M{^{r_2-\operatorname{tw{}$ 由提供

(12)

$$\开始{align}\left（\pi_{1\star}f1^{star}\mathrm{T}（T）_{\马塔尔{十} _1个}\oplus\pi{2\star}f2^{star}\mathrm{T}（T）_{\马塔尔{十} _2}\右）^\vee。\结束{对齐}$$

因此，我们有一个具有完美障碍理论的三角形

并希望为美元\psi$ 给出一个兼容的三元组。有自然形态 $\mathrm美元{T}（T）_{\马塔尔{十} _ i}\到p_i^\star\mathrm{T} X（_X）$ 在 $\mathcal美元{十} _ i$ 因此，我们获得

$$\开始{align*}\pi_{1\star}f1^{star}\mathrm{T}（T）_{\马塔尔{X} 1个}\oplus\pi{2\star}f2^{star}\mathrm{T}（T）_{\马塔尔{十} _2}到\pi_{0\star}f_0^{star}\mathrm{T} _X。\结束{align*}$$

（如定理的证明2.1，这源于投影公式和通过沿着粗化图向前推来保留各种通用曲线的结构槽轮的事实；参见[参考文献阿布拉莫维奇、奥尔森和维斯托利4，定理3.1]。）将圆锥体二元化、移位并取下，我们得到

$$开始{align*}\left（\pi_{1\star}f1^{star}\mathrm{T}（T）_{\马塔尔{十} _1个}\oplus\pi{2\star}f2^{star}\mathrm{T}（T）_{\马塔尔{十} _2}\右）^\vee\to\mathbf{电子}_\psi\向左（\pi_{0\star}f_0^\star\mathrm{T} X（_X）\右）^\vee[1]\xrightarrow{[1]}。\结束{align*}$$

四引理的几个应用表明 $\mathbf美元{电子}_\磅/平方英寸$ 是一个相对完善的障碍理论美元\psi$ .

最后，我们希望比较美元\psi$ 和美元\varphi$ 在图表中(10). 对于任何根堆栈 $\mathcal{Y}=Y_{D，r}$ 带gerby除数 $\mathcal{D}$ ，局部计算给出了以下精确序列：

$$\开始{align*}0\到\mathrm{T}（T）_{\mathcal{Y}}\到p^\star\mathrm{T} Y（_Y）\至\mathcal{O}（O）_{（r-1）\mathcal{D}}（r\mathcal{D}）\到0。\结束{align*}$$

由此我们得到了短精确序列的一个态射

snake引理的一个应用在 $\mathcal{X}$ :

(13)

$$\开始{align}0\to\mathrm{T}（T）_｛\mathcal｛X｝｝\到p_1^\star\mathrm{T}（T）_｛\数学{十} _1个}\oplus p_2^\星\mathrm{T}（T）_{\马塔尔{十} _2}\到p^\star\mathrm{T} X（_X）\到0。\结束{对齐}$$

应用 $\pi_\star f^\star$ ，我们看到完美障碍理论的回落美元\psi$ 符合完美的障碍理论美元\varphi$ 在图表中(10). 然后，该定理遵循虚拟回拉和向前推的可交换性[参考Manolache19，定理4.1]，因为图中的底部水平箭头(10)程度合适 $1$ .

3.3本地-本地通信

建立了相关乘积公式后，我们现在可以直接证明定理2.1在凸面设置中。

凸目标定理2.1的证明。再次考虑图表(7). 定理3.1给出了以下关系 $\mathsf{K}（X）$ :

$$\begin{align*}（\rho\circ\nu）_\star[\mathsf{K}（\ mathcal{X}）]^{\operatorname{virt}}=（\rho _1）_\star[\mathsf{K}（\fathcal{十} _1个)]^{\operatorname{virt}}\cdot（\rho_2）_\star[\mathsf{K}（\mathcal{十} _2)]^｛\operatorname｛virt｝｝。\结束{align*}$$

对于最大接触设置，结果紧接着是光滑因子的局部-对偶对应和局部理论的障碍束分裂 $\mathcal美元{O} X（_X）（-D_1）\oplus\mathcal{O} X（_X）（-D_2）$ .□

这个结果可以通过虚拟回调方法推广到凸嵌入。这是一件相当平常的事情：例如，请参阅[参考Battistella和Nabijou6，附录A]。由于§2已经建立了完全通用的结果，我们省略了这里的细节。

3.4与朴素不变量的比较

从调用[参考Nabijou21,参考Nabijou和Ranganathan22]对于一个简单的正态交叉对美元（X，D）$ 具有X（X）凸的，定义了朴素的虚拟类（属 $0$ )作为对数虚类的乘积

$$\begin{align*}[\mathsf{N}（X\mid D）]^{\operatorname{virt}}:=\prod_{i=1}^N（\rho_i）_\star[\mathsf{K}（X\mid D_i）]^}\operator name{virt}}\end{aling*}$$

里面 $\mathsf{K}（X）$ 我们还对纤维产品进行了改进 $\mathsf{N}（X\mid D）$ ，但我们最感兴趣的是其推动 $\mathsf{K}（X）$ 该定义通过虚拟拉回扩展到任意凸嵌入。定理的直接结果3.1是orbifold和naive不变量的标识。

推论3.4。对于美元（X，D）$ 凸嵌入，关系

$$\开始{align*}\rho_\star\left[\mathsf{K}\left（X_{D，\vec{r}}\right）\right]^{\operatorname{virt}}=[\mathsf{N}（X\mid D）]^{\ operatorname{virt{}}\end{align**}$$

保持在内部 $\mathsf{K}（X）$ （用于兼容的联系订单选择）。

鉴于此[参考Nabijou和Ranganathan22，§1]和[参考Nabijou21§3.4]表明，球形不变量和对数不变量通常不同，并且该缺陷不限于最大接触设置。

朴素空间为探索多根空间的地理和不变量提供了另一种视角。的迭代爆破构造[参考Nabijou和Ranganathan22]给出了对数不变量与天真/轨道不变量的比较方法；另请参阅[参考Ranganathan25,参考Herr16]用于处理相关想法。

致谢

我们感谢Druv Ranganathan博士就相关想法进行的对话，以及对手稿草稿的评论。我们还感谢Michel van Garrel和Leo Herr的有益讨论。最后，我们感谢裁判对论文的透彻阅读和许多有益的评论。

第一位作者得到了德国卓越战略EXC-2181/1-390900948（海德堡卓越结构集群）下的德国研究基金会（DFG）的支持。第二位作者得到了赫切尔·史密斯基金会的支持。第三位作者得到西蒙斯基金会合作拨款的部分支持。第四位作者得到了EPSRC拨款EP/R013349/1的支持。

竞争性利益

没有。

工具书类

阿布拉莫维奇,D。,卡德曼,C、。和明智,J。,相对和球形Gromov-Writed不变量,阿尔盖布。几何。 4(4) (2017),472–500.谷歌学者

阿布拉莫维奇,D。和陈,问：。,定界分数对II的稳定对数映射,亚洲数学杂志。 18(三) (2014),465–488.交叉参考谷歌学者

阿布拉莫维奇,D。和凡泰基,B。,退化公式中的Orbifold技术,Ann.Sc.规范。超级的。比萨Cl.Sci。(5) 16(2) (2016),519–579.谷歌学者

阿布拉莫维奇,D。,奥尔森,M。和维斯托利,答：。,扭曲稳定贴图以驯服Artin堆栈,J.代数几何。 20(三) (2011),399–477.交叉参考谷歌学者

阿布拉莫维奇,D。和维斯托利,答：。,稳定映射空间的压缩,J.Amer。数学。Soc公司。 15(1) (2002),27–75.交叉参考谷歌学者

巴蒂斯泰拉,L。和纳比茹,N。,相对拟映射和镜像公式,国际数学。Res.不。IMRN公司 2021(10) (2021),7885–7931.交叉参考谷歌学者

布索,第页。,布里尼,答：。和范加雷尔,M。,'关于曲面边界的local-log原则'，预打印，2019,https://arxiv.org/abs/1908.04371.谷歌学者

布索,第页。,布里尼,答：。和范加勒尔,M。，'到Looijenga对的稳定映射'，预打印，2020,https://arxiv.org/abs/2011.08830.谷歌学者

布索,第页。,布里尼,答：。和范加雷尔,M。,'到Looijenga对的稳定映射：Orbifold示例’,莱特。数学。物理学。 111(4) (2021)，37，第109号论文。谷歌学者

卡德曼,C、。和陈,L。,与光滑立方相切的有理平面曲线的计数,高级数学。 219(1) (2008),316–343.交叉参考谷歌学者

科茨,T。,科尔蒂,答：。,伊里塔尼,H。和郑,高-高。,计算类零扭曲Gromov-Writed不变量,杜克大学数学。J。 147(三) (2009),377–438.交叉参考谷歌学者

风扇,H。,郑,高-高。和你,F、。,根堆栈和相关对的镜像定理,选择数学。（未另行规定） 25(4) (2019), 54.交叉参考谷歌学者

风扇,H。和吴,L。,Witten–Dijkgraaf–Verlinde–Verlinder方程及其在相对Gromov–Witten理论中的应用.国际数学。Res.不。IMRN公司,2021(13)2021,9834–9852,https://doi.org/10.1093/imrn/rnz353.交叉参考谷歌学者

富尔顿,西。,交集理论第二版，Ergebnisse der Mathematik und ihrer Grenzgebiete(Springer-Verlag公司,柏林,1998).交叉参考谷歌学者

总量,M。,潘达利潘德,R。和西伯特,B。,热带顶点,杜克大学数学。J。 153(2) (2010),297–362.交叉参考谷歌学者

先生,L。,'对数乘积公式'，预打印，2019,https://arxiv.org/abs/1908.04936.谷歌学者

约翰逊,第页。,潘达利潘德,R。和郑,高-高。，'本地注释

${\mathbf{P}}^1$ 眼眶’(2008),https://people.math.ethz.ch网站/~rahul/lPab.ps.谷歌学者

克莱姆,答：。和潘达利潘德,R。,Calabi-Yau 4倍的枚举几何,公共数学。物理学。 281(三) (2008),621–653.交叉参考谷歌学者

马诺拉切,C、。,虚拟回拉,J.Algebr。几何。 21(2) (2012),201–245.交叉参考谷歌学者

马诺拉切,C、。,虚拟向前推,地理。白杨。 16(4) (2012),2003–2036.交叉参考谷歌学者

纳比茹,N。,对数Gromov–Witten理论和拟映射理论中的递归公式，博士论文，2018,伦敦帝国理工学院,https://www.dpmms.cam.ac.uk/~nn333/Nabijou论文.pdf.谷歌学者

纳比茹,N。和兰加纳坦,D。,Gromov–Witten最大接触理论论坛数学。西格玛 10(2022)，e5。交叉参考谷歌学者

西努,T。和西伯特,B。,复曲面品种和热带曲线的复曲面退化,杜克大学数学。J。 135(2006),1–51.交叉参考谷歌学者

奥尔森,M。,（对数）扭曲曲线,作曲。数学。 143(2) (2007),476–494.交叉参考谷歌学者

兰加纳坦,D。,“关于成对乘积中曲线循环的注释'，预打印，2019,https://arxiv.org/abs/1910.00239.谷歌学者

郑,高-高。和你,F、。，“无对数几何的简单法向交叉对的Gromov书面理论”，预印本，2020,https://arxiv.org/abs/2008.04844.谷歌学者

郑,高-高。和你,F、。,多根堆栈的镜像定理及其应用'，预打印，2020,https://arxiv.org/abs/2006.08991.谷歌学者

郑,高-高。和你,F、。,高等属相对和球形Gromov–Witten不变量,地理。白杨。 24(6) (2020),2749–2779.交叉参考谷歌学者

范加雷尔,M。,抓取器,T。和Ruddat公司,小时。,局部Gromov-Writed不变量是日志不变量,高级数学。 350(2019),860–876.交叉参考谷歌学者