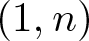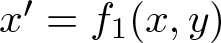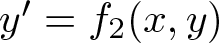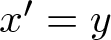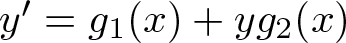2.1.案例1: $a_{0,1}=0$
$a_{0,1}=0$
在这种情况下,系统(2)成为
这个系统的分歧是
施加条件(c1),即。, $\mathrm{Tr}Df\lt 0$为所有人
$\mathrm{Tr}Df\lt 0$为所有人 $(x,y)\in\mathbb{R}^2$,我们必须拥有它米是均匀的,并且
$(x,y)\in\mathbb{R}^2$,我们必须拥有它米是均匀的,并且
具有 $\alpha_i,\beta_i\in\mathbb{R}$和
$\alpha_i,\beta_i\in\mathbb{R}$和 $\beta_i\ne 0$所以,系统(三)成为
$\beta_i\ne 0$所以,系统(三)成为
注意,如果 十亿美元_{0,1}-a_{1,0}+b{m,1}\prod_{i=1}^{m/2}(\alpha_i^2+\beta_i^2)=0$,然后是线路x个=0由平衡填充,因此这是不可能的。所以
十亿美元_{0,1}-a_{1,0}+b{m,1}\prod_{i=1}^{m/2}(\alpha_i^2+\beta_i^2)=0$,然后是线路x个=0由平衡填充,因此这是不可能的。所以 十亿美元_{0,1}-a_{1,0}+b_{m,1}\prod_{i=1}^{m/2}(\alpha_i^2+\beta_i^2)\ne 0$和
十亿美元_{0,1}-a_{1,0}+b_{m,1}\prod_{i=1}^{m/2}(\alpha_i^2+\beta_i^2)\ne 0$和 $(0,0)$是系统的唯一平衡点(4)得出该条件(c2)是满足的。
$(0,0)$是系统的唯一平衡点(4)得出该条件(c2)是满足的。
另一方面,矩阵 美元f(0,0)$具有特征值
美元f(0,0)$具有特征值 $a_{1,0}$和
$a_{1,0}$和 十亿美元_{0,1}-a_{1,0}+b{m,1}\prod_{i=1}^{m/2}(\alpha_i^2+\beta_i^2)$.施加条件(c3)并考虑到
十亿美元_{0,1}-a_{1,0}+b{m,1}\prod_{i=1}^{m/2}(\alpha_i^2+\beta_i^2)$.施加条件(c3)并考虑到 十亿美元_{0,1}-a_{1,0}+b_{m,1}\prod_{i=1}^{m/2}(\alpha_i^2+\beta_i^2)\ne 0$,我们一定有
十亿美元_{0,1}-a_{1,0}+b_{m,1}\prod_{i=1}^{m/2}(\alpha_i^2+\beta_i^2)\ne 0$,我们一定有 $a_{1,0}\lt 0$和
$a_{1,0}\lt 0$和 十亿美元_{0,1}-a_{1,0}+b{m,1}\prod_{i=1}^{m/2}(\alpha_i^2+\beta_i^2)\lt 0$,在这种情况下,原点是稳定节点。
十亿美元_{0,1}-a_{1,0}+b{m,1}\prod_{i=1}^{m/2}(\alpha_i^2+\beta_i^2)\lt 0$,在这种情况下,原点是稳定节点。
现在,我们将证明原点是全局渐近稳定的。任何解决方案方程式(4)具有初始条件 $(x_0,y_0)$由提供
$(x_0,y_0)$由提供 $(x(y),y(t))$具有
$(x(y),y(t))$具有 $x(t)=x_0\,{\rm e}^{a_{1,0}吨}$和年(吨)由于常量方法的变化,即设置,可以计算
$x(t)=x_0\,{\rm e}^{a_{1,0}吨}$和年(吨)由于常量方法的变化,即设置,可以计算
我们得到,
自 $a_{1,0}\lt 0$和
$a_{1,0}\lt 0$和 $x_0{\rm e}^{a_{1,0}吨}\至0$什么时候
$x_0{\rm e}^{a_{1,0}吨}\至0$什么时候 $t\到+\infty$,存在T型>0,以便
$t\到+\infty$,存在T型>0,以便 $t\ge吨$,我们得到
$t\ge吨$,我们得到
那么,对于 $t,\tau\ge t$,我们有
$t,\tau\ge t$,我们有 $0\le{\rme}^{\int_\tau^ta\,{\rmd}s}\le{\trme}^{a^*(t-\tau)}$和
$0\le{\rme}^{\int_\tau^ta\,{\rmd}s}\le{\trme}^{a^*(t-\tau)}$和 ${\rm e}^{a_{1,0}i\tau}{\rme}^{\int_{\tau}^ta(s)\,{\rmd}s}\le{\rme}^{a_{1,0}i \tau+a^*(t-\tau)}$因此,对于
${\rm e}^{a_{1,0}i\tau}{\rme}^{\int_{\tau}^ta(s)\,{\rmd}s}\le{\rme}^{a_{1,0}i \tau+a^*(t-\tau)}$因此,对于 $t,t_0\ge t$和
$t,t_0\ge t$和 $t\ge t_0$,
$t\ge t_0$,
如果 $a^*\neia_{1,0}$对于任何
$a^*\neia_{1,0}$对于任何 $i=0,1,\ldot,n$、和
$i=0,1,\ldot,n$、和
如果存在 $i^*\在\{0,1,\ldot,n\}中$这样的话
$i^*\在\{0,1,\ldot,n\}中$这样的话 $a^*=i^*a{1,0}$。
$a^*=i^*a{1,0}$。
在这两种情况下都使用 $a_{1,0}\lt 0$和
$a_{1,0}\lt 0$和 $a^*\lt 0$,我们得到了任何解决方案
$a^*\lt 0$,我们得到了任何解决方案 美元(x(t),y(t))$具有初始条件
美元(x(t),y(t))$具有初始条件 $(x_0,y_0)$时间吨 0倾向于原点
$(x_0,y_0)$时间吨 0倾向于原点 $t\到+\infty$因此原点是全局渐近稳定的。在这种情况下证明了定理的证明。
$t\到+\infty$因此原点是全局渐近稳定的。在这种情况下证明了定理的证明。
2.2.案例2: $a_{0,1}\n一个0$
$a_{0,1}\n一个0$
在这种情况下,引入变量的变化:
方程式(2)写入
它也写
为了避免繁琐的符号,我们重命名了变量(X(X),Y(Y))再次作为(x个,年)和新参数 $\波浪线b_{i,0}=a_{0,1}b_{i,0}-a{1,0}b{i-1,1}$对于
$\波浪线b_{i,0}=a_{0,1}b_{i,0}-a{1,0}b{i-1,1}$对于 $i=1,\ldot,p$,其中
$i=1,\ldot,p$,其中
考虑到这一点
和施加条件(c1),即。 $\mathrm{Tr}Df\lt 0$为所有人
$\mathrm{Tr}Df\lt 0$为所有人 $(x,y)\in\mathbb{R}^2$,我们必须拥有它米是均匀的,并且
$(x,y)\in\mathbb{R}^2$,我们必须拥有它米是均匀的,并且
具有α我, $\beta_i\in\mathbb{R}$和
$\beta_i\in\mathbb{R}$和 $\beta_i\ne 0$因此,系统(5)成为
$\beta_i\ne 0$因此,系统(5)成为
哪里 $A=b_{m,1}\prod_{i=1}^{m/2}(\alpha_i^2+\beta_i^2)$和
$A=b_{m,1}\prod_{i=1}^{m/2}(\alpha_i^2+\beta_i^2)$和 $b_{m,1}\prod_{i=1}^{m/2}\big((x-\alpha_i)^2+\beta_i^2\big)-A$没有常数项。
$b_{m,1}\prod_{i=1}^{m/2}\big((x-\alpha_i)^2+\beta_i^2\big)-A$没有常数项。
案例2.2:p奇数
注意,如果 $\波浪线b_{10}\ne 0$,矩阵
$\波浪线b_{10}\ne 0$,矩阵 美元f(0,0)$具有特征值:
美元f(0,0)$具有特征值:
和强制条件(c3),我们必须 $\波浪线b_{1,0}\lt 0$,自A类<0,原点是稳定节点,如果
$\波浪线b_{1,0}\lt 0$,自A类<0,原点是稳定节点,如果 $A^2+4\波浪线b_{1,0}\ge 0$和稳定的焦点,如果
$A^2+4\波浪线b_{1,0}\ge 0$和稳定的焦点,如果 $A^2+4\波浪线b_{1,0}\lt 0$。
$A^2+4\波浪线b_{1,0}\lt 0$。
如果 $\波浪线b_{1,0}=0$,然后我们得到系统(7)其起源是半双曲线。根据案例2.1,如果
$\波浪线b_{1,0}=0$,然后我们得到系统(7)其起源是半双曲线。根据案例2.1,如果 $\波浪线b_{2,0}\ne 0$,则原点是鞍节点,这是不可能的。所以,
$\波浪线b_{2,0}\ne 0$,则原点是鞍节点,这是不可能的。所以, $\颚化符b_{2,0}=0$.现在应用定理三至系统(8),我们明白了
$\颚化符b_{2,0}=0$.现在应用定理三至系统(8),我们明白了 $Y=-\tilde b_{3,0}X^3/A+\c点$然后
$Y=-\tilde b_{3,0}X^3/A+\c点$然后 $F(X,Y)=-\tilde b_{3,0}X^3/A^2+\cdots$也就是说,如果
$F(X,Y)=-\tilde b_{3,0}X^3/A^2+\cdots$也就是说,如果 $\颚化符b_{3,0}\ne 0$,要使原点成为节点,必须
$\颚化符b_{3,0}\ne 0$,要使原点成为节点,必须 $\波浪线b_{3,0}\lt 0$.如果
$\波浪线b_{3,0}\lt 0$.如果 $\波浪线b_{3,0}=0$,那么为了满足条件(c3),我们必须
$\波浪线b_{3,0}=0$,那么为了满足条件(c3),我们必须 $\波浪线b_{4,0}=0$简而言之,如果满足系统的条件(c3)(7),必须存在奇数
$\波浪线b_{4,0}=0$简而言之,如果满足系统的条件(c3)(7),必须存在奇数 $i^*\在\{1,\ldot,n\}中$对于其中
$i^*\在\{1,\ldot,n\}中$对于其中 $\波浪线b_{i^*,0}\lt 0$和系统(7)写入
$\波浪线b_{i^*,0}\lt 0$和系统(7)写入
请注意 $p-i美元^*$是偶数,那个等式
$p-i美元^*$是偶数,那个等式 $\sum_{i=0}^{p-i^*}\波浪线b_{i+i^*,0}x^{i}=0$不能有真正的解决方案(否则条件(c2)不满足)。考虑到这一点,我们可以写
$\sum_{i=0}^{p-i^*}\波浪线b_{i+i^*,0}x^{i}=0$不能有真正的解决方案(否则条件(c2)不满足)。考虑到这一点,我们可以写
在这种情况下,系统的起源(6)是系统的唯一平衡点(6)和采取 $\波浪线b_{i^*,0}\lt 0$和A类<0,满足所有条件(c1)–(c3)。请注意
$\波浪线b_{i^*,0}\lt 0$和A类<0,满足所有条件(c1)–(c3)。请注意
从那以后 $\波浪线b_{i^*,0}\lt 0$,这意味着
$\波浪线b_{i^*,0}\lt 0$,这意味着 $\颚化符b_{p,0}\lt 0$。
$\颚化符b_{p,0}\lt 0$。
我们记得第页很奇怪,米是均匀的,并且 $b_{p,0}\lt 0$.研究(参见[参考Dumortier和Herssens6])庞加莱球面上原点附近的这种系统构成了证明的支柱。在这种情况下,系统(6)是一个广义Liénard微分系统第页奇数,米甚至,
$b_{p,0}\lt 0$.研究(参见[参考Dumortier和Herssens6])庞加莱球面上原点附近的这种系统构成了证明的支柱。在这种情况下,系统(6)是一个广义Liénard微分系统第页奇数,米甚至, 百万美元+1$和
百万美元+1$和 $\颚化符b_{p,0}\lt 0$.我们确实可以进行缩放
$\颚化符b_{p,0}\lt 0$.我们确实可以进行缩放
和系统(6)成为
哪里 $\hat b_{2i,1}$,
$\hat b_{2i,1}$, $\hat b_{m,1}$,
$\hat b_{m,1}$, $\hat\alpha_i$和
$\hat\alpha_i$和 $\hat\beta_i$是新参数,以及
$\hat\beta_i$是新参数,以及 $Y X ^米$为-1。
$Y X ^米$为-1。
注意,现在系统(9)是一个广义Liénard微分系统第页奇数,米偶数,以及系数X(X)第页等于−1。使用的差速器系统(3)[参考Dumortier和Herssens6]带有ɛ= 1,米奇数和n个偶数[参考Dumortier和Herssens6]),我们得到系统的无穷大(9)必须是图5(3)、图6(1)、图7(3)和图8(6)和图9(3)相图中描述的以下五个无穷大之一。
从前面的这些图中,我们可以得出图5(3)、图6(1)和图7(3)中的无穷大是一个排斥器(有来自无穷大的轨道,但没有通向无穷大的轨),或者图8(6)和图9(3)没有来自无穷大或走向无穷大的任何轨道。
注意,由于系统的发散性是负的(条件(c1)),这要归功于庞加莱-本迪克森定理(例如,参见[参考Dumortier、Llibre和Artés7,定理7.10]),不存在周期轨道,条件(c1)–(c3)以及前面描述的无穷远处的行为意味着原点是全局渐近稳定的。这就是定理的证明1。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()



![]()
![]()

![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()








![]()
![]()

![]()
![]()



![]()
![]()
![]()


![]()

![]()
![]()
![]()


![]()
![]()
![]()
![]()

![]()


![]()
![]()

![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()




![]()


![]()
![]()

![]()
![]()



![]()





![]()

![]()


![]()





![]()

![]()
![]()
![]()













![]()


![]()






![]()
![]()





![]()
![]()
![]()