1本说明的范围

Praeger–Xu图形，由Praege和Xu于[推荐人Praeger和Xu2]相对于顶点数，具有指数级的大组自同构。这一事实导致许多自然问题出现各种复杂情况。

在他们最近的工作中[参考Jajcay、Potočnik和Wilson1]，贾凯等。给出了Praeger–Xu图成为Cayley图的一个充要条件。明确地说[参考Jajcay、Potočnik和Wilson1，定理1.1]指出，对于任何正整数 $n\geq第3季度$ , $n\ne 4个$ ，对于任何正整数 $k\leq n-1$ ，Praeger–Xu图 $\textrm{PX}（n，k）$ 是Cayley图，当且仅当下列条件之一成立时：

1. （i）多项式 $t^{n}+1$ 有度的除数 n-k美元$ 在里面 $\mathbb美元{Z}（Z）_{2} [吨]$ ;

2. （ii） n个是偶数，并且存在多项式 $f_{1}，f_{2}，g_{1{，g_2}，u，v\in\mathbb{Z}（Z）_{2} [吨]$ 这样的话 $u，v$ 是程度的回文 n-k美元$ 、和

   (1.1) $$开始{align}t^{n}+1=f_{1}。\结束{对齐}$$

我们这里的目的是证明（ii）意味着（i），从而获得以下精化。（可以验证 $\textrm{PX}（4,1）$ , $\textrm{PX}（4,2）$ 和 $\textrm{PX}（4,3）$ 是Cayley图。）

使用因子分解 $t^{n}+1$ 在里面 $\mathbb美元{Z}（Z）_{2} [吨]$ ，我们给出了Cayleness的一个纯算术条件 $\textrm{PX}（n，k）$ .让 美元\varphi$ 成为欧拉 美元\varphi$ -函数和，对于每个正整数d日，让

$$\begin{align*}\omega（d）：=\min\lbrace c\in\mathbb{N}\midd\text{divides}2^{c} -1个\rbrace\end{align*}$$

是的乘法顺序 $2$ 模d日。

推论1.2。让一是一个非负整数，让b条是一个奇数正整数，让 $n:=2^{a} b条$ 具有 $n\geq第3季度$ 然后让k个是一个正整数 $k\leq n-1$ .Praeger–Xu图 $\mathrm{PX}（n，k）$ 是Cayley图当且仅当k个可以写为

(1.2) $$\begin{align}k=\sum_{d\mid-b}\alpha_{d}\omega（d），\quad\text{用于某些整数}\alfa_{d{\text{与}0\leq\alpha_a{d}\ leq\frac{2^{a}\varphi（d）}{\omega。\结束{对齐}$$

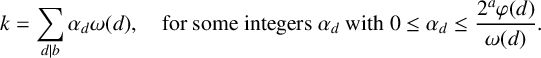
2定理1.1的证明

假设（ii）成立。我们的目标是证明 $t^{n}+1$ 可被次数多项式整除 n-k美元$ 在里面 $\mathbb美元{Z}（Z）_{2} [吨]$ ，表示（i）。特色工作 $2$ , (1.1)可以写为

$$开始{align*}t^{n}+1=f_{1}^{2}$$

简言之，

（2.1） $$\开始{align}t^{n}+1=f_{1}^{2} u个+tg{1}^{2} v（v）=f_{2}^{2} v（v）+tg{2}^{2} 美国。\结束{align}$$

如果 $g_{1}=0$ 或者如果 $g_{2}=0$ ，则结果如下(2.1)以及以下事实u个和v（v）有学位 n-k美元$ 因此，对于剩下的论证，我们可以假设 $g_{1}，g_{2}\ne 0$ 此外，请注意 $f_{1}，f_{2}\ne 0$ ，因为t吨不可分割 $t^{n}+1$ 。

我们引入四个多项式 $u{e}，u{o}，v{e}，v{o}\in\mathbb{Z}（Z）_{2} [吨]$ 这样的话

$$\开始{align*}u:=u{e}^{2}+tu{o}^{2]，\quad v:=v{e}^{2{+tv{o}^}。\结束{align*}$$

将这些扩展替换为u个和v（v）英寸(2.1),

$$\开始{align*}t^{n}+1&=f_{1}^{2} 单位_{e} ^{2}+t^{2} 克_{1}^{2} v（v）_{o} ^｛2｝+t（f_｛1｝^{2} u个_{o} ^{2}+g{1}^{2} v（v）_{e} ^{2}），\\[5pt]t^{n}+1&=f_{2}^{2} v（v）_{e} ^{2}+t^{2} 克_{2}^{2} u个_{o} ^{2}+t（f_{2}^{2} v（v）_{o} ^{2}+g{2}^{2} u个_{e} ^{2}）。\结束{align*}$$

回想一下n个是均匀的。通过将方程分解为奇偶度项，我们得到

$$\开始{align*}t^{n}+1&=f_{1}^{2} u个_{e} ^{2}+t^{2} 克_{1}^{2} v（v）_{o} ^{2}，\quad 0=t（f_{1}^{2} u个_{o} ^{2}+g{1}^{2} v（v）_{e} ^{2}），\\[5pt]t^{n}+1&=f_{2}^{2} v（v）_{e} ^{2}+t^{2} 克_{2}^{2} 单位_{o} ^{2}，\quad 0=t（f_{2}^{2} 五_{o} ^{2}+g{2}^{2} u个_{e} ^｛2｝）。\结束{align*}$$

设置 $m:=无$ .因为我们的工作很有特色 $2$ ,

(2.2) $$\开始{align}&t^{m}+1=f_{1} u个_{e} +总重量_{1} v（v）_{o} ，\四元t^{m}+1=f_{2} v（v）_{e} +总重量_{2} u个_{o} ，\结束{align}$$

(2.3) $$\开始{align}&\hspace{-42pt}f_{1} u个_{o} =克_{1} v（v）_{e} ，\qquad\qquad_f_{2} v（v）_{o} =克_{2} u个_{e} ●●●●。\结束{对齐}$$

自u个和v（v）根据假设是回文的，我们得到 $1=u（0）=u{e}（0）$ 和 ${1=v（0）=v{e}（0）}$ 尤其是，两者 $u_{e}$ 和 $v_{e}$ 不为零。发件人(2.2)和(2.3),

(2.4) $$\begin{align}f_{1}=&\frac{t^{m}+1}{u_{e} v（v）_{e} +tu_{o} 五_{o} }v{e}，\quad g{1}=\frac{t^{m}+1}{u_{e} 五_{e} +tu_{o} v（v）_{o} ｛u_｛o｝，\非成员\\f_｛2｝=&&frac｛t^｛m｝+1｝｛u_{e} v（v）_{e} +tu_{o} v（v）_{o} }u{e}，\quad g{2}=\frac{t^{m}+1}{u_{e} v（v）_{e} +tu_{o} v（v）_{o} }v{o}。\结束{对齐}$$

我们想要除数的候选者 $t^{n}+1$ 是 $s:=u_{e} v（v）_{e} +tu_{o} v（v）_{o}（o）$ 让我们先展示一下 $\deg=n-k$ .自 $u（美元）_{e} v（v）_{电子}$ 和 $u（美元）_{o} v（v）_{o}（o）$ 我们推断，具有均匀度

$$\开始{align*}\deg（s）=\max\{\deg_{e} v（v）_{e} ），\deg（tu_{o} v（v）_{o} ）\}。\结束{align*}$$

召回 $u=u{e}^{2}+tu{o}^{2]$ 和 $v=v_｛e｝^｛2｝+tv_｛o｝^｛2｝$ .如果 n-k美元$ 那就平分秋色了

$$\begin{align*}\deg（u{e}）=\deg。\结束{align*}$$

但是，如果 n-k美元$ 那就奇怪了

$$\begin{align*}\deg（u{e}），\deg。\结束{align*}$$

因此，在这两种情况下， $\度=n-k$ 。

还有待证明秒划分 $t^{n}+1$ .自 $f_1}，g_1}、f_2}、g_2}$ 是多项式，由(2.4),秒划分

$$开始{align*}\gcd（（t^{m}+1）v{e}，（t^}m}+1”）v{o}，“（t^[m}+1]）u{e}.”。\结束{align*}$$

请注意 $\gcd（v{e}，v{o}，u{e}.，u{o}.）$ 划分 $f美元_{1} u个_{e} +总重量_{1} v（v）_{o}（o）$ ，因此，考虑到(2.2), $\gcd（v{e}，v{o}，u{e}.，u{o}.）$ 划分 $t^{m}+1$ 因此，秒划分 ${（t^{m}+1）^{2}=t^{n}+1}$ 。

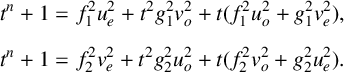
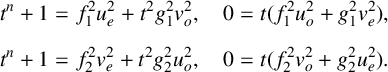
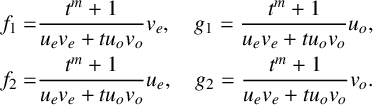
三推论1.2的证明

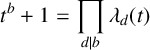
根据定理1.1，决定是否为Praeger–Xu图 $\textrm{PX}（n，k）$ 是Cayley图就等于决定 $t^{n}+1$ 接受除数k个在里面 $\mathbb美元{Z}（Z）_{2} [吨]$ .立即着手的方法是研究如何 $t^{n}+1$ 可以分解为不可约多项式。

让 $n=2^{a} b$ ，使用 $\gcd（2，b）=1$ .因为我们是有特色的 2美元$ ,

$$\开始{align*}t^{n}+1=t^{2^{a} b条}+1=（t^{b}+1）^{2^{a}}。\结束{align*}$$

此外，如果 $\lambda_{d}（t）\in\mathbb{Z}[t]$ 表示d日第个分圆多项式，则

$$\开始{align*}t^{b}+1=\prod_{d|b}\lambda_{d}（t）\end{align**}$$

是因子分解 $t^{b}+1$ 上的不可约多项式 $\mathbb{Q}[t]$ 根据高斯定理。由于Galois群的任何域的扩展 $\mathbb美元{Z}（Z）_{2}$ 是由Frobenius自同构生成的循环群，它是 $\lambda_{d}（t）$ 在里面 $\mathbb美元{Z}（Z）_{2} [吨]$ 是最小的c（c）这样d日th本原根 $\泽塔$ 被提升到权力 $2^{c}$ 是 $\泽塔$ 也就是说， $\omega（d）$ 因此， $\lambda_{d}（t）$ 在里面 $\mathbb美元{Z}（Z）_{2} [吨]$ 将因子分解为 $\varphi（d）/\omega（d）$ 不可约多项式，每个多项式都有度 $\omega（d）$ 。

因此， $t^{n}+1\in\mathbb{Z}（Z）_{2} [吨]$ 有度的除数k个当且仅当k个可以写成一些 $\omega（d）$ 术语，每个摘要最多重复一次 $2^{a}\varphi（d）/\omega（d）$ 时间，确切地说(1.2).