我从计划中的假期回来后上一篇博客文章，我整个一月份都在玩图的代数并尝试寻找有趣且有用的构建图形的方法，重点是编写多态代码，这些代码可以操作图形表达式，而无需将其转换为具体的数据结构。我整理了一个小工具箱，里面有一些古怪的类型，我想在这篇博客文章中与大家分享。如果你不熟悉图的代数，请阅读介绍性博客帖子第一。

更新：这一系列博客文章是作为功能珍珠在2017年哈斯克尔研讨会上。

图形转置

可以应用于图形的最简单变换之一是反转其所有边的方向。它通常很容易实现，但无论您使用什么数据结构来表示图形，您至少要花费O（1）是时候修改它了（比如，通过翻转治疗为换位旗帜）；通常，您必须遍历数据结构并翻转每一条边，从而O（|V|+|E|）时间复杂性。如果我告诉你，通过使用Haskell的类型系统，我们可以在零时间？听起来可疑吗？让我们看看这是如何工作的。

考虑以下内容图表实例：

新类型 转座克= T型{转置::g｝实例 图表 克 => 图表(转座 克)哪里
    类型 顶点(转座g）= 顶点克空的= T型空的顶点= T型 .顶点覆盖x y= T型 $转置x`覆盖`转置y连接x y= T型 $转置y`连接`转置x--翻转

我们将图形包装在新类型将参数的顺序颠倒为连接。让我们检查一下是否有效：

λ>边缘列表$ 1* (2 + 三) *4[(1,2),(1,三),(1,4),(2,4),(三,4)]λ>边缘列表$转置$ 1* (2 + 三) *4[(2,1),(三,1),(4,1),(4,2),(4,三)]

酷！而且它的运行时成本为零，因为我们所做的只是包装和解包新类型，这是保证免费作为练习，验证转置是反同态在图形上，即：

• T（ε）=ε
• T（v）=v
• T（x+y）=T（x）+T（y）
• T（x→y）=T（y）→T（x）

此外，转置是其自身的逆运算：转置。转置=id.

为了确保转置仅应用于多态图，我们不导出构造函数T型，因此唯一的呼叫方式转置是给它一个多态参数，并让类型推理将其解释为类型的值转座。类型签名有点令人不满意：

λ> :t转置转置 :: 转座 克 -> 克

从类型上看，函数是否在图上运行一点也不清楚。你有什么改进意见吗？

用函子合并图顶点

这里有一个难题：你能实现一个函数吗gmap（gmap）给定函数的a->b以及顶点为类型的多态图一将生成具有类型顶点的多态图b条将函数应用于每个顶点？是的，这几乎是一个Functor（仿真器）但它没有通常的类型签名，因为图表不是更高种类的类型。

我的解决方案如下，但我觉得可能有更简单的解决方案：

新类型 图形Functor一=
    GF公司{g对于::所有g. 图表克=>（a）-> 顶点g）->克}实例 图表(图形Functor 一)哪里
    类型 顶点(图形Functora）=一空的= GF公司 $ \_->空的顶点x= GF公司 $ \（f）->顶点（f x）覆盖x y= GF公司 $ \（f）->gmap f x`覆盖`gmap f y连接x y= GF公司 $ \（f）->gmap f x`连接`gmap f ygmap（gmap） :: 图表 克 =>(一 -> 顶点 克)-> 图形Functor 一 -> 克gmap（gmap）= 轻弹gfor公司

本质上，我们正在定义另一个新类型包装器，它将给定的函数一直推向顶点。这没有运行时成本，就像以前一样，尽管在每个顶点对给定函数的实际求值当然不是免费的。让我们测试一下！

λ>邻接列表$ 1*2*三 + 4*5[(1,[2,三]),(2,[三]),(三,[]),(4,[5]),(5,[])]λ> :t gmap(+1)$ 1*2*三 + 4*5gmap（gmap）(+1)$ 1*2*三 + 4*5 ::(图表克, 号码(顶点g） ）=>克λ>邻接列表$gmap（gmap）(+1)$ 1*2*三 + 4*5[(2,[三,4]),(三,[4]),(4,[]),(5,[6]),(6,[])]

如您所见，我们可以通过映射函数增加每个顶点的值(+1)在图表上。根据需要，得到的表达式是多态图。同样，我们做了一些有用的工作，但没有将图形转换为具体的数据结构。作为练习，展示一下gmap（gmap）满足函子定律：gmap id=id和gmap文件。gmap g=gmap（f.g）。有用的第一步是证明映射函数是同态:

• M（M）_（f）(ε) = ε
• M（M）_（f）（v） =f（v）
• M（M）_（f）（x+y）=M_（f）（x） +M（百万美元）_（f）（年）
• M（M）_（f）（x→y）=M_（f）（x） →M_（f）（年）

警惕的读者可能会想：如果函数将两个原始顶点映射到同一个顶点，会发生什么？他们将被合并！合并图顶点是一个有用的函数，所以让我们用以下术语定义它gmap（gmap）:

合并顶点 :: 图表 克 =>(顶点 克 -> 布尔)-> 顶点 克
    -> 图形Functor(顶点g）->克合并顶点p v=gmap（gmap）$ \单位-> 如果对u然后v（v）其他的单位λ>邻接列表$合并顶点古怪的 三 $ 1*2*三 + 4*5[(2,[三]),(三,[2,三]),(4,[三])]

该函数接受图顶点和目标顶点上的谓词，并将满足谓词的所有顶点映射到目标顶点，从而合并它们。在我们的示例中，所有奇数顶点{1，3，5}合并为3，特别是创建自循环3→3。注意：这需要线性时间O（|g|）的合并顶点将谓词应用于每个顶点（g是表达式g的大小），这可能比合并具体数据结构中的顶点效率更高；例如，如果图形由邻接矩阵表示，则可能需要从头开始重建生成的矩阵，这需要O（|V|^2）时间。因为对于许多图，我们有|g|=O（|V|），基于矩阵合并顶点将磨合O（|g|^2）.

将顶点展开为子图（嘿，单子！）

删除顶点和拆分顶点的操作有什么共同点？它们都可以通过将图的每个顶点替换为（可能为空）子图并展平结果来实现。听起来很熟悉吗？你可能会认出这是莫纳德的绑定函数或Haskell运算符>>=，它非常有用，甚至可以Haskell的徽标.我们将实施绑定把图包装成另一个图新类型:

新类型 GraphMonad（图形单体）一=
    总经理{绑定::对于所有g. 图表克=>（a）->g）->克}实例 图表(GraphMonad（图形单体） 一)哪里
    类型 顶点(GraphMonad（图形单体）a）=一空的= 总经理 $ \_->空的顶点x= 总经理 $ \（f）->f x（f x）--这就是诀窍！覆盖x y= 总经理 $ \（f）->绑定x f`覆盖`绑定y f连接x y= 总经理 $ \（f）->绑定x f`连接`绑定y f

如您所见，实现几乎与gmap（gmap）：而不是包装值（f） x到顶点，我们应该保持原样。得到的变换也是同态。让我们看看如何利用工具箱中的这种新类型。

我们首先要实现一个类似过滤器的函数诱导在给定顶点谓词和图的情况下，将计算诱导子图关于通过将所有其他顶点转化为满足谓词的顶点集空子图并将结果展平。

诱导 :: 图表 克 =>(顶点 克 -> 布尔)-> GraphMonad（图形单体）(顶点g）->克诱导pg=绑定g$ \v（v）-> 如果p v值然后顶点v其他的空的λ>边缘列表$集团[0..4][(0,1),(0,2),(0,三),(0,4),(1,2),(1,三),(1,4),(2,三),(2,4),(三,4)]λ>边缘列表$诱导(<三)$集团[0..4][(0,1),(0,2),(1,2)]λ>诱导(<三)（集团[0..4])==（集团[0..2]:: 基本 国际)真的

如您所见，通过在我们喜欢的顶点子集上诱导团(<3)，我们得到了一个较小的集团，正如预期的那样。

我们现在可以实施删除顶点通过诱导:

移除顶点 ::(等式(顶点 克),图表 克)=> 顶点 克
    -> GraphMonad（图形单体）(顶点g）->克移除顶点v=诱导(/=v）λ>邻接列表$移除顶点2 $ 1* (2 + 三)[(1,[三]),(三,[])]

删除边并不是那么简单。我怀疑这与相应的转换似乎不是同态这一事实有关。实际上，您会发现满足R上的最后一个同态要求很难_x→y:

• R（右）_x→y（x→y）=R_x→y（x） →R_x→y（年）

然而，我们可以实现一个函数断开删除两个之间的所有边不同的顶点如下：

断开 ::(等式(顶点 克),图表 克)=> 顶点 克 -> 顶点 克
    -> GraphMonad（图形单体）(顶点g）->克断开uv g=删除顶点`覆盖`移除顶点v gλ>邻接列表$断开1 2 $ 1* (2 + 三)[(1,[三]),(2,[]),(三,[])]

也就是说，我们创建了两个图：一个没有u，另一个没有v，并对其进行叠加，从而删除u→v和v→u边。我仍然没有一个只删除单个边u→v，甚至只删除自循环v→v的解决方案（注意：断开v v=删除Vertex v). 也许你能找到解决方案？(更新：Arseniy Alekseyev找到了一种去除自循环的解决方案，可以推广用于去除边缘，请参阅博客文章末尾的注释。）

奇怪的是，我们可以稍微缩短断开，因为返回图形的函数也可以给定图表实例：

实例 图表 克 => 图表(一 -> 克)哪里
    类型 顶点（a）->g）= 顶点克空的=纯空顶点=纯净的.顶点覆盖x y=覆盖<$>x<*>年连接x y=连接<$>x<*>年断开 ::(等式(顶点 克),图表 克)=> 顶点 克 -> 顶点 克
    -> GraphMonad公司(顶点g）->克断开uv=移除顶点u`覆盖`移除顶点v

最后，正如所承诺的，下面是如何使用绑定功能：

splitVertex（分割顶点） ::(等式(顶点 克),图表 克)=> 顶点 克
    ->[顶点克]-> GraphMonad（图形单体）(顶点g）->克splitVertex v vs g=绑定g$
    \单位-> 如果单位==v（v）然后顶点vs其他的顶点uλ>邻接列表$splitVertex（分割顶点）1[0, 1]$ 1* (2 + 三)[(0,[2,三]),(1,[2,三]),(2,[]),(三,[])]

这里，顶点1被拆分为具有相同连接性的一对顶点{0，1}。

构造De Bruijn图

为了证明我们可以使用所提供的工具包构建相当复杂的图形，让我们试试德布鲁因图是一个有趣的组合对象，经常出现在计算机工程和生物信息学中。我的实现相当简短，但需要一些解释：

德布鲁因 ::(图表 克,顶点 克~ [一])=> 国际 ->[一]-> 克deBruijn-len字母表=绑定骨架展开哪里重叠= 地图M(常量字母表）[2..长度]骨架=从边缘列表[(左侧秒, 赖特s）|秒<-重叠]展开v=顶点[任一（[a]++) (++[a] ）v|一<-字母]

该函数构建一个De Bruijn维度图伦恩从给定的符号字母表.图的顶点都是可能的长度词伦恩包含的符号字母表，当删除x的第一个符号和y的最后一个符号后，只要x和y匹配，两个单词就连接x→y（相当于当某些符号a和b的x=az和y=zb时）。下图（右）显示了字母{0，1}上的三维De Bruijn图的示例。

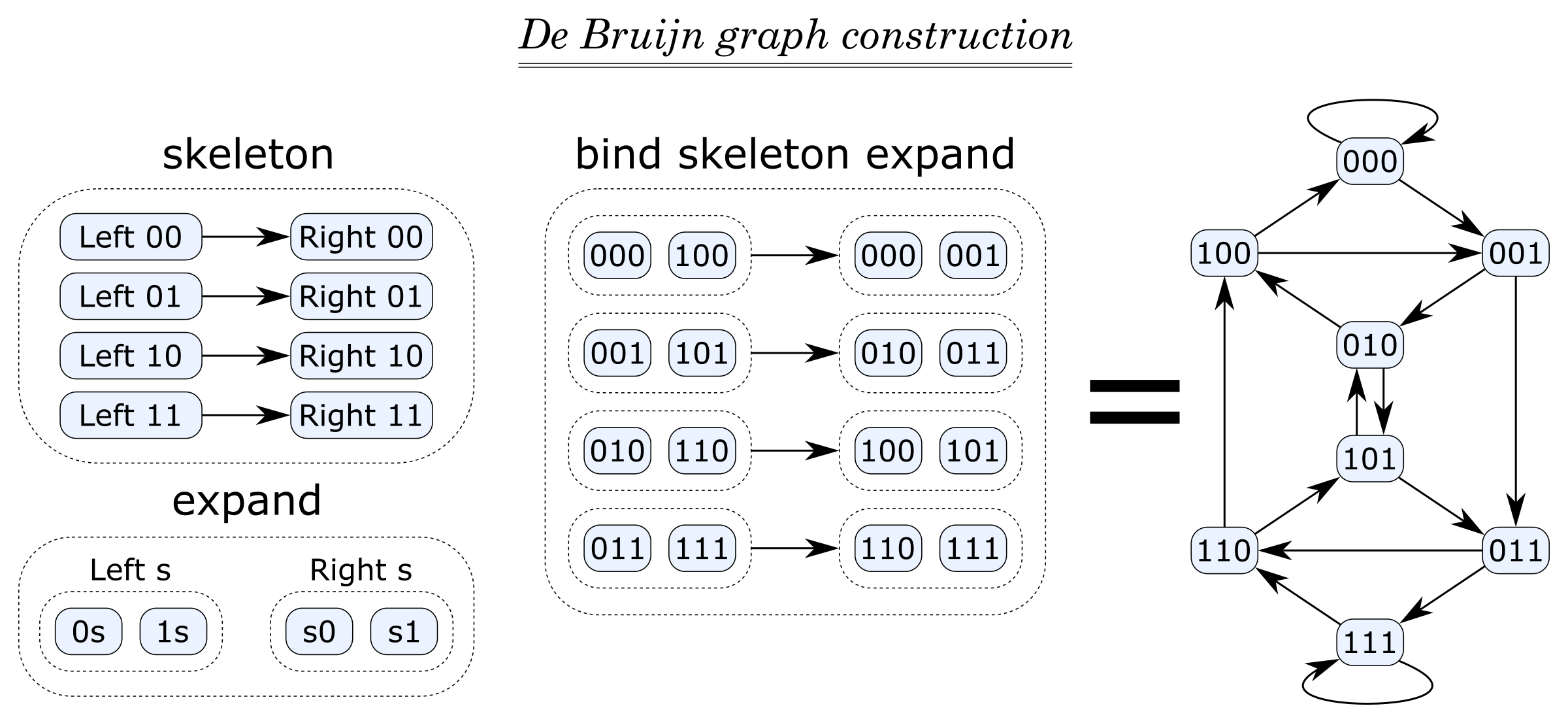
以下是溶液的所有成分：

• 重叠包含所有可能长度的单词透镜-1对应于连接顶点的重叠。
• 骨架是每个重叠有一条边的图左侧和赖特充当临时占位符的顶点（参见图表）。
• 我们替换一个顶点 左侧s具有两个顶点的子图{0秒,1秒}，即后缀为秒对称地， 右侧被两个顶点的子图取代{第0集,s1}. 这由函数捕获扩大.
• 通过计算得出结果绑定骨架展开，如上所示。

……这与预期相符：

λ>边缘列表$德布鲁因三 "01"[("000","000"),("000","001"),("001","010"),("001","011"),("010","100"),("010","101"),("011","110"),("011","111"),("100","000"),("100","001"),("101","010"),("101","011"),("110","100"),("110","101"),("111","110"),("111","111")]λ> 全部的(\（x）,年）-> 滴 1x==拖放结束1年）$边缘列表$德布鲁因9 “abc”
真的
λ> 设置.大小$顶点集$德布鲁因9 “abc”
19683 --即3^9

现在就到此为止！我希望我已经说服了您，在构建图形时，您不一定需要操作具体的数据结构。通过使用Haskell的类型将多态图表达式解释为映射、绑定和其他熟悉的转换，您可以编写高效且可重用的代码。给我任何旧图，我会给你写一个新的类型来构造它！😉

附言：图的代数在藻类图书馆。

更新：Arseniy Alekseyev找到了一个很好的解决方案来消除自锁。让R_v（v）表示移除顶点v的操作，并且R_v→v表示移除自循环v→v的操作。然后，后者可定义如下：

• R（右）_v→v(ε) = ε
• R（右）_v→v（x） =x
• R（右）_v→v（x+y）=R_v→v（x） +R（右）_v→v（年）
• R（右）_v→v（x→y）=R_v（v）（x） →R_v→v（y） +R（右）_v→v（x） →R_v（v）（年）

这不是同态，但似乎有效。酷！此外，我们可以概括上述内容并实现操作R_u→v删除边u→v：

• R（右）_u→v(ε) = ε
• R（右）_u→v（x） =x
• R（右）_u→v（x+y）=R_u→v（x） +R（右）_u→v（年）
• R（右）_u→v（x→y）=R_单位（x） →R_u→v（y） +R（右）_u→v（x） →R_v（v）（年）

请注意，由于应用了此类操作，表达式的大小可能会大幅增加。给定大小为|g|的表达式g，结果的最坏可能大小|R是多少_u→v（g） |？