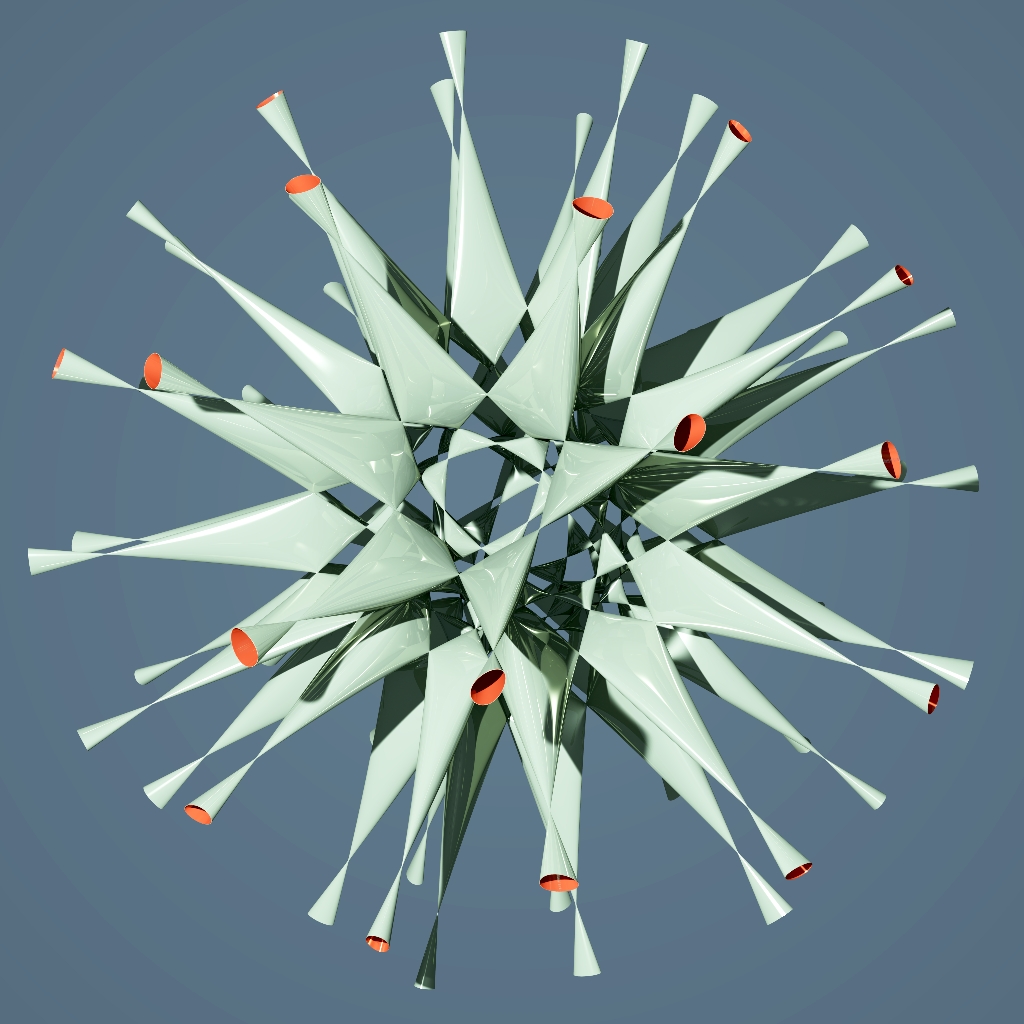
Barth Decic–Abdelaziz Nait Merzouk
A类分度面是由10次多项式方程定义的。这个Barth decic公司,由绘制阿卜杜拉齐兹·奈特·默祖克,是目前已知数量最多的普通双点:也就是说,它看起来像由定义的三维空间中圆锥体原点的点
$$x^2+y^2=z^2$$
它有345个普通的双点,而最著名的分度曲面的上限是360,除了这种奇点外,它是光滑的。
Barth decic由四个变量(w,x,y,z)中的10次齐次多项式方程定义:
$$开始{数组}{c}8(x^2–\Phi^4y^2)(y^2–\ Phi^4 z^2)\\
+(3+5\Phi)w^2\left(x^2+y^2+z^2–w^2\\right)^2\ left(x ^2+y ^2+z ^2–(2-\Phi$$
哪里
$$\Phi=\frac{\sqrt{5}+1}{2}$$
是黄金比例。该等式确定了具有复数维2的子集(S\subset\mathbb{C}^4)。注意,如果\(w,x,y,z\in\mathbb{C}^4\)是一个解,那么任何倍数\((cw,cx,cy,cz)\也是一个解。我们可以这样投射\(S\),将任何解决方案视为与该解决方案的任何倍数“相同”。结果是代数簇\(X\)在复射影空间\(\mathbb{C}\mathrm{P}^3\)。这种变体具有复杂的维度2,因此称为复杂曲面为了得到一个普通的实二维曲面,我们可以取它与\(\mathbb{C}\mathrm{P}^3)中的\(\mathbb{R}\mathr m{P{^3)的副本的交集。
坐在(mathbb{R}\mathrm{P}^3)里面,我们又有许多普通三维空间的副本。上面的图片显示了其中一个副本中的巴特·德克部分。具体来说,这包括上述方程的实际解,其中\(w=1\)。
但我们也有“无穷远点”。如果你沿着\(mathbb{R}^3)中两个相反方向中的任何一个前进,你将在无穷远处接近其中一个点。无穷远处的点构成射影平面,即,\(\mathbb{R}\mathrm{P}^2\)的副本。具体地说,这些无穷远点是\(mathbb{R}\mathrm{P}^2)中的点,它们来自\(x,y,z,w)\ in\mathbb}R}^4)和\(w=0)。
巴思分局有345个普通的双分。然而,其中45个点位于无穷远处,因此它们在上图或下图中不可见:

Barth Decic–Abdelaziz Nait Merzouk
我们可以通过稍微旋转\(\mathbb{R}\mathrm{P}^3\)来观察无穷远处的双点。如果我们对生成的曲面进行切片以更好地看到它,则会得到如下图片:

旋转Barth Decic–Abdelaziz Nait Merzouk
我们也可以将(mathbb{R}^3)压缩成一个球,这样无穷远处的点就位于这个球的表面上。更准确地说,这个球的表面是一个2球,一个\(\mathbb{R} P(P)^2),所以这个2球体中的任何对反点对应于无穷远处的同一点。
这给出了以下对巴特判决的看法:

压缩Barth Decic–Abdelaziz Nait Merzouk
你可以直观地看到,压缩后的巴思分贝在10个大圆内与2个球体相遇。为了从数学上看到这一点,我们可以取Barth decic的方程,并设置(w=0):
$$开始{数组}{c}(x^2–\Phi^4y^2)(y^2–\ Phi^4 z^2)$$
这包括10个线性函数:
$$(x–\Phi^2 y)(x+\Phi|2 y)$$
每一个都在$\mathbb{R}^3$中定义了一个平面,它与单位2-球体的交点是10个大圆中的一个。这10个大圆与穿过正十二面体对角的直线正交:

带十二面体的压缩Barth Decic–Abdelaziz Nait Merzouk
你可以在十二面体的每个面上看到5个双点,在每个边的中点看到1个,总共\(5\乘以12+30=90\)。然而,球体上的反足点在无穷远处算为同一点,因此我们在无穷远处得到了总共的(90/2=45)个双点。
有关更多相关图片,请参见:
•Abdelaziz Nait Merzouk,Barth decic和十二面体.
值得比较的是巴思六分仪:
•巴思六分仪.
二十面体的旋转和反射对称组{A} _5个times\mathbb{Z}/2)充当了巴思六分仪和巴思分度仪的对称性。Barth在这里介绍了这些表面:
•Wolf Barth,两个具有多个节点的投影曲面,承认二十面体的对称性,代数几何杂志 5(1994), 173–186.
普通的双倍积分也称为节点1984年,宫崎骏证明了只有有理双点的$\mathbb{C}\mathrm{P}^3$中的十进制曲面最多可以有360个这样的点:
•Y.Miyaoka,给定数值不变量曲面上商奇异的最大数目,数学。安。 268(1984), 159–171.
视觉洞察力是一个分享有助于解释高等数学主题的醒目图像的地方。我一直在寻找真正美丽的图像,所以如果你知道,请留言在这里让我知道!