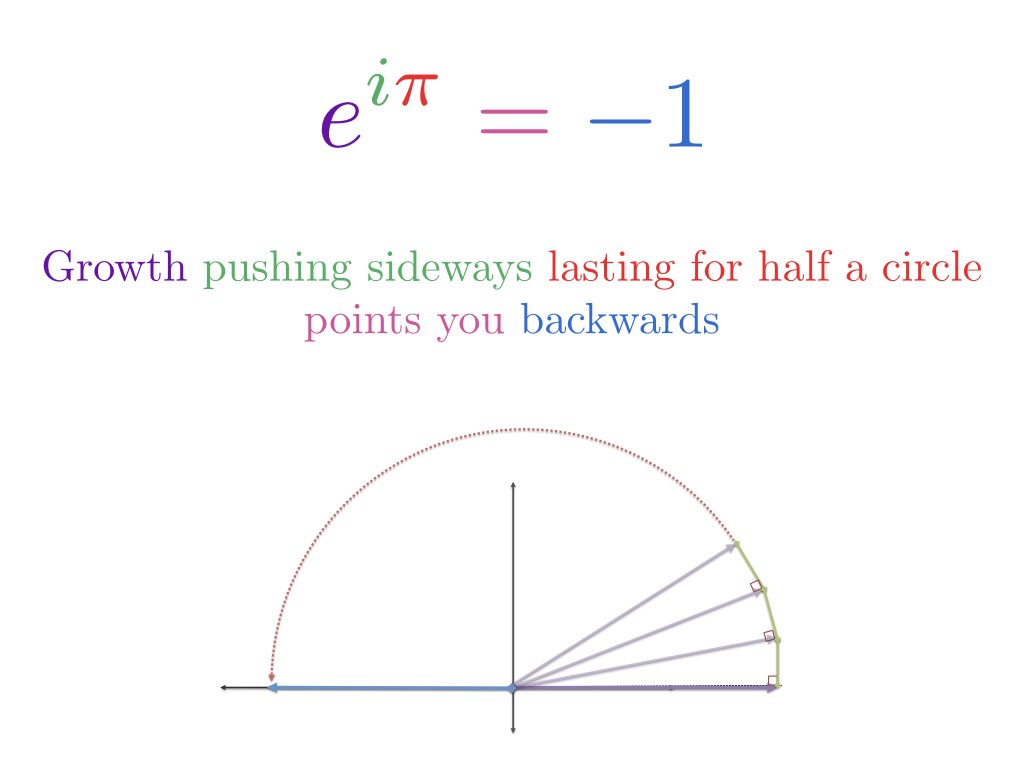对欧拉公式的直观理解—

欧拉的身份似乎令人困惑：

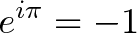
$\显示样式{e^{i\pi}=-1}$

它来源于一个更一般的公式：

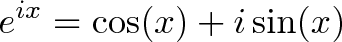
$\显示样式{e^{ix}=\cos（x）+i\sin（x）}$

尤扎——我们正在讲述一个虚指数正弦和余弦！不知怎么地，插入π会得到-1？这可能是直观的吗？

根据19世纪数学家本杰明·皮尔斯的说法：

这绝对是自相矛盾的；我们无法理解它，也不知道它意味着什么，但我们已经证明了它，因此我们知道它一定是真理。

啊，这种态度让我热血沸腾！公式不是需要记住的魔法咒语：我们必须，必须，必须找到洞察力。这是我的：

欧拉公式描述了两种等效的圆周运动方式。

就这样？这个惊人的方程式是关于旋转的？是的，我们可以通过几个类比来理解：

从数字1开始，将乘法视为转型这将更改数字：$1\cdot e^{i\pi}$
常规指数增长连续不断地增加1按一定比率计算一段时间；想像的指数持续增长旋转一段时间内为1
增加“π”时间单位意味着增加π弧度围绕一个圆
因此，$e^{i\pi}$意味着从1开始，旋转pi（绕圆的一半）以达到-1

这是高层视图，让我们深入了解细节。顺便说一句，如果有人想用$e^{i\pi}=-1$给你留下深刻印象，问问他们我到我-次幂。如果他们想不透，欧拉的公式对他们来说仍然是一个魔咒。

更新：在写作时，我认为视频可能有助于更清楚地解释这些想法：

理解cos（x）+i*sin（x）

等号过载。有时我们指的是“将一件事设置为另一件事”（比如x=3），而其他的我们指的则是“这两件事描述了相同的概念”（比如$\sqrt{-1}=i$）。

欧拉公式是后者：它给出了两个解释如何在圆周中运动的公式。如果我们使用三角和行程x弧度检查圆周运动：

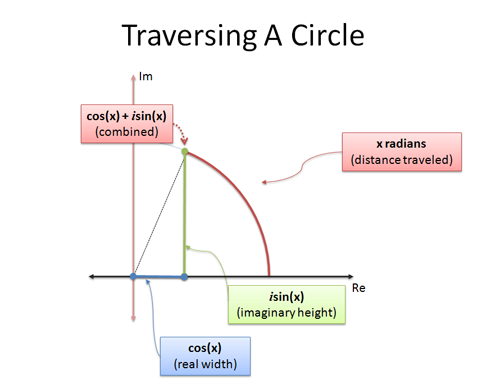
cos（x）是x坐标（水平距离）
sin（x）是y坐标（垂直距离）

声明

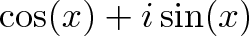
$\显示样式{\cos（x）+i\sin（x）}$

是将x和y坐标涂抹为单个数字的聪明方法。“复数是二维的”这一类比帮助我们将单个复数解释为圆上的位置。

当我们将x设置为$\pi$时，我们沿着单位圆的外侧移动$\pi$units。因为总周长是$2\pi$，所以普通的$\pi$在一半左右，使我们处于-1。

Neato：欧拉公式（$\cos（x）+i\sin（x）$）的右侧用虚数描述圆周运动。现在让我们想想e（电子）等式的一边完成了它。

什么是想象增长？

将x和y坐标组合成一个复数是很棘手的，但可以管理。但想象中的指数意思是？

让我们退一步。当我看到$3^4$时，我这样想：

3是最终结果以ln（3）的速度快速生长（使用e）。换句话说：$3=e^{ln（3）}$
$3^4$与增长到3相同，但增长的时间是原来的4倍。所以$3^4=e^{ln（3）\cdot4}=81$

你可以把这些数字看作是我们必须“成长”的东西，而不是看到它们自己的数字。实数，如3，给出ln（3）=1.1的利率，这就是e在不断增长的过程中“收集”的值。

常规增长很简单：它不断地向原来的方向“推动”一个数字。3×3向原始方向推动，使其增大3倍（9）。

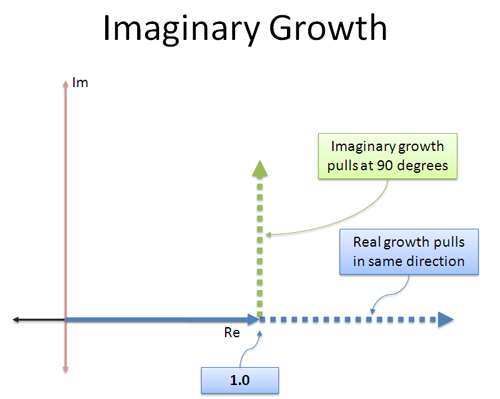
想象中的增长是不同的：我们赚取的“利息”方向不同！这就像是一个侧面捆绑着的喷气发动机——我们不是向前推进，而是开始以90度角推进。

恒定的正交（垂直）推力最妙的地方在于，它不会加速或减慢你的速度——它会旋转你！取任意数并乘以我不会改变它的大小，只会改变它所指向的方向。

直觉上，我是这样看的连续假想增长率：“当我成长的时候，不要把我推向已经前进的方向，而是让我旋转。”

但我们不应该越来越快地旋转吗？

我也很奇怪。有规律的生长复合物在我们原来的方向上，所以我们用1、2、4、8、16，每次乘以2倍，并保持实数不变。我们可以考虑这个$e^{ln（2）x}$，这意味着在“x”秒内以ln（1）的速率立即增长。

嘿，如果我们的增长速度是2 ln（2）vs ln（1）的两倍，那么它看起来就像增长了两倍的时间（2 x vs x）。e的魔力让我们可以互换汇率和时间；ln（2）下的2秒与2ln（2中）下的1秒增长相同。

现在，假设我们有一些纯粹的想象增长率（Ri），它使我们旋转，直到达到i，或向上90度。如果我们把速率加倍到2Ri，会发生什么呢？

不！速率为2Ri意味着我们旋转的速度是原来的两倍，或者说，以R的速率旋转的时间是原来的二倍，但我们仍停留在圆周上。旋转两倍的长度意味着我们现在面对180度。

一旦我们意识到某个指数增长率可以将我们从1带到i，增加这个速度只会使我们旋转更多。我们永远无法摆脱这个圈子。

然而，如果我们的增长率很复杂（a+bi vs Ri），那么实部（a）将使我们像正常一样增长，而虚部（bi）使我们旋转。但我们不要想当然：欧拉公式$e^{ix}$是关于纯粹虚构的让我们保持循环的增长（稍后会详细介绍）。

快速健康检查

写作时，我必须为自己澄清几个问题：

为什么使用$e^x$，我们不是在旋转数字1吗？

e（电子）表示从1开始，在1个单位时间内以100%的利息持续增长的过程。

当我们写作时e（电子）我们用一个数字来描述整个过程，e代表了持续增长的所有繁琐。实际上，$e^x$是说“从1开始，在x秒内以100%的速度连续增长”，并且像我们希望的那样从1开始。

但作为指数，我该做什么呢？

对于像$3^4$这样的常规指数，我们会问：

隐性增长率是多少？我们从1增长到3（指数的基数）。
我们该怎么做改变增长率是多少？我们将其按4x（指数的幂）进行缩放。

我们可以将我们的增长转换为“e”格式：我们的瞬时速率是ln（3），然后将其增加到ln（3*4。再一次，指数（4）的威力只是衡量了我们的增长率。

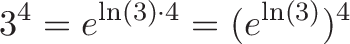
$\显示样式{3^4=e^{ln（3）\cdot 4}=$

当最高指数为i（如$3^i$）时，我们只需将隐式增长率乘以i。因此，我们不是以普通的ln（3）增长，而是以ln（3*i增长。

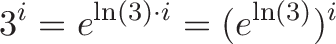
$\显示样式{3^i=e^{ln（3）\cdoti}=（e^{ln（三）}）^i}$

指数的顶部修改底部的隐式增长率。

细腻细腻的细节

让我们仔细看看。记住以下定义e（电子）以下为：

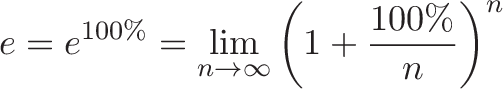
$\显示样式{e=e^{100\%}=lim_{n\to\infty}\左（1+frac{100\%}{n}\右）^n}$

这$\frac{100\%}{n}$代表了我们在每个微观时期赚取的部分利息。我们假设实际利率为100%，但如果在想象的方向上利率为100%呢？

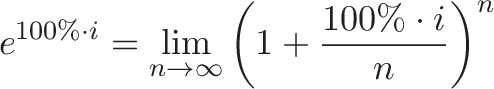
$\显示样式{e^{100\%\cdoti}=\lim_{n\to\infty}\left（1+frac{100\%\cdoti}{n}\right）^n}$

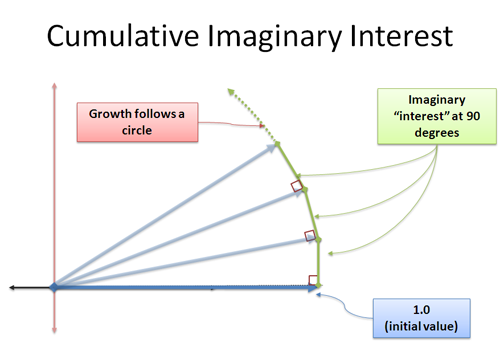
现在，我们新形成的兴趣在90度方向上增加了我们。令人惊讶的是，这并没有改变我们的长度——这是一个棘手的概念，因为它似乎是一个三角形，其中斜边必须更大。我们正在处理一个极限，而额外的距离在我们指定的误差范围内。这是我想改天再解决的问题，但请相信我的话：持续的垂直增长会让你旋转。这是正弦和余弦的中心，你的变化垂直于你当前的位置，你在一个圆内移动。

我们申请我增长单位以无限小的增量递增，每一个都以90度角推动我们。没有“越来越快”的旋转——相反，我们沿着周长爬行一段距离|i|=1（i量级）。

嘿，绕着一个圆圈爬行的距离是一个弧度！我们找到了另一种描述圆周运动的方法！

要进行圆周运动：以90度角（又称假想增长率）旋转，连续变化。

所以，欧拉的公式是说“指数，想象中的增长会画出一个圆”。这条路径与在假想平面中使用正弦和余弦在圆周中移动的路径相同。

在这种情况下，“指数”一词令人困惑，因为我们以恒定的速度绕着圆圈运动。在大多数讨论中，假设指数增长具有累积复合效应。

一些示例

你真的不相信我，是吗？这里有几个例子，以及如何直观地思考它们。

示例：$e^i$

x在哪里？啊，只有1。直观地说，在不使用计算器的情况下，我们知道这意味着“沿单位圆移动1弧度”。在我的脑海中，我看到了“e”尝试在同一方向上以100%的速度增长1，但我不断移动球，并迫使“1”沿着圆的边缘增长：

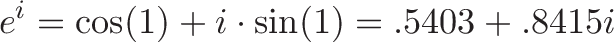
$\显示样式{e^i=\cos（1）+i\cdot\sin（1）=.5403+.8415i}$

虽然不是最漂亮的数字，但它确实存在。输入时，请记住将计算器设置为弧度模式。

示例：$3^i$

这很棘手——它不是我们的标准格式。但请记住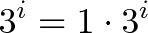， $\显示样式{3^i=1\cdot 3^i}$

我们希望在周期结束时初始增长为3倍，或者瞬时增长率为ln（3）。但是我并将ln（3）的速率更改为“i*ln（三）”：

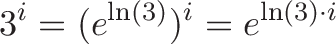
$\显示样式{3^i=（e^{ln（3）}）^i=e^{in（3）\cdot i}}$

我们思想我们将以ln（3）的常规速率进行转化，因为e约为2.718，所以比100%的连续增长略快。但噢，不，我旋转我们：现在我们正在以想象的速度变换，这意味着我们只是在旋转。如果我如果是一个像4这样的常规数字，我们的增长速度就会提高4倍。现在，我们以ln（3）的速度增长，但横向增长。

我们应该期望单位圆上有一个复数——增长率中没有任何东西可以增加我们的规模。求解方程式：

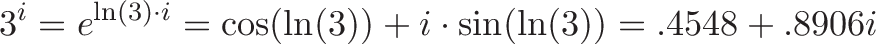
$\显示样式{3^i=e^{ln（3）\cdoti}=\cos$

所以，不是围绕圆圈结束“1”个单位（比如$e^i$），而是围绕圆圈以（3）个单位结束。

示例：$i^i$

几个月前，这会让我流泪。今天不行！让我们来分解一下转换：

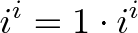
$\显示样式{i^i=1\cdot i^i}$

我们从1开始，想改变它。像解$3^i$一样，用我作为基地？

小时。通常，我们会使用ln（x）来获得在1个单位时间结束时达到x所需的增长率。但以一个假想的速率呢？我们需要把这件事处理一下。

为了从1开始并增长到我我们需要从一开始就开始轮换。有多快？我们需要在1个时间单位内得到90度（π/2弧度）。所以我们的价格是$i\frac{\pi}{2}$。记住我们的速度必须是虚构的，因为我们在旋转，而不是增长！普通的旧$\frac{\pi}{2}$约为1.57，导致正常增长。

这应该是有意义的：将1.0改为我在1个单元的末尾，我们应该在这段时间内旋转$\frac{\pi}{2}$弧度（90度）。所以，为了得到“i”，我们可以使用$e^{i\frac{\pi}{2}$。

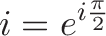
$\显示样式{i=e^{i\frac{\pi}{2}}}$

唷。这将i描述为基础。指数怎么样？

嗯，这个其他我告诉我们改变我们的利率——是的，这是我们花了这么长时间计算出来的利率！因此，不要以$i\frac{\pi}{2}$的速度旋转，这是我也就是说，我们将比率转换为：

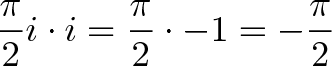
$\显示样式{\frac{\pi}{2} 我\cdot i=\frac{\pi}{2}\cdot-1=-\frac}\pi}{2}}$

我取消了，让增长率再次成为现实！我们旋转了我们的速度，把自己推到了负数。负增长率意味着我们正在收缩——我们应该期望美元能使事情变得更小。它确实做到了：

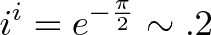
$\显示样式{i^i=e^{-\frac{\pi}{2}}\sim.2}$

塔达！（在谷歌上搜索“i^i”以使用其计算器）

稍作休息：你可以直观地计算出虚基和虚指数的行为。哇哦。

作为奖励，你计算出ln（i）——使$e^x$变为i，使e旋转$\frac｛\pi｝｛2｝$弧度。

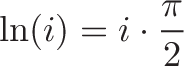
$\displaystyle｛\ln（i）=i\cdot\frac｛\pi｝｛2｝｝$

示例：（i^i）^i

双虚指数？如果你坚持的话。首先，我们知道括号内的增长率是多少：

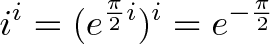
$\显示样式{i^i=（e^{frac{pi}{2} 我})^i=e^{-\frac{\pi}{2}}$

我们得到负（收缩）增长率-pi/2。现在我们修改这个比率再一次通过我以下为：

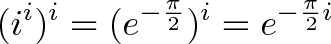
$\显示样式{（i^i）^i=（e^{-\frac{\pi}{2}}）^i=e^{-\frac}\pi}{2} 我}}$

现在我们有一个负旋转！我们以每单位时间$-\frac{\pi}{2}$的速度绕着圆圈转。我们要走多久？好吧，在这个指数链的最顶端有一个隐含的“1”时间单位；隐含的默认值是使用1个时间单位（就像$e=e^1$）。1时间单位表示$-\frac{\pi}{2}$弧度（-90度）或-i！

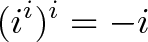
$\显示样式{（i^i）^i=-i}$

而且，仅就踢球而言，如果我们把这个疯狂的结果平方起来：

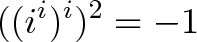
$\显示样式｛（（i^i）^i）^2=-1｝$

它是旋转的“刚好”两倍：2是一个规则的数字，所以我们的旋转速度是单位时间内旋转180度的两倍。或者，您可以将其视为连续两次应用-90度旋转。

乍一看，这些真的是奇怪的指数。但通过我们的类比，我们可以从容应对。

复杂增长

我们可以同时有真实的和想象的增长：真实部分放大我们，想象部分旋转我们：

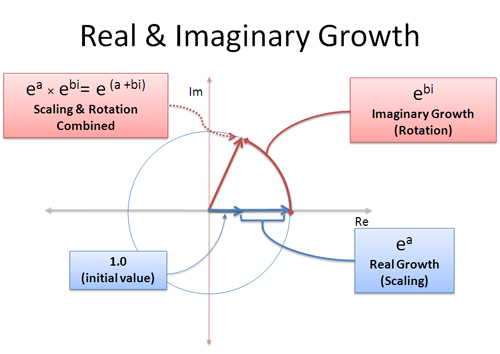
像（A+bi）这样的复杂增长率是实增长和虚增长的混合。实际部分a表示“100%增长一秒”，虚部b表示“旋转b条秒”。记住，旋转并没有得到复合的好处，因为你一直在不同的方向“推动”——旋转是线性增加的。

记住这一点，我们可以用（a+bi）表示任意大小的圆上的任意点！半径为$e^a$，角度由$e^{bi}$决定。这就像将数字放入expand-o-tron中两个循环：一次将其增大到合适的大小（a秒），另一次将它旋转到合适的角度（b秒）。或者，你可以先旋转它，然后再生长！

假设我们想知道达到6+8i的增长量。这实际上是在问一个虚数的自然对数：我们如何增长e才能得到（6+8i）？

半径：我们需要多大的圆圈？那么，震级是$\sqrt{6^2+8^2}=\sqrt}100}=10$。这意味着我们需要增加ln（10）=2.3秒才能达到这个数量。
旋转量：该点的角度是多少？我们可以用反正切来计算：atan（8/6）=53度=.93弧度。
合并结果：ln（6+8i）=2.3+.93i

也就是说，如果使用$e^{2.3+.93i}$，我们可以到达随机点（6+8i）。

为什么这很有用？

欧拉公式为我们提供了另一种描述圆周运动的方法。但我们已经可以用正弦和余弦来做了，有什么特别的？

这都是关于视角的。正弦和余弦用栅格，绘制水平和垂直坐标。

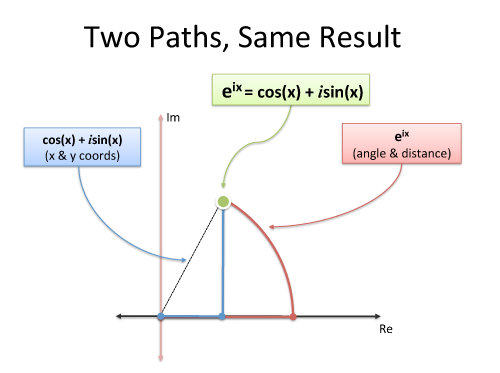
欧拉公式使用极坐标——角度和距离是多少？同样，这是描述运动的两种方法：

电网系统：向东3个单位，向北4个单位
极坐标：以53.13度角移动5个单位

根据问题的不同，极坐标或直角坐标更有用。欧拉公式允许我们在两者之间进行转换，以使用最佳工具完成工作。此外，由于$e^{ix}$可以转换为正弦和余弦，我们可以将trig中的公式重写为e的变体，这非常方便（无需记住sin（a+b），您可以推导它——改天再推导）。每一个数字，无论是真的还是复数，都是e的变体，这很美。

但实用性、灵活性：最重要的结果是认识到，通过正确的类比，令人困惑的方程可以变得直观。不要让欧拉公式这样漂亮的方程式成为魔咒--以类比为基础你知道要看到方程式中的洞察力。

快乐数学。